A Scalable Montgomery Modular Multiplication Architecture with Low Area-Time Product Based on Redundant Binary Representation
Abstract
:1. Introduction
- Low and customizable area cost: our area cost is mainly affected by the pipeline-stage-num. When using a memory outside our module, area cost will be lower by storing the temporary result outside.
- Small critical path: our critical path is smaller by cutting calculating into precalculate quotient logic and multiplication-shift logic.
- Low memory bandwidth requirement: compared with RBR-MMM, which needs whole operators simultaneously, our design only needs two words every cycle and only writes one word out. The word size is determined by the multiplier used in our design.
- Low and customizable latency: we adapt the algorithm to the pipeline to prevent the 2-cycle delay between each stage. Latency will be determined by the stage num and input width.
2. Algorithm Fundamentals
| Algorithm 1 Basic Radix- RBR-MMM (). |
| INPUT: |
| M is prime; X,Y,M are in RBR: |
| ; |
| ; |
| ; |
| ; |
| OUTPUT: |
| 1: |
| ; |
| ; |
| 2: |
| 3: for to do |
| 4: |
| 5: |
| //computing quotient logic |
| 6: |
| //parallel computing o’ |
| 7: for to do |
| 8: |
| 9: end for |
| //parallel computing shift right logic to cal new_o |
| 10: for to do |
| 11: |
| 12: end for |
| //convert y to binary representation |
| 13: if do |
| 14: |
| 15: end if |
| 16: end for |
| 17: return O |
3. Pipeline Precalculate Redundant Binary Representation Montgomery Modular Multiplication
| Algorithm 2 Basic Radix- PPCRBR-MMM (). |
| INPUT: |
| M is prime; X,Y,M are in RBR: |
| ; |
| ; |
| ; |
| ; |
| OUTPUT: |
| 1: |
| ; |
| ; |
| ; |
| 2: |
| // totally 2n iteration, each j means one pipeline stage |
| 3: for to do |
| 4: |
| 5: |
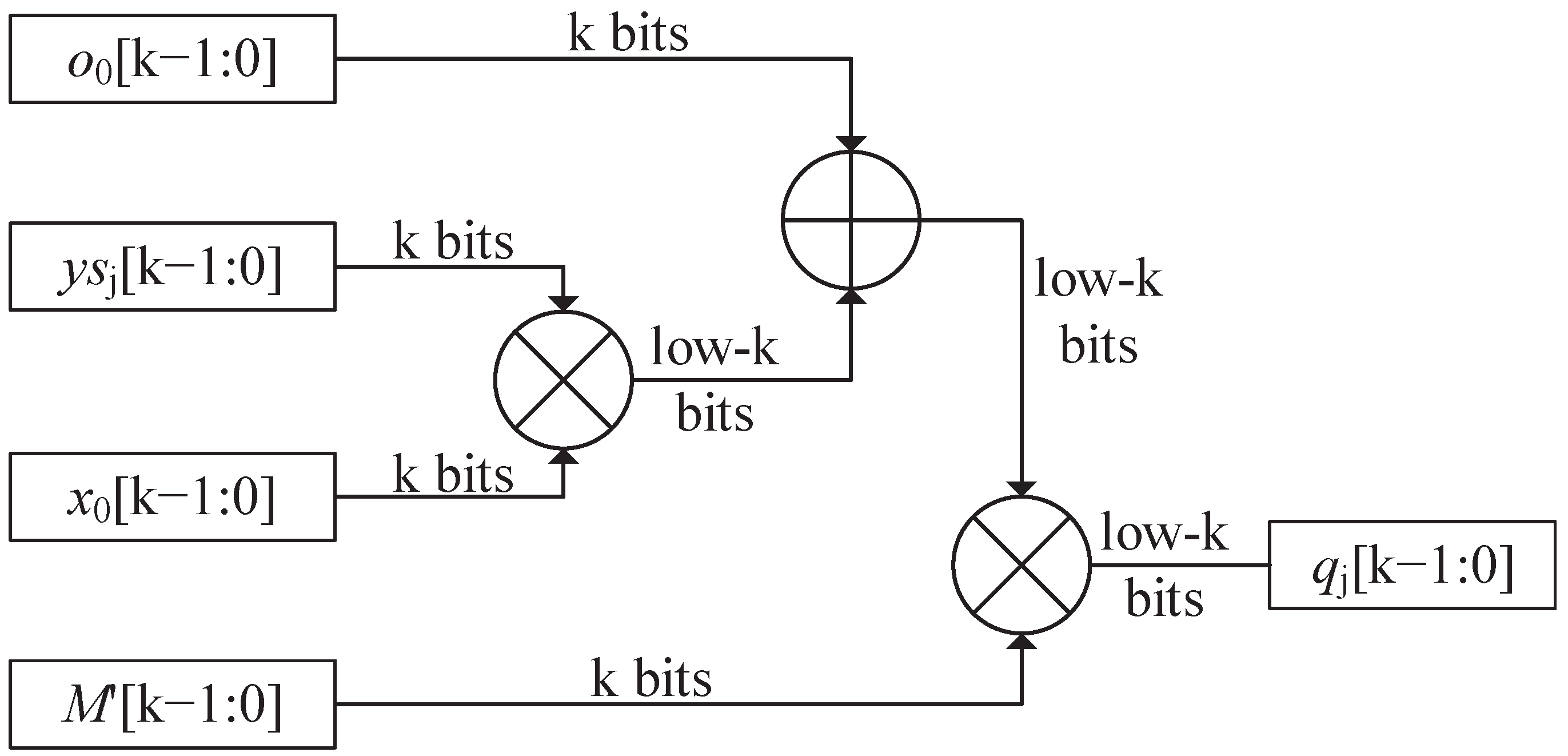
| //computing quotient logic |
| 6: |
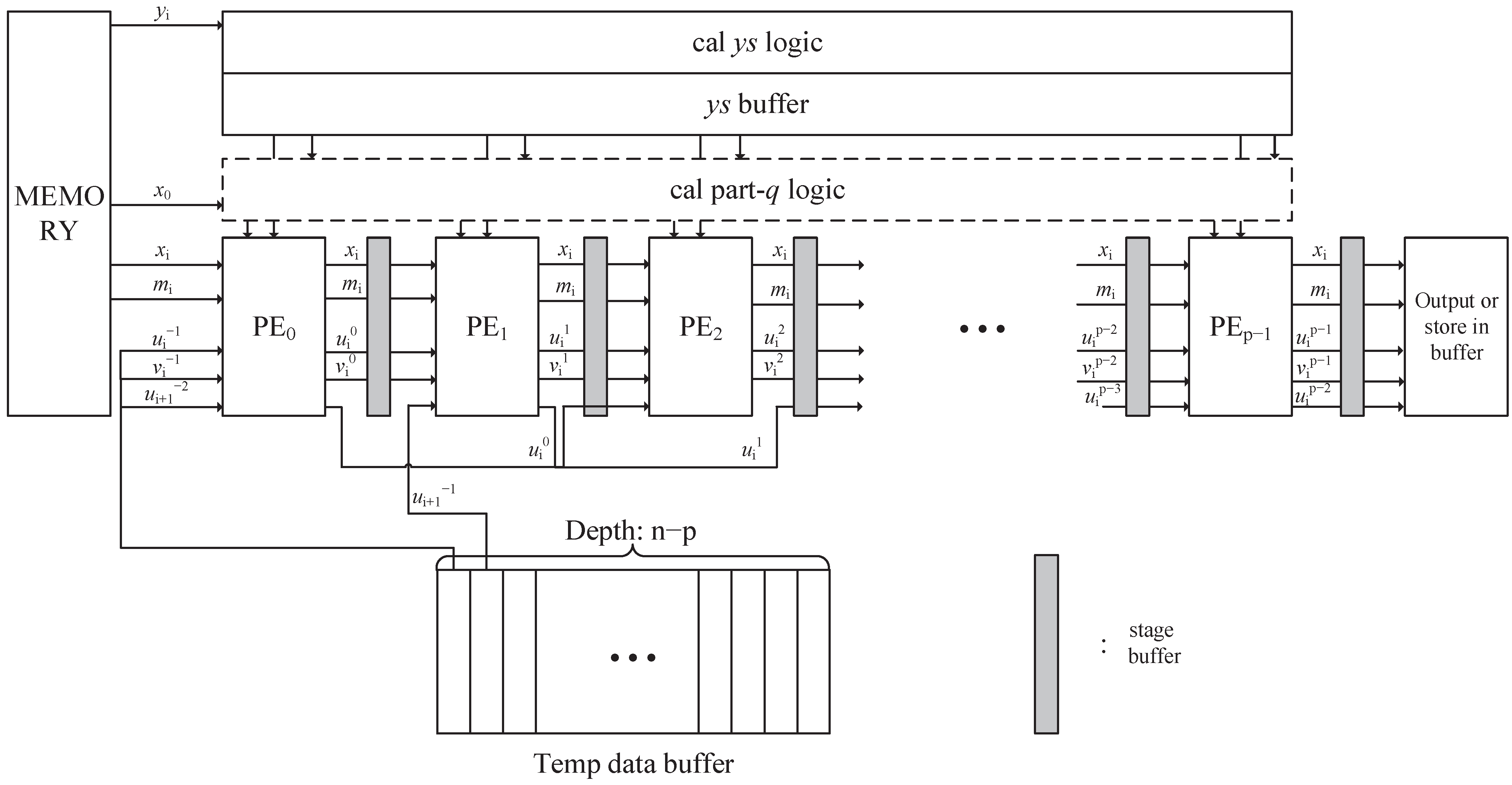
| //inner-loop: for each pipeline, n cycles are needed |
| 7: for to do |
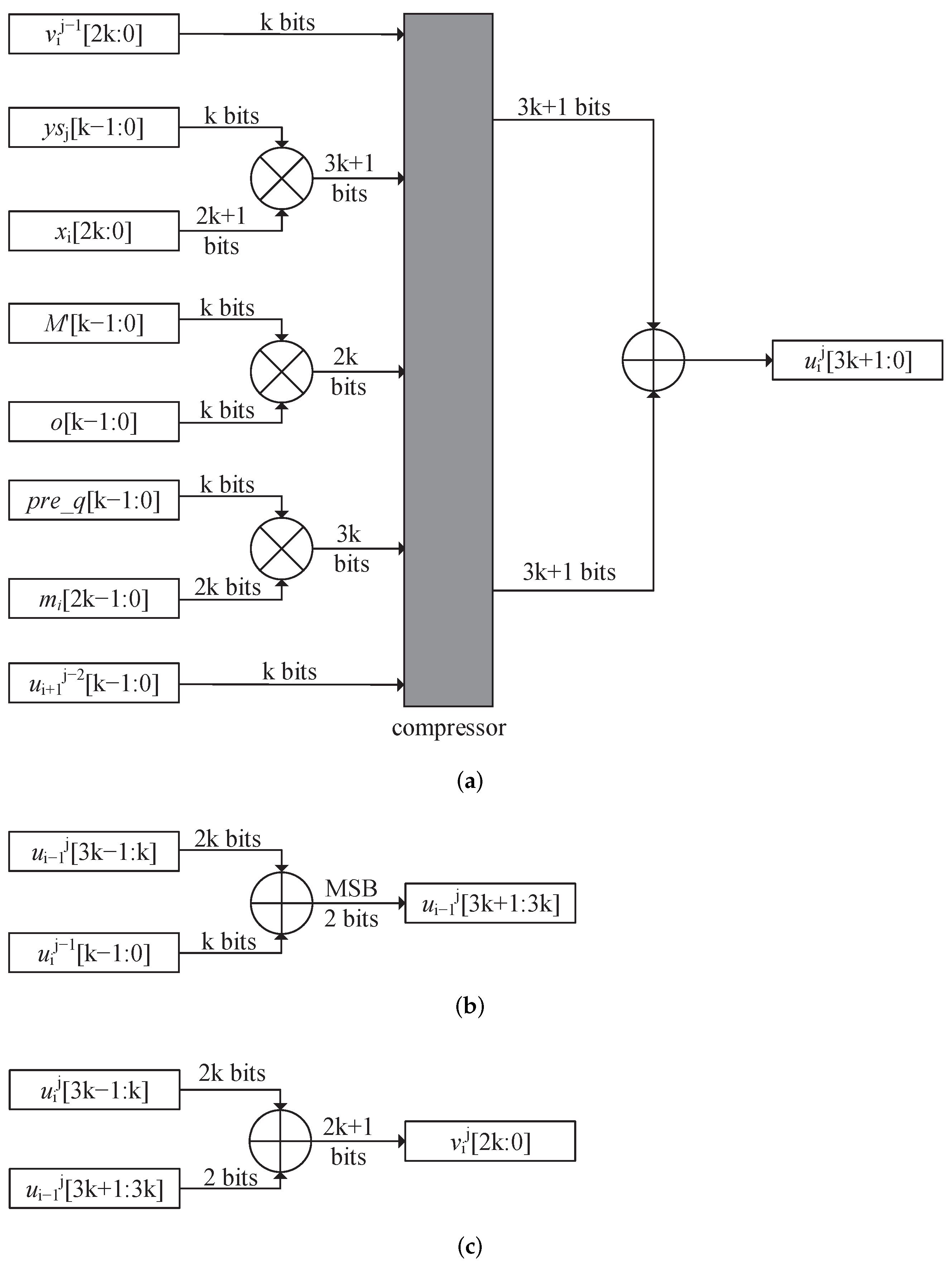
| 8: |
| 9: |
| 10: |
| 11: end for |
| //convert y to binary representation |
| 12: if do |
| 13: |
| 14: end if |
| 15: end for |
| 16: //two more cycles are needed for output |
| 17: for to do |
| 18: |
| 19: end for |
| 20: return O |
4. Analysis of PPCRBR-MMM
4.1. Timing Analysis
4.2. Critical Path Analysis
4.3. Area Analysis
5. Experimental Results and Comparisons
5.1. Experiments of PPCRBR-MMM and RBR-MMM Algorithms
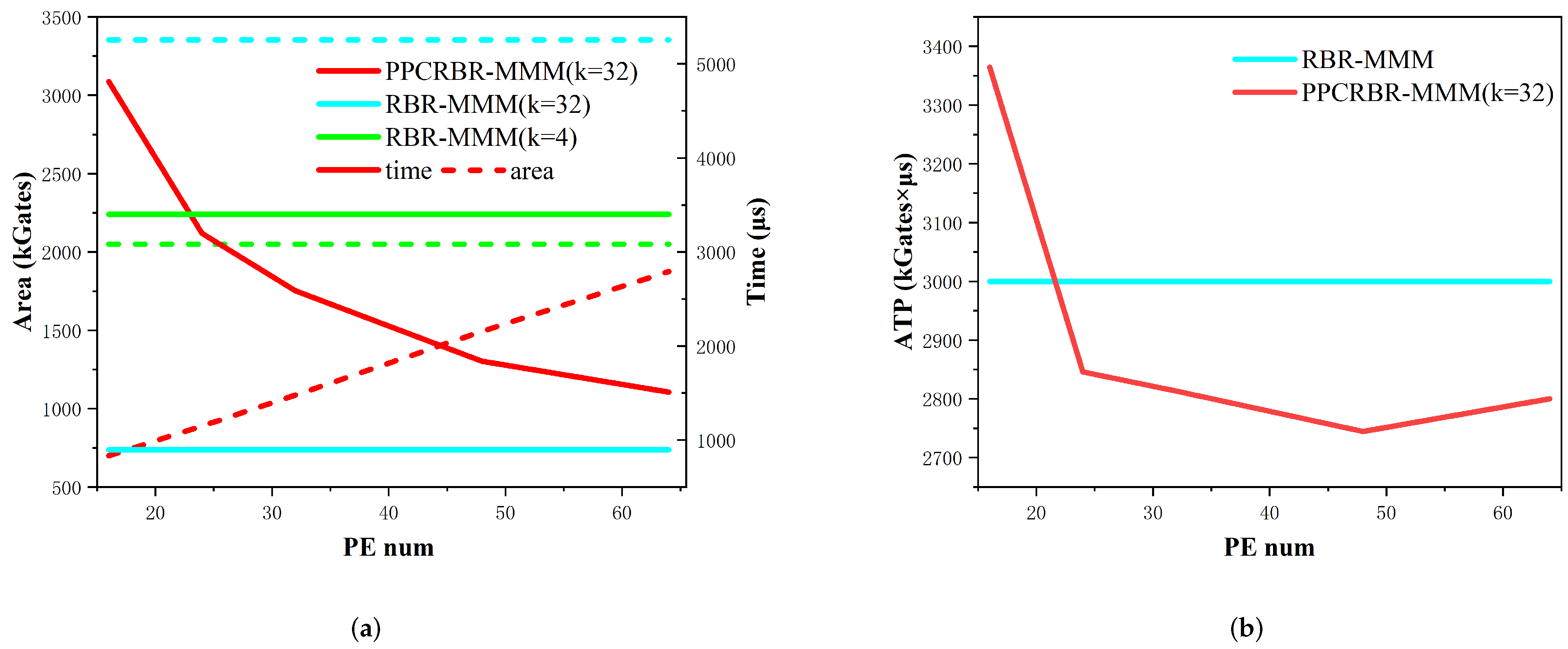
5.2. Results and Comparisons
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MMM | Montgomery Modular Multiplication |
| RBR | Redundant Binary Representation |
References
- Montgomery, P.L. Modular multiplication without trial division. Math. Comput. 1985, 44, 519–521. [Google Scholar] [CrossRef]
- Ding, J.; Li, S. A low-latency and low-cost Montgomery modular multiplier based on NLP multiplication. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1319–1323. [Google Scholar] [CrossRef]
- Gu, Z.; Li, S. A division-free Toom–Cook multiplication-based Montgomery modular multiplication. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 1401–1405. [Google Scholar] [CrossRef]
- Dai, W.; Chen, D.D.; Cheung, R.C.; Koc, C.K. Area-time efficient architecture of FFT-based montgomery multiplication. IEEE Trans. Comput. 2016, 66, 375–388. [Google Scholar] [CrossRef]
- Mo, Y.; Li, S. Design of an 8192-bit RNS montgomery multiplier. In Proceedings of the 2017 International Conference on Electron Devices and Solid-State Circuits (EDSSC), Hsinchu, Taiwan, 18–20 October 2017; pp. 1–2. [Google Scholar]
- Kolagatla, V.R.; Desalphine, V.; Selvakumar, D. Area-Time Scalable High Radix Montgomery Modular Multiplier for Large Modulus. In Proceedings of the 2021 25th International Symposium on VLSI Design and Test (VDAT), Surat, India, 16–18 September 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, S.H.; Lin, W.C.; Ye, J.H.; Shieh, M.D. Fast scalable radix-4 Montgomery modular multiplier. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems (ISCAS), Seoul, Korea, 20–23 May 2012; pp. 3049–3052. [Google Scholar] [CrossRef]
- Rentería-Mejía, C.P.; Trujillo-Olaya, V.; Velasco-Medina, J. 8912-bit Montgomery multipliers using radix-8 booth encoding and coded-digit. In Proceedings of the 2013 IEEE 4th Latin American Symposium on Circuits and Systems (LASCAS), Cusco, Peru, 27 February–1 March 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Erdem, S.S.; Yanık, T.; Çelebi, A. A General Digit-Serial Architecture for Montgomery Modular Multiplication. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2017, 25, 1658–1668. [Google Scholar] [CrossRef]
- Nti, R.B.; Ryoo, K. Area-efficient design of modular exponentiation using montgomery multiplier for RSA cryptosystem. In Advanced Multimedia and Ubiquitous Engineering; Springer: Berlin/Heidelberg, Germany, 2018; pp. 431–437. [Google Scholar]
- Kuang, S.R.; Wu, K.Y.; Lu, R.Y. Low-cost high-performance VLSI architecture for Montgomery modular multiplication. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2015, 24, 434–443. [Google Scholar] [CrossRef]
- Sassaw, G.; Jiménez, C.J.; Valencia, M. High radix implementation of Montgomery multipliers with CSA. In Proceedings of the 2010 International Conference on Microelectronics, Cairo, Egypt, 19–22 December 2010; pp. 315–318. [Google Scholar] [CrossRef]
- Mahapatra, P.P.; Agrawal, S. RSA Cryptosystem with Modified Montgomery Modular Multiplier. In Proceedings of the 2017 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Coimbatore, India, 14–16 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Zode, P.P.; Deshmukh, R.B. Fast modular multiplication using parallel prefix adder. In Proceedings of the 2014 2nd International Conference on Emerging Technology Trends in Electronics, Communication and Networking, Surat, India, 26–27 December 2014; pp. 1–4. [Google Scholar]
- Sutter, G.D.; Deschamps, J.P.; Imaña, J.L. Modular multiplication and exponentiation architectures for fast RSA cryptosystem based on digit serial computation. IEEE Trans. Ind. Electron. 2010, 58, 3101–3109. [Google Scholar] [CrossRef]
- Fatemi, S.; Zare, M.; Khavari, A.F.; Maymandi-Nejad, M. Efficient implementation of digit-serial Montgomery modular multiplier architecture. IET Circuits Devices Syst. 2019, 13, 942–949. [Google Scholar] [CrossRef]
- Srinitha, S.; Niveda, S.; Rangeetha, S.; Kiruthika, V. A High Speed Montgomery Multiplier used in Security Applications. In Proceedings of the 2021 3rd International Conference on Signal Processing and Communication (ICPSC), Coimbatore, India, 13–14 May 2021; pp. 299–303. [Google Scholar] [CrossRef]
- Ibrahim, A.; Gebali, F.; Elsimary, H. New and improved word-based unified and scalable architecture for radix 2 Montgomery modular multiplication algorithm. In Proceedings of the 2013 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing (PACRIM), Victoria, BC, Canada, 27–29 August 2013; pp. 153–158. [Google Scholar] [CrossRef]
- Shieh, M.D.; Lin, W.C. Word-Based Montgomery Modular Multiplication Algorithm for Low-Latency Scalable Architectures. IEEE Trans. Comput. 2010, 59, 1145–1151. [Google Scholar] [CrossRef]
- Tenca, A.; Koc, C. A scalable architecture for modular multiplication based on Montgomery’s algorithm. IEEE Trans. Comput. 2003, 52, 1215–1221. [Google Scholar] [CrossRef]
- Li, B.; Wang, J.; Ding, G.; Fu, H.; Lei, B.; Yang, H.; Bi, J.; Lei, S. A high-performance and low-cost montgomery modular multiplication based on redundant binary representation. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2660–2664. [Google Scholar] [CrossRef]
- Ding, Y.; Hu, J.; Wang, D.; Tan, H. A High-Performance RSA Coprocessor Based on Half-Carry-Save and Dual-Core MAC Architecture. Chin. J. Electron. 2018, 27, 70–75. [Google Scholar] [CrossRef]
- Miyamoto, A.; Homma, N.; Aoki, T.; Satoh, A. Systematic design of RSA processors based on high-radix Montgomery multipliers. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2010, 19, 1136–1146. [Google Scholar] [CrossRef]
- Wu, T. Reducing memory requirements in CSA-based scalable Montgomery modular multipliers. In Proceedings of the 2014 12th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Guilin, China, 28–31 October 2014; pp. 1–3. [Google Scholar]
- Lin, W.C.; Ye, J.H.; Shieh, M.D. Scalable Montgomery Modular Multiplication Architecture with Low-Latency and Low-Memory Bandwidth Requirement. IEEE Trans. Comput. 2014, 63, 475–483. [Google Scholar] [CrossRef]


| Alg | Param | Tech | Freq (MHz) | Area (KGates) | Cycles | Time (ns) | ATP |
|---|---|---|---|---|---|---|---|
| 1024-bit MMM | |||||||
| RBR-MMM | k = 4 | 65 nm | 685 | 121.8 | 258 | 377 | 45.92 |
| 90 nm | 435 | 108.7 | 258 | 593 | 64.47 | ||
| k = 16 | 65 nm | 385 | 304.4 | 66 | 166 | 50.53 | |
| PPCRBR-MMM | p = 16 k = 16 | 65 nm | 617 | 185.4 | 164 | 266 | 49.28 |
| p = 24 k = 16 | 65 nm | 617 | 222.4 | 114 | 185 | 41.09 | |
| 90 nm | 392 | 198.5 | 114 | 291 | 57.69 | ||
| 2048-bit MMM | |||||||
| RBR-MMM | k = 4 | 65 nm | 654 | 224.8 | 514 | 786 | 176.69 |
| k = 32 | 65 nm | 302 | 900.0 | 66 | 218 | 196.63 | |
| PPCRBR-MMM | p = 16 k = 32 | 65 nm | 485 | 506.3 | 164 | 338 | 171.19 |
| p = 24 k = 32 | 65 nm | 485 | 707.1 | 114 | 235 | 166.22 | |
| 90 nm | 308 | 631.1 | 114 | 370 | 233.37 | ||
| 8192-bit MMM | |||||||
| RBR-MMM | k = 4 | 65 nm | 603 | 878.1 | 2050 | 3400 | 2985.25 |
| 130 nm | 200 | 945.5 | 2050 | 10250 | 9691.38 | ||
| k = 32 | 65 nm | 288 | 3353.9 | 258 | 896 | 3006.70 | |
| PPCRBR-MMM | p = 16 k = 32 | 65 nm | 452 | 699.2 | 2178 | 4816 | 3367.41 |
| p = 24 k = 32 | 65 nm | 446 | 889.9 | 1428 | 3203 | 2850.12 | |
| p = 32 k = 32 | 65 nm | 446 | 1087.0 | 1156 | 2593 | 2818.12 | |
| p = 48 k = 32 | 65 nm | 428 | 1493.8 | 788 | 1842 | 2751.53 | |
| 130 nm | 142 | 1608 | 788 | 5554 | 8932.61 | ||
| p = 64 k = 32 | 65 nm | 425 | 1875.2 | 644 | 1516 | 2841.92 | |
| Ref | Tech | Freq (MHz) | Area (KGates) | Cycles | Time (ns) | ATP |
|---|---|---|---|---|---|---|
| 1024-bit MMM | ||||||
| [22] | 90 nm | 369 | 47.2 | 1153 | 3124 | 147.45 |
| [23] | 90 nm | 472 | 11.4 | 2207 | 4680 | 53.35 |
| [10] | 90 nm | 885 | 84.0 | 1026 | 1159 | 97.36 |
| [24] | 90 nm | 909 | 97.0 | 595 | 655 | 63.54 |
| [25] | 90 nm | 595 | 103.0 | 1485 | 2496 | 257.07 |
| Ours | 90 nm | 392 | 198.5 | 114 | 291 | 57.69 |
| 2048-bit MMM | ||||||
| [11] | 90 nm | 227 | 336.0 | 1724 | 7646 | 2569.06 |
| Ours | 90 nm | 308 | 631.1 | 114 | 370 | 233.37 |
| 8192-bit MMM | ||||||
| [5] | 130 nm | 263 | 1240.0 | 2118 | 8056 | 9989.44 |
| Ours | 130 nm | 142 | 1608 | 788 | 5554 | 8932.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, P. A Scalable Montgomery Modular Multiplication Architecture with Low Area-Time Product Based on Redundant Binary Representation. Electronics 2022, 11, 3712. https://doi.org/10.3390/electronics11223712
Zhang Z, Zhang P. A Scalable Montgomery Modular Multiplication Architecture with Low Area-Time Product Based on Redundant Binary Representation. Electronics. 2022; 11(22):3712. https://doi.org/10.3390/electronics11223712
Chicago/Turabian StyleZhang, Zhaoji, and Peiyong Zhang. 2022. "A Scalable Montgomery Modular Multiplication Architecture with Low Area-Time Product Based on Redundant Binary Representation" Electronics 11, no. 22: 3712. https://doi.org/10.3390/electronics11223712
APA StyleZhang, Z., & Zhang, P. (2022). A Scalable Montgomery Modular Multiplication Architecture with Low Area-Time Product Based on Redundant Binary Representation. Electronics, 11(22), 3712. https://doi.org/10.3390/electronics11223712





