Hiding and Extracting Important Information in Encrypted Images by Using the Transformation of All Possible Permutations and VQ Codebook

Abstract

Due to its applications in cloud computing, research on reversible data hiding in encrypted images (RDHEI) is becoming more and more important. This paper proposes a reversible data hiding scheme for encrypted images that utilizes an all-permutation technique to embed data into encrypted images. The proposed scheme follows a block-wise data hiding process. Message extraction and image restoration are performed by the receiver using the trained vector quantization (VQ) codebook. This scheme can provide a high embedding rate and reduce the hardware burden on the receiver.

1. Introduction

1.1. Background Introduction

With the rapid development of cloud storage and cloud computing technologies, more and more users are processing their images through cloud-based social networking applications. However, some unauthorized attackers may intercept, leak, or even tamper with sensitive image data during transmission, resulting in compromised user security. The combination of image encryption and data hiding techniques is a potential solution to protect the privacy of information while enabling the transmission of messages.

Image encryption is a technique that usually uses an encryption key to encrypt a plaintext image into a ciphertext image, and only the recipient with the decryption key can decrypt the image [1]. Data hiding methods are mainly divided into two types: reversible and irreversible. Reversible Data Hiding (RDH) [2,3,4,5,6] can extract the secret data and restore the original image without distortion. Irreversible Data Hiding (IRDH) [7,8] can only extract the secret data and does not restore the original image losslessly.

Reversible data hiding (RDHEI) in encrypted images has become increasingly important in recent years. There are three hypothetical users in the RDHEI scheme, including content owners, data hiders, and receivers. The whole process is that the content owner encrypts the original image with the image encryption key, and then the data hider embeds additional data such as timestamp, watermark, and copyright information into the encrypted image. The receiver with the data hiding key can extract the embedded data, and the decrypted image can be obtained with the image encryption key. Existing spatial RDHEI schemes can be mainly divided into two categories: (1) reserving the spare room before image encryption (RRBE) [9,10,11] and (2) vacating the spare room after image encryption (VRAE) [12,13,14,15,16,17,18,19,20,21,22,23,24,25]. Figure 1 shows the general process of RDHEI, and briefly shows the difference between RRBE and VRAE.

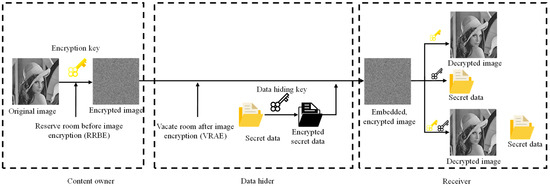
Figure 1. The overall process of RDHEI.

In the RRBE scheme, the spare space is reserved before the image is encrypted, that is, the spare space is reserved in the plaintext image. Because meaningful images have some correlation between their adjacent pixels, these redundant spaces can be reserved for data embedding. It is obvious that the RRBE scheme requires a significant amount of complex preprocessing to compress the original image before image encryption. However, it is difficult to require each content owner to perform specific preprocessing on the images before uploading them, and therefore the VRAE scheme is sometimes more appropriate than RRBE.

In VRAE schemes, the content owner simply encrypts the original image. The spare room used to embed the data is freed up in the process of encrypting the image. Because there is little correlation between the adjacent pixels of encrypted images, some early VRAE schemes cannot recover the original image and extract the embedded data losslessly. To improve the embedding rate and avoid errors, some block-based VRAE schemes have been proposed in recent years. In these schemes, the original image is first divided into non-overlapping blocks, and each block is encrypted with the same key. By doing this, the correlation between pixels in the block is preserved.

In this paper, we propose a permutation-based RDHEI scheme (P-RDHEI) that can be directly applied to encrypted images. In each encrypted image block of size $p\times q$, the image block is divided into n sub-blocks for all permutations, and multi-bit secret data are embedded by replacing the permutation of the image blocks. The original arrangement can be predicted from the VQ codebook to restore the image and extract information. When restoring encrypted blocks, the original arrangement can be predicted from the VQ codebook to restore the image and extract information. Most encrypted blocks can be fully recovered because the codewords in the VQ codebook are inherently representative of the pixel distribution of natural image blocks. The main contributions of our scheme are summarized as follows:

(1) Compared with traditional VRAE schemes, the P-RDHEI scheme significantly improves the embedding rate using all permutations, which can embed 0.9562 bpp of secret data into encrypted images.

(2) The proposed P-RDHEI scheme can achieve lossless data extraction and image restoration when the VQ codebook is relatively large.

(3) Compared with the CNN network required for extraction in the scheme in [12], the P-RDHEI scheme only needs the VQ codebook to complete the function of extracting and restoring images, effectively reducing the hardware burden on the receiver.

(4) Encrypted images and embedded encrypted images are fully encrypted. Because our proposed scheme only changes the order of the pixels in each block, the statistical properties and textures of the original image are not exposed.

The rest of this paper is organized as follows. Section 2 introduces the VQ compression techniques used in this paper and the related work that this paper mainly refers to. Section 3 illustrates the proposed scheme P-RDHEI. In Section 4, experimental results, comparisons, and discussions are given. Conclusions are provided in Section 5.

1.2. Literature Review

In this section, related literature is reviewed. After many years of development, the traditional RDH method has achieved many effective results in many fields [2,3,4,5,6,7,8]. Chang [2] trained generative adversarial networks (GANs) to reinvigorate the regular-singular (RS) method. This network generates a synthetic image and uses it as a reference to provide guidance for data embedding and image recovery. Ref. [3] combines VQ compression [4] with multiple linear regression prediction to further compress the VQ index using multiple linear regression prediction, which improves the embedding capability of images. In Ref. [5], using the feature that 3D space points have more moveable directions, Chi et al. used the prediction error of PVO to locate 3D space coordinate points to obtain more embedding space and designed clever displacement rules to reduce image distortion. In [6], a new data encryption method is proposed to reduce the size of encrypted data and improve the spatial efficiency. In [7], a very classical data hiding method is proposed, where the mapping space corresponding to the pixel pair coordinates is divided into the shape of a turtle shell, and then the secret numbers are embedded into each pixel pair under the guidance of the turtle shell. In [8], the identity of the lip image is hidden in the image itself using modulation techniques without hindering the recognition rate of the biometric system, thus reducing the possibility of template misuse.

In the RRBE domain, in [9], a local difference predictor is used to calculate the prediction error of the central pixel of each block with the other pixels, and the blocks are classified into different types based on these prediction errors, freeing up room for high embedding capacity before the original image is encrypted. The method of [10] improves the embedding capability of reversible data hiding methods based on encrypted images using public key encryption by preprocessing the images using differential expansion (DE) before encryption. The method of [11] performs the preprocessing of histogram shrinkage before encryption and then embeds the data into the LSB plane of the ciphertext pixels.

In the VRAE domain, in [12], the Arnold transform was used in the data embedding of the encrypted block, and the number of Arnold transforms of the encrypted block was determined according to the decimal of the embedded data. A convolutional neural network (CNN) model was then used to restore the image and extract information. Ref. [13] also uses pixel rotation technology to embed data into encrypted images and embeds different secret data according to the position of the maximum value in different rotation states. The block complexity is used to recover the original state of the pixel block. A method for embedding watermarks in encrypted images using the mean property and using mean preservation to extract hidden messages is discussed in [14]. Ming et al. introduced a histogram shift-based RDH scheme for encrypted images in [15]. By using homomorphic addition, the shifted histogram for data hiding will be created for the purpose of data hiding. In [16,19], the secret data are embedded by flipping the least significant bits (LSBs) of the encrypted pixel blocks. Ref. [17] improved the algorithm for calculating the smoothness in [16] to reduce the error rate of image recovery. Huang et al. [20] applied the histogram shifting technique to the prediction error histogram derived from each encrypted block for data embedding using a two-layer strategy. An RDH method for encrypted domains using the Laplacian-like distribution high-frequency coefficients of integer wavelet transform and the independence of orthogonal coefficients is detailed in [21]. Ref. [23] uses a median edge detection (MED) predictor to predict the bit-plane and then recursively processes all the bit-planes of the image to improve the hiding ability. Ref. [24] used matrix coding to embed the data to the location of the highest significant bit (MSB). To recover the image, high accuracy MSB prediction based on the orthogonal projection technique is preprocessed on the original image, and the prediction is self-embedded to help recover the image. An RDHEI method using adaptive difference recovery (ADR) was proposed in [25]. The range of the original disparity between the overlay pixel and the reference pixel can be determined adaptively based on the marker disparity generated by the bit substitution technique. The pixels can be recovered by the range of the original disparity and the reference pixel.

2. Related Works

2.1. Vector Quantization (VQ)

In 1984, Gray first proposed a method for compressing images called VQ compression [4]. As shown in Figure 2, there are three steps when using VQ compression.

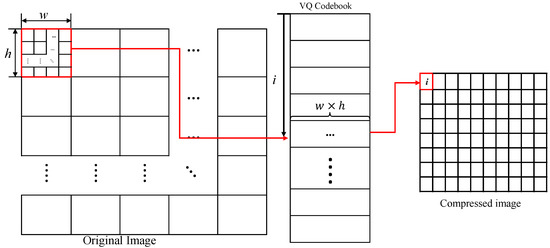
Figure 2. The encoding method of VQ.

Step 1: Divide the original image of size $W\times H$ into pixel blocks of size $w\times h$. Each block has $k=w\times h$ pixels, forming a $k$-dimensional vector. These vectors are called codewords.

Step 2: Obtain $L=2^l$ groups of codewords that can best represent these pixel blocks from multiple images to form a codebook.

Step 3: In this type of scheme, the pixel block is replaced with the index value of the codeword closest to the original image pixel block in the codebook. In the scheme proposed in this paper, we will take advantage of this feature to assist us in restoring images and then extracting information.

That is to say, the codewords in the VQ codebook can represent the pixel distribution of normal image pixel blocks to a certain extent. When decompressing, we only need to use the index value to return to the codebook, cut the corresponding codeword, and paste it back into the image like a tile. With many image blocks, when the distance between an image block and the VQ codebook is the shortest, the distribution of pixels in that image block is closest to the real image block, or most likely to be the real image block.

We use the Euclidean distance as the distance between the codeword and the vector. Let $x=\left(x_1 ,x_2 ,...,x_k \right)$ be the $k$-dimensional vector to be compression encoded and $Y=\left\{Y_1 ,Y_2 ,... ,Y_L \right\}$ be our codebook. There are $L=2^l$ codewords; each codeword is a $k$-dimensional vector, i.e., $Y_i=\left\{Y_{i1} ,Y_{i2} ,... ,Y_{ik} \right\}$. When the encoding of vector $x$ is $c$ (i.e., the $c$-th codeword in the codebook is closest to vector $x$), each VQ index is represented as $l={\log }_{2}L$ bits. The minimum distance formula is as follows, where $t$ is in the range $\left[1, 2^l \right]$.

$$\sqrt{{\displaystyle \sum }_{v=1}^k{\left(x_v-Y_{cv}\right)}^2}=\underset{t\in \left[1,2^l\right]}{\min }\sqrt{{\displaystyle \sum }_{v=1}^k{\left(x_v-Y_{tv}\right)}^2}$$

(1)

In order to better explain the VQ compression method, we have given an example in Figure 3. As shown in Figure 3, we obtain a 4 × 4 block of pixels from the original image and expand it to form a 16-dimensional array. We find that the 18th codeword in the VQ codebook is the closest to this array, in distance, so we can use the index value ‘18’ of this codeword to represent the information of this pixel block.

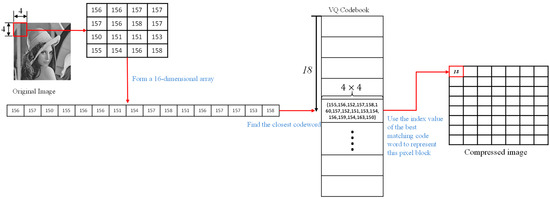
Figure 3. An example of VQ compression.

2.2. Panchikkil et al.’s Method

Panchikkil et al. proposed a novel encrypted image-based data hiding method [12] that uses block Arnold transform to embed secret data into the encrypted image, and then uses the convolutional neural network (CNN) model for data extraction and image restoration. Arnold transform is usually used in image encryption direction in image processing, but Panchikkil et al. cleverly used it for data embedding.

In this method, the data hider first divides the encrypted image into non-overlapping pixel blocks of $n\times n$ size. According to the size of the pixel block, we can use the Arnold transform technique to calculate the number of transformations for the pixel block. Each pixel block can have a list of Arnold transforms. We convert the secret data we want to embed into a decimal as the index value, and then we use the transform corresponding to the index to replace the pixels in the block.

When extracting the secret message and restoring the image, the receiver needs to first train a CNN model with the normal image dataset that can identify what kind of pixel block the normal image pixel block is. Then, the receiver divides the received image into $n\times n$ pixel blocks and integrates all Arnold transforms of the current pixel block into a list to extract the secret message, that is, the current index value. The receiver then decrypts all items in that list and uses the CNN model to determine the pixel blocks of the normal image for image restoration.

3. Proposed Scheme

In this section, we propose an all permutation-based data hiding technique to embed data into encrypted images (P-RDHEI). The original image is encrypted by the content owner using stream cipher encryption technology. For the data hider, the encrypted image is divided into non-overlapping $p\times q$ sized blocks; all blocks are then divided into n sub-blocks. Next, the data hider performs an all permutation of the n sub-blocks to obtain a list with all permutations. The original permutations are then replaced with the corresponding permutations in the list based on the secret data as an index. In the data extraction and image restoration phases, we need to first train a $p\times q$ dimensional VQ codebook for image restoration. We also divide the received stego image into non-overlapping $p\times q$ blocks, divide all blocks into n sub-blocks, and then perform an all permutation of these n sub-blocks to obtain a list with all permutations. Next, we decrypt all the permutations in the list. Then, the original permutation is found from the list according to the VQ codebook, and then the index of the permutation of the stego pixel block is extracted. Figure 4 shows the framework of our proposed P-RDHEI. The detailed phase of image encryption, data embedding, data extraction, and image restoration will be described in the following subsections.

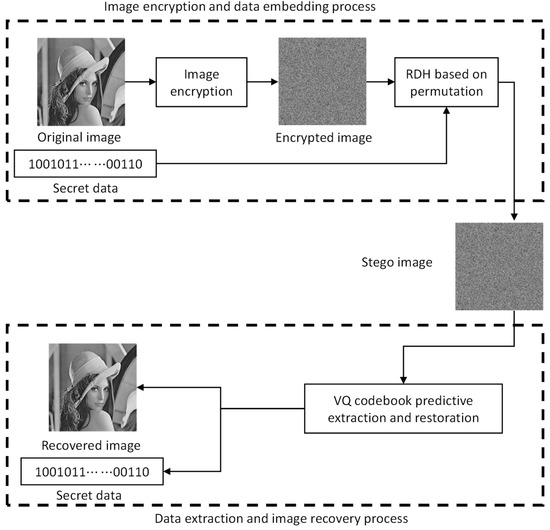
Figure 4. The overall flow of the proposed scheme P-RDHEI.

3.1. The Image Encryption

First, we encrypt the original image $O$ of size $M\times N$ into encrypted image E of size $M\times N$. This paper chooses the stream cipher encryption method to ensure the security of the encrypted image. To conduct the image encryption, a pseudo-random matrix sized $M\times N$ is used as the encryption key, $K_E$, where each value of the random stream ranges from 0 to 255. The original image, $O$, is then encrypted according to the following steps.

Step 1: Each pixel of the original image, $O$, and the corresponding encryption key, $K_E$, are converted into an 8-bit binary system according to Equation (2).

$$\begin{gathered} O{\left(i,j\right)}^x={\displaystyle ⎣}\frac{O\left(i,j\right)}{2^{x-1}}{\displaystyle ⎦} mod 2 \\ {K}_E{\left(i,j\right)}^x={\displaystyle ⎣}\frac{K_E\left(i,j\right)}{2^{x-1}}{\displaystyle ⎦} mod 2 \end{gathered}$$

(2)

where $\left(i,j\right)$ represents the coordinates, and the ranges of $i$ and $j$ are $\left[1, M\right]$ and $\left[1, N\right]$, respectively. The order of bits from back to front is denoted as $x\left(x=1,2,\cdots ,8\right)$.

Step 2: According to Equation (3), a bit-level XOR operation is performed on the original image, O, and the encryption key, $K_E$.

Step 3: The final decimal encrypted image, $E$, can be obtained by converting the binary number to decimal by Equation (4).

$$E{\left(i,j\right)}^x=O{\left(i,j\right)}^x\oplus K_E{\left(i,j\right)}^x$$

(3)

$$E\left(i,j\right)={\displaystyle \sum }_{x=1}^{8}E{\left(i,j\right)}^x\times 2^{x-1}$$

(4)

3.2. The Data Embedding Phase

After receiving the encrypted image, E, it is first divided into $\left(M\times N\right)/\left(p\times q\right)$ non-overlapping $p\times q$ sized blocks, where $E{B}_{\theta }$ denotes the θ-th encrypted block. For each $p\times q$ sized encrypted block, $E{B}_{\theta }$, we divide it equally into $n$ sub-blocks of the same size (the maximum value of n is $p\times q$), and then we perform a non-repeated all permutation operation on these n sub-blocks to generate a list sorted from small to large. That is to say, we list all the random permutations of n sub-blocks and delete duplicate permutations. According to the order from top to bottom and from left to right, the pixel value of each permutation is then extracted to form a $p\times q$-dimensional array, and all permutations are then sorted according to these arrays. Next, we find the $E{B}_{\theta }$ permutation from the list and set the index of the current permutation as 0. The other permutations are cyclically numbered along the current item. Assuming that there are W items in the list generated by the encrypted block, $E{B}_{\theta }$, we can then embed $k=⎣{\log }_{2}W⎦$ bits of secret data into this block. The specific operation removes the k-bit secret data to be embedded in the block, converts it to decimal $D$, finds the permutation numbered $D$ in the list, uses it to replace the current permutation, and the embedding operation is completed. As shown in the list in Figure 5, the 4 × 4 encrypted block is divided into 4 sub-blocks of the same size by the red line. All possible random permutations of these 4 sub-blocks are then listed, resulting in 24 different permutations. We then extract the pixel values from top to bottom and left to right for each permutation to form 24 16-dimensional arrays. Finally, according to the value of these arrays, 24 different permutations are sorted from small to large, and finally our permutation list is generated. We then find the original permutation of encrypted blocks in this list and number its index as 0. The index values of other permutations are numbered from 0 down in the order of the list. In Figure 5, we can see that when the index number is 1, we have numbered the last item of the list, but the permutations above index 0 in the list have not been numbered. Therefore, we loop to the first permutation in the list, and number down along the previous index until all permutations that do not have an index value are numbered. There are 24 items in the list, so we can embed $k=⎣{\log }_{2}24⎦=4$ bits of secret data in this encrypted block. Because the secret data are ${\left(0011\right)}_2={\left(3\right)}_{10}$, we use the permutation where the index is 3 to replace the original permutation as the stego block.

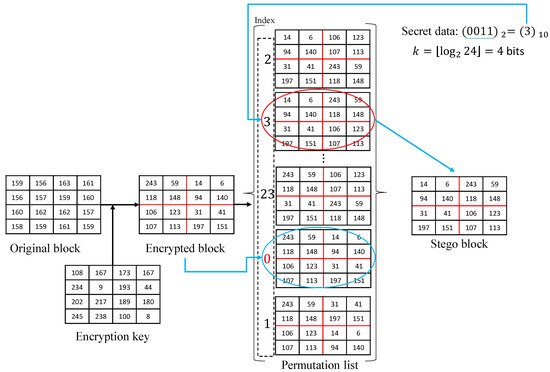
Figure 5. An example of the embedding process in which the 4 × 4 pixel block is divided into 4 sub-blocks.

From the process of embedding data, as long as we can correctly find the permutation with the index value of 0, we can accurately extract the index value of the received stego block permutation and then use the permutation with the index value of 0 to restore the image.

3.3. The Data Extraction and Image Recovery Phase

After receiving the stego encrypted image, the receiver needs to use natural images to train a VQ codebook with $L=2^l$ codewords to assist the receiver in restoring the image and extracting the secret data. The training method of the VQ codebook is described in detail in Section 2.1. In general, the value of $l$ is an integer greater than 3. The more codewords in the VQ codebook, the more accurate the prediction of the VQ codebook; however, the more codewords there are in the VQ codebook, the more storage space will be required. Therefore, after weighing the accuracy and storage space, the value of $l$ is 6 and 7 in the subsequent experiments.

The stego encrypted image is then divided into non-overlapping $p\times q$ sized blocks, where $EB{\prime }_{\theta }$ denotes the θ-th stego encrypted block. Similar to the operation during embedding, we divide $E{B\prime }_{\theta }$ into n sub-blocks, and then perform a non-repeated all permutation operation on these n sub-blocks to generate a list sorted from small to large. Next, we perform a decryption operation for each item in this list using the encryption key, $K_E$, as shown in Equations (5) and (6).

$$IT{\left(i,j\right)}_v{}^x=E{\left(i,j\right)}_v{}^x\oplus K_E{\left(i,j\right)}^x$$

(5)

$$IT{\left(i,j\right)}_v={\displaystyle \sum }_{x=1}^{8}IT{\left(i,j\right)}_v{}^x\times 2^{x-1}$$

(6)

where $\left(i,j\right)$ represents the coordinates, and the ranges of $i$ and $j$ are $\left[1, M\right]$ and $\left[1, N\right]$, respectively. $E{\left(i,j\right)}_v$ represents the encrypted value at position $\left(i,j\right)$ of the v-th item in the permutation list, $IT{\left(i,j\right)}_v$ represents the decrypted value at the position $\left(i,j\right)$ of the v-th item in the permutation list, and the range of v is $\left[1, W\right]$.

We then have a decrypted list with W items, of which only one is a permutation of the original image block. Due to the characteristics of stream encryption, only the correct arrangement can decrypt pixel blocks with normal pixel distribution, and other arrangements will decrypt some garbled characters. What the receiver must do is find the permutation of the natural image; we use the characteristics of the VQ codebook, which means the pixels in the natural image pixel block can be replaced by the best matching codeword in the VQ codebook to find the permutation that best matches the VQ codebook in the decryption list. Because the distribution of elements in the decrypted garbled blocks is irregular, their matching degree with the VQ codebook will be very low. That is to say, they are very different from the codewords of the VQ codebook. As such, we can use the shortest distance of the permutation to the VQ codebook to find the permutation of the original image block in the decryption list. We need to calculate the shortest distance between the W items in the decryption list and the VQ codebook, and then the permutation with the shortest distance is what we think is the natural permutation. After we have determined which item in the list is the original pixel permutation, we number the index of the current permutation as 0. The other items are cyclically numbered along the current item. This way, we can find the index of the received permutation in the list. By extracting this index and converting it into a k-bit binary number ($k=⎣{\log }_{2}W⎦$), the secret data embedded in the block by the data hider can be obtained. Figure 6 is an example of pixel block recovery and information extraction, where the pixel block size is 4 × 4 and is divided into 4 sub-blocks for permutation. As shown in the list in Figure 6, the 4 × 4 encrypted stego block is divided into 4 sub-blocks of the same size by the red line. We thanlist all possible random permutations of these 4 sub-blocks, resulting in 24 different permutations. We then extract the pixel values from top to bottom and left to right for each permutation to form 24 16-dimensional arrays. According to the value of these arrays, 24 permutations are sorted from small to large, and the permutation list is generated. We then decrypt all 24 permutations in the list in order to obtain the decrypted permutation list. Only one of the 24 decrypted permutations is the permutation of the original pixel block, and the others are irregular garbled codes; that is, only one permutation of the 24 decrypted permutations has the general characteristics of the image pixel block. The codeword of the VQ codebook may be a judgment criterion that can be used as a universal feature of an image pixel block. Therefore, we calculate the shortest distance between these 24 decrypted permutations and the VQ codebook, respectively. When the shortest distance of a permutation is the smallest among all permutations, we number its index value as 0, and we consider this permutation to be the permutation of our original pixel block. At this point, we can restore the pixel block. The next step is extracting our secret data. The index values of other permutations are numbered from 0 down in the order of the list. In Figure 6, we can see that when the index number is 1, we have numbered the last item of the list, but the permutations above index 0 in the list have not been numbered. We loop to the first permutation in the list and number down along the previous index until all permutations that do not have an index value are numbered. In the decrypted permutation list, we find the same permutation as the decrypted received stego block, extract its index value ${\left(3\right)}_{10}$, and then convert the index value into a $k$-bit $\left( k=⎣{\log }_{2}24⎦=4\right)$ binary number. Therefore, our secret data are ${\left(0011\right)}_2$.

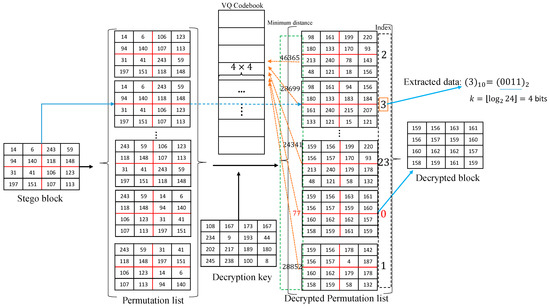
Figure 6. An example of the extraction process in which the 4 × 4-pixel block is divided into 4 sub-blocks.

4. Experimental Results

In this section, some experimental results were conducted in the R2017a version MATLAB environment on a Windows PC operating system to evaluate the performance of our proposed scheme and compare it with state-of-the-art schemes. We mainly tested different schemes on four commonly used grayscale images “Airplane”, “Baboon”, “Boat”, and “Peppers” with $512\times 512$ pixels, as shown in Figure 7.

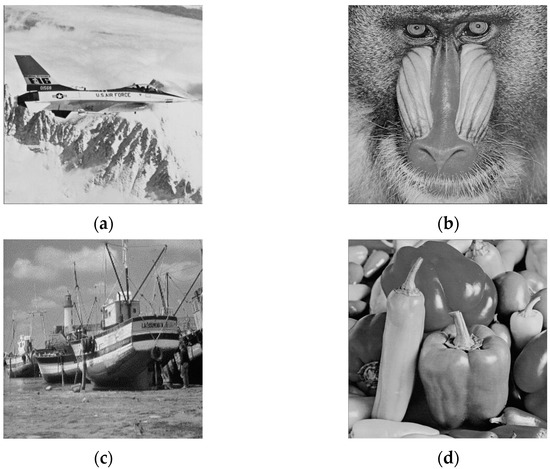
Figure 7. Test images. (a) Airplane; (b) Baboon; (c) Boat; (d) Peppers.

Two important metrics, PSNR (dB) and SSIM, are used to evaluate the image distortion between the original image and the recovered image and can be calculated by:

$$MSE=\frac{1}{M\times N}{\sum }_{i=1}^M{\sum }_{j=1}^N{(O_{i,j}-D_{i,j})}^2,$$

(7)

$${\mathrm{PSNR}=10\mathit{log}}_{10}\frac{{\left(255\right)}^2}{\mathit{MSE}}\left(\mathrm{dB}\right),$$

(8)

$$\phi \left(o_{\alpha }, d_{\alpha }\right)=\frac{\left(2{\mu }_o^{\alpha }{\mu }_d^{\alpha }+c_1\right)\left(2{\sigma }_{od}^{\alpha }+c_2\right)}{\left[{\left({\mu }_o^{\alpha }\right)}^2+{\left({\mu }_d^{\alpha }\right)}^2+c_1\right]\left[{\left({\sigma }_o^{\alpha }\right)}^2+{\left({\sigma }_d^{\alpha }\right)}^2+c_2\right]},$$

(9)

$$\mathrm{SSIM}=\frac{1}{b}{\sum }_{\alpha =1}^b\phi \left(o^{\alpha }, d^{\alpha }\right).$$

(10)

In Equation (9), $\mu$ and $\sigma$ denote the mean value and standard deviation and set two constants, $c_1$ and $c_2$, near to zero, respectively. In Equation (10), $b$ and $\alpha$ represent the total block number and block index, respectively. The embedding rate reveals the average number of bits that can be embedded into one pixel, which is obtained by:

$$\gamma =\frac{\left|Ad\right|}{M\times N}.$$

(11)

The error rate measures the data extraction and image recovery accuracies in this paper, which can be calculated by:

$$\epsilon =\frac{Error block number}{Total block number}.$$

(12)

Meanwhile, the information entropy is chosen to test the security of the encrypted image, i.e., calculate the randomness of the image histogram by:

$$H\left(I\right)=-{\sum }_{ı=0}^{255}\mathsf{\Theta }({\rho }_{ı})\log 2\left(\mathsf{\Theta }({\rho }_{ı}\right)),$$

(13)

where $I$ is an input grayscale image with 256 gray-levels, ${\rho }_{ı}$ ($0\le ı\le$255), and $\mathsf{\Theta }({\rho }_{ı})$ denotes the probability of ${\rho }_{ı}$. The information entropy value is closer to 8 if an encrypted image has a higher randomness. We first evaluate our proposed scheme in different scenarios in Section 4.1 and provide some execution results and a security analysis in Section 4.2. The comparisons with other state-of-the-art schemes are given in Section 4.3.

4.1. Performances of Our Proposed Schemes

Because the block size, number of sub-blocks, and codebook size will affect the embedding rate and the image block recovery accuracy, we first tested the performance of our proposed scheme in different block sizes, numbers of sub-blocks, and codebook sizes. For comparison purposes, we tested different block sizes of 4 × 4, 8 × 8, 16 × 16, and 32 × 32. For each block composed of different block sizes, we divided it into four or eight sub-blocks. This is because the size of the pixel blocks we divide determines that we cannot define the number of sub-blocks as multiples of 3. When the number of sub-blocks is 2, the amount of data that can be embedded in a pixel block will be small. When the number of sub-blocks is greater than 8, the time cost of calculating the full arrangement of sub-blocks will be large. To sum up, we chose to define the number of sub-blocks as 4 or 8 after weighing the embedding ability and the time cost. Therefore, each block can carry $lo{g}_{2}4!$ or $lo{g}_{2}8!$ secret bits, so that the embedding rates for these two scenarios are 0.2866 bpp and 0.9562 bpp, 0.0716 bpp and 0.2391 bpp, 0.0179 bpp and 0.0598 bpp, and 0.0045 bpp and 0.0149 bpp, with block sizes from 4 × 4 to 32 × 32. From Table 1, Table 2, Table 3 and Table 4, except for ‘Airplane’ and ‘Baboon’ in the case of block size 32 × 32, in most cases the error rates are growing while the block size decreases, so that the PSNRs and SSIMs are gradually decreasing. When the block size is larger, such as 16 × 16 or 32 × 32, most images can be totally recovered. While the images ‘Airplane’ and ‘Baboon’ have a block size of 16 × 16 or 32 × 32, due to some randomness of the stream cipher, the error rate suddenly increases occasionally in multiple experiments. Our table shows the average error rate of multiple experiments, so there will be an increase in the value. Generally, the error rates when choosing 4 sub-blocks are much lower than when the number of sub-blocks is 8, because there are more recovered block states compared to when the number of sub-blocks is 8, and they are more prone to be misjudged. The error rate decreases as the size of the VQ codebook increases, because the larger the size of the VQ codebook, the codewords in it can express more image features, and we can better judge the permutation of the original pixel blocks. From our experimental results, when the size of the VQ codebook is 128 and the number of sub-blocks is 4, the error rate is lower than other cases.

Table 1. Performances when number of sub-blocks = 4 and codebook size = 64.

Images	Block Size	$\mathbf{Embedding} \mathbf{Rate} \mathit{\gamma }$ (bpp)	PSNR (dB)	SSIM	$\mathbf{Error} \mathbf{Rate} \mathit{\epsilon }$ (%)
Airplane	4 × 4	0.2866	36.3807	0.9956	0.0044
	8 × 8	0.0716	46.2754	0.9997	0.0002
	16 × 16	0.0179	35.8955	0.9977	0.0029
	32 × 32	0.0045	Inf	1	0
Baboon	4 × 4	0.2866	30.0085	0.9813	0.0206
	8 × 8	0.0716	46.1674	0.9997	0.0005
	16 × 16	0.0179	Inf	1	0
	32 × 32	0.0045	Inf	1	0
Boat	4 × 4	0.2866	34.3157	0.9913	0.0090
	8 × 8	0.0716	36.3722	0.9976	0.0022
	16 × 16	0.0179	40.1909	0.9994	0.0010
	32 × 32	0.0045	Inf	1	0
Peppers	4 × 4	0.2866	35.8851	0.9927	0.0078
	8 × 8	0.0716	46.5244	0.9997	0.0002
	16 × 16	0.0179	38.2135	0.9994	0.0010
	32 × 32	0.0045	Inf	1	0

Table 2. Performances when number of sub-blocks = 4 and codebook size = 128.

Images	Block Size	$\mathbf{Embedding} \mathbf{Rate} \mathit{\gamma }$ (bpp)	PSNR (dB)	SSIM	$\mathbf{Error} \mathbf{Rate} \mathit{\epsilon }$ (%)
Airplane	4 × 4	0.2866	42.4206	0.9987	0.0018
	8 × 8	0.0716	47.9849	0.9998	0.0002
	16 × 16	0.0179	Inf	1	0
	32 × 32	0.0045	Inf	1	0
Baboon	4 × 4	0.2866	34.8421	0.9938	0.0081
	8 × 8	0.0716	47.1214	0.9997	0.0002
	16 × 16	0.0179	Inf	1	0
	32 × 32	0.0045	Inf	1	0
Boat	4 × 4	0.2866	36.0354	0.9960	0.0037
	8 × 8	0.0716	36.1620	0.9976	0.0022
	16 × 16	0.0179	Inf	1	0
	32 × 32	0.0045	Inf	1	0
Peppers	4 × 4	0.2866	39.0904	0.9975	0.0024
	8 × 8	0.0716	Inf	1	0
	16 × 16	0.0179	38.4969	0.9991	0.0001
	32 × 32	0.0045	Inf	1	0

Table 3. Performances when number of sub-blocks = 8 and codebook size = 64.

Images	Block Size	$\mathbf{Embedding} \mathbf{Rate} \mathit{\gamma }$ (bpp)	PSNR (dB)	SSIM	$\mathbf{Error} \mathbf{Rate} \mathit{\epsilon }$ (%)
Airplane	4 × 4	0.9562	28.0438	0.9573	0.0992
	8 × 8	0.2391	35.6202	0.9958	0.0071
	16 × 16	0.0598	34.0751	0.9960	0.0059
	32 × 32	0.0149	36.8924	0.9987	0.0031
Baboon	4 × 4	0.9562	20.8189	0.7899	0.3775
	8 × 8	0.2391	36.5928	0.9966	0.0073
	16 × 16	0.0598	Inf	1	0
	32 × 32	0.0149	Inf	1	0
Boat	4 × 4	0.9562	26.3119	0.9261	0.1343
	8 × 8	0.2391	31.2961	0.9901	0.0146
	16 × 16	0.0598	34.9084	0.9967	0.0068
	32 × 32	0.0149	Inf	1	0
Peppers	4 × 4	0.9562	27.8656	0.9552	0.0745
	8 × 8	0.2391	35.5764	0.9957	0.0063
	16 × 16	0.0598	33.3352	0.9952	0.0088
	32 × 32	0.0149	31.1752	0.9933	0.0156

Table 4. Performances when number of sub-blocks = 8 and codebook size = 128.

Images	Block Size	$\mathbf{Embedding} \mathbf{Rate} \mathit{\gamma }$ (bpp)	PSNR (dB)	SSIM	$\mathbf{Error} \mathbf{Rate} \mathit{\epsilon }$ (%)
Airplane	4 × 4	0.9562	28.7802	0.9658	0.0874
	8 × 8	0.2391	38.0761	0.9979	0.0049
	16 × 16	0.0598	46.1583	0.9997	0.0001
	32 × 32	0.0149	36.5631	0.9984	0.0117
Baboon	4 × 4	0.9562	21.7144	0.8130	0.4152
	8 × 8	0.2391	39.0186	0.9980	0.0054
	16 × 16	0.0598	Inf	1	0
	32 × 32	0.0149	Inf	1	0
Boat	4 × 4	0.9562	26.6285	0.9297	0.1337
	8 × 8	0.2391	31.9629	0.9918	0.0122
	16 × 16	0.0598	35.2929	0.9967	0.0068
	32 × 32	0.0149	Inf	1	0
Peppers	4 × 4	0.9562	28.8480	0.9645	0.0754
	8 × 8	0.2391	40.0998	0.9984	0.0032
	16 × 16	0.0598	37.8925	0.9986	0.0020
	32 × 32	0.0149	37.4123	0.9987	0.0039

4.2. Execution Results and Security Analysis

Some execution results, i.e., images in different phases, are given in Figure 8. After encrypting the image, the pixel values are disordered, and no meaningful information can be observed. Therefore, the pixel distributions of the encrypted images are even in a histogram. Because our proposed data embedding scheme only scrambles the encrypted pixel locations, the pixel distributions of the embedded encrypted images are not changed. When the number of sub-blocks is 8, codebook size is 64, and block size is 4 × 4, 0.9562 bpp can be embedded; however, the recovered image has some errors, as shown in Figure 8a4. When the number of sub-blocks is 4, codebook size is 128, and block size is 16 × 16, after extracting 0.0179 bpp of additional data, the original image can be totally recovered without any errors.

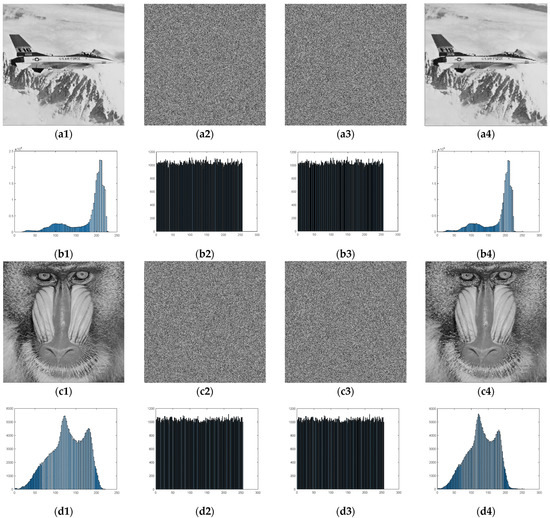
Figure 8. Execution results of our proposed scheme: (a1) The original “Airplane” image with $512\times 512$ pixels. (a2,a3) are the encrypted image and embedded encrypted image (the number of sub-blocks = 8, codebook size = 64, block size = 4 × 4, and $\gamma =$ bpp). (a4) is the decrypted image (PSNR $=$ dB). (b1–b4) are the corresponding histograms of (a1–a4). In (c,d), the results of “Baboon” (the number of sub-blocks = 4, codebook size = 128, block size = 16 × 16, $\gamma =$ 0.0179 bpp, and PSNR $=$ Inf dB) are given.

Additionally, we also analyze the security of our proposed scheme based on information entropy. The original images, encrypted images, and embedded encrypted images of different block sizes are shown in Table 5. Obviously, the entropy values of the encrypted image and the embedded encrypted image for each image are all the same, because our proposed scheme only scrambles the encrypted pixel locations. On the other hand, the entropy values of different encrypted images are very close to 8 and are much higher than those of the original images. Therefore, the distribution of pixel values in the encrypted images have a higher randomness so that security can be better guaranteed.

Table 5. Information Entropy of Different Images in Two Scenarios.

Images	Original Image	Encrypted Image	Block Size	Embedded Encrypted Image
				4 Sub-Blocks	8 Sub-Blocks
Airplane	6.7059	7.9994	4 × 4	7.9994	7.9994
			8 × 8	7.9994	7.9994
			16 × 16	7.9994	7.9994
			32 × 32	7.9994	7.9994
Baboon	7.3579	7.9992	4 × 4	7.9992	7.9992
			8 × 8	7.9992	7.9992
			16 × 16	7.9992	7.9992
			32 × 32	7.9992	7.9992
Boat	7.1914	7.9994	4 × 4	7.9994	7.9994
			8 × 8	7.9994	7.9994
			16 × 16	7.9994	7.9994
			32 × 32	7.9994	7.9994
Peppers	7.5944	7.9993	4 × 4	7.9993	7.9993
			8 × 8	7.9993	7.9993
			16 × 16	7.9993	7.9993
			32 × 32	7.9993	7.9993
Average	7.2124	7.9993	/	7.9993	7.9993

Furthermore, the correlation between the adjacent pixels of an image is also an important part of image security analysis. Therefore, we further analyzed some statistical features and provided some results, including horizontal correlation and vertical correlation. Table 6, Table 7, Table 8 and Table 9 show the correlation distribution between the encrypted image and the original image in different directions when embedding using different pixel block sizes, respectively. As shown in Table 6, Table 7, Table 8 and Table 9, there is some similarity between adjacent pixels in the original image, i.e., both horizontal and vertical correlations are high. Because stream encryption is used, the correlation distribution of the encrypted image in different directions does not change with the pixel block size, as long as the stream cipher key remains unchanged. The correlations of both the encrypted image and the embedded encrypted image are close to 0, indicating a high difference in the values of adjacent pixels, because the stream cipher encryption fully encrypts the image and all of the permutation embedding retains the encrypted pixel values. After image encryption, most of the pixels are not equal to the original pixels, so no image content is exposed.

Table 6. Correlation distribution of images in different directions when the pixel block size is 4 × 4.

Images	Horizontal Correlation				Vertical Correlation
	Original Image	Encrypted Image	Embedded Encrypted Image		Original Image	Encrypted Image	Embedded Encrypted Image
			4 Sub-Blocks	8 Sub-Blocks			4 Sub-Blocks	8 Sub-Blocks
Airplane	0.9606	−0.0043	0.0031	0.0040	0.9584	0.0032	0.0025	−0.0012
Baboon	0.8667	−0.0048	−0.0044	−0.0039	0.7498	0.0032	−0.0032	0.0022
Boat	0.9383	−0.0026	0.0030	−0.0025	0.9715	0.0045	0.0040	−0.0022
Peppers	0.9730	0.0030	0.0025	−0.0022	0.9762	0.0026	0.0013	0.0015

Table 7. Correlation distribution of images in different directions when the pixel block size is 8 × 8.

Images	Horizontal Correlation				Vertical Correlation
	Original Image	Encrypted Image	Embedded Encrypted Image		Original Image	Encrypted Image	Embedded Encrypted Image
			4 Sub-Blocks	8 Sub-Blocks			4 Sub-Blocks	8 Sub-Blocks
Airplane	0.9606	−0.0043	−0.0028	0.0039	0.9584	0.0032	−0.0034	−0.0028
Baboon	0.8667	−0.0048	−0.0036	−0.0033	0.7498	0.0032	0.0025	−0.0022
Boat	0.9383	−0.0026	0.0016	0.0012	0.9715	0.0045	−0.0047	−0.0032
Peppers	0.9730	0.0030	0.0039	0.0025	0.9762	0.0026	0.0011	0.0016

Table 8. Correlation distribution of images in different directions when the pixel block size is 16 × 16.

Images	Horizontal Correlation				Vertical Correlation
	Original Image	Encrypted Image	Embedded Encrypted Image		Original Image	Encrypted Image	Embedded Encrypted Image
			4 Sub-Blocks	8 Sub-Blocks			4 Sub-Blocks	8 Sub-Blocks
Airplane	0.9606	−0.0043	0.0021	−0.0041	0.9584	0.0032	0.0036	−0.0025
Baboon	0.8667	−0.0048	0.0029	−0.0032	0.7498	0.0032	−0.0030	0.0032
Boat	0.9383	−0.0026	−0.0018	0.0025	0.9715	0.0045	−0.0031	−0.0038
Peppers	0.9730	0.0030	0.0031	−0.0027	0.9762	0.0026	−0.0026	0.0029

Table 9. Correlation distribution of images in different directions when the pixel block size is 32 × 32.

Images	Horizontal Correlation				Vertical Correlation
	Original Image	Encrypted Image	Embedded Encrypted Image		Original Image	Encrypted Image	Embedded Encrypted Image
			4 Sub-Blocks	8 Sub-Blocks			4 Sub-Blocks	8 Sub-Blocks
Airplane	0.9606	−0.0043	−0.0044	0.0036	0.9584	0.0032	−0.0037	0.0021
Baboon	0.8667	−0.0048	0.0039	−0.0030	0.7498	0.0032	0.0034	0.0038
Boat	0.9383	−0.0026	−0.0035	0.0031	0.9715	0.0045	−0.0039	−0.0056
Peppers	0.9730	0.0030	0.0048	−0.0039	0.9762	0.0026	−0.0018	0.0017

4.3. Comparison with State-of-the-Art Schemes

In this section, we mainly compare our proposed scheme with the scheme in [12], and we carry out an embedding rate comparison with some state-of-the-art schemes. In Table 10, the embedding rates of our proposed scheme are all higher than those in [12], except for when the number of sub-blocks is 4 and the block size is 32. Especially when dividing each block into 8 parts, the embedding rates have tremendous improvements. Because the image quality of the recovery image mainly depends on the error rate, we further compare our proposed scheme with [12] in terms of error rate. As shown in Table 11, [12] has lower errors in the most cases, because the CNN model was only trained on these four images. Our proposed scheme trained the VQ codebook on other images, so the error rates are relatively higher. Nevertheless, the error rates remain at a low level, so they are still acceptable, especially in the larger block sizes.

Table 10. Comparison of Embedding Rate $\gamma$ (bpp).

Images	Block Size	[12]	4 Sub-Blocks	8 Sub-Blocks
Airplane	4 × 4	0.1563	0.2866	0.9562
	8 × 8	0.0547	0.0716	0.2391
	16 × 16	0.0176	0.0179	0.0598
	32 × 32	0.0054	0.0045	0.0149
Baboon	4 × 4	0.1563	0.2866	0.9562
	8 × 8	0.0547	0.0716	0.2391
	16 × 16	0.0176	0.0179	0.0598
	32 × 32	0.0054	0.0045	0.0149
Boat	4 × 4	0.1563	0.2866	0.9562
	8 × 8	0.0547	0.0716	0.2391
	16 × 16	0.0176	0.0179	0.0598
	32 × 32	0.0054	0.0045	0.0149
Peppers	4 × 4	0.1563	0.2866	0.9562
	8 × 8	0.0547	0.0716	0.2391
	16 × 16	0.0176	0.0179	0.0598
	32 × 32	0.0054	0.0045	0.0149

Table 11. Comparison of Error Rate $\epsilon$ (%).

Images	Block Size	[12]	Codebook Size = 64		Codebook Size = 128
			4 Sub-Blocks	8 Sub-Blocks	4 Sub-Blocks	8 Sub-Blocks
Airplane	4 × 4	0	0.0044	0.0992	0.0018	0.0874
	8 × 8	0	0.0002	0.0071	0.0002	0.0049
	16 × 16	0	0.0029	0.0059	0	0.0001
	32 × 32	0	0	0.0031	0	0.0117
Baboon	4 × 4	0.0004	0.0206	0.3775	0.0081	0.4152
	8 × 8	0	0.0005	0.0073	0.0002	0.0054
	16 × 16	0	0	0	0	0
	32 × 32	0	0	0	0	0
Boat	4 × 4	0.0004	0.0090	0.1343	0.0037	0.1337
	8 × 8	0	0.0022	0.0146	0.0022	0.0122
	16 × 16	0	0.0010	0.0068	0	0.0068
	32 × 32	0	0	0	0	0
Peppers	4 × 4	0.0001	0.0078	0.0745	0.0024	0.0754
	8 × 8	0	0.0002	0.0063	0	0.0032
	16 × 16	0	0.0010	0.0088	0.0001	0.0020
	32 × 32	0	0	0.0156	0	0.0039

Because the spare room of our proposed scheme is vacated after image encryption, we make the embedding rate comparison with some VRAE schemes [10,11,12,14,15,16,17,18,21,22], as shown in Table 12. In [12], and in our proposed scheme, we set the block size to 8 × 8 and the number of sub-blocks to 8. It can be observed that our proposed scheme has outstanding embedding rates compared to other schemes. This is because we are using the all-permutation technique in mathematics, which generates more permutations than other permutation techniques, so our embedding rate is better.

Table 12. Maximum Embedding Rate Comparison in Different Schemes.

Images	$\mathit{\gamma } \left(\mathbf{bpp}\right)$
	[10]	[11]	[12]	[14]	[15]	[16]	[17]	[18]	[21]	[22]	Proposed
Airplane	0.0039	0.0039	0.0030	0.0020	0.0040	0.0080	0.0080	0.0039	0.0400	0.0547	0.2391
Baboon	0.0039	0.0039	0.0010	0.0020	0.0040	0.0080	0.0080	0.0039	0.0400	0.0547	0.2391
Boat	0.0039	0.0039	0.0030	0.0020	0.0040	0.0080	0.0080	0.0039	0.0400	0.0547	0.2391
Peppers	0.0039	0.0039	0.0030	0.0020	0.0040	0.0080	0.0080	0.0039	0.0400	0.0547	0.2391
Average	0.0039	0.0039	0.0025	0.0020	0.0040	0.0080	0.0080	0.0039	0.0400	0.0547	0.2391

5. Conclusions

In this paper, we proposed a reversible data hiding scheme in encrypted images that directly embeds data into encrypted images using the all-permutation technique (P-RDHEI). In the process of extracting information and restoring images, the scheme combines the characteristics of the VQ codebook, which effectively reduces the burden on the receiver. The encrypted image of our scheme and the embedded encrypted image of our scheme are fully encrypted without exposing the statistical properties and texture of the original image. It has a high payload capacity of 0. 9562 bpp when dividing a 4 × 4 size image block into 8 sub-blocks, and our P-RDHEI scheme has a higher embedding efficiency and larger embedding capacity compared to many other existing similar RDHEI schemes. When a 32 × 32 size image block is divided into four sub-blocks for embedding, our scheme is able to achieve total image recovery, that is, full image recovery can be achieved using VQ codebook-assisted image restoration, which is also better than some existing replacement-based RDHEI schemes.

When the number of sub-blocks is greater than 8, the time cost of computing the full sub-block arrangement will be large. After weighing the embedding capability and time cost, we choose to define the number of sub-blocks as 4 or 8. In future research, we will try to design other methods to obtain more embeddable space without increasing the time cost. We can also introduce deep learning techniques to further optimize the algorithm to improve the decrypted image quality of our P-RDHEI scheme.