Multi-Gbps LDPC Decoder on GPU Devices
Abstract
1. Introduction
- (1)
- We propose a high decoding parallelism GPU-based LDPC design scheme, which further optimizes intra-codeword and inter-codeword parallelisms to improve the throughput performance.
- (2)
- We propose a new GPU-based data scheduling strategy, which enhances the off-chip memory utilization to match well with different rates and lengths of LDPC codes and meet the requirements of large-scale data processes.
- (3)
- Combined with the high decoding parallel design scheme and data scheduling strategy, we implement GPU-based high-throughput decoders on GGPU and EGPU devices, respectively. The experimental results show that the proposed decoder outperforms the state-of-the-art work in scenarios that need to process large-scale data.
2. LDPC Codes and Decoding Algorithms
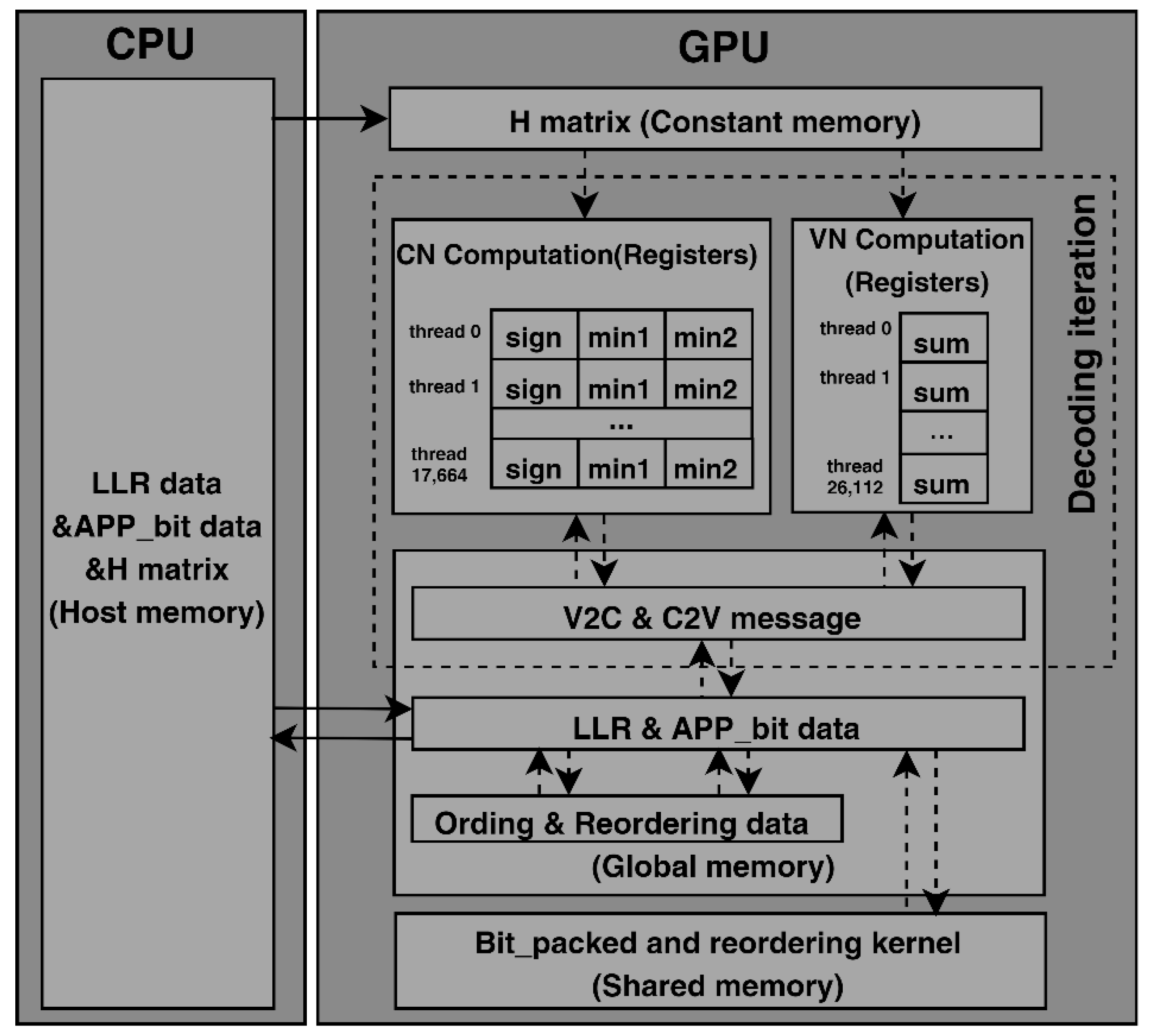
3. Proposed High-Throughput GPU-Based LDPC Decoder
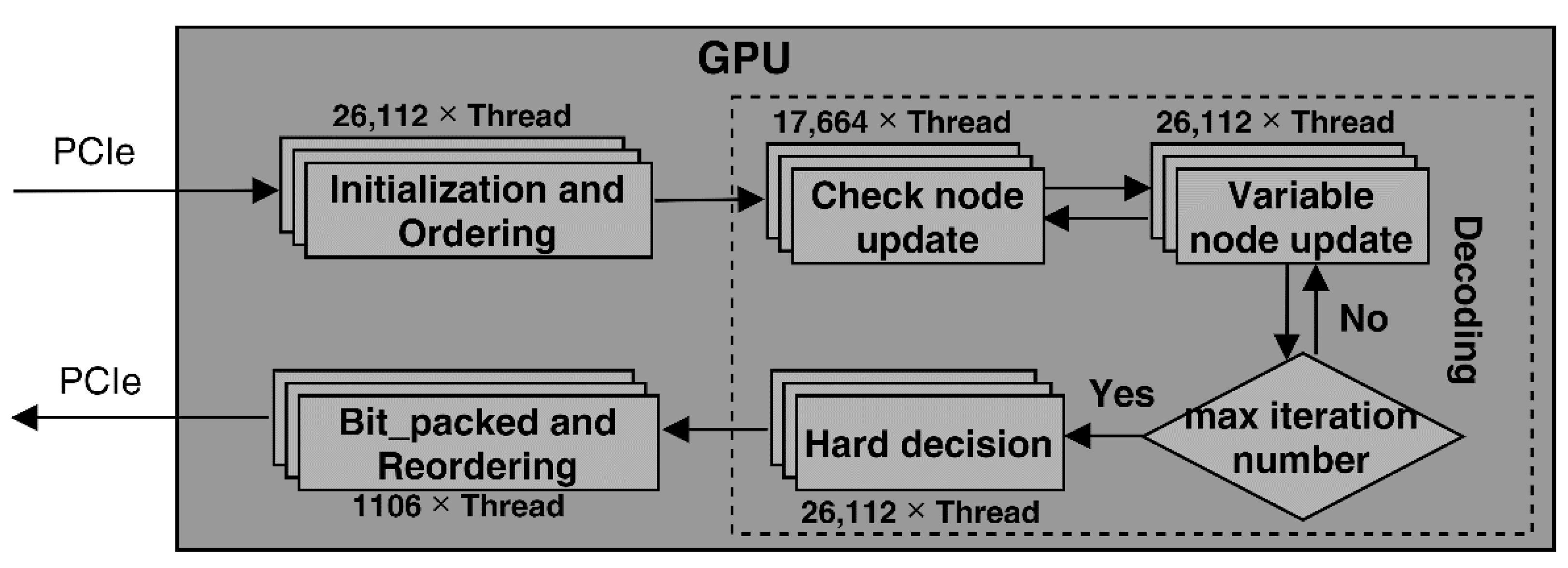
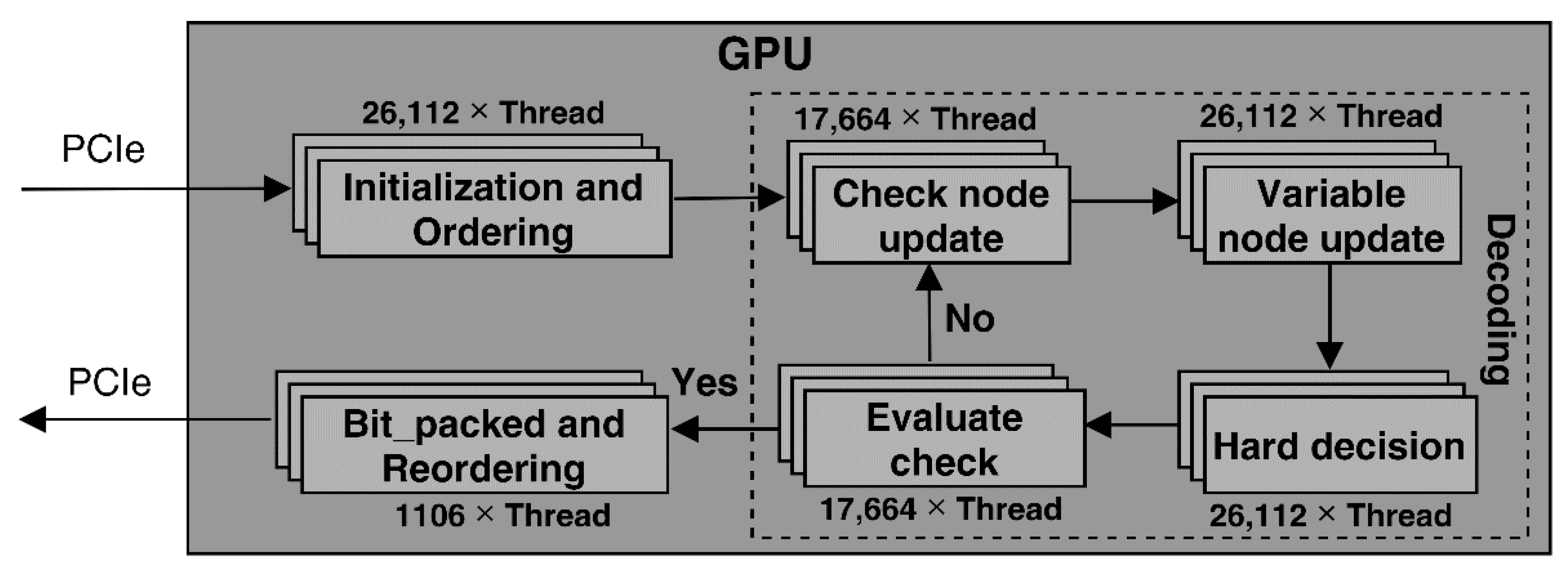
3.1. High Decoding Parallelism Design Scheme
3.1.1. Initialization and Ordering
3.1.2. Check Node Update
3.1.3. Variable Node Update
3.1.4. Hard Decision
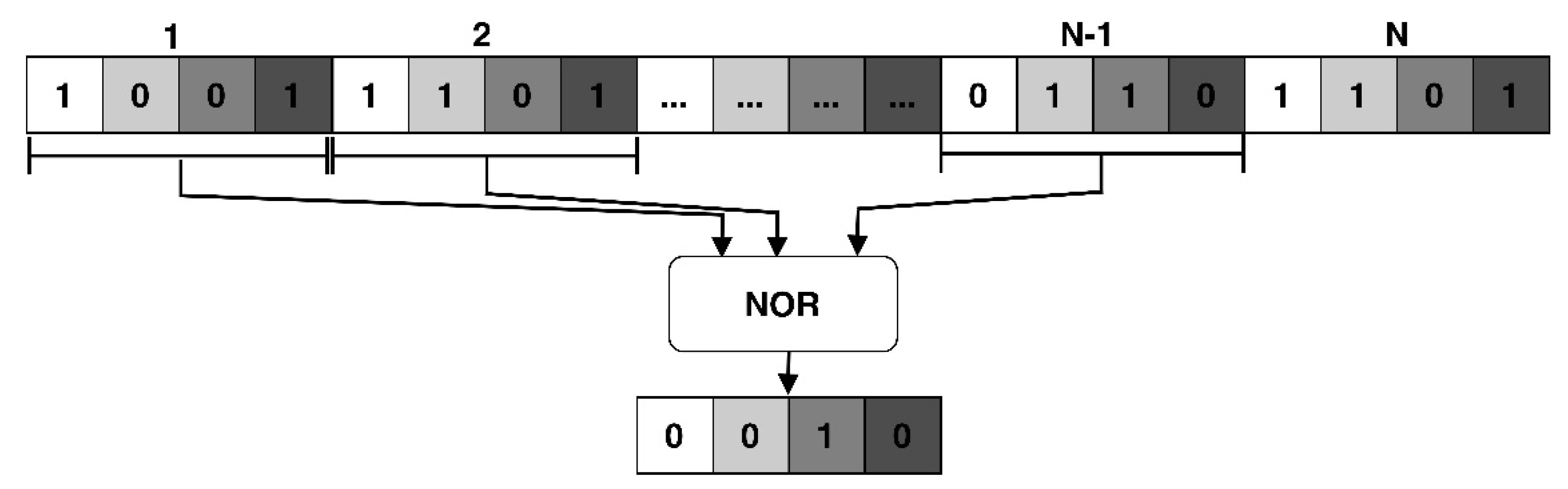
3.1.5. Evaluate Check
3.1.6. Bit Packed and Reordering
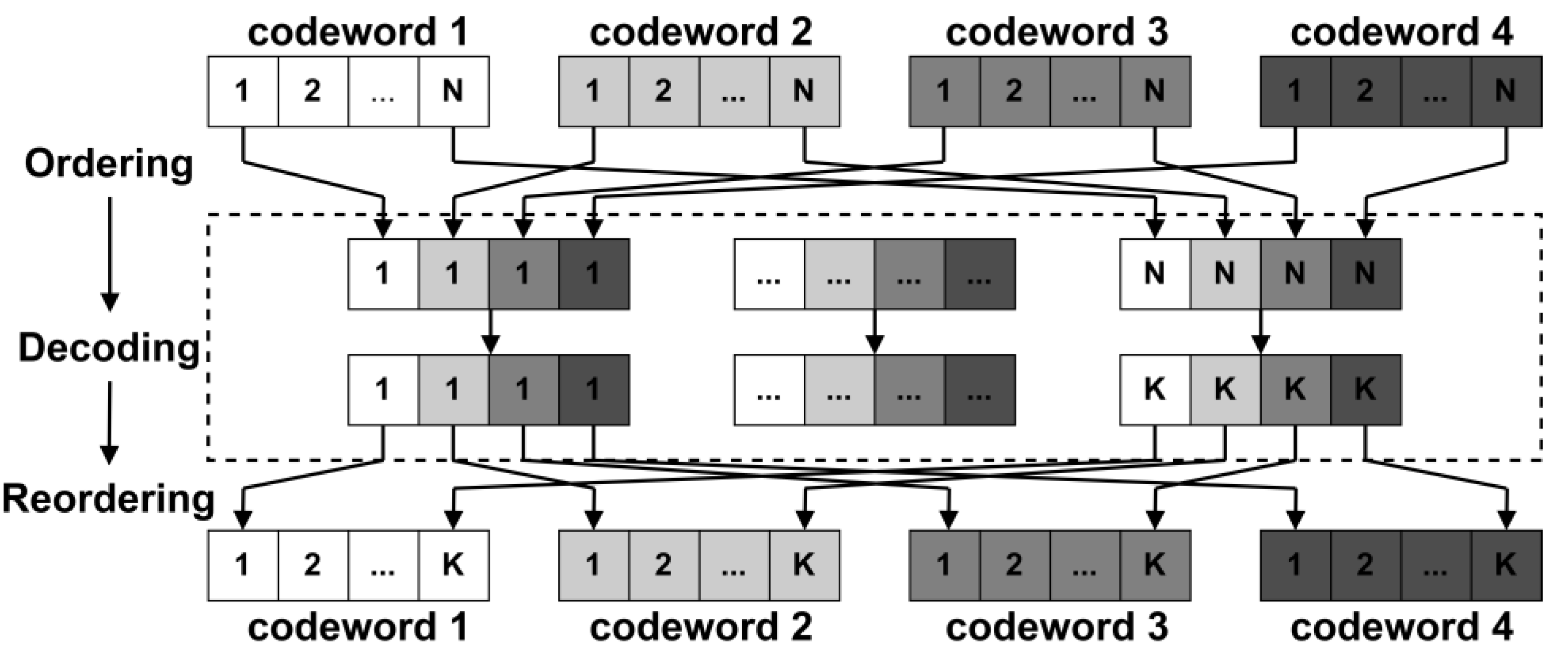
3.2. Data Scheduling Strategy
3.2.1. Memory Allocation Strategy during Decoding
3.2.2. Storage Method for PCM
3.2.3. Data Transfer Strategy
4. Experimental Results and Analysis
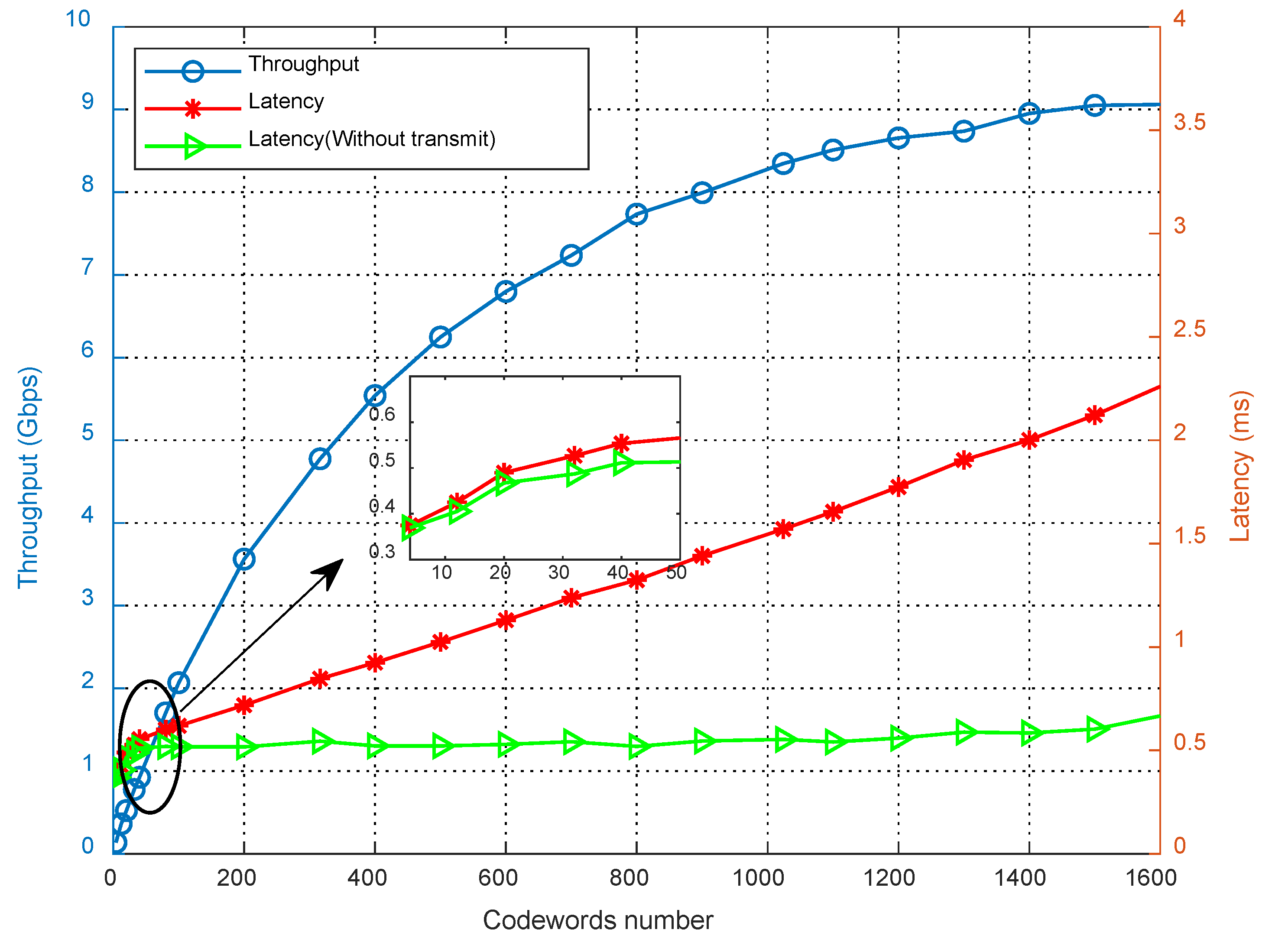
4.1. Throughput and Latency Performance Analysis
4.2. Performance Analysis on the EGPU Device
4.3. Performance Analysis under Multiple-Stream Mode
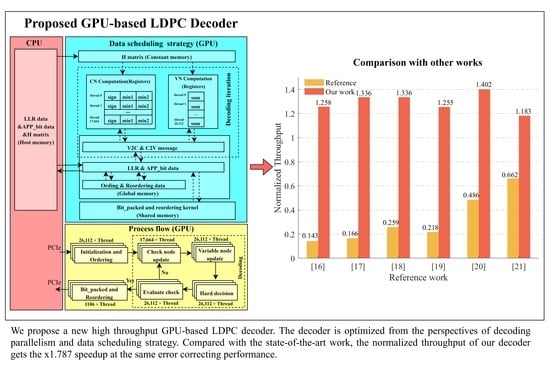
4.4. Comparison with Other Works
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gallager, R. Low-Density Parity-Check Codes. IEEE Trans. Inform. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- MacKay, D.J.C.; Neal, R.M. Near shannon limit performance of low density parity check codes. Electron. Lett. 1996, 33, 457–458. [Google Scholar] [CrossRef]
- Session Chairman (Nokia). Chairman’s Notes of Agenda Item 7.1.5 Channel Coding and Modulation. 3GPP TSG RAN WG1 Meeting No. 87, R1-1613710. 2016. Available online: https://portal.3gpp.org/ngppapp/CreateTdoc.aspx?mode=view&contribu-tionId=752413 (accessed on 14 August 2022).
- A 802.11 Wireless LANs; TGn Sync Proposal Technical Specification. IEEE Standard Association: Piscataway, NJ, USA, 2004.
- Std IEEE 802.16e; Part 16: Air Interface for Fixed and Mobile Broadband Wireless Access Systems. IEEE Standard Association: Piscataway, NJ, USA, 2008.
- Chen, S.; Peng, K.; Song, J.; Zhang, Y. Performance Analysis of Practical QC-LDPC Codes: From DVB-S2 to ATSC 3.0. IEEE Trans. Broadcast. 2019, 65, 172–178. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Li, Y.; Xu, B.; Ma, L.; Yang, J.; Huang, W. High-throughput GPU layered decoder of multi-edge type low density parity check codes in continuous-variable quantum key distribution systems. Sci. Rep. 2020, 10, 14561. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Liu, X.; Wu, F.; Lu, Z.; Xie, C. A Low Bit-Width LDPC Min-Sum Decoding Scheme for NAND Flash. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 1971–1975. [Google Scholar] [CrossRef]
- Wang, C.X.; Haider, F.; Gao, X.Q.; You, X.H.; Yang, Y.; Yuan, D.F.; Aggoune, H.M.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular architecture and key technologies for 5G wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef]
- Lin, C.H.; Wang, C.X.; Lu, C.K. LDPC Decoder Design Using Compensation Scheme of Group Comparison for 5G Communication Systems. Electronics 2021, 10, 2010. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, W.; Li, H.; Dai, S.; Han, C.; Yang, J. Iterative Decoding of LDPC-Based Product Codes and FPGA-Based Performance Evaluation. Electronics 2020, 9, 122. [Google Scholar] [CrossRef]
- Thi Bao Nguyen, T.; Nguyen Tan, T.; Lee, H. Low-Complexity High-Throughput QC-LDPC Decoder for 5G New Radio Wireless Communication. Electronics 2021, 10, 516. [Google Scholar] [CrossRef]
- Verma, A.; Shrestha, R. Low Computational-Complexity SOMS-Algorithm and High-Throughput Decoder Architecture for QC-LDPC Codes. IEEE Trans. Veh. Technol. 2022, 1–14. [Google Scholar] [CrossRef]
- Duarte, L.; Gomes, R.; Ribeiro, C.; Caldeirinha, R.F.S. A Software-Defined Radio for Future Wireless Communication Systems at 60 GHz. Electronics 2019, 8, 1490. [Google Scholar] [CrossRef]
- Richter, L.; Reimers, U.H. A 5G New Radio-Based Terrestrial Broadcast Mode: System Design and Field Trial. IEEE Trans. Broadcast. 2022, 68, 475–486. [Google Scholar] [CrossRef]
- Fernandes, G.; Silva, V.; Sousa, L. How gpus can outperform asics for fast ldpc decoding. In Proceedings of the International Conference Supercomputing, New York, NY, USA, 8–12 June 2009; pp. 390–399. [Google Scholar]
- NVIDIA Corporation. NVIDIA CUDA C Programming Guide Version 4.0[M]; NVIDIA CUDA Group: Santa Clara, CA, USA, 2011; pp. 1–5. [Google Scholar]
- OpenCL—The Open Standard for Parallel Programming of Heterogeneous Systems. Available online: http://khronos.org/opencl/ (accessed on 13 August 2022).
- Wang, Z.; Jiang, Z.; Wang, Z.; Tang, X.; Liu, C.; Yin, S.; Hu, Y. Enabling Latency-Aware Data Initialization for Integrated CPU/GPU Heterogeneous Platform. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2020, 39, 3433–3444. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Liu, C.; Hu, Y. Understanding and tackling the hidden memory latency for edge-based heterogeneous platform. In Proceedings of the 3rd USENIX Workshop on Hot Topics in Edge Computing (HotEdge 20), 25–26 June 2020. [Google Scholar]
- Le Gal, B.; Jego, C.; Crenne, J. A High Throughput Efficient Approach for Decoding LDPC Codes onto GPU Devices. IEEE Embed. Syst. Lett. 2014, 6, 29–32. [Google Scholar] [CrossRef]
- Keskin, S.; Kocak, T. GPU-Based Gigabit LDPC Decoder. IEEE Commun. Lett. 2017, 21, 1703–1706. [Google Scholar] [CrossRef]
- Yuan, J.; Sha, J. 4.7-Gb/s LDPC Decoder on GPU. IEEE Commun. Lett. 2018, 22, 478–481. [Google Scholar] [CrossRef]
- Li, R.C.; Zhou, X.; Pan, H.Y.; Su, H.Y.; Dou, Y. A High-Throughput LDPC Decoder Based on GPUs for 5G New Radio. In Proceedings of the IEEE Symposium on Computers and Communications (ISCC), Rennes, France, 7–10 July 2020; pp. 1–7. [Google Scholar]
- Tarver, C.; Tonnemacher, M.; Chen, H.; Zhang, J.Z.; Cavallaro, J.R. GPU-Based, LDPC Decoding for 5G and Beyond. IEEE Open J. Circuits Syst. 2021, 2, 278–290. [Google Scholar] [CrossRef]
- Ling, J.; Cautereels, P. Fast LDPC GPU Decoder for Cloud RAN. IEEE Embed. Syst. Lett. 2021, 13, 170–173. [Google Scholar] [CrossRef]
- Wymeersch, H. Iterative Receiver Design; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Tanner, R.M. A Recursive Approach to Low Complexity Codes. IEEE Trans. Inf. Theory 1981, 27, 533–547. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Good Error-Correcting Codes Based on Very Sparse Matrices. IEEE Trans. Inform. Theory 1999, 45, 399–431. [Google Scholar] [CrossRef]
- Fossorier, M.P.C.; Mihaljevic, M.; Imai, H. Reduced complexity iterative decoding of low density parity check codes based on belief propagation. IEEE Trans. Commun. 1999, 47, 673–680. [Google Scholar] [CrossRef]
- Chen, J.; Fossorier, M.P.C. Near Optimum Universal Belief Propagation Based Decoding of Low-Density Parity Check Codes. IEEE Trans. Commun. 2002, 50, 406–414. [Google Scholar] [CrossRef]
- Chen, J.; Fossorier, M.P.C. Density Evolution for Two Improved BP-Based Decoding Algorithms of LDPC Codes. IEEE Commun. Lett. 2002, 6, 208–210. [Google Scholar] [CrossRef]
- Le Gal, B.; Jego, C. High-Throughput Multi-Core LDPC Decoders Based on x86 Processor. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 1373–1386. [Google Scholar] [CrossRef]
- Hocevar, D.E. A reduced complexity decoder architecture via layered decoding of LDPC codes. In Proceedings of the IEEE Workshop on Signal Processing Systems (SIPS), Austin, TX, USA, 13–15 October 2004; pp. 107–112. [Google Scholar]
- Zhang, J.; Fossorier, M.P.C. Shuffled iterative decoding. IEEE Trans. Commun. 2005, 53, 209–213. [Google Scholar] [CrossRef]
- Li, M.; Nour, C.A.; Jégo, C.; Douillard, C. Design and FPGA prototyping of a bit-interleaved coded modulation receiver for the DVB-T2 standard. In Proceedings of the IEEE Workshop On Signal Processing Systems (SIPS), San Francisco, CA, USA, 6–8 October 2010; pp. 162–167. [Google Scholar]
- Falcao, G.; Sousa, L.; Silva, V. Massively LDPC decoding on multicore architectures. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 309–322. [Google Scholar] [CrossRef]
- Falcao, G.; Andrade, J.; Silva, V.; Sousa, L. GPU-based DVB-S2 LDPC decoder with high throughput and fast error floor detection. Electron. Lett. 2011, 47, 542–543. [Google Scholar] [CrossRef]
- Duff, I.S.; Grimes, R.G.; Lewis, J.G. Sparse matrix test problems. ACM Trans. Math. Softw. 1989, 15, 1–14. [Google Scholar] [CrossRef]





| Number | 4 × 1 | 4 × 16 | 4 × 32 | 4 × 128 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | T | L1 | L2 | T | L1 | L2 | T | L1 | L2 | T | L1 | L2 |
| (8448, 25,344) | 0.124 | 0.816 | 0.810 | 1.536 | 1.056 | 0.959 | 2.719 | 1.193 | 0.998 | 6.590 | 1.969 | 1.190 |
| (2560, 12,800) | 0.143 | 0.358 | 0.355 | 1.447 | 0.566 | 0.516 | 2.564 | 0.639 | 0.542 | 6.375 | 1.028 | 0.601 |
| (2488, 4896) | 0.134 | 0.145 | 0.144 | 1.205 | 0.259 | 0.235 | 2.142 | 0.292 | 0.245 | 5.342 | 0.469 | 0.281 |
| (2000, 4000) | 0.113 | 0.141 | 0.140 | 1.089 | 0.235 | 0.215 | 1.855 | 0.275 | 0.236 | 4.871 | 0.420 | 0.266 |
| (972, 1944) | 0.072 | 0.107 | 0.106 | 0.567 | 0.219 | 0.209 | 1.049 | 0.237 | 0.218 | 3.110 | 0.320 | 0.245 |
| Decoder | [26] | Our Work | ||
|---|---|---|---|---|
| Code rate | (8448, 26,112) | (8448, 26,112) | ||
| Device | GPGPU | GPGPU | EGPU | |
| Scheduling | Layered | Flooding | Flooding | Flooding |
| Iterations | 10 | 20 | 20 | 20 |
| Power (W) | 40.000 | 116.500 | 8.805 | 10.844 |
| Throughput (Gbps) | 1.800 | 7.959 | 0.567 | 0.610 |
| Efficiency (Mbps/W) | 45.000 | 68.317 | 64.395 | 56.252 |
| Parameter | Proposed Decoder | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number | 6144 | 7168 | 8192 | ||||||
| 1 | 2 | 4 | 1 | 2 | 4 | 1 | 2 | 4 | |
| 6144 | 3072 | 1536 | 7168 | 3584 | 1792 | 8192 | 4096 | 2048 | |
| Throughput | 7.783 | 8.690 | 8.626 | 7.928 | 8.720 | 8.974 | 7.936 | 8.753 | 9.114 |
| Latency | 20.626 | 18.467 | 18.616 | 23.620 | 21.488 | 20.864 | 26.970 | 24.443 | 23.438 |
| Code Rate | Boost Frequency (CUDA) of Ref. | Scheduling of Ref. | Iterations | Throughput | N_Throughput | Speedup | |||
|---|---|---|---|---|---|---|---|---|---|
| Ref. | Our | Ref. | Our | Ref. | Our | ||||
| (2000, 4000) | 1545 (4352) [21] | Layered | 10 | 20 | 0.965 | 8.463 | 0.143 | 1.258 | 8.797 |
| (972, 1944) | 1531 (3584) [22] | Flooding | 10 | 10 | 0.913 | 8.984 | 0.166 | 1.336 | 8.048 |
| (972, 1944) | 1582 (3584) [23] | Flooding | 10 | 10 | 1.474 | 8.984 | 0.259 | 1.336 | 5.274 |
| (1760, 2080) | 1545 (4352) [24] | Layered | 10 | 20 | 1.380 | 8.444 | 0.218 | 1.255 | 5.756 |
| (8448, 26,112) | 1770 (4608) [25] | Flooding | 5 | 5 | 3.964 | 9.427 | 0.486 | 1.402 | 2.884 |
| (8448, 26,112) | 1770 (1536) [26] | Layered | 10 | 20 | 1.800 | 7.959 | 0.662 | 1.183 | 1.787 |
| Decoder | Scheduling | Max Iteration Number | SNR (dB) | Throughput (Gbps) |
|---|---|---|---|---|
| [23] | Flooding | 10 | 1.0~5.5 | 1.153~4.771 |
| Layered | 10 | 1.0~5.5 | 0.708~3.672 | |
| Our work | Flooding | 10 | −3.5~5.5 | 6.508~10.013 |
| Flooding | 20 | −4.5~5.5 | 4.688~10.013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Yin, H.; Lv, Y.; Xu, W.; Yang, Z. Multi-Gbps LDPC Decoder on GPU Devices. Electronics 2022, 11, 3447. https://doi.org/10.3390/electronics11213447
Dai J, Yin H, Lv Y, Xu W, Yang Z. Multi-Gbps LDPC Decoder on GPU Devices. Electronics. 2022; 11(21):3447. https://doi.org/10.3390/electronics11213447
Chicago/Turabian StyleDai, Jingxin, Hang Yin, Yansong Lv, Weizhang Xu, and Zhanxin Yang. 2022. "Multi-Gbps LDPC Decoder on GPU Devices" Electronics 11, no. 21: 3447. https://doi.org/10.3390/electronics11213447
APA StyleDai, J., Yin, H., Lv, Y., Xu, W., & Yang, Z. (2022). Multi-Gbps LDPC Decoder on GPU Devices. Electronics, 11(21), 3447. https://doi.org/10.3390/electronics11213447