Abstract
After the great success of mobile wallets, the Internet of Things (IoT) leaves the door wide open for consumers to use their connected devices to access their bank accounts and perform routine banking activities from anywhere, anytime, and with any device. However, consumers need to feel safe when interacting with IoT-based payment systems, and their personal information should be protected as much as possible. Unlike what is usually found in the literature, in this paper, we introduce two lightweight and secure IoT-based payment protocols based on an identity-based signature scheme. We adopt a server-aided verification technique to construct the first scheme. This technique allows to outsource the heavy computation overhead on the sensor node to a cloud server while maintaining the user’s privacy. The second scheme is built upon a pairing-free ECC-based security protocol to avoid the heavy computational complexity of bilinear pairing operations. The security reduction results of both schemes are held in the Random Oracle Model (ROM) under the discrete logarithm and computational Diffie–Hellman assumptions. Finally, we experimentally compare the proposed schemes against each other and against the original scheme on the most commonly used IoT devices: a smartphone, a smartwatch, and the embedded device Raspberry Pi. Compared with existing schemes, our proposed schemes achieve significant efficiency in terms of communication, computational and storage overheads.
1. Introduction
Financial services and the payment industry are constantly evolving to meet customer requirements and to create a competitive advantage by providing better banking and financial services, improving operational efficiency and reducing costs. After plastic cards were successfully replaced by the mobile wallet (m-Wallet) [1], the Internet of Things (IoT) leaves the door wide open for consumers to use their connected devices to access their bank accounts and perform routine banking activities from anywhere, anytime, and with any device. For instance, a connected watch can be used by a customer to conduct payment at a store, while a driver can pay for parking and fuel via a connected car. Furthermore, more milk can be bought automatically through a connected refrigerator. All these payment scenarios are categorized in the so-called IoT-based payment systems. The trend toward IoT-based payment systems started in the last few years and accelerated in 2018 [2].
As one of the effective methods of IoT-based payment systems, an in-vehicle payment solution has recently been launched by two leading credit card companies: Visa and MasterCard. In this solution, the driver is alerted when he/she is near a smart parking meter or fuel pump. At payment time, the amount of the purchased service is displayed in the dashboard. Afterwards, the entire payment process is simply completed with just a touch of a button. In addition to in-vehicle payments, wearable payment systems [3,4] have innovatively integrated payment methods into wearable devices such as smartwatches, jewelry, wristbands, fitness bands, and other adaptable wearables.
An IoT-based payment system offers substantial efficiency benefits for both buyers and sellers, and both individuals and businesses. The consumers receive shorter transaction time with high comfort and fast real-time response. Furthermore, their financial habits will improve as the IoT-based payment system supports them to spend their money wisely. For example, to prevent oversupply, reordering only occurs when the product is running low. On the other hand, the traders can gain more customers by ensuring IoT-friendliness, automating their logistics processes using smart shelves, and optimizing checkout and customer service by accepting IoT wallets.
Along with the many benefits of the IoT-based payment system, the associated risks and threats [5,6] cannot be omitted. With so many payment data shared across many IoT devices and things, it is inevitable that hackers and malicious users will try to obtain access to these most valuable and vulnerable data.
1.1. Motivations
Most breaches have financial motivations. These breaches aim to obtain information such as financial account information, users’ credentials, or online banking details. Once the users’ credentials are stolen, hackers misuse them to gain illegal access to the victim’s account, defraud institutions, or commit other financial crimes.
To ensure that clients derive the maximum benefits and enjoy the appealing features of IoT-based payment systems, credit card companies and their partners should consider the following challenges. First, it is essential to guarantee that nobody is allowed to impersonate any customer or create a fake payment request to steal funds. Otherwise, forgery and fraud will abort the invention of IoT-based payments in its initial stages. Second, anonymity and privacy have a significant influence on a user’s attitude toward IoT-based payment systems. To increase the usage, acceptance, and adoption of IoT-based payment systems, the personal information of consumers should be protected as much as possible. Furthermore, consumers need to feel safe when interacting with IoT-based payment systems. Third, the IoT embedded devices are extremely limited in resources such as storage capacity, processing capabilities, communication bandwidth, and battery lifetime. Therefore, traditional encryption and authentication methods cannot be directly applied on sensor nodes in the IoT-based payment scenarios. This issue could be resolved by outsourcing the heavy computation overhead on sensor nodes to cloud servers while maintaining the user’s privacy. Another solution lies in adopting pairing-free ECC-based security protocols. In this paper, both solutions are adopted to introduce two lightweight and agile IoT-based payment protocols.
A digital signature [7] is a fundamental cryptographic primitive that offers nonrepudiation, unforgeability, and authenticity of electronic payment systems. However, the traditional public key-based digital signature suffers from the complex certificate management. Fortunately, due to its certificate-free property, the identity-based signature (IBS) [8,9] has been introduced to simplify the complexity and reduce the heavy cost of certificate management in traditional public key-based digital signatures. Therefore, it is interesting and challenging to design a lightweight and secure IoT-based payment method based on the idea of an identity-based signature.
1.2. Contribution
Motivated by the limited resources of IoT devices, we introduce two lightweight and secure IoT-based payment protocols based on an identity-based signature scheme, where each run a different lightweight computation and communication costs to suit the varying capabilities of IoT devices with limited resources. Then, we experimentally compare the proposed schemes against each other and against existing schemes on the most commonly used IoT devices: a smartphone, a smartwatch, and the embedded device Raspberry Pi. To summarize, the major contributions of this article are twofold:
- We introduce a lightweight and secure IoT-based payment scheme based on an identity-based signature scheme. To preserve the limited resources of IoT embedded devices and to meet the IoT-based payment system’s goal of conserving bandwidth consumption, energy, and processing power, we adopt a server-aided verification technique to reduce the heavy verification overhead. We further provide a security analysis of our proposed protocol to examine its correctness and soundness.
- We propose an alternative solution of using a server-aided verification technique in the IoT-based payment scheme by adopting a pairing-free ECC-based security protocol. We then experimentally compare our pairing-free IoT-based payment scheme against original and server-aided verification protocols. The security reduction results of the second proposed scheme are held in the Random Oracle Model (ROM) under the discrete logarithm assumption.
The rest of this paper is organized as follows. In Section 2, we discuss works related to our study. A high-level description of the proposed protocols and mathematical backgrounds are given in Section 3. In Section 4, the details of the proposed IoT-based payment protocols are presented. Through Section 5 and Section 6, a security analysis and performance evaluation are analyzed, followed by the conclusion and future work in Section 7.
2. Related Work
Throughout time, cashless-based payment systems have evolved several times from smart cards to smart phones and Internet banking. The current trends for cashless-based payment systems include the debit and credit cards, Samsung Pay, Google Pay, Apple Pay, Wechat Pay, AliPay, and many more mobile banking applications. This paper is primarily related to electronic payment systems, mobile wallets, micropayments, and contactless payment systems.
2.1. Electronic Payment Systems
The financial technology (FinTech) sector [10] is an industry that leverages new technologies to provide secure, instant, and efficient financial services. Its services (e.g., mobile banking apps) have been widely adopted by financial institutions. However, as revealed by the recent study [11], the FinTech financial services are not as secure as we expected. The study discovered thousands of vulnerabilities in 693 banking apps across over 80 countries, many of which could cause serious consequences, such as sensitive information leakage (e.g., PIN code, user name, or users’ credentials). Once the users’ credentials are stolen, hackers misuse them to gain illegal access to the victim’s account, defraud institutions, and other such financial and identity crimes.
In academia, many electronic payment systems have been proposed [12,13,14,15,16]. These systems aim to deliver payments from consumers to merchants in the most effective, efficient, and error-free way, particularly in combination with attractive security properties. Unfortunately, each system is limited in some aspect.
2.2. Contactless Payment
Google Wallet launched the first (contactless) payment system in 2011. Subsequently, it was followed by both Apple and Samsung Pay in 2014 and 2015, respectively. Additionally in 2015, Android Pay was announced as a new contactless system. Traditional contactless payments use cards. Now, the majority of them follow Europay, MasterCard, and Visa (EMV) contactless specifications [17]. In a mobile contactless payment system, the user is allowed to use the virtual debit and credit card information to securely pay for the purchases in store with those cards by waving the smart phone in front of the near-field communication point-of-sale (NFC-POS).
The contactless payment can be classified according to the amount of money transferred into two main types: micro and macro [18]. In a micro payment, the user makes a small contactless transaction with touch-and-go practice, while in the macro payment, the user conducts a big amount transaction with touch-and-confirm practice.
Despite the great convenience brought by mobile contactless payment systems, fraud remains a significant consumer concern. Recent research [19] showed that 38% of users have a strong feeling that contactless payments are insecure, and around half (51%) are very or extremely concerned about fraud. As a result, 30% of all users with contactless cards still do not use them.
2.3. Mobile Wallet
A mobile wallet (m-Wallet) is a virtual wallet that keeps payment card information on a mobile device. Mobile wallets are a convenient way for a consumer to conduct in-store, in-app, or online payments. In 2017, Qin et al. [1] introduced a secure and privacy-preserving mobile wallet by incorporating the certificateless signature and pseudo identity technique. Their approach significantly reduces the computation overhead in a resource-limited mobile device by offloading the heavy computation overhead on the user side to the untrusted cloud server. However, their payment protocol is insecure against a collusion attack between the customer, Alice, and the cloud server at the server-aided verification phase, as proved in [20]. Because the cloud server is untrusted, there is no way to verify whether the returned information is valid or not. By considering the benefits of certificate-free property, Yeh and Chen et al. [21,22] proposed IoT-based payment protocols based on certificateless cryptography primitives. However, despite the security proofs, Zirui et al. [23] proved that the Yeh [21] protocol is insecure against public key replacement attack, while Chen et al. [22] suffers from perfect forward secrecy and replay attacks, as shown in [24]. The work by Şengel et al. [25] proposed a new mobile payment cryptographic solution model, and this solution stores clients’ credentials in the memory of the device; however, keeping users’ credentials (private keys and PIN) in the memory of a handset is very risky as these credentials can be easily compromised. A fully offline transaction e-commerce system model based on mobile payment, which includes the offline POS terminal, mobile device, and payment center, was proposed by Li et al. [26], but it has limitations in day-to-day customer–merchant transactions, as it requires an additional POS terminal.
Despite the security requirements of IoT-based payment seeming similar to those identified in the literature, the limited resources of IoT devices such as storage capacity, processing capabilities, communication bandwidth, and battery lifetime make the problem very novel and challenging. Furthermore, to the best of our knowledge, none of the state-of-the-art systems are designed to operate over IoT devices with limited resources.
3. Preliminaries
In this section, we first describe the system model. Then, the basic definitions and assumptions that are needed in the remainder of the paper are presented.
3.1. System Model
The scope of this section is to provide an overview of our proposed model. Our system model consists of the following participants:
- Buyer: Alice. A consumer who wants to purchase products or services from the seller.
- Seller: Bob. A trader who offers goods or services for sale either online or in store.
- Payment Service Provider (): Responsible for ensuring payment security and privacy. The performs cryptographic initialization and user management.
- Cloud server provider (): This entity performs server-aided verification to reduce the heavy computational overhead on the sensor node.
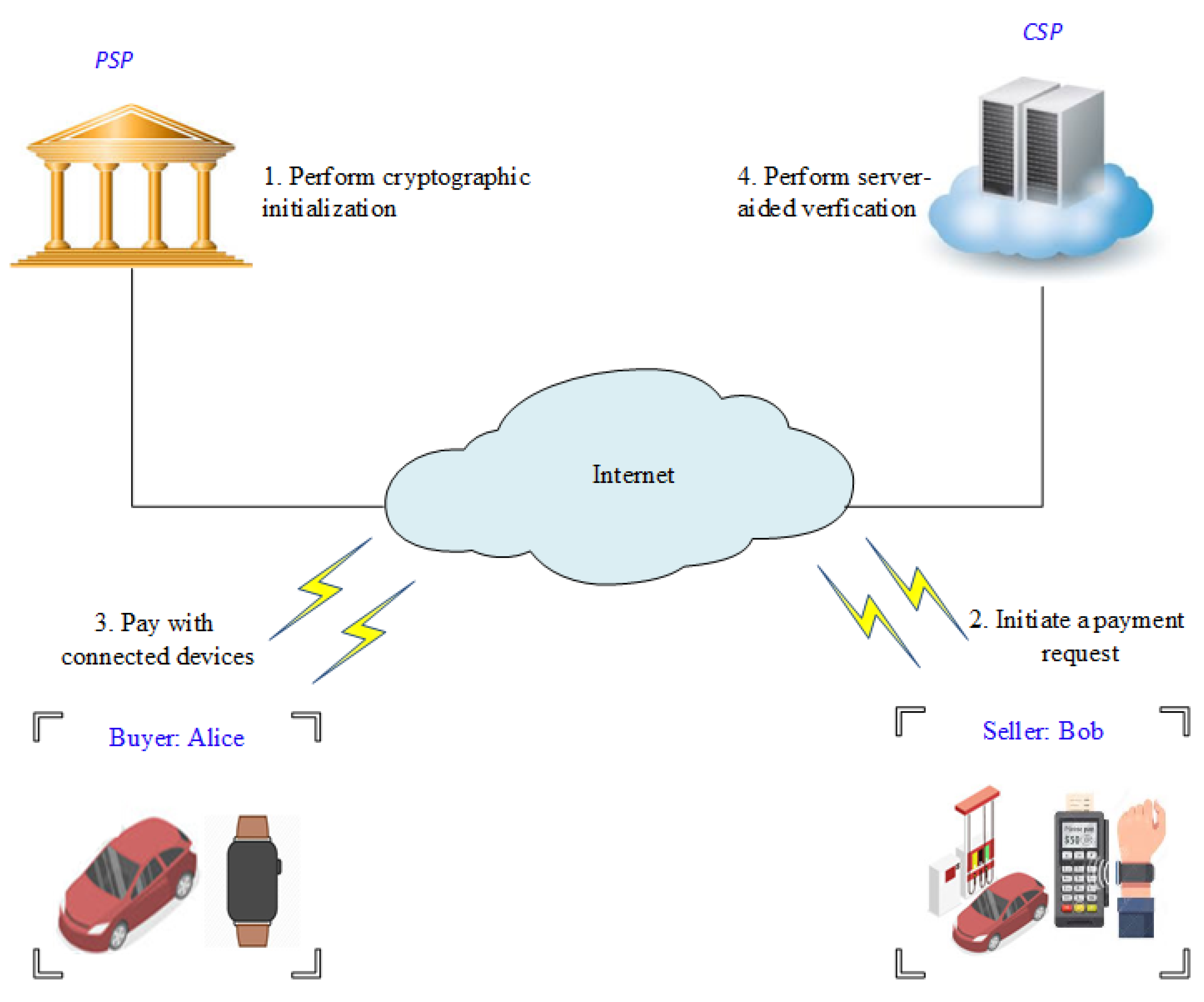
The interaction scenario between the above participants is expressed graphically in Figure 1. Alice and Bob communicate with each other and with the other entities using short-range wireless communication protocol standards, such as NFC (IEEE 802.11), Bluetooth (IEEE 802.15.1), WiFi, or Zig-Bee (IEEE802.15.4), whereas the and are located and operated in the fixed network. The players take part in the following three phases of an IoT-based payment system: the initialization phase, payment phase, and verification phase. In the initialization phase, the initializes and assigns the system parameters for each user. Then, it anonymously generates the user’s pseudo identity using a tamper-proof device. In IoT-based payment systems, the IoT smart device alerts the user to purchase the necessary goods or services. For example, in our model, a smart refrigerator reminds Alice to buy more milk, whereas her smart vehicle notifies her when she is near a smart parking meter or fuel pump. In the payment phase, Alice uses her connected device to conduct the payment. There are three payment options that correspond to IoT smart devices: in-store, in-app or online. For an in-store payment, Alice tries to conduct a payment transaction using her wearable or handheld device and Bob’s near-field communication point-of-sale (NFC-POS). To perform this, Bob initiates a payment request on his NFC-POS. Afterward, Alice waves her wearable device near the NFC-POS, then she confirms the payment with her digital signature. For an in-app payment, Alice uses application program interfaces (APIs) to handle payments and transactions with just a touch of a button. For online payments, Alice performs the payment transaction remotely over the Internet, using a wireless connection. Once Alice has completed the payment process, Bob uses Alice’s public key to check the validity of Alice’s signature and to ensure the payment integrity. Finally, after Alice’s payment has passed the verification, Bob uses his private key to sign a receipt for the amount that he received.
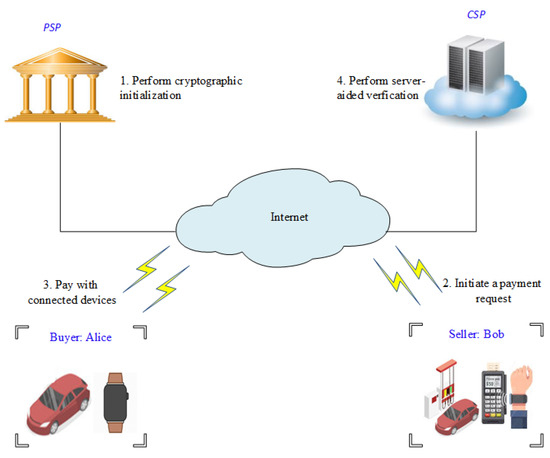
Figure 1.
System architecture.
3.2. Elliptic Curves Cryptography (ECC)
Miller and Koblitz [27,28] individually suggested the use of elliptic curves in cryptography in the middle of the 1980s. Several years later, elliptic curves cryptography (ECC) has attracted much attention from scientists, engineers, and researchers worldwide. Today, ECC plays an important role in public key cryptography. Compared with RSA, ECC-based cryptosystems provide a high security level with a small key size and more efficient implementations [29]. Let be a prime number and be a nonsingular elliptic curve over , which can be defined as the Weierstrass form.
where with the discriminant . A point is an elliptic curve point if it satisfies Equation (1), and the point is called the negative of P, i.e., . The points together with a point (called point at infinity) form an additive cyclic group , that is, and of prime order q. Scalar multiplication over can be computed as follows:
3.3. Bilinear Pairing
Let and be two cyclic groups of the same large prime q. Let be generators of . Assume that the discrete logarithm in and are hard. Let be an admissible pairing that satisfies the following properties:
- Bilinear: Given , we have.For any , we have.
- Non-degenerate: There exists such that . This means that if and are two generators of , then is a generator of .
- Computability: There is an efficient algorithm to compute for all .
3.4. Computational Hardness Assumption
Our scheme is based on the hardness assumptions as follows:
- Discrete logarithm (DL) problem: Given a generator of a cyclic group with order q, then compute for a random .
- Computational Diffie–Hellman (CDH) problem: Given (g, , ) then compute , where is the generator and is unknown.
3.5. Design Goals
To maintain the IoT-based payment security, our protocols should be able to satisfy the following requirements:
- Unforgeability: Only authorized users are allowed to make transactions. In other words, nobody can impersonate Alice or Bob to create a fake payment request or a fake or illegal receipt. Let be a CDH attacker which attacks the IoT-based payment protocol and be a forger who attacks the identity-based signature scheme (IBS). The forger performs the IoT-based payment protocol instead of the without knowing the ’s secret master key. The attacker plays the following game with .
- (a)
- Setup: The runs the setup algorithm to generate the system’s parameters and sends them to the forger .
- (b)
- Queries: The forger performs a series of queries to the following oracles:
- Extract query: Key extraction oracle: returns private keys for arbitrary identities.
- Sign query: Signature oracle: produces signatures on arbitrary messages using the private key corresponding to arbitrary identities.
- (c)
- Forgery: produces a triple (, , ) made of an identity , whose private key was never extracted, and a message–signature pair (, ) such that (, ) was not submitted to the signature oracle. She wins if the verification algorithm accepts the triple (, , ).
- Anonymity: The real identity of Alice is only known to the and Alice herself. Alice should be able to deal with Bob without disclosing her real identity. The same holds true when Bob signs a receipt.
- Traceability and Revocation: The real identity of the malicious user must be traceable and revoked, but only by the . Malicious users must be prevented from accessing the tamper-proof device. Malicious users must be revoked and kicked out of the payment protocol, but only by the .
- Unlinkability: In our protocols, any user can conduct multiple payment transactions without others being able to link these transactions to a particular user. The proposed IoT-based payment protocols cannot be hacked by an attacker with any linkable information.
- Nonrepudiation: Alice should not be able to deny the confirmed transaction. Bob also cannot deny that he received the amount paid by Alice.
- Resistance to Replay Attack: An adversary cannot reuse the previously exchanged valid information to obtain the corresponding service.
- Resistance to Impersonation Attack: An adversary cannot impersonate Alice or Bob to create a fake payment request or a fake or illegal receipt.
- Mutual Authentication: Alice and Bob should authenticate each other before actual communication occurs to avoid the potential malicious attacks.
In addition to the above security requirements, low energy and bandwidth consumption with other low-cost design capabilities are extremely desired properties in IoT-based payment systems.
4. Proposed Schemes
In this section, we concretely construct two lightweight IoT-based payment schemes. Both schemes are built upon an identity-based signature scheme. The first protocol is constructed based on Tzeng et al.’s scheme [30], and the second protocol relies on the Hu et al. scheme [31]. We employ server-aided verification protocols [32] to introduce the first scheme, while the second scheme is constructed based on a pairing-free approach. For convenience, the notations of the proposed scheme are defined in Table 1.

Table 1.
Notations.
4.1. Scheme I: IoT-Based Payment Scheme with Server-Aided Verification
An IoT-based payment scheme with a server-aided verification consists of the following phases:
- Initialization PhaseIn this phase, the initializes and assigns the system parameters for each user. These include two groups, and , of prime order q and a bilinear pairing . Let and denote two generators in . It next randomly selects its secret master key and computes its public master key . It also selects two hash functions, and . For the first registration of Alice and Bob, assigns real identities and passwords and for Alice and Bob, respectively. then stores into the tamper-proof device. Finally, announces the public parameters: , where .
- Payment PhaseAccording to IoT device capabilities, there are three payment options: in-store, in-app, or online. For in-store payments, Alice tries to conduct a payment transaction using her wearable or handheld device and Bob’s near-field communication point-of-sale (NFC-POS), whereas APIs are used to handle payments and transactions with just a touch of a button in the in-app payment scenario. For online payments, Alice conducts a payment transaction remotely over the Internet, using a 4G/5G or WiFi wireless connection. The following steps illustrate how this can be performed:
- Step 1: Bob initiates a payment request on his NFC-POS, app, or website by encoding the payment amount information into a message M.
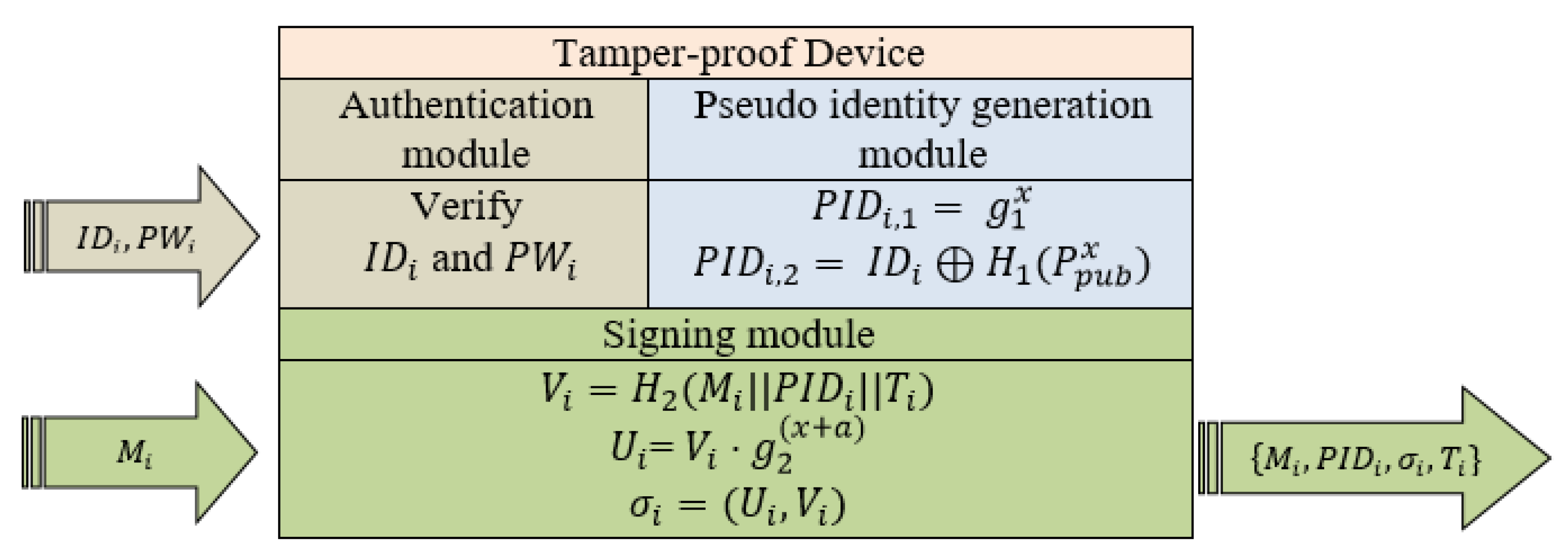
- Step 2: Upon receiving the payment request, Alice logs in into the tamper-proof device using her real identity and password . If an incorrect or is entered, the tamper-proof device terminates the current process and refuses to perform further modules. On the other hand, if Alice passes the authentication module, then her real identity is transferred to the next module, the pseudo identity generation module. Figure 2 shows the procedures and modules of the tamper-proof device.
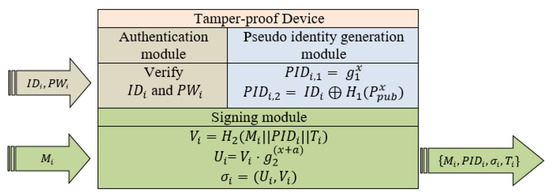 Figure 2. The tamper-proof device for Scheme I.
Figure 2. The tamper-proof device for Scheme I. - Step 3: The pseudo identity generation module composes Alice’s pseudo identity into and . It then picks and computes the pseudo identity as follows:Finally, the pseudo identity generation module sets Alice’s pseudo identity as .
- Step 4: Alice inputs the message M into the tamper-proof device. The tamper-proof device uses Alice’s pseudo identity , x and a current timestamp T to generate the signature of M as follows:
- -
- Compute .
- -
- Compute .
Afterward, Alice obtains the final and sends it to Bob.
- Verification PhaseUpon receiving the final message from Alice, Bob checks the validity of the signature to ensure the integrity of the payment information. To preserve the limited resources and help to meet the IoT-based payment system’s goal of conserving bandwidth consumption, energy, and processing power, we adopt a server-aided verification technique to minimize the number of pairing operations in the original verification process. The details of the original and server-aided verifications are described as follows.
- (a)
- Original verification: Given the final message sent by Alice, Bob uses the public parameters published by the to check the validity of the signature as follows.
- Step 1: To resist the replaying attack, Bob checks the freshness of the final message. Assume that the receiving time is . Bob checks whether . If it does, then Bob continues; otherwise, he rejects it.
- Step 2: Bob verifies the signature by checking whether holds or not. If it does, output is valid, otherwise output is ⊥.
- (b)
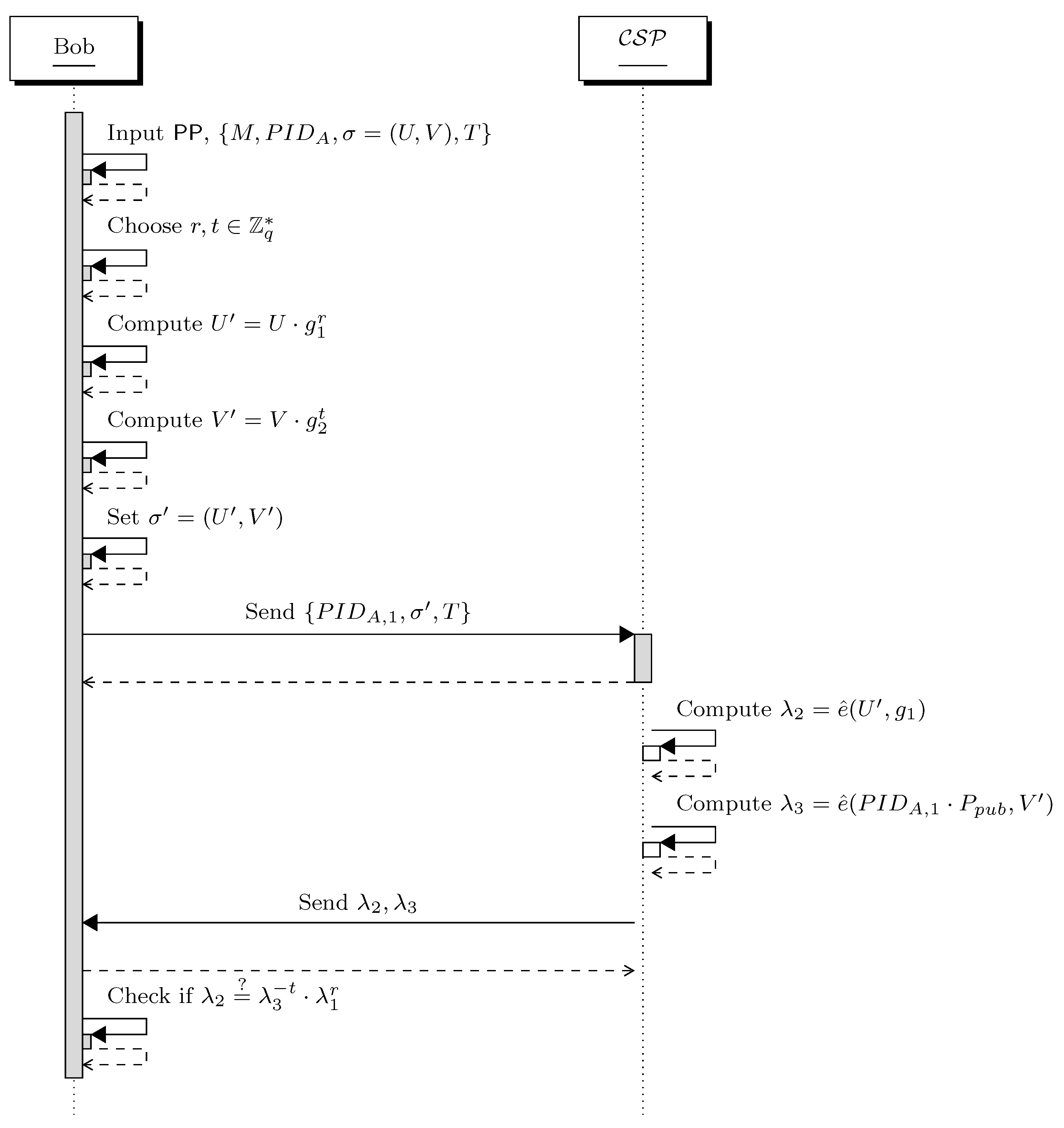
- Server-aided verification: As indicated in Step 2 during the original verification, two pairing operations are required to verify the signature. However, a bilinear pairing operation is computationally more expensive than other operations over elliptic curve groups. To minimize the number of pairing operations, Bob delegates an untrusted cloud server provider to perform server-aided verification. The following steps and Figure 3 illustrate how Bob and interact with each other.
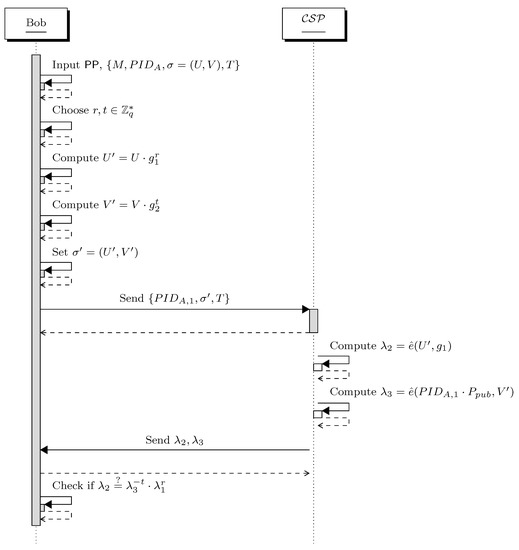 Figure 3. Interaction between Bob and in server-aided verification.
Figure 3. Interaction between Bob and in server-aided verification.- Step 1: To check the freshness of the final message, Step 1 of the original verification is repeated here.
- Step 2: Given public parameters and the final message , Bob randomly chooses and computes and . He then sets . Afterward, he sends the message and blind signature to the .
- Step 3: Upon the receiving from Bob, it computes and . It then sends to Bob.
- Step 4: Bob checks if . If it does, output is valid, otherwise output is ⊥.
4.2. Scheme II: Pairing-Free IoT-Based Payment Scheme
In this section, our second pairing-free IoT-based payment scheme is introduced. This scheme is constructed based on Hu et al.’s scheme. Our second scheme consists of three phases, as in Scheme I: the initialization phase, the payment phase, and the verification phase.
- Initialization phaseInitially, the inputs the security parameters k and determines the tuple{} as defined in Section 3.2. Then, it picks the secret master key and computes its public master key . Next, chooses two hash functions, and . Finally, the publishes the system parameters: .
- Payment PhaseSteps 1 and 2 are the same as steps 1 and 2 of Scheme I during the same phase. The main differences are in step 3 and step 4.
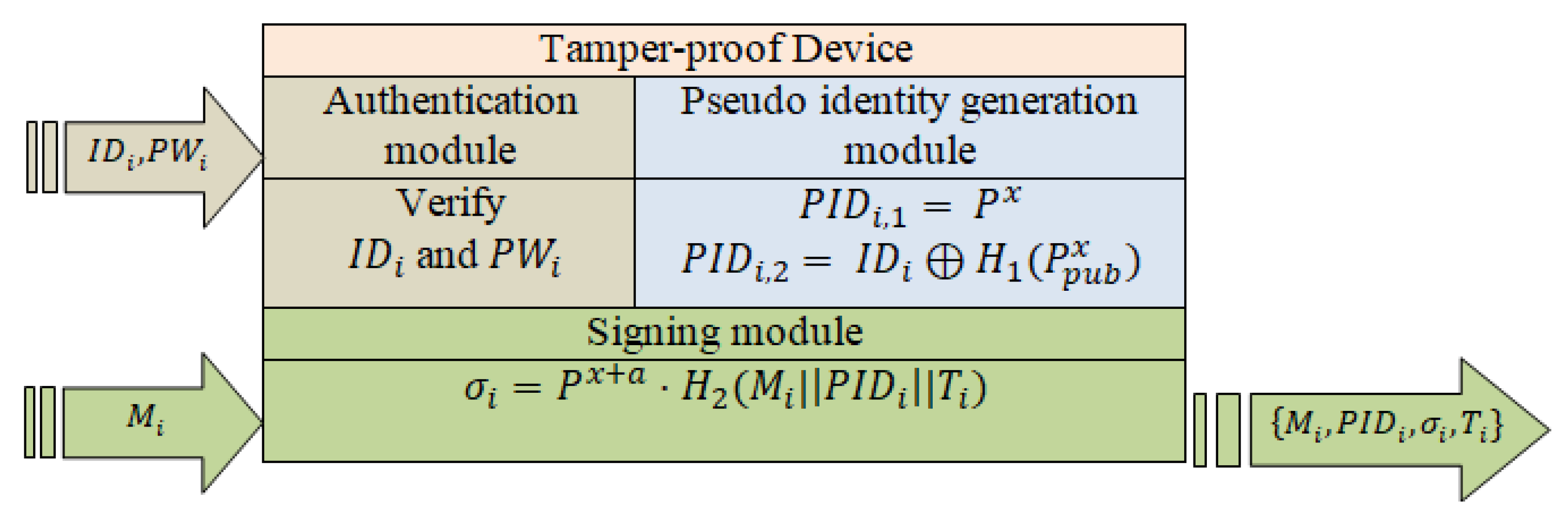
- Step 3: The pseudo identity generation module composes Alice’s pseudo identity into and . It then picks and computes pseudo identity as follows:Finally, the pseudo identity generation module sets Alice’s pseudo identity as .
- Step 4: Alice inputs the message M into the tamper-proof device that is shown in Figure 4, The tamper-proof device uses Alice’s pseudo identity , x and a current timestamp T to generate the signature of M as
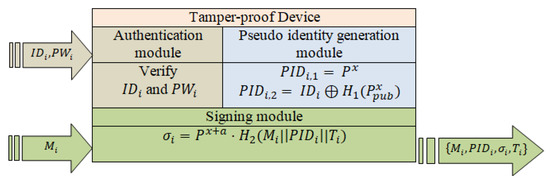 Figure 4. The tamper-proof device for Scheme II.Next, Alice obtains the final message and sends it to Bob.
Figure 4. The tamper-proof device for Scheme II.Next, Alice obtains the final message and sends it to Bob.
- Verification PhaseGiven the final message sent by Alice, Bob uses the public parameters published by the to check the validity of the signature as follows.
- Step 1: For freshness, Bob repeats step 1 of the original verification of Scheme I.
- Step 2: Bob verifies the signature by checking whetherholds or not. If it does, output is valid, otherwise output is ⊥.
5. Security Analysis
Considering the security requirements of an IoT-based payment system as a part of the system model of this article, in this section we discuss how these requirements can be achieved through both proposed protocols. The unforgeability property of each scheme is proved separately, while the other security properties are proved for both schemes together.
5.1. Correctness
For Scheme I, the correctness of signatures is described as follows.
For Scheme II, the correctness of signatures is described as follows.
5.2. Security Proof Sketch
Theorem 1 (Unforgeability).
Only authorized users are allowed to make transactions. In other words, nobody can impersonate Alice or Bob to create a fake payment request or a fake or illegal receipt. Let be a CDH attacker which attacks the IoT-based payment protocol and be a forger who attacks the identity-based signature scheme (IBS). The forger performs the IoT-based payment protocol instead of the without knowing the ’s secret master key.
Proof.
Our Scheme I is existentially unforgeable against adaptive chosen message attacks in the Random Oracle Model if any adversary with runtime t wins the game in detention with a probability at most ϵ after issuing at most q signing queries. Let be a CDH attacker who receives a CDH challenge tuple (, , ) for and . interacts with as simulated in the game that is defined in detention 1. We show how may use to solve the CDH problem.
Initial. Firstly, calculates given , , for some unknown . sets the public parameters including and . Finally, gives to the .
Queries. In this phase, answers ’s oracle queries as follows:
- queries. randomly chooses , where times queries. Whenever requests the hash value of for , performs the following:
- saves a list which is initially empty.
- tests whether , if the value of already exists on the list in a tuple , then outputs as a response to ’s query.
- Otherwise, if , picks and sets and returns to .
- Sign queries. Once receives a signing query for message from , performs the following:
- In spite of the fact that does not know the private key, it can still produce the signature as follows. looks for the tuple , if does not exist, picks and . It then produces the signature as and . The validity of the produced signature can be checked as follows..
- If the tuple already exists on the , picks another and , and produces the signature again. It then returnsto the and saves the tuple in the . For the adversary , all signatures produced by are indistinguishable from those signatures computed by the legitimate user.
Forgery. Eventually, receives two valid forged signatures and with the same random “α-value" but different hash values in a polynomial time, where
Finally, has successfully obtained the solution of the CDH problem. However, this breaks the assumption that the CDH is hard. It implies that an attacker cannot impersonate any customer or forge the signature on a payment receipt. Therefore, the unforgeability, nonrepudiation, and authenticity of payment receipt (message M) are achieved in our first proposed scheme. □
Proof.
Our Scheme II is existentially unforgeable against adaptive chosen message attacks in the Random Oracle Model if and only if the DL is hard.
We describe how a challenger can use an adversary as a subroutine to solve a random given instance to compute for a random and .
Initial. picks a random integer and sets . gives to the .
Queries. In this phase, makes a sequence of oracle queries. These queries are answered by as in the unforgeability game in detention 1.
- queries. randomly picks , where times queries. Whenever requests the hash value of for , performs the following:
- keeps a list which is initially empty.
- tests whether , if the value of already exists on the list in a tuple , then outputs as a response to the ’s query.
- Otherwise, if , picks and sets and returns to .
- queries. When requests the hash value of for , deals with this request as follows:
- If the value of already exists on the list in a tuple, then outputs as a response to the ’s query.
- Otherwise, picks and sets and returns to .
- Sign queries. Upon receiving a query on message , it randomly picks and computes the signature as follows.The produced signature looks valid from ’s view because
Forgery. According to the Forking Lemma [33], can obtain two forged signatures, and . The forged signatures satisfy the following:
□
Theorem 2 (Anonymity of Scheme I and Scheme II).
In our proposed IoT-based payment schemes, Scheme I and II, the real identity of Alice is only known to the and Alice herself. Alice should be able to deal with Bob without disclosing her real identity. The same holds true when Bob signs a receipt.
Proof.
As shown in the pseudo identity generation module in Figure 2, Figure 4 and Step 3 during the payment phase, the real identity of Alice is converted into two anonymous and random pseudo identities for unknown . Consequently, the only way to determine the the real identity from the anonymous and pseudo identity pair is to know the secret master key a from or the private key x from , as depicted in the traceability process below. Moreover, the anonymous identity pair is an ElGamal-type ciphertext, which is secure against chosen-plaintext attacks (CPAs). As a result, our proposed schemes provide the unconditional anonymity. □
Theorem 3 (Traceability).
When a dispute occurs during the payment process, the PSP should be able to identify the disputing parties; it then tries to resolve the dispute, in case none of the disputing parties is a malicious party. Otherwise, the malicious parties are revoked and kicked out of the payment protocol.
Proof.
Given the anonymous identity pair , only can trace the real identity of the user as follows.
It is clear that the can easily trace the malicious users and find out their identities in order to revoke them from payment protocol. □
Theorem 4 (Revocation).
Malicious users must be prevented from accessing the tamper-proof device. Malicious users must be revoked and kicked out of payment protocol, but only by .
Proof.
If misbehavior is detected, the identity of the violating user can be easily traced by , as shown in the proof of Theorem 3. The then deletes the malicious user information from the tamper-proof device. Thus, the malicious users can be easily revoked and kicked out of payment protocol in our proposed schemes. □
Theorem 5 (Unlinkability).
For both schemes, any client can conduct multiple payment transactions without others being able to link these transactions to a particular client.
Proof.
Each signature on message partially consists of pseudo identity and timestamp , which are changed every time. Furthermore, as shown in the proof of Theorem 2 and Theorem 3, it impossible to determine or even guess the real identity of a user from his/her anonymous identity without prior knowledge of the secret master key a and private key x. Therefore, there is no way to link two or more messages to a particular user, so the security property of unlinkability is achieved in both our schemes. □
Theorem 6 (Resistance to Impersonation Attack).
An adversary cannot impersonate Alice or Bob to create a fake payment request or a fake or illegal receipt.
Proof.
Assume that an adversary attempts to send a valid payment request to Alice while impersonating as a legitimate merchant (Bob) to steal funds. To this end, it should generate the current timestamp and a signature for the message (payment request). However, to sign the message, the adversary needs to have the knowledge of the master secret key , private key x, and a current timestamp T. Any adversary cannot generate a valid payment request without these secrets. Similarly, no adversary can successfully impersonate the legitimate user (Alice). Thus, our protocols can resist the impersonation attack. □
Theorem 7 (Resistance to Replay Attack).
The previously transmitted payment request and receipt cannot be reused by adversaries to obtain the corresponding responses from the legitimate entity.
Proof.
An adversary intends to prove its legitimate identity through delivering the previous valid signature of a legitimate entity to the receiver. However, in our protocol, this attack cannot be launched with success since the invalid timestamp condition results in the failure of authentication. Hence, our protocols can prevent the replay attack. □
Theorem 8 (Mutual Authentication).
In our protocols, mutual authentication allows the merchant (Bob) to return the confirmation message signed with its private key to the buyer (Alice) if the received signature is valid, and vice versa.
Proof.
For Scheme I, given the final message sent by Alice, Bob uses the public parameters published by the to check the validity of the signature, as follows.
- Step 1: To resist the replaying attack, Bob checks the freshness of the final message. Assume that the receiving time is . Bob checks whether . If it does, then Bob continues; otherwise, he rejects it.
- Step 2: Bob verifies the signature by checking whether holds or not. If it does, output is valid, otherwise output is ⊥.
This verification can be performed as server-aided verification by the cloud server provider , as shown in Figure 3.
For Scheme II, given the final message sent by Alice, Bob uses the public parameters published by the to check the validity of the signature as follows.
- Step 1: For freshness, Bob checks the freshness of the final message.
- Step 2: Bob verifies the signature by checking whetherholds or not. If it does, output is valid, otherwise output is ⊥.
□
6. Performance Evaluation
6.1. Computation Overhead
To experimentally evaluate the performance of the proposed IoT-based payment protocols, we adopt the following most commonly used IoT devices: smartphone (HUAWEI P9 Lite 2017), smartwatch (HUAWEI Watch 2), and embedded device Raspberry Pi 3 Model B. The specifications of these devices are shown in Table 2. The performance evaluation is conducted based on the results in [34], in which the relative times of various cryptographic operations are averaged by repeated experiments in Java using the JPBC library [35].

Table 2.
IoT devices specifications.
For convenience, we adopt the following notations: for bilinear pairing and for exponentiation on (implemented as scalar multiplication of an elliptic-curve point). Multiplication and hash function operations are denoted by and , respectively. The consuming times of these operations are shown in Table 3.

Table 3.
Cryptographic Operations time in IoT devices.
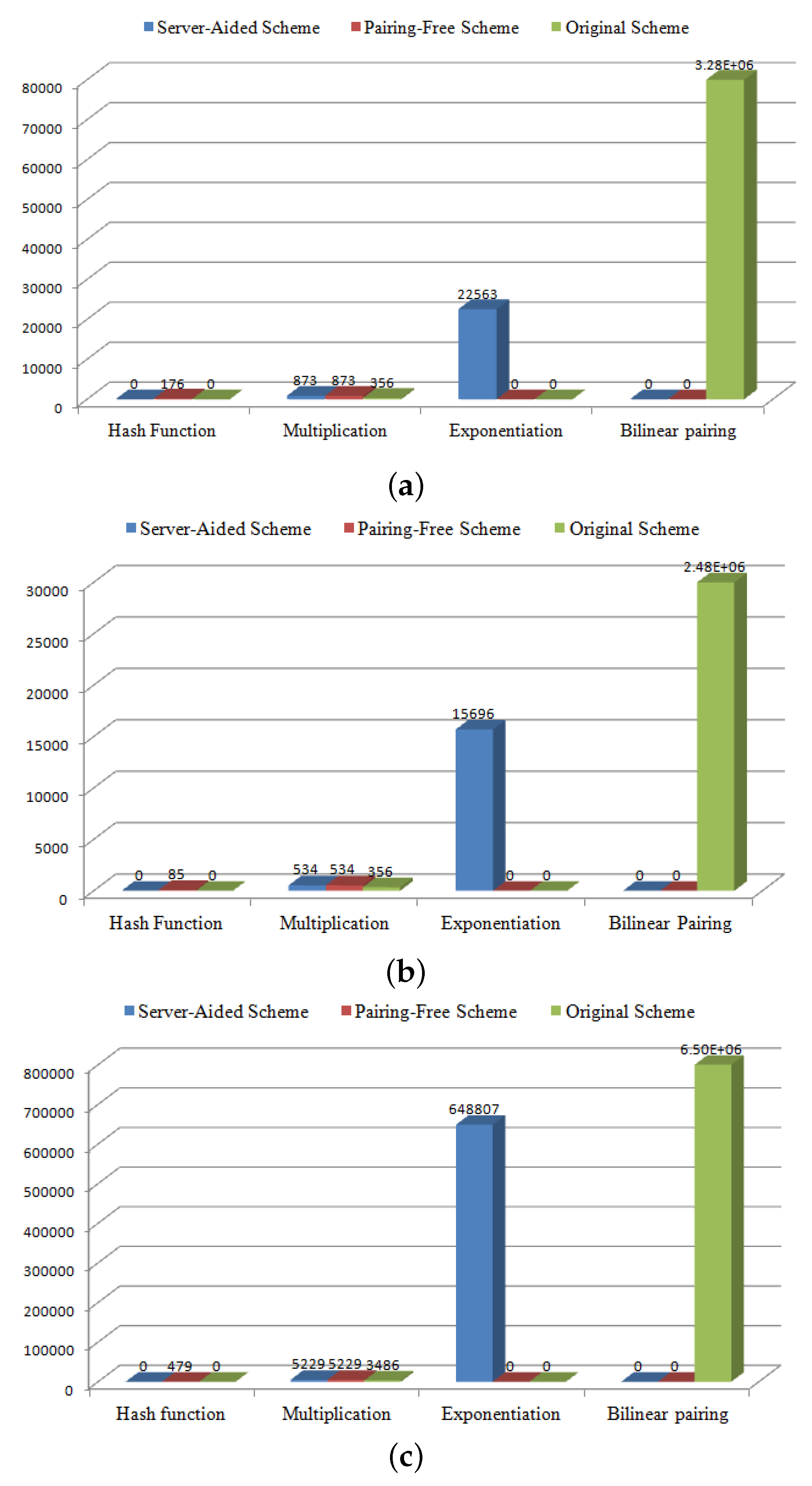
In the following, the efficiency of the proposed server-aided and pairing-free schemes are compared against each other and against the original scheme. From the efficiency comparison outlined in Table 4, Table 5 and Table 6, we figure out that in each device, the computational complexity for all the schemes are similar at the signing stage. However, the difference appears clearly during the verification process. As indicated in Table 4, the total running times in the smartwatch platform of our schemes during the verification process are 23.436 s and 1.049 s for server-aided and pairing-free schemes, respectively, whereas the original scheme needs 3285.052 s at the same stage for the same device. From the results of the smartphone platform that are detailed in Table 5, our server-aided and pairing-free schemes only require 16.23 and 0.619 s for the verification process, against 2480.826 s for the original scheme at the same stage.

Table 4.
Efficiency comparison in smartwatch platform.

Table 5.
Efficiency comparison in smartphone platform.

Table 6.
Efficiency comparison in embedded device Raspberry Pi 1 Model B.
The results in Table 6 also indicate that, compared with the original scheme, the total running times of our schemes are reduced by approximately 10 times and up to 1140 times for server-aided and pairing-free schemes, respectively, in embedded device Raspberry Pi 1 Model B for the verification process. Figure 5a–c show the number of operations of our schemes versus the original scheme. It is worth mentioning that the original scheme is overshadowed by a heavy computational complexity of bilinear pairing operations.
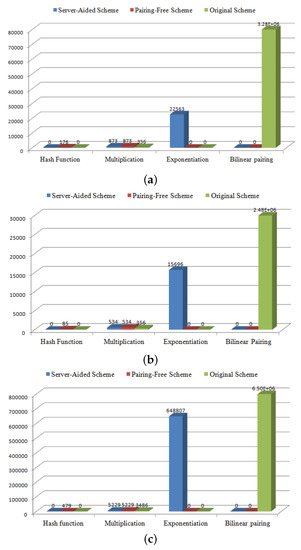
Figure 5.
(a) Efficiency comparison in smartwatch platform; (b) efficiency comparison in smartphone platform; (c) efficiency comparison in embedded device Raspberry Pi 1 Model B.
6.2. Communication Overhead
The communication cost of our protocols and related payment protocols are analyzed in this subsection. We adopt the security level of 1024 bits RSA algorithm. In our experiment, we choose an Ate pairing since the size in bilinear pairing operation is 512 bit (64 bytes), and the modulus size of q in ECC operation is 512 bits (note that although the size of the elements in is 160 × 16 = 2560 bits, the final size of one time scale multiplication on ECC should be 512 bits because of the modulus q). In addition, let the sizes of an identity, a timestamp, and a general hash function be 32 bits, 32 bits, and 160 bits. Then, an 8-character, 64-bit password is adopted in our protocols to defend against offline dictionary attacks. These parameters are summarized in Table 7. The analysis process is shown below.

Table 7.
Length of the group in bilinear pairing and ECC.
6.2.1. Scheme I (Server-Aided Verification Scheme)
- Registration phase:In this phase, assigns real identities and passwords and for Alice and Bob, respectively. The overhead of these messages are bits = 272 bytes.
- Payment phase:In the payment phase, Alice send the tuple to Bob. From this tuple . Therefore, the communication cost for this phase is bits = 395 bytes
- Server-aided verificationIn this phase, Bob sends the message and blind signature to the , and he receives from . In these transmitted messages,and are . Hence, the communication overheads in this phase are bits = 512 bytes.
6.2.2. Scheme II (Pairing-Free ECC-Based Scheme)
- Registration phase:In this phase, assigns real identities and passwords and for Alice and Bob, respectively. The overheads of these messages are bits = 88 bytes.
- Payment phase:In the payment phase, Alice send the tuple to Bob. From this tuple . Therefore, the communication cost for this phase is bits = 84 bytes.
To sum up, the overall communication overheads of our schemes are summarized in the Table 8. As shown in this table, our proposed schemes have certain advantages in communication overhead. Specifically, our Scheme II incurs lower communication overhead in comparison with the other two schemes [36,37]. Our Scheme I is slightly more than Zeng et al.’s [36] scheme, but significantly less than Thammarat’s [37]. Furthermore, in our Scheme I, communication–computation trade-off is provided. As the processing capabilities of IoT devices is extremely limited, we adopt a server-aided verification technique to outsource the heavy computation overhead on the sensor node to a cloud server. This technique decreased the computation overhead by 89% in the Raspberry Pi 3 Model B, and 99% in the smartphone and smartwatch, but on the other hand, the communication overhead increased by 56%.

Table 8.
Comparison of communication costs (in bytes).
6.3. Storage Overhead
In general, sensor node, IoT devices, and smartcard have far less storage capacity than the payment service provider (). Therefore, reduction of the requirements of the storage capacity of sensor node and IoT devices is essential for IoT-based applications. We kept this issue in mind when designing our IoT-based payment protocols. To this end, in the initialization phase, stores . These parameters are equivalent to bit, while sensor node stores nothing in its memory during all stages of the protocol, but the user needs to memorize the password.
7. Conclusions
This paper raises the challenging question of how to increase convenience and enable clients to derive maximum benefits and to enjoy the appealing features of IoT-based payment systems. To answer this question, we proposed two lightweight and secure IoT-based payment protocols based on the identity-based signature scheme. The security analysis demonstrates that the proposed protocols are provably secure in the Random Oracle Model under the discrete logarithm and computational Diffie–Hellman assumptions. In addition, the performance evaluation results show that the proposed protocols have lower computational and communication costs, which will enable us to satisfy the IoT-based payment system’s goal of conserving bandwidth consumption, energy, and processing power. The long-term results of this effort are to continue to improve the communication and computation costs at the sensor node.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qin, Z.; Sun, J.; Wahaballa, A.; Zheng, W.; Xiong, H.; Qin, Z. A Secure and Privacy-preserving Mobile Wallet with Outsourced Verification in Cloud Computing. Comput. Stand. Interfaces 2017, 54, 55–60. [Google Scholar] [CrossRef]
- Turban, E.; Outland, J.; King, D.; Lee, J.K.; Liang, T.P.; Turban, D.C. Mobile commerce and the internet of things. In Electronic Commerce; Springer: Cham, Switzerland, 2018; pp. 205–248. [Google Scholar]
- Cha, B.R.; Lee, S.H.; Park, S.B.; Ji, Y.; Lee, G.K. Design of micro-payment to strengthen security by 2 factor authentication with mobile & wearable devices. Adv. Sci. Technol. Lett. 2015, 109, 28–32. [Google Scholar]
- Zhou, T.T.; Zhou, D.T.; Zhou, A.H. One-Touch Payment Using Haptic Control via a Messaging and Calling Multimedia System on Mobile Device and Wearable Device, Currency Token Interface, Point of Sale Device, and Electronic Payment Card. U.S. Patent 8,985,442, 24 March 2015. [Google Scholar]
- Bhardwaj, A.; Kaushik, K.; Kumar, M. Taxonomy of Security Attacks on Internet of Things. In Security and Privacy in Cyberspace; Kaiwartya, O., Kaushik, K., Gupta, S.K., Mishra, A., Kumar, M., Eds.; Springer Nature: Singapore, 2022; pp. 1–24. [Google Scholar] [CrossRef]
- Wheelus, C.; Zhu, X. IoT network security: Threats, risks, and a data-driven defense framework. IoT 2020, 1, 259–285. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-key Cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Paterson, K. ID-based signatures from pairings on elliptic curves. Electron. Lett. 2002, 38, 1025–1026. [Google Scholar] [CrossRef]
- Hess, F. Efficient Identity Based Signature Schemes Based on Pairings. In Proceedings of the Revised Papers from the 9th Annual International Workshop on Selected Areas in Cryptography, SAC ’02, St. Johns, NL, Canada, 15–16 August 2002; Springer: London, UK, 2003; pp. 310–324. [Google Scholar]
- Chen, C.C.; Liao, C.C. Research on the development of Fintech combined with AIoT. In Proceedings of the 2021 IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Penghu, Taiwan, 15–17 September 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Chen, S.; Su, T.; Fan, L.; Meng, G.; Xue, M.; Liu, Y.; Xu, L. Are mobile banking apps secure? What can be improved? In Proceedings of the 2018 26th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Lake Buena Vista, FL, USA, 4–9 November 2018; pp. 797–802. [Google Scholar]
- Hassan, M.A.; Shukur, Z.; Hasan, M.K. An efficient secure electronic payment system for e-commerce. Computers 2020, 9, 66. [Google Scholar] [CrossRef]
- Wang, F.; Yang, N.; Shakeel, P.M.; Saravanan, V. Machine learning for mobile network payment security evaluation system. Trans. Emerg. Telecommun. Technol. 2021, e4226. [Google Scholar] [CrossRef]
- Deng, X.; Gao, T. Electronic payment schemes based on blockchain in VANETs. IEEE Access 2020, 8, 38296–38303. [Google Scholar] [CrossRef]
- Tut, D. FinTech and the Covid-19 pandemic: Evidence from electronic payment systems. SSRN 2020. [Google Scholar] [CrossRef]
- Shanmugapriyan, J.; Parthasarathy, R.; Sathish, S.; Prasanth, S. Secure Electronic Transaction Using AADHAAR Based QR Code and Biometric Authentication. In Proceedings of the 2022 International Conference on Communication, Computing and Internet of Things (IC3IoT), Chennai, India, 10–11 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar]
- Basin, D.; Sasse, R.; Toro-Pozo, J. The EMV Standard: Break, Fix, Verify. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 1766–1781. [Google Scholar] [CrossRef]
- Gupta, B.B.; Narayan, S. A key-based mutual authentication framework for mobile contactless payment system using authentication server. J. Organ. End User Comput. (JOEUC) 2021, 33, 1–16. [Google Scholar] [CrossRef]
- Nilsson, H. Trust issues? The need to secure contactless biometric payment cards. Biom. Technol. Today 2021, 2021, 5–8. [Google Scholar] [CrossRef]
- Liao, Y.; He, Y.; Li, F.; Zhou, S. Analysis of a mobile payment protocol with outsourced verification in cloud server and the improvement. Comput. Stand. Interfaces 2018, 56, 101–106. [Google Scholar] [CrossRef]
- Yeh, K.H. A secure transaction scheme with certificateless cryptographic primitives for IoT-based mobile payments. IEEE Syst. J. 2017, 12, 2027–2038. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Peng, L.; Zhang, H. Light-weight and privacy-preserving authentication protocol for mobile payments in the context of IoT. IEEE Access 2019, 7, 15210–15221. [Google Scholar] [CrossRef]
- Qiao, Z.; Yang, Q.; Zhou, Y.; Zhang, M. Improved Secure Transaction Scheme With Certificateless Cryptographic Primitives for IoT-Based Mobile Payments. IEEE Syst. J. 2022, 16, 1842–1850. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, Y.; Jin, C.; Kumari, S. Efficient and Privacy-Preserving Authentication Protocol for Heterogeneous Systems in IIoT. IEEE Internet Things J. 2020, 7, 11713–11724. [Google Scholar] [CrossRef]
- Şengel, Ö.; Aydin, M.A.; Sertbaş, A. A survey on white box cryptography model for mobile payment systems. In International Telecommunications Conference; Springer: Berlin/Heidelberg, Germany, 2019; pp. 215–225. [Google Scholar]
- Li, S.; Hu, X.; Fengling; Zhang, Y.; Dong, W.; Ye, J.; Sun, H. Research on Offline Transaction Model in Mobile Payment System. In International Conference on Frontier Computing; Hung, J.C., Yen, N.Y., Hui, L., Eds.; Springer: Singapore, 2019; pp. 1815–1820. [Google Scholar]
- Miller, V.S. Use of elliptic curves in cryptography. In Proceedings of the Advances in Cryptology CRYPTO 85 Proceedings, Santa Barbara, CA, USA, 18–22 August 1985; Springer: Berlin/Heidelberg, Germany, 1985; pp. 417–426. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Bos, J.W.; Halderman, J.A.; Heninger, N.; Moore, J.; Naehrig, M.; Wustrow, E. Elliptic curve cryptography in practice. In International Conference on Financial Cryptography and Data Security; Springer: Berlin/Heidelberg, Germany, 2014; pp. 157–175. [Google Scholar]
- Tzeng, S.F.; Horng, S.J.; Li, T.; Wang, X.; Huang, P.H.; Khan, M.K. Enhancing Security and Privacy for Identity-Based Batch Verification Scheme in VANETs. IEEE Trans. Veh. Technol. 2016, 66, 3235–3248. [Google Scholar] [CrossRef]
- Hu, X.; Wang, J.; Xu, H.; Liu, Y.; Zhang, X. Secure and Pairing-Free Identity-Based Batch Verification Scheme in Vehicle Ad-Hoc Networks. In Proceedings of the Intelligent Computing Methodologies: 12th International Conference, ICIC 2016, Lanzhou, China, 2–5 August 2016; Proceedings, Part III. Huang, D.S., Han, K., Hussain, A., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 11–20. [Google Scholar]
- Xu, L.; Li, J.; Tang, S.; Baek, J. Server-Aided Verification Signature with Privacy for Mobile Computing. Mob. Inf. Syst. 2015, 1–11. [Google Scholar] [CrossRef]
- Pointcheval, D.; Stern, J. Security Arguments for Digital Signatures and Blind Signatures. J. Cryptol. 2000, 13, 361–396. [Google Scholar] [CrossRef]
- Malina, L.; Hajny, J.; Martinasek, Z. Privacy-preserving authentication systems using smart devices. In Proceedings of the 2016 39th International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, 27–29 June 2016; pp. 11–14. [Google Scholar] [CrossRef]
- De Caro, A.; Iovino, V. jPBC: Java pairing based cryptography. In Proceedings of the 16th IEEE Symposium on Computers and Communications, ISCC 2011, Corfu, Greece, 28 June–1 July 2011; pp. 850–855. [Google Scholar]
- Zeng, X.; Xu, G.; Zheng, X.; Xiang, Y.; Zhou, W. E-AUA: An efficient anonymous user authentication protocol for mobile IoT. IEEE Internet Things J. 2018, 6, 1506–1519. [Google Scholar] [CrossRef]
- Thammarat, C. Efficient and secure NFC authentication for mobile payment ensuring fair exchange protocol. Symmetry 2020, 12, 1649. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).