Mitigation of Thermal Stability Concerns in FinFET Devices †
Abstract
1. Introduction
2. Measuring SHE in the Devices and Systems
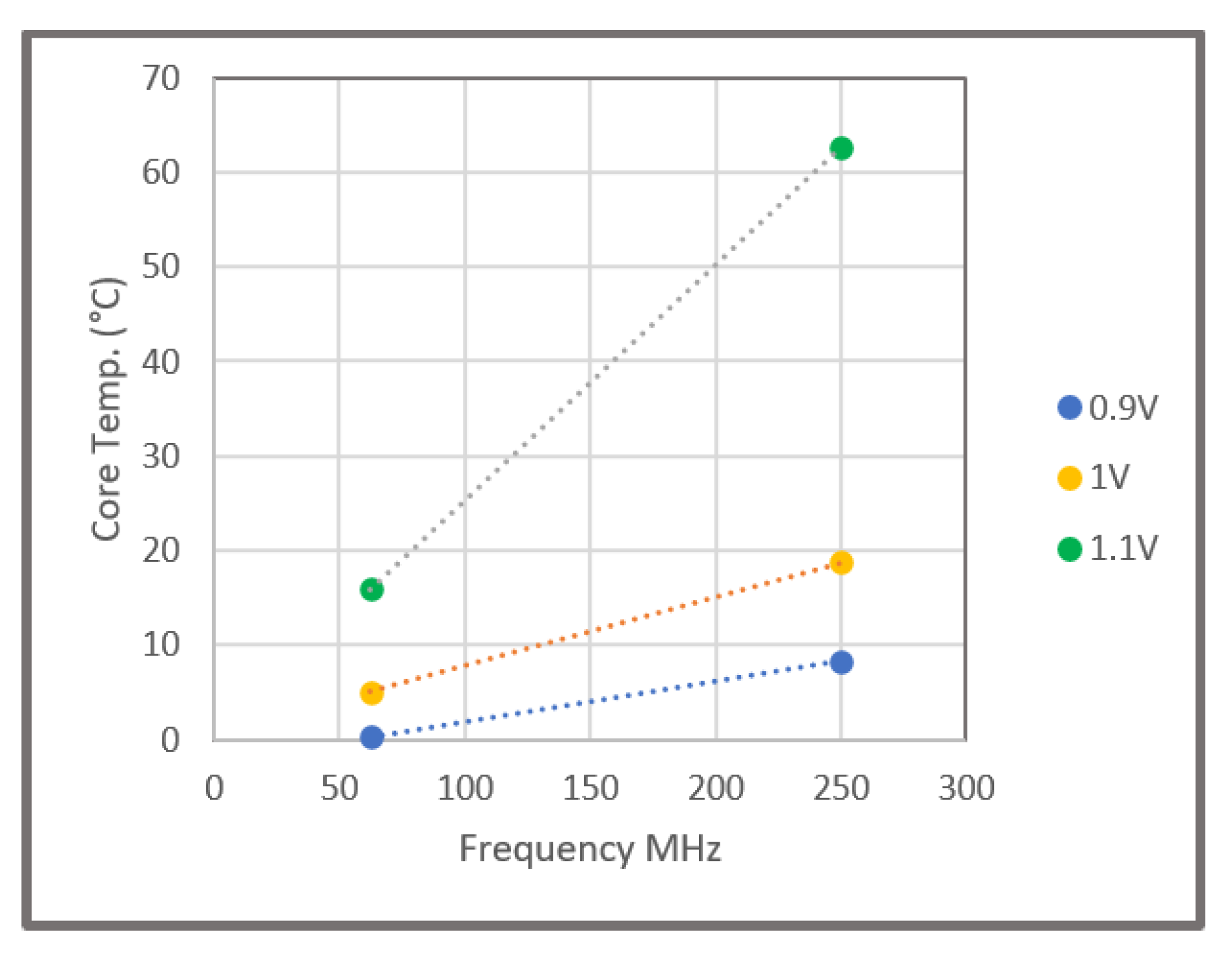
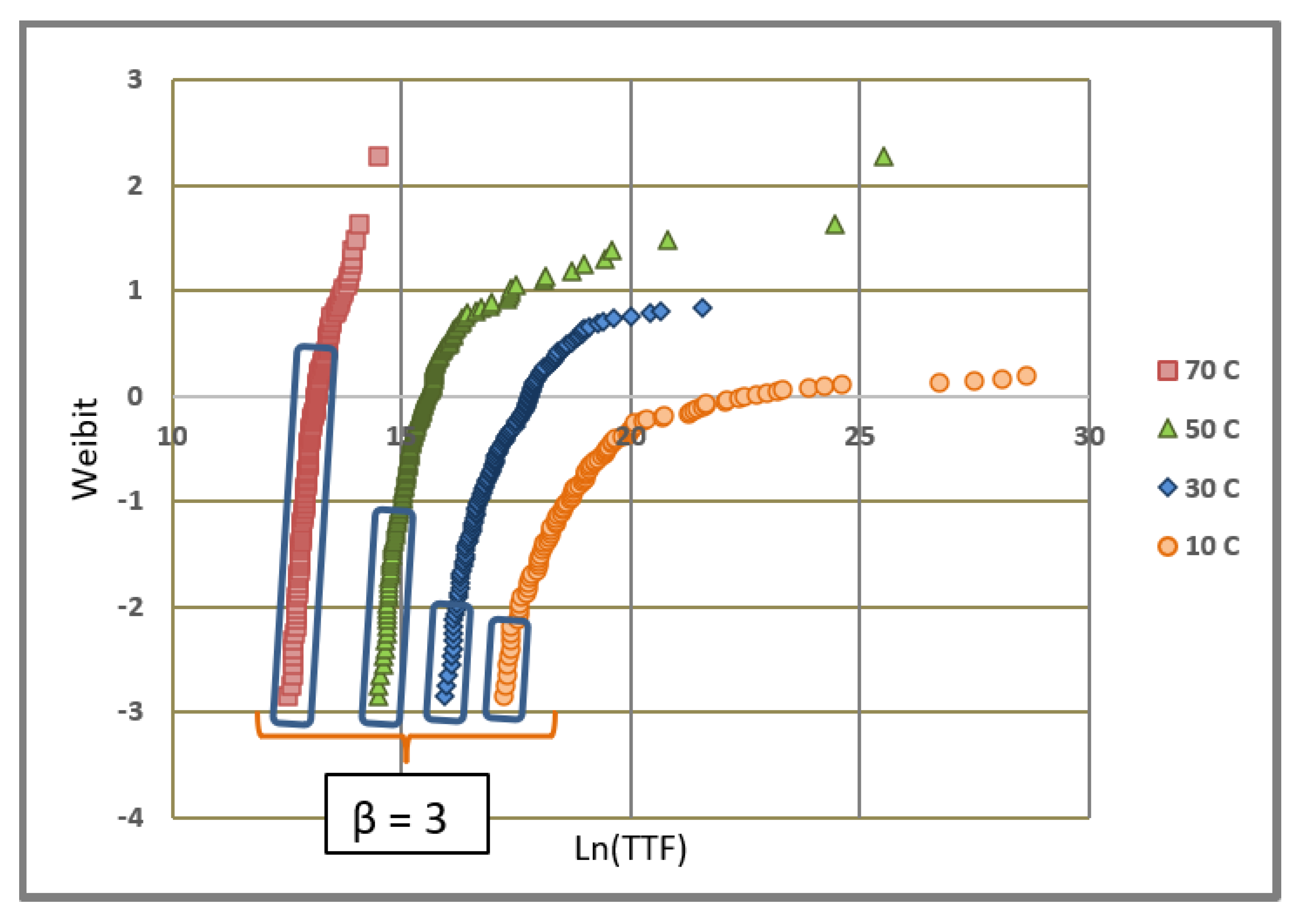
2.1. Device-Level Testing and Results
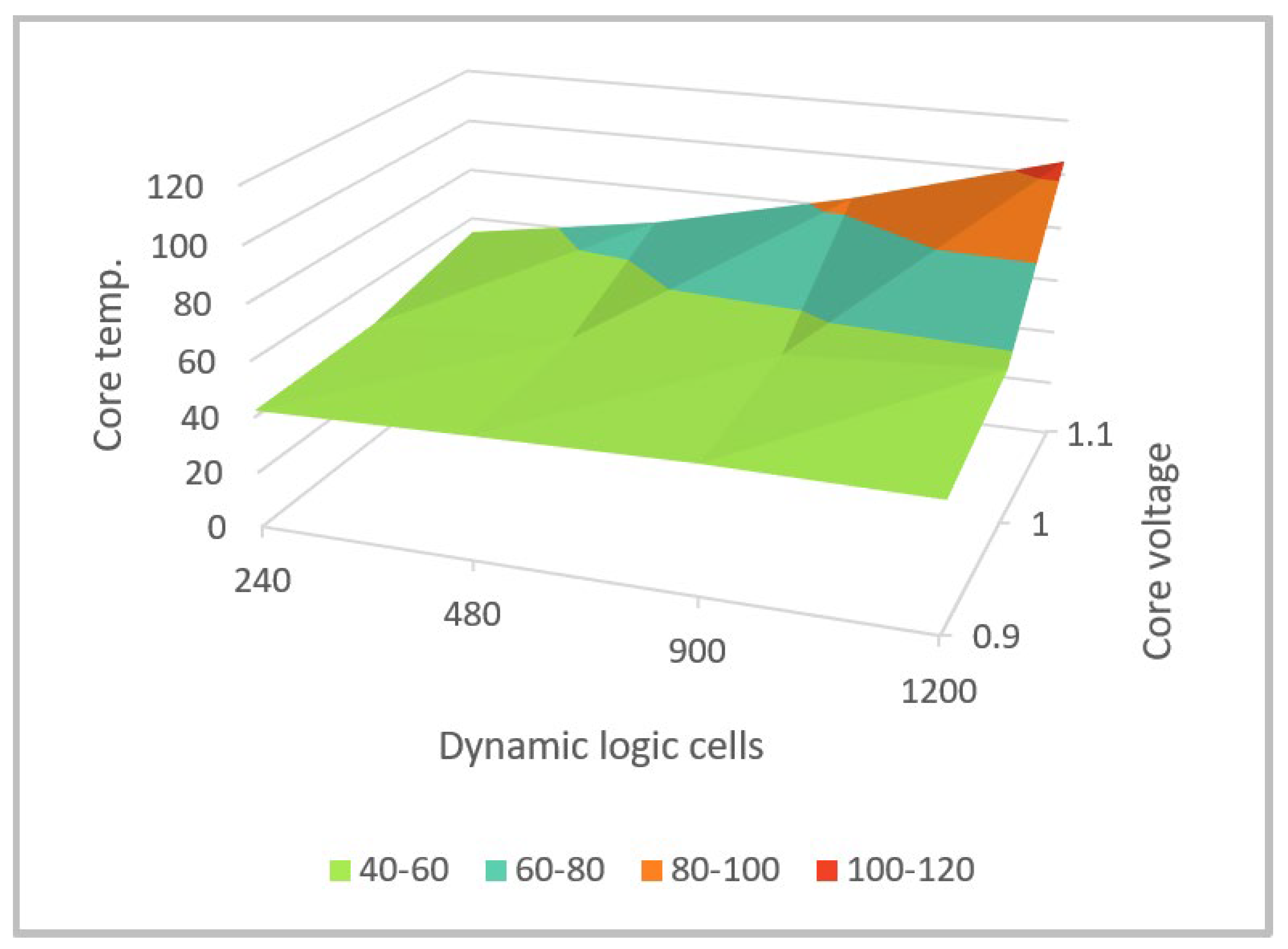
2.2. System-Level Testing and Results
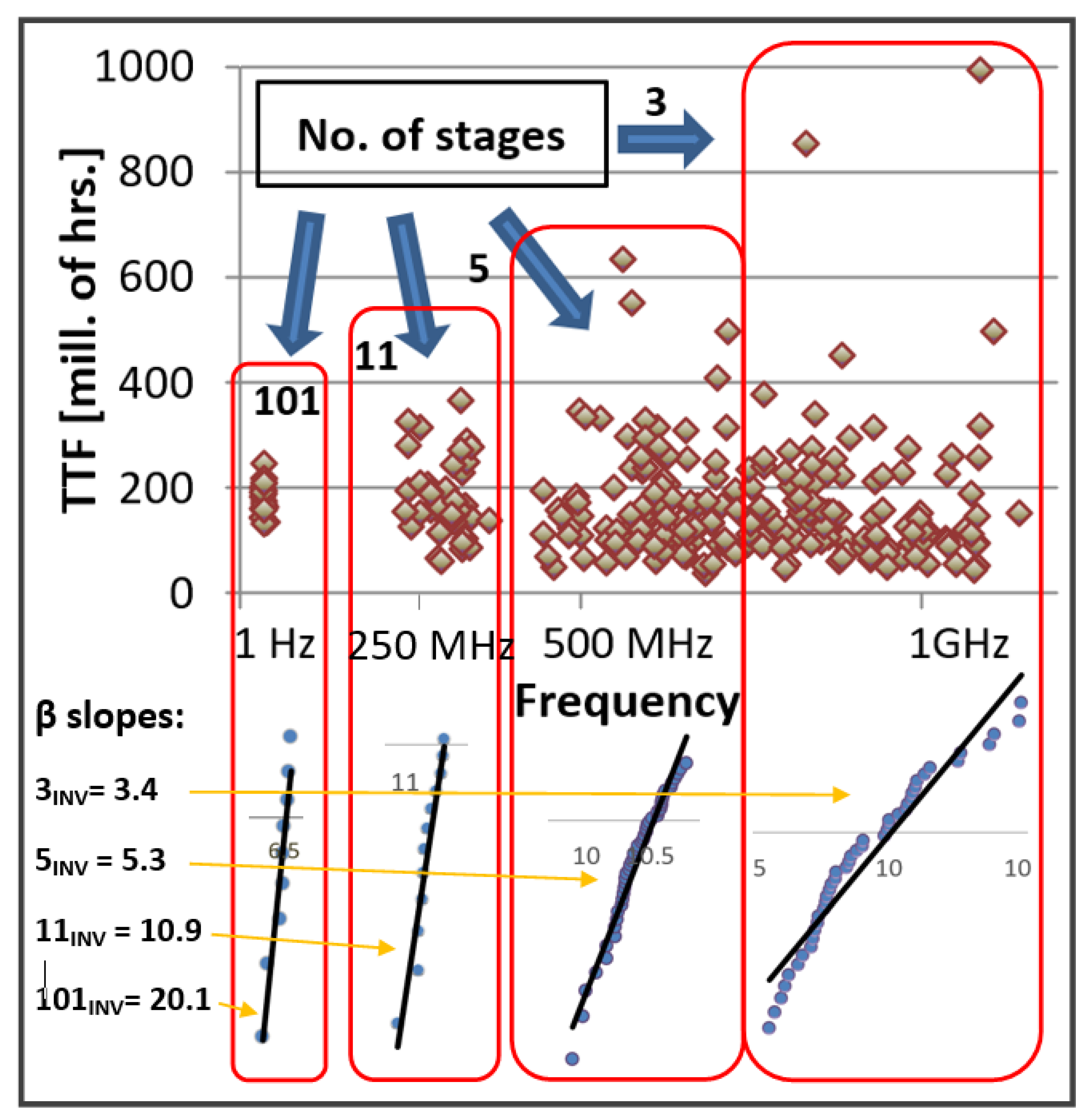
2.3. Modification of System-Level Testing Using External Clocking
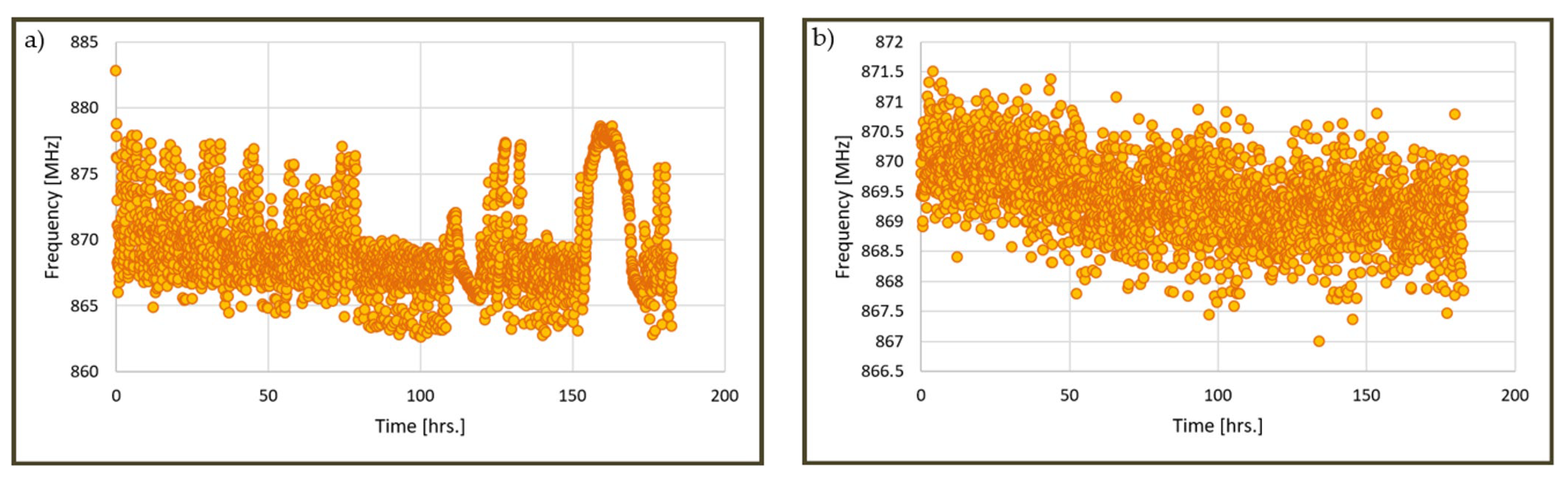
3. Degradation Signal Tempering Using Noise Reduction Techniques
3.1. Degradation Data Correction with Temperature Compensation
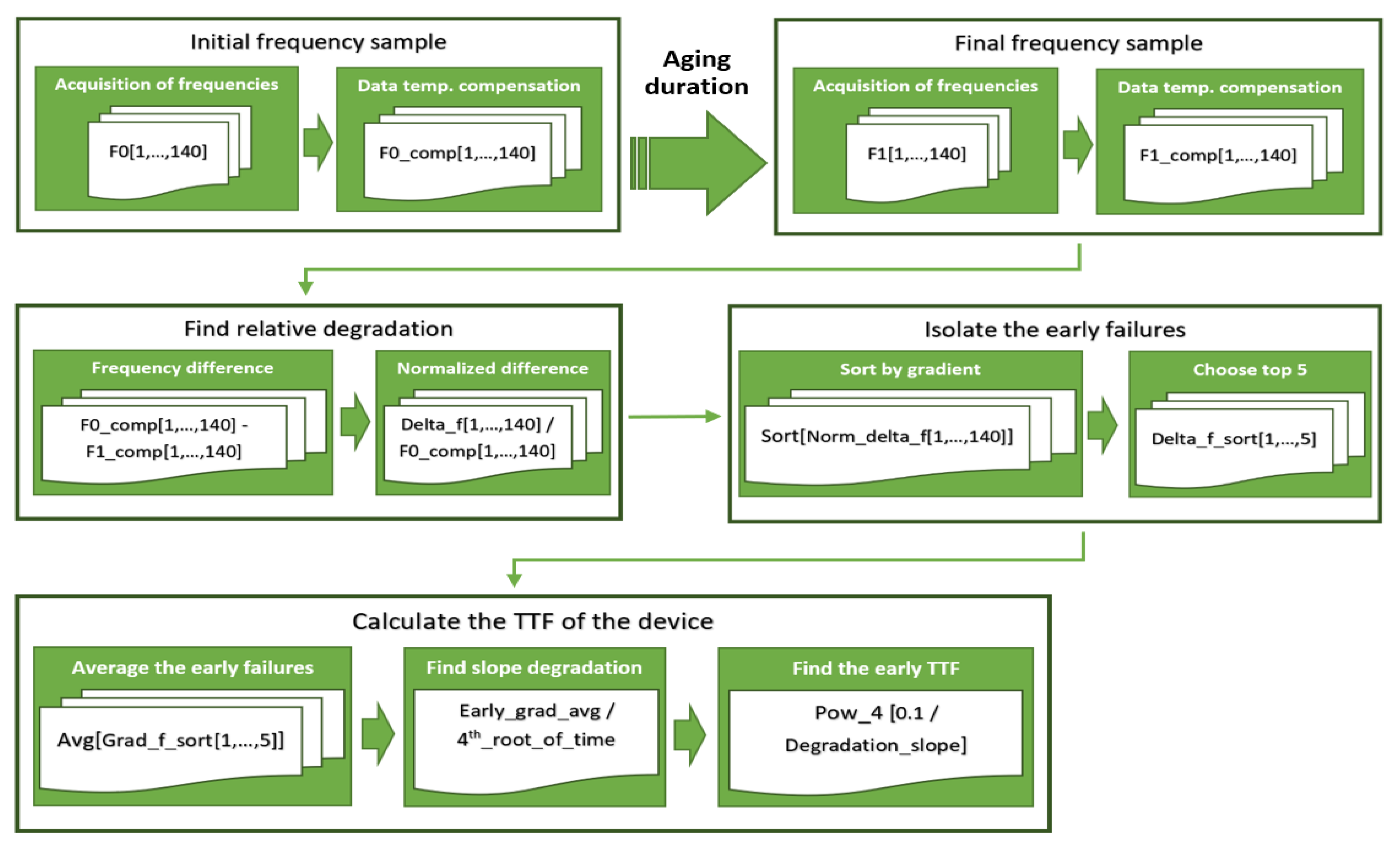
3.2. Accurate Lifetime Calculations Using Early Failures
4. Algorithm to Calculate the TTF of Early Failures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sagong, H.C.; Choi, K.; Kim, J.; Jeong, T.; Choe, M.; Shim, H.; Kim, W.; Park, J.; Shin, S.; Pae, S. Modeling of FinFET Self-Heating Effects in multiple FinFET Technology Generations with implication for Transistor and Product Reliability. In Proceedings of the IEEE 2018 Symposium on VLSI Technology, Honolulu, HI, USA, 18–22 June 2018; pp. 121–122. [Google Scholar] [CrossRef]
- Myeong, I.; Son, D.; Kim, H.; Shin, H. Analysis of Self Heating Effect in DC/AC Mode in Multi-Channel GAA-Field Effect Transistor. IEEE Trans. Electron Dev. 2019, 66, 4631–4637. [Google Scholar] [CrossRef]
- Kumar, A.; Srinivas, P.S.T.N.; Tiwari, P.K. Physical Insight into Self-heating Effects in Ultrathin Junctionless Gate-All-Around FETs. In Proceedings of the 2019 IEEE 9th International Nanoelectronics Conferences (INEC), Kuching, Malaysia, 3–5 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Liao, M.-H.; Hsieh, C.-P.; Lee, C.-C. Systematic Investigation of Self-Heating Effect on CMOS Logic Transistors From 20 to 5 nm Technology Nodes by Experimental Thermoelectric Measurements and Finite Element Modeling. IEEE Trans. Electron Dev. 2017, 64, 646–648. [Google Scholar] [CrossRef]
- Sootkaneung, W.; Howimanporn, S.; Chookaew, S. Thermal Effect on Performance, Power, and BTI Aging in FinFET-Based Designs. In Proceedings of the IEEE 2017 Euromicro Conference on Digital System Design, Vienna, Austria, 30 August–1 September 2017; pp. 345–351. [Google Scholar] [CrossRef]
- Drego, N.; Chandrakasan, A.; Boning, D. An All-Digital, Highly Scalable Architecture for Measurement of Spatial Variation in Digital Circuits. In Proceedings of the IEEE Asian Solid-State Circuits Conference, Fukuoka, Japan, 3–5 November 2008; pp. 393–396. [Google Scholar]
- Bender, E.; Bernstein, J.B. Microchip Health Monitoring System Using the FLL Circuit. Sensors 2021, 21, 2285. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, J.B.; Gurfinkel, M.; Li, X.; Walters, J.; Shapira, Y.; Talmor, M. Electronic circuit reliability modeling. Microelectron. Reliab. 2006, 46, 1957–1979. [Google Scholar] [CrossRef]
- Bernstein, J.B.; Gabbay, M.; Delly, O. Reliability matrix solution to multiple mechanism prediction. Microelectron. Reliab. 2014, 54, 2951–2955. [Google Scholar] [CrossRef]
- Ultra96 Hardware User’s Guide, version 0.9; Avnet Inc.: Phoenix, AZ, USA, 2018.
- Bender, E.; Bernstein, J.B. Self-Heating Effects Measured in Fully Packaged FinFET Devices. In Proceedings of the IEEE 32nd International Conference on Microelectronics (Miel), Niš, Serbia, 12–14 September 2021. [Google Scholar]
- Jiang, H.; Liu, X.; Xu, N.; He, Y.; Du, G.; Zhang, X. An Investigation of DC/AC Hot Carrier Degradation in Multiple-fin SOI FinFETs. IEEE Electron Device Lett. 2015, 36, 1258–1260. [Google Scholar] [CrossRef]
- Paliwoda, P.; Chbili, Z.; Kerber, A.; Nigam, T.; Singh, D.; Nagahiro, K.; Manik, P.; Cimino, S.; Misra, D. Self-heating effects on Hot carrier degradation and its impact on Ring Oscillator reliability. In Proceedings of the 2018 International Integrated Reliability Workshop (IIRW), South Lake Tahoe, CA, USA, 7–11 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Choi, J.; Monga, U.; Park, Y.; Shim, H.; Kwon, U.; Pae, S.; Kim, D. Impact of BEOL Design on Self-heating and heating and Reliability in Highly-scaled FinFETs. In Proceedings of the International Conference on Semiconductor Processes and Devices (SISPAD), Udine, Italy, 4–6 September 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Kim, J.; Hong, K.; Shim, H.; Rhee, H.; Shin, H. Comparative Analysis of Hot Carrier Degradation (HCD) in 10-nm Node nMOS/pMOS FinFET Devices. IEEE Trans. Electron Dev. 2020, 67, 5396–5402. [Google Scholar] [CrossRef]
- Stellari, F.; Jenkins, K.A.; Weger, A.J.; Linder, B.; Song, P. Self-Heating Characterization of FinFET SOI Devices using 2D Time Resolved Emission Measurements. In Proceedings of the IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 19–23 April 2015; pp. 2B.1.1–2B.1.6. [Google Scholar] [CrossRef]
- Bernstein, J.B.; Bensoussan, A.; Bender, E. Reliability Prediction of FinFET FPGAs by MTOL. Microelectron. Reliab. 2020, 114, 113809. [Google Scholar] [CrossRef]
- Qu, Y.; Lin, X.; Li, J.; Cheng, R.; Zheng, Z.; Lu, J.; Chen, B.; Zhao, Y. Ultra Fast (<1 ns) Electrical Characterization of Self-Heating Effect and Its Impact on Hot Carrier Injection in 14nm FinFETs. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; pp. 39.2.1–39.2.4. [Google Scholar] [CrossRef]
- Zhang, G.; Gu, Y.; Li, J.; Tao, H. An Improved Model of Self-Heating Effects for Ultrathin Body SOI nMOSFETs Based on Phonon Scattering Analysis. IEEE Electron Device Lett. 2015, 36, 534–536. [Google Scholar] [CrossRef]
- Makovejev, S.; Olsen, S.; Raskin, J.-P. RF Extraction of Self-Heating Effects in FinFETs. IEEE Trans. Electron Dev. 2011, 53, 3335–3341. [Google Scholar] [CrossRef]
- Bernstein, J.B.; Bensoussan, A.; Bender, E. Reliability prediction with MTOL. Microelectron. Reliab. 2017, 68, 91–97. [Google Scholar] [CrossRef]
- UltraScale Architecture System Monitor, V1.10. AMD Xilinx. Available online: https://docs.xilinx.com/v/u/en-US/ug580-ultrascale-sysmon (accessed on 7 October 2022).
- DP800 Series Programmable Linear Power Supply; Rigol Technologies, Inc.: Beijing, China, 2015.
- Bender, E.; Bernstein, J.B. Product Failure Time Assessments using Early Degradation Filtering. Eng. Technol. Open Acc. 2021, 3, 555625. [Google Scholar] [CrossRef]
- McPheirson, M.P. Reliability and Physics Engineering; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Drego, N.; Chandrakasan, A.; Boning, D.; Shah, D. Reduction of Variation-Induced Energy Overhead in Multi-Core Processors. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2011, 30, 891–904. [Google Scholar] [CrossRef]
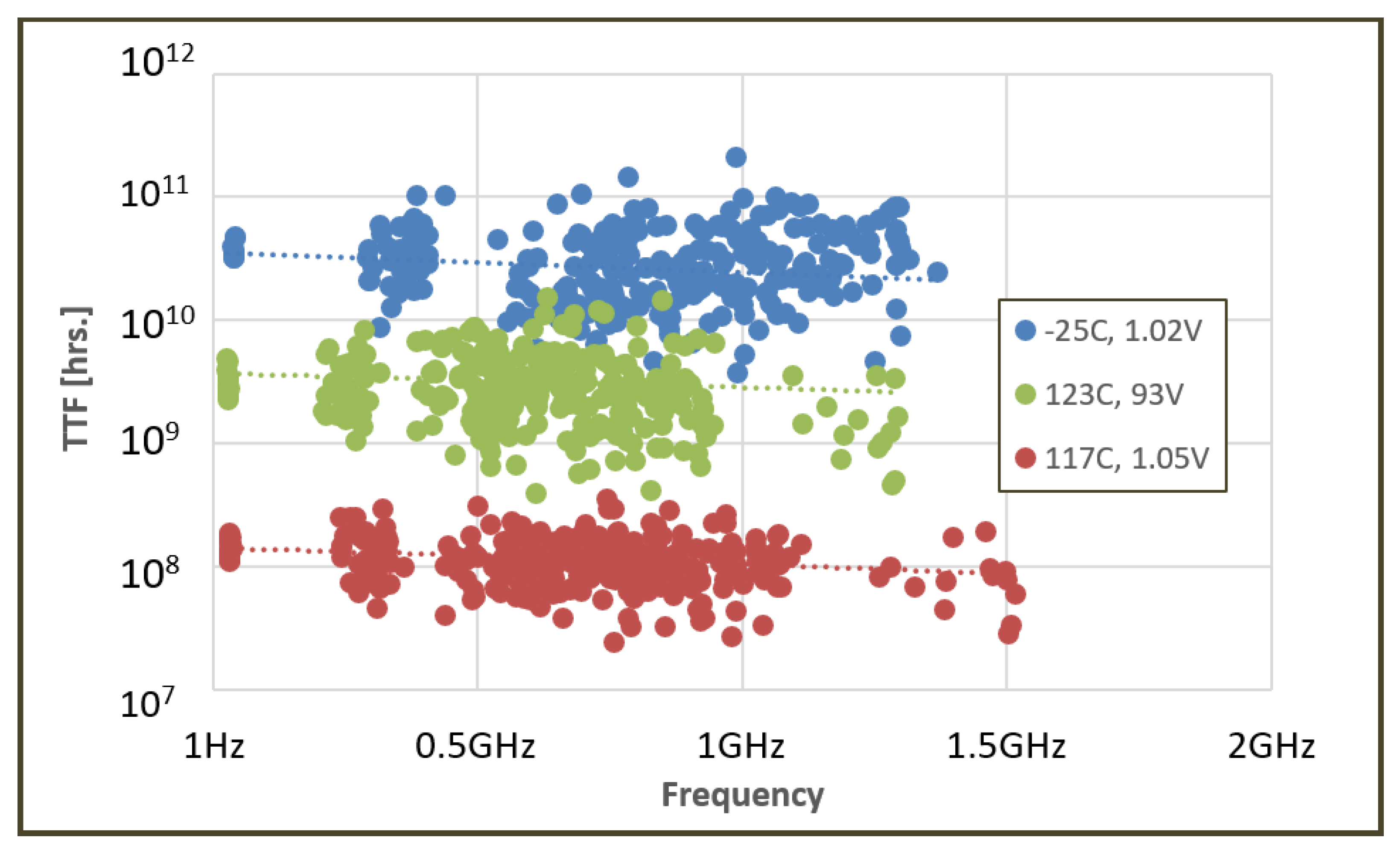
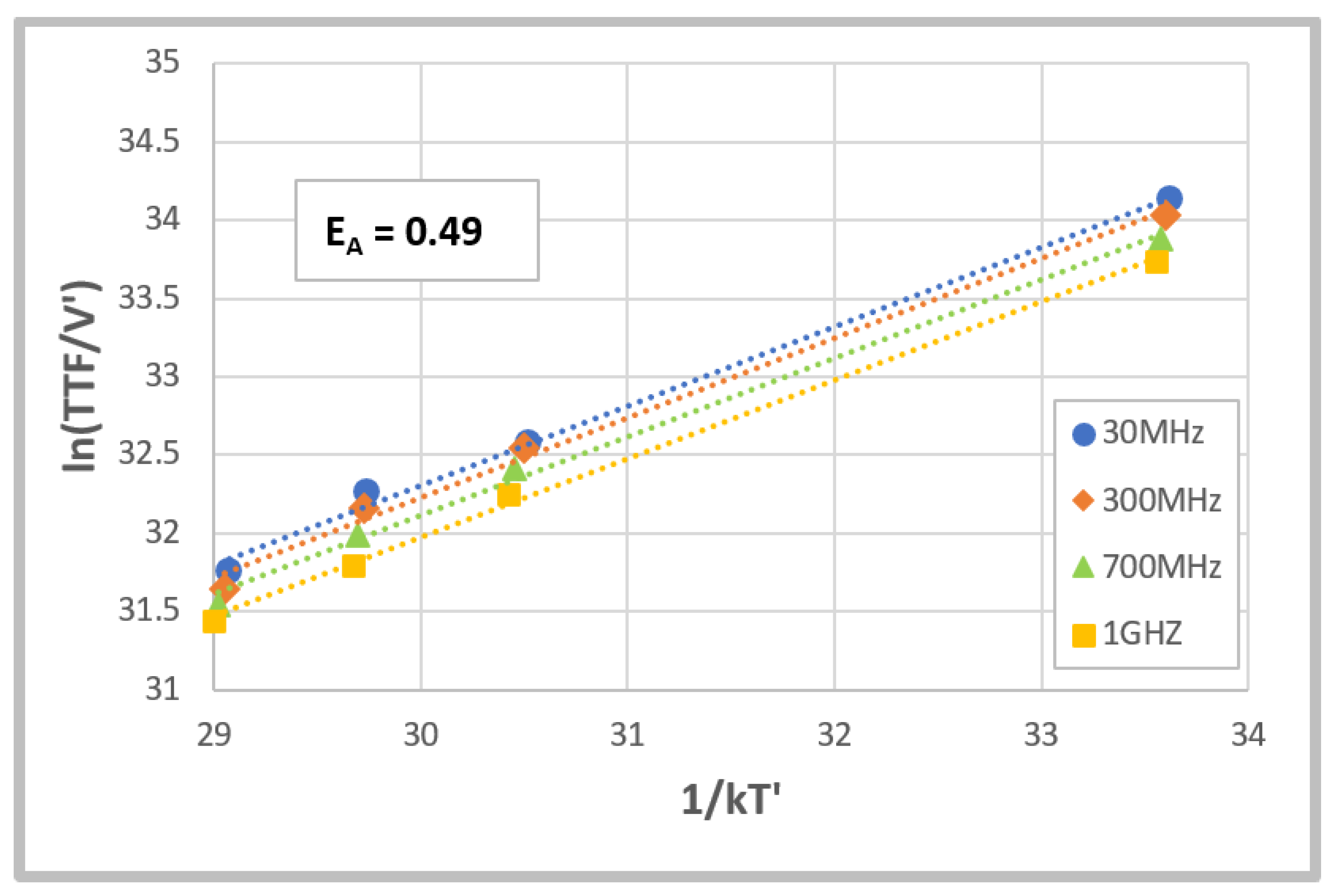

| Stress Values | TTF at 30 MHz (h) | TTF at 1 GHz (h) | Change in TTF |
|---|---|---|---|
| −15 °C, 1.02 V | 72% | ||
| 123 °C, 0.93 V | 83% | ||
| 117 °C, 1.05 V | 73% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bender, E.; Bernstein, J.B.; Boning, D.S. Mitigation of Thermal Stability Concerns in FinFET Devices. Electronics 2022, 11, 3305. https://doi.org/10.3390/electronics11203305
Bender E, Bernstein JB, Boning DS. Mitigation of Thermal Stability Concerns in FinFET Devices. Electronics. 2022; 11(20):3305. https://doi.org/10.3390/electronics11203305
Chicago/Turabian StyleBender, Emmanuel, Joseph B. Bernstein, and Duane S. Boning. 2022. "Mitigation of Thermal Stability Concerns in FinFET Devices" Electronics 11, no. 20: 3305. https://doi.org/10.3390/electronics11203305
APA StyleBender, E., Bernstein, J. B., & Boning, D. S. (2022). Mitigation of Thermal Stability Concerns in FinFET Devices. Electronics, 11(20), 3305. https://doi.org/10.3390/electronics11203305







