Strengthening Quality of Chaotic Bit Sequences
Abstract
1. Introduction
2. The XOR Process of Mixed-Mode Signals
2.1. The XOR Mixing Process
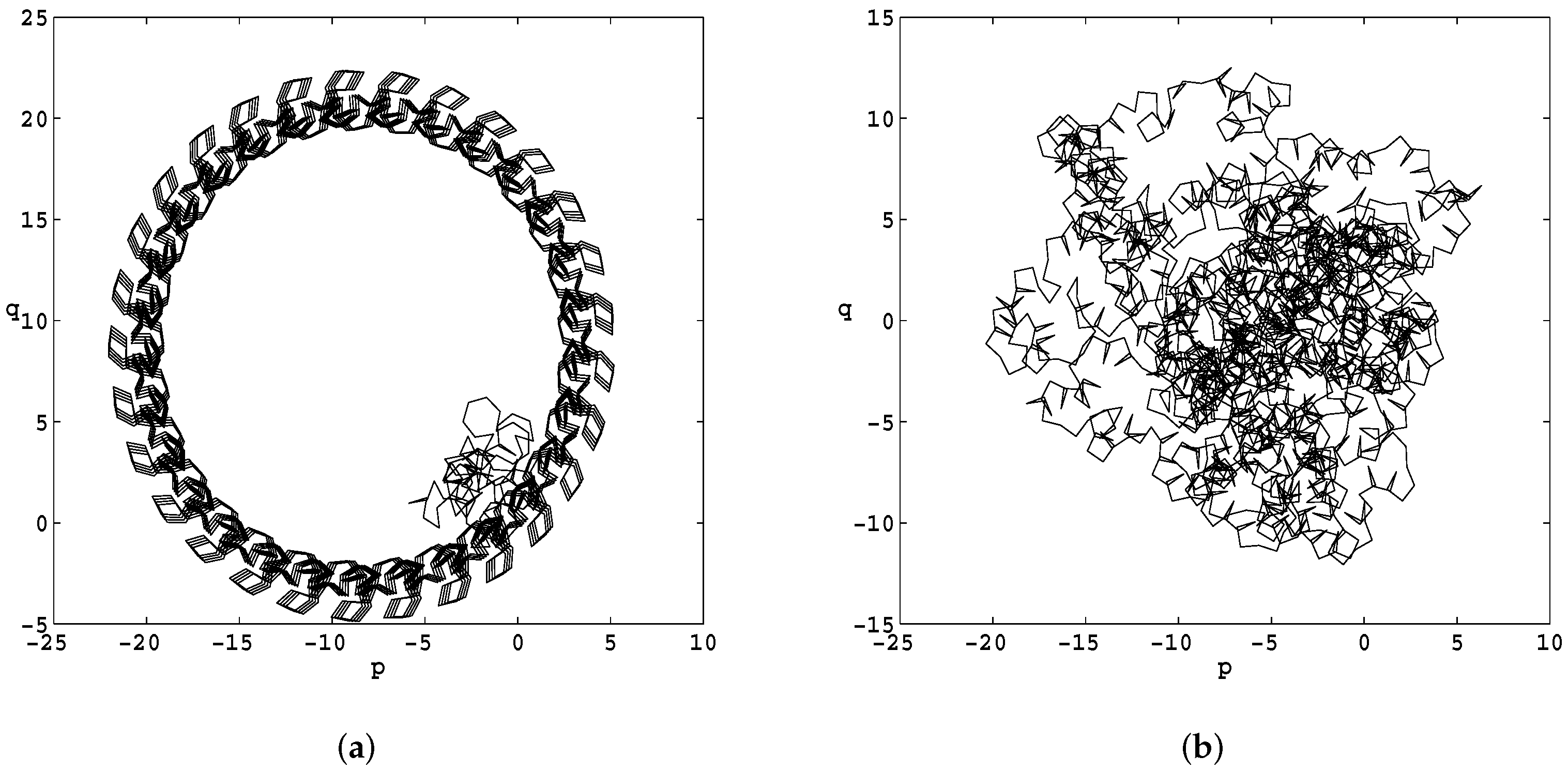
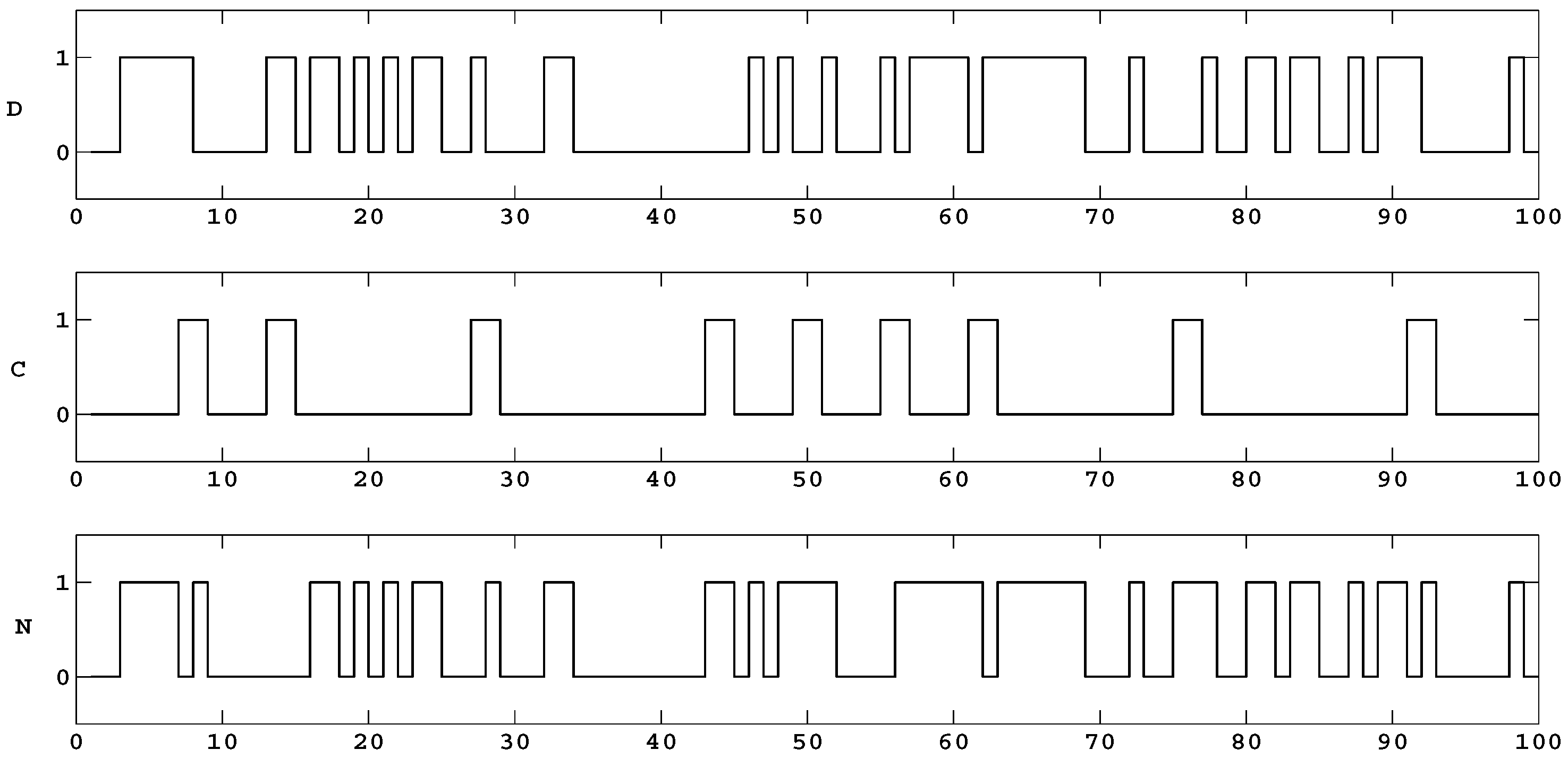
2.2. Generation of Chaotic Bits
3. Computational Results
4. The XORed Sequences and Their Quality
4.1. The Nine Sequences and Their Visual Quality
4.2. The ent Test Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The 0-1 Test (for Chaos)
Appendix B. The ent Test (for Random Signals)
- Entropy level test. For a sequence of ASCII characters, we obtain randomness if the entropy level is around the value of 8. The lower the entropy level, the more likely it is to have a non-random sequence of ASCII characters.
- Compression test. Random sequences should have their compression levels close to .
- (chi-square) test. Randomness is confirmed in this test if a sequence falls into the interval of to . As explained in [25], such an interval is achieved primarily in cases of radioactive isotope decay. Furthermore, the chi-square distribution is calculated for the stream of bytes in the sequence and expressed as two values (see Table 2): an absolute number and a percentage which indicates how frequently a truly random sequence should exceed the calculated value. For example, for sequence , the distribution is , and randomly should exceed this value of the time.
- Arithmetic mean value (AMV) test with the output value close to for random sequences. In this test all input bytes are summed up and divided by the total number of bytes.
- The Monte-Carlo (MC ) test indicating a random sequence if the result is a single percentage digit. For very long input streams this value will be close to 0, meaning an accurate approximation of .
- The serial correlation coefficient (SCC) test yielding the number close to for random sequences. This test checks the dependence of each byte on the previous one. If there is no dependence between bytes, then the SCC value is close to .
References
- Kanaso, A.; Smaoui, N. Logistic chaotic for binary numbers generations. Chaos Solitions Fractals 2009, 40, 2557–2568. [Google Scholar] [CrossRef]
- Yalcin, M.E.; Suykens, J.A.K.; Vandewalle, J. True random bit generation from a double-scroll attractor. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 1394–1404. [Google Scholar] [CrossRef]
- Posadas-Castillo, C.; Cruz-Hernandez, C.; Lopez-Gutierrez, R.M. Experimental realization of synchronization in complex networks with Chua’s circuits like nodes. Chaos Solitons Fractals 2009, 40, 1963–1975. [Google Scholar] [CrossRef]
- Wu, X.; Chen, G.; Cai, J. Chaos synchronization of the master-slave generalized Lorenz systems via linear state error feedback control. Physica D 2007, 229, 52–80. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, F. Synchronization for chaotic systems and chaos-based secure communications via both reduced-order and step-by-step sliding mode observers. Commun. Nonl. Sci. Numer. Simul. 2013, 18, 926–937. [Google Scholar] [CrossRef]
- Cuomo, K.M.; Oppenheim, A.V.; Strogatz, S.H. Synchronization of Lorenz-based chaotic circuits with applications to communications. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1993, 40, 626–633. [Google Scholar] [CrossRef]
- Persohn, K.J.; Povinelli, R.J. Analyzing logistic map pseudorandom number generators for periodicity inducted by finite precision floating-point representation. Chaos Solitions Fractals 2012, 45, 238–244. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Breaking an encrypted scheme based on chaotic baker map. Phys. Lett. A 2006, 352, 78–82. [Google Scholar] [CrossRef]
- Özkaynaka, F.; Yavuzb, S. Security problems for a pseudorandom sequence generator based on the Chen chaotic system. Comput. Phys. Commer. 2013, 184, 2178–2181. [Google Scholar] [CrossRef]
- Handkiewicz, A.; Katarzynski, P.; Szczesny, S.; Naumowicz, M.; Melosik, M.; Sniatala, P.; Kropidłowski, M. Design automation of a lossless multiport network and its application to image filtering. Expert Syst. Appl. 2014, 41, 2211–2221. [Google Scholar] [CrossRef]
- Handkiewicz, A.; Szczesny, S.; Naumowicz, M.; Katarzynski, P.; Melosik, M.; Sniatala, P.; Kropidłowski, M. SI-Studio, a layout generator of current mode circuits. Expert Syst. Appl. 2015, 42, 3205–3218. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, S. A valid algorithm of converting chaos sequences to uniformity pseudo-random ones. In Proceedings of the International Symposium on Information Engineering and Electronic Commerce (IEEC-2009), Ternopil, Ukraine, 16–17 May 2009; pp. 295–298. [Google Scholar]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. Proc. R. Soc. Lond. 2003, 460, 603–611. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. Testing for chaos in deterministic systems with noise. Physica D 2005, 212, 100–110. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. On the implementation of the 0–1 test for chaos. SIAM J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]
- Melosik, M.; Marszalek, W. On the 0-1 test for chaos in continuous systems. Bull. Pol. Acad. Sci. Tech. Sci. 2016, 64, 521–528. [Google Scholar] [CrossRef][Green Version]
- Walczak, M.; Marszalek, W.; Sadecki, J. Using the 0-1 test for chaos in nonlinear continuous systems with two varying parameters: Parallel computations. IEEE Access 2019, 7, 154375–154385. [Google Scholar] [CrossRef]
- Marszalek, W.; Walczak, M.; Sadecki, J. Testing deterministic chaos: Incorrect results of the 0-1 test and how to avoid them. IEEE Access 2019, 7, 183245–183251. [Google Scholar] [CrossRef]
- Matsumoto, T.; Chua, L.O.; Komuro, M. The double scroll. IEEE Trans. Circuits Syst. 1985, 32, 798–818. [Google Scholar] [CrossRef]
- ID Quantique SA, White Paper Version 3.0. Random Number Generation Using Quantum Physics. 2019. Available online: http://www.idquantique.com (accessed on 12 December 2021).
- IDQ Random Numbers. 2019. Available online: https://www.idquantique.com/random-number-generation/overview/ (accessed on 12 December 2021).
- Melosik, W.; Marszalek, W. Trojan attack on the initialization of pseudo-random bit generators using synchronization of chaotic input sources. IEEE Access 2021, 9, 161846–161853. [Google Scholar] [CrossRef]
- Yu, W.K.; Li, S.; Yao, X.R.; Liu, X.F.; Wu, L.A.; Zhai, G.J. A protocol based on compressed sensing for high-speed authentication and cryptographic key distribution over a multiparty optical network. Appl. Opt. 2013, 52, 7882–7888. [Google Scholar] [CrossRef]
- von Neumann, J. Various techniques used in connection with random digits. Appl. Math. Ser. 1951, 12, 36–38. [Google Scholar]
- Walker, J. ENT A Psudorandom Number Sequence Test Program. 2019. Available online: http://www.fourmilab.ch/random/ (accessed on 12 December 2021).
- Tehranipoor, M.; Wang, C. (Eds.) Introduction to Hardware Security and Trust; Springer: New York, NY, USA, 2012. [Google Scholar]
- Marszalek, W.; Trzaska, Z. Mixed-mode oscillations in a modified Chua’s circuit. Circuits Syst. Signal Process. 2010, 29, 1075–1087. [Google Scholar] [CrossRef]
- Marszalek, W. Circuits with oscillatory hierarchical Farey sequences and fractal properties. Circuits Syst. Signal Process. 2012, 31, 1279–1296. [Google Scholar] [CrossRef]
- Marszalek, W.; Trzaska, Z. Memristive circuits with steady-state mixed-mode oscillations. Electr. Lett. 2014, 50, 1275–1277. [Google Scholar] [CrossRef]
- Melosik, M.; Marszalek, W. Using the 0-1 test for chaos to detect hardware trojans in chaotic bit generators. Electr. Lett. 2016, 52, 919–920. [Google Scholar] [CrossRef]
- Colbeck, R.; Kent, A. Private randomness expansion with untrusted devices. J. Phys. A Math. Theor. 2011, 44, 095305. [Google Scholar] [CrossRef]
- Lai, Q.; Kuate, P.D.K.; Liu, F.; Iu, H.H.-C. An extremely simple chaotic system with infinitely many coexisting attractors. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1129–1133. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kengne, L.K.; Kuate, P.D.K.; Chen, C. Two-memristor-based chaotic system with infinite coexisting attractors. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2197–2201. [Google Scholar] [CrossRef]








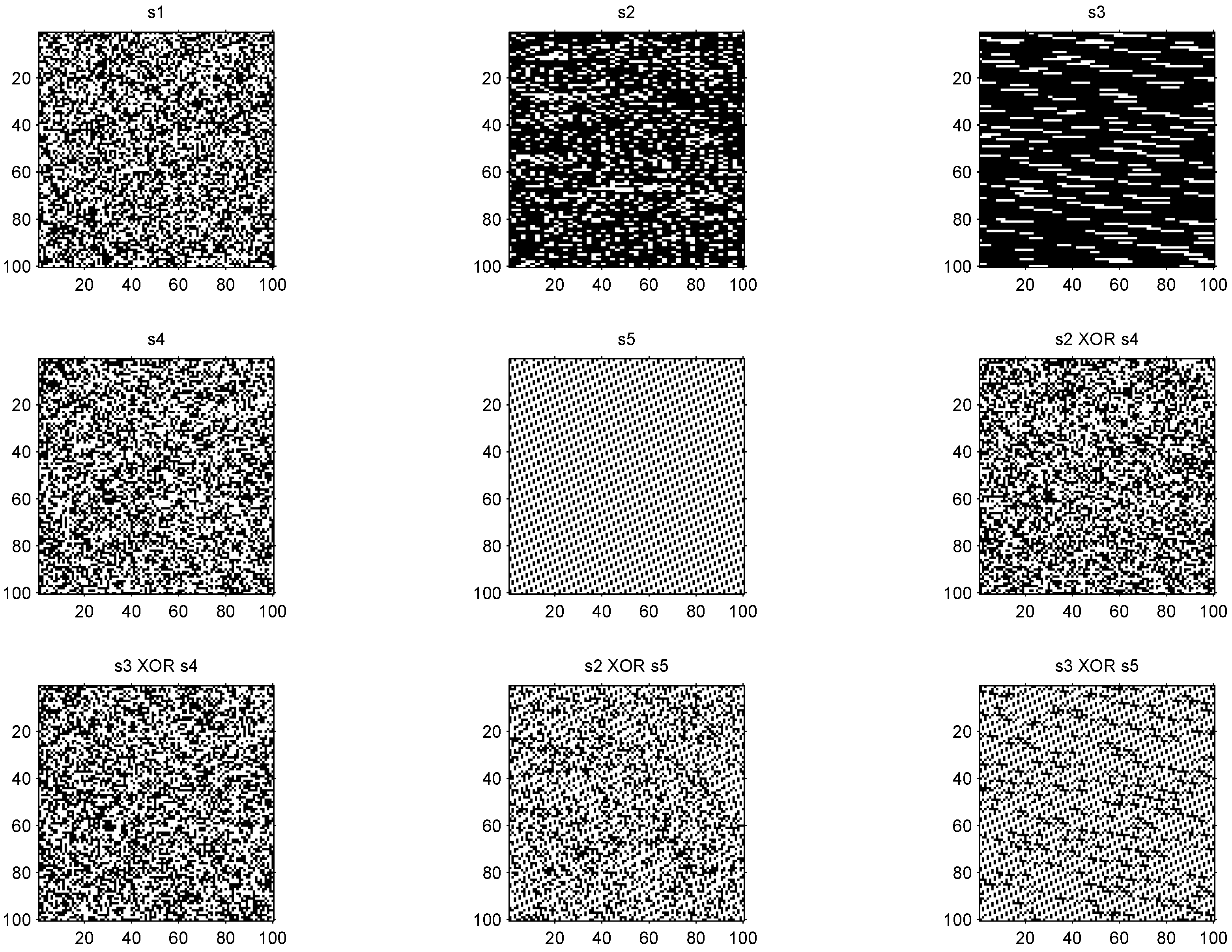
| Sequence | Source |
|---|---|
| s1 | QUANTIS (reference sequence of high entropy) [20,21] |
| s2 | chaotic bits from Lorenz system |
| s3 | chaotic bits from Chua circuit |
| s4 | chaotic bits from logistic eqn. (32 bits , see Figure 2) |
| s5 | chaotic bits from logistic eqn. (10 bits , see Figure 2) |
| s6 | sequence s2 XOR sequence s4 |
| s7 | sequence s3 XOR sequence s4 |
| s8 | sequence s2 XOR sequence s5 |
| s9 | sequence s3 XOR sequence s5 |
| sn | Entropy | Comp. % | Value; % | AMV | MC % | SCC |
|---|---|---|---|---|---|---|
| s1 | 7.869559 | 1 | 213.91; 95 | 127.4415 | 1.07 | 0.005292 |
| s2 | 3.884870 | 51 | 36,200.14; 0.01 | 62.4149 | 21.87 | 0.119915 |
| s3 | 1.829749 | 77 | 162,993.87; 0.01 | 39.1188 | 27.32 | 0.111901 |
| s4 | 7.850575 | 1 | 263.07; 50 | 131.5946 | 4.81 | 0.051919 |
| s5 | 2.845031 | 64 | 44,492.49; 0.01 | 181.7886 | 44.22 | 0.037565 |
| s6 | 7.851689 | 1 | 251.59; 50 | 129.7392 | 2.06 | 0.013551 |
| s7 | 7.837249 | 2 | 270.84; 25 | 131.6376 | 2.67 | 0.043232 |
| s8 | 6.266494 | 21 | 5044.32; 0.01 | 155.7672 | 16.14 | 0.102282 |
| s9 | 4.512645 | 43 | 22,535.47; 0.01 | 166.5360 | 32.67 | 0.073107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melosik, M.; Marszalek, W. Strengthening Quality of Chaotic Bit Sequences. Electronics 2022, 11, 272. https://doi.org/10.3390/electronics11020272
Melosik M, Marszalek W. Strengthening Quality of Chaotic Bit Sequences. Electronics. 2022; 11(2):272. https://doi.org/10.3390/electronics11020272
Chicago/Turabian StyleMelosik, Michal, and Wieslaw Marszalek. 2022. "Strengthening Quality of Chaotic Bit Sequences" Electronics 11, no. 2: 272. https://doi.org/10.3390/electronics11020272
APA StyleMelosik, M., & Marszalek, W. (2022). Strengthening Quality of Chaotic Bit Sequences. Electronics, 11(2), 272. https://doi.org/10.3390/electronics11020272






