Signal Tables: An Extensible Exchange Format for Simulation Data
Abstract
:1. Introduction
- Clocked variables are only defined at clock ticks, and are undefined otherwise.
- In the recently published FMI 3.0 [5], array sizes can change at event points.
2. Overview of Existing Formats
2.1. CSV Format
| Listing 1. Example of a CSV file with a time event at 0.1 s. |
 |
2.2. DSRES Format
- The string vector name contains the names of the signals. An index i of this vector characterizes the corresponding signal i. An array variable is flattened into scalar variables. For example, a vector v of length 3 with name "v" is flattened into three signals: name = ["v[1]", "v[2]", "v[3]"].
- The string vector description contains a description text for every signal. The unit of a variable is stored at the end of every description text, e.g., "…[N*m]".
- The integer matrix dataInfo[:,4] contains information on where and how a signal is stored. A signal i is stored:
- in matrix data_j (see next item) with j = dataInfo[i,1];
- in column |k| of matrix data_j with sign(k) as a sign where k=dataInfo[i,2];
- with an interpolation type dataInfo[i,3] (0: linear interpolation);
- with an extrapolation type dataInfo[i,4] (=: undefined outside matrix, 0: keep first/last value outside matrix, 1: linear interpolation through first/last two points outside matrix).
- The core data is stored in the matrices data_j, where every column of a matrix contains the time series of one signal. The first column is the independent variable. Different matrices can have different time axes, that is, a different number of rows. Typically, two data matrices are present: one matrix with two rows that stores the parameters as time series with the first and the last time points, and one matrix with the time-varying signal data, which corresponds to the data stored in CSV file format.
2.3. HDF5-Based Formats
2.4. Recon Format
3. Signal Tables
3.1. Simple Example of a Signal Table
| Listing 2. Simple Signal Table. |
 |
| Listing 3. Information about simple Signal Table. |
 |
3.2. Formal Definition of a Signal Table
- A Var (=abbreviation for Variable) dictionary has a required key "values" with an associated value that is a multi-dimensional array of any element type and has one of the following formats (where is variable k and v_k is the associated value of the key "values"):
- −
- v_k is a vector within the i-th Var that has attribute "independent" = true:v_k[:] are the values of independent variable .
- −
- v_k is a vector with only one independent variable defined:v_k[i] is the value of scalar variable at independent variable .
- −
- v_k is a matrix with only one independent variable defined:v_k[i,j] is the value of at independent variable .
- −
- v_k is an array with two or more dimensions:v_k[i1,i2,…in,j1,j2,…jm] is the value ofat independent variables .
- A Par (=abbreviation for Parameter) dictionary has a required key "value" representing a parameter of any type and does not depend on the independent variables.
- A Map dictionary has no required keys, and collects attributes/metadata that are associated with a Signal Table or a Var or Par dictionary.
- using the tool and build information on the respective operating system,
- instantiating the corresponding model,
- initializing variables with the start attributes,
- using the values of the parameters from value,
- simulating with the attributes from Map experiment (see Table A3),
- setting absolute and relative tolerances with the help of the nominal, unbounded, tolerance attributes (for details, see FMI 3.0 [5]).
3.3. Examples
3.3.1. Various Signal Table Types
| Listing 4. Signal Table with various types. |
 |
| Listing 5. Information about Signal Table with various types. |
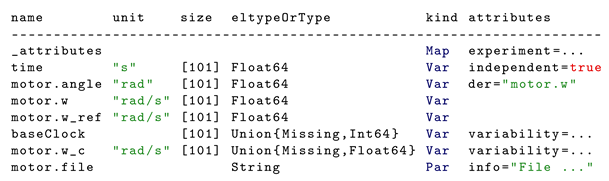 |
| Listing 6. Post-processing of Signal Table with various types. |
 |
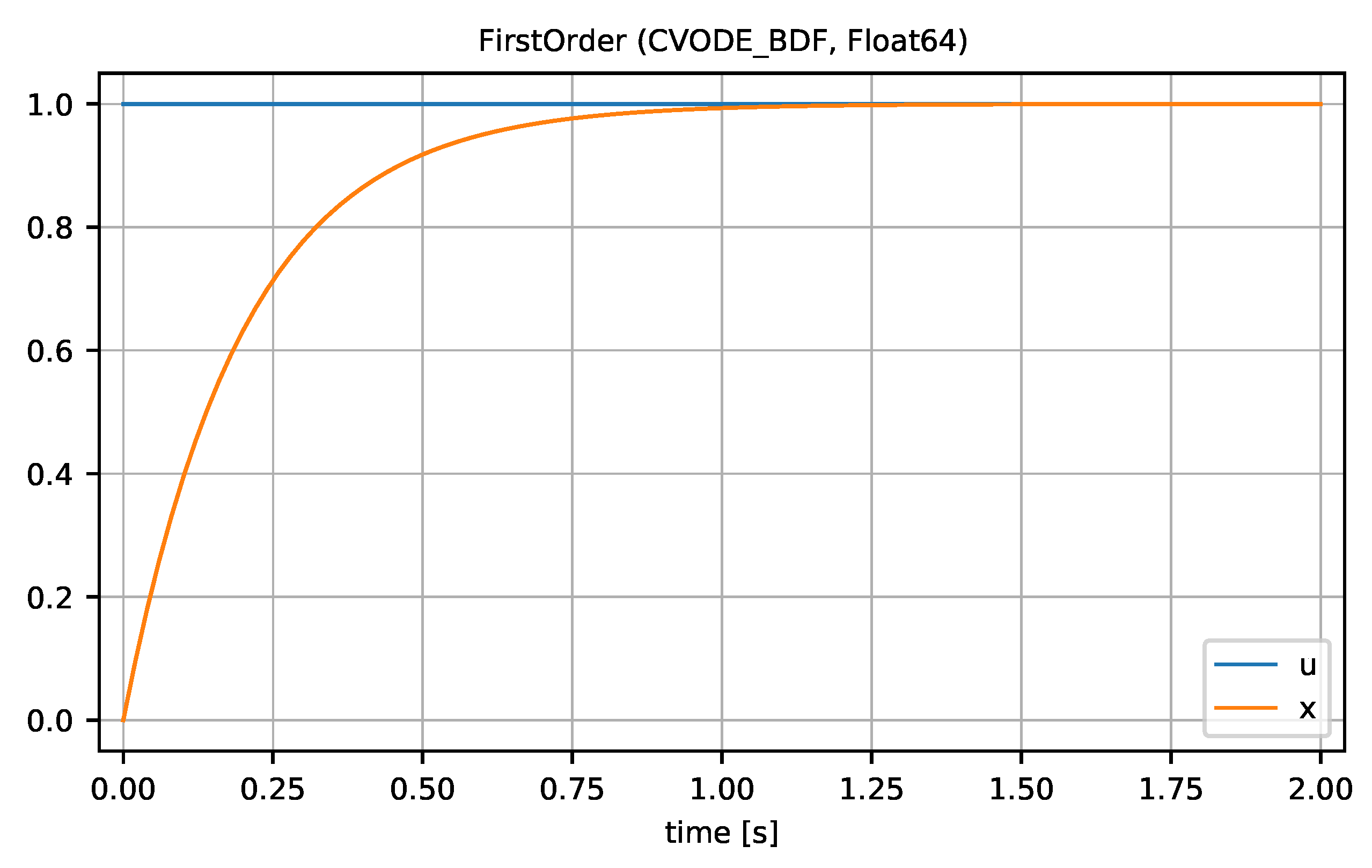
3.3.2. Transient Simulation
| Listing 7. Signal Table of one simulation of model firstOrder. |
 |
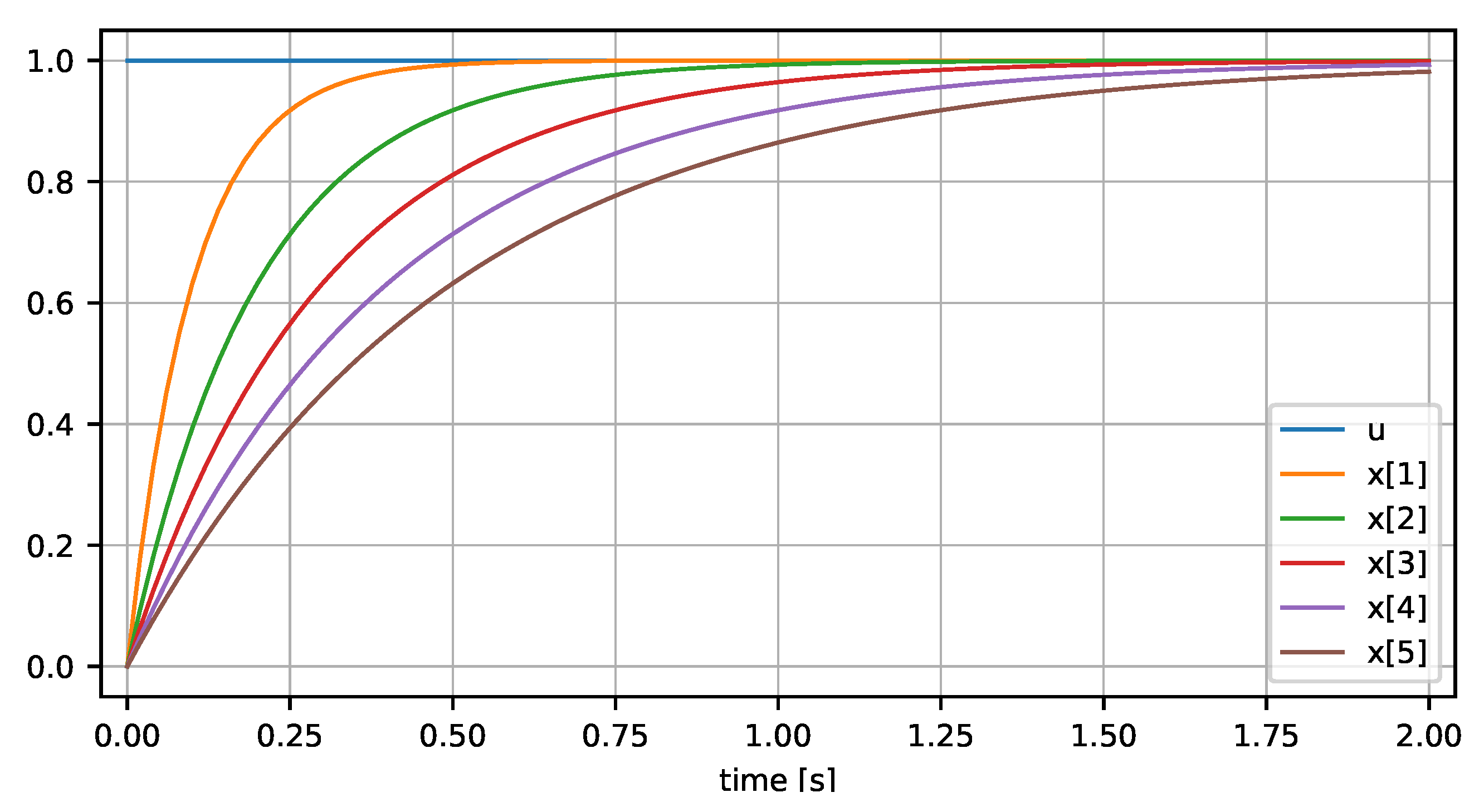
| Listing 8. Parameter variation of model firstOrder resulting in one Signal Table based on five simulations where the first independent variable is "time" and the second independent variable is "T" with values = 0.1, 0.2, 0.3, 0.4, 0.5. |
 |
| Listing 9. Parameter variation of model firstOrder resulting in one Signal Table based on 5 × 3 simulations in which the first independent variable is "time", the second independent variable is "T" with values = 0.1, 0.2, 0.3, 0.4, 0.5, and the third independent variable is "k" with values = 0.7, 0.8, 0.9. |
 |
| Listing 10. Parameter variation of model firstOrder resulting in one Signal Table based on 15 simulations in which the first independent variable is "time" and the second independent variable is "run" with values = 1, 2, …, 15. |
 |
| Listing 11. Signal Table of a Monte Carlo Simulation run where the parameter k is defined with a Uniform distribution in the range 0.7 . . . 1.1. |
 |
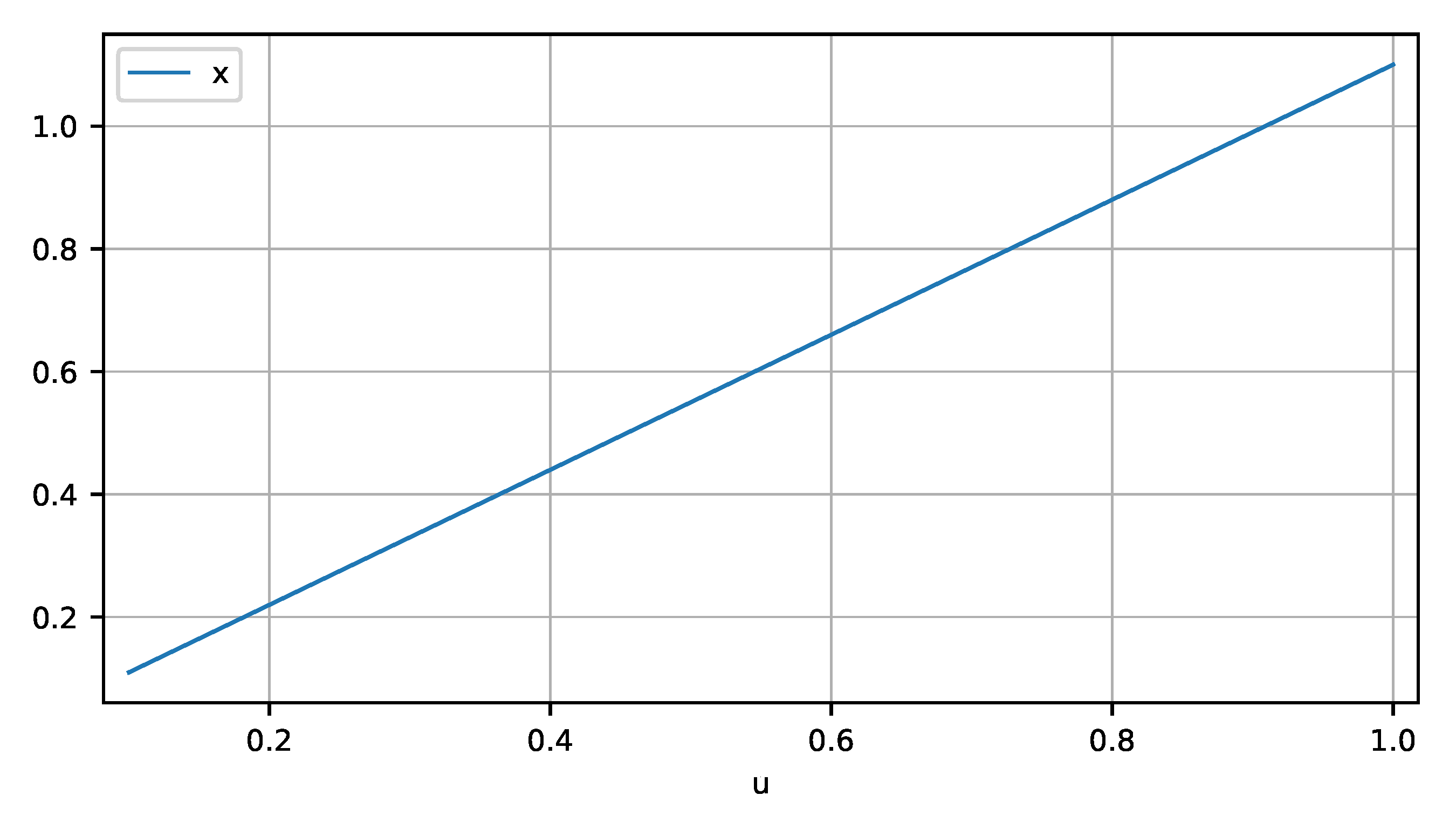
3.3.3. Steady-State Simulation
| Listing 12. Steady-state simulations of model firstOrder resulting in one Signal Table. |
 |
3.4. Missing Values
- In the Julia language, a missing value of any type is represented by the value missing. The properties of this design (no efficiency degradation, small memory overhead) are discussed in a blog posting (https://julialang.org/blog/2018/06/missing/, accessed on 30 July 2022).
- In the R programming language (https://www.r-project.org/, accessed on 30 July 2022), a missing value is represented by the value NA (https://rlang.r-lib.org/reference/missing.html, accessed on 30 July 2022), which is converted to a type-specific missing value.
- In Python, there is no dedicated missing value; instead, NaN is used for floating-point types and None is used for Python objects (https://jakevdp.github.io/PythonDataScienceHandbook/03.04-missing-values.html, accessed on 30 July 2022). Certain packages, such as pandas, have special support to make this more convenient.
- In MATLAB, a missing value is supported for certain data types and is represented by the value missing, which is converted to a type-specific value (https://www.mathworks.com/help/matlab/data_analysis/missing-data-in-matlab.html, accessed on 30 July 2022).
- In JSON, a missing value of any type is represented by the value null.
3.5. Signal Tables on File
- A dictionary of type SignalTable, Var, Par, Map is stored as a JSON object with an additional element "_class":"<kind>", for example, "_class":"Var".
- An array with more than one dimension is stored as a JSON object with additional information. For example, a Float32 matrix with 4 rows and 2 columns and with values = [11 12; 21 22; 31 32; 41, 42] is stored as a JSON object as shown in Listing 13. Note, the elements of the matrix are stored in a vector in column-major ordering.
Listing 13. JSON object of a Float32 matrix with values = [11 12; 21 22; 31 32; 41, 42]. - The "values" and "value" elements of a signal are not written on file if the key "alias" is present. In Julia, the "values" and "value" data of alias signals are present only once and are referenced from corresponding alias signals. When writing to file, the parent alias "values" and "value" data is written on file, while the data of the child alias signals (identified by the "alias" key) are not stored on file. The compression is thus somewhat less than with the DSRES format sketched in Section 2.2 as negative alias signals are not specially handled. In object-oriented modeling, trivial equations of the form often occur. In the DSRES format, the data of one of these variables is stored. With a Signal Table, the data of two of these variables is stored (). This is similar to FMI 3.0 [5], in which negative alias variables are not supported in order to simplify the FMI description (in FMI 1 and FMI 2 [4], negative alias variables are supported).
| Listing 14. Commands to store sigTable2 from Listing 4 in JSON format on file. |
 |
| Listing 15. Commands to store sigTable2 from Listing 4 in HDF5 format on file. |
 |
4. Conclusions and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Predefined Attributes of a Signal Table
| Key | Value | Value |
|---|---|---|
| Type | Description | |
| "info" | String | Short description of signal. |
| "independent" | Bool | = true, if independent variable (i-th independent variable is i-th Var in signal
table with "independent" = true). If not present, "independent" = false. |
| "values" | Any | See Section 3.2. Elements have units defined with attribute "unit". |
| "alias" | String | Key of alias signal (see caption). |
| "unit" | String | Unit of all signal elements, e.g., "kg*m*s^2". |
| String Array | unit is unit of variable element . | |
| "displayUnit" | String | Display "values" with respect to "displayUnit". using "displayUnit" for all signal elements. |
| String Array | displayUnit is display unit of variable element . | |
| "start" | Any | Initial value of variable. |
| "fixed" | Bool | = true, if the variable value is "start" after initialization. = false, if the variable value is "start" before initialization (default = false). |
| "nominal" | Float64 | Nominal value of all variable elements. |
| "unbounded" | Bool | = true indicates that during time integration, the variable gets values much larger than its nominal value. Typically, relative tolerance is set to zero to increase numerical stability, see FMI 3.0 [5] (default = "false"). For example, the rotation angle of a vehicle shaft would be typically defined with "unbounded=true". |
| "variability" | String | = "continuous", "clocked", "clock", "discrete" or "tunable". "tunable" is similar to "discrete" but characterizes a parameter that is changed/tuned during simulation (default = "continuous"). |
| "state" | Bool | = true, if signal is a (continuous, clocked or discrete) state (default = false). |
| "der" | String | Key of variable that is the derivative of the variable with respect to the first independent variable. |
| "previous" | String | Key of variable that is the previous value of the variable at the current clock tick. ("variability" must be "clocked" or "clock"). |
| "clock" | String | Key of clock associated with variable (values is only defined at clock ticks and otherwise is missing). |
| "interpolation" | String | Interpolation of signal points (= "linear" or "none"). If not provided, "interpolation" is deduced from "variability" and otherwise it is "linear". |
| "extrapolation" | String | Extrapolation outside the values of the independent signal (= "none", "HoldLastPoint", "LastTwoPoints"; default = "none"). |
- Multiplication is characterized by "*" in Unitful and by "." in Modelica.
- Exponentiation is characterized by "^" in Unitful and without a symbol in Modelica.
- Degree is characterized by "°" in Unitful and by "deg" in Modelica.
| Key | Value | Value |
|---|---|---|
| Type | Description | |
| "info" | String | Short description of signal. |
| "value" | Any | Value of any type (does not depend on independent signals). |
| "alias" | String | Key of alias signal (see caption). |
| "unit" | String | Unit of all signal elements, e.g., "kg*m*s^2". |
| String Array | unit[j1,j2,…] is unit of variable element . | |
| "displayUnit" | String | Display "value" with respect to "displayUnit". using "displayUnit" for all signal elements. |
| String Array | displayUnit[j1,j2,…] is display unit of variable element . | |
| "index1" | String | See example of Listing 10. |
| Key | Value | Value |
|---|---|---|
| Type | Description | |
| "unitFormat" | String | Format of the string representation of units(= "Unitful", "Modelica" or a tool specific format). |
| "model" | Map | Attributes defining the model that was used to generate
the Signal Table. Example for Modia: model = Map(name="FirstOrder", url="https://github.com/ModiaSim/Modia.jl/blob/main/test/TestFirstOrder.jl", line=16, commit="abd3f4ca053775e288e0fd1eff7b9b2ab3b2a372" Example for Modelica: model=Map(name="Modelica.Blocks.Examples.PID_Controller", url="https://github.com/modelica/ModelicaStandardLibrary/blob/master/Modelica/Blocks/package.mo", line=12, commit="8d090810980e1e2e51559721cdd4c267a4c849ae"). A model might use models from other libraries and also other resources like configuration files, tables, files defining the reference motion etc. All this information should be included with additional tool specific attributes. |
| "instantiation" | Map | Attributes defining the instantiation of the model with tool
specific attributes. Example for Modia: instantiation = Map(FloatType="Float64", evaluateParameters=true, logCode=true, logTiming=true) |
| "experiment" | Map | Attributes defining the setup of one simulation run. Example for Modia: experiment = Map(startTime=0.0, stopTime=10.0, interval=0.02, tolerance=1e-6, algorithm="CVODE_BDF", dtmax=0.1, log=true). Attributes startTime, stopTime, interval, tolerance are standardized. startTime, stopTime, interval are with respect to the unit defined for the first independent variable. tolerance is the relative tolerance. All other attributes are tool specific. |
| "statistics" | Map | The statistics of the simulation run or the
simulation runs that produced the Signal Table in form of
tool specific attributes. Example for Modia: statistics = Map(nResults = 501, nf_total = 1248, nf_integrator = 745, nf_zeroCrossings = 0, …) |
| "tool" | Map | Attributes defining the tool that was used to
simulate the model. Example for Modia: tool = Map(name="Modia", version="0.9.2", uuid="cb905087-75eb-5f27-8515-1ce0ec8e839e", url="https://github.com/ModiaSim/Modia.jl/releases/tag/v0.9.2", commit="2948cdd8d57c977ddbbb73bc806670a014572652") Example for OpenModelica: tool = Map(name="OpenModelica", version="1.19.2", url="https://build.openmodelica.org/omc/builds/windows/releases/1.19/2/64bit/OpenModelica-v1.19.2-64bit.exe"). |
| "environment" | Map | Attributes defining the environment in which the tool was used.
Example for Julia: environment = Map(name="Julia", version="1.7.3", url="https://julialang-s3.julialang.org/bin/winnt/ x64/1.7/julia-1.7.3-win64.zip") |
| "system" | Map | Attributes defining the operating system and the processor. Example: system = Map(name="Microsoft Windows 10 Enterprise", build="10.0.19044", processor="Intel64 Family 6 Model 142 1919 MHz", RAM="32.575 MB"). |
References
- Gall, L.; Otter, M.; Reiner, M.; Schäfer, M.; Tobolář, J. Continuous Development and Management of Credible Modelica Models. In Proceedings of the 14th International Modelica Conference, Linköping, Sweden, 20–24 September 2021; pp. 359–372. [Google Scholar] [CrossRef]
- Modelica Association. Modelica—A Unified Object-Oriented Language for Systems Modeling. Language Specification Version 3.5. 2021. Available online: https://specification.modelica.org/maint/3.5/MLS.pdf (accessed on 30 July 2022).
- Blochwitz, T.; Otter, M.; Akesson, J.; Arnold, M.; Clauss, C.; Elmqvist, H.; Friedrich, M.; Junghanns, A.; Mauss, J.; Neumerkel, D.; et al. Functional Mockup Interface 2.0: The Standard for Tool independent Exchange of Simulation Models. In Proceedings of the 9th International Modelica Conference, München, Germany, 3–5 September 2012; pp. 173–184. [Google Scholar] [CrossRef]
- Modelica Association. Functional Mock-up Interface for Model Exchange and Co-Simulation—Version 2.0.3. 2021. Available online: https://github.com/modelica/fmi-standard/releases/download/v2.0.3/FMI-Specification-2.0.3.pdf (accessed on 30 July 2022).
- Modelica Association. Functional Mock-up Interface Specification—Version 3.0. 2022. Available online: https://fmi-standard.org/docs/3.0/ (accessed on 30 July 2022).
- Zimmer, D. Equation-Based Modeling of Variable-Structure Systems. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2010. [Google Scholar] [CrossRef]
- Tinnerholm, J.; Pop, A.; Sjölund, M. A Modular, Extensible, and Modelica-Standard-Compliant OpenModelica Compiler Framework in Julia Supporting Structural Variability. Electronics 2022, 11, 1772. [Google Scholar] [CrossRef]
- Pfeiffer, A.; Bausch-Gall, I.; Otter, M. Proposal for a Standard Time Series File Format in HDF5. In Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012; pp. 495–505. [Google Scholar] [CrossRef]
- Tiller, M.; Harman, P. Recon—Web and network friendly simulation data formats. In Proceedings of the 10th International Modelica Conference, Lund, Sweden, 10–12 March 2014; pp. 1081–1093. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Elmqvist, H.; Otter, M.; Neumayr, A.; Hippmann, G. Modia—Equation Based Modeling and Domain Specific Algorithms. In Proceedings of the 14th International Modelica Conference, Linköping, Sweden, 20–24 September 2021; pp. 73–86. [Google Scholar] [CrossRef]
- Otter, M.; Reiner, M.; Tobolář, J.; Gall, L.; Schäfer, M. Towards Modelica Models with Credibility Information. Electronics 2022, 11, 2728. [Google Scholar] [CrossRef]
- Viotti, J.C.; Kinderkhedia, M. A Survey of JSON-compatible Binary Serialization Specifications. arXiv 2022, arXiv:2201.02089. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otter, M. Signal Tables: An Extensible Exchange Format for Simulation Data. Electronics 2022, 11, 2811. https://doi.org/10.3390/electronics11182811
Otter M. Signal Tables: An Extensible Exchange Format for Simulation Data. Electronics. 2022; 11(18):2811. https://doi.org/10.3390/electronics11182811
Chicago/Turabian StyleOtter, Martin. 2022. "Signal Tables: An Extensible Exchange Format for Simulation Data" Electronics 11, no. 18: 2811. https://doi.org/10.3390/electronics11182811
APA StyleOtter, M. (2022). Signal Tables: An Extensible Exchange Format for Simulation Data. Electronics, 11(18), 2811. https://doi.org/10.3390/electronics11182811











