Study of Breakdown Voltage Stability of Gas-Filled Surge Arresters in the Presence of Gamma Radiation †
Abstract
1. Introduction
2. Experimental Method
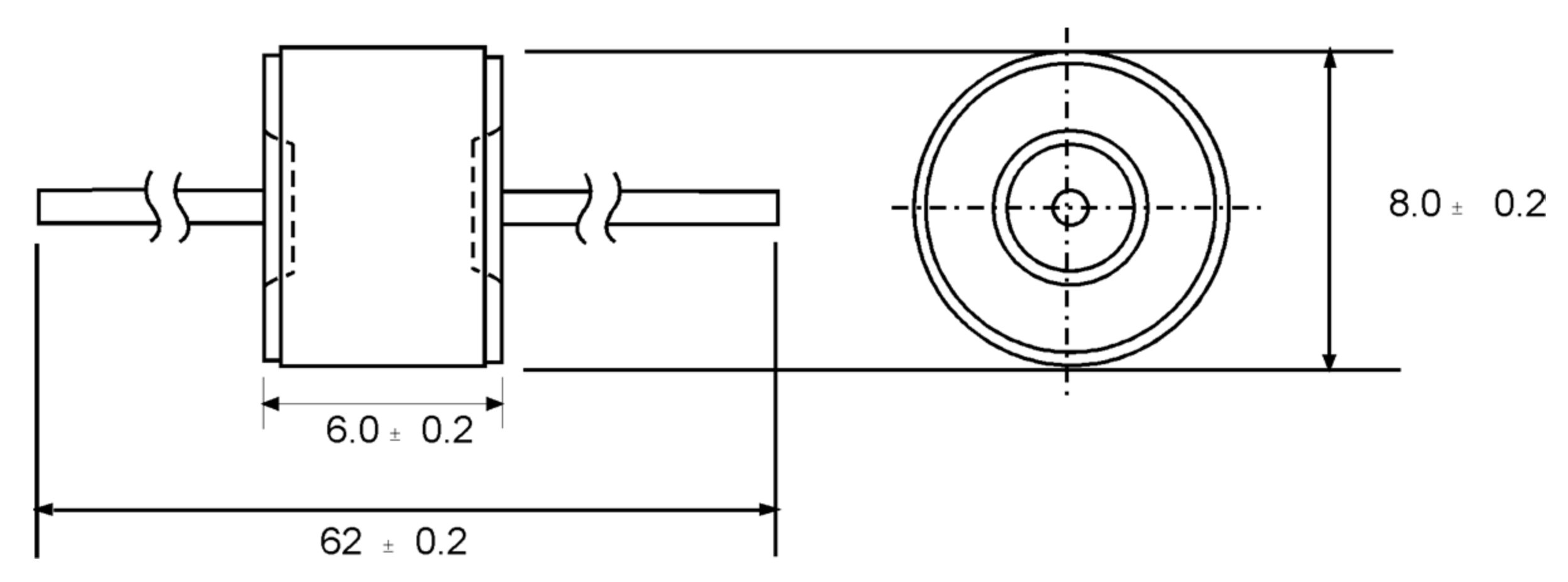
2.1. Experimental Used Component
2.2. The Source of Gamma Radiation
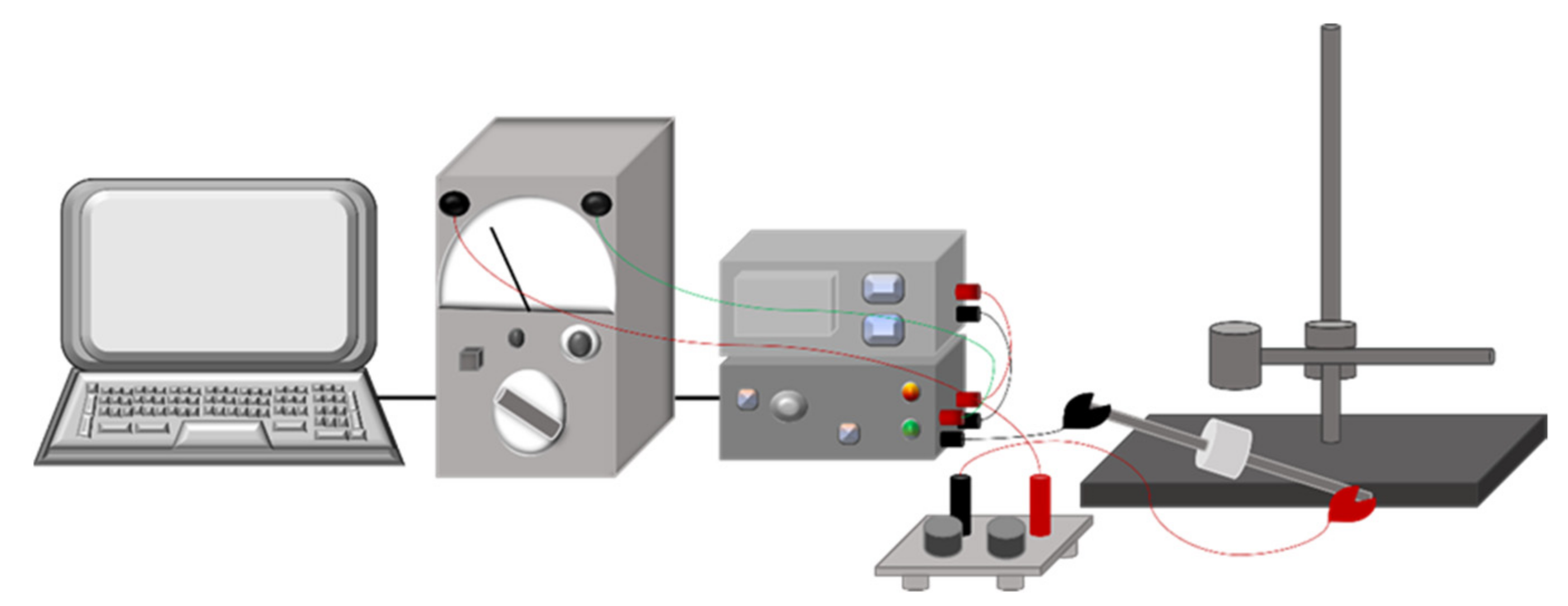
2.3. Experimental Procedure
- -
- the computer, through which the parameters are set, activates the software and collects the data;
- -
- DC high voltage source, step voltage generator and digital subsystem;
- -
- source of radiation;
- -
- gas-filled surge arrester.
3. Results and Discussion
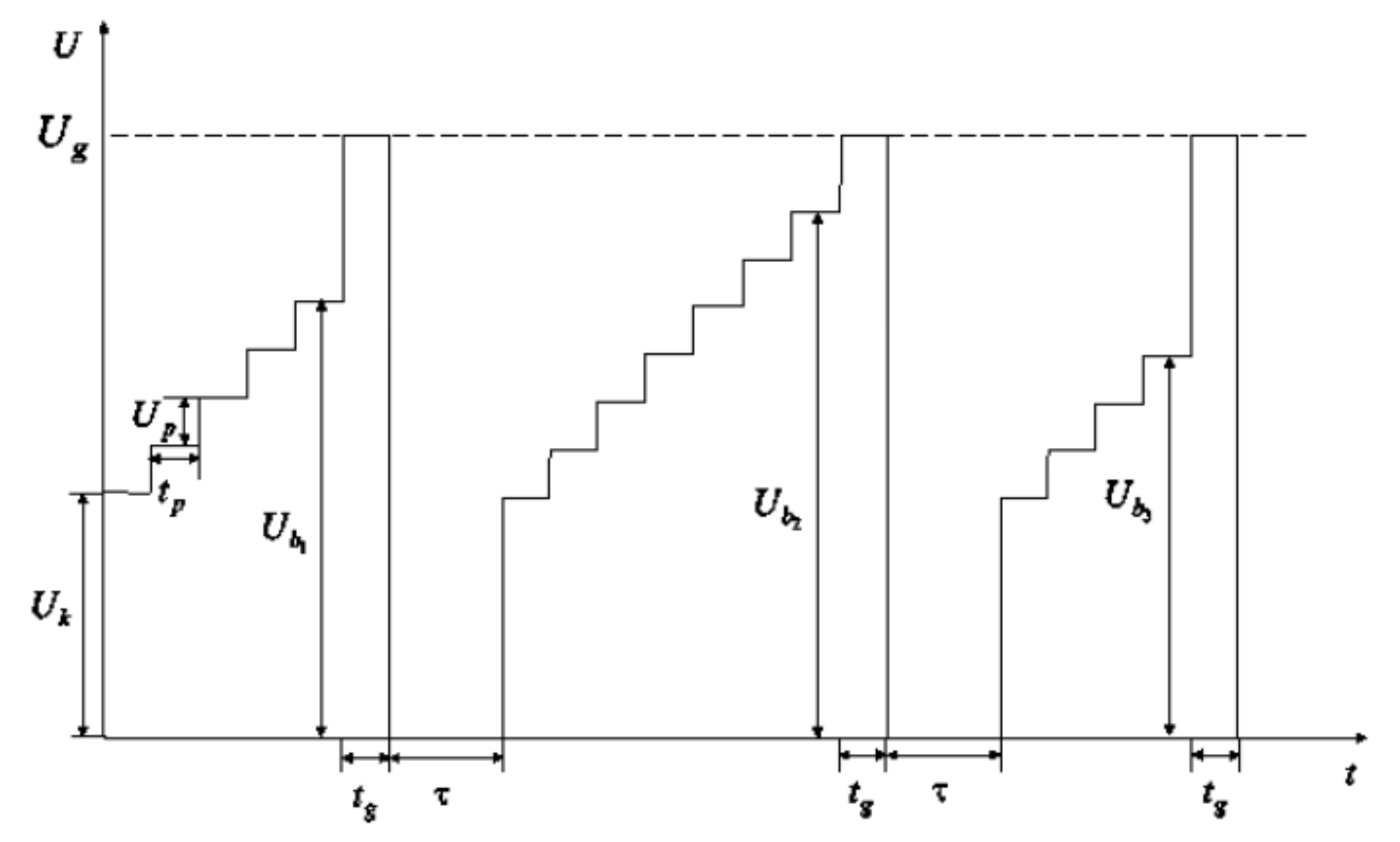
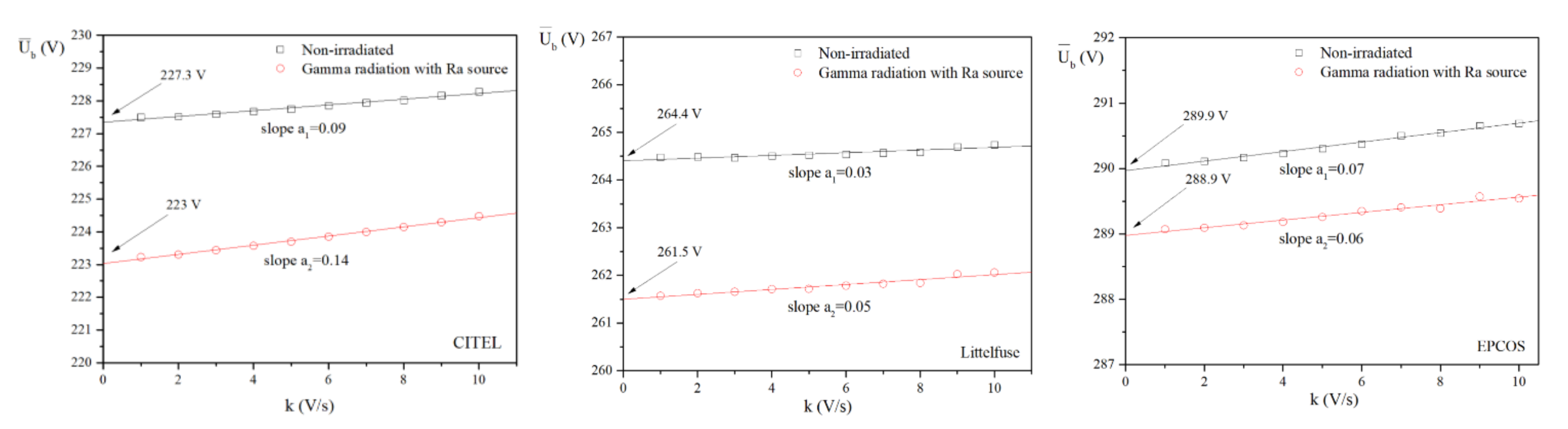
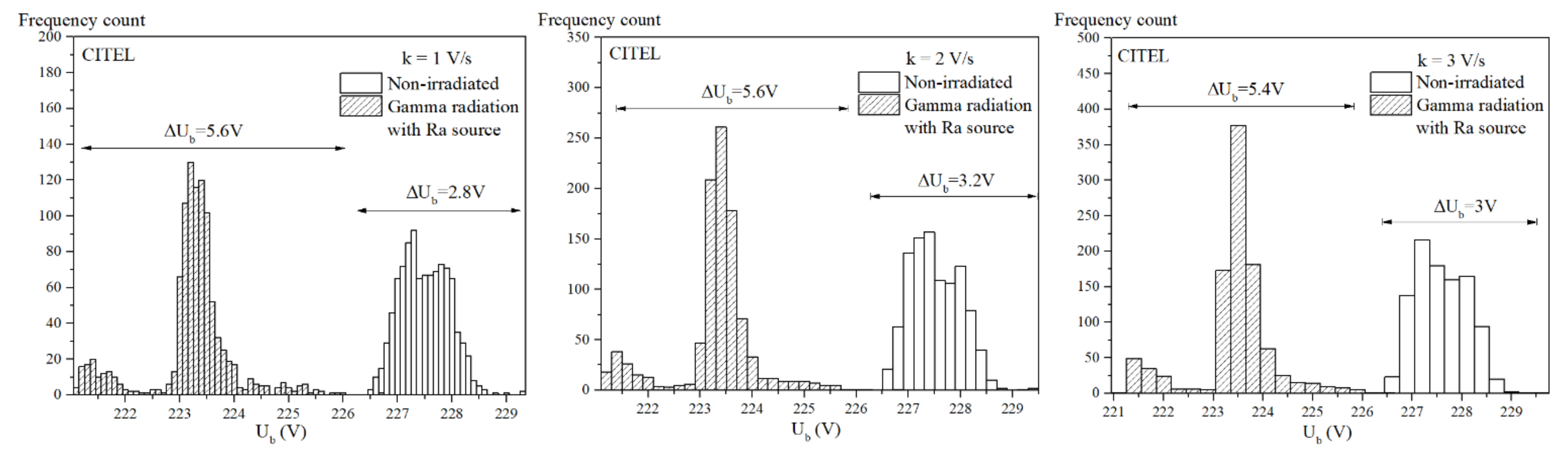
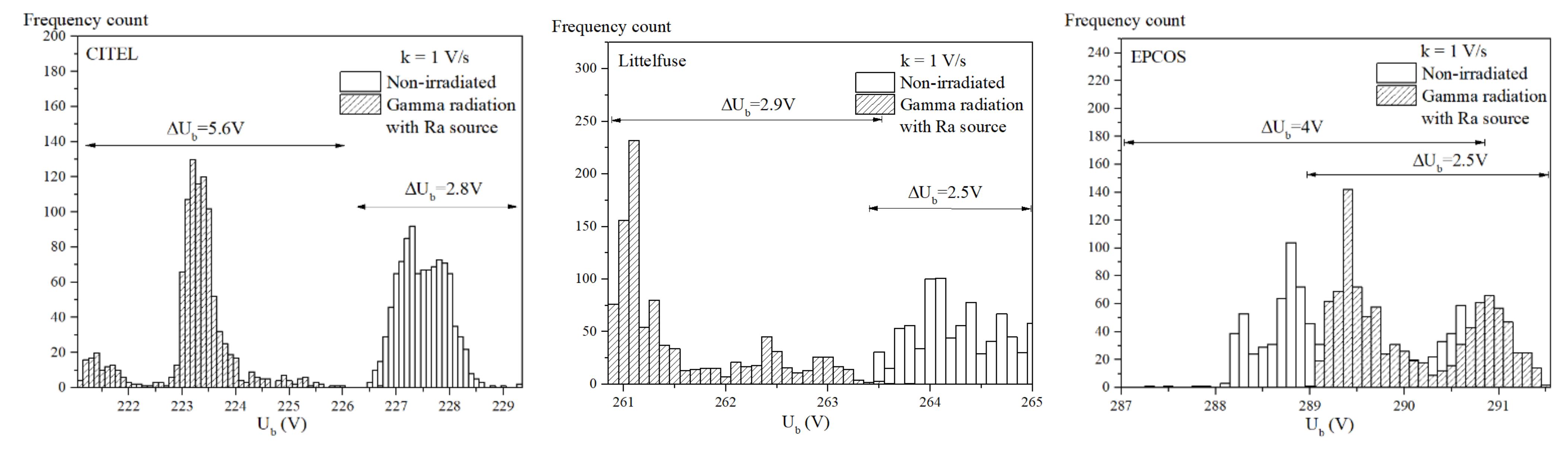
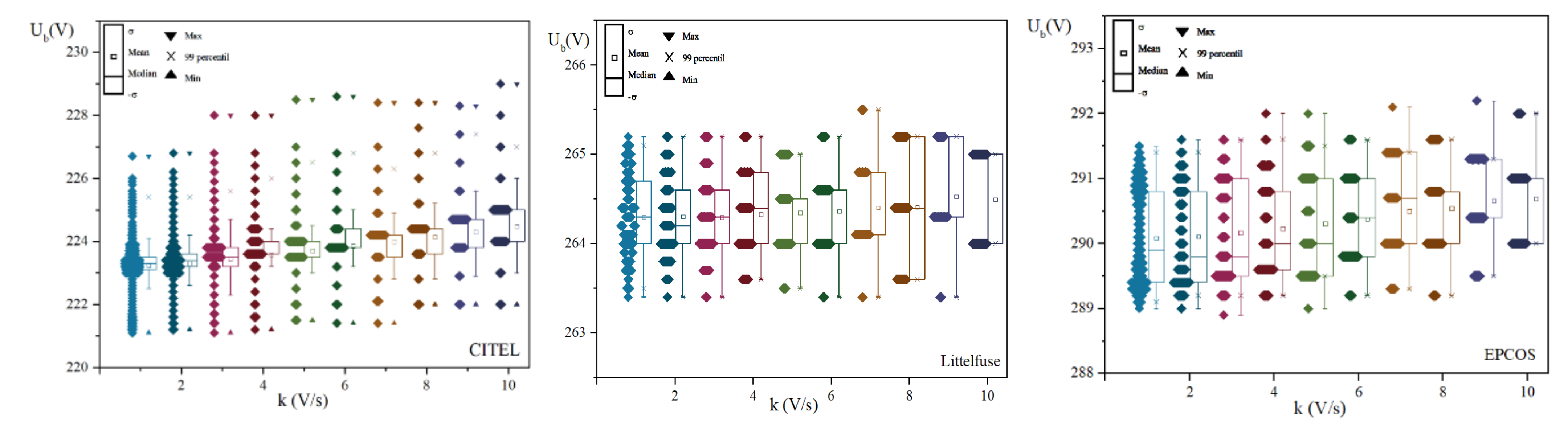
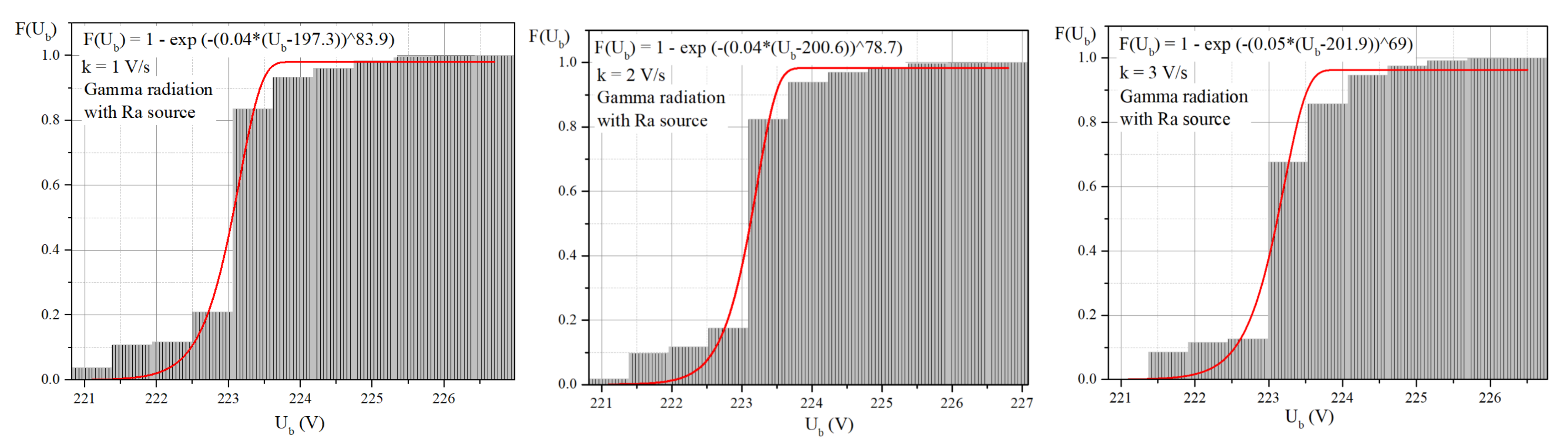
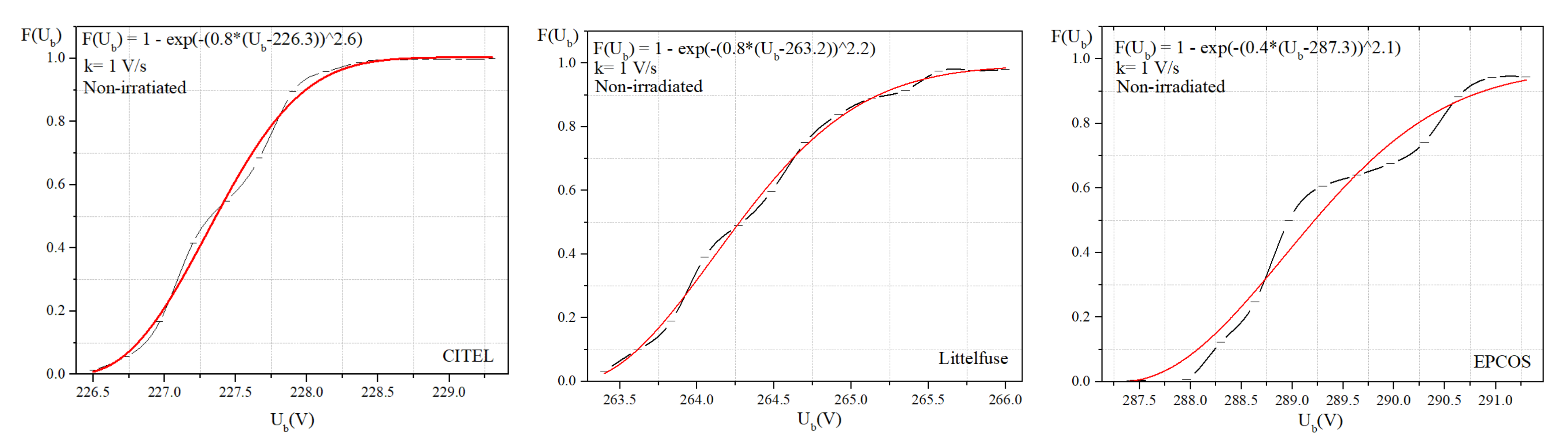
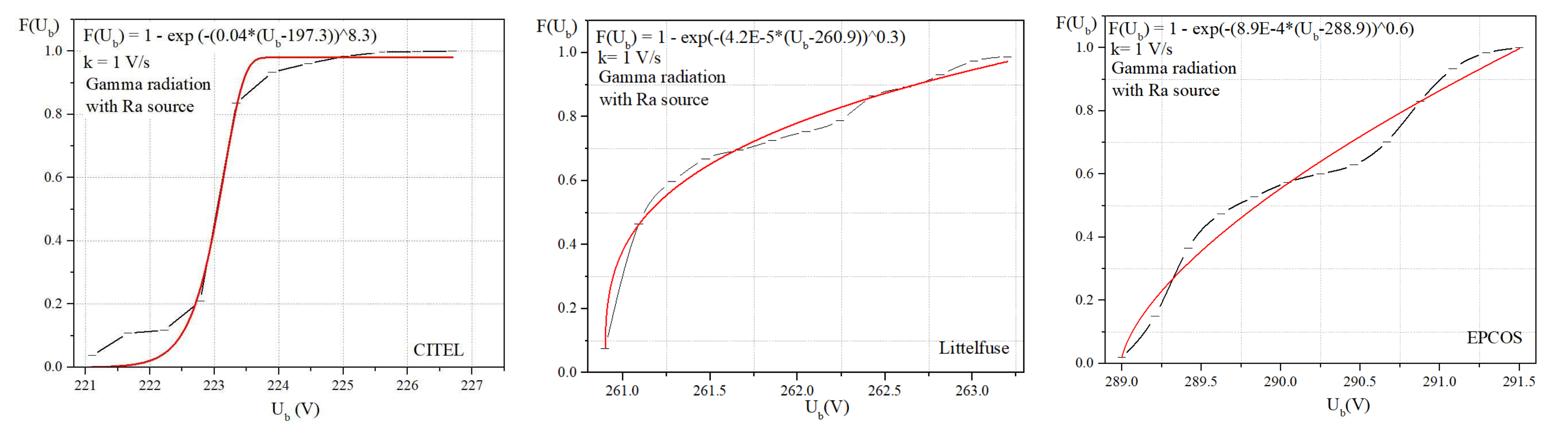
3.1. Statistical Analysis of Breakdown Voltage
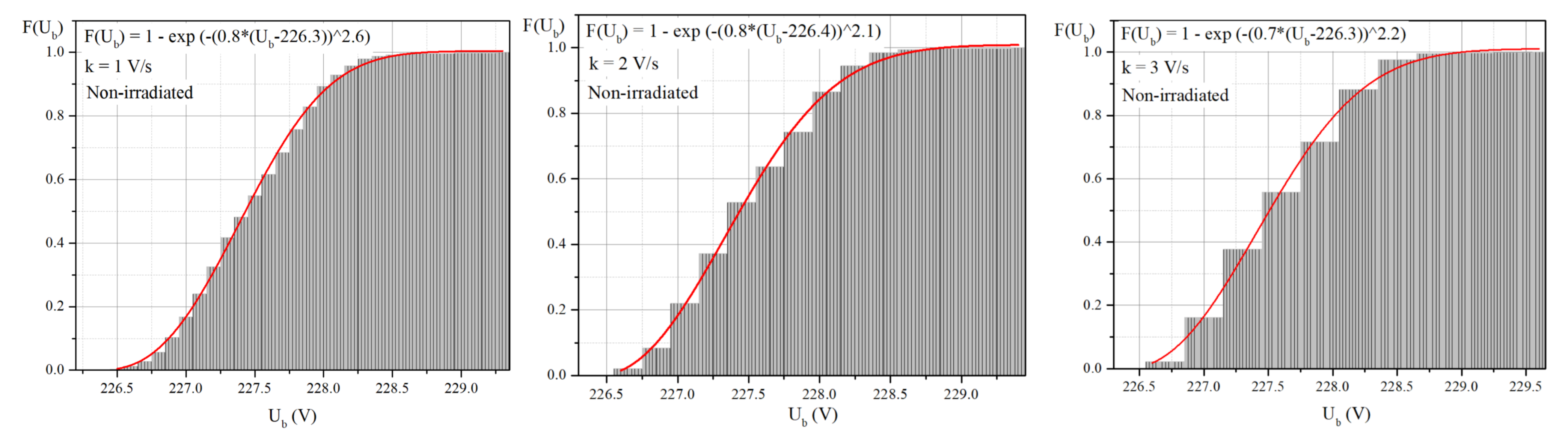
3.2. The Weibull Distribution and Parameters Estimation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Živković, M.; Dimitrijević, N.; Živanović, E. Statistical Analysis of Breakdown Voltage of Citel Gas-filled Surge Arrester. In Proceedings of the 32nd International Conference on Microelectronics, Niš, Serbia, 12–14 September 2021; pp. 113–116. [Google Scholar]
- Pejović, M.M. Introduction to Electrical Gas Discharges. Gas Electronic Components, Chapter 8; University of Niš, Faculty of Electronic Engineering: Niš, Serbia, 2008; pp. 124–128. [Google Scholar]
- Pham, C.D.; Crevenat, V.; Gannac, Y. Empirical model of the impulse voltage-time characteristic of gas discharge tube. In Proceedings of the 35th International Conference on Lightning Protection, Colombo, Sri Lanka, 20–26 September 2021. [Google Scholar]
- Gannac, Y.; Leduc, G.; Pham, C.-D.; Crevenat, V. 8/20 and 10/350 surges behaviour of a gas discharge tube according to gas pressure. Electr. Pow. Syst. Res. 2021, 197, 107302. [Google Scholar] [CrossRef]
- Huttner, L.; Jurcacko, L.; Valent, F.; Ehrhardt, A.; Schreiter, S.; Rock, M. Basic problems and solution of the encapsulation of a low-voltage spark gap with arc splitter chamber. J. Electric. Eng. 2012, 63, 103–108. [Google Scholar] [CrossRef][Green Version]
- Finis, G.; Wetter, M.; Meyer, T. New spark-gap technology with efficient line-follow current suppression for the protection of powerful LV distribution systems. In Proceedings of the 33rd International Conference on Lightning Protection, Estoril, Portugal, 25–30 September 2016. [Google Scholar]
- Rozman, R. Gas Discharge Tube Assemblies. U.S. Patent 2020/0161073 A1, 12 May 2020. [Google Scholar]
- Tsovilis, T.E. Critical insight into performance requirements and test methods for surge protective devices connected to low-voltage power systems. IEEE Trans. Pow. Del. 2021, 36, 3055–3064. [Google Scholar] [CrossRef]
- Arbutina, D.S.; Vasić-Milovanović, A.I.; Nedić, T.M.; Janićijević, A.J.; Timotijević, L.B. Possibility of Achieving an Acceptable Response Rate of Gas-Filled Surge Arresters by Substitution of Alpha Radiation Sources by Selection of Electrode Material and the Electrode Surface Topography. Nucl. Technol. Radiat. Prot. 2020, 35, 223–234. [Google Scholar] [CrossRef]
- Osmokrović, P.; Vasić, A.; Živić, T. The Influence of the Electric Field Shape on the Gas Breakdown Under Low Pressure and Small Inter-Electrode Gap Conditions. IEEE Transactions on Plasma Science 2005, 33, 1677–1681. [Google Scholar] [CrossRef]
- Osmokrović, P.; Živić, T.; Lončar, B.; Vasić, A. The Validity of the General Similarity Law for Electrical Break down of Gases. Plasma Sources Sci. Technol. 2006, 15, 703–713. [Google Scholar] [CrossRef]
- Stanković, K.; Alimpijević, M. Free-Electron Gas Spectrum Uniqueness in the Mixture of Noble Gases. Contrib. Plasma Phys. 2016, 56, 126–133. [Google Scholar] [CrossRef]
- Pejović, M.M.; Nešić, N.T.; Pejović, M.M.; Brajović, D.V.; Denić, I.V. Investigation of Post-Discharge Processes in Nitrogen at Low Pressure. Phys. Plasmas 2012, 19, 123512. [Google Scholar] [CrossRef]
- Živanović, E. Influence of combined gas and vacuum breakdown mechanisms on memory effect in nitrogen. Vacuum 2014, 107, 62–67. [Google Scholar] [CrossRef]
- Lucchini, F.; Marconato, N.; Bettini, P. Automatic Optimization of Gas Insulated Components Based on the Streamer Inception Criterion. Electronics 2021, 10, 2280. [Google Scholar] [CrossRef]
- Deng, S.; Morrison, A.P.; Guo, Y.; Teng, C.; Chen, M.; Cheng, Y.; Liu, H.; Xiong, X.; Yuan, L. Design of a Real-Time Breakdown Voltage and On-Chip Temperature Monitoring System for Single Photon Avalanche Diodes. Electronics 2021, 10, 25. [Google Scholar] [CrossRef]
- Vavilov, V.S.; Ukhin, H.A. Radiation Effects in Semiconductors and Semiconductors Devices, 1st ed.; Consultants Bureau: New York, NY, USA, 1977. [Google Scholar]
- Stojadinović, N.; Djorić-Veljković, S.; Davidović, V.; Golubović, S.; Stanković, S.; Prijić, A.; Prijić, Z.; Manić, I.; Danković, D. NBTI and irradiation related degradation mechanisms in power VDMOS transistors. Microelectron. Realibaility 2018, 88–90, 135–141. [Google Scholar] [CrossRef]
- Djorić-Veljković, S.; Manić, I.; Davidović, V.; Danković, D.; Golubović, S.; Stojadinović, N. Annealing of Radiation-Induced Defects in Burn-in Stressed Power VDMOSFETs. Nucl. Technol. Radiat. Prot. 2011, 26, 18–24. [Google Scholar] [CrossRef]
- Martínez, P.J.; Maset, E.; Martín-Holgado, P.; Morilla, Y.; Gilabert, D.; Sanchis-Kilders, E. Impact of Gamma Radiation on Dynamic RDSON Characteristics in AlGaN/GaN Power HEMTs. Materials 2019, 12, 2760. [Google Scholar] [CrossRef] [PubMed]
- Rubinjoni, L.; Karadžić, K.; Lončar, B. Influence of Gamma Radiation on Gas-Filled Surge Arresters. In Use of Gamma Radiation Techniques in Peaceful Applications; Chapter 13; Almayah, B.A., Ed.; IntechOpen: London, UK, 2019. [Google Scholar]
- Živanović, E.; Veljković, S.; Živković, M.; Pejović, M. Reliability of various type of gas-filled surge arresters under DC discharge. In Proceedings of the 31st International Conference on Microelectronics, Niš, Serbia, 16–18 September 2019; pp. 113–116. [Google Scholar]
- Živanović, E.; Živković, M.; Pejović, M. The Evolution of Breakdown Voltage and Delay Time Under High Overvoltage for Different Types of Surge Arresters. Facta Univ. Ser. Electron. Energetics 2021, 34, 307–322. [Google Scholar] [CrossRef]
- Pejović, M.M.; Pejović, M.M. Investigation of breakdown voltage and time delay of gas-filled surge arresters. J. Phys. D Appl. Phys. 2006, 39, 4417–4422. [Google Scholar] [CrossRef]
- Lončar, B.; Vujisić, M.; Stanković, K.; Aranđić, D.; Osmokrović, P. Radioactive Resistance of Some Commercial Gas Filled Surge Arresters. In Proceedings of the 26th International Conference on Microelectronics, Niš, Serbia, 11–14 May 2008; pp. 587–590. [Google Scholar]
- CITEL Surge Protection. Available online: https://citel.fr/en/gdt/2-electrode (accessed on 6 July 2022).
- Littelfuse Surge Protection. Available online: https://www.littelfuse.com/media?resourcetype=datasheets&itemid=e3c9bc9e-6b2c-4bc9-92b2-d903d0925a22&filename=littelfuse-gdt-ac-cg3-datasheet (accessed on 6 July 2022).
- EPCOS Surge Protection. Available online: https://docs.rs-online.com/c5e1/A700000008614351.pdf (accessed on 6 July 2022).
- Ropp, R.C. The Alkaline Earths as Metals. In Encyclopedia of the Alkaline Earth Compounds, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 1–23. [Google Scholar]
- Gad, S.C. Radium. In Encyclopedia of Toxicology, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 44–45. [Google Scholar]
- Pejović, M.; Živanović, E.; Stojanović, M. Xenon-filled diode performance under influence of low doses of gamma radiation. Appl. Radiat. Isot. 2022, 184, 110207. [Google Scholar] [CrossRef]
- Pejović, M.M. Digital system for vacuum and gas-filled devices testing. Rev. Sci. Instrum. 2005, 76, 015102. [Google Scholar] [CrossRef]
- Pejović, M.M.; Milosavljević, Č.S.; Pejović, M.M. The estimation of static breakdown voltage for gas-filled tubes at low pressures using dynamic method. IEEE Trans. Plasma Sci. 2003, 31, 776–781. [Google Scholar] [CrossRef]
- Živanović, E.; Maluckov, Č. Investigation of statistical behaviour of electrical breakdown voltage distribution for nitrogen-filled diode at 13.3 mbar pressure. Contrib. Plasma Phys. 2018, 58, 293–301. [Google Scholar] [CrossRef]
- Müller, P.H.; Neumann, P.; Storm, R. Tafeln der Mathematischen Statistik; VEB Fachbuchverlag: Leipzig, Germany, 1973. [Google Scholar]
- Lai, C.-D.; Pra Murthy, D.N.; Xie, M. Weibull Distributions and Their Applications; Chapter 2, Springer Handbook of Engineering Statistics; Pham, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 63–78. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Larsen, R.J.; Marx, M.L. An Introduction to Mathematical Statistics and Its Applications, 5th ed.; Pearson Education, Inc.: London, UK, 2012; pp. 221–280. [Google Scholar]
- Electromagnetic Pulse (EMP) Protection and Resilience Guidelines for Critical Infrastructure and Equipment, National Coordinating Center for Communications (NCC), Unclassified, National Cybersecurity and Communications Integration Center Arlington, 2019, Virginia, USA. pp. 1–133. Available online: https://michaelmabee.info/electromagnetic-pulse-emp-protection-and-resilience-guidelines/ (accessed on 6 July 2022).
- Tsovilis, T.E.; Topcagic, Z. DC overload behavior of low-voltage varistor-based surge protective devices. IEEE Trans. Power Deliv. 2020, 35, 2541–2543. [Google Scholar] [CrossRef]
| Specifications of Gas-Filled Surge Arresters | ||||||||
|---|---|---|---|---|---|---|---|---|
| Component’s Manufacturer | Operating Voltage AC (V) | Breakdown Voltage in the dc Mode (V) | DC Breakdown-Typical (V) | Insulation Resistance (GΩ) | Capacitance (pF) | Arc Voltage-on State Voltage (V) | Nominal Impulse Discharge Current (8/20 μs) (kA) | Impulse Sparkover Voltage (1.2/50 µs/6 kV) |
| CITEL | 230 | 184 to 276 | 230 | 10 | <0.8 | ~30 | 25 | <900 |
| Littelfuse | 230 | 184 to 276 | 230 | 10 | <1.5 | ~15 | 20 | <700 |
| EPCOS | 230 | 196 to 264 | 230 | 10 | <1.5 | ~12 | 10 | <700 |
| k (V/s) | B | Ua | d | R2 | χ2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Non- Irradiated | Irradiated | Non- Irradiated | Irradiated | Non- Irradiated | Irradiated | Non- Irradiated | Irradiated | Non- Irradiated | Irradiated | |
| 1 | 0.8 | 0.04 | 226.3 | 197.3 | 2.6 | 8.3 | 0.996 | 0.882 | 0.00016 | 0.00320 |
| 2 | 0.7 | 0.04 | 226.4 | 200.6 | 2.1 | 8.7 | 0.995 | 0.991 | 0.00079 | 0.00295 |
| 3 | 0.7 | 0.05 | 224.3 | 201.9 | 2.9 | 6.9 | 0.988 | 0.855 | 0.00157 | 0.00438 |
| k = 1 V/s Component | B | Ua | d | R2 | χ2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Non- Irradiated | Irradiated | Non- Irradiated | Irradiated | Non- Irradiated | Irradiated | Non- Irradiated | Irradiated | Non- Irradiated | Irradiated | |
| CITEL | 0.8 | 0.04 | 226.3 | 197.3 | 2.6 | 8.3 | 0.996 | 0.882 | 0.00023 | 0.00320 |
| Littelfuse | 0.8 | 4.2 × | 223.2 | 260.9 | 2.2 | 0.3 | 0.997 | 0.992 | 0.00036 | 0.00196 |
| EPCOS | 0.4 | 8.9 × | 287.3 | 288.9 | 2.1 | 0.6 | 0.979 | 0.976 | 0.00152 | 0.00318 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Živanović, E.; Živković, M.; Veljković, S. Study of Breakdown Voltage Stability of Gas-Filled Surge Arresters in the Presence of Gamma Radiation. Electronics 2022, 11, 2447. https://doi.org/10.3390/electronics11152447
Živanović E, Živković M, Veljković S. Study of Breakdown Voltage Stability of Gas-Filled Surge Arresters in the Presence of Gamma Radiation. Electronics. 2022; 11(15):2447. https://doi.org/10.3390/electronics11152447
Chicago/Turabian StyleŽivanović, Emilija, Marija Živković, and Sandra Veljković. 2022. "Study of Breakdown Voltage Stability of Gas-Filled Surge Arresters in the Presence of Gamma Radiation" Electronics 11, no. 15: 2447. https://doi.org/10.3390/electronics11152447
APA StyleŽivanović, E., Živković, M., & Veljković, S. (2022). Study of Breakdown Voltage Stability of Gas-Filled Surge Arresters in the Presence of Gamma Radiation. Electronics, 11(15), 2447. https://doi.org/10.3390/electronics11152447








