Abstract
Deep Learning (DL) is moving towards deploying workloads not only in cloud datacenters, but also to the local devices. Although these are mostly limited to inference tasks, it still widens the range of possible target architectures significantly. Additionally, these new targets usually come with drastically reduced computation performance and memory sizes compared to the traditionally used architectures—and put the key optimization focus on the efficiency as they often depend on batteries. To help developers quickly estimate the performance of a neural network during its design phase, performance models could be used. However, these models are expensive to implement as they require in-depth knowledge about the hardware architecture and the used algorithms. Although AI-based solutions exist, these either require large datasets that are difficult to collect on the low-performance targets and/or limited to a small number of target platforms and metrics. Our solution exploits the block-based structure of neural networks, as well as the high similarity in the typically used layer configurations across neural networks, enabling the training of accurate models on significantly smaller datasets. In addition, our solution is not limited to a specific architecture or metric. We showcase the feasibility of the solution on a set of seven devices from four different hardware architectures, and with up to three performance metrics per target—including the power consumption and memory footprint. Our tests have shown that the solution achieved an error of less than 1 ms (2.6%) in latency, 0.12 J (4%) in energy consumption and 11 MiB (1.5%) in memory allocation for the whole network inference prediction, while being up to five orders of magnitude faster than a benchmark.
1. Introduction
Due to its high demand for computational power, Deep Learning was mostly restricted to cloud datacenters for the training and inference. In recent years, the industry moved more and more towards deploying Deep Learning workloads directly to the local hardware, removing the need for cloud processing. This has multiple reasons, including the demand for more privacy, lower latency, and stand-alone solutions that do not rely on a network connection or remote datacenter. This shift was enabled by the increasing compute performance and efficiency of mobile and embedded hardware, as well as novel hardware developments, such as new vector-extensions [1] and dedicated AI accelerators [1,2,3], but also new software developments such as kernel libraries [4,5] and dedicated frameworks [6,7,8], as well as optimization techniques, such as quantization [9,10] and pruning [11].
Although this enabled developers to utilize Deep Learning in novel ways and applications that did not allow for cloud processing, such as Industry 4.0, control loops and new ways for users to interact with their devices (Radar-based gesture recognition like Google Soli: https://atap.google.com/soli/ (accessed on 25 May 2022)), it also makes the deployment of AI workloads more complicated: As the range of possible targets becomes increasingly more varied and diverse, not all targets can achieve the best performance through the same means. Different targets require different executors and libraries to achieve optimal performance for the intended workloads. This makes it more time consuming to optimize and deploy a workload to a certain target.
Another problem is that this makes it more difficult for developers to estimate the model performance on the set of intended targets during the model architecture definition. They could either deploy different iterations to the hardware target—requiring them to have access to all target devices and to optimize the workload before the deployment—or utilize a performance model for each target, which needs to be implemented by experts that can model the interactions of the hardware architecture and Deep Learning algorithms correctly.
As an alternative to handcrafted performance models, which are rarely provided by device manufacturers, we suggest an AI-based flow that does not require any knowledge about the hardware architecture, Deep Learning algorithms, or hardware-specific optimization strategies, as it learns from recorded benchmarking data and operates almost completely automated. Although performance predictions are not a new topic in research, we are aiming at finding a solution that is able to generate estimates with a reasonable accuracy without the huge cost in hardware, computation time, or working time of expensive experts that is required for some of the related publications—making our solution more accessible for developers and groups with more limited resources. In this work, we aim to showcase our solution that automatically collects benchmarking data and trains AI-based regression models on these datasets. This system operates in a layerwise fashion, by predicting the performance impact of each layer of the Deep Learning model based on its hyperparameters individually and adding these predictions up to estimate the performance for the inference of the entire model.
To prove its feasibility, we implemented and deployed this flow on a diverse set of targets and with multiple different performance metrics. The devices range from server-grade CPUs (Intel Xeon E5-2680v3) and GPUs (Nvidia Tesla K80 and A100) over consumer hardware (Intel Core i7-4790 and Nvidia GTX 980Ti) to mobile devices (ARM Mali T628 MP6 GPU and ARM Cortex-A72 CPU).
A key benefit of this approach is the portability as models can be created for any performance metric on any hardware architecture and software framework, as long as the relevant metrics can be measured precisely.
For the performance models, different regression techniques were evaluated, including XGBoosted Trees [12], Extremely Random Trees [13], but also linear regression, k-Nearest Neighbours, and multi-layer perceptrons [14].
The key contributions of our work are:
- Targeting implementations that have been generated by a search-based compiler instead of a math kernel library;
- Enabling the prediction of various performance metrics;
- Reducing the data collection effort by sampling from a set of representative workload configurations instead of randomly from the space of possible configurations;
- Showcasing its portability, allowing for its use on any hardware architecture and with every code generation flow, from high-performance to mobile hardware, CPUs to GPUs and LLVM [15], CUDA [16], or OpenCL [17] code;
- Using simple AI-based models that can be trained on moderately sized datasets, making this approach available for developers that do not have the means of some of the related publications.
The first section after the related work will explain the data collection and model training flow. The second section will be the evaluation, starting with layerwise evaluations and finishing with a full network inference case study.
2. Related Work
Many publications have already researched the implementation of performance models for various use cases. These works either focus on general purpose applications or specialize on Deep Learning use cases. Different methods were used to predict the performance, from analytic models to AI-based solutions.
2.1. Performance Prediction for General Purpose Applications
The precise calculation of the execution time of a program is a very complicated task and can be seen as an extension of the halting problem [18] as it does not only need to predict if a program finishes, but also when it is going to halt. Most of the publications listed in this section use various methods to estimate the runtime instead. These estimates are based on different metrics and parameters that have been extracted from the source or the compiled representation of the program.
Works such as those of Huang et al. [19] extract relevant data from the source of the program and use it as input for regression models, while Braun et al. [20] and Sun et al. [21] use the compiled programs to generate their features: Braun et al. [20] gathers information from the compiled PTX (Nvidia PTX developer documentation: https://docs.nvidia.com/cuda/parallel-thread-execution/ (accessed on 25 May 2022)) code using the CUDA Flux profiler [22] that extracts the instruction count, kernel launch parameters, and more data from it. Sun et al. [21] instrument the source using a modified version of clang [15]. It relies on extracted information about the number of variable assignments, branches, loops, and the MPI communication. The disadvantage of relying on the compiled representation of the program for the feature extraction is that the additional effort must be spent to compile it in the first place, increasing the required time and compute resources to generate the estimation. This can be especially problematic for automated solutions that require the rapid exploration of a large design space during their search (i.e., network architecture search for Deep Learning models).
Shafiabadi et al. [23,24] uses regression models to estimate the performance of OpenCL [17] programs on a specific AMD GPU architecture.
Nadeem et al. [25] uses template matching to predict the program execution time. Instead of implementing or training complicated models, a database with recordings of previously executed programs is kept. When a program has been executed, its configuration and measured performance data will be added to the database. The performance estimation for a new program is made by finding the closest match in the database. This solution is similar to k-Nearest Neighbors, but does not extrapolate between the closest neighbors. Instead only the closest match will be returned. No features are extracted from the source or compiled representation of the programs as the input arguments are used as input for the search. The benefit of such a solution is that it improves its accuracy throughout its use, but the limitation to launch parameters does limit its accuracy for the estimation of entire programs and also requires a large dataset of already seen examples to provide accurate estimates as no extrapolation between known samples is used. Additionally, the distance needs to be manually defined for the current search space and might depend on the targeted hardware environment.
These publications show two major differences from our own contribution: They try to estimate the performance for general purpose programs—this makes it much more complicated as no assumptions about the program structure and control flow can be made. This results in the second major difference: the need for sophisticated feature extraction steps or alternatives that are less expressive—as no easily available data can be used for the modeling.
2.2. Performance Prediction for Deep Learning Applications
The focus on the prediction of performance metrics for Deep Learning applications allows for certain simplifications in the approach: Deep Learning models usually are strictly sequential in their execution, which means that they do not contain any control flow operations, such as loops and branching, and are made up of similar building blocks—the layers. These layers execute only a limited set of operations, such as convolutions, matrix multiplication, the application of activation functions, or pooling, and their main difference is the configuration of their function kernels through hyperparameters. The related work regarding the performance prediction of Deep Learning workloads is mostly focused on GPU and HPC environments and targets the Deep Learning training process in addition to the inference for the performance prediction.
Kaufman et al. [26] use a graph neural network for the performance modeling of Deep Learning programs on Google’s CloudTPU [27] accelerators. Instead of relying on extracted or hand-selected features, it operates directly on the neural network graph and autonomously extracts the important data from it. This approach comes with certain disadvantages: it requires a large dataset for the training of the models, which is expensive and not always feasible for researchers and developers to collect, especially, when targeting multiple devices.
PALEO by Qi et al. [28] use a much simpler analytic approach instead. The strictly sequential nature of Deep Learning models is exploited by estimating the execution time of the individual layers and adding them up to calculate the total estimated execution time of the whole network. This simplification has also been used by multiple other publications (see the column layerwise estimate in Table 1 for an overview). A simple model is used to estimate the performance of a single layer. This model assumes that the execution of the layer consists of three consecutive steps: the loading of the data, the computation, and the write back of the result. Each step is calculated based on the number of memory transactions or FLOPs that are required for its execution and the memory bandwidth or computation performance provided by the target device. The separation of the workload in three sequential steps assumes that the underlying hardware architecture does not support any form of concurrency for these operations, which does not always hold up for all hardware targets.
The analytic predictions are scaled with an additional factor that has been set by comparing the estimates with real measurements to account for a non-optimal utilization of the device. This assumes a constant scaling factor across the entire configuration space for workloads, which is also unlikely to hold up for all target devices.
Justus et al. [29] use the same layerwise approach and combine it with a batchwise extension by calculating the execution time of a single batch during training and accumulating the estimates for all batches to the total training time. An AI-based regression model is used instead of an analytic solution and it is able to target different devices with a single model by adding the hardware configuration to the model inputs. We assume that this enables the prediction for unseen devices, but is most likely limited to similar hardware architectures, such as a specific GPU generation, and could make retraining the models more difficult when a new device is added to the dataset. We have decided to use one regression model per triplet of device, layer type and performance metric instead, which also allows us to further simplify each model.
Lattuada et al. [30] suggest a solution to the problems of Justus et al. [29], but do not use a layerwise approach. Instead, the neural network is described by using the number of occurrences of the different layer types and the total FLOPs as input features.
Yu et al. [31] combine neural network-based regression with wave scaling. Wave scaling is a method to convert an already seen performance measurement for a kernel configuration from one GPU type to another by using their ratios of compute performance and memory bandwidth. This method is also only applicable to targets of similar hardware architectures that vary only in terms of the number of processing elements and their memory bandwidth.
Wang et al. [32] operate similar to Justus et al. [29], but specifically target heterogeneous systems that contain a CPU and a GPU. This is achieved by accounting for the initial data transfer and final return of the result to and from the GPU memory in addition to the solution suggested in previous works. However, this assumes certain characteristics about the target platform, such as dedicated memories for both devices, which does not always hold up as mobile SoCs usually share the memory between all devices.

Table 1.
Comparison of related work with our own contribution. The performance data reflects what these publications reported.
Table 1.
Comparison of related work with our own contribution. The performance data reflects what these publications reported.
| Target Application | Target Environment | Implementation | Prediction | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Related Work | General Purpose | Deep Learning Training | Deep Learning Inference | Search-based Deep Learning Compiler | (CUDA) GPUs | CPUs | HPC/Workstation | Mobile/Embedded | AI | NN | Relies on layerwise Estimate | Execution Time | Power Consumption | Memory Allocation | Hardware Utilization | Reported Performance 1 |
| Huang et al. [19] | ✓ | ✓ | ✓ | ✓ | ✓ | Accuracy: | ||||||||||
| Braun et al. [20] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | MAPE: 8.86–52% (Time) | |||||||||
| MAPE: 1.84–2.94% (Power) | ||||||||||||||||
| Nadeem et al. [25] | ✓ | ✓ | ✓ | ✓ | - | |||||||||||
| Sun et al. [21] | ✓ | ✓ | ✓ | ✓ | ✓ | MAE: | ||||||||||
| Shafiabadi et al. [23,24] | ✓ | ✓ 2 | ✓ | ✓ | - | |||||||||||
| Kaufman et al. [26] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Accuracy: | |||||||||
| Qi et al. [28] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | MAE: 3 | |||||||||
| Justus et al. [29] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | - 4 | ||||||||
| Yu et al. [31] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Error: | ||||||||
| Wang et al. [32] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | MAPE: | |||||||
| Yeung et al. [33] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | - 5 | |||||||||
| Gianniti et al. [34] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Error: 10–23% | ||||||||
| Lattuada et al. [30] | ✓ | ✓ | ✓ | ✓ | ✓ | Error: | ||||||||||
| Cai et al. [35] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Accuracy: 88.24% (Runtime) | ||||||||
| Accuracy: 88.34% (Power) | ||||||||||||||||
| Accuracy: 97.21% (Energy) | ||||||||||||||||
| Bouhali et al. [36] | ✓ | ✓ 6 | ✓ | ✓ | ✓ | MAPE: | ||||||||||
| Velasco-Montero et al. [37] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Error: 3–10% | ||||||||
| Lu et al. [38] | ✓ | ✓ 7 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Accuracy: (Runtime) | ||||||
| Accuracy: (Energy) | ||||||||||||||||
| Our Work | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ 8 | Error: (Time) | |||
| Error: (Energy) | ||||||||||||||||
| Error: (Memory) | ||||||||||||||||
1 self-reported by author; 2 targets specific AMD GPU architecture; 3 according to our own test with a reimplementation of PALEO; 4 only provided RMSE data; 5 only provided RMSLE data; 6 embedded GPU of Nvidia Jetson TX2; 7 embedded GPU of Nvidia Jetson TK1, TX1; 8 not evaluated in this work, but possible as same interface was used to read the power information on CUDA GPUs
Yeung et al. [33] is the only publication listed here, which does not target the estimation of the execution time. Instead, only the device utilization is predicted. This information is then used to optimize the scheduling of Deep Learning jobs in an HPC environment by exploiting co-location, i.e., the placement of multiple concurrent tasks on a single GPU. This improves the efficiency of the HPC system by better utilizing the available hardware.
Gianniti et al. [34] follow the same approach as Justus et al. [29], but do not use the layer hyperparameters directly. Instead, a complexity metric was derived from them, which was then used as an input feature for the regression models. This allows for smaller training sets and models that generalize better to unseen configurations. However, the complexity metric probably depends on the targeted hardware architecture and is very closely related to the number of compute operations (FLOPs) that are required to execute the layer.
Cai et al. [35] also operate in a layerwise fashion and enable the prediction of the execution time and power consumption of Deep Learning workloads on HPC GPUs.
The following works target the performance modeling for Deep Learning inference tasks on mobile and embedded devices instead of high performance cluster and workstation environments. Bouhali et al. [36] exclusively target the Nvidia Jetson TX2 (Nvidia Jetson TX2 product sheet: https://developer.nvidia.com/embedded/jetson-tx2 (accessed on 25 May 2022)). Their solution describes networks as a whole and does not operate layerwise, similar to Lattuada et al. [30]. Similarly to in the majority of works, the measurement configurations that are used to train the models are randomly sampled from the search space.
Velasco-Montero et al. [37] predict the energy consumption and execution time of inference workloads by operating in the already known layerwise fashion and using the number of operations and memory transactions, as well as the number of weights used by the layer. Simple linear regression models are fitted for each combination of layer type and predicted metric. The estimated performance values are then used by a neural network that searches for the optimal network architecture for the current use case.
Lu et al. [38] predict the execution time, energy usage, and memory allocation for Deep Learning inference tasks on the Nvidia Jetson TK1 (Nvidia Jetson TK1 product sheet: https://developer.nvidia.com/embedded/jetson-tk1-developer-kit (accessed on 25 May 2022)) and TX1 (Nvidia Jetson TX1 product sheet: https://developer.nvidia.com/embedded/jetson-tx1 (accessed on 25 May 2022)). They also operate with a layerwise approach and uses regression models (linear for CPUs, more advanced for GPU) to predict the performance metrics using the layer’s FLOPs, as well as the matrix multiplication problem size of the layer function as parameters. This assumes that all layers utilize matrix multiplications for the implementation of their functionality, which does not hold up. For example, pooling layers, activation functions, and other layers do not rely on matrix multiplications for their implementation.
None of the cited publications target the prediction of performance metrics for Deep Learning programs that have been optimized by a search-based compiler, such as TVM [39]. These compilers try to find the optimal implementation for the current layer hyperparameter configurations in combination with the targeted hardware environment. The referenced publications target Deep Learning frameworks, such as Caffe [40], Theano [41], TensorFlow [42], and PyTorch [43] instead, which rely on math-kernel libraries such as Intel MKL [44,45], Nvidia cuDNN [46], ARM CMSIS [4], and others to provide hand-optimized—but static—kernels for each combination of workload type and specific hardware target. TVM utilizes an AI-based solution called autoTVM [47]. This solution tries to automatically find the best function kernel implementation for the current scenario of hyperparameter configurations and hardware environment. To reduce the number of on-device sampling runs a performance model is trained that allows for the estimation of the performance of different kernel implementations without having to benchmark them. It uses XGBoosted Trees [12] for the regression models and simplifies the task by assigning relative scores to the different configurations instead of predicting the absolute performance numbers. This solution is not directly comparable to the related work and our own contribution as it is designed for a very different use case.
A comparison and overview of all related publications can be found in Table 1.
2.3. Datasets and Data Acquisition
Zheng et al. [48] provide a dataset of measured samples of Deep Learning inference workloads on various (mostly HPC GPU) targets. The current size of the dataset is 51 million samples, consisting of differently sized subgraphs and their measured runtime. We did not use this dataset for our own work as it is designed for autotuning solutions that search for the optimal kernel implementations and does not contain memory allocation or power consumption data.
Rodrigues et al. [49] describe a solution that allows for the fine-grained measurement of the energy usage of Deep Convolutional Neural Networks on the Nvidia Jetson TX1 and was used as a reference for our own work. However, this solution relies on the built-in sensors of the platform, which are not available or accessible on all embedded devices.
3. Overview
Our work is similar to some of the related approaches by relying on layerwise estimates that are accumulated for the total network inference cost. However, instead of randomly sampling measurement configurations from the configuration space, we operate on a set of representative Deep Learning layer workloads from where the most important layer types and configurations are extracted. This allows us to reduce the amount of sampling that needs to be performed.
The data collection itself is built using TVM to be able to target a wide range of platforms and automatically apply the best target-specific optimizations. For this work, the execution time, power consumption, and memory allocation have been recorded. However, due to its modular design, every metric that can be measured during the layer workload execution can be recorded.
Once the required datasets have been collected, the performance models are trained. These models are implemented using AI-based regression methods. The current approach is to train one model per triplet of target-device, workload type and performance metric. Multiple different regression methods are used and the model that shows the best performance on the validation set is selected. This approach has two major benefits:
- Already trained models can be kept when new workloads or targets are added, as these are added by training additional models;
- The best regression method can be selected for each target triplet (target, workload, metric) independently.
The total network inference cost is estimated by accumulating the individual layer predictions.
No access to the target devices is required once the models have been trained, as developers can query them to obtain an performance estimate for the current architecture configuration. Alternatively, the regression models can be improved over time, by gradually adding occasionally collected new measurements—similar to the template matching by Nadeem et al. The performance models are quicker to query than a full deployment and benchmark run on the target device. Another advantage is that the data collection and model training is a one-time cost: the usage of the models is more efficient than individual benchmarks as soon as more queries have been processed than samples were collected for the training datasets as the cost of the regression model fitting and the prediction runs is diminishingly small compared to the data collection. The entire flow has also been visualized in Figure 1.
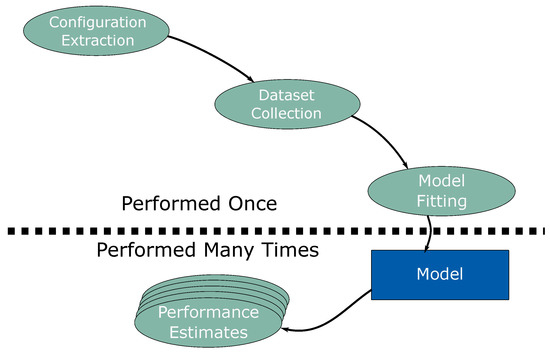
Figure 1.
A visualization of the entire flow. The configuration extraction, data collection, and model training steps are only completed once, while the trained model will perform many predictions.
4. Data Collection
TVM [39] was chosen as a base for the data collection due to its wide range of supported target devices and code generation flows that are able to automatically optimize the Deep Learning workload for the specified target and its advanced profiling capabilities. TVM is a Deep Learning compiler that is able to process already trained networks from most Deep Learning frameworks and toolkits and optimize their inference for a wide range of platforms during the compilation process. It consists of two major parts:
- The compiler stack, which transforms the Deep Learning model from the framework (i.e., TensorFlow, PyTorch, etc.) to its own representation, optimizes and compiles it;
- The executor, which performs the model inference on the target device. For this project, the graph runtime was used, especially its debug version that has additional profiling capabilities, to execute the workloads.
One key difference between the function kernels of TVM and those that are used by frameworks such as PyTorch and TensorFlow is that the later are static handwritten kernels, while TVM optimizes the function kernel itself for the targeted combination of layer configuration and hardware target. This makes the prediction of the performance for these kernels more difficult as the underlying function kernels can vary across configurations in terms of loop unrolling, memory tiling, and more.
A recent pull request (PAPI interface: https://github.com/apache/tvm/pull/7983 (accessed on 21 July 2021)) to TVM added an additional profiling interface. This allowed for the easy and modular extension of the debug executor with data collectors that act as interfaces to other platform or vendor specific profiling and benchmarking libraries and tools. We further modified the profiling infrastructure of TVM to accommodate for the collection of power consumption information across all evaluated target devices.
However, this approach is not limited to TVM, our collected performance data, or layer types, and could also be applied to other toolchains and frameworks, as long as they are capable of instrumenting the individual layer workloads to measure their performance footprint in all relevant metrics.
Our modified version of TVM with the additional profiling capabilities will be made available on GitHub (TVM Power Measurement Tools: https://github.com/MaxS1996/tvm (accessed on 25 May 2022)).
4.1. Sampling
As the regression models are kept relatively simple by using a low number of input features, the majority of time and resources are spent on the profiling of the workloads to create the training datasets for the AI-based performance models. A smart sampling strategy could therefore allow for a significant decrease in resources required for this step.
To reduce the number of samples that need to be profiled, the sample configurations should be similar to typical Deep Learning workloads: possible hyperparameter configurations for each layer type create an n-dimensional space with an infinite amount of possible workloads within this space. However, only a small subset of it is actually used in Deep Learning models. This allows for the training of regression models that only need to achieve accurate estimates in the same subspace of the layer configuration space instead of the entire configuration space. In addition, the most compute operations of the neural network inference are contributed by a small set of layer types. To exploit these observations, the Keras model zoo was explored to find the most computation-intense layer types and configurations: layers that were found are convolutional, dense, maximum, and average pooling layers. To further extend the dataset to cover more operation types, the found convolutional layers were augmented by adding new group and filter configurations, as well as dilation rates, to also be able to cover depthwise and dilated convolutional workloads. These are special types of convolutional operations. Depthwise convolutions are often used in the mobile or embedded scenario to cut down the computational workload without sacrificing too much prediction performance by applying each filter to only one channel of the input feature map. Dilated convolutions extend the filter kernel by adding strides between its kernel elements and are primarily used for image segmentation tasks.
As some layer parameters are target-dependent, such as the input, weight, and output tensor layout, the most suitable configuration for the target was selected for those parameters. The profiled batch sizes are also target dependent as the maximum viable batch size of each workload depends on the available system memory.
4.1.1. Dense Workloads
Due to the low number of unique samples and the close similarity of the found samples, another strategy was required to generate a configuration dataset for dense workloads. Dense layers have a very small set of relevant hyperparameters that are independent of the target device: the number of input features and the number of units inside the layer. As these two hyperparameters do not constrict each others values, sample configurations for dense workloads were randomly drawn and added to the configurations found in the model zoo.
4.1.2. Pooling Workloads
The found pooling workloads suffered from the same shortage of unique samples as the dense layers. To increase the number of samples in the sample set, additional configurations were created by augmenting existing samples with different pooling sizes, while keeping the input tensor dimensions.
4.1.3. Convolutional Workloads
The model zoo contains 2916 convolutional layer configurations only 542 of which are unique. Although this number is small, more samples can be generated by augmenting the data for different batch sizes as it is the case for all layer types. More samples could be artificially generated, but it is a non-trivial problem to generate representative workload configurations as convolutional layers have a larger set of hyperparameters that are not independent of each other. Therefore, we avoided generating completely new convolutional workloads and chose to augment existing standard convolutional workloads instead.
4.2. Benchmarking Flow
As multiple thousands of samples need to be processed for each target, no optimizations with extended runtimes such as Auto-Tuning or Auto-Scheduling have been performed, which causes additional noise in the dataset.
The time required to collect the necessary datasets mostly depends on the target device and the amount and type of recorded metrics: if only the inference latency is required, the data collection can be completed in hours. The required time increases drastically, if memory allocation and power consumption data need to be collected, as the libraries and APIs used to gather this information operate on low sampling rate and often produce very noisy measurements that require multiple runs to obtain an accurate result. This can increase the time from hours to days or weeks.
However, this data collection only needs to take place once per target device and can be sped up by using multiple instances of the same device. In addition, only the initial setup and selection of relevant metrics needs human interaction, while the long data recording process is fully automated. The reliance on standard tools such as PAPI [50], powercap [51], RAPL [52], and NVML (NVIDIA Management Library (NVML) is a C-based API to manage and monitor various information about Nvidia GPUs: https://developer.nvidia.com/nvidia-management-library-nvml (accessed on 25 May 2022)) to collect performance data also further simplifies the setup process.
A possible way to collect such datasets for a large number of targets would be a direct integration of the flow into TVM’s runtime, allowing all users to easily participate in the process to refine the performance models of their hardware targets by contribution measurements from their own hardware automatically.
There are two versions of the compilation flow, which are optimized for the different circumstances under which the data collection could take place.
The benchmarking flow will be published in a separate repository on GitHub(TVM Profiler: https://github.com/MaxS1996/TVM_Profiler (accessed on 25 May 2022)), as it can either be used with the TVM main branch or our modified power measurement version.
4.2.1. Online Flow
The first variant performs the compilation on the target itself, which is usually the best option for the server- and desktop-grade devices that have enough compute performance and system memory to process the compilation locally. The profiling of a single workload starts with the extraction of the workload description (i.e., layer type and hyperparameter settings) from the set of representative configurations that was created during the sampling step. A single stored sample configuration is profiled with different batch sizes. The batch sizes to be profiled are configured for each target individually to account for the difference in available memory and compute performance.
As shown in Figure 2, the following steps are repeated for each batch size on a single workload configuration:
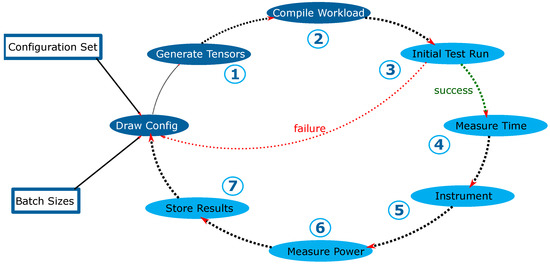
Figure 2.
A visualization of the benchmarking and measurement flow: the boxes on the left are the datasets that are provided, containing the extracted workload configurations and batch sizes that will be profiled, dark blue bubbles marks operations that are performed on the offline device in case of the precompiled flow. Light blue bubbles will be executed on the target device itself in both flow variants.
- The input and (optional) weight tensors are generated according to the workload specification and filled with random numbers of the required data type;
- The workload is compiled by TVM to optimize it for the selected target platform;
- An initial test execution is performed. If the compilation or execution fail, the flow starts over with the next workload description from the sampled configuration set, skipping the remaining batch sizes for this workload description;
- The execution time is recorded multiple times after performing a burn-in to operate on warm (already filled) caches;
- The workload is instrumented for the additional metrics that need to be recorded;
- The metrics are recorded, using multiple repetitions, each with its own burn-in phase;
- The collected raw data is cleaned up by performing outlier removal and only the median of each metric is used as a label.
The skipping of remaining batch sizes for a workload configuration helps to further speed up the collection of the dataset: if the compilation or execution fails due to an error that is not related to the batch size, all batch size configurations are going to fail for this workload and can, therefore, be skipped. If the error is related to the batch size, it is most likely due to a lack of available memory. As the batch sizes are profiled in an ascending order, the required memory will only increase with each evaluated batch size.
As many power measurement tools have a minimum sampling period that is much longer than the execution time of a single neural network layer inference (i.e., NVML: 1/6 s), the workload is looped to extend the runtime over the sampling time window during the measurement of metrics other than the inference time. Due to measurement noise, the measurements need to be repeated multiple times for each sample, depending on the target device and the used power consumption measurement interface, up to 50 repetitions were required to achieve an accurate and reproducible result on most targets.
4.2.2. Precompiled Flow
Since low-powered mobile and embedded platforms, which are not capable of executing the compilation, should also be targeted by this flow, a cross-compiler-based solution was required. The key difference in this version is that the compilation and tensor generation is performed on a different device beforehand using the appropriate code generation flow for the target. The compiled executable and tensors are transferred alongside the workload configuration data to the target device afterwards. The execution and profiling flow on the device itself is identical to the online version. This variant has been used for the Cortex-A CPU and Mali GPU targets.
On mobile and low-powered devices with limited system memory, TVM’s function metadata system (workspace size metadata: https://github.com/apache/tvm/pull/7938 (accessed on 21 July 2021)) was used to calculate the memory allocation sizes of the function workspace and IO tensors during compilation.
5. Dataset
To save time and resources, only the compute-intense layer types, such as 2D-convolutions, dense as well as maximum and average 2D-pooling layers were profiled. The reason is that these layer types make up the majority of the total neural network inference workload. However, the compilation and data collection flow can be applied to every workload type that can be represented with TVM’s Relay graph-level representation.
Smaller workloads, like activation functions, are currently not considered during the performance prediction as their impact is often negligible, especially after performing compiler optimizations, such as layer fusion, which combine the activation functions with the previously executed compute workload. This removes the need to read and write the intermediate feature maps from memory again just for the activation function, which significantly reduces their performance impact.
Table 2 shows an overview of the devices that have been targeted for this work and which metrics were recorded, as well as which measurement tool was used for each metric. At the time of writing this paper, seven different target devices have been profiled. We included four different architectures using x86 Intel CPUs, CUDA GPUs, an ARM Cortex-A CPU, and a ARM Mali GPU. Table 3 shows the number of collected samples for each tuple of target device and workload type. A key benefit of extracting the samples for the profiling from a model zoo is that most popular layer configurations will already be part of the training data. This enables very accurate predictions for these workloads, as they are already seen data for the regression models. The collected data will be available alongside the trained performance models in a GitHub repository (TVM Profiling Dataset: https://github.com/MaxS1996/TVM_Profiling_Dataset (accessed on 25 May 2022)).

Table 2.
Overview of profiled targets and measured metrics.

Table 3.
Overview of the collected datasets. The XU4 has been measured with and without the recording of the power consumption during the execution.
An investigation of the collected training data shows that the convolutional datasets contain samples with significantly longer execution times compared to similar workload configurations. In some cases, a change of the input dimensions by just one pixel in height or width resulted in a reduced performance and increased the execution time of these workloads by up to one order of magnitude. A closer inspection of the generated source code of these samples shows a lack of parallelization and optimization for the function kernels, resulting in completely sequential kernels without any vectorization. This is caused by the lack of auto-tuning during the sample collection, as previously mentioned: the autotuning solutions use a function template that is optimized for the combination of current workload and target device during an AI-feedback driven optimization loop that tries to find the best optimization parameters for the current case. As several thousands of convolutional operations need to be compiled and profiled on multiple targets, the time requirement of the autotuning process (30 min to 60 min per convolutional workload) was not feasible for this publication. Although this work is supposed to showcase the feasibility of this approach, a real use in a production environment would require the datasets to consist of tuned examples. This could be achieved by utilizing the TVM runtime to collect the data during the auto-tuning process directly from the users and accumulating it into one central and publicly accessible data repository.
However, this is mostly a TVM specific limitation that does not affect toolchains that do not rely on tuning and could be used as an additional tool for tuning-based frameworks. The performance predictor could be used in combination with tuning-based solutions to identify workloads within the network that have the biggest optimization potential by comparing the prediction with the real-world measurement for the same workload. If the measured execution time is significantly longer than the prediction, it is most likely a badly configured function kernel that would improve its performance by applying tuning to it. In addition, AutoTVM is mostly used for trainable layers and this limitation does not apply for the pooling workloads that are also part of the dataset.
6. Performance Model
Similar to the majority of the related work, we have chosen to model the total network cost as the sum of its layer costs. The calculation of the total network cost depends on the targeted performance metric: the total execution time is the sum of the individual layer execution times, as shown in Equation (1) (n is the index of the individual layers).
Most tools measure the average power consumption in the last time frame, therefore only the layer power consumption, instead of the energy usage, will be measured in most cases. To calculate the total neural network inference energy usage estimate, the individual layer energy estimates need to be calculated from the individually predicted power consumptions and execution times before accumulating the values for the total energy, as shown in Equation (2).
The calculation of the total memory allocation is more complicated, as TVM employs various memory optimization techniques. We suggest two methods to estimate the memory allocation. The first more pessimistic method uses the sum of the two largest layer estimates for the total memory allocation. This approach accounts for memory reuse and the simultaneous liveness of two intermediate feature maps at each point of the inference. It is pessimistic because it assumes that the two largest intermediate feature maps are live at the same time. A second more optimistic approach has been described in Equation (3). It also accounts for the simultaneous liveness of two intermediate feature maps, but does not assume that the two largest ones will be live at the same time. Both approaches assume a strictly feed-forward network architecture without parallel branches.
Due to this layerwise approach, the performance models are implemented as regression models that predict the performance metrics for each layer type based on the hyperparameter configuration. As the research field of Deep Learning is always in a state of rapid innovation—regularly producing new layer types and approaches—we have decided to train one model per triplet of target, workload type, and performance metric. This allows for a modular structure, where performance models for novel layer types and newly collected metrics can be added without the need to retrain the existing models. Other benefits of this approach are the feasibility of adapting each model’s input vector to the relevant hyperparameters of the layer type and the possibility to collect independent datasets for each metric. This is especially important as certain metrics are more time consuming to collect than others.
Different regression methods have been evaluated: XGBoostes Trees (XGB) were used as they are already utilized by TVM as part of the autoTVM flow and are usually able to achieve good results for regression tasks [12]; and Extremely Randomized Trees (ERT) were included in this testing, as they are known to achieve state-of-the-art regression performance as well [13]. The key benefit of these tree-based regressors is that they were able to achieve reasonable prediction performance while not needing any preprocessing—besides one-hot-encoding of discrete features—being applied to the datasets.
However, as we wanted to evaluate as many different regression algorithms as possible, we added a scaling step to the preprocessing pipeline and applied more traditional regression methods as well. These methods included k-Nearest Neighbor regression (kNN), decision tree regression (dTr), linear regression (linR), multi-layer perceptrons (MLP), and support vector regression (SVR). With the exception of XGB, scikit-learn [14] was used to preprocess the data and train the regression models.
7. Evaluation
As the trained performance models are solving a regression task, we are using the coefficient of determination (R2), mean (MAE) as well as median absolute error (MEDAE), the mean percentage error (MAPE), and the maximum error (MaxE) to evaluate the prediction performance. Although the absolute and maximum errors cannot be directly compared between metrics or devices, due to significantly different ranges of the predicted values, their ratio compared to the maximum, mean, and median of the ground truth data can be a helpful indicator.
7.1. Performance Prediction without Feature Augmentation
The first test was carried out by applying kFold cross-validation on the initially collected datasets. The presented evaluation numbers in this section always represent the mean of all k runs. The use of kFold cross-validation allowed for the evaluation of all workloads and metrics, even if they are not part of the final full network test case. The inference time and power consumption was predicted for all targets. On CUDA GPUs, each workload’s memory allocation was measured and on mobile devices, the workspace and IO allocation was calculated by the TVM compiler based on the generated function kernels.
For this test, no further preprocessing outside of a scaling step and the one-hot encoding of categorical features was applied to the sample representation. To account for the lack of tuning of the recorded samples, an outlier removal algorithm was used to eliminate the most obvious unoptimized samples from the training and validation sets. This was performed by using isolation forests that identified outliers based on the hyperparameter configurations and their execution time. As these outliers are a TVM specific limitation and would not occur with frameworks and toolflows that do not rely on an auto-tuning step, this outlier removal is probably not necessary for alternative toolchains such as TensorFlow and PyTorch.
The input features of the regression models were restricted to hyperparameters and architectural information available from the neural network definition, including the dimensions of the involved input, weight and output tensors to avoid the need for additional compilation steps. Relying on information that is only available after the compilation would limit the usability of the trained regression models, by increasing the time and resource footprint of each performance estimation drastically. This would reduce the benefit of such performance models—their small resource and time footprint compared to simulators and benchmarks on the target—for many use cases, as an additional compilation step reduces the amount of network configurations that can be evaluated in a certain time. As certain applications, such as network architecture search (NAS) systems, often rely on the trial of large amounts of configurations in a short period of time, this is not an option for them.
The best performing models across all target devices and workloads consistently were tree-based methods, especially ERT and XGB, as well as the MLP models. These methods generally achieved the best R2, MAE, MEDAE, and MaxE scores across all metrics, workload types, and target devices. Although the MLP regressor was able to achieve competitive results, it required significantly more time to train the models compared to the tree-based alternatives (multiple seconds instead of sub-second runtimes). Detailed results can be found in the dataset repository on Github, which also contains the model training scripts and protocols of past evaluations.
7.1.1. CUDA Targets
The initial test showed promising results across all layer types and recorded metrics for the CUDA targets, as shown in Figure 3. Although there are some outliers in the overall performance (i.e., power consumption of dense workloads on the Tesla K80), these are most likely caused by the usage of multiple different GPU instances for the Tesla targets, adding additional noise to the dataset.
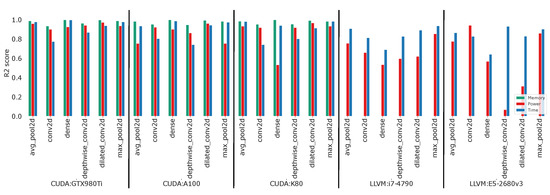
Figure 3.
The R2 scores of the best regression models out of the tested methods across all metrics and workload types for the CUDA and x86 targets of the currently collected datasets without the application of any feature augmentation.
The memory allocation was the metric with the smallest error on most workloads, achieving an MAPE score of less than 3% on all workload types except the pooling operations (MAPE of up to 13%) across all CUDA targets.
The results for the power consumption prediction seem to indicate that the usage of multiple target instances to collect samples of the same workload type—as was done for the Tesla A100 dataset—can introduce additional noise in power data which results in reduced prediction performance, as the A100 power models only achieved an MAPE of 5% to 13%, while the K80 and 980 Ti power models achieved score between 1% and 10%.
The inference latency was the metric with the highest variation between workload types: the models for the prediction of dense layers achieved the best performance with an MAPE of as low as 4% on the 980 Ti, while pooling workloads could be predicted with an error of around 30%. The highest MAPE value was measured for the prediction on standard and depthwise convolutional workloads, with up to 52%. This is most likely caused by the search-based TVM compilation that results in the usage of different kernel implementations across the hyperparameter configuration space. Dilated convolutions achieved better results, however, these were likely caused by the construction of its sample set—creating many similar samples that only differ at the dilation rate—and the low performance impact of the dilation rate on CUDA targts.
7.1.2. X86 Targets
Only the inference latency and power consumption were measured on the x86 targets, as the memory allocation of the network inference is less relevant with the large available system memories of typical cluster nodes and workstations. Additionally, the power consumption for workloads on the Xeon and Core-i7 CPU was measured using different tools: for the Xeon CPU HDEEM [53] was used to measure the power consumption directly, while the desktop Core-i7 relied on powercap (Linux Kernel-Powercap: https://www.kernel.org/doc/html/latest/power/powercap/powercap.html (accessed on 25 May 2022)) and RAPL [54] to measure its energy use and derive the power consumption from the measured energy and execution time. This makes the results of the power prediction on these targets less comparable as it introduces different amounts of noise into the datasets.
The overall prediction performance on the x86 targets seems to be similar to the CUDA targets, as shown in Figure 3, although the power consumption prediction quality is lower compared to the CUDA GPUs. This can be caused by two reasons: the background noise of the OS and other processes on the CPU, while the GPUs are used exclusively for the task and the difference in the measurement setup between these targets.
Another observation was the lower prediction accuracy for the execution time of dense workloads on both CPU types and the increased accuracy for the convolutional workloads on these targets, which are most likely caused by the different memory hierarchy and code generation that affects these workload types differently on the CPU and GPU targets. However, this is only a assumption.
The low prediction quality on the i7 for the power consumption of depthwise and dilated convolutions is most likely caused by an error during the collection of the dataset—which relied on the chain of PAPI, powercap, and, finally, RAPL to perform the measurement—as the minimal power consumption of the dataset was also reported to be zero.
7.1.3. Mobile Targets
Due to their lower amount of accessible memory and the high number of iterations required to measure a reproducible power consumption reading, the datasets for these targets were much smaller. This resulted in a number of workload types where no predictors could be trained for the Cortex-A target, as well as overall lower performance on the smaller datasets, as shown in Figure 4. To showcase a overall feasibility, an additional measurement run without power consumption data was collected on the Mali GPU to validate the feasibility of the approach on mobile targets.
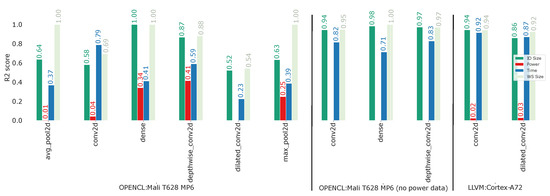
Figure 4.
The R2 scores of the best regression models out of the tested methods across all metrics and workload types for the mobile targets of the currently collected datasets without the application of any feature augmentation.
On the other workload types, the IO and workspace allocations achieved almost perfect results, which is not surprising as these calculated values are deterministic and do not contain any noise.
The power consumption prediction, however, did not achieve a significant prediction accuracy for most workloads. The most likely reason is that the total board power was measured for the these targets and the difference in power consumption between different layer configurations was too small to be detected among the overall noise. Nevertheless, the different workload types showed distinct distributions in their measured power consumption, allowing for an MAPE score of 7% to 13% for the trained power consumption models.
The low inference latency prediction performance on the Mali GPU dataset that includes the power consumption data is caused by the small datasets as many of the sample configurations were too large to fit the limited resources of the mobile platform. The inclusion of more mobile and embedded focused model zoos into the sample configuration dataset could help to improve the dataset size for this kind of target platform. An additional data collection run that did not include the power measurements was able to collect more samples for some layer workloads, which resulted in a drastically improved model performance.
7.1.4. Summary of the Non-Augmented Prediction
The initial evaluation has shown that a useful prediction quality can be achieved by our approach. However, the individual performance seems to depend on the hardware architecture, dataset size, code generation, and measurement utilities, as the performance impact of different hyperparameters seems to shift between targets and the feasible accuracy depends on the accuracy of the underlying measurements.
7.2. Prediction Performance with Feature Augmentation
Although the initial results looked promising, we aimed to improve the overall performance and generalizability of the models for unseen configurations.
As works such as PALEO [28] and Gianniti et al. [34] were able to perform accurate predictions based on simple features that have been derived from the layer configuration, four additional features were added to the model inputs: the sizes of the involved input, weight, and output tensors, as well as the number of operations required to execute the workload if a standard function kernel is assumed. These features are used in conjunction with the layer hyperparameters, do not require any additional compilation steps and can be acquired at the same graph-level representation of the neural network as before.
The additional features enabled the memory allocation prediction across all targets to achieve an almost perfect R2 score of over 0.99 and an MAPE of less than 1%. The inference latency prediction did show a major improvement for pooling layers across all target devices, often drastically improving the MAPE score by an order of magnitude from 30% to 5% on CUDA targets and the Xeon CPU, as well as from 120% to 12% on the Core-i7. For the power consumption prediction quality no major improvement could be seen on the tested workloads and targets. Detailed data about the model training and evaluation can be found in the dataset repository.
As the additional features have improved the performance for most datasets, they have been added to the feature vector during the following tests.
7.3. Dataset Size
Although the usage of the model zoo for the sampling of measurement data enabled the training of accurate regression models on small datasets, the collection of this dataset was still the most time-consuming part of the entire flow. An additional reduction in the dataset sizes could therefore improve the efficiency of the approach further.
For the test of the required dataset size, only the GTX 980 Ti GPU and the Core-i7 CPU were evaluated, as they were representative for their hardware architectures. The mobile targets were not considered for this test, as their datasets were too small to be further reduced.
To evaluate the minimal dataset size the datasets were randomly divided into a validation and a training set. The training set was split into 15 equally sized, randomly sampled subsets while the validation set stayed unchanged. The regression models were trained on the initial subset of the training set and evaluated on the validation set. After each evaluation, the training set is increased by 1 of the 15 subsets and the models are re-instantiated, removing all knowledge from previous training iterations, before being retrained with the extended training set.
7.3.1. Dense Layers
The dense dataset is the largest out of the measured workload types on most target devices, with up to 20,000 samples, while dense workloads have the lowest number of hyperparameters out of the evaluated layer types. Accordingly, the largest savings were expected for this layer type.
As shown in Figure 5, the CUDA target already achieved an R2 score of 0.997 and an MAPE of 4.7% for the inference latency after the first iteration with just 1260 samples. The initial iterations show a steep reduction in the MAPE score until the improvement slowed down after 8820 samples with a MAPE score of 3.6%. The further development was rather small, with final scores of 0.998 and 3.4% on a training set of 18,900 samples. The power consumption and memory allocation showed smaller improvements after the first iterations, starting with MAPE scores of 2.2% and 0.3%, respectively, slightly reducing their error until the last iteration down to 1.8% and 0.07%.
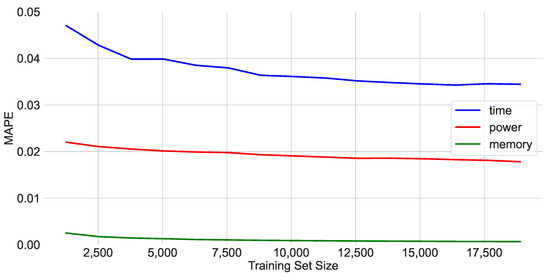
Figure 5.
The development of the MAPE scores for the dense workload performance metrics on the GTX 980 Ti with an increasing training set size.
Although the inference time models did not achieve the same quality for dense workloads on the x86 targets, the reason does not seem to be the significantly smaller dataset, as the MAPE score in Figure 6 does not show a major decrease in the prediction error across iterations.
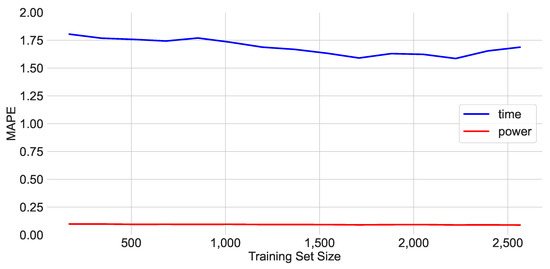
Figure 6.
The development of the MAPE scores for the dense workload performance metrics on the Core-i7 4790 with an increasing training set size.
The power consumption prediction did not show any significant improvement between the first and the last iteration as well, as the error could only be decreased by 1.1%, while the training set was drastically increased from 171 to 2565 samples.
The conclusion for dense workloads is that the training set can be shrunken significantly from the used 20,000 samples without a larger reduction in the model performance, and that the lower quality on the x86 targets is not caused by a lack of training samples.
7.3.2. Convolutional Layers
The observation of the inference latency prediction across iterations for convolutional workloads shows a drastic improvement after the first iterations for the GTX 980 Ti: during the third iteration, using a training set of 300 samples, the MAPE score of all models decreased significantly from over 100% to as low as 57%. After the fourth iteration only gradual improvements could be seen, with a final MAPE score of 40% that was achieved by the ERT model. On the Core-i7 dataset, the MAPE score of the inference latency prediction model showed a similar behavior, reducing the error from 175% during the first iteration to 90% after the fifth iteration with 500 samples. Additional iteration reduced the error gradually until it reached 72% while learning from the entire training set.
The power consumption model already achieved a low MAPE value on the first iteration with an error of 5% on the Intel CPU and 2% on the CUDA GPU, which were decreased to less than 1% on the GPU and 2% on the CPU.
The memory allocation prediction on the GTX 980 Ti showed a similar behavior with only small improvements in its error from 9% to 8% across all iterations.
Although the power consumption and memory allocation training set can most likely be reduced, an increase in samples might benefit the inference time prediction performance for this workload.
7.3.3. Pooling Layers
As both pooling workload types show similar behavior, they have been grouped together for this evaluation. The behavior for the GTX 980 Ti is similar to the convolutional workloads: a steep decrease in the observed error of the inference latency prediction in the initial iterations until a saturation point is reached. For pooling layers, this point seems to be around 1800 samples for average pooling workloads and just 800 samples for maximum pooling layers. The other metrics show an already low MAPE score in the first iterations and only small improvements for larger training sets.
The same observation was made for these workloads on the Core-i7 target, only the saturation point seems to be reached much earlier with just 135 maximum and 235 average pooling samples.
7.3.4. Summary of the Dataset Size Exploration
Although these results seem to indicate that some sample configuration sets could be reduced in size, significantly speeding up the data collection process, they also show a difference in the number of required samples for some workloads that seems to depend on the target device.
An additional observation is that the power consumption prediction rarely shows significant improvements after the first few iterations. As the reproducible measurement of the power consumption requires the most time in the data collection loop, this suggests that considerable time savings are possible by only collecting the power information for a small subset of the total samples.
Further research might be necessary to find a solution that selects the most important workload configurations for each individual hardware architecture to achieve large time savings without reducing the prediction quality. Alternatively techniques to identify the appropriate training set size automatically based on the target device, initial measurements and the accuracy that is required by the intended performance model use case could be explored.
7.4. Full Network Inference
The last test was the prediction of the performance of a full network inference run instead of a layerwise comparisons. The test network was inspired by DarkNet-19 and the Tesla A100 was used to benchmark the entire network inference. The model was not part of the model zoo that was used to prepare the collected workload configurations.
A key difference between the standalone workloads in the training set and their equivalent in the test networks is that TVM performs layer fusion, which adds the activation function to the executed function kernel. However, this should only have an minimal impact on the overall performance as the cost of applying the activation function is diminishingly small compared to the function kernels that are executed prior.
The network consists of standard and pointwise convolutions, pooling layers, and different activation functions. The final classification is implemented through a global pooling layer before applying a softmax function. The total layer count is 22, with 14 convolutional, five max pooling and one global average pooling, and a flatten and a softmax activation layer. Out of these layers, only the convolutional and max pooling layers are considered by the performance predictor as the impact of the other layers is expected to be too small to make a significant difference in the overall inference footprint. The batch size was set to 16. The full architecture is shown in Table 4. The layerwise comparisons of measurements and estimates from the different prediction approaches can be found in Table 5 and Table 6.

Table 4.
Overview of the layer configurations of the test network. The layer configuration of the convolutional layer with the large underestimation of the inference latency is marked in red, the green row represents a similar layer which achieved a significantly shorter inference latency.

Table 5.
Comparison of the layerwise measurements of the execution time with the predictions of the different approaches. The layer configuration of the convolutional layer with the large underestimation of the inference latency is marked in red, the green row represents a similar layer which achieved a significantly shorter inference latency. The inference latency was measured and predicted in ms. The last line compares the total inference times with and without the inclusion of the erroneous layer.

Table 6.
Comparison of the layerwise measurements of the execution power with the predictions of the different approaches. The layer configuration of the convolutional layer with the large underestimation of the inference latency is marked in red, the green row represents a similar layer which achieved a significantly shorter inference latency. The inference power was measured and predicted in Watt. The last line compares the total inference times with and without the inclusion of the erroneous layer.
7.4.1. Prediction Performance
The measured and predicted results for the individual layer execution times can be seen in Table 5 and Figure 7. The layerwise power consumption measurements and estimates can be found in Table 6 and Figure 8.
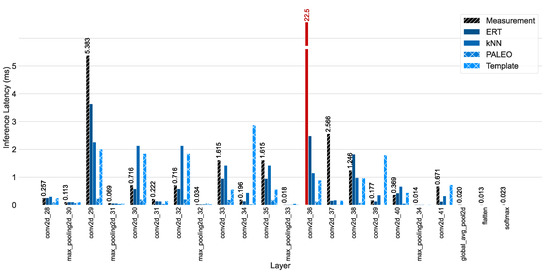
Figure 7.
The measured and estimated layerwise inference latency of the test network. The measurement outlier has been marked with red and is represented by an interrupted bar to fit into the figure.
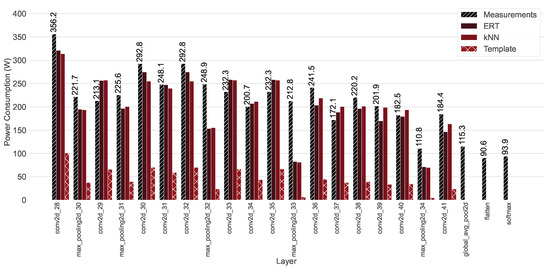
Figure 8.
The measured and estimated layerwise power consumption of the test network. The total energy consumption of the whole network inference was calculated by multiplying each layers power consumption estimate with its inference time prediction and accumulating the products of all layers.
The full network inference was measured with a latency of 38.5 ms, an inference energy consumption of 8.93 J, and a memory footprint of 787.64 MiB. Of the total inference latency, only 0.056 ms were contributed to by the layers that will be ignored during the performance prediction and 0.2667 ms (less than 1%) were caused by the maximum pooling workloads. This hints at the possibility that a performance prediction model for these workloads is also unnecessary, however, it might just be the case for this specific network architecture.
The remaining 38.2 ms are spent on the convolutional layer workloads. An interesting observation is that a single convolutional layer requires 22.45 ms (conv2d_36) of the total inference time—which hints at another performance outlier as described before, because a very similar layer (conv2d_38) in the network required significantly less time (1.25 ms) to complete its operation.
ERT and kNN regression models have been evaluated for this test. Although ERT showed the best performance in the previous tests, the kNN model was selected with a configuration of k = 3 and a uniform weighting of the neighbors as an attempt to reduce the impact of performance outliers in the training set that was observed in the previous tests. PALEO and the template matching approach were chosen for the comparison as they are representative for their respective strategy out of the related work.
The ERT model predicted an execution time of 12.6 ms and an energy consumption of 2.94 J. Although the predictions for the pooling workloads were quite accurate (0.225 ms), the main disparity was caused by the slow convolutional layer (conv2d_36) as it was predicted with an inference latency of just 2.48 ms instead of over 22 ms. The kNN model predicted an inference latency of 14.1 ms and an inference energy of 3.4 J. It achieved a similar accuracy for the maximum pooling layers with 0.225 ms and its main prediction error was caused by the same convolutional layer, which has been predicted with an inference latency of 1.15 ms. The template matching approach predicted 15.1 ms and 3.31 J, while PALEO with an assumed computer performance of 19.5TFLOP and a memory bandwidth of 1555 GB for the Tesla A100 estimated a total inference time of 1.72 ms—PALEO did not describe a way to estimate other performance metrics, limiting it to the inference latency for this test.
If the unoptimized layer is removed from the consideration, the total inference time is reduced to 12.8 ms, while the inference energy is 2.94 J. The ERT model predicts 9.84 ms with an energy of 2.38 J, while the kNN model is much more accurate with 12.5 ms and an energy of 3.06 J. This equals an error of 23% for the inference latency and 18.9% for the inference energy for the ERT model and 2.6%, as well as 4.1% for the kNN model. This showcases that the selected kNN model configuration can compensate the outliers in the training set. The template matching solution achieved a similar result with an estimated inference time of 13.53 ms and an inference energy of 2.97 J—resulting in an error of 5.6% for the inference time and less than one percent for the energy. PALEO, which was used without a scaling factor, predicted a significantly lower inference time of 1.58 ms.
This experiment showcases that an AI-based performance prediction for Deep Learning inference workloads is possible. However, the special tuning-based approach of TVM makes it more complicated to achieve accurate results. Nevertheless, the combination of a performance prediction solution with a tuning-based solution like TVM can be utilized to identify subgraphs of the Deep Learning model that can benefit the most from additional attention during the optimization and tuning process by comparing the actual measurements against the estimates of the performance models. The surprisingly high accuracy of the template matching approach also shows that the selection strategy for the training set is able to cover the most important parts of the layer hyperparameter configuration spaces.
The estimation of the total memory footprint of the full network inference based on the individual layer predictions is more complicated than for the other metrics, which only require an accumulation of the individual values. As TVM performs multiple optimizations that reduce the overall inference memory footprint, a simple approximation of their impact is required. A pessimistic and simple approach that can estimate an upper bound for the required memory space of a strictly sequential neural network is the accumulation of the two biggest layerwise estimates. This solution takes the liveness analysis based optimizations and memory reuse into account. For ERT, the two largest memory footprints are 522 MiB and 537 MiB, resulting in a sum of 1059 MiB, which is much larger than the measured 787.64 MiB. The kNN model predicted 509 MiB and 524 MiB, resulting in a similar sum and error from the measurement. The template matching solution achieved a similar estimate with 514 MiB and 524 MiB.
These estimates are very pessimistic in their assumption. This was a deliberate decision, as the memory footprint is often the deciding factor, if a Deep Learning workload can be deployed to a platform. A more optimistic approach is based on the average of the layerwise memory estimates, which is multiplied by two, to account for the simultaneous liveness of the input and output feature map of each layer. This approach results in an estimate of 776 MiB for the ERT model, 879 MiB for the kNN model and the template matching, which is much closer to the measurement than the other solution, but tends to underestimate the value. However, a more deterministic approach that does not rely on (AI-based) estimates might be a more suitable solution for the memory usage calculation, as the main contributes stem from the (intermediate) feature maps and not the function kernels.
7.4.2. Prediction Time
The total score time for all metric of all considered layers was 46.9 ms for the ERT model and 93.75 ms for the kNN model on a standard mobile computer, while the benchmark of the inference took 81.4 ms to transform the model from its Keras representation to TVM’s graph-level IR, 118.037 s to compile it, 4.3 s to do the initial time measurement and 16.5 min to perform the power measurement for the entire network on a high-end cluster node. This underlines the benefit of the AI-driven performance models in terms of the spent time as each of the steps required to benchmark the workload takes (significantly) more time than the querying of the trained models.
Therefore, the querying of the ERT performance models is 23,000 times faster than the deployment and benchmark for this test model, while the kNN model is still 11,865 times faster. Another benefit in terms of the required time to obtain an estimate is that the query time of the performance models grows linearly with the layer count, while the complexity of the compilation and optimization is difficult to quantize and the time spent on the following measurements mostly depends on the number of FLOPs required, as well as the accuracy and sampling rate of the measurement tools. This large difference in the required query time should allow this approach to quickly reach its break-even point when the expensive data collection and model training step is considered as well, especially if the findings of the previous section about the required dataset size are considered.
8. Conclusions and Future Work
We introduced an AI-driven performance model for Deep Learning inference workloads that can be applied to all hardware architectures and metrics as long as the desired characteristics can be measured for individual layer workloads. Although our prototype was built using TVM and targeted search-based tuning solutions, it can be implemented with all major Deep Learning frameworks and compilers, as long as accurate performance measurements can be performed.
We showcased that the system is able to produce competitive predictions (see Table 1 for a comparison of the self-reported accuracy)—even when using a tuning-reliant Deep Learning compiler such as TVM—and is by multiple orders of magnitude faster than a real benchmark on the target device. The estimates are solely based on information that is available at the network architecture level, enabling the use of these models in various applications. As models could be trained on moderately sized datasets, this solution does not have the same barrier of entry as some of the related publications, as a single hardware instance is enough to collect the datasets in a tolerable time window.
Future work can take two different directions. The first direction is the improvement of the current concept and execution to further advance the efficiency and quality of the prediction flow. The data collection step is currently a brute force solution that measures all found workload configurations on all target platforms. Our tests seem to indicate that this is likely not the best approach, as the prediction quality between targets differed while using the same set of workload configurations to collect their datasets. Possible reasons are the different influences of the hyperparameters depending on the hardware architecture that executes the function kernel. Based on these differences in influence, the relevance of different samples also changes depending on the target. Future work could focus on a more sophisticated approach to select the most relevant workloads for the measurement on the target to build meaningful performance models on a minimal dataset. Alternatively, the regression models could be refined to increase the quality of their output—for example, implementing AutoML functionality to automate the model refinement just as the current data collection and training flow of predefined regression models.
The second direction is the usage of these models in other applications. We identified the ability to locate performance outliers during the evaluation, where a large discrepancy between the predicted and measured performance can indicate further optimization potential for a workload. Other use cases are the provision of performance estimates during the model design phase, which can take place either manually or automated (NAS), and allows for the consideration of additional performance characteristics such as the power consumption in addition to the inference time. A use in combination with a NAS system such as DONNA [55] that is able to estimate a models inference accuracy without having to train it, could enable fundamental new approaches of designing Deep Learning models and applications.
The metrics that can be predicted are not limited to those which were used for this publication—as every characteristic that can be measured during the inference and is impacted by the change in the layer configuration could be targeted by the performance predictors. Another use case is the utilization of our solution to support the mapping and scheduling of Deep Learning inference workloads across heterogeneous and distributed systems, by estimating the performance of the individual workloads on the available target devices, allowing for the fastest or most efficient mapping to be found.
Author Contributions
Conceptualization, M.S., B.W. and A.K.; methodology, M.S.; software, M.S.; validation, M.S., B.W. and A.K.; formal analysis, M.S.; investigation, M.S.; resources, B.W. and A.K.; data curation, M.S.; writing—original draft preparation, M.S.; writing—review and editing, B.W. and A.K.; visualization, M.S.; supervision, B.W. and A.K.; project administration, B.W.; funding acquisition, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available in a publicly accessible repository that does not issue DOIs Publicly available datasets were analyzed in this study. These data can be found here: https://github.com/MaxS1996/TVM_Profiling_Dataset (accessed on 25 May 2022).
Acknowledgments
The authors are grateful to the Center for Information Services and High Performance Computing [Zentrum für Informationsdienste und Hochleistungsrechnen (ZIH)] at TU Dresden for providing its facilities for high throughput calculations.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| API | Application Programming Interface |
| CPU | Central Processing Unit |
| CUDA | Compute Unified Device Architecture |
| dTr | Decision Trees |
| DL | Deep Learning |
| ERT | Extremely Randomized Trees |
| GPU | Graphics Processing Unit |
| HDEEM | High Definition Energy Efficiency Monitoring |
| IO | Input/Output |
| kNN | k-Nearest Neighbors |
| linR | Linear Regression |
| NAS | Network Architecture Search |
| NN | Neural Network |
| NVML | Nvidia Management Library |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MaxE | Maximum Error |
| MEDAE | Median Absolute Error |
| MLP | Multi-Layer Perceptron |
| OS | Operating System |
| PAPI | Performance API |
| R2 | Coefficient of Determination |
| RAPL | Running Average Power Limit |
| SVR | Support Vector Regression |
| TPU | Tensor Processing Unit |
| TVM | Tensor Virtual Machine |
| XGB | XGBoosted Trees |
References
- Skillman, A.; Edso, T. A Technical Overview of Cortex-M55 and Ethos-U55: Arm’s Most Capable Processors for Endpoint AI. In Proceedings of the 2020 IEEE Hot Chips 32 Symposium (HCS), Palo Alto, CA, USA, 16–18 August 2020; pp. 1–20. [Google Scholar] [CrossRef]
- Chen, Y.H.; Yang, T.J.; Emer, J.; Sze, V. Eyeriss v2: A flexible accelerator for emerging deep neural networks on mobile devices. IEEE J. Emerg. Sel. Top. Circuits Syst. 2019, 9, 292–308. [Google Scholar] [CrossRef]
- Farshchi, F.; Huang, Q.; Yun, H. Integrating NVIDIA Deep Learning Accelerator (NVDLA) with RISC-V SoC on FireSim. In Proceedings of the 2019 2nd Workshop on Energy Efficient Machine Learning and Cognitive Computing for Embedded Applications (EMC2), Washington, DC, USA, 17 February 2019; pp. 21–25. [Google Scholar] [CrossRef]
- Lai, L.; Suda, N.; Chandra, V. CMSIS-NN: Efficient Neural Network Kernels for Arm Cortex-M CPUs. arXiv 2018, arXiv:1801.06601. [Google Scholar]
- Garofalo, A.; Rusci, M.; Conti, F.; Rossi, D.; Benini, L. Pulp-nn: A computing library for quantized neural network inference at the edge on risc-v based parallel ultra low power clusters. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 33–36. [Google Scholar]
- David, R.; Duke, J.; Jain, A.; Reddi, V.J.; Jeffries, N.; Li, J.; Kreeger, N.; Nappier, I.; Natraj, M.; Regev, S.; et al. TensorFlow Lite Micro: Embedded Machine Learning on TinyML Systems. arXiv 2021, arXiv:2010.08678. [Google Scholar]
- Rotem, N.; Fix, J.; Abdulrasool, S.; Catron, G.; Deng, S.; Dzhabarov, R.; Gibson, N.; Hegeman, J.; Lele, M.; Levenstein, R.; et al. Glow: Graph Lowering Compiler Techniques for Neural Networks. arXiv 2019, arXiv:1805.00907. [Google Scholar]
- Lin, W.F.; Tsai, D.Y.; Tang, L.; Hsieh, C.T.; Chou, C.Y.; Chang, P.H.; Hsu, L. ONNC: A Compilation Framework Connecting ONNX to Proprietary Deep Learning Accelerators. In Proceedings of the 2019 IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS), Hsinchu, Taiwan, 18–20 March 2019; pp. 214–218. [Google Scholar] [CrossRef]
- Guo, Y. A Survey on Methods and Theories of Quantized Neural Networks. arXiv 2018, arXiv:1808.04752. [Google Scholar]
- Wu, B.; Waschneck, B.; Mayr, C. Squeeze-and-Threshold Based Quantization for Low-Precision Neural Networks. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Halkidiki, Greece, 25–27 June 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 232–243. [Google Scholar]
- Wang, H.; Qin, C.; Zhang, Y.; Fu, Y. Emerging Paradigms of Neural Network Pruning. arXiv 2021, arXiv:2103.06460. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lattner, C. LLVM and Clang: Next generation compiler technology. In Proceedings of the BSD Conference, Ottawa, ON, Canada, 16–17 May 2008; Volume 5, pp. 1–20. [Google Scholar]
- Nvidia. Compute Unified Device Architecture Programming Guide; Nvidia: Santa Clara, CA, USA, 2007. [Google Scholar]
- Munshi, A. The OpenCL specification. In Proceedings of the 2009 IEEE Hot Chips 21 Symposium (HCS), Stanford, CA, USA, 23–25 August2009; pp. 1–314. [Google Scholar] [CrossRef]
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. J. Math. 1936, 58, 5. [Google Scholar]
- Huang, L.; Jia, J.; Yu, B.; Chun, B.G.; Maniatis, P.; Naik, M. Predicting Execution Time of Computer Programs Using Sparse Polynomial Regression. 2010. Available online: https://proceedings.neurips.cc/paper/2010/hash/995665640dc319973d3173a74a03860c-Abstract.html (accessed on 29 June 2022).
- Braun, L.; Nikas, S.; Song, C.; Heuveline, V.; Fröning, H. A Simple Model for Portable and Fast Prediction of Execution Time and Power Consumption of GPU Kernels. ACM Trans. Archit. Code Optim. 2021, 18, 1–25. [Google Scholar] [CrossRef]
- Sun, J.; Sun, G.; Zhan, S.; Zhang, J.; Chen, Y. Automated Performance Modeling of HPC Applications Using Machine Learning. IEEE Trans. Comput. 2020, 69, 749–763. [Google Scholar] [CrossRef]
- Braun, L.; Fröning, H. CUDA Flux: A Lightweight Instruction Profiler for CUDA Applications. In Proceedings of the 2019 IEEE/ACM Performance Modeling, Benchmarking and Simulation of High Performance Computer Systems (PMBS), Denver, CO, USA, 18 November 2019; pp. 73–81. [Google Scholar] [CrossRef]
- Shafiabadi, M.H.; Pedram, H.; Reshadi, M.; Reza, A. Comprehensive regression-based model to predict performance of general-purpose graphics processing unit. Clust. Comput. 2020, 23, 1505–1516. [Google Scholar] [CrossRef]
- Shafiabadi, M.; Pedram, H.; Reshadi, M.; Reza, A. An accurate model to predict the performance of graphical processors using data mining and regression theory. Comput. Electr. Eng. 2021, 90, 106965. [Google Scholar] [CrossRef]
- Nadeem, F.; Fahringer, T. Using Templates to Predict Execution Time of Scientific Workflow Applications in the Grid. In Proceedings of the 2009 9th IEEE/ACM International Symposium on Cluster Computing and the Grid, Shanghai, China, 18–21 May 2009; pp. 316–323. [Google Scholar] [CrossRef]
- Kaufman, S.J.; Phothilimthana, P.M.; Zhou, Y.; Mendis, C.; Roy, S.; Sabne, A.; Burrows, M. A Learned Performance Model for Tensor Processing Units. arXiv 2021, arXiv:2008.01040. [Google Scholar]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Qi, H.; Sparks, E.R.; Talwalkar, A. Paleo: A Performance model for deep neural networks. In Proceedings of the 5th International Conference on Learning Representations, (ICLR 2017), Toulon, France, 24–27 April 2017; Available online: https://openreview.net/forum?id=SyVVJ85lg (accessed on 25 May 2022).
- Justus, D.; Brennan, J.; Bonner, S.; McGough, A.S. Predicting the Computational Cost of Deep Learning Models. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 3873–3882. [Google Scholar] [CrossRef]
- Lattuada, M.; Gianniti, E.; Ardagna, D.; Zhang, L. Performance prediction of deep learning applications training in GPU as a service systems. Clust. Comput. 2022, 25, 1279–1302. [Google Scholar] [CrossRef]
- Yu, G.X.; Gao, Y.; Golikov, P.; Pekhimenko, G. Habitat: A {Runtime-Based} Computational Performance Predictor for Deep Neural Network Training. In Proceedings of the 2021 USENIX Annual Technical Conference (USENIX ATC 21), Online, 14–16 July 2021; pp. 503–521. [Google Scholar]
- Wang, C.C.; Liao, Y.C.; Kao, M.C.; Liang, W.Y.; Hung, S.H. PerfNet: Platform-Aware Performance Modeling for Deep Neural Networks. In Proceedings of the International Conference on Research in Adaptive and Convergent Systems (RACS’20), Gwangju, Korea, 13–16 October 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 90–95. [Google Scholar] [CrossRef]
- Yeung, G.; Borowiec, D.; Friday, A.; Harper, R.; Garraghan, P. Towards GPU Utilization Prediction for Cloud Deep Learning. In Proceedings of the 12th USENIX Workshop on Hot Topics in Cloud Computing (HotCloud 20), Online, 13–14 July 2020. [Google Scholar]
- Gianniti, E.; Zhang, L.; Ardagna, D. Performance Prediction of GPU-Based Deep Learning Applications. In Proceedings of the 2018 30th International Symposium on Computer Architecture and High Performance Computing (SBAC-PAD), Lyon, France, 24–27 September 2018; pp. 167–170, ISSN 1550-6533. [Google Scholar] [CrossRef]
- Cai, E.; Juan, D.C.; Stamoulis, D.; Marculescu, D. NeuralPower: Predict and Deploy Energy-Efficient Convolutional Neural Networks. In Proceedings of the Ninth Asian Conference on Machine Learning. PMLR, Seoul, Korea, 15–17 November 2017; pp. 622–637, ISSN 2640-3498. [Google Scholar]
- Bouhali, N.; Ouarnoughi, H.; Niar, S.; El Cadi, A.A. Execution Time Modeling for CNN Inference on Embedded GPUs. In Proceedings of the 2021 Drone Systems Engineering and Rapid Simulation and Performance Evaluation: Methods and Tools Proceedings, Budapest, Hungary, 18–20 January 2021; Association for Computing Machinery: New York, NY, USA, 2021. DroneSE and RAPIDO ’21. pp. 59–65. [Google Scholar] [CrossRef]
- Velasco-Montero, D.; Fernandez-Berni, J.; Carmona-Galan, R.; Rodriguez-Vazquez, A. PreVIous: A Methodology for Prediction of Visual Inference Performance on IoT Devices. IEEE Internet Things J. 2020, 7, 9227–9240. [Google Scholar] [CrossRef]
- Lu, Z.; Rallapalli, S.; Chan, K.; Pu, S.; Porta, T.L. Augur: Modeling the Resource Requirements of ConvNets on Mobile Devices. IEEE Trans. Mob. Comput. 2021, 20, 352–365. [Google Scholar] [CrossRef]
- Chen, T.; Moreau, T.; Jiang, Z.; Zheng, L.; Yan, E.; Shen, H.; Cowan, M.; Wang, L.; Hu, Y.; Ceze, L.; et al. TVM: An Automated End-to-End Optimizing Compiler for Deep Learning. In Proceedings of the 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18), Carlsbad, CA, USA, 8–10 October 2018; pp. 578–594. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional Architecture for Fast Feature Embedding. arXiv 2014, arXiv:1408.5093. [Google Scholar]
- Al-Rfou, R.; Alain, G.; Almahairi, A.; Angermueller, C.; Bahdanau, D.; Ballas, N.; Bastien, F.; Bayer, J.; Belikov, A.; Belopolsky, A.; et al. Theano: A Python framework for fast computation of mathematical expressions. arXiv 2016, arXiv:1605.02688. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for Large-Scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 7994–8005. [Google Scholar]
- Basics, L.S. Intel® Math Kernel Library 2005. Available online: https://www.intel.com/content/www/us/en/developer/tools/oneapi/onemkl.html (accessed on 29 June 2022).
- Wang, E.; Zhang, Q.; Shen, B.; Zhang, G.; Lu, X.; Wu, Q.; Wang, Y. Intel math kernel library. In High-Performance Computing on the Intel® Xeon Phi™; Springer: Berlin/Heidelberg, Germany, 2014; pp. 167–188. [Google Scholar]
- Chetlur, S.; Woolley, C.; Vandermersch, P.; Cohen, J.; Tran, J.; Catanzaro, B.; Shelhamer, E. cudnn: Efficient primitives for deep learning. arXiv 2014, arXiv:1410.0759. [Google Scholar]
- Chen, T.; Zheng, L.; Yan, E.; Jiang, Z.; Moreau, T.; Ceze, L.; Guestrin, C.; Krishnamurthy, A. Learning to Optimize Tensor Programs. arXiv 2019, arXiv:1805.08166. [Google Scholar]
- Zheng, L.; Liu, R.; Shao, J.; Chen, T.; Gonzalez, J.E.; Stoica, I.; Ali, A.H. TenSet: A Large-Scale Program Performance Dataset for Learned Tensor Compilers. In Proceedings of the Neural Information Processing Systems Track on Datasets and Benchmarks, Virtual, 6 December 2021; Available online: https://openreview.net/forum?id=aIfp8kLuvc9 (accessed on 29 June 2022).
- Rodrigues, C.F.; Riley, G.; Luján, M. Fine-grained energy profiling for deep convolutional neural networks on the Jetson TX1. In Proceedings of the 2017 IEEE International Symposium on Workload Characterization (IISWC), Seattle, WA, USA, 1–3 October 2017; pp. 114–115. [Google Scholar] [CrossRef][Green Version]
- Mucci, P.J.; Browne, S.; Deane, C.; Ho, G. PAPI: A Portable Interface to Hardware Performance Counters. In Proceedings of the Department of Defense HPCMP Users Group Conference, Montery, CA, USA, 7–10 June 1999; pp. 7–10. [Google Scholar]
- Power Capping Framework—The Linux Kernel Documentation. Available online: https://www.kernel.org/doc/html/latest/power/powercap/powercap.html (accessed on 29 June 2022).
- Intel® 64 and IA-32 Architectures Software Developer’s Manual Combined Volumes: 1, 2A, 2B, 2C, 2D, 3A, 3B, 3C, 3D, and 4. 2022. pp. 3345–3354. Available online: https://cdrdv2.intel.com/v1/dl/getContent/671200 (accessed on 29 June 2022).
- Hackenberg, D.; Ilsche, T.; Schuchart, J.; Schöne, R.; Nagel, W.E.; Simon, M.; Georgiou, Y. HDEEM: High Definition Energy Efficiency Monitoring. In Proceedings of the 2014 Energy Efficient Supercomputing Workshop, New Orleans, LA, USA, 16–21 November 2014; pp. 1–10. [Google Scholar] [CrossRef]
- Hähnel, M.; Döbel, B.; Völp, M.; Härtig, H. Measuring energy consumption for short code paths using RAPL. ACM Sigmetrics Perform. Eval. Rev. 2012, 40, 13–17. [Google Scholar] [CrossRef]
- Moons, B.; Noorzad, P.; Skliar, A.; Mariani, G.; Mehta, D.; Lott, C.; Blankevoort, T. Distilling optimal neural networks: Rapid search in diverse spaces. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 12229–12238. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).