Abstract
In light of the problem of difficult model parameter selection and poor resonance effects in traditional bearing fault detection, this paper proposes a parameter-adaptive stochastic resonance algorithm based on an improved whale optimization algorithm (IWOA), which can effectively detect bearing fault signals of rotating machinery. First, the traditional WOA was improved with respect to initial solution distribution, global search ability and population diversity generalization, effectively improving the global convergence of the WOA. Then, the parameters of the bistable stochastic resonance model were optimized using the improved WOA, and adaptive adjustment of the stochastic resonance parameters was realized. Finally, the Case Western Reserve University bearing data set and the XJTU-SY bearing data set were used as fault data for the actual bearing to be tested for experimental verification. The signal-to-noise ratios of the detected fault frequencies for the above two data sets were −20.5727 and −21.1289, respectively. Among the algorithms compared, the IWOA proposed in this paper had the highest signal-to-noise ratio of the detected fault frequencies. The experimental results show that the proposed method can effectively detect a weak bearing fault signal in enhanced noise.
1. Introduction
Rotating machinery, such as gas turbines, blowers, water pumps, etc., represents a very important type of power equipment used in industry. Bearings, as an important part of rotating mechanical systems, may fail when overloaded for a long time, affecting the safe and stable operation of the equipment. Because the characteristic signal of bearing failure is often submerged in the intense noise of rotating machinery operation, it can be difficult to detect and analyze effectively. Thus, it is of great importance to investigate how to detect weak bearing fault signals in intense noise to ensure the safe and stable operation of rotating machinery.
At present, there are several research directions relating to the detection of weak signals of bearing faults. One is to detect weak signals by suppressing noise, such as by using one of the following methods: the wavelet transform method [1], the coherence analysis method [2], the chaotic oscillator method [3], Hilbert variation [4], empirical mode decomposition [5], variable Partial mode decomposition [6] and others. The second is to detect weak signals based on data-driven and deep learning methods [7,8]. These methods can obtain a comprehensive evaluation, with high accuracy, of the system operation and fault conditions using the experience and knowledge of many subject experts to process and analyze various types of information concerning system operation. However, due to the large number of experimental samples required, such methods are not suitable for all fault diagnostic purposes. The third is to use noise energy to enhance the signal energy to be tested—an example of this approach is the stochastic resonance (SR) method [9,10]. SR has the advantage that it can superimpose part of the noise energy on the signal and achieve enhanced detection of weak signals when the input and output signals of the system are synchronized [11]. Benzi et al. proposed the use of an SR algorithm when they studied paleo-meteorological glaciers [12,13]. Over the past two decades, the theory underpinning the stochastic resonance method has continued to develop, and application of the method has been extended to mechanical fault diagnosis [14], image processing [15], optics [16], medical information processing [17], and many other areas.
The stochastic resonance (SR) method has been applied to bearing fault diagnosis of rotating machinery [18,19]. Relevant studies have shown that the selection of the model parameters of the stochastic resonance directly affects the resonance effect and has a significant impact on the fault diagnosis results obtained. Therefore, investigation of parameter-adaptive stochastic resonance has become one of the main research directions in this field. Using an intelligent optimization method to select stochastic resonance parameters has also been a major research direction in recent years [20]. However, available research suggests that problems remain, such as optimization results easily falling into local optima and low computational efficiency [21,22]. Therefore, obtaining the stochastic resonance parameters by selecting an appropriate intelligent optimization algorithm is very important to ensure the accuracy of fault diagnosis.
Whale optimization algorithms (WOAs) are a new group of intelligent optimization algorithms proposed by Seyedali Mirjalili et al. in 2016 [23]. Based on the foraging behavior of humpback whales, the algorithm constructs theoretical models of searching, encircling and hunting to achieve the optimal solution to a target problem. Compared with other optimization algorithms, WOA has the advantages of using a unique search mechanism, having fewer parameters, and being easier to understand. However, similar to other swarm intelligence algorithms, WOA also has the problems of slow convergence speed and ease of falling into local optima.
In this paper, parameter-adaptive stochastic resonance is used to detect and study the bearing fault signal. In view of the difficulty in selecting parameters for the stochastic resonance algorithm and the slow convergence speed of the whale optimization algorithm, their ease of falling into local optima, poor optimization accuracy, and other problems, combined with previous research concerning these issues, a parameter-adaptive SR using an improved whale optimization algorithm (IWOA) is proposed. The method uses chaotic iterative mapping to generate the initial whale population, which makes the initial solution distribution in the solution space uniform. Nonlinear time-varying factors and inertial weights are used to balance and improve the global search and local development capabilities and are combined with stochastic learning strategies to increase the population diversity during the iterative process. Last, but not least, Cauchy mutation is used to improve the ability of the algorithm to jump out of local optima. Experiments undertaken show that the method proposed has the advantages of using a simple model, having few algorithm parameters, exhibiting fast convergence speed, and having the capacity to detect bearing fault signals accurately and efficiently.
2. Parameter-Adaptive Stochastic Resonance
2.1. Bistable Stochastic Resonance
The theory of stochastic resonance concerns the detection of weak characteristic signals through a noise transfer mechanism in nonlinear systems. Generally, the process of stochastic resonance can be described by the Langevin equation, which was first used to explain the irregular motion of Brownian particles in fluids. The expression is as follows
where, is the SR output signal, is a potential function of the nonlinear system, is an input signal, is a noise signal, is the quality of the particle, and is the friction factor.
The potential function expression of the classical bistable model is as follows:
In Equation (2), and are the parameters of the nonlinear bistable model, , . The potential function chart of the traditional bistable model is shown in Figure 1. The bistable model has two steady points and one unsteady point ; the barrier height is .
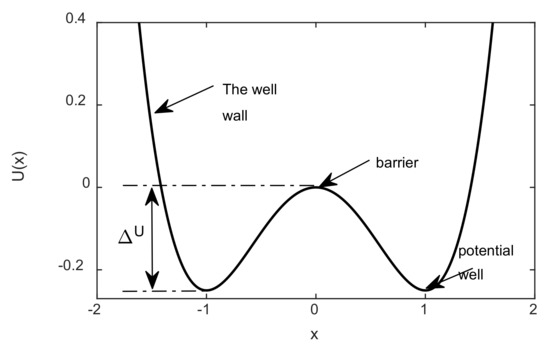
Figure 1.
Potential function diagram of classical bistable model.
The one-dimensional overdamped motion in the double potential well provides a description of the stochastic process of the classical bistable system. By neglecting the inertia term in Equation (1), setting the damping ratio , changing into the potential function of the classical bistable model, and adding noise with intensity D to the system, the Langevin equation of classical bistable system is obtained:
The trajectory of Brownian particles in the classical bistable system conforms to the description of Formula (3). When the noise of the system , there is only a weak periodic input signal. If the input signal amplitude is less than the threshold () of this system, the Brownian particle only oscillates in a single-sided potential well, and the position of the particles in the unilateral potential trap depends on the initial state. If the input amplitude is greater than the threshold , the Brownian particles cross the potential barrier under the driving force, and an inter-well transition occurs. If noise is added to the system, driven by the periodic force, the potential well of the nonlinear model potential function of the system will switch periodically.
Where the input signal amplitude is sufficiently small, an effective resonance can be achieved among the noise, the signal and the nonlinear classical bistable system. The particles can transition under noise, enabling detection of weak periodic signals.
2.2. Determination of Parameter Ranges
Kramers’ rate is an important index to describe the transition ability of particles in the two potential wells. According to the classical SR principle, the SR phenomenon occurs in the output of the system when the Kramers’ rate is equal to half of the signal frequency, namely:
The traditional stochastic resonance method is often used for weak signal detection with low frequency (frequency less than 1 Hz), but the frequency of the signal to be measured is often very large in practice. Generally, the signal frequency is compressed and sampled using a rescaling technique [24] and the compression ratio is set to .
The relationship between the input periodic signal and the system parameter and the calculation step are shown below:
where is a constant in [0, 1].
The input signal amplitude is not less than , that is
So
The particles can jump over a higher barrier height by accumulating energy as a result of the effect of noise. According to the research theory [25,26,27], and many simulation experiments, the range of parameter is set as [0, 0.5], and the value range of is set as [0, 10].
3. Improved Whale Optimization Algorithm
3.1. WOA
The whale optimization algorithm (WOA) is a new heuristic optimization algorithm proposed by Mirjalili to imitate the hunting behavior of humpback whales. In nature, humpback whales swim spirally to their prey and shrink the enclosure at the same time, as shown in Figure 2. This predation behavior is named the bubble net predation strategy, and the following is its mathematical model expression.
where, represents the optimal solution in each iteration, and are the coefficient vectors and is a position vector. It is important to note that each iteration should update the optimal solution, unless the optimal solution in the current iteration is better than that in the next iteration. The coefficient vectors and are shown as
where, as the number of iterations increases, linearly decays from 2 to 0. To enable some agents to reach optimal positions, is an arbitrary vector in [0, 1].

Figure 2.
Humpback whale hunting behavior.
In the process of humpback whale capturing prey in a spiral route, it is assumed that the chance of choosing the constriction encirclement system and the spiral model to update the whale’s position are half to half, and the following is its mathematical model expression:
where, is a random number in [0, 1] and is a constant that defines the shape of the spiral. is a random number in the range [−1, 1]. The following is the formula for calculating .
The following is the mathematical model formula for humpback whales looking for food:
where, is the randomly selected whale position vector.
3.2. Improved Whale Optimization Algorithm
The article presents an improved whale optimization algorithm. Firstly, this algorithm uses a chaotic iterative map to generate the initial whale population. Secondly, nonlinear time-varying factors and inertia weights are used to balance and improve the global search and local development capabilities. Then stochastic learning strategies are combined to increase the population diversity during optimization. Last, but not least, Cauchy variation is used to prevent the algorithm from falling into a local optimum.
3.2.1. Chaos Sequence Initialization
A chaotic iterative map is used to generate the initial whale population model to solve the problem of uneven distribution of the initial population position. The mathematical expression of the iterative map is:
where, is the control parameter, , and is given in the paper.
3.2.2. Linear Time-Varying Factors and Adaptive Weights
If the traditional WOA does not search the prey thoroughly in the preceding phase, then the convergence speed during the later hunting process is slow due to the linear descent of the convergence factor . Therefore, a piecewise nonlinear convergence factor is proposed in the paper, which is described as follows
Compared with the original convergence factor , enhances the ability for global exploration in the preceding phase and local development in the later period.
Because the update of the whale group location will be affected by the prey target, an adaptive weight strategy is added to optimize the position update of whales in the process of hunting, which is:
So, the formula for updating the position becomes the following:
The adaptive weight gradually increases with the number of iterations in the middle and late period of this iteration, which enhances the local development ability of the algorithm, enabling the whale swarm to find the target solution more quickly and accurately. The improvement effectively strengthens the optimization performance of the algorithm, accelerates the algorithm convergence and improves algorithm stability.
3.2.3. Random Learning Strategy
A random learning strategy [28] is added to simulate the learning mode of discussion and communication between whales. This model optimizes its own position by learning from better individuals, thereby improving the global optimization ability. The better individuals are selected in our method by comparing fitness values between individual and a randomly selected individual from the population. The optimized location of better individuals can be expressed as
where, the learning factor is a random number between (0, 1), which represents the difference of each individual’s learning ability. The randomness learning of individuals enhances the information-sharing ability and the diversity of the population, and effectively improves the global optimization performance of the algorithm.
3.2.4. Cauchy Mutation Strategy
A Cauchy mutation strategy is introduced to solve the problem that the whale optimization algorithm easily falls into local optimization. The optimal individual position update with Cauchy mutation equation can be expressed as
where, represents the new value obtained from the current optimal value after Cauchy disturbance, and is a Cauchy operator. The standard Cauchy distribution function formula [29] is
According to the mathematical theory, the extension of the Cauchy distribution at both ends can generate random numbers far from the origin, which can enable the disturbed whales to have the ability to quickly avoid local traps. At the same time, compared with other functions, if the highest peak of the Cauchy distribution is lower, which can shorten the time spent by individuals in this search space, then the convergence speed of the algorithm is accelerated.
To verify the performance of the proposed algorithm and other optimization algorithms, four typical benchmark test functions were selected (Table 1), where F4 represents the unimodal benchmark function, F10 and F11 represent the complex multimodal benchmark functions, and F15 represents the fixed-dimension multimodal benchmark function. The algorithms involved in the comparison were the whale optimization algorithm (WOA), gray wolf optimization (GWO), bat optimization algorithm (BOA), gravity search algorithm (GSA), particle swarm optimization (PSO), and the artificial bee colony (ABC).

Table 1.
Benchmark function.
The population size was set to 30, the maximum number of iterations was 500, and each algorithm ran independently 30 times. The mean value (mean) and standard deviation (std) of the optimal simulation results were used as the algorithm performance evaluation index. The results are shown in Table 1.
It can be seen from Table 2 that when the average value of the optimal value was used as the evaluation index, among the four test functions of F4, F10, F11, and F15, the optimization results of the IWOA algorithm were all the best. Taking the standard deviation of the optimal value as the evaluation index of the algorithm stability, it can be seen from 30 independent simulation calculations that the stability of the IWOA algorithm proposed in this paper was worse than that of ABC in F15, but in F4, F10, and F11, the stability was better than the other six optimization algorithms, so the overall stability was still the best.

Table 2.
Comparison of the results for IWOA and other optimization algorithms.
In order to more intuitively reflect the convergence speed of the algorithm proposed in this paper and the ability to jump out of the local optimum, the convergence curve of each algorithm is shown in Figure 3. As can be seen from the figure, the IWOA algorithm proposed had the fastest optimization process for the four test functions of F4, F10, F11, and F15, which can effectively save optimization time.
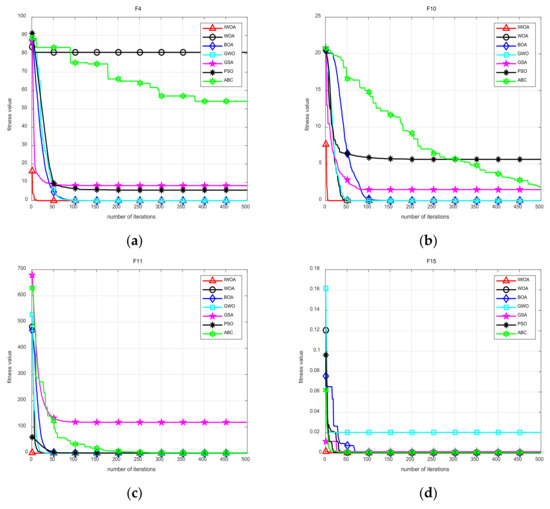
Figure 3.
Algorithm convergence curve: (a) test function F4, (b) test function F10, (c) test function F11, (d) test function F15.
4. Stochastic Resonance Parameter Adaptive Strategy
4.1. Stochastic Resonance Parameter Adaptation Based on Improved Whale Optimization Algorithm
The signal-to-noise ratio (SNR) is widely used to evaluate the output of SR systems. WOA focuses on searching parameters to minimize the objective function values, so this paper uses the inverse of the SNR as the fitness function. Below is the expression for SNR:
where, is the amplitude of the target frequency, is the amplitude of the input signal at a frequency other than the target frequency, and is the number of agents.
According to the above analysis, the flow chart of rotating machinery fault signal detection based on the improved whale algorithm to optimize SR parameters is shown in Figure 4.
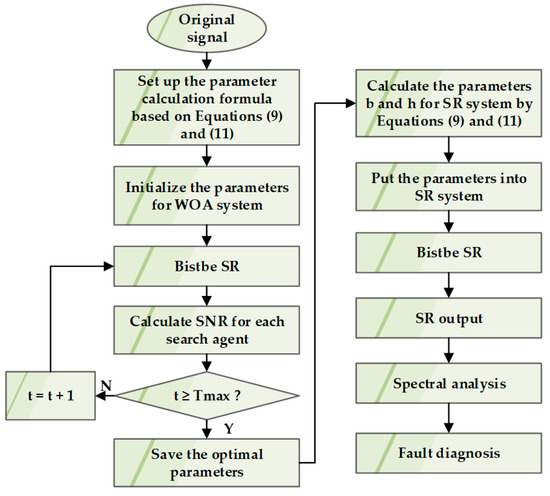
Figure 4.
SR fault diagnosis flowchart based on IWOA.
The steps of optimizing SR parameters for fault signal detection of rotating machinery based on the improved whale algorithm are as follows:
- Step 1:
- Input the noisy signal, establish the calculation process of Formulas (9) and (11), and initialize the parameters of the whale optimization system. The value ranges of , , and are [0, 0.5], [0, 1], [0, 10], respectively. The maximum iteration time is 200 and the whale population is 30.
- Step 2:
- Optimize SR parameters through IWOA and calculate the SNR. Update the best position for particles until the maximum number of iterations.
- Step 3:
- Obtain the optimal solution of , , by IWOA. Then the parameters and are calculated according to Equations (9) and (11).
- Step 4:
- Substitute , , into the stochastic resonance system to run, and convert the calculation results into the frequency domain through Fourier transform. Diagnose the fault signal by analyzing the results of the frequency domain.
4.2. Simulation
The correctness of the method proposed in this article was confirmed by simulation experiments. The amplitude of the input signal , the target frequency , the phase angle , the sampling frequency , the sample data length , the noise intensity , and . The waveforms in the time and frequency domains of the input signal are shown in Figure 5. As shown in Figure 5, the target frequency of the input signal was difficult to capture under the influence of noise. The SR parameters obtained after IWOA optimization and calculation were , , and . The three parameters, , and h, were then substituted into the stochastic resonance system to obtain the time-domain and frequency-domain waveforms of its output, as shown in Figure 5. The SNR of the output was , which, compared with the input signal-to-noise ratio, increased by 10.0471 dB. According to the frequency domain waveform in Figure 6, a significant spike was observed at the target frequency, and the amplitude of the frequency at the spike was much greater than the amplitude of the other surrounding frequencies. Thus, the method proposed can accurately detect weak signals.
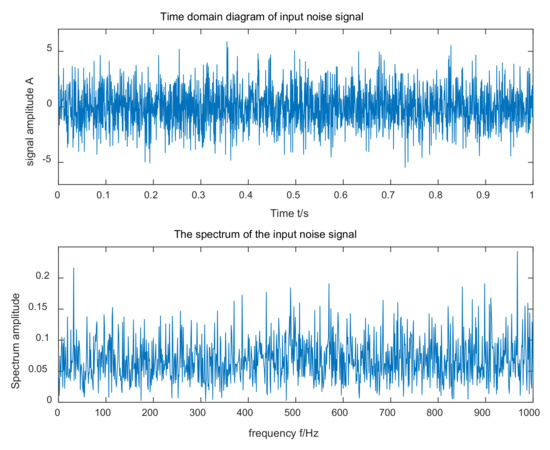
Figure 5.
Input signal time domain waveform and FFT spectrum of the simulation model.
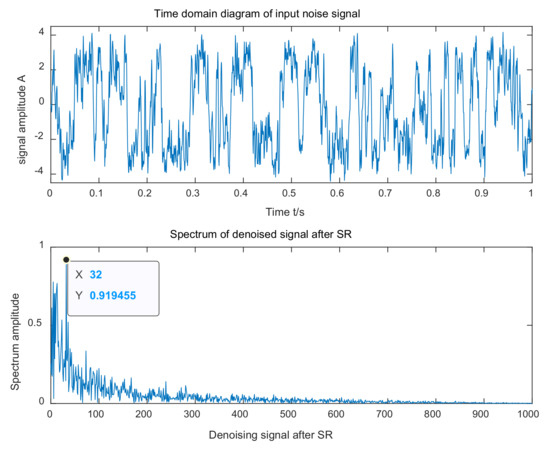
Figure 6.
The output signal processed by the mentioned method of the simulation model.
5. Bearing Fault Detection Experiment
5.1. Bearing Fault Detection Based on IWOA
6205-2RS JEM SKF deep groove ball bearings and LDK UER204 bearings were used as the research objects to detect the inner ring signal of the faulty bearing, and the main parameters of the bearing are shown in Table 3 and Table 4, respectively. The fault signal data of the actual bearing to be tested were the data of the electrical engineering laboratory of Case Western Reserve University [30] and the XJTU-SY bearing dataset [31], respectively. Since the rotation speed used in the Case Western Reserve University dataset is 1750 rpm, it can be calculated that the fault characteristic frequency of the inner loop is 158 Hz, the sampling frequency is 12 kHz, and the data length of the signal is 12,000. The rotation speed used in the XJTU-SY bearing data set is 2250 rpm, so it can be calculated that the fault characteristic frequency of the inner ring is 184.38 Hz, while the sampling frequency and the data length of the signal are 14.2 kHz and 14,200 respectively.

Table 3.
6205-2RS JEM SKF Bearing Parameters.

Table 4.
LDK UER204 Bearing Parameters.
The time domain and frequency domain waveforms of the original signal input from the Case Western Reserve University dataset are shown in Figure 7. The optimal parameters of the IWOA were , , . Then, the parameters and were calculated through Formulas (10) and (12). The three parameters , , and were substituted into the SR system to obtain the frequency domain waveform of the output, as shown in Figure 8. In Figure 8, the ordinate of the fault frequency point is the amplitude of the target frequency. It can be observed that the amplitude of the fault characteristic frequency was the largest, and the output SNR can be calculated as −20.5727, with less interference components around it. It can be seen that the method proposed in this paper can achieve the adaptive selection of stochastic resonance parameters and detect the bearing fault signal.
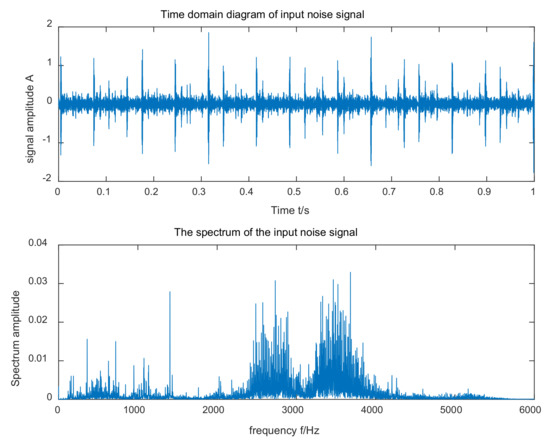
Figure 7.
Input signal time domain waveform and FFT spectrum for the Western Reserve University dataset.
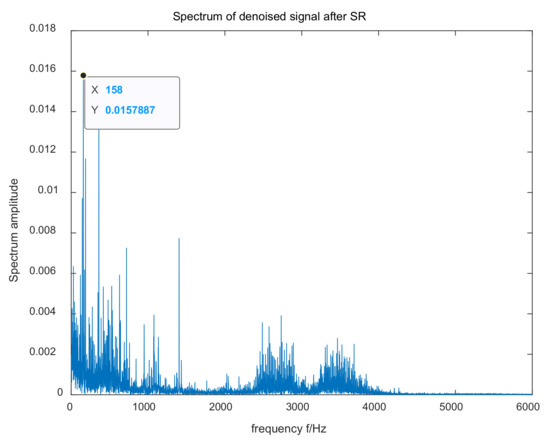
Figure 8.
The output signal processed by the mentioned method for the Western Reserve University dataset.
The original signal time domain and frequency domain waveforms input from the XJTU-SY bearing dataset are shown in Figure 9. The optimization of the SR parameters by IWOA were , , . The frequency domain waveform of the SR output results is shown in Figure 10. Since the amplitude of the fault characteristic frequency is the largest, and there are fewer interference components around it, the fault characteristic frequency can be easily observed—the output signal-to-noise ratio was −21.1289. Therefore, the algorithm proposed can effectively detect the bearing fault frequency in different datasets.
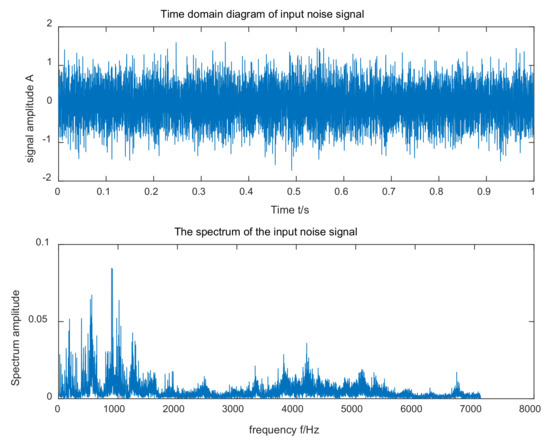
Figure 9.
Input signal time domain waveform and FFT spectrum for the XJTU-SY bearing dataset.
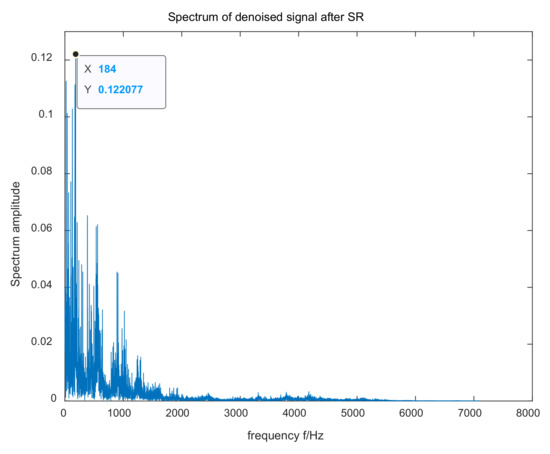
Figure 10.
The output signal processed by the mentioned method for the XJTU-SY bearing dataset.
5.2. Comparison with Other Methods
To assess the advantages of the IWOA method proposed with respect to convergence and detection effectiveness, bearing fault detection experiments were carried out using a variety of adaptive SR parameters, such as the whale optimization algorithm (WOA) [32], the spotted hyena optimizer (SHO) [33], the gray wolf optimization (GWO) [34], the bat optimization algorithm (BOA) [35], the aquila optimizer (AO) [36] and particle swarm optimization (PSO) [37].
A comparison of fault detection results for the Case Western Reserve University dataset are shown in Figure 11. Figure 11a–f, respectively, show the fault frequencies detected after optimization of the SR parameters by WOA, SHO, GWO, BOA, AO and PSO. The optimized SR parameters and the detection effects are shown in Table 5. It is evident from Figure 11 that the amplitudes of the fault characteristic frequencies processed by the above six methods were all the largest. These optimization algorithms could obtain reasonable SR parameters and apply them to signal detection, and the effects were consistent with those obtained by the proposed method. It can be seen in Table 5 that, in terms of signal-to-noise ratio, the proposed method has a larger signal-to-noise ratio compared with the above six methods, and enables easier observation of the fault characteristic frequency. In terms of time performance, except for the BOA algorithm, the calculation time for the proposed algorithm was the shortest. In the field of fault diagnosis, the signal-to-noise ratio is one of the main metrics. Therefore, the method proposed in this paper has certain advantages.
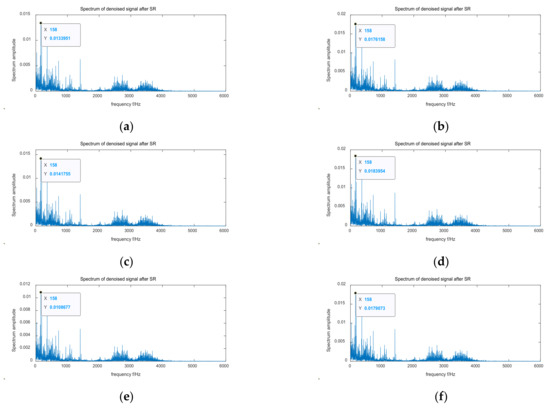
Figure 11.
The output signal processed by the mentioned method: (a) WOA, (b) SHO, (c) GWO, (d) BOA, (e) AO, (f) PSO.

Table 5.
Experimental parameter results.
A comparison of the fault detection results of the XJTU-SY bearing dataset using the above optimization algorithms is shown in Table 6. Although the running time of the algorithm in this paper was not the fastest, it was very close to the fastest time, and the detected fault frequency signal-to-noise ratio was still the highest.

Table 6.
Experimental parameter results.
According to the experimental results for the above two datasets, the proposed parameter-adaptive SR algorithm based on the IWOA has some advantages in terms of convergence speed and detection effect.
6. Conclusions
To solve the problem that the parameters of the traditional SR model are difficult to obtain, a parameter-adaptive SR with an improved whale optimization algorithm was proposed. This method represents an improvement compared to the traditional WOA with respect to initial solution distribution, global search ability and population diversity generalization, and can adaptively select the parameters of the SR model. A 6205-2RS JEM SKF deep groove ball bearing and an LDKUER204 bearing were used as the research objects. Bearing fault detection was performed on the Case Western Reserve University dataset and the XJTU-SY bearing dataset. The experimental results showed that the proposed method can be used to detect bearing fault signals and can effectively enhance fault signals in the noise. Compared with stochastic resonance parameters optimized by other intelligent algorithms, the method has the advantages of fast convergence speed and accurate optimization of parameters.
Author Contributions
Conceptualization, W.H. and S.J.; methodology, W.H. and S.J.; software, G.Z.; validation, W.H. and G.Z.; formal analysis, W.H.; investigation, S.J. and J.W.; resources, W.H. and G.Z.; data curation, J.W.; writing—original draft preparation, G.Z.; writing—review and editing, W.H.; visualization, W.H. and G.Z.; supervision, W.H., S.J. and J.W.; project administration, W.H. and S.J.; funding acquisition, S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Natural Science Foundation (NNSF) of China NO.62073258, 62003261, 61871318), the Natural Basic Science Research Program of Shaanxi Province of China (NO. 2020JQ-650), and the Scientific Research Program funded by the Shaanxi Education Department (NO. 20JK0788).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tyagi, S.; Panigrahi, S.K. A Simple Continuous Wavelet Transform Method for Rolling Bearing Fault Detection and Its Comparison with Envelope Detection. J. Res. Sci. Eng. 2021, 3, 1033–1040. [Google Scholar]
- Waters, W.M.; Jarrett, B.R. Bandpass Signal Sampling and Coherent Detection. IEEE Trans. Aerosp. Electron. Syst. 1982, 18, 731–736. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Li, X.Y.; Hu, C.Y.; Yan, X.S.; Gong, W.Y. Chaotic-based grey wolf optimizer for numerical and engineering optimization problems. Memetic Comput. 2020, 12, 371–398. [Google Scholar] [CrossRef]
- Mahata, S.; Shakya, P.; Babu, N.R. A robust condition monitoring methodology for grinding wheel wear identification using Hilbert Huang transform. Precis. Eng. 2021, 70, 77–91. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Cexus, J.C. EMD-Based Signal Filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Ren, G. An improved adaptive VMD method and its application in wear condition monitoring of main bearing. Vibroeng. Procedia 2021, 38, 26–31. [Google Scholar]
- Chen, H.T.; Jiang, B.; Zhang, T.Y.; Lu, N.Y. Data-driven and deep learning-based detection and diagnosis of incipient faults with application to electrical traction systems. Neurocomputing 2020, 396, 429–437. [Google Scholar] [CrossRef]
- Jiang, Y.C.; Yin, S.; Kaynak, O. Optimized Design of Parity Relation Based Residual Generator for Fault Detection, Data-Driven Approaches. IEEE Trans. Ind. Inform. 2021, 17, 1449–1458. [Google Scholar] [CrossRef]
- Shi, H.T.; Li, Y.Y.; Zhou, P.; Tong, S.H.; Guo, L.; Li, B.C.; Forte, P. Weak Fault Detection for Rolling Bearings in Varying Working Conditions through the Second-Order Stochastic Resonance Method with Barrier Height Optimization. Shock Vib. 2021, 2021, 5539912. [Google Scholar] [CrossRef]
- Fraņcois, C.B.; Godivier, X. Theory of stochasticresonance in signal transmission by static nonlinear systems. Phys. Rev. E 1997, 55, 1478–1495. [Google Scholar]
- Ren, Y.; Huang, J.; Hu, L.M.; Chen, H.P.; Li, X.K.; Zhou, L. Research on Fault Feature Extraction of Hydropower Units Based on Adaptive Stochastic Resonance and Fourier Decomposition Method. Shock Vib. 2021, 2021, 6640040. [Google Scholar] [CrossRef]
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys.-Math. Gen. 1981, 14, L453–L457. [Google Scholar] [CrossRef]
- Benzi, R.; Parisi, G.; Vulpiani, S.A. A Theory of Stochastic Resonance in Climatic Change. SIAM J. Appl. Math. 1983, 43, 565–578. [Google Scholar] [CrossRef]
- Mba, C.U.; Makis, V.; Marchesiello, S.; Fasana, A.; Garibaldi, L. Condition monitoring and state classification of gearboxes using stochastic resonance and hidden Markov models. Measurement 2018, 126, 76–95. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z. Binary image enhancement based on aperiodic stochastic resonance. IET Image Process. 2015, 9, 1033–1038. [Google Scholar] [CrossRef]
- Zhang, L.; Cao, L.; Wu, D.J. Effect of correlated noises in an optical bistable system. Phys. Rev. A 2008, 77, 015801. [Google Scholar] [CrossRef]
- Rodrigo, G.; Stocks, N.G. Suprathreshold Stochastic Resonance behind Cancer. Trends Biochem. Sci. 2018, 43, 483–485. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Wang, J.; Liu, Y.; Dai, D.; Kong, F. Multiscale noise tuning of stochastic resonance for enhanced fault diagnosis in rotating machines. Mech. Syst. Signal Process. 2012, 28, 443–457. [Google Scholar] [CrossRef]
- Tan, J.; Chen, X.; Wang, J.; Chen, H.; Cao, H.; Zi, Y.; He, Z. Study of frequency-shifted and re-scaling stochastic resonance and its application to fault diagnosis. Mech. Syst. Signal Process. 2009, 23, 811–822. [Google Scholar] [CrossRef]
- Chi, K.; Kang, J.S.; Tong, R.; Zhang, X.H. An adaptive stochastic resonance method based on multi-agent cuckoo search algorithm for bearing fault detection. J. Vibroeng. 2019, 21, 1296–1307. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Yang, X.S.; Alavi, A.H. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization. Eng. Comput. 2014, 31, 1198–1220. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Guo, J.; Zhu, L.; Lv, S. Research on mud pulse signal detection based on adaptive stochastic resonance. J. Pet. Sci. Eng. 2017, 157, 643–650. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- He, B.; Huang, Y.; Wang, D.; Yan, B.; Dong, D. A parameter-adaptive stochastic resonance based on whale optimization algorithm for weak signal detection for rotating machinery. Measurement 2019, 136, 658–667. [Google Scholar] [CrossRef]
- Li, G.; Li, J.; Wang, S.; Chen, X. Quantitative evaluation on the performance and feature enhancement of stochastic resonance for bearing fault diagnosis. Mech. Syst. Signal Process. 2016, 81, 108–125. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; He, Z. Adaptive stochastic resonance method for impact signal detection based on sliding window. Mech. Syst. Signal Process. 2013, 36, 240–255. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Liu, Z.; He, Z. An adaptive stochastic resonance method based on grey wolf optimizer algorithm and its application to machinery fault diagnosis. ISA Trans. 2017, 71, 206–214. [Google Scholar] [CrossRef]
- Bi, X.J.; Li, Y.; Chen, C.Y. A self-adaptive teaching-and-learning-based optimization algorithm with a mixed strategy. J. Harbin Eng. Univ. 2016, 37, 842–848. [Google Scholar]
- He, Q.; Lin, J.; Xu, H. Hybrid Cauchy Mutation and Uniform Distribution of Grasshopper Optimization Algorithm. Control Decis. 2021, 36, 1558–1568. [Google Scholar]
- Available online: http://www.eecs.cwru.edu/laboratory/bearing/download.html (accessed on 10 April 2018).
- Wang, B.; Lei, Y.; Li, N.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2018, 69, 401–412. [Google Scholar] [CrossRef]
- Li, M.D.; Xu, G.H.; Fu, Y.W.; Zhang, T.W.; Du, L. Improved whale optimization algorithm based on variable spiral position update strategy and adaptive inertia weight. J. Intell. Fuzzy Syst. 2022, 42, 1501–1517. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer, a novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Arora, S.; Singh, S. Butterfly optimization algorithm, a novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila Optimizer, a novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Tong, L.; Li, X.; Hu, J.; Ren, L. A PSO Optimization Scale-Transformation Stochastic-Resonance Algorithm with Stability Mutation Operator. IEEE Access 2017, 6, 1167–1176. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).