Abstract
Fractional calculus is an emerging topic in artificial neural network training, especially when using gradient-based methods. This paper brings the idea of fractional derivatives to spiking neural network training using Caputo derivative-based gradient calculation. We focus on conducting an extensive investigation of performance improvements via a case study of small-scale networks using derivative orders in the unit interval. With particle swarm optimization we provide an example of handling the derivative order as an optimizable hyperparameter to find viable values for it. Using multiple benchmark datasets we empirically show that there is no single generally optimal derivative order, rather this value is data-dependent. However, statistics show that a range of derivative orders can be determined where the Caputo derivative outperforms first-order gradient descent with high confidence. Improvements in convergence speed and training time are also examined and explained by the reformulation of the Caputo derivative-based training as an adaptive weight normalization technique.
1. Introduction
Neural networks have been around in machine learning for decades by now [1,2,3,4]. They evolved from implementing elementary logical gates through solving everyday, monotonic tasks, such as character recognition, to exceeding human intelligence in complex intellectual tasks, such as chess or go. However these static, artificial neural networks (ANNs) still work in a digital manner, they work well on time-multiplexed machines, such as CPUs and GPUs. The next step in their evolution came with the first spiking neural networks (SNNs). These SNNs are analog-valued, dynamic simulations of biological neurons based on more complex mathematical representations when compared to ANNs. They transmit information between neurons via strictly timed spikes, rather than real values, thus they resemble the behavior of human brains and natural intelligence.
Along with the practical data encoding, SNNs novelty relies on their specific hardware architecture. In the last few years, there were several artificial neural arrays designed to work with various SNN models, and training methods. When it comes to the energy efficiency of these neuromorphic processors, all models report a huge improvement, with three or four orders of magnitude less energy consumed than a regular CPU or GPU. Even modern TPUs cannot achieve as low training and inference energies as specifically designed SNN processors; therefore, SNN technology favors energy-efficient applications [5,6,7]. Recently developed memristive approaches might widen this gap even more [8].
While ANN-to-SNN conversion-based training has been a hot topic in the last few years [9,10], direct SNN training should also be considered as an alternative. Direct SNN trainings are mostly based on local learning rules which are native operations on a neuromorphic computing device. These are mostly variants of Spike-Time Dependent Plasticity (STDP) learning [11,12] and gradient learning. STDP-like learning rules are local in the sense, that they only need the pre- and postsynaptic spikes to apply appropriate weight modifications. There are successful mixed applications where gradient-based or evolutionary operators are used in addition to local plasticity, to handle global convergence [13,14].
The third main method for SNN training is the gradient-based, global approach [15,16], which is the focus of this paper as well. Gradient-based methods use spike-timing, or rate-based metrics to interpret the outputs of the SNN, and therefore use these metrics to formulate cost functions too.
From the gradient-based SNN architectures in our case study, we utilize the Tempotron model [17]. The errors in this model are the excess or absent voltages compared to the spiking threshold. These voltage differences are in the end functions of the weight parameters, and by taking their gradients, classic Gradient Descent (GD) learning can be used. While Tempotron is not the latest architecture, its various applications and enhancements are carried out by numerous research groups even nowadays [18,19,20]. Such reusability of classical methods can be observed in the field of artificial intelligence in general [21,22,23,24].
As this paper is a pioneer in applying Caputo fractional derivative in gradient-based SNN training, we use a simple two-layer architecture without any backpropagation (BP) tricks used to bypass the thresholding step function, and carry out extensive optimization experiments with more than 10,000 SNNs trained. We will also apply restrictions and use first-to-spike encoding to pass information between spiking neurons, and evaluate results. For the experiments, we use four basic classification datasets also used for introducing Caputo derivative-based ANNs by [25], so our work will be comparable in the sense of improvement. Of course, as we explore basic ideas in this paper, the aim of this comparison is not to outperform similar ANNs (especially as SNN models tend to be less accurate compared to structurally similar ANNs), but rather to highlight empirical analogies.
Looking back to these ANN training possibilities, several recent studies are reporting more efficient, and more precise learning, when standard, integer-order derivatives are replaced with fractional-order derivatives [25,26]. These methods interpolate between the cost function and the gradient of it based on different mathematical methods described by fractional calculus. Recent studies include joint first and fractional-order methods and global proofs of convergence when using these methods with ANNs [27,28], thus making them a promising future research path.
The theorem of fractional calculus dates back several hundred years; however, the possibility of its effective use has only become relevant in the last few decades. The basic idea of fractional calculus is the extension of derivative orders from the integers to reals or even imaginary numbers. There is a crucial property of these fractional-order derivatives which is important when it comes to gradient-based training. fractional-order derivatives are not local properties, rather they are interpreted over an interval. This means that every single point of the fractional gradient includes information from an interval of the cost manifold. Altogether using Caputo derivatives leads to a small, but significant improvement in training, and thus they are to be used when training artificial neural networks [25].
In most cases, when training ANNs with fractional-order derivatives, the Caputo derivative, defined by [29] is one of the best operators to use, while the ideal order of this derivative is around [25]. Caputo derivative has also been proven to be useful when calculating SNN neural dynamics [30], however to the best of our knowledge, it has not been used for gradient-based SNN training before.
In this paper, as a case study, we propose a method for utilizing Tempotron-like [17] learning using Caputo derivatives, in the training of two-layer spiking neural networks, which later could serve as a basis of fractional-order training of more complex models. The main contributions of the paper are as follows:
- We propose the Caputron optimizer, an efficient matrix formula for computing fractional-order derivative-based weight updates of Tempotron-like architectures.
- By using shallow models and basic benchmark datasets extensive experiments are carried out to show how Caputron with derivative orders from the open interval outperforms classic first-order derivative-based optimization in terms of categorization accuracy and convergence speed.
- Using particle swarm optimization [31] we search for near-optimal derivative orders for specific datasets and investigate if there is a generally suitable value for the derivative order which is viable for multiple datasets.
- We discuss the possible reformulation of Caputo-derivative-based learning as an adaptive weight normalization, which introduces a degree of sparsity to the network architecture.
With this case study, we wish to provide empirically suitable values for Caputo derivative orders for SNN training based on a large number of model evaluations. We also aim to encourage discussion and future research of more complex fractional-order derivative-based SNN architectures, which can achieve state-of-the-art performance due to a higher number of parameters and more complex information flow.
The structure of this paper is as follows. In Section 2, Tempotron learning rule is used in our case study, and the mathematical background of the Caputo derivative is introduced. Section 3 presents the used algorithms for SNN simulation and Caputron, a novel Caputo derivative-based Tempotron optimizer. Section 4 contains various tests, on standard benchmark datasets, and summarizes our experiments and comparisons. Section 5 draws conclusions, possible future work is also presented here.
2. Problem Statement
2.1. Fractional Derivatives in Tempotron Learning
The Tempotron SNN model was introduced in Nature by [17]. The model uses spike-time-based information representation. Rather than solving a differential equation, this SNN model has a kernel function, which is an ordinary function derived from neural dynamics. This kernel function takes the elapsed times from every presynaptic spike as arguments, to calculate the postsynaptic potentials (PSPs). The weighted sum of these gives the momentary membrane potential of the postsynaptic neuron. The kernel function is given by Equation (1).
where is the kernel function, is the normalization coefficient, t is the current simulation time, is the presynaptic spiketime, and are the membrane and synaptic time constants, respectively. A representation of the kernel function with common time constants and unit normalization coefficient is shown in Figure 1.
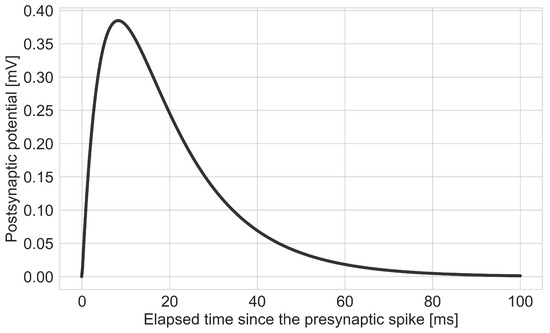
Figure 1.
Tempotron kernel function with example neural parameters. With parameters: mV, ms and ms.
The postsynaptic neuron’s potential is then calculated according to Equation (2).
where denotes the membrane potential of postsynaptic neuron j, is the synaptic weight between presynaptic neuron i and postsynaptic neuron j, is the series of spiketimes of the presynaptic neuron i, and is the equilibrium potential of the neuron.
Tempotron is trained in a classical gradient-based manner, based on the cost function’s first order partial derivative with respect to the weights. A learning rate is also applied when calculating the weight updates. The main idea behind the Tempotron cost function is the following. If there was a desired spike, but the neuron was inactive, the error is the difference between the firing threshold and the maximal membrane potential. If there is an undesired neuron activation, the error is the voltage difference by which the maximal membrane potential exceeds the firing threshold. The cost function’s definition is given by Equation (3).
The above mentioned derivative of this cost function and the weight update rules are as follows (Equations (4) and (5)).
where the cases are the same as in Equation (3). here is the simulation time at which the membrane potential of output neuron j had the highest value.
where is the weight change and is the learning rate.
A schematic of the forward and backward pass of two neurons in the Tempotron model is depicted in Figure 2. Here T denotes the discrete simulation time steps, and are spike times of neuron i and j, respectively. Neurons form two layers the presynaptic one is denoted by I the postsynaptic layer is denoted by J the weight parameter of the synapse between neuron i and j is described by . is the postsynaptic potential derived from presynaptic spike . is the maximal membrane potential of neuron j at time step . is the Tempotron loss calculated from the output spikes, target spike times, and maximal membrane potentials. is the partial derivative of the loss with respect to the weight parameter. The weights are updated based on this derivative the formulation of which depends on the derivative order, as it can be either 1 or a fractional value for the Caputo derivative between 0 and 1. Inspired by results in ANN research [25,26] this paper aims to investigate the effect of replacing the first-order partial derivative with a fractional-order Caputo derivative.
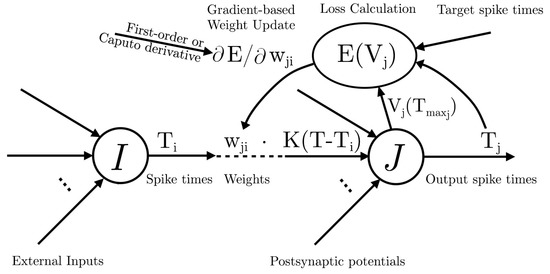
Figure 2.
Forward and backward pass for each synapse between two layers of spiking neurons using Tempotron loss. The forward pass includes the calculation of neural dynamics in layer I and J by utilizing K Tempotron kernel function and as spike times. weights represent the synapses and are the learnable parameters of this architecture. The network outputs spike times of the postsynaptic layer. The backward pass includes the calculation of Tempotron loss according to Equation (3). Then the weights are updated based on the partial derivative which can be calculated with an integer or a fractional Caputo order as well.
2.2. Caputo Derivative
In the following section, we introduce the specified fractional-order derivative we used for training our spiking neural network.
There have been several definitions for fraction-order derivatives such as the Grünwald–Letnikov or the Riemann–Liouville definition. In this paper, we would like to utilize the most promising one based on ANN studies, this is the fractional-order derivative by Caputo. The main mathematical reason for this choice is that Caputo and the ordinary first-order derivative have the same initial value for differential equations. Another useful advantage is that the derivative of a constant is always 0.
where F is a constant function and is the Caputo derivative operator of order over interval .
The definition of Caputo fractional-order derivative of order is defined in Equation (7).
where is the fractional derivative order, n is the upper integer neighbor of , is the Gamma function and function is differentiable on interval. This Caputo derivative is valid on the same interval.
Simplifying Equation (7) is possible with the restriction of the derivative order. Equation (8) presents the situation where is between 0 and 1.
It is important to emphasize, that in the case is then according to the definition Caputo derivative becomes the first integral, furthermore in the case is 1, then we obtain the first integer-order derivative of the original function. Since even with the simplified version of Caputo derivative calculation there is a wide range of values to choose from, this paper aims to give an empirical overview of the most suitable values for the derivative order and even investigate the existence of data-independent optima based on experimental results.
3. Proposed Algorithm
In this section, the proposed algorithms for SNN training and evaluation are presented. First, the used SNN layers are described. These are spiking neurons simulated at discrete time steps only. Then the Caputron (Caputo derivative-based Tempotron) optimizer is introduced. After these, an artificial swarm intelligence-based hyperparameter-optimizer is presented, which we used for derivative order selection.
3.1. Proposed Spiking Neuron Model
As neuromorphic processors are not widely available, for SNN simulation we used a CPU-based architecture. This means using analog values for simulation is impossible. This implies the need for numerical differential equation solvers, to find the exact moment of threshold crossings. In this work, some simplifications are used, to eliminate the need for these computationally demanding operations, while maintaining relatively low error rates. The idea of these simplifications was experimentally validated in previous works [32,33].
The simulation (e.g., membrane potentials, PSPs, spikes) is evaluated at discrete, equidistant time steps only. Threshold value comparison and spike generation only happen at these steps.
Each input is presented to the network for several time steps constantly. Input layers take the role of spike generation in an integrate-and-fire way. After the preset number of time steps elapsed, the neural potentials are reset to their default values, while the weights are kept.
The information carried by spikes is interpreted in a first-to-spike manner, therefore only one spike per neuron is allowed. Membrane potentials are saved for later evaluation and it is not to be recalculated in the upcoming time steps.
In this paper, we only consider single-label classification problems, this means that the first spike in the output layer may halt the simulation with only a marginally increment of error rates, thus saving time and computational power.
For training, we built two shallow (two-layer) models, one for the UCI datasets, and one for the MNIST benchmark dataset. The output layers of these neural networks are the same Leaky Integrate-and-Fire Layers. For processing the inputs different input layers are used, Gaussian Receptive Field Layer for the UCI datasets and Integrate-and-Fire Layer for the MNIST dataset.
3.1.1. Leaky Integrate-and-Fire Layer
This layer consists of a column of leaky integrate-and-fire neurons. These neurons use the kernel function defined in the original Tempotron paper [17] which is presented in Section 2.1. The effect of presynaptic spikes, after a quick jump, is slowly decreasing over time, and the effects of presynaptic spikes are commulated for each postsynaptic neuron. The former characteristic makes the layer “Leaky”, and the latter implies the integrate-and-fire naming.
Membrane potentials are updated in a discretized manner similarly to Equation (2). The above-mentioned simplification of one spike per neuron makes it easier to detect spikes too. The direction of threshold crossing can only be rising, so only a simple comparison is needed with the threshold potential, to determine if a spike is generated or not. Equation (9) describes the base mechanisms of this process.
here T is the discrete simulation time which follows a series of time steps with equal differences . is the time step at which the i-th presynaptic neuron elicits a spike.
As an enhancement we introduced a layer-wide winner-take-all mechanism for this layer, meaning that the first neuron to spike suppresses other neurons which will not be able to spike. Spikes in the same simulation time step are not differentiated, thus if no neuron fired before, multiple “first spikes” can occur. Winner-take-all is observed to enable neural networks to solve optimization problems much more efficiently [34]. This mechanism is implemented in a computationally beneficial way, meaning the first output spike will interrupt the simulation.
This layer is used as the output layer in the two-layer models.
3.1.2. Gaussian Receptive Field Layer
This layer consists of a column of at least two integrate-and-fire neurons, which are excited by positive Gaussian receptive fields over a real-valued input dimension. For every input dimension, the minimal and maximal input value is given for all expected inputs. The first two neurons’ receptive field’s maxima are assigned to the minimum and maximum of the input dimension. The other receptive fields are arranged equally between the first two. Each receptive field has a deviation equal to the distance between the two receptive field centers. Each receptive field is evaluated over an input value every time step and the result is added to the membrane potential of the corresponding neuron. A representation of the receptive fields scaled by of a 4 neuron layer with input minimum and input maximum 1 is pictured in Figure 3. Generated spike timings can be directly derived from the excitation of each receptive field, therefore they will be characteristic for a small interval of the input values.
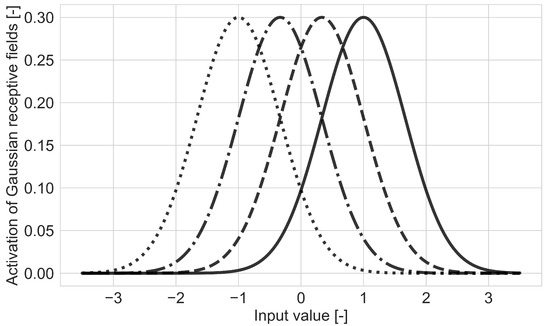
Figure 3.
Gaussian receptive fields of a 4 neuron layer with equally placed maxima over the interval of expected input values. Gaussians here are scaled by . Activation values are added to each neuron’s membrane potential.
This layer is used for spike generation receiving the inputs directly from every dimension of the real-valued input data. Of course, this is a loss-making representation of these input dimensions, however, it is easy to control the resolution of this spike generation method via the number of neurons assigned to each dimension, and the resolution of simulation time steps.
3.1.3. Integrate-and-Fire Layer
This layer consists of a column of integrate-and-fire neurons. These neurons are excited by constant input values, which are scaled down enough to create meaningful results over several time steps. These input values are added to the membrane potential every time step until the firing threshold is reached. This structure was used to generate spikes from serialized images in the authors’ previous work with success [32].
In this paper, this layer is utilized in training on the MNIST [35] database, where the serialized pixel lightness values are fed to the network.
3.2. Caputron Learning
As described in Section 2, Caputo derivative can be utilized to calculate the partial derivative of the Tempotron cost function with respect to synaptic weights. To acquire the equation by which each weight could be updated using this novel Caputo-based Tempotron (Caputron) optimizer, first the Caputo derivative of the cost function should be considered over a restricted interval of the weight values , and with a derivative order between 0 and 1, similarly to Equation (8).
where notations are similar to Equation (8), but c is the minimum of weight values corresponding to the j-th postsynaptic neuron, is the weight between the i-th presynaptic and j-th postsynaptic neuron. Here, is a function of weights () belonging to postsynaptic neuron j, where N is the neuron count of the presynaptic layer.
The first order partial derivative in Equation (10) is constant with respect to weight values, and is defined in Equation (4). With the simplifications and restrictions defined at the beginning of this section, the first order derivative of the cost function only has to take one spike into account, thus the sum has only one member.
After simplification, the following formula is acquired.
where is the sign correction coefficient derived from the cost value of postsynaptic neuron j. has the same effect as the signs in Equation (4), it is negative when expected output spike did not occur, positive when an unexpected spike occurred, and zero in any other case.
In conclusion the update rule for a single weight with Caputron learning, taking into account that each neuron can only spike once in this architecture, is defined in Equation (12).
For efficient weight updates Equation (12) must be reformulated with matrix operations. Using the definition of a single weight update, some matrices and vectors should be constructed to obtain the final formula of mass weight updates.
where N and M are the number of neurons in the pre- and postsynaptic layers, respectively. is the matrix of synaptic weights, is the vector of sign correction coefficients for each postsynaptic neuron, is the matrix of kernel function values, where is . If no spike happened before was reached, is set to 0. Vector contains minimal weight values for every postsynaptic neuron (i.e., it consists of the minima of each row in matrix ), this vector is in dimensions. Symbols ⊙ and denote the element-wise multiplication and element-wise power operators, respectively.
This definition of the Caputron optimizer can be used with shallow (two-layer) spiking neural networks, where information is represented in a time-to-first spike or spike order-based manner. A weight update of Equation (13) is performed after each training step when the simulation stops. Maximal membrane potential and PSP values are stored and updated along with the simulation time, during the evaluation of each time step. The data processing diagram of these networks is depicted in Figure 4.
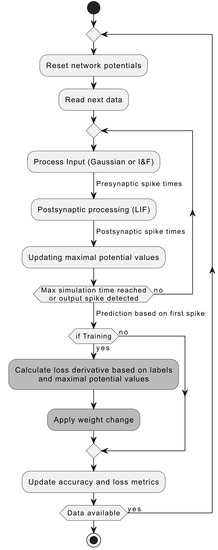
Figure 4.
Training and inference process of simulated Tempotron SNNs. The steps enhanced by Caputron are denoted by dark gray color.
3.3. Particle Swarm Optimization of Derivative Order
As it is visible from Section 3.2, the Caputron optimizer highly depends on the derivative order used for calculations. To observe the impact of this parameter’s value on the accuracy of the whole model, a simple hyperparameter-optimizer is utilized. As there are infinite values for this parameter, and testing is complex, and intelligent optimizer should be used. Rather than using a grid or gradient-based algorithm, the authors propose to use a particle swarm optimizer (PSO) [31] here, while leaving other hyperparameters (like learning rate, or network dimensions) unchanged.
Particle swarm optimization is a swarm method that uses a set of search points in the parameter space, often referred to as individuals or swarm members. These individuals start with a random velocity at a random or pre-assigned point in the parameter space. In each step, these individuals are evaluated, and their fitness value is stored. After evaluation, the velocity of each individual is changed. They accelerate towards their personal best and to the global best of the whole swarm with random coefficients. Using this new velocity a simple step is performed, adding each velocity vector to the last position of the corresponding individual. These steps are described by Equations (14) and (15) originally published in [31].
Here, and are the position and velocity of a swarm member in the search space. and are samples from uniform distributions where the upper limit is described by two constants and which correspond to the accelerations towards the personal best of the swarm member and the global best g. Upper indices denote discrete timesteps t and .
PSO was successfully used for numerous parameter optimization problems in the last few decades, with recent achievements ranging from engineering applications, such as distributed generator integration of smart cities [36] to federated learning aggregation [37] and large-scale hyperparameter optimization of deep learning networks [38].
To observe the effect of parameter change, and seek the optimal value of it, this PSO optimizer has a one-dimensional search space bound with a minimal and maximal value. Individuals (swarm members) are bound between these values and cannot leave the predefined interval. Here, choosing the best fitting initialization, starting velocities are chosen randomly, and the population is equally distributed over the above-mentioned interval, including one initial search point on each boundary value too. The pseudocode of this hyperparameter search is described by Algorithm 1.
| Algorithm 1 Derivative order optimization via PSO |
|
4. Experimental Results
Experiments were carried out on a desktop environment with regular multi-core CPUs (Intel i5-8300H@) used for training.
The networks were constructed in Python using NumPy [39] and SciPy [40] for mathematical operations, and Seaborn for visualization.
For evaluating model performances we used categorization accuracy. We compared the results on the test set. To make accuracy values stable and less initialization-dependent, when performing PSO-based derivative order parameter search we take averages of test accuracy values of multiple trainings with different initializations. For measuring convergence speed we take the number of epochs needed to reach the best performing model state during training. When performing PSO-based derivative order parameter search we average these values as well for trainings of the same derivative order.
4.1. UCI Dataset Results
Using the novel Caputron learning rule several tests were carried out. First, three UCI [41] datasets were examined, to compare Caputron optimizer and first order Gradient Descent. The datasets we used were the same as the ones used by [25] for ANN training. These datasets are Iris (4 input features, 3 classes, 150 samples), Liver (6 input features, 2 classes), and Sonar (60 input features, 2 classes, 208 samples), all three are categorization problems.
For finding the optimal derivative order values a 20 generations long particle swarm optimization [31] was carried out for each dataset separately. To cover the search space, initially, the swarm members were distributed equally between and 1 along the derivative order axis. The swarm had 8 individuals in it. The coefficients for accelerating towards the global best were randomly drawn from a uniform distribution between 0 and , while coefficients for accelerating towards personal best results were drawn from a uniform distribution between 0 and . Each dataset was split into a train and test subset with of test data. The learning rate was , for every evaluation.
A two-layer model was constructed with a Gaussian receptive field layer as an input layer and a leaky integrate-and-fire layer as an output layer with a weight matrix between them. The input layer had 15 neurons per dimension, while the output layer’s neuron count was equal to the number of classes the dataset had. The Gaussian receptive fields were scaled down by . The threshold potential and normalization coefficient () was 1 for all neurons, while the resting potential was set to 0. The membrane and synaptic time constants were 15 ms and 5 ms, respectively.
Each parameter evaluation of an individual returned a score of average best validation accuracy, where these best validation accuracies were accumulated from 10 different trainings over the same dataset, where the weight matrices were randomly reinitialized, drawn from a uniform distribution from 0 to 1. Each training lasted for 30 epochs from which the best one’s validation accuracy was passed on for averaging. Each input was presented to the neural network for 50 equitemporal steps between 0 ms and 15 ms.
It is important to note, that when setting exactly the optimizer was changed to a simple, first integer-order derivative-based Gradient Descent optimizer, described in Section 2.1. Although Caputron with derivative order should theoretically also work such as classical Gradient Descent, to avoid any mid-computation imprecision the algorithm was changed to solely use the mathematical expression from Equation (5).
After the first optimizations over all three datasets, another one was carried out, to let the PSO work more on the interval with the best results. The second intention behind another hyperparameter optimization was, to see if there is a clear convergence to any given constants for all the datasets, or if the existence of this optimal derivative order is not that trivial. With only the interval lower boundary changed to , all the other parameters remained the same.
Results are presented in Figure 5, Figure 6 and Figure 7, and Table 1. For each dataset, all derivative orders evaluated by the two PSO runs are plotted, with the average test accuracies. The average training epochs used to reach Gradient Descent’s accuracy for each evaluation during the second run are also presented as a third diagram. Those alpha values were excluded in this diagram, where average test accuracy was under Gradient Descent’s test accuracy. Horizontal dashed lines indicate the performance of Gradient Descent, while in the third subplot for each dataset shades of gray, and the star marker refers to the best final test accuracy of the given training.
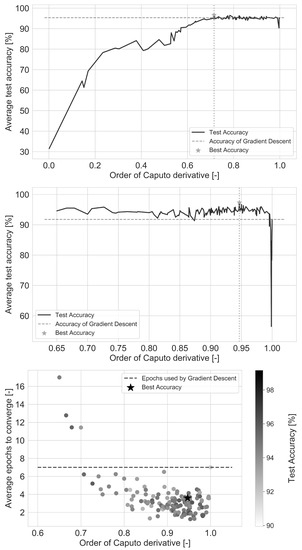
Figure 5.
Average test categorical accuracy of the two PSO runs, and the average training epochs taken to reach Gradient Descent’s accuracy for the second run (from top to bottom) on the Iris dataset.
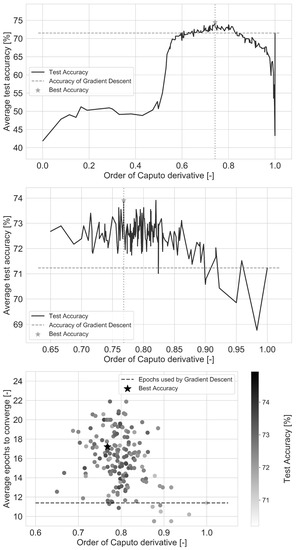
Figure 6.
Average test accuracy of the two PSO runs, and the average training epochs taken to reach Gradient Descent’s accuracy for the second run (from top to bottom) on the Liver dataset.
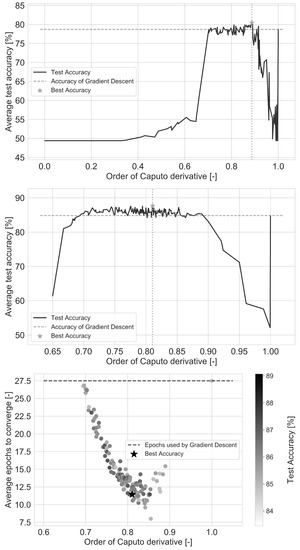
Figure 7.
Average test accuracy of the two PSO runs, and the average training epochs taken to reach Gradient Descent’s accuracy for the second run (from top to bottom) on the Sonar dataset.

Table 1.
Comparison of Gradient Descent and Caputron including the best fractional derivative orders for each dataset with the classification error reduction induced by replacing Gradient Descent with Caputron, and the percentage of epochs taken to reach Gradient Descent’s accuracy by Caputron (with Gradient Descent training epochs being ).
Table 1 concludes the best average accuracy values, with the best gradient order parameters. As an indicator of improvement, the ratio of erroneously classified test cases was reduced by the percentage shown in the table, when Caputron was used instead of Gradient Descent. Additionally, the percentage of training epochs taken until reaching Gradient Descent’s accuracy by Caputron-with respect to epochs taken by Gradient Descent-is also presented.
For every dataset, Caputron was more accurate, and in most cases, it provided faster convergence too, or at least there is a derivative order, where the convergence was faster for the same test accuracy reached by the first order optimizer. It is clear that no overall optimal alpha value was found, it is most likely data-dependent. However, the derivative orders, where Caputron outperforms Gradient Descent are mostly between and for all observed benchmark tests. This recommended interval is a safe parameter choice, as the second, refined PSO searches point out. For all three datasets together 355 alpha values were observed in the interval, on average using of these observed derivative orders resulted in improved accuracy compared to first order Gradient Descent. Therefore it can be concluded that using this interval as a thumb rule of derivative order selection is a safe choice based on our experimental results.
These results of SNN experiments are similar to ANN training results by [25]. These ANN experiments found that the suitable range for Caputo derivative orders is between and .
Although our shallow Caputron optimized model cannot compete with more complex, deep architectures, it outperforms SpikeProp-based brain-inspired SNN architectures on the Iris dataset [42] despite having only two layers compared to the 3-layer architecture of the compared SpikeProp models. The performance increases from classification accuracy to in the case of our approach.
4.2. MNIST Results
Caputron learning of a shallow SNN has also been tested on the MNIST [35] benchmark dataset of handwritten digits, which contains 60,000 images for training and 10,000 images for testing. These grayscale 8 bit images were scaled down by 1536, so the maximal input value was .
PSO here was not utilized, only an equally spread population of 21 search points were used with the evaluation similar to those with the UCI Datasets. The only difference is the number of reinitializations, which in this case is halved, using only 5 different random weight initializations to determine an average best epoch accuracy.
A two-layer model was constructed here as well with an integrate-and-fire and a leaky integrate-and-fire layer in this order. The input layer has one neuron for each pixel, resulting in an input size of 784, as MNIST images are images. The output layer contains a neuron for every decimal digit, thus the output layer size is 10. Individual neuron parameters remain the same.
Results are presented in Figure 8 and Table 1. Similarly to the UCI Datasets, Caputron performed better than Gradient Descent. The ideal interval of the derivative order remained the same .
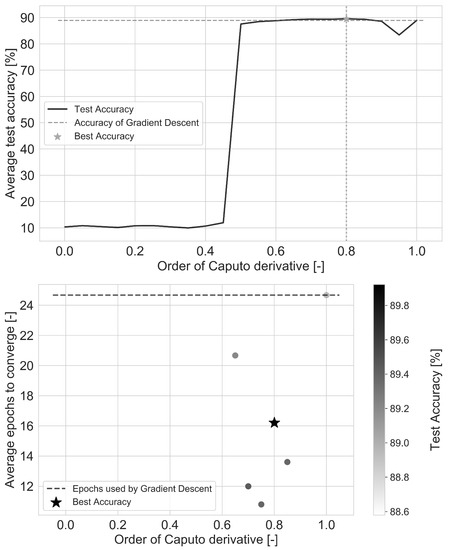
Figure 8.
Average test accuracy, and the average training epochs taken to reach Gradient Descent’s accuracy (from top to bottom) on the MNIST dataset.
Training times for the best derivative order and the first order derivative can be compared, with an average training time of 2830 s for Caputron, and 2910 s for Gradient Descent, resulting in a drop in training time when using Caputron. As the first spikes with the winner-take-all mechanism introduced in Section 3.1.1 would halt the simulation, we examined training times with this mechanism turned off. The results showed the same tendency with Caputron taking 3588 s, and Gradient Descent taking 3691 s on average. The same drop in training time can be observed here. To investigate, even more, we compare the calculation speed of both optimizers for the weight matrix used by MNIST. For a million randomized updates Gradient Descent became an average weight update time of , while for Caputron it took to perform a full weight matrix update. Although in weight updates Caputron is slower, when it comes to network simulation Caputron regains its lead over Gradient Descent, with earlier fire times resulting in more sparse and slightly faster computations.
When evaluating the MNIST database, information about the improvements of Caputo derivative-based ANN training is available. We observe a closely located peak of test accuracy at derivative order, where as [25] reports as their best candidate. Thus, it can be concluded that both ANN and SNN architectures have the same ideal value for Caputo derivative-based training, while SNN test accuracies are lower than those achieved by their ANN counterparts, the error reduction rates are in a similar range around 5– depending on network size.
Compared to the reimplementation of the original Tempotron [17] (denoted by Gradient Descent accuracy in Table 1) our model performed slightly better on the MNIST dataset, reaching test accuracy over the original but this improvement still lacks the performance of modern architectures. To reach state-of-the-art performance on MNIST more complex deep neural networks have to be used with refined temporal simulation. Such models achieve % testing categorical accuracy on the digit dataset without convolution [43]. We expect improvements of the same magnitude over these results when applying fractional-order optimization, however, no research on this has been conducted yet according to the best of our knowledge.
4.3. Inherent Adaptive Weight Normalization
To this point, experiments indicate a significant performance increase without providing insights into the underlying causes. To address the question, of why Caputron is better than standard Gradient Descent, the reformulation of Equation (12) is necessary. For this single spike per neuron scenario, the sums from Equation (5) of basic Gradient Descent weight update are reduced to a single member. Thus, in Equation (16) the factors from Gradient Descent are gathered together.
where is the weight change caused by standard Gradient Descent, and
is an adaptive weight normalization function of the difference of the weight and the minimal weight value corresponding to the same postsynaptic neuron.
The limit of this weight normalization value is as follows , thus indicating the theoretical equivalence of Gradient Descent and first integer-order Caputron learning. In this case, no adaptive weight normalization happens.
The behavior of this weight normalization coefficient is visualized in Figure 9. Caputron multiplicatively reduces the value of weight changes near the minimal weight value. The minimal weight of each training step is hardly ever changed. However, the weight change of much higher weights is multiplicatively increased. For values other than 1 these functions have no upper bound, however, loss changes mostly prevent them from exploding. The order of fractional derivative here controls the curve of weight normalization and sets the point where the coefficient reaches the value of 1.
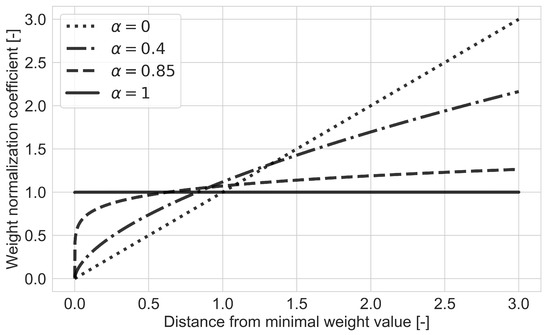
Figure 9.
Inherent adaptive weight normalization coefficient of Caputron.
This effect makes it harder for inhibitory synapses to change, or eventually become excitatory, while excitatory synapses can converge in larger steps, thus reaching the needed amplification value if they remain excitatory, or changing to inhibitory type synapse if their value is updated to be negative. This enforces a certain level of sparsity concerning inhibitory and excitatory neurons.
Since the information from the network is extracted in a “first-to-spike” manner, even when no negative weights (i.e., no inhibitory synapses) are present in the network, lower weight values are more stable. This results in the same effect of insignificant synapses changing slowly, while significant, excitatory connections are easier to change.
5. Conclusions
As experiments in Section 4 have demonstrated, the usage of fractional-order Caputo derivative increases the performance of shallow Tempotron SNNs. Caputo derivative is successfully applied for weight updates of shallow Tempotron SNNs, with one spike per neuron, thus creating the novel method of Caputron learning. Training models on different datasets point out, that the high-performance range for the derivative order is between and for the benchmark datasets observed in this paper, while the results are not comparable to that of the latest deep architectures, our aim to verify the effectiveness of Caputron learning over Gradient Descent was achieved. Not only Caputron learning is better than first-order Gradient Descent in increasing classification accuracy, but faster convergence is also observed in most cases. Based on the results we propose to replace classic first-order derivative-based Gradient Descent with fractional-order Caputo-derivative having an order in the range of , as it leads to higher accuracy in approximately of the examined test cases with a marginal increase, or even decrease in training time. Handling as an optimizable hyperparameter for Caputron training is also recommended, as the preferred derivative orders are data-dependent.
The problem of backpropagation, a wider range of possible and learning rate values, and handling multiple spikes per neuron, as well as using learning method enhancements such as momentum, AdaDelta or attention [44], which proved to be successful in applied Deep Learning [45,46] are to be addressed in future works.
Although two-layer spiking neural architectures have been utilized in multiple real-world applications [18,19,32] we would like to promote the adaptation of fractional-order derivative-based optimization for more complex state-of-the-art architectures as well. These architectures require further theoretical investigation and a wide range of experiments. Such research on event-based fractional derivative optimized SNN architectures is being conducted currently by the authors.
Author Contributions
Conceptualization, N.M.G. and J.B.; methodology, N.M.G. and G.E.; software, N.M.G. and G.E.; validation, N.M.G. and G.E.; formal analysis, N.M.G. and J.B.; investigation, N.M.G.; resources, N.M.G.; data curation, N.M.G. and G.E.; writing—original draft preparation, N.M.G. and J.B.; writing—review and editing, J.B. and N.M.G.; visualization, N.M.G.; supervision, J.B.; project administration, J.B; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Supporting code is available at: https://github.com/nata108/Caputron (accessed on 2 July 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, T.; Wang, J.; Yang, B.; Wang, X. Facial expression recognition method with multi-label distribution learning for non-verbal behavior understanding in the classroom. Infrared Phys. Technol. 2021, 112, 103594. [Google Scholar] [CrossRef]
- Zhang, Z.; Lai, C.; Liu, H.; Li, Y.F. Infrared facial expression recognition via Gaussian-based label distribution learning in the dark illumination environment for human emotion detection. Neurocomputing 2020, 409, 341–350. [Google Scholar] [CrossRef]
- Wu, H.; Liu, Y.; Liu, Y.; Liu, S. Fast facial smile detection using convolutional neural network in an intelligent working environment. Infrared Phys. Technol. 2020, 104, 103061. [Google Scholar] [CrossRef]
- Liu, H.; Nie, H.; Zhang, Z.; Li, Y.F. Anisotropic angle distribution learning for head pose estimation and attention understanding in human-computer interaction. Neurocomputing 2021, 433, 310–322. [Google Scholar] [CrossRef]
- Indiveri, G.; Sandamirskaya, Y. The importance of space and time for signal processing in neuromorphic agents: The challenge of developing low-power, autonomous agents that interact with the environment. IEEE Signal Process. Mag. 2019, 36, 16–28. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Wan, L.; Liu, J.; Harkin, J.; Cao, Y. An efficient, low-cost routing architecture for spiking neural network hardware implementations. Neural Process. Lett. 2018, 48, 1777–1788. [Google Scholar] [CrossRef]
- Paul, A.; Tajin, M.A.S.; Das, A.; Mongan, W.M.; Dandekar, K.R. Energy-Efficient Respiratory Anomaly Detection in Premature Newborn Infants. Electronics 2022, 11, 682. [Google Scholar] [CrossRef]
- Varshika, M.L.; Corradi, F.; Das, A. Nonvolatile Memories in Spiking Neural Network Architectures: Current and Emerging Trends. Electronics 2022, 11, 1610. [Google Scholar] [CrossRef]
- Mostafa, H. Supervised learning based on temporal coding in spiking neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3227–3235. [Google Scholar] [CrossRef] [Green Version]
- Stöckl, C.; Maass, W. Optimized spiking neurons can classify images with high accuracy through temporal coding with two spikes. Nature Mach. Intell. 2021, 3, 230–238. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Legenstein, R.; Pecevski, D.; Maass, W. A Learning Theory for Reward-Modulated Spike-Timing-Dependent Plasticity with Application to Biofeedback. PLoS Comput. Biol. 2008, 4, e1000180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kasabov, N. Integrative connectionist learning systems inspired by nature: Current models, future trends and challenges. Natural Comput. 2009, 8, 199–218. [Google Scholar] [CrossRef]
- Tan, C.; Šarlija, M.; Kasabov, N. Spiking neural networks: Background, recent development and the NeuCube architecture. Neural Process. Lett. 2020, 52, 1675–1701. [Google Scholar] [CrossRef]
- Neftci, E.O.; Mostafa, H.; Zenke, F. Surrogate gradient learning in spiking neural networks: Bringing the power of gradient-based optimization to spiking neural networks. IEEE Signal Process. Mag. 2019, 36, 51–63. [Google Scholar] [CrossRef]
- Anwani, N.; Rajendran, B. Training multi-layer spiking neural networks using NormAD based spatio-temporal error backpropagation. Neurocomputing 2020, 380, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Gütig, R.; Sompolinsky, H. The tempotron: A neuron that learns spike timing–based decisions. Nature Neurosci. 2006, 9, 420–428. [Google Scholar] [CrossRef]
- Iyer, L.R.; Chua, Y. Classifying Neuromorphic Datasets with Tempotron and Spike Timing Dependent Plasticity. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Kasi, S.K.; Das, S.; Biswas, S. Energy-efficient event pattern recognition in wireless sensor networks using multilayer spiking neural networks. Wirel. Netw. 2021, 27, 2039–2054. [Google Scholar] [CrossRef]
- Shi, C.; Wang, T.; He, J.; Zhang, J.; Liu, L.; Wu, N. DeepTempo: A Hardware-Friendly Direct Feedback Alignment Multi-Layer Tempotron Learning Rule for Deep Spiking Neural Networks. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1581–1585. [Google Scholar] [CrossRef]
- Liu, H.; Fang, S.; Zhang, Z.; Li, D.; Lin, K.; Wang, J. MFDNet: Collaborative Poses Perception and Matrix Fisher Distribution for Head Pose Estimation. IEEE Trans. Multimed. 2022, 24, 2449–2460. [Google Scholar] [CrossRef]
- Liu, T.; Liu, H.; Li, Y.F.; Chen, Z.; Zhang, Z.; Liu, S. Flexible FTIR Spectral Imaging Enhancement for Industrial Robot Infrared Vision Sensing. IEEE Trans. Ind. Inform. 2020, 16, 544–554. [Google Scholar] [CrossRef]
- Li, D.; Liu, H.; Zhang, Z.; Lin, K.; Fang, S.; Li, Z.; Xiong, N.N. CARM: Confidence-aware recommender model via review representation learning and historical rating behavior in the online platforms. Neurocomputing 2021, 455, 283–296. [Google Scholar] [CrossRef]
- Liu, H.; Zheng, C.; Li, D.; Shen, X.; Lin, K.; Wang, J.; Zhang, Z.; Zhang, Z.; Xiong, N.N. EDMF: Efficient Deep Matrix Factorization With Review Feature Learning for Industrial Recommender System. IEEE Trans. Ind. Inform. 2022, 18, 4361–4371. [Google Scholar] [CrossRef]
- Wang, J.; Wen, Y.; Gou, Y.; Ye, Z.; Chen, H. Fractional-order gradient descent learning of BP neural networks with Caputo derivative. Neural Netw. 2017, 89, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Bao, C.; Pu, Y.; Zhang, Y. Fractional-order deep backpropagation neural network. Comput. Intell. Neurosci. 2018, 2018, 7361628. [Google Scholar] [CrossRef]
- Zhang, H.; Pu, Y.F.; Xie, X.; Zhang, B.; Wang, J.; Huang, T. A global neural network learning machine: Coupled integer and fractional calculus operator with an adaptive learning scheme. Neural Netw. 2021, 143, 386–399. [Google Scholar] [CrossRef]
- Pu, Y.f.; Wang, J. Fractional-order global optimal backpropagation machine trained by an improved fractional-order steepest descent method. Front. Inf. Technol. Electron. Eng. 2020, 21, 809–833. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Alidousti, J.; Ghaziani, R.K. Spiking and bursting of a fractional order of the modified FitzHugh-Nagumo neuron model. Math. Model. Comput. Simulations 2017, 9, 390–403. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Gyöngyössy, N.M.; Domonkos, M.; Botzheim, J.; Korondi, P. Supervised Learning with Small Training Set for Gesture Recognition by Spiking Neural Networks. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2201–2206. [Google Scholar]
- Kheradpisheh, S.R.; Ganjtabesh, M.; Thorpe, S.J.; Masquelier, T. STDP-based spiking deep convolutional neural networks for object recognition. Neural Netw. 2018, 99, 56–67. [Google Scholar] [CrossRef] [Green Version]
- Lynch, N.; Musco, C.; Parter, M. Winner-Take-All Computation in Spiking Neural Networks. arXiv 2019, arXiv:1904.12591. [Google Scholar]
- LeCun, Y.; Cortes, C. MNIST Handwritten Digit Database. 2010. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 2 July 2022).
- Rizwan, M.; Waseem, M.; Liaqat, R.; Sajjad, I.A.; Dampage, U.; Salmen, S.H.; Obaid, S.A.; Mohamed, M.A.; Annuk, A. SPSO Based Optimal Integration of DGs in Local Distribution Systems under Extreme Load Growth for Smart Cities. Electronics 2021, 10, 2542. [Google Scholar] [CrossRef]
- Park, S.; Suh, Y.; Lee, J. FedPSO: Federated Learning Using Particle Swarm Optimization to Reduce Communication Costs. Sensors 2021, 21, 600. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Li, J.Y.; Zhan, Z.H. Efficient Hyperparameter Optimization for Convolution Neural Networks in Deep Learning: A Distributed Particle Swarm Optimization Approach. Cybern. Syst. 2021, 52, 36–57. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nature Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: http://archive.ics.uci.edu/ml/ (accessed on 2 July 2022).
- Yu, Q.; Tang, H.; Tan, K.C.; Yu, H. A brain-inspired spiking neural network model with temporal encoding and learning. Neurocomputing 2014, 138, 3–13. [Google Scholar] [CrossRef]
- Comsa, I.M.; Potempa, K.; Versari, L.; Fischbacher, T.; Gesmundo, A.; Alakuijala, J. Temporal Coding in Spiking Neural Networks with Alpha Synaptic Function. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 8529–8533. [Google Scholar] [CrossRef] [Green Version]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Xiao, H.; Hu, Z. Feature-similarity network via soft-label training for infrared facial emotional classification in human-robot interaction. Infrared Phys. Technol. 2021, 117, 103823. [Google Scholar] [CrossRef]
- Ju, J.; Zheng, H.; Li, C.; Li, X.; Liu, H.; Liu, T. AGCNNs: Attention-guided convolutional neural networks for infrared head pose estimation in assisted driving system. Infrared Phys. Technol. 2022, 123, 104146. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).