A Novel Bus Arrival Time Prediction Method Based on Spatio-Temporal Flow Centrality Analysis and Deep Learning
Abstract
:1. Introduction
2. Related Works
3. Methodology
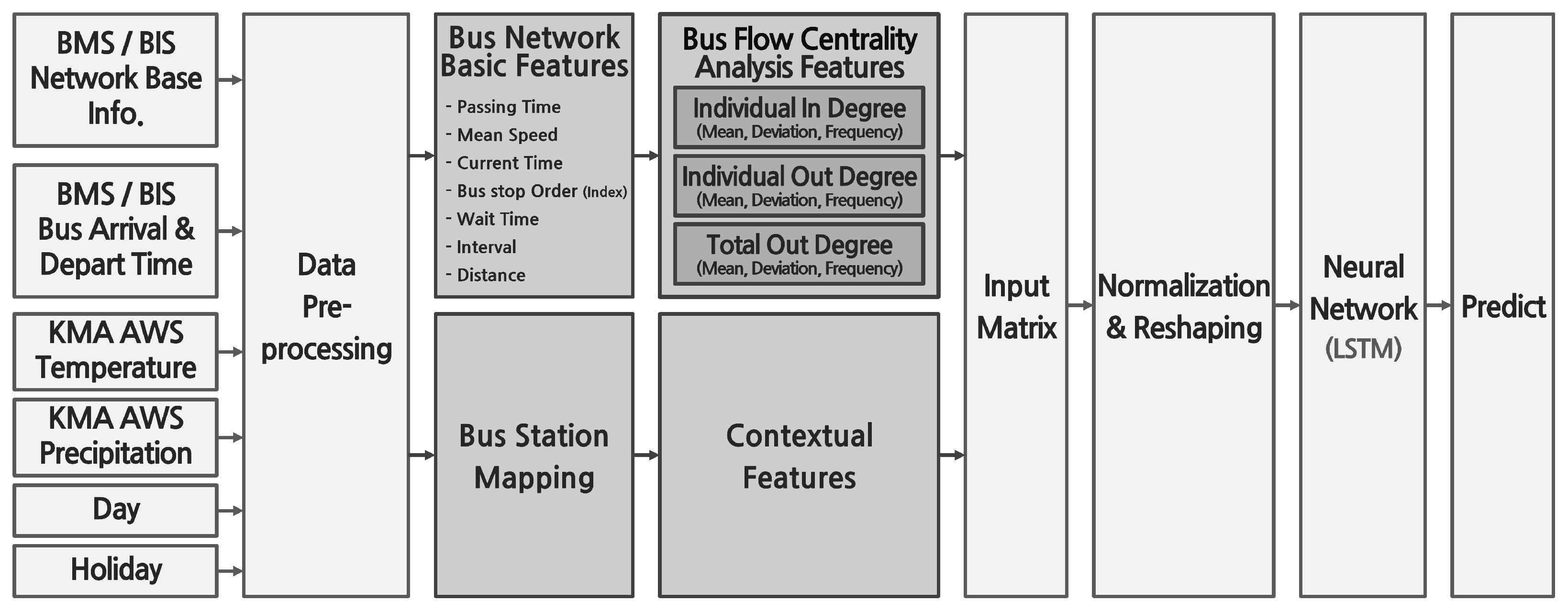
3.1. Feature Extraction
3.1.1. Bus Network Basic Features
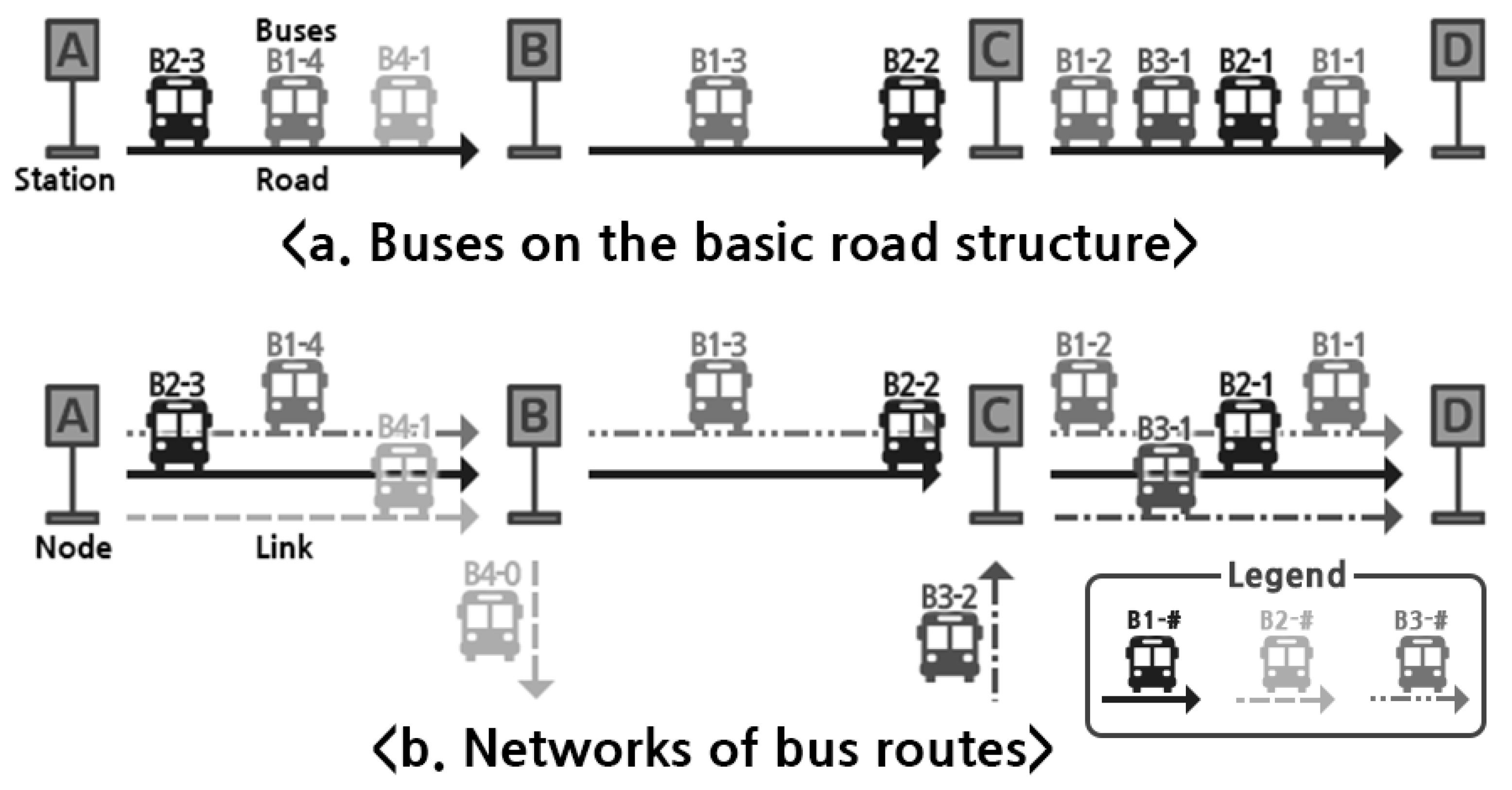
- Passing Timeis the required time in seconds for the jth bus of the route i to arrive at the kth stop from the preceding k− 1th stop. is the difference between arrival time and departure time , as shown in Equation (1). We do not compute starting station’s as there is no preceding station.For example, as shown in Figure 2, bus B2-2 arriving at stop C is denoted as . The time taken for bus B2-2 to arrive at stop C from stop B can be expressed as . Moreover, the time at which this bus departs from the next stop C can be expressed as .
- Mean SpeedMean Speed (m/s) is divided by Distance d as shown in Equation (2). Here, d is the distance between stop and stop k on bus route i.
- Wait TimeWait Time is the amount of time a bus temporarily stays at the bus stop for loading and unloading passengers or a short break, as shown in Equation (3).
- Inter-Arrival Time IInter-Arrival Time I between buses on a bus route is given in Equation (4). We obtain I by subtracting the time when the j− 1th bus on the bus route i arrived at stop k from the time when the jth bus on i arrived at the same stop.
- Distance dDistance d in meters is the Euclidean distance between stops and and on bus route i given their coordinates as shown in Equation (5).
- Current TimeCurrent time of is the time in which the hour, minute, and second information is converted into seconds.
- Bus Stop Order IndexThe Bus Stop Order Index (BSOI) of k denotes the sequential order of station k for bus route i. Each bus route is composed of bus stops in a different order. For instance, in Figure 2, the BSOI of bus stops A, B, C, and D for route B2 are 1, 2, 3, and 4, respectively.
3.1.2. Bus Flow Centrality Analysis Features
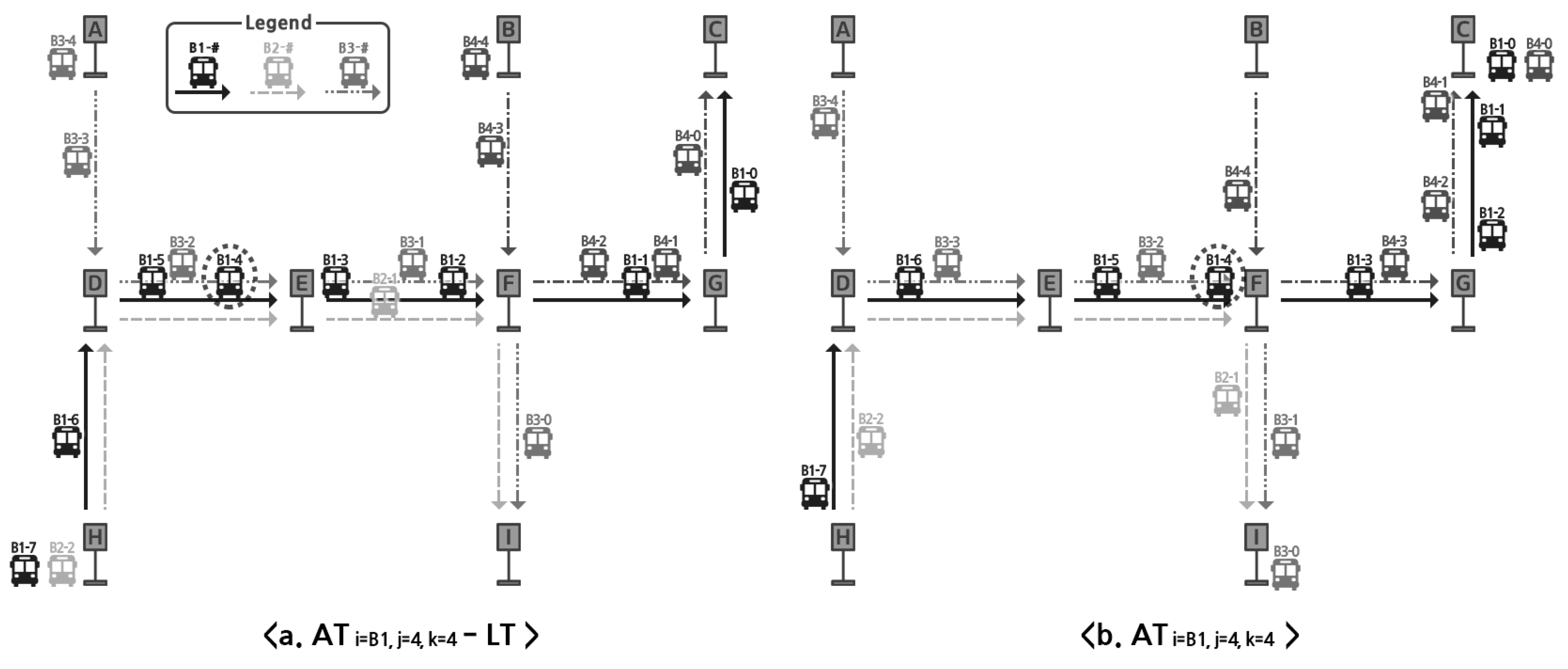
- Individual In Degreerefers to a set of times buses took to pass a given stop within a certain amount of time to pass through a specific link. Suppose is given. From a preset time period in the past () to , we retrieve of every bus j on route i passing stop k via (denoted as ). In other words, can be regarded as a set of buses including j and other buses ahead on the same route i that represent the overall inbound spatial flows upon the point when j passes bus station k. The pseudo-code for obtaining is presented in Algorithm 1.An intuitive example is provided in Figure 3. Bus B1 is en route, passing stops in the order of H, D, E, F, G, and C. Figure 3a,b show a snapshot at and , respectively, where F is the fourth stop for route . Bus B1-4 on sub-figure a is in between stops D and E. Later on, sub-figure b shows B1-4 arriving at stop F. In this case, the buses involved in producing are B1-2, B1-3, and B1-4.Spatial flow information is embedded further into a low-dimensional vector. We construct this vector by applying Equations (6)–(8) to a given . The embedding process is carried out for every stop and every bus. Note that, by using such embedding, we represent not only spatial information but also the different temporal dynamics of every bus on the route.
- Individual Out Degreerepresents the outbound spatial flow when a bus j leaves station k for bus stop . Suppose is provided. From a preset time period in the past () to , we retrieve of every bus j on route i that left station k for the next stop (denoted as ). is expected to be another factor for influencing the time a bus takes to reach the next stop. can be obtained by the running the pseudo-code presented in Algorithm 2.As shown in Figure 3, buses B1-1 and B1-2 that departed stop G are ahead of B1-4. of B1-1 and B1-2 can provide a clue for B1-4 on the condition of the link to the next stop.
- Total Out Degreeis computed for a particular route. On the other hand, is a set of PTs of buses on all routes heading toward the next stop from stations k. represents the aggregate flow pattern on the link to the next stop. Buses not moving to are not considered in constructing . For example, in Figure 3, buses on route B3 are not considered for computing for station G via F. It is because the buses on B3 head toward stop I from F instead. Set can be obtained by executing Algorithm 3. is embedded into the latent vector using Equation (6), Equation (7), and Equation (8). Along with , we keep IODs separately for all stops and buses to account for microscopic flow patterns that can affect the travel time prediction to the next stations.
| Algorithm 1: Individual In Degree . |
 |
| Algorithm 2: Individual Out Degree . |
 |
| Algorithm 3: Total Out Degree . |
 |
3.1.3. Contextual Features
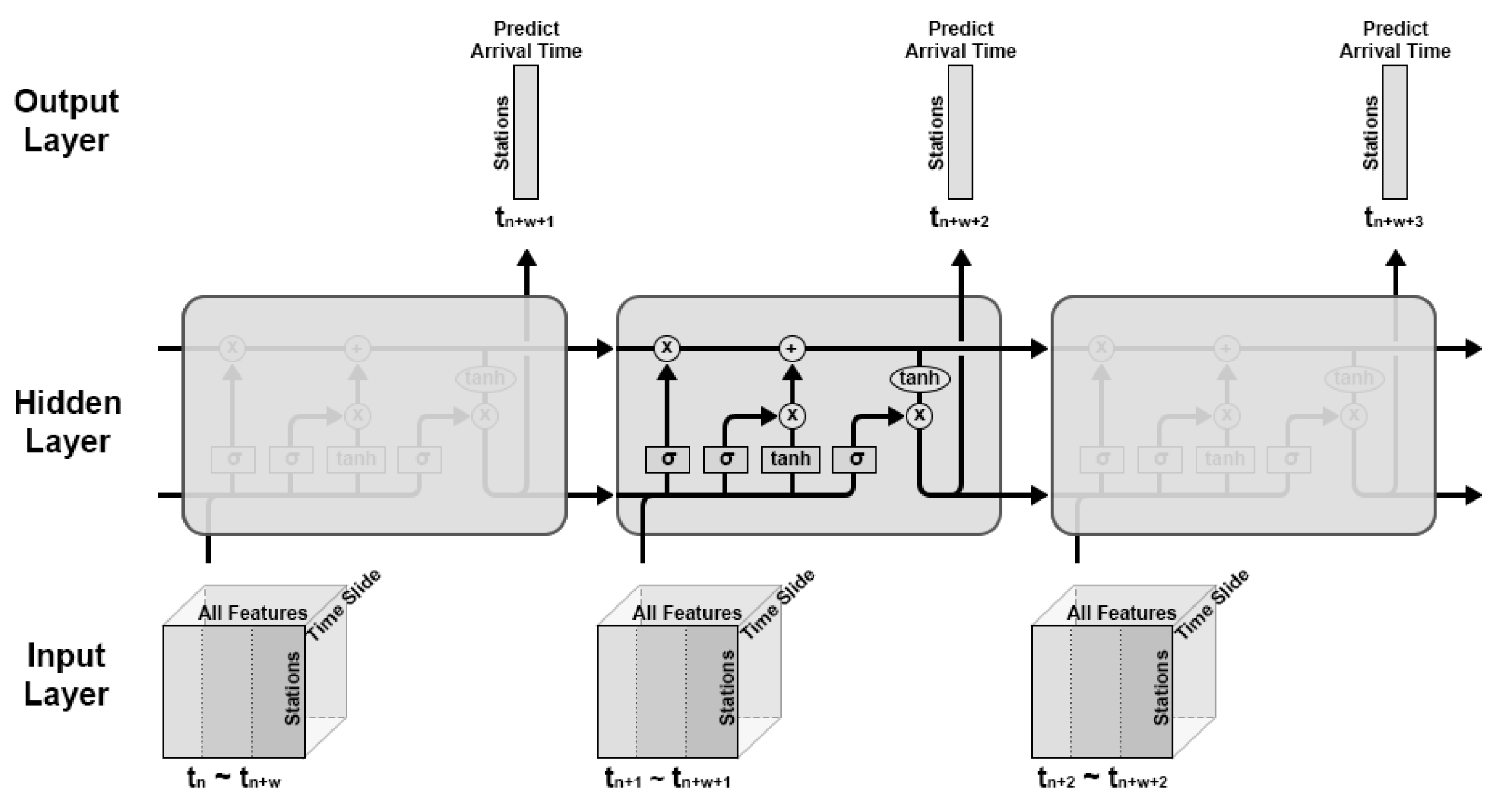
3.2. Models
4. Evaluation
- Buses pass through stops in order;
- A bus x cannot overtake the other bus y ahead if x and y are on the same route;
- Algorithm 4 implements linear interpolation between two points. However, interpolation cannot be carried out for the time intervals, with consecutive nulls appearing at the beginning or end of the sequence.
| Algorithm 4: Interpolation function. |
 |
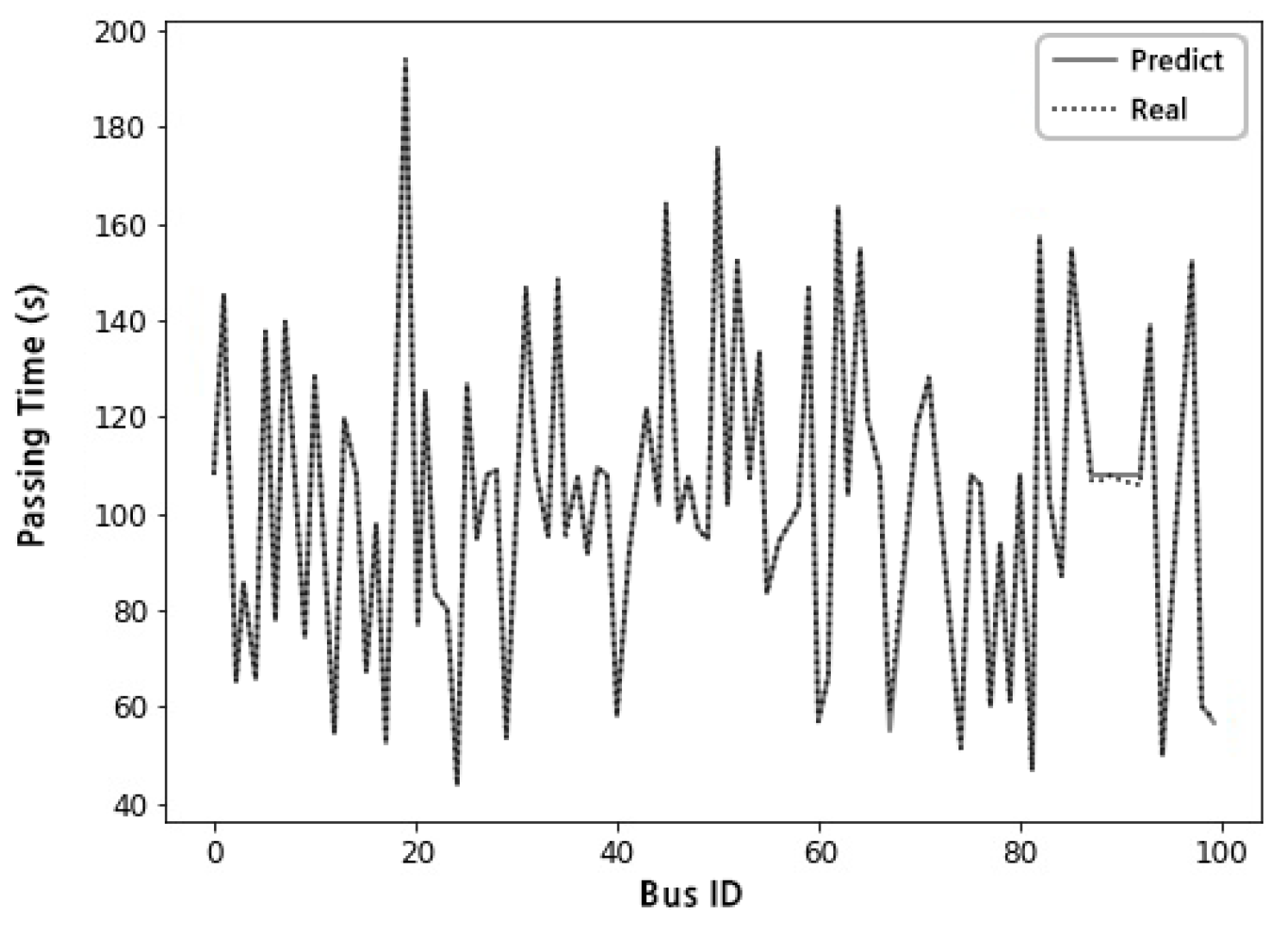
4.1. Measuring Prediction Performance
4.2. Measuring the Predictive Performance of Random Forest Models
4.3. Measuring the Predictive Performance of Multi-Linear Regression Models
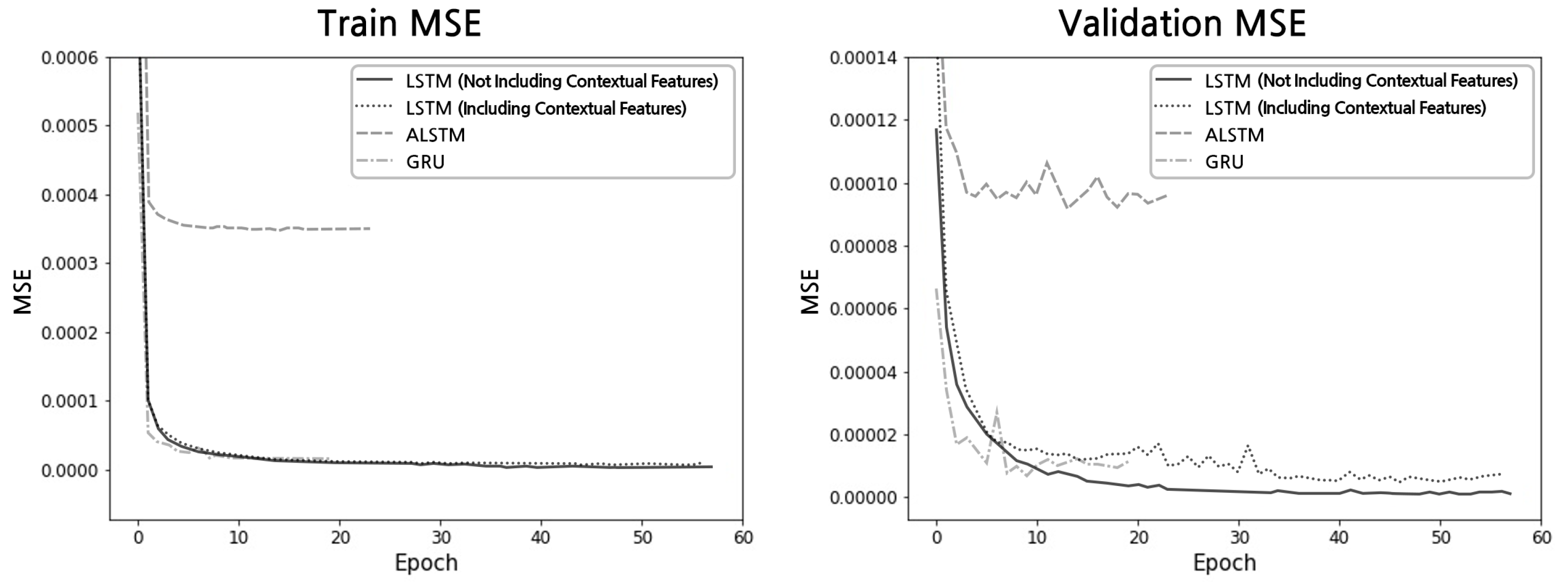
4.4. Measuring the Predictive Performance of LSTM Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BFC | Bus Flow Centrality; |
| IID | Individual In Degree; |
| IOD | Individual Out Degree; |
| TOD | Total Out Degree; |
| PT | Passing Time; |
| AT | Arrival Time. |
References
- Kim, S.; Lewis, M.E.; White, C.C. Optimal vehicle routing with real-time traffic information. IEEE Trans. Intell. Transp. Syst. 2005, 6, 178–188. [Google Scholar] [CrossRef]
- Ying, S.; Yang, Y. Study on vehicle navigation system with real-time traffic information. In Proceedings of the 2008 International Conference on Computer Science and Software Engineering, Wuhan, China, 12–14 December 2008; Volume 4, pp. 1079–1082. [Google Scholar]
- Daganzo, C.; Anderson, P. Coordinating Transit Transfers in Real Time. 2016. Available online: https://escholarship.org/uc/item/25h4r974 (accessed on 29 April 2022).
- Kujala, R.; Weckström, C.; Mladenović, M.N.; Saramäki, J. Travel times and transfers in public transport: Comprehensive accessibility analysis based on Pareto-optimal journeys. Comput. Environ. Urban Syst. 2018, 67, 41–54. [Google Scholar] [CrossRef]
- Kager, R.; Bertolini, L.; Te Brömmelstroet, M. Characterisation of and reflections on the synergy of bicycles and public transport. Transp. Res. Part A Policy Pract. 2016, 85, 208–219. [Google Scholar] [CrossRef] [Green Version]
- Leduc, G. Road traffic data: Collection methods and applications. Work. Pap. Energy Transp. Clim. Chang. 2008, 1, 1–55. [Google Scholar]
- Dafallah, H.A.A. Design and implementation of an accurate real time GPS tracking system. In Proceedings of the The Third International Conference on e-Technologies and Networks for Development (ICeND2014), Beirut, Lebanon, 29 April–1 May 2014; pp. 183–188. [Google Scholar]
- Lee, C.; Yoon, Y. Context-Aware Link Embedding with Reachability and Flow Centrality Analysis for Accurate Speed Prediction for Large-Scale Traffic Networks. Electronics 2020, 9, 1800. [Google Scholar] [CrossRef]
- Treethidtaphat, W.; Pattara-Atikom, W.; Khaimook, S. Bus arrival time prediction at any distance of bus route using deep neural network model. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 988–992. [Google Scholar]
- Zhou, X.; Dong, P.; Xing, J.; Sun, P. Learning dynamic factors to improve the accuracy of bus arrival time prediction via a recurrent neural network. Future Internet 2019, 11, 247. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Xu, H.; Yan, Y.; Cai, Z.; Sun, T.; Li, W. Bus arrival time prediction based on LSTM and spatial-temporal feature vector. IEEE Access 2020, 8, 11917–11929. [Google Scholar] [CrossRef]
- Petersen, N.C.; Rodrigues, F.; Pereira, F.C. Multi-output bus travel time prediction with convolutional LSTM neural network. Expert Syst. Appl. 2019, 120, 426–435. [Google Scholar] [CrossRef] [Green Version]
- Jeong, R.; Rilett, R. Bus arrival time prediction using artificial neural network model. In Proceedings of the 7th International IEEE Conference on Intelligent Transportation Systems (IEEE Cat. No. 04TH8749), Washington, WA, USA, 3–6 October 2004; pp. 988–993. [Google Scholar]
- Lin, W.H.; Zeng, J. Experimental study of real-time bus arrival time prediction with GPS data. Transp. Res. Rec. 1999, 1666, 101–109. [Google Scholar] [CrossRef] [Green Version]
- Gong, J.; Liu, M.; Zhang, S. Hybrid dynamic prediction model of bus arrival time based on weighted of historical and real-time GPS data. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 972–976. [Google Scholar]
- Han, Q.; Liu, K.; Zeng, L.; He, G.; Ye, L.; Li, F. A bus arrival time prediction method based on position calibration and LSTM. IEEE Access 2020, 8, 42372–42383. [Google Scholar] [CrossRef]
- Chien, S.I.J.; Ding, Y.; Wei, C. Dynamic bus arrival time prediction with artificial neural networks. J. Transp. Eng. 2002, 128, 429–438. [Google Scholar] [CrossRef]
- Bin, Y.; Zhongzhen, Y.; Baozhen, Y. Bus arrival time prediction using support vector machines. J. Intell. Transp. Syst. 2006, 10, 151–158. [Google Scholar] [CrossRef]
- Yu, B.; Lam, W.H.; Tam, M.L. Bus arrival time prediction at bus stop with multiple routes. Transp. Res. Part Emerg. Technol. 2011, 19, 1157–1170. [Google Scholar] [CrossRef]
- Agafonov, A.; Yumaganov, A. Bus arrival time prediction with lstm neural network. In International Symposium on Neural Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 11–18. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Seber, G.A.; Lee, A.J. Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 329. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Ferris, B.; Watkins, K.; Borning, A. OneBusAway: Results from providing real-time arrival information for public transit. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Atlanta, GA, USA, 10–15 April 2010; pp. 1807–1816. [Google Scholar]
- Zhang, F.; Shen, Q.; Clifton, K.J. Examination of traveler responses to real-time information about bus arrivals using panel data. Transp. Res. Rec. 2008, 2082, 107–115. [Google Scholar] [CrossRef]
- Reinhoudt, E.M.; Velastin, S. A dynamic predicting algorithm for estimating bus arrival time. IFAC Proc. Vol. 1997, 30, 1225–1228. [Google Scholar] [CrossRef]
- Bin, Y.; Zhong-zhen, Y.; Qing-cheng, Z. Bus arrival time prediction model based on support vector machine and kalman filter. China J. Highw. Transp. 2008, 2, 89. [Google Scholar]
- Liu, T.; Ma, J.; Guan, W.; Song, Y.; Niu, H. Bus arrival time prediction based on the k-nearest neighbor method. In Proceedings of the 2012 Fifth International Joint Conference on Computational Sciences and Optimization, Heilongjiang, China, 23–26 June 2012; pp. 480–483. [Google Scholar]
- Suwardo, W.; Napiah, M.; Kamaruddin, I. ARIMA models for bus travel time prediction. J. Inst. Eng. Malays. 2010, 2010, 49–58. [Google Scholar]
- Lingqiu, Z.; Guangyan, H.; Qingwen, H.; Lei, Y.; Fengxi, L.; Lidong, C. A LSTM Based Bus Arrival Time Prediction Method. In Proceedings of the 2019 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Leicester, UK, 19–23 August 2019; pp. 544–549. [Google Scholar]
- Panovski, D.; Zaharia, T. Long and Short-Term Bus Arrival Time Prediction With Traffic Density Matrix. IEEE Access 2020, 8, 226267–226284. [Google Scholar] [CrossRef]
- Zhang, K.; Lai, Y.; Jiang, L.; Yang, F. Bus Travel-Time Prediction Based on Deep Spatio-Temporal Model. In International Conference on Web Information Systems Engineering; Springer: Cham, Switzerland, 2020; pp. 369–383. [Google Scholar]
- Kim, D.H.; Hwang, K.Y.; Yoon, Y. Prediction of Traffic Congestion in Seoul by Deep Neural Network. J. Korea Inst. Intell. Transp. Syst. 2019, 18, 44–57. [Google Scholar] [CrossRef]
- Panovski, D.; Zaharia, T. Public transportation prediction with convolutional neural networks. In International Conference on Intelligent Transport Systems; Springer: Cham, Switzerland, 2019; pp. 150–161. [Google Scholar]
- He, P.; Jiang, G.; Lam, S.K.; Tang, D. Travel-time prediction of bus journey with multiple bus trips. IEEE Trans. Intell. Transp. Syst. 2018, 20, 4192–4205. [Google Scholar] [CrossRef]
- Pang, J.; Huang, J.; Du, Y.; Yu, H.; Huang, Q.; Yin, B. Learning to predict bus arrival time from heterogeneous measurements via recurrent neural network. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3283–3293. [Google Scholar] [CrossRef]
- Baimbetova, A.; Konyrova, K.; Zhumabayeva, A.; Seitbekova, Y. Bus Arrival Time Prediction: A Case Study for Almaty. In Proceedings of the 2021 IEEE International Conference on Smart Information Systems and Technologies (SIST), Nur-Sultan, Kazakhstan, 28–30 April 2021; pp. 1–6. [Google Scholar]
- Leong, S.H.; Lam, C.T.; Ng, B.K. Bus Arrival Time Prediction for Short-Distance Bus Stops with Real-Time Online Information. In Proceedings of the 2021 IEEE 21st International Conference on Communication Technology (ICCT), Tianjin, China, 13–16 October 2021; pp. 387–392. [Google Scholar]
- Zhong, G.; Yin, T.; Li, L.; Zhang, J.; Zhang, H.; Ran, B. Bus travel time prediction based on ensemble learning methods. IEEE Intell. Transp. Syst. Mag. 2022, 14, 174–189. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the ICML, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ruder, S. An Overview of Gradient Descent Optimization Algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Nguyen, B.P. Prediction of FMN binding sites in electron transport chains based on 2-D CNN and PSSM Profiles. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 18, 2189–2197. [Google Scholar]
- Tng, S.S.; Le, N.Q.K.; Yeh, H.Y.; Chua, M.C.H. Improved Prediction Model of Protein Lysine Crotonylation Sites Using Bidirectional Recurrent Neural Networks. J. Proteome Res. 2021, 21, 265–273. [Google Scholar] [CrossRef]
- Ying, R.; Bourgeois, D.; You, J.; Zitnik, M.; Leskovec, J. GNN explainer: A tool for post-hoc explanation of graph neural networks. arXiv 2019, arXiv:1903.03894. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]

| Model | Data Type | Data Range | MAPE (%) | |||
|---|---|---|---|---|---|---|
| GPS | Flow Embedding | Contextual | Temporal Range | Spatial Range | ||
| ALSTM [11] | ✓ | - | - | 1 month | 1 route | 4 |
| Weighted LSTM [16] | ✓ | - | ✓ | 8 month | 1 route | 4.89 |
| LSTM [32] | ✓ | - | - | 12 month | 1 route | 3.6 |
| ConvLSTM [12] | ✓ | - | - | 6 month | 1 route | 4.19 |
| Ensemble ML [41] | - | - | ✓ | 1 month | 1 route | 19.64 |
| LSTM-RNN [38] | - | - | - | 1 month | 47 routes | 11.75 |
| DA-RNN [40] | - | - | ✓ | unknown | 4 routes | 18 |
| BFC-LSTM | - | ✓ | - | 1 month | 100+ routes | 1.19 |
| - | ✓ | ✓ | 1 month | 100+ routes | 2.90 | |
| Data | Status | Time (by Bus Stop ID) | Temperature | Precipitation | Day | Holiday |
|---|---|---|---|---|---|---|
| Mean | - | - | −1.72 | 0.00 | - | - |
| Median | - | - | −1.7 | 0.0 | - | - |
| Max | 1 (Arrival) | 1-January-2018 00:00:00 | 9.5 | 1.0 | 1 | 1 |
| Min | 0 (Depart) | 1-December-2017 00:00:00 | −16.9 | 0.0 | 0 | 0 |
| Unit | - | DD-MM-YYYY hh:mm:ss | °C | mm | - | - |
| Time Interval | Each Bus | 1-s | 1-min | 1-min | 1-day | 1-day |
| Type | Binary | Int | Float | Float | Binary | Binary |
| Model | Passing Time Feature | Basic Features | BFC Features | Contextual Features | MAPE (%) |
|---|---|---|---|---|---|
| Linear Regression | ✓ | - | - | - | 54.6 |
| Random Forest | ✓ | - | - | - | 20.8 |
| Multi-Linear Regression | ✓ | ✓ | ✓ | - | 18.8 |
| - | - | 22.4 | |||
| LSTM | ✓ | ✓ | ✓ | - | 1.19 |
| ✓ | ✓ | 2.91 | |||
| - | - | 31.7 | |||
| - | ✓ | 34.9 | |||
| GRU | ✓ | ✓ | ✓ | - | 2.03 |
| - | - | 34.1 | |||
| ALSTM | ✓ | ✓ | ✓ | - | 4.71 |
| - | - | 38.7 |
| Number of Perceptrons | Previous Model MAPE (%) | BFC Model MAPE (%) | ||||
|---|---|---|---|---|---|---|
| LSTM | GRU | ALSTM | LSTM | GRU | ALSTM | |
| 64 | 35.0 | 37.8 | 42.8 | 1.64 | 2.76 | 5.87 |
| 128 | 31.7 | 34.1 | 39.1 | 1.19 | 2.03 | 4.92 |
| 256 | 32.1 | 34.3 | 38.7 | 1.22 | 2.11 | 4.71 |
| 512 | 31.9 | 34.4 | 39.0 | 1.21 | 2.08 | 4.74 |
| MAPE (%) | T | ||||||
|---|---|---|---|---|---|---|---|
| 25 | 50 | 75 | 100 | 150 | 200 | ||
| D | 10 | 22.08 | 21.97 | 21.95 | 21.93 | 21.92 | 21.91 |
| 15 | 21.29 | 21.13 | 21.13 | 21.03 | 21.00 | 20.98 | |
| 20 | 21.25 | 21.02 | 21.02 | 20.90 | 20.87 | 20.85 | |
| 25 | 21.23 | 21.01 | 21.01 | 20.89 | 20.86 | 20.84 | |
| 30 | 21.26 | 21.03 | 21.03 | 20.91 | 20.86 | 20.84 | |
| 35 | 21.24 | 21.02 | 21.02 | 20.90 | 20.86 | 20.84 | |
| BFC Features LT (min.) | With Contextual Features MAPE (%) | Without Contextual Features MAPE (%) |
|---|---|---|
| - | 22.41 | 22.36 |
| 5 | 21.26 | 21.22 |
| 10 | 20.36 | 20.35 |
| 15 | 20.03 | 20.00 |
| 20 | 19.66 | 19.66 |
| 30 | 19.24 | 19.23 |
| 45 | 18.92 | 18.92 |
| 60 | 18.83 | 18.83 |
| 120 | 18.84 | 18.84 |
| 180 | 18.84 | 18.84 |
| LT (min.) | With Contextual Features | Without Contextual Features | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE (%) | MAE | RMSE | MAPE (%) | |
| 5 | 3.84 | 8.29 | 3.71 | 1.62 | 4.23 | 1.65 |
| 10 | 3.09 | 6.50 | 3.05 | 1.15 | 2.91 | 1.19 |
| 15 | 2.94 | 5.75 | 3.01 | 1.16 | 2.92 | 1.21 |
| 20 | 2.94 | 5.80 | 2.98 | 1.22 | 2.99 | 1.26 |
| 30 | 2.88 | 5.68 | 2.90 | 1.32 | 3.10 | 1.37 |
| 45 | 3.00 | 5.80 | 3.10 | 1.30 | 3.12 | 1.37 |
| 60 | 3.07 | 5.98 | 3.09 | 1.37 | 3.21 | 1.42 |
| 120 | 3.08 | 6.23 | 3.16 | 1.43 | 3.49 | 1.47 |
| 180 | 3.36 | 6.51 | 3.42 | 1.39 | 3.25 | 1.47 |
| Number of Time Windows | MAE | RMSE | MAPE (%) |
|---|---|---|---|
| 5 | 1.16 | 2.92 | 1.19 |
| 10 | 1.33 | 3.27 | 1.37 |
| 15 | 1.38 | 3.38 | 1.44 |
| 20 | 1.36 | 3.44 | 1.40 |
| 25 | 1.42 | 3.38 | 1.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Yoon, Y. A Novel Bus Arrival Time Prediction Method Based on Spatio-Temporal Flow Centrality Analysis and Deep Learning. Electronics 2022, 11, 1875. https://doi.org/10.3390/electronics11121875
Lee C, Yoon Y. A Novel Bus Arrival Time Prediction Method Based on Spatio-Temporal Flow Centrality Analysis and Deep Learning. Electronics. 2022; 11(12):1875. https://doi.org/10.3390/electronics11121875
Chicago/Turabian StyleLee, Chanjae, and Young Yoon. 2022. "A Novel Bus Arrival Time Prediction Method Based on Spatio-Temporal Flow Centrality Analysis and Deep Learning" Electronics 11, no. 12: 1875. https://doi.org/10.3390/electronics11121875
APA StyleLee, C., & Yoon, Y. (2022). A Novel Bus Arrival Time Prediction Method Based on Spatio-Temporal Flow Centrality Analysis and Deep Learning. Electronics, 11(12), 1875. https://doi.org/10.3390/electronics11121875






