Adaptive Fuzzy Observer Control for Half-Car Active Suspension Systems with Prescribed Performance and Actuator Fault
Abstract
:1. Introduction
- 1.
- The half-car active suspension is analyzed in the presence of uncertain parameters and actuator failures to guarantee ride comfort, suspension deflection, and driving safety;
- 2.
- FLSs are applied to approximate the unknown functions of parametric uncertainties and different masses of passengers. Then, the adaptive fault-tolerant control is designed to compensate for the actuator fault problem;
- 3.
- The PPF technique is incorporated into the control technique to constrain chassis displacement and angular motion within the small boundaries.
2. System Description
2.1. Half Car Suspension Model
2.2. Actuator Fault Formulation and Preliminaries
- (1)
- Lock-in-place type: In this case, the actuator is stuck and cannot respond to the input control signal. Then, the actual signal can be described by and , in which is the constant values of the float fault of and is the constant values of the float fault of .
- (2)
- Loss of effectiveness model: The actual control cannot satisfy the complete value of signal control in this case. This means that some effectiveness is lost, which is denoted by the coefficient factor and . For example, indicates that the remaining coefficient actuator is while the loss signal of the vertical control actuator is .
- (1)
- Ride comfort: The chassis movement must be stabilized and isolated from the external violation of road disturbance, which can improve the passenger comfort;
- (2)
- Handling stability: The active suspension must guarantee the suspension deflection within the mechanical structure. To meet this requirement, the relative suspension deflection (RSD) has to be smaller than 1.
- (3)
- Driving safety: This objective is considered to ensure that the tire should always contact with the road profile. For this purpose, the relative tire fore (RTF) must be kept less than 1.
3. Adaptive Fuzzy Observer Control with Prescribed Performance
3.1. Prescribed Performance Function
3.2. Adaptive Fuzzy Observer Controller with Prescribed Performance
3.3. Handling Stability and Driving Safety Analysis
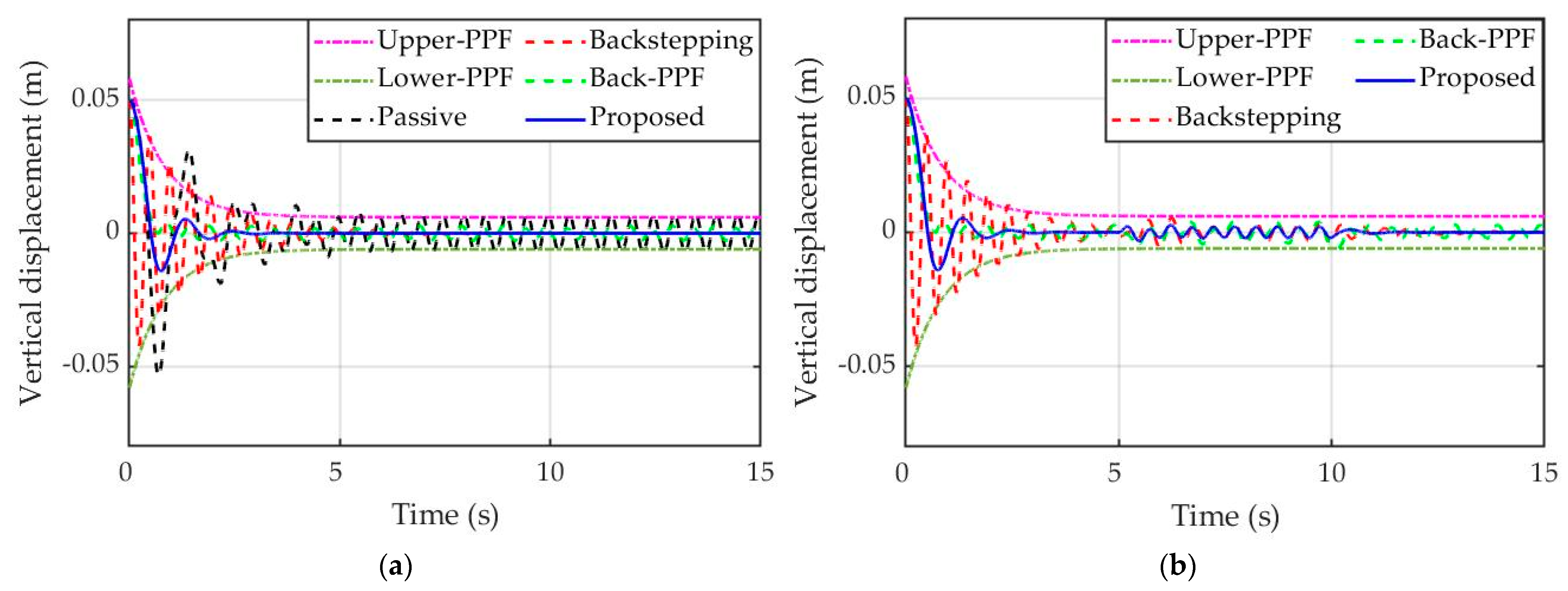
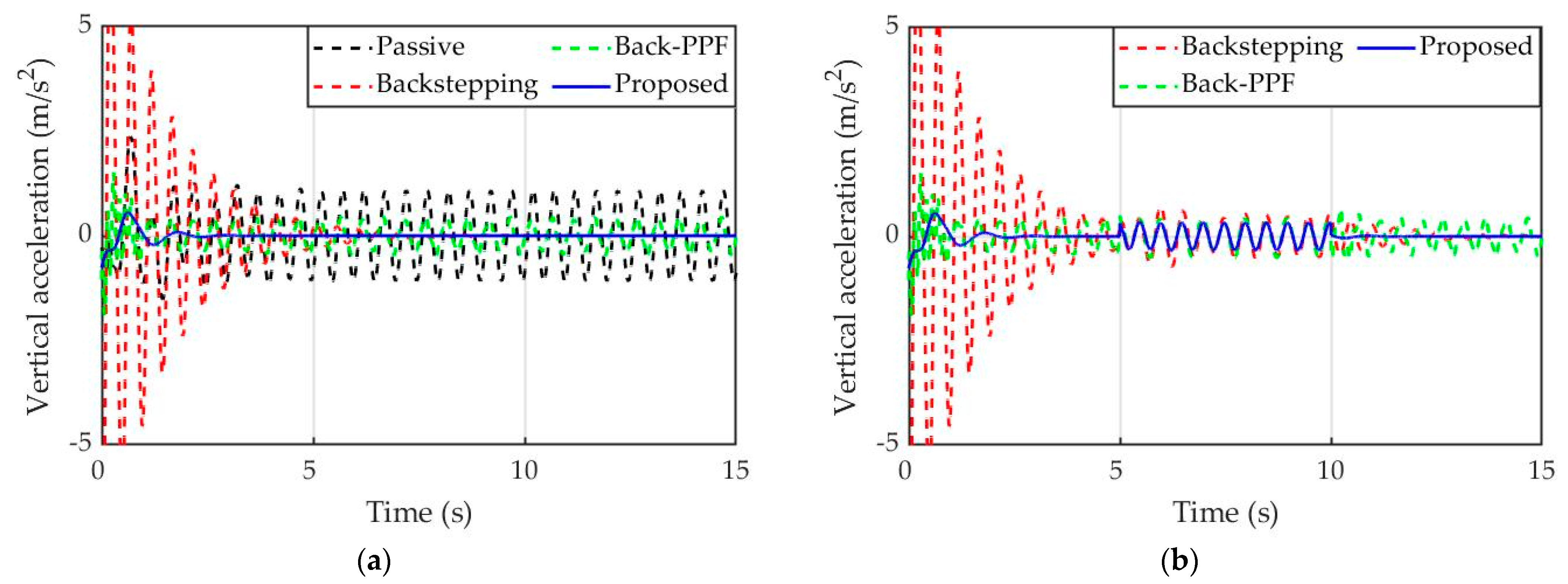
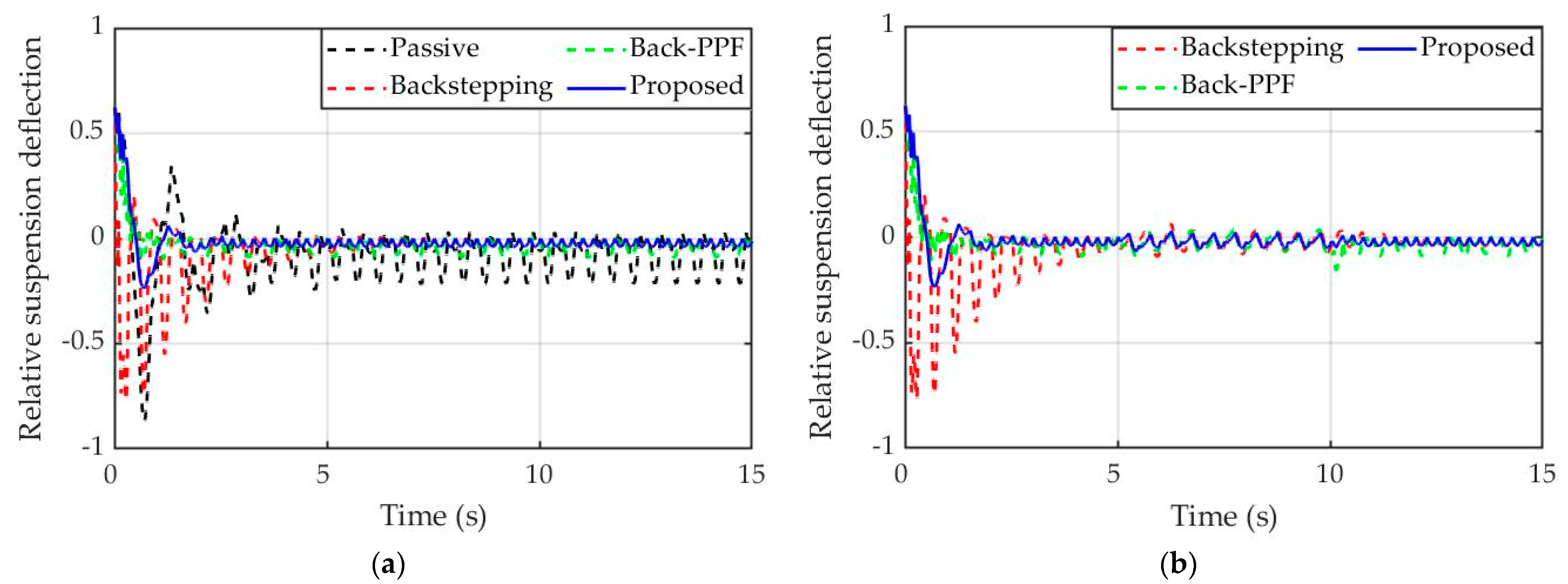
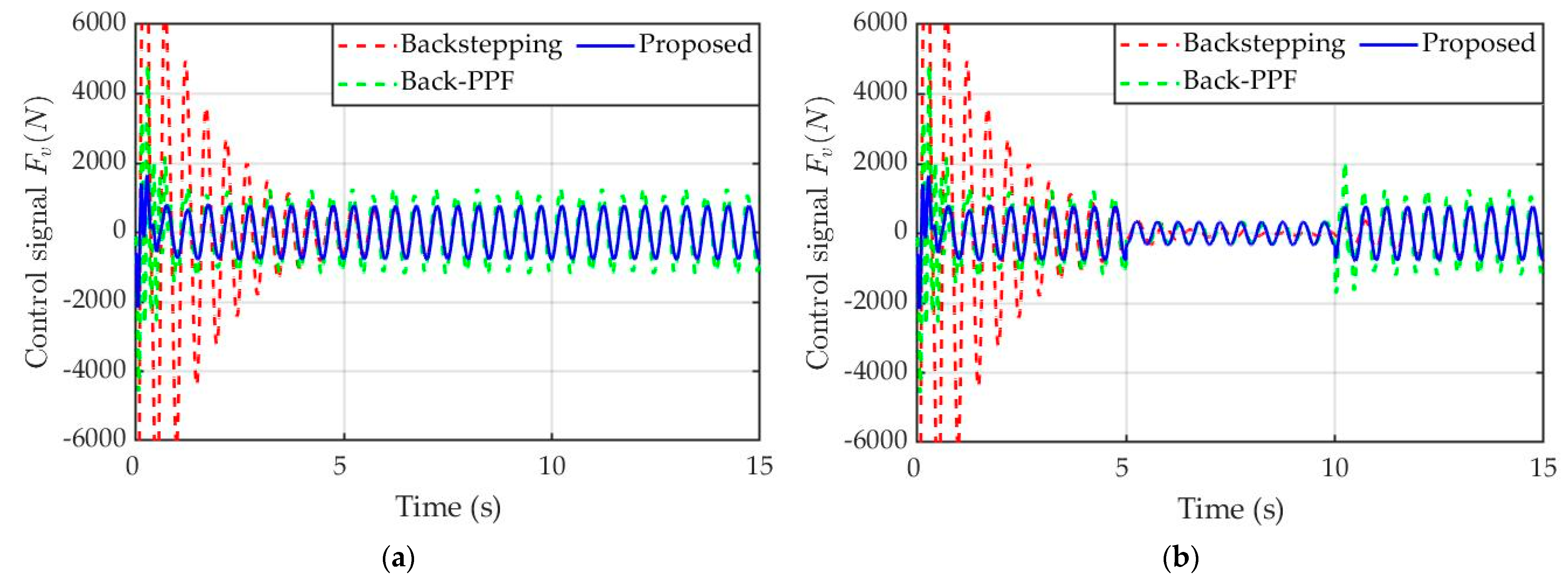
4. Simulation Results and Discussion
4.1. Simulation Description
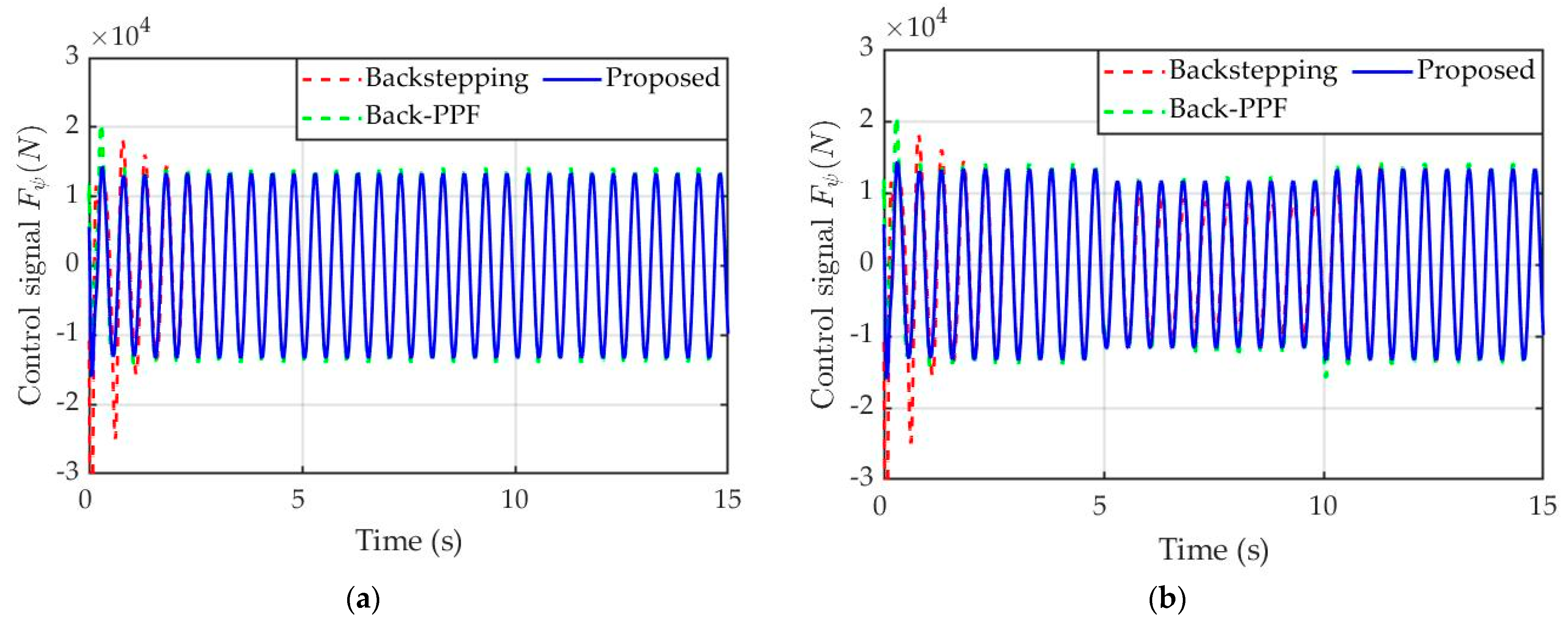
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Rath, J.J.; Defoort, M.; Sentouh, C.; Karimi, H.R.; Veluvolu, K.C. Output-Constrained Robust Sliding Mode Based Nonlinear Active Suspension Control. IEEE Trans. Ind. Electron. 2020, 67, 10652–10662. [Google Scholar] [CrossRef]
- Lin, B.; Su, X. Fault-tolerant Controller Design for Active Suspension System with Proportional Differential Sliding Mode Observer. Int. J. Control Autom. Syst. 2019, 17, 1751–1761. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Zeng, Q.; Liu, L.; Tong, S. An Adaptive Neural Network Controller for Active Suspension Systems with Hydraulic Actuator. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 5351–5360. [Google Scholar] [CrossRef]
- Pan, J.; Li, W.; Zhang, H. Control Algorithms of Magnetic Suspension Systems Based on the Improved Double Exponential Reaching Law of Sliding Mode Control. Int. J. Control Autom. Syst. 2018, 16, 2878–2887. [Google Scholar] [CrossRef]
- Choi, H.D.; Lee, C.J.; Lim, M.T. Fuzzy Preview Control for Half-vehicle Electro-hydraulic Suspension System. Int. J. Control Autom. Syst. 2018, 16, 2489–2500. [Google Scholar] [CrossRef]
- Jing, H.; Wang, R.; Li, C.; Bao, J. Robust finite-frequency H control of full-car active suspension. J. Sound Vib. 2019, 441, 221–239. [Google Scholar] [CrossRef]
- Yan, G.; Fang, M.; Xu, J. Analysis and experiment of time-delayed optimal control for vehicle suspension system. J. Sound Vib. 2019, 446, 144–158. [Google Scholar] [CrossRef]
- Pan, H.; Sun, W. Nonlinear Output Feedback Finite-Time Control for Vehicle Active Suspension Systems. IEEE Trans. Ind. Inform. 2019, 15, 2073–2082. [Google Scholar] [CrossRef]
- Ho, C.M.; Tran, D.T.; Ahn, K.K. Adaptive sliding mode control based nonlinear disturbance observer for active suspension with pneumatic spring. J. Sound Vib. 2021, 509, 116241. [Google Scholar] [CrossRef]
- Sun, W.; Gao, H.; Kaynak, O. Adaptive Backstepping Control for Active Suspension Systems with Hard Constraints. IEEE ASME Trans. Mechatron. 2013, 18, 1072–1079. [Google Scholar] [CrossRef]
- Kazemipour, A.; Novinzadeh, A.B. Adaptive fault-tolerant control for active suspension systems based on the terminal sliding mode approach. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 501–511. [Google Scholar] [CrossRef]
- Pusadkar, U.S.; Chaudhari, S.D.; Shendge, P.D.; Phadke, S.B. Linear disturbance observer based sliding mode control for active suspension systems with non-ideal actuator. J. Sound Vib. 2019, 442, 428–444. [Google Scholar] [CrossRef]
- Pang, H.; Zhang, X.; Chen, J.; Liu, K. Design of a coordinated adaptive backstepping tracking control for nonlinear uncertain active suspension system. Appl. Math. Model. 2019, 76, 479–494. [Google Scholar] [CrossRef]
- Li, W.; Xie, Z.; Zhao, J.; Wong, P.K.; Li, P. Fuzzy finite-frequency output feedback control for nonlinear active suspension systems with time delay and output constraints. Mech. Syst. Signal Processing 2019, 132, 315–334. [Google Scholar] [CrossRef]
- Ho, C.M.; Tran, D.T.; Nguyen, C.H.; Ahn, K.K. Adaptive Neural Command Filtered Control for Pneumatic Active Suspension with Prescribed Performance and Input Saturation. IEEE Access 2021, 9, 56855–56868. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Wang, Z.; Bai, R.; Liu, L. Neural networks-based adaptive dynamic surface control for vehicle active suspension systems with time-varying displacement constraints. Neurocomputing 2020, 408, 176–187. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Yan, H.; Xie, X. Adaptive Event-Triggered Fuzzy Control for Uncertain Active Suspension Systems. IEEE Trans. Cybern. 2019, 49, 4388–4397. [Google Scholar] [CrossRef]
- Wen, S.; Chen, M.Z.Q.; Zeng, Z.; Yu, X.; Huang, T. Fuzzy Control for Uncertain Vehicle Active Suspension Systems via Dynamic Sliding-Mode Approach. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 24–32. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust Adaptive Control of Feedback Linearizable MIMO Nonlinear Systems with Prescribed Performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, J.; Yue, D. Prescribed performance control of one-DOF link manipulator with uncertainties and input saturation constraint. IEEE CAA J. Autom. Sin. 2019, 6, 148–157. [Google Scholar] [CrossRef]
- Wang, M.; Yang, A. Dynamic Learning from Adaptive Neural Control of Robot Manipulators with Prescribed Performance. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2244–2255. [Google Scholar] [CrossRef]
- Huang, Y.; Na, J.; Wu, X.; Gao, G. Approximation-Free Control for Vehicle Active Suspensions with Hydraulic Actuator. IEEE Trans. Ind. Electron. 2018, 65, 7258–7267. [Google Scholar] [CrossRef]
- Na, J.; Huang, Y.; Wu, X.; Gao, G.; Herrmann, G.; Jiang, J.Z. Active Adaptive Estimation and Control for Vehicle Suspensions with Prescribed Performance. IEEE Trans. Control Syst. Technol. 2018, 26, 2063–2077. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Jiang, B.; Mao, Z.; Ding, S.X. Adaptive Backstepping Based Fault-tolerant Control for High-speed Trains with Actuator Faults. Int. J. Control Autom. Syst. 2019, 17, 1408–1420. [Google Scholar] [CrossRef]
- Pan, H.; Li, H.; Sun, W.; Wang, Z. Adaptive Fault-Tolerant Compensation Control and Its Application to Nonlinear Suspension Systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1766–1776. [Google Scholar] [CrossRef]
- Chen, L.; Li, X.; Xiao, W.; Li, P.; Zhou, Q. Fault-tolerant Control for Uncertain Vehicle Active Steering Systems with Time-delay and Actuator Fault. Int. J. Control Autom. Syst. 2019, 17, 2234–2241. [Google Scholar] [CrossRef]
- Ho, C.M.; Ahn, K.K. Design of an Adaptive Fuzzy Observer-Based Fault Tolerant Controller for Pneumatic Active Suspension with Displacement Constraint. IEEE Access 2021, 9, 136346–136359. [Google Scholar] [CrossRef]
- Liu, B.; Saif, M.; Fan, H. Adaptive Fault Tolerant Control of a Half-Car Active Suspension Systems Subject to Random Actuator Failures. IEEE ASME Trans. Mechatron. 2016, 21, 2847–2857. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, H.; Luo, X.; Xiao, J. Adaptive sliding fault tolerant control for nonlinear uncertain active suspension systems. J. Frankl. Inst. 2016, 353, 180–199. [Google Scholar] [CrossRef]
- Wang, L.-X.; Mendel, J.M. Fuzzy basis functions, universal approximation, and orthogonal least squares learning. IEEE Trans. Neural Netw. 1992, 3, 807–814. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.-X. Stable adaptive fuzzy control of nonlinear systems. IEEE Trans. Fuzzy Syst. 1993, 1, 146–155. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Liu, X.; Wang, H. Adaptive Neural Network Prescribed Performance Bounded- Hinfinity Tracking Control for a Class of Stochastic Nonlinear Systems. IEEE Trans. Neural. Netw. Learn. Syst. 2020, 31, 2140–2152. [Google Scholar] [CrossRef] [PubMed]






| Parameter | Value | Unit |
|---|---|---|
| 1200 | kg | |
| 100 | kg | |
| 100 | kg | |
| 600 | kgm2 | |
| 15,000 | Nm−1 | |
| 150,000 | Nm−1 | |
| 200,000 | Nm−1 | |
| 1500 | Nsm−1 | |
| 1100 | Nsm−1 | |
| 1200 | Nsm−1 | |
| 1.2 | m | |
| 1.5 | m |
| Controller | Parameter |
|---|---|
| Backstepping | |
| Back-PPF | |
| Proposed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, C.M.; Nguyen, C.H.; Ahn, K.K. Adaptive Fuzzy Observer Control for Half-Car Active Suspension Systems with Prescribed Performance and Actuator Fault. Electronics 2022, 11, 1733. https://doi.org/10.3390/electronics11111733
Ho CM, Nguyen CH, Ahn KK. Adaptive Fuzzy Observer Control for Half-Car Active Suspension Systems with Prescribed Performance and Actuator Fault. Electronics. 2022; 11(11):1733. https://doi.org/10.3390/electronics11111733
Chicago/Turabian StyleHo, Cong Minh, Cong Hung Nguyen, and Kyoung Kwan Ahn. 2022. "Adaptive Fuzzy Observer Control for Half-Car Active Suspension Systems with Prescribed Performance and Actuator Fault" Electronics 11, no. 11: 1733. https://doi.org/10.3390/electronics11111733
APA StyleHo, C. M., Nguyen, C. H., & Ahn, K. K. (2022). Adaptive Fuzzy Observer Control for Half-Car Active Suspension Systems with Prescribed Performance and Actuator Fault. Electronics, 11(11), 1733. https://doi.org/10.3390/electronics11111733







