Requirement Analysis and Teardrop-Based Design of High Antenna Isolation for FMCW Radar
Abstract
:1. Introduction
2. FMCW Radar and Requirements for Antenna Isolation
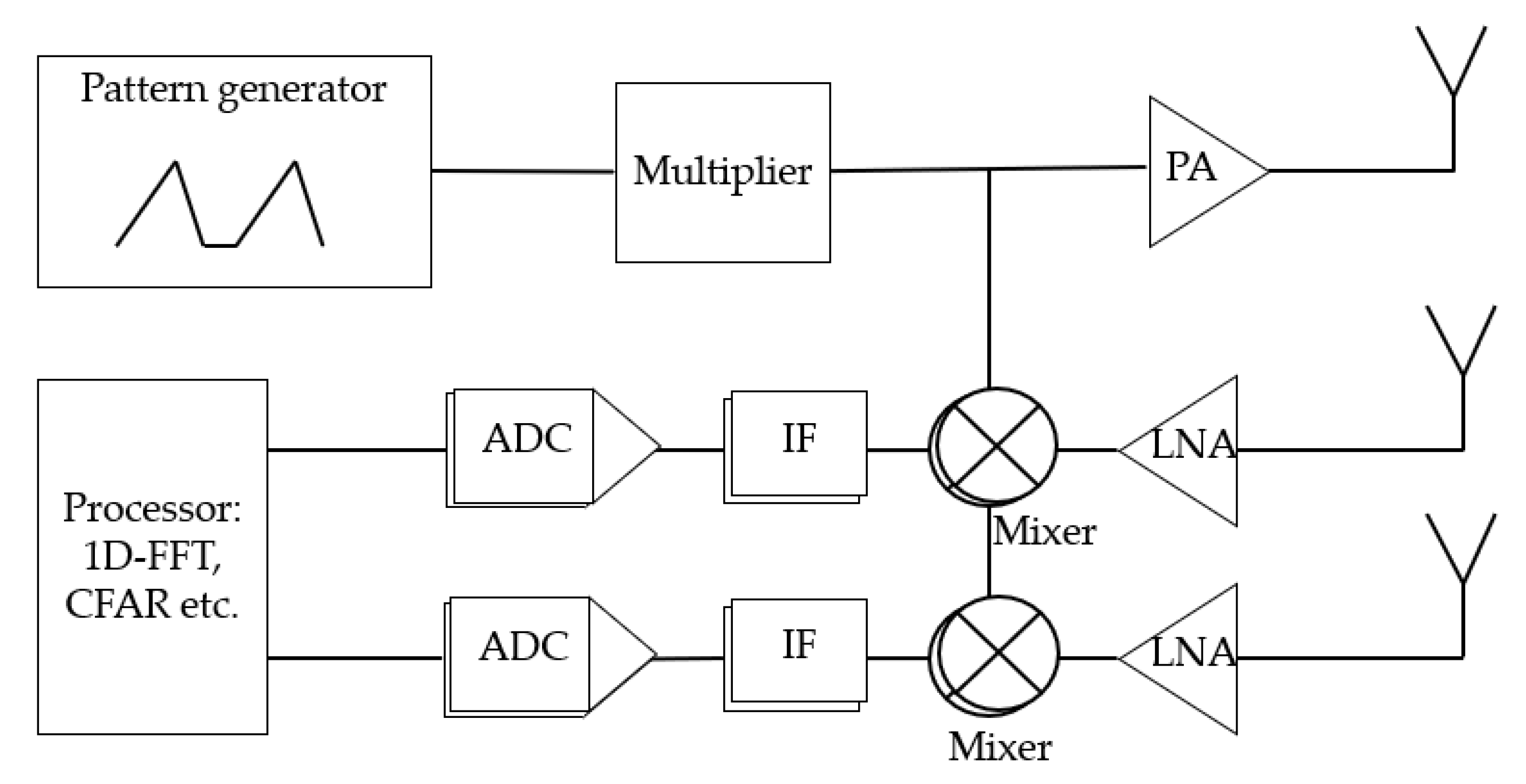
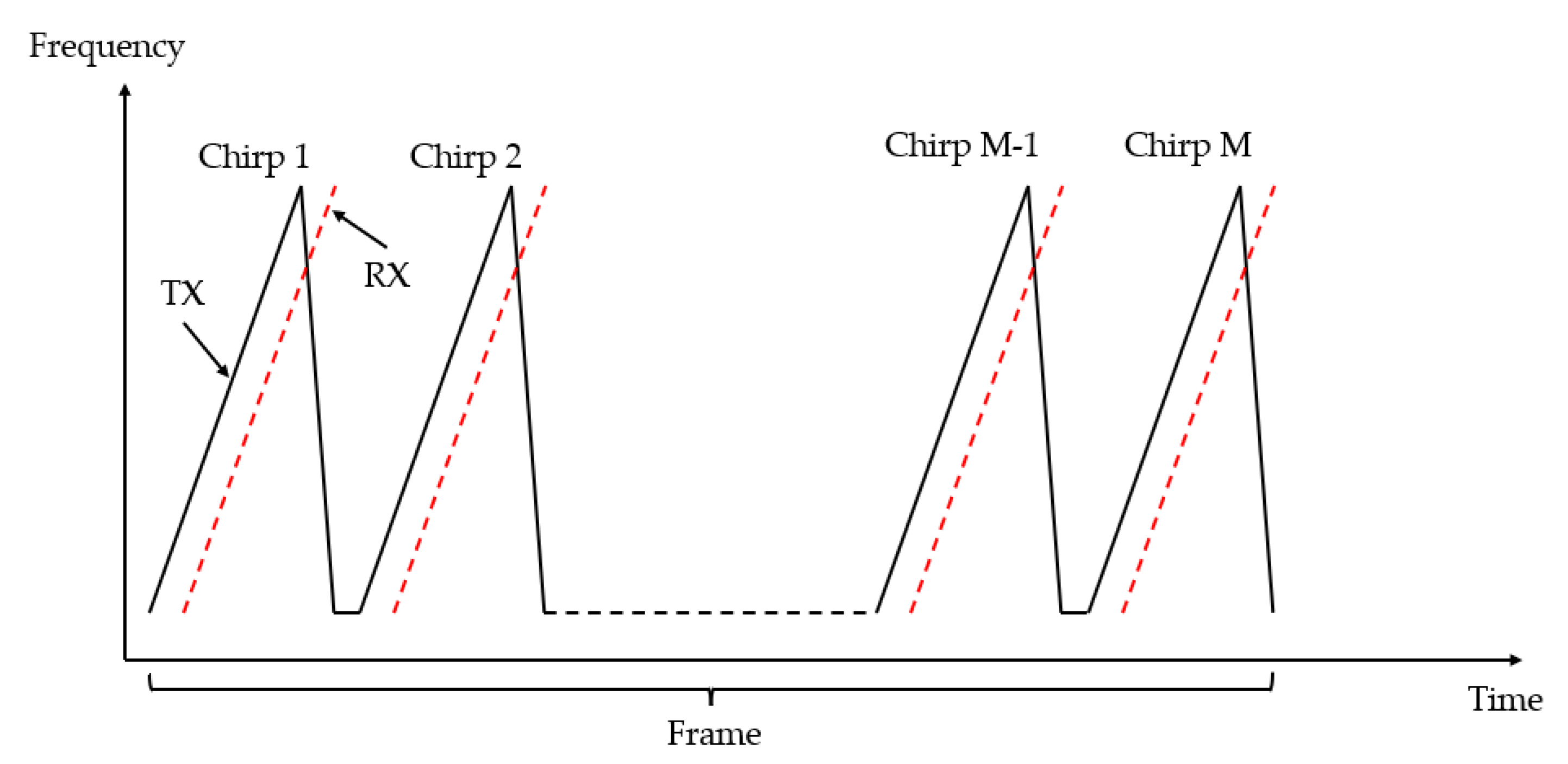
2.1. FMCW Radar Principle
2.2. Antenna Isolation Influence on the Radar Range Equation
3. Experimental Analysis of the Isolation Impact on System Performance
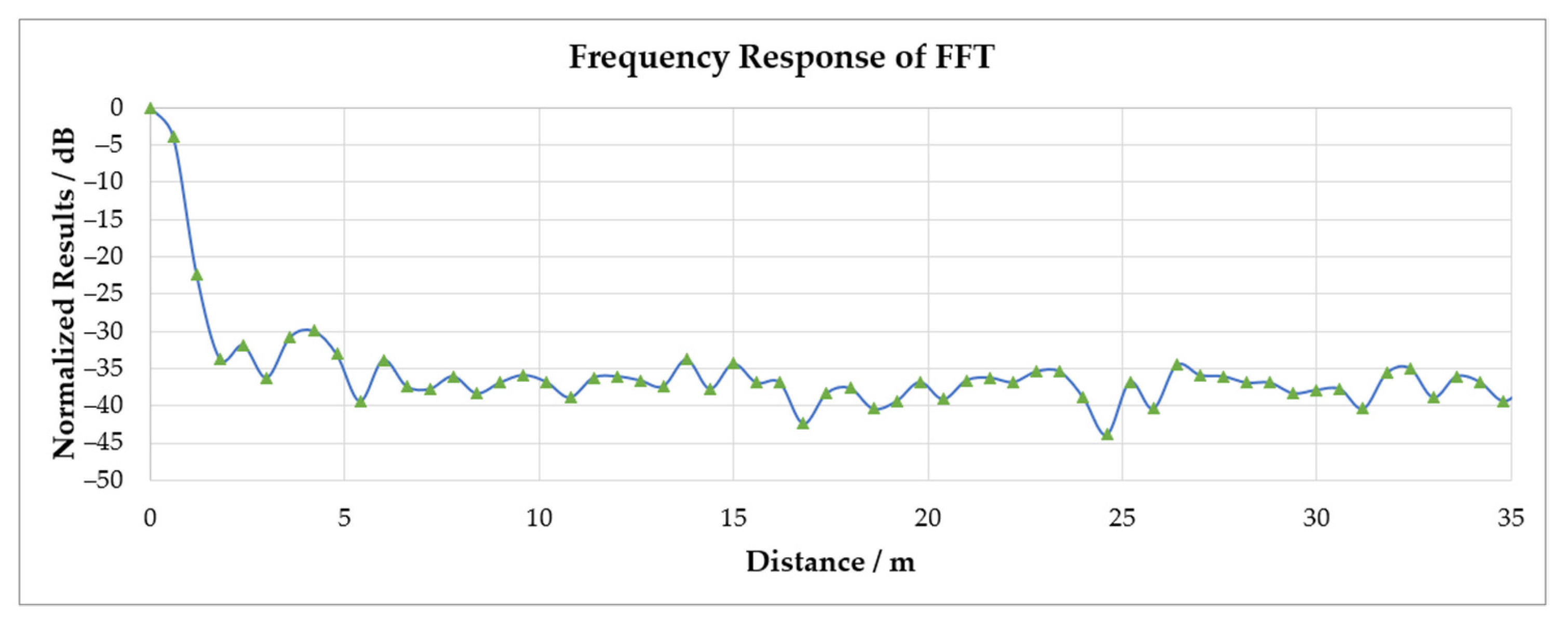
3.1. Experimental Results in an Anechoic Chamber
3.2. Experimental Results in an Open Environment
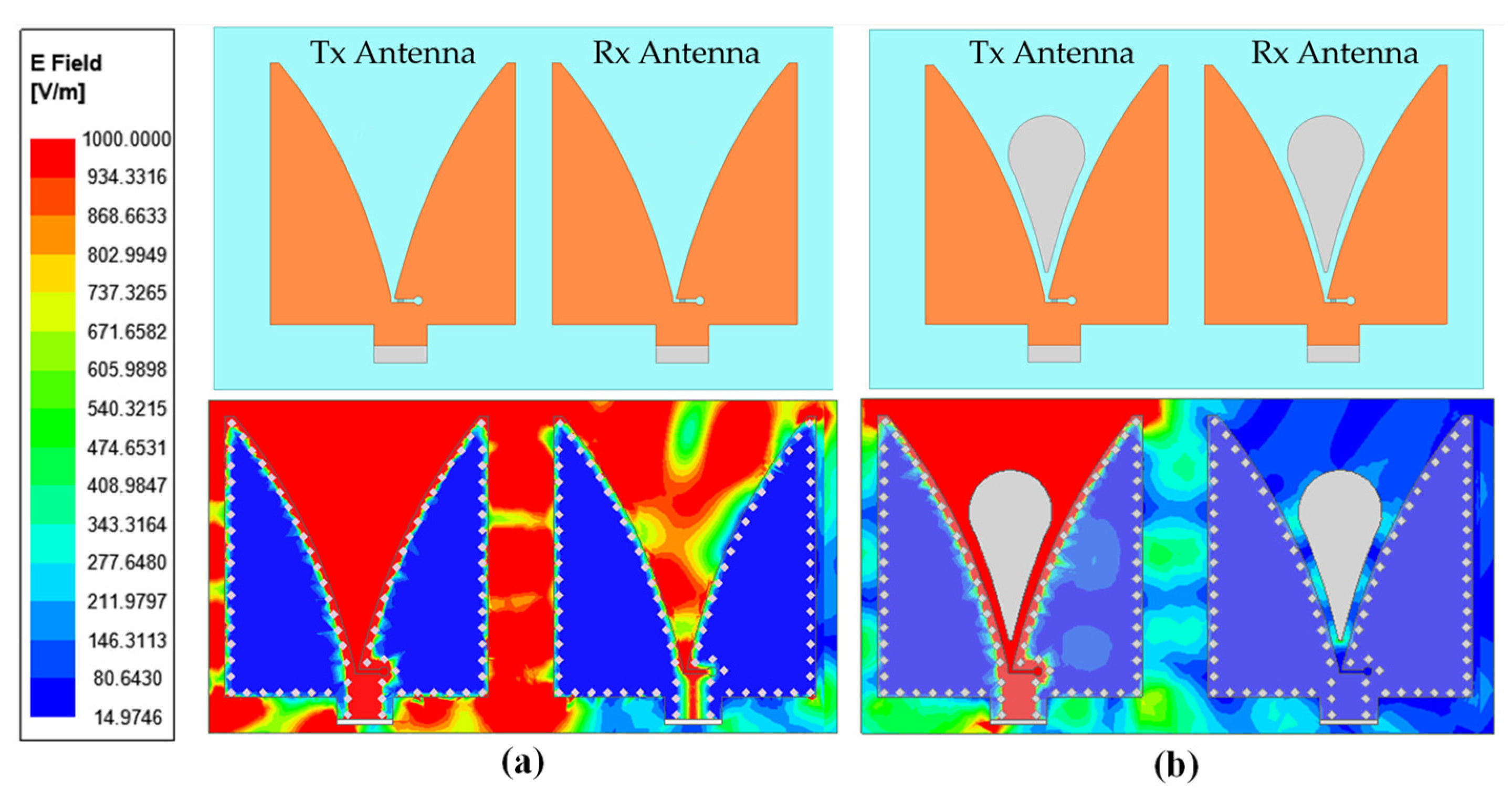
4. Vivaldi Antenna with Teardrop Loaded Design
4.1. Teardrop Loaded Vivaldi Antenna Configuration
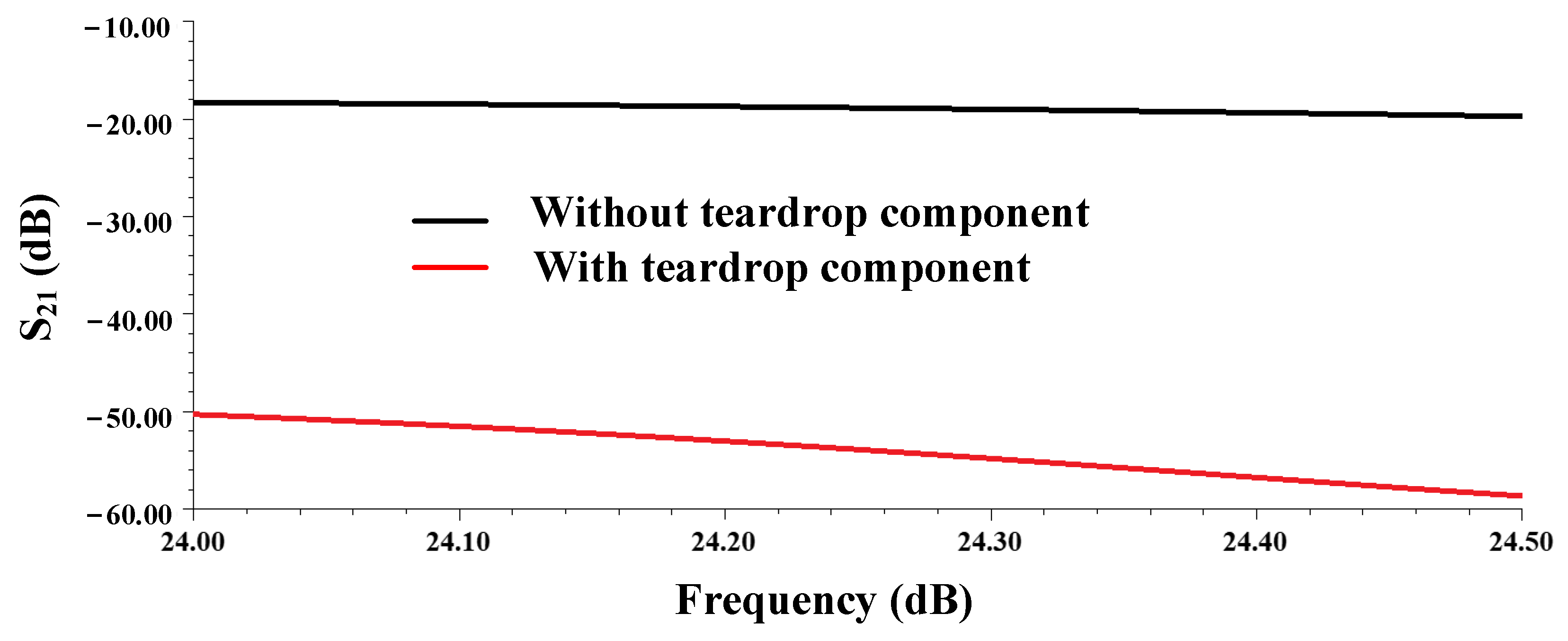
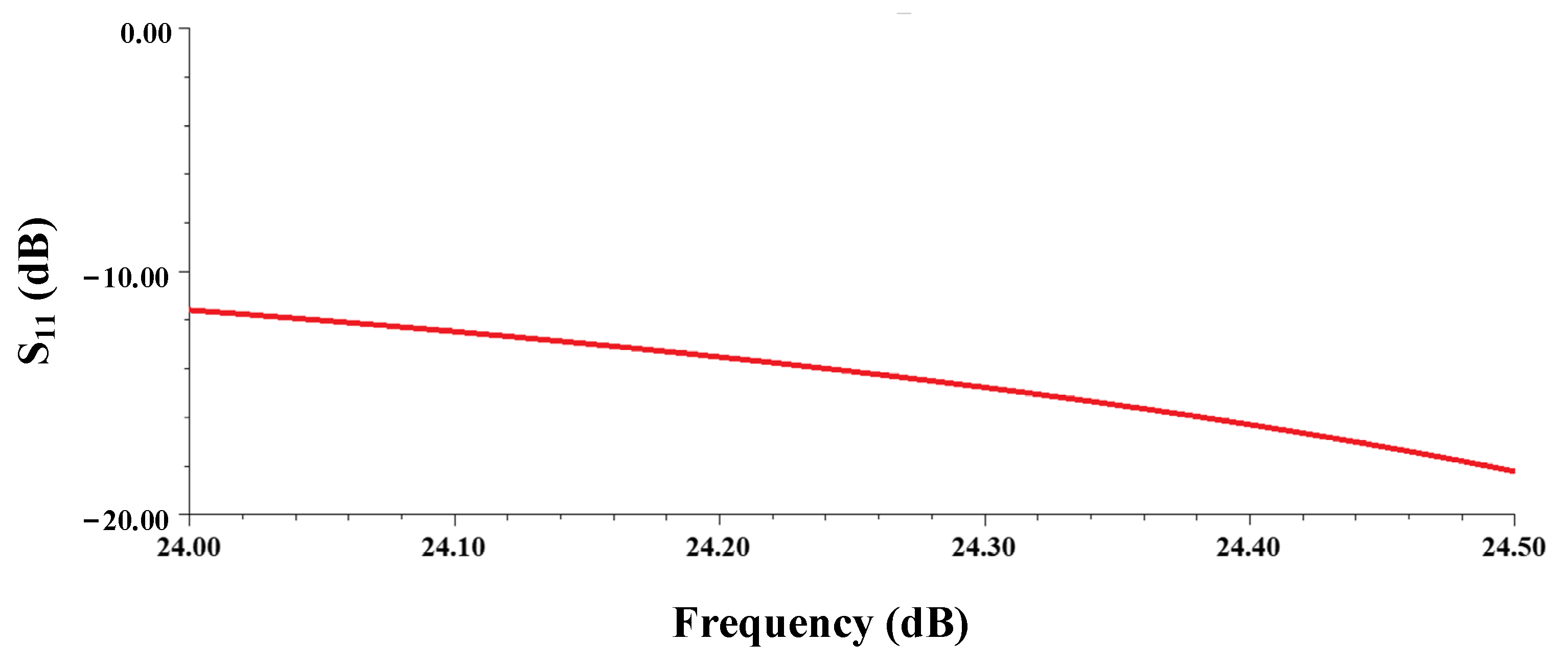
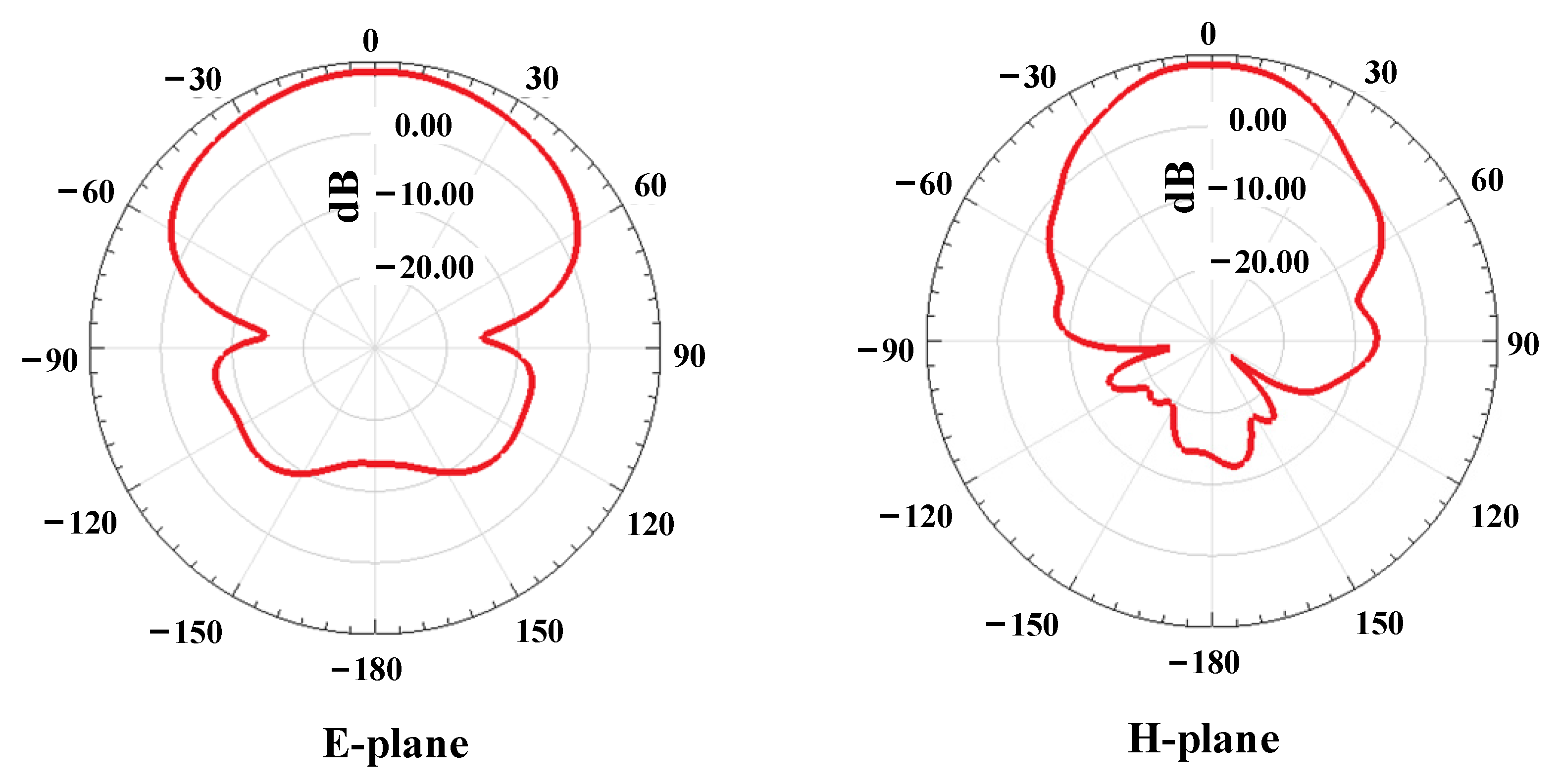
4.2. Antenna Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, S.; Jeon, Y.; Park, G.; Myung, J.; Lee, S.; Lee, O.; Moon, H.; Nam, I. A 24-GHz RF Transmitter in 65-nm CMOS for In-Cabin Radar Applications. Electronics 2020, 9, 2005. [Google Scholar] [CrossRef]
- Senigagliesi, L.; Ciattaglia, G.; De Santis, A.; Gambi, E. People Walking Classification Using Automotive Radar. Electronics 2020, 9, 588. [Google Scholar] [CrossRef] [Green Version]
- Passafiume, M.; Rojhani, N.; Collodi, G.; Cidronali, A. Modeling Small UAV Micro-Doppler Signature Using Millimeter-Wave FMCW Radar. Electronics 2021, 10, 747. [Google Scholar] [CrossRef]
- Gouveia, C.; Loss, C.; Pinho, P.; Vieira, J. Different Antenna Designs for Non-Contact Vital Signs Measurement: A Review. Electronics 2019, 8, 1294. [Google Scholar] [CrossRef] [Green Version]
- Bhatia, J.; Dayal, A.; Jha, A.; Vishvakarma, S.K.; Joshi, S.; Srinivas, M.B.; Yalavarthy, P.K.; Kumar, A.; Lalitha, V.; Koorapati, S.; et al. Classification of Targets Using Statistical Features from Range FFT of mmWave FMCW Radars. Electronics 2021, 10, 1965. [Google Scholar] [CrossRef]
- Tang, T.; Wu, C.; Elangage, J. Analyze the FMCW Waveform Skin Return of Moving Objects in the Presence of Stationary Hidden Objects Using Numerical Models. Electronics 2021, 10, 28. [Google Scholar] [CrossRef]
- Qi, A.; Ma, M.; Luo, Y.; Fernandes, G.; Shi, G.; Fan, J.; Qi, Y.; Ma, J. WISe: Wireless Intelligent Sensing for Human Centric Applications. IEEE Wirel. Commun. 2022. [Google Scholar] [CrossRef]
- Cidronali, A.; Passafiume, M.; Colantonio, P.; Collodi, G.; Florian, C.; Leuzzi, G.; Pirola, M.; Ramella, C.; Santarelli, A.; Traverso, P. System Level Analysis of Millimetre-wave GaN-based MIMO Radar for Detection of Micro Unmanned Aerial Vehicles. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium—Spring (PIERS—Spring), Rome, Italy, 17–20 June 2019. [Google Scholar]
- Melzer, A.; Onic, A.; Starzer, F.; Huemer, M. Short-Range Leakage Cancelation in FMCW Radar Transceivers Using an Artificial On-Chip Target. IEEE J. Sel. Top. Signal Process. 2015, 9, 1650–1660. [Google Scholar] [CrossRef]
- Adela, B.B.; van Zeijl, P.T.M.; Johannsen, U.; Smolders, A.B. On-Chip Antenna Integration for Millimeter-Wave Single-Chip FMCW Radar, Providing High Efficiency and Isolation. IEEE Trans. Antennas Propag. 2016, 64, 3281–3291. [Google Scholar] [CrossRef]
- Yoo, B.-Y.; Park, J.-H.; Yang, J.-R. Quasi-Circulator Using an Asymmetric Coupler for Tx Leakage Cancellation. Electronics 2018, 7, 173. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Muñoz-Ferreras, J.; Gu, C.; Li, C.; Gómez-García, R. Application of Linear-Frequency-Modulated Continuous-Wave (LFMCW) Radars for Tracking of Vital Signs. IEEE Trans. Microw. Theory Tech. 2014, 62, 1387–1399. [Google Scholar] [CrossRef]
- Beck, C.; Ng, H.J.; Agethen, R.; PourMousavi, M.; Forstner, H.P.; Wojnowski, M.; Pressel, K.; Weigel, R.; Hagelauer, A.; Kissinger, D.; et al. Industrial mmWave Radar Sensor in Embedded Wafer-Level BGA Packaging Technology. IEEE Sens. J. 2016, 16, 6566–6578. [Google Scholar] [CrossRef]
- Nasr, I.; Jungmaier, R.; Baheti, A.; Noppeney, D.; Bal, J.S.; Wojnowski, M.; Karagozler, E.; Raja, H.; Lien, J.; Poupyrev, I.; et al. A Highly Integrated 60 GHz 6-Channel Transceiver with Antenna in Package for Smart Sensing and Short-Range Communications. IEEE J. Solid-State Circuits 2016, 51, 2066–2076. [Google Scholar] [CrossRef]
- S5 Series K-band mmWave Sensor. Available online: https://www.iclegend.com/en/sensor.html (accessed on 10 April 2022).
- Liu, K.; Liu, N.W.; Fu, G. Isolation Improvement of Dual-polarized Microstrip Array Antenna by Using DGS Scheme. In Proceedings of the ICEICT—2021 IEEE 4th International Conference on Electronic Information and Communication Technology, Xi’an, China, 18–20 August 2021. [Google Scholar]
- Moallem, M.; Crawford, Z.; Kulak, R.; Dewilde, M.; Chi, C.; Lin, A.; Ginsburg, B. High Performance mm-Wave MIMO Radar with Integrated Antenna-on-Package. In Proceedings of the 2020 IEEE 70th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 3–30 June 2020. [Google Scholar]
- Kim, S.; Kim, D.K.; Kim, Y.; Choi, J.; Jung, K. A 24 GHz ISM-Band Doppler Radar Antenna with High Isolation Characteristic for Moving Target Sensing Applications. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1532–1536. [Google Scholar] [CrossRef]
- Yang, Y.; Chi, L.; Luo, Y.; Qi, A.; Miao, M.; Qi, Y. Antenna Design of Millimeter Wave Radar for Smart Toilet. In Proceedings of the 13th International Symposium on Antennas, Propagation and EM Theory (ISAPE 2021), Zhuhai, China, 1–4 December 2021. [Google Scholar]
- Ngo, A.; Bauer, M.P.; Resch, M. A Sensitivity Analysis Approach for Evaluating a Radar Simulation for Virtual Testing of Autonomous Driving Functions. In Proceedings of the 2022 7th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS 2022), Singapore, 17–19 July 2020. [Google Scholar]
- Martínez-Vázquez, M. Overview of design challenges for automotive radar MMICs. In Proceedings of the International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 11–16 December 2021. [Google Scholar]
- Gandhi, P.P.; Kassam, S.A. Analysis of CFAR processors in nonhomogeneous background. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 427–445. [Google Scholar] [CrossRef]
- David, M.P. Microwave Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Luo, Y.; Qi, A.; Shi, G.; Miao, M.; Qi, Y.; Ma, J. Millimeters Wave Radar for Wireless Intelligent Sensing. In Proceedings of the 13th International Symposium on Antennas, Propagation and EM Theory (ISAPE 2021), Zhuhai, China, 1–4 December 2021. [Google Scholar]


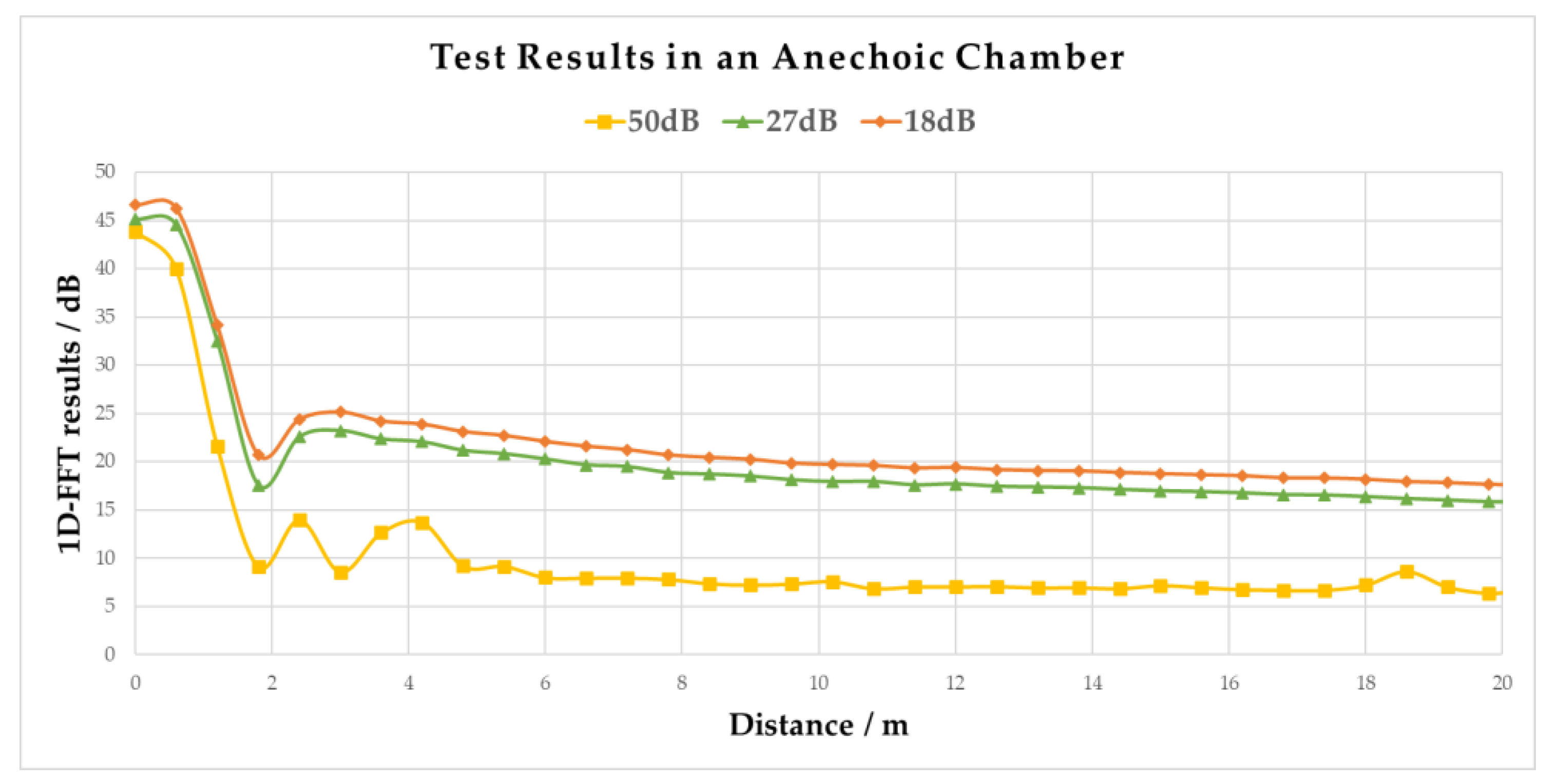
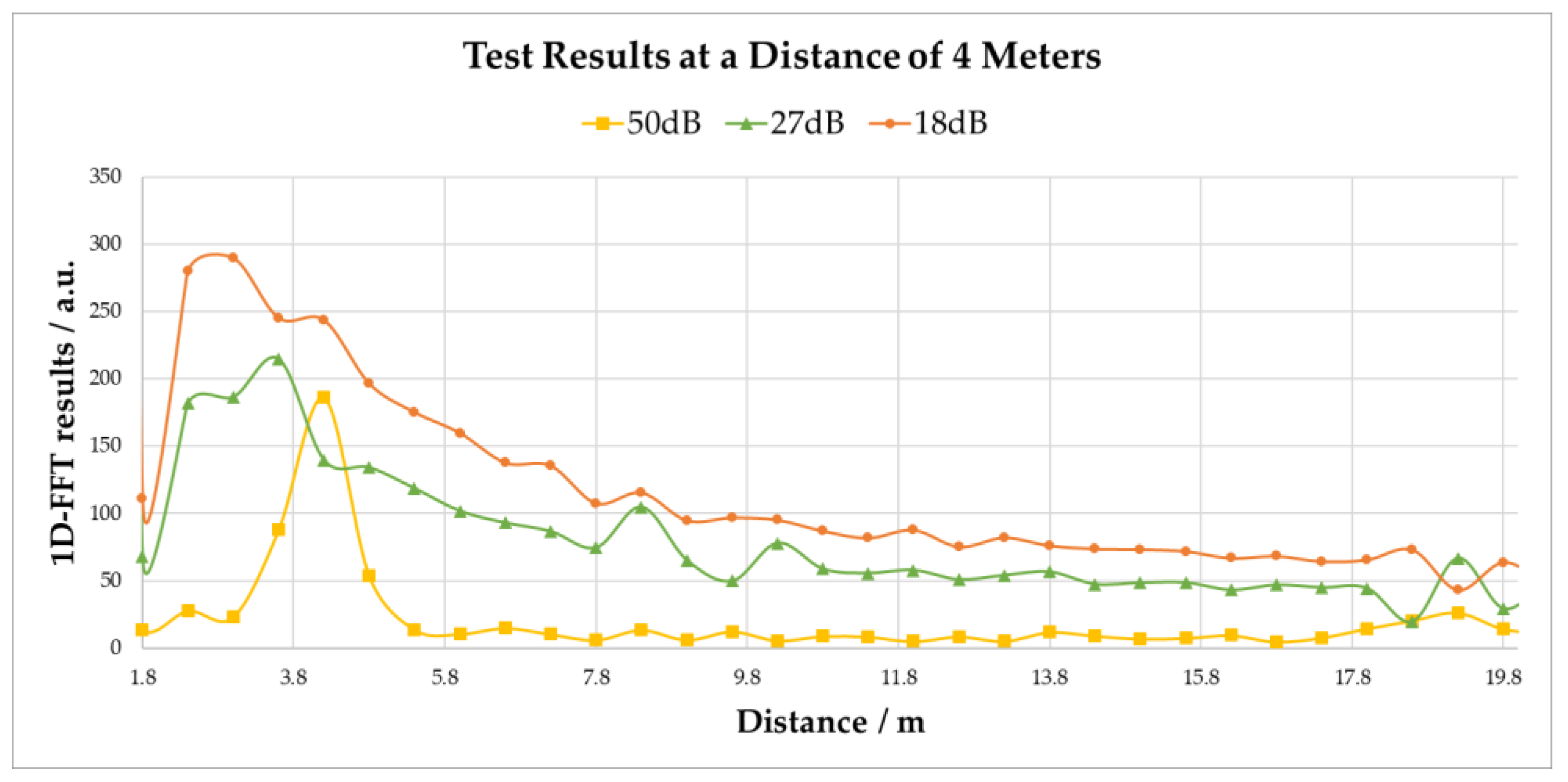


| Distance | SNR Corresponding to 50 dB Isolation | SNR Corresponding to 27 dB Isolation | SNR Corresponding to 18 dB Isolation |
|---|---|---|---|
| 2 m | 11.67 dB | 3.5 dB | 0.96 dB |
| 4 m | 10.09 dB | 2.16 dB | 0.77 dB |
| 8 m | 6.24 dB | 1.13 dB | 0.03 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Chi, L.; Qi, A.; Ma, J.; Qi, Y. Requirement Analysis and Teardrop-Based Design of High Antenna Isolation for FMCW Radar. Electronics 2022, 11, 1687. https://doi.org/10.3390/electronics11111687
Luo Y, Chi L, Qi A, Ma J, Qi Y. Requirement Analysis and Teardrop-Based Design of High Antenna Isolation for FMCW Radar. Electronics. 2022; 11(11):1687. https://doi.org/10.3390/electronics11111687
Chicago/Turabian StyleLuo, Yunlong, Lidong Chi, Alex Qi, Jianhua Ma, and Yihong Qi. 2022. "Requirement Analysis and Teardrop-Based Design of High Antenna Isolation for FMCW Radar" Electronics 11, no. 11: 1687. https://doi.org/10.3390/electronics11111687
APA StyleLuo, Y., Chi, L., Qi, A., Ma, J., & Qi, Y. (2022). Requirement Analysis and Teardrop-Based Design of High Antenna Isolation for FMCW Radar. Electronics, 11(11), 1687. https://doi.org/10.3390/electronics11111687








