A Hybrid Predictive Type-3 Fuzzy Control for Time-Delay Multi-Agent Systems
Abstract
:1. Introduction
1.1. Literature Review
1.2. Motivations and Objectives
- MASs with time-delay perturbations and uncertain dynamic models have rarely been studied.
- In most studies, distributed control policies have been designed for MASs with known dynamics and only some parametric uncertainties are considered.
- Most of the aforementioned works study linear MASs or the dynamics of the nodes are considered to be Lipschitz type.
- Among all the existing studies, type-3 FLS-based controllers have not been developed for heterogeneous MASs.
1.3. Main Contributions
- Based on a compact form of the agent dynamics, the consensus problem of MASs with time delays, heterogeneous structures, unknown dynamic models, and nonlinear terms is analyzed via a novel distributed learning-based control policy.
- An error dynamic system is established for the consensus problem and the stability/robustness analysis of the error dynamics is investigated via an appropriate Lyapunov–Krasovskii functional.
- The optimization problem in the framework of LMIs is suggested and the solution to the optimization problem leads to the gain of a distributed controller.
- Type-3 FLS of [23] is formulated to study the nonlinearities of heterogeneous MASs and design a novel hybrid controller. It should be noted that the type-3 FLS-based control of MASs with the aforementioned perturbations has not been studied. In addition, novel online tuning rules for T3-FLS are presented in this paper.
2. Preliminaries and Problem Definition
2.1. Graph Theory
2.2. Problem Definition
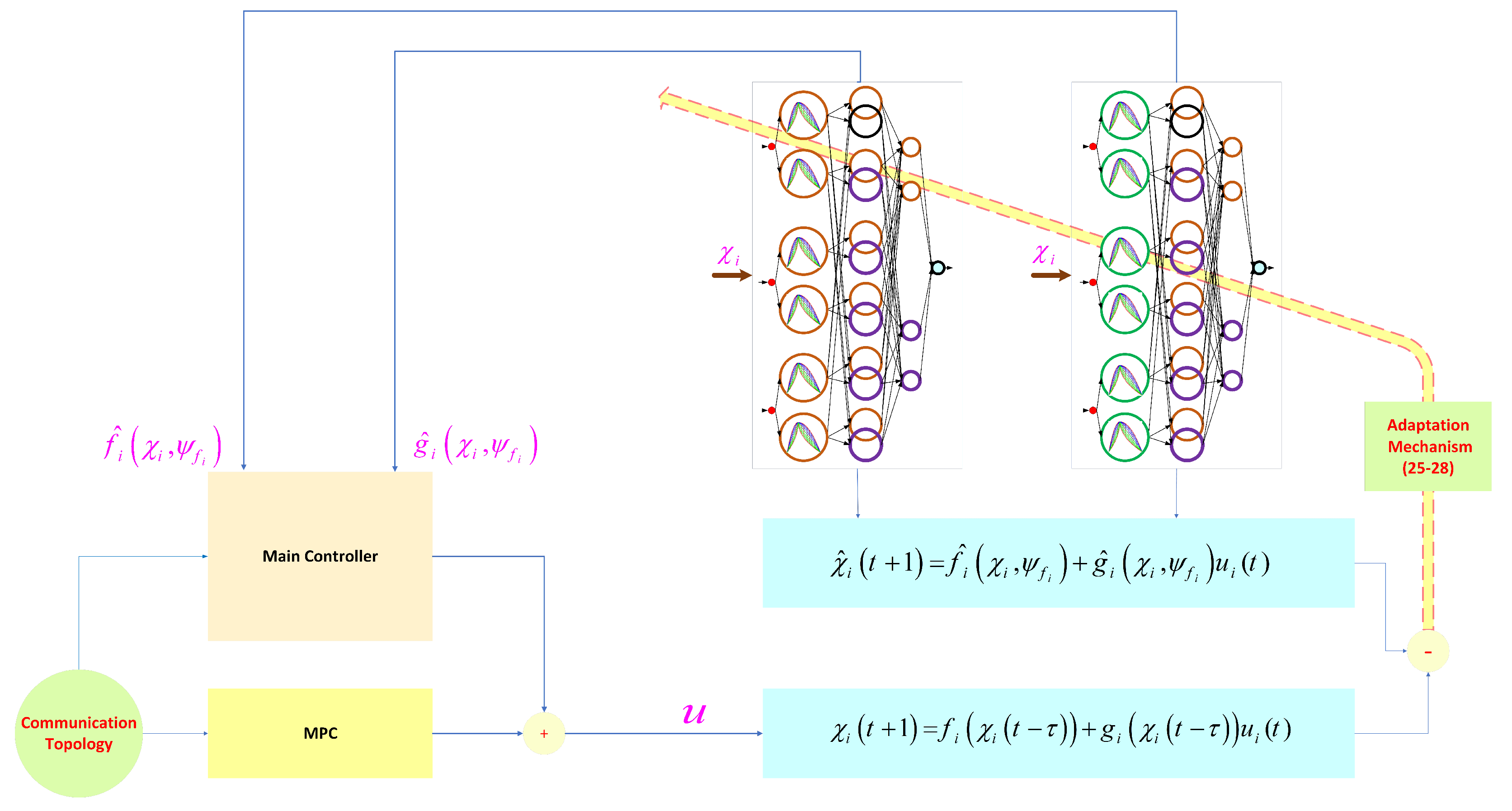
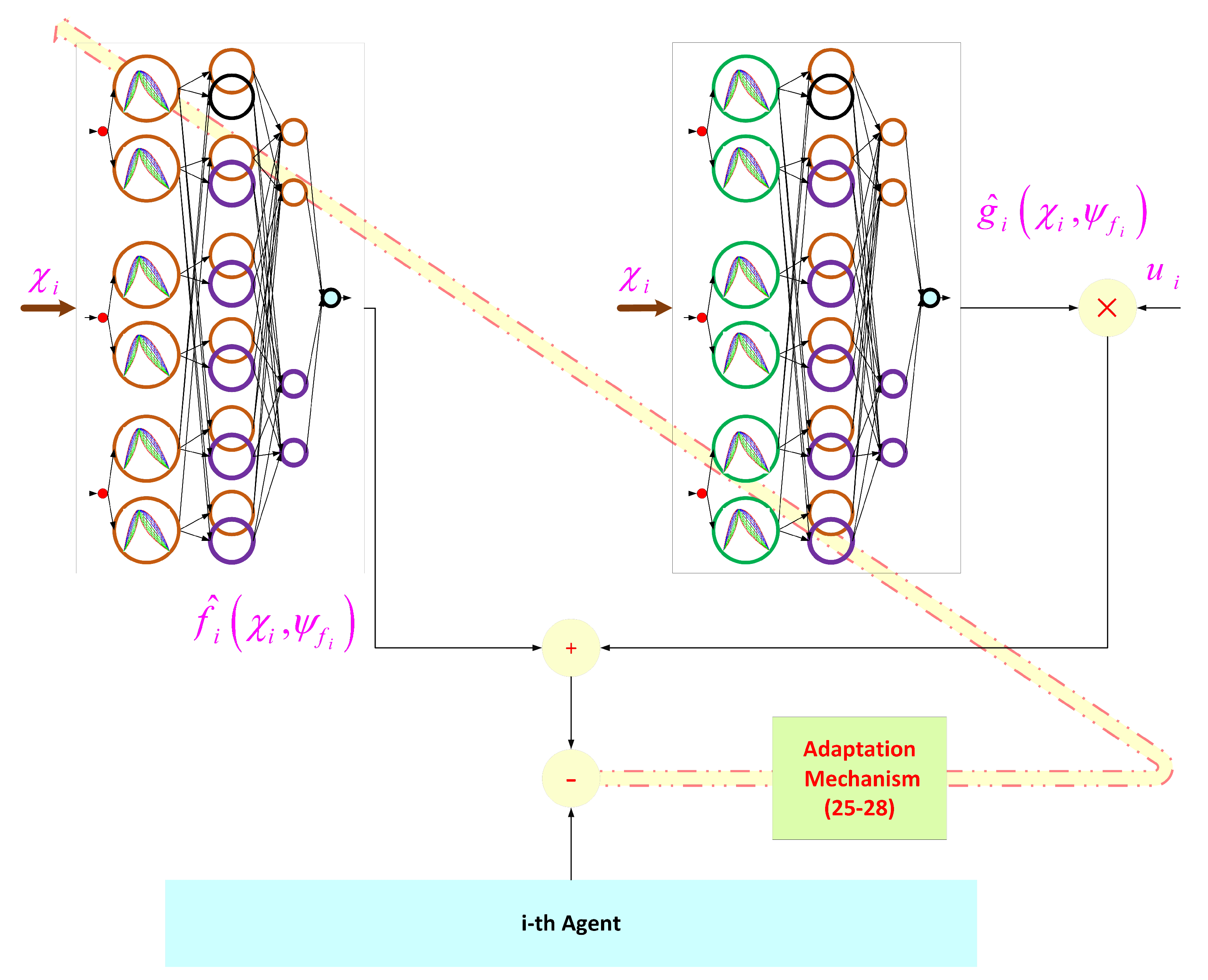
3. Type-3 FLS
Compact Form
4. MPC
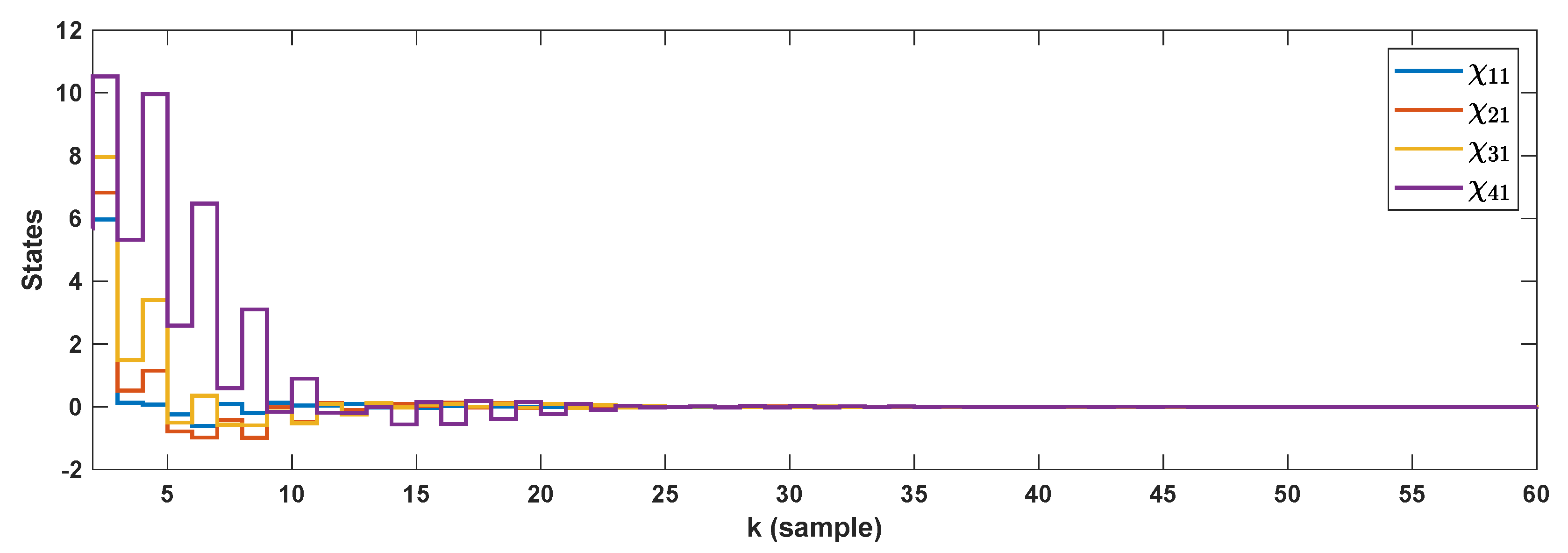
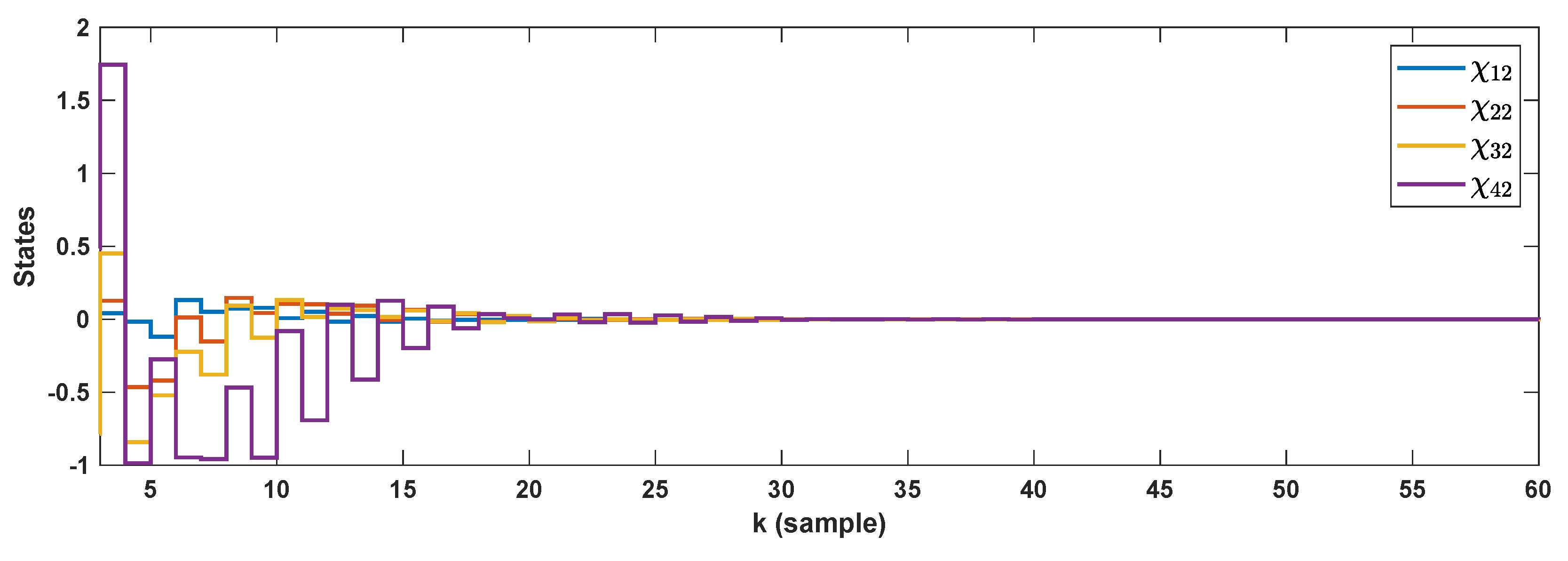
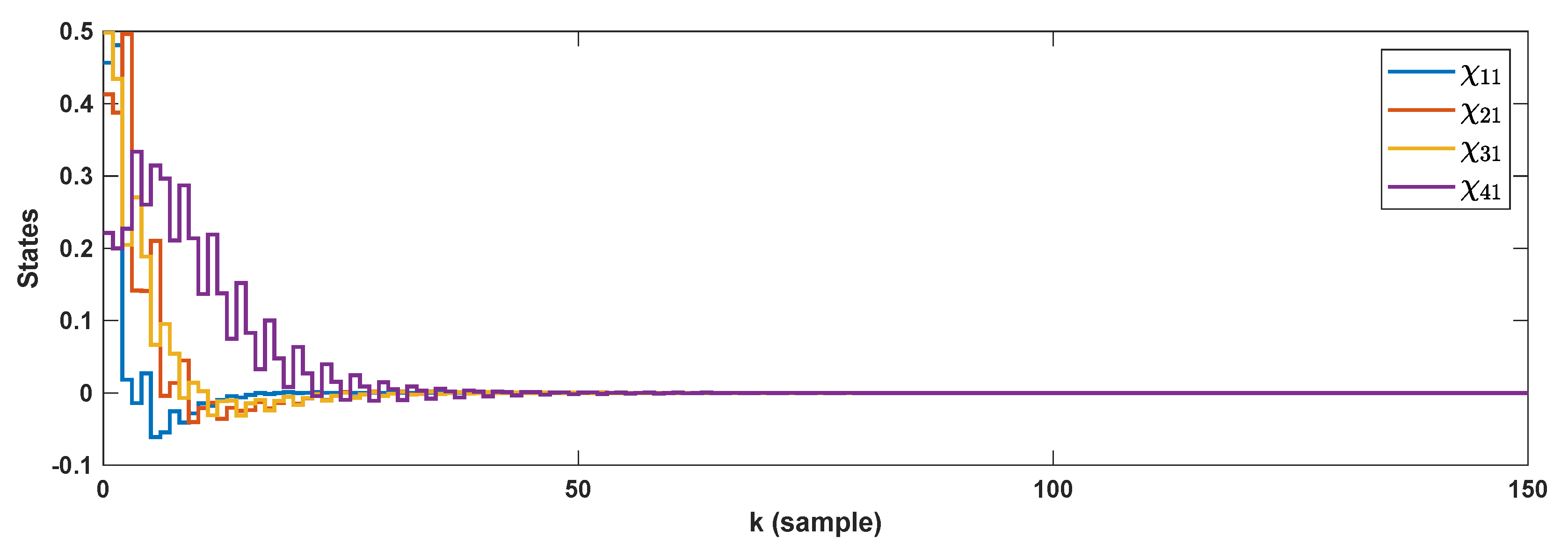
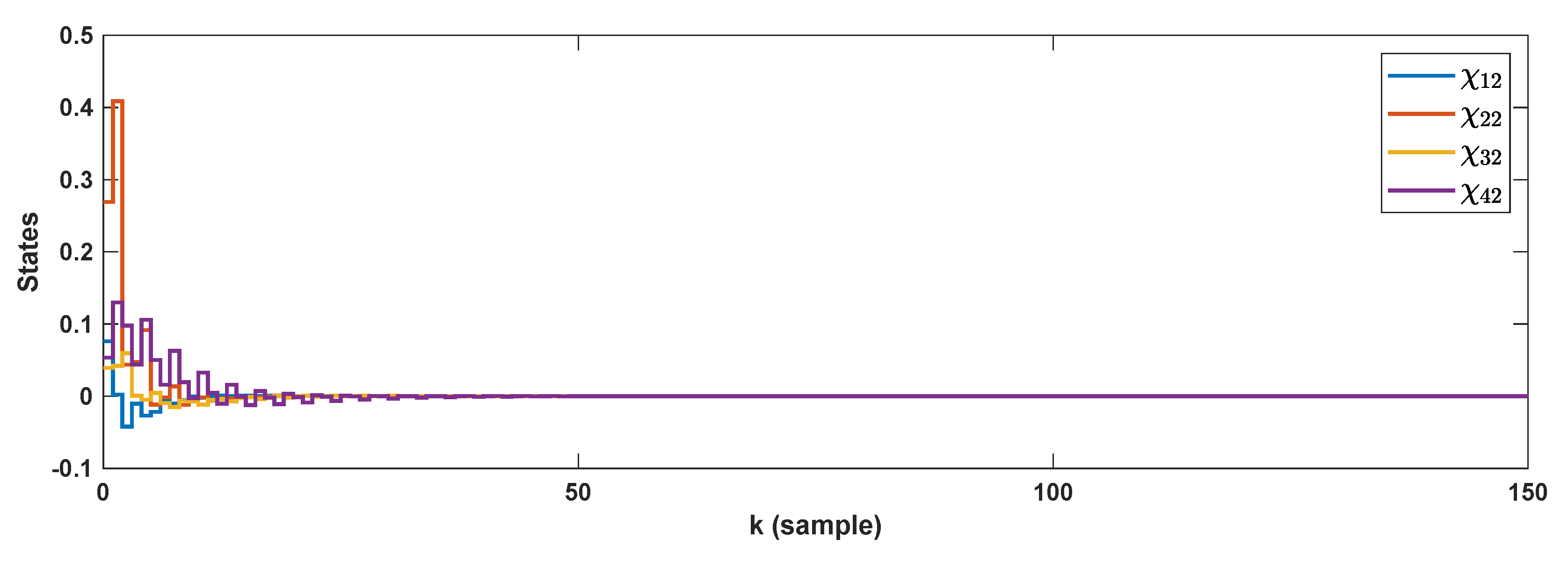
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Lin, Z.; Sun, Z. Distributed Event-Triggered Approach for Multi-Agent Formation Based on Cooperative Localization with Mixed Measurements. Electronics 2021, 10, 2265. [Google Scholar] [CrossRef]
- Shi, X.; Lin, Z.; Yang, T.; Wang, X. Distributed dynamic event-triggered algorithm with minimum inter-event time for multi-agent convex optimisation. Int. J. Syst. Sci. 2021, 52, 1440–1451. [Google Scholar] [CrossRef]
- Jin, X.; Lü, S.; Deng, C.; Chadli, M. Distributed adaptive security consensus control for a class of multi-agent systems under network decay and intermittent attacks. Inf. Sci. 2021, 547, 88–102. [Google Scholar] [CrossRef]
- Nan, X.; Lv, Y.; Duan, Z. On bipartite consensus of linear MASs with input saturation over directed signed graphs: Fully distributed adaptive approach. IET Control Theory Appl. 2021, 15. [Google Scholar] [CrossRef]
- Shi, X.; Lin, Z.; Zheng, R.; Wang, X. Distributed dynamic event-triggered algorithm with positive minimum inter-event time for convex optimisation problem. Int. J. Control 2020. [Google Scholar] [CrossRef]
- Seyboth, G.S.; Dimarogonas, D.V.; Johansson, K.H.; Frasca, P.; Allgöwer, F. On robust synchronization of heterogeneous linear multi-agent systems with static couplings. Automatica 2015, 53, 392–399. [Google Scholar] [CrossRef]
- Jiao, J.; Trentelman, H.L.; Camlibel, M.K. A suboptimality approach to distributed H2 control by dynamic output feedback. Automatica 2020, 121, 109164. [Google Scholar] [CrossRef]
- Zuo, S.; Lewis, F.L.; Davoudi, A. Resilient Output Containment of Heterogeneous Cooperative and Adversarial Multigroup Systems. IEEE Trans. Autom. Control 2020, 65, 3104–3111. [Google Scholar] [CrossRef]
- Rahimi, N.; Binazadeh, T. Robust model predictive control of heterogeneous time-delay multi-agent systems with polytopic uncertainties and input amplitude constraints. J. Vib. Control 2021, 27, 1098–1112. [Google Scholar] [CrossRef]
- Nojavanzadeh, D.; Liu, Z.; Saberi, A.; Stoorvogel, A.A. H∞ and H2 almost output and regulated output synchronization of heterogeneous multi-agent systems: A scale-free protocol design. J. Frankl. Inst. 2021. [Google Scholar] [CrossRef]
- Liu, Z.; Nojavanzadeh, D.; Saberi, D.; Saberi, A.; Stoorvogel, A.A. Scale-free protocol design for regulated state synchronization of homogeneous multi-agent systems with unknown and non-uniform input delays. Syst. Control Lett. 2021, 152, 104927. [Google Scholar] [CrossRef]
- Li, K.; Li, Y. Fuzzy adaptive optimal consensus fault-tolerant control for stochastic nonlinear multi-agent systems. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Huang, H.C.; Xu, J.J. Evolutionary Machine Learning for Optimal Polar-Space Fuzzy Control of Cyber-Physical Mecanum Vehicles. Electronics 2020, 9, 1945. [Google Scholar] [CrossRef]
- Huang, H.C.; Tao, C.W.; Chuang, C.C.; Xu, J.J. FPGA-based mechatronic design and real-time fuzzy control with computational intelligence optimization for Omni-Mecanum-wheeled autonomous vehicles. Electronics 2019, 8, 1328. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.C.; Chuang, C.C. Artificial Bee Colony Optimization Algorithm Incorporated With Fuzzy Theory for Real-Time Machine Learning Control of Articulated Robotic Manipulators. IEEE Access 2020, 8, 192481–192492. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y. Discrete Non-iterative Centroid Type-Reduction Algorithms on General Type-2 Fuzzy Logic Systems. Int. J. Fuzzy Syst. 2021, 23, 704–715. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, J. Containment control of interval type-2 fuzzy multi-agent systems with multiple intermittent packet dropouts and actuator failure. J. Frankl. Inst. 2020, 357, 6096–6120. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Zhang, W. Dynamic programming strategy based on a type-2 fuzzy wavelet neural network. Nonlinear Dyn. 2019, 95, 1661–1672. [Google Scholar] [CrossRef]
- Valdez, F.; Castillo, O.; Cortes-Antonio, P.; Melin, P. A survey of Type-2 fuzzy logic controller design using nature inspired optimization. J. Intell. Fuzzy Syst. 2020, 39, 6169–6179. [Google Scholar] [CrossRef]
- Chen, C.H.; Jeng, S.Y.; Lin, C.J. Mobile robot wall-following control using fuzzy logic controller with improved differential search and reinforcement learning. Mathematics 2020, 8, 1254. [Google Scholar] [CrossRef]
- Lee, C.L.; Lin, C.J. Integrated computer vision and type-2 fuzzy CMAC model for classifying pilling of knitted fabric. Electronics 2018, 7, 367. [Google Scholar] [CrossRef] [Green Version]
- Qasem, S.N.; Ahmadian, A.; Mohammadzadeh, A.; Rathinasamy, S.; Pahlevanzadeh, B. A type-3 logic fuzzy system: Optimized by a correntropy based Kalman filter with adaptive fuzzy kernel size. Inf. Sci. 2021, 572, 424–443. [Google Scholar] [CrossRef]
- Chen, C.; Lewis, F.L.; Xie, K.; Xie, S.; Liu, Y. Off-policy learning for adaptive optimal output synchronization of heterogeneous multi-agent systems. Automatica 2020, 119, 109081. [Google Scholar] [CrossRef]
- Jiang, Y.; Fan, J.; Gao, W.; Chai, T.; Lewis, F.L. Cooperative adaptive optimal output regulation of nonlinear discrete-time multi-agent systems. Automatica 2020, 121, 109149. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Kaynak, O. A novel general type-2 fuzzy controller for fractional-order multi-agent systems under unknown time-varying topology. J. Frankl. Inst. 2019, 356, 5151–5171. [Google Scholar] [CrossRef]
- Li, S.; Er, M.J.; Zhang, J. Distributed Adaptive Fuzzy Control for Output Consensus of Heterogeneous Stochastic Nonlinear Multiagent Systems. IEEE Trans. Fuzzy Syst. 2018, 26, 1138–1152. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Ren, C.E.; Du, T. Fuzzy Observed-Based Adaptive Consensus Tracking Control for Second-Order Multiagent Systems With Heterogeneous Nonlinear Dynamics. IEEE Trans. Fuzzy Syst. 2016, 24, 906–915. [Google Scholar] [CrossRef]
- Zou, W.; Ahn, C.K.; Xiang, Z. Fuzzy-Approximation-Based Distributed Fault-Tolerant Consensus for Heterogeneous Switched Nonlinear Multiagent Systems. IEEE Trans. Fuzzy Syst. 2021, 29, 2916–2925. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, C.Z. Adaptive Fuzzy Leader-Follower Synchronization of Constrained Heterogeneous Multiagent Systems. IEEE Trans. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Shi, P.; Yu, J. Dissipativity-Based Consensus for Fuzzy Multiagent Systems Under Switching Directed Topologies. IEEE Trans. Fuzzy Syst. 2021, 29, 1143–1151. [Google Scholar] [CrossRef]
- Jiao, J.; Trentelman, H.L.; Camlibel, M.K. H2 suboptimal output synchronization of heterogeneous multi-agent systems. Syst. Control Lett. 2021, 149, 104872. [Google Scholar] [CrossRef]




| − 1, 0, 1 | |
| 0.5 | |
| 0.5 | |
| 0.7, 0.8, 0.9 | |
| 0.2, 0.3, 0.4 | |
| 9 |
| Delay Samples | |||
|---|---|---|---|
| State | 1 | 5 | 10 |
| 1.2651 | 1.2670 | 1.3021 | |
| 1.0137 | 1.0172 | 1.0201 | |
| 1.3560 | 1.3641 | 1.3692 | |
| 1.0200 | 1.0205 | 1.0212 | |
| 1.5083 | 1.5302 | 1.6301 | |
| 1.0290 | 1.0322 | 1.0392 | |
| 2.4010 | 2.4105 | 2.4532 | |
| 1.0738 | 1.0802 | 1.0890 | |
| FLSs | |||
|---|---|---|---|
| State | T3-FLS | T2-FLS | T1-FLS |
| 1.2651 | 1.8710 | 2.0678 | |
| 1.0137 | 1.9850 | 2.2001 | |
| 1.3560 | 1.5101 | 1.7041 | |
| 1.0200 | 1.8501 | 2.0254 | |
| 1.5083 | 1.5241 | 1.6950 | |
| 1.0290 | 1.7014 | 2.0025 | |
| 2.4010 | 2.5155 | 2.6036 | |
| 1.0738 | 1.7408 | 1.9052 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taghieh, A.; Aly, A.A.; Felemban, B.F.; Althobaiti, A.; Mohammadzadeh, A.; Bartoszewicz, A. A Hybrid Predictive Type-3 Fuzzy Control for Time-Delay Multi-Agent Systems. Electronics 2022, 11, 63. https://doi.org/10.3390/electronics11010063
Taghieh A, Aly AA, Felemban BF, Althobaiti A, Mohammadzadeh A, Bartoszewicz A. A Hybrid Predictive Type-3 Fuzzy Control for Time-Delay Multi-Agent Systems. Electronics. 2022; 11(1):63. https://doi.org/10.3390/electronics11010063
Chicago/Turabian StyleTaghieh, Amin, Ayman A. Aly, Bassem F. Felemban, Ahmed Althobaiti, Ardashir Mohammadzadeh, and Andrzej Bartoszewicz. 2022. "A Hybrid Predictive Type-3 Fuzzy Control for Time-Delay Multi-Agent Systems" Electronics 11, no. 1: 63. https://doi.org/10.3390/electronics11010063
APA StyleTaghieh, A., Aly, A. A., Felemban, B. F., Althobaiti, A., Mohammadzadeh, A., & Bartoszewicz, A. (2022). A Hybrid Predictive Type-3 Fuzzy Control for Time-Delay Multi-Agent Systems. Electronics, 11(1), 63. https://doi.org/10.3390/electronics11010063









