POSIT vs. Floating Point in Implementing IIR Notch Filter by Enhancing Radix-4 Modified Booth Multiplier
Abstract
:1. Introduction
- (1)
- Enhancing the POSIT multiplication operation by implementing a special type of multiplier called ERMBM, which significantly enhances the area, speed, and energy compared with the regular multiplier proposed previously in [5].
- (2)
- Implementing the POSIT cosine function along with the division arithmetic unit utilizing a shared hardware that is based on the Taylor series technique to reduce the design area.
- (3)
- (4)
- Comparing the performances of POSIT when utilizing a regular multiplier with floating point which results in better accuracy and area enhancement.
2. Background
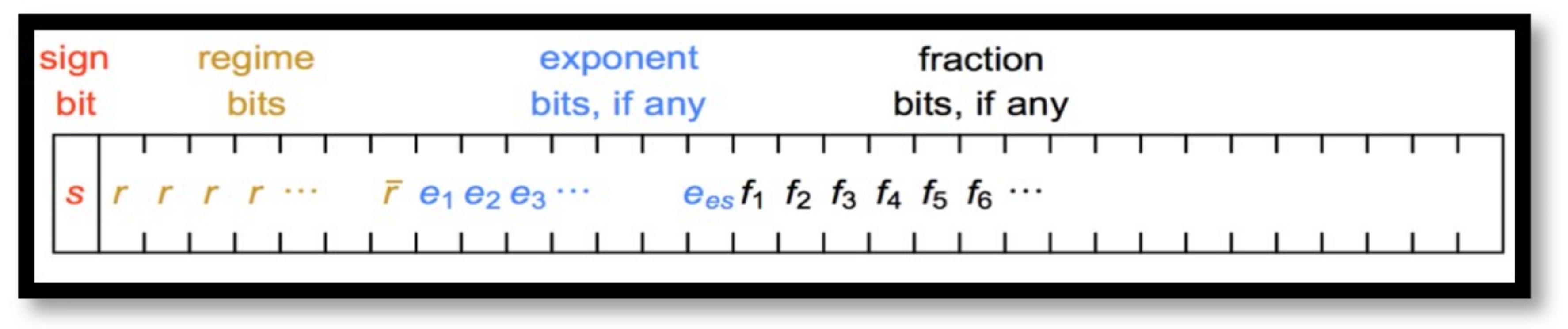
2.1. POSIT
2.2. IIR Filter
3. Related Work
3.1. IIR Filter
3.2. POSIT Numbering System
4. Components Design
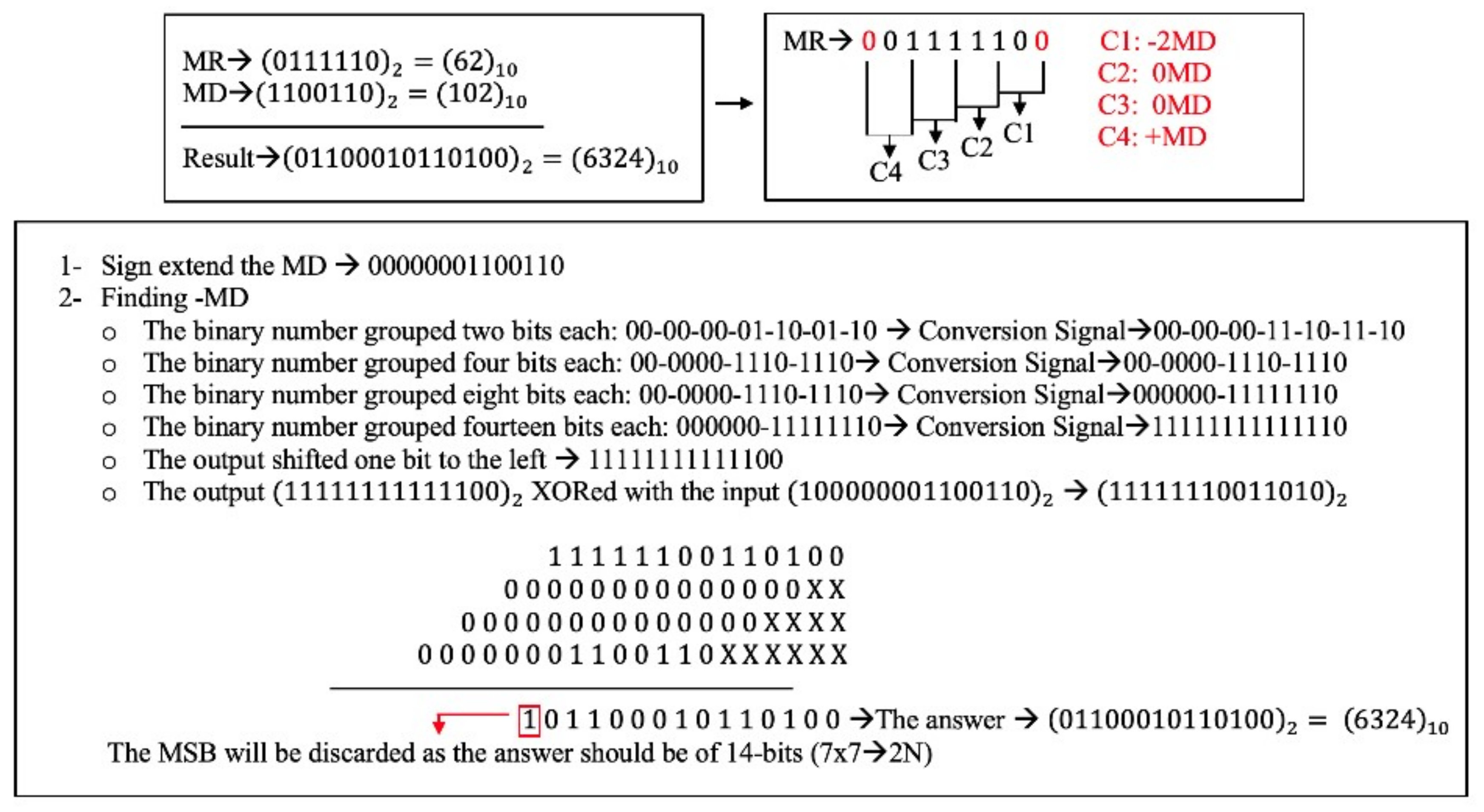
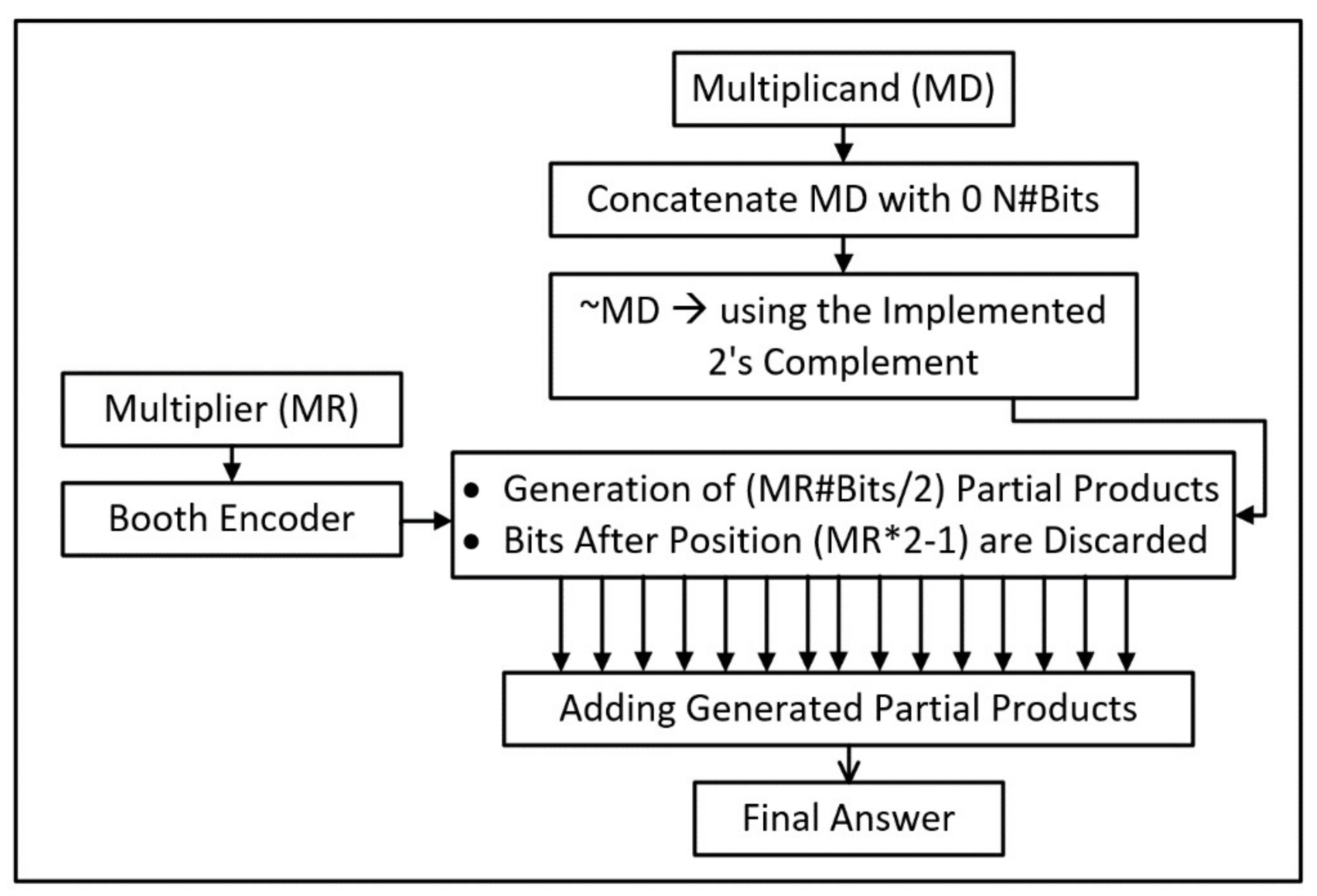
4.1. Enhanced Radix-4 Modified Booth Multiplier
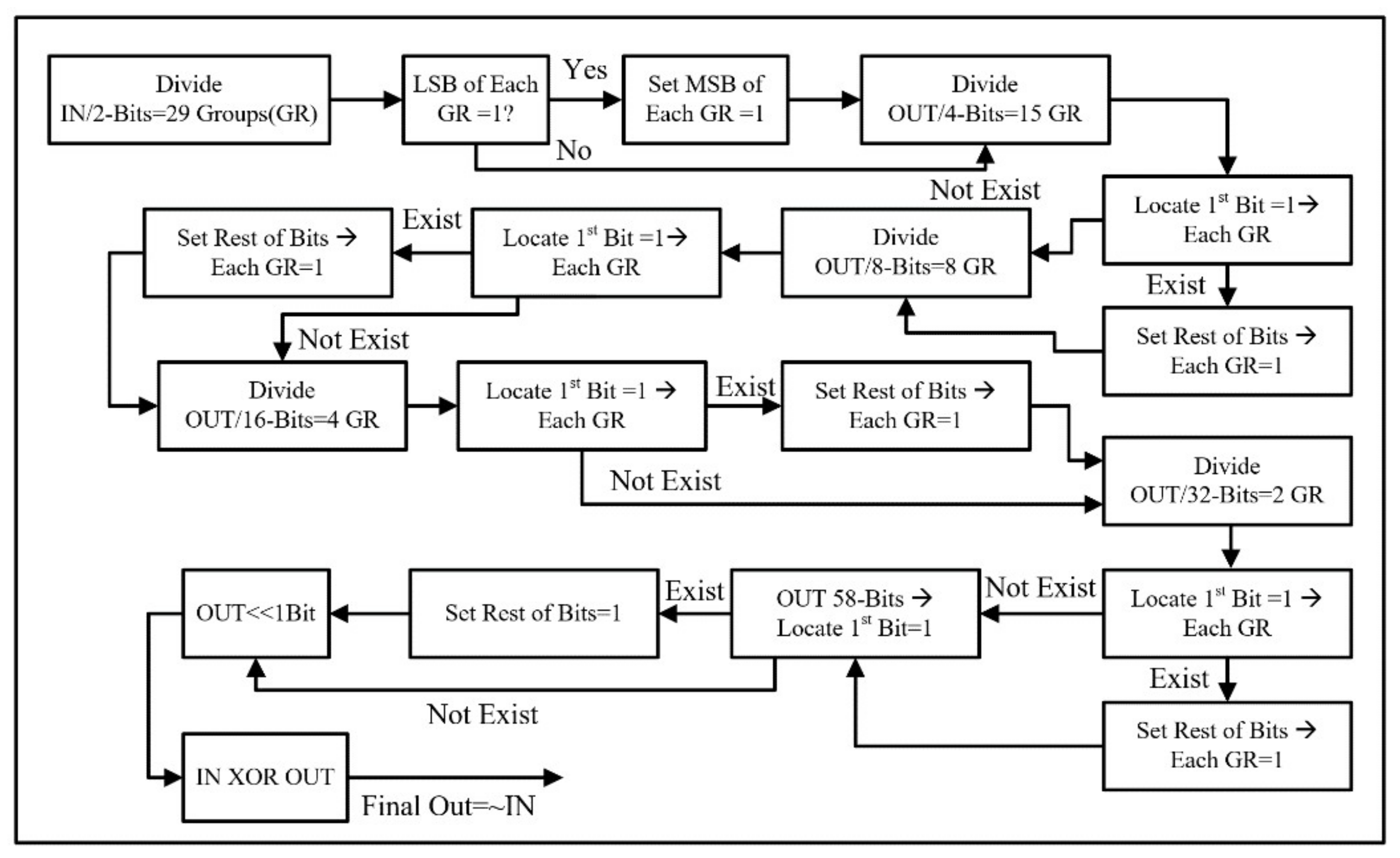
4.1.1. Computing 2′s Complement
4.1.2. Encoding the Multiplier
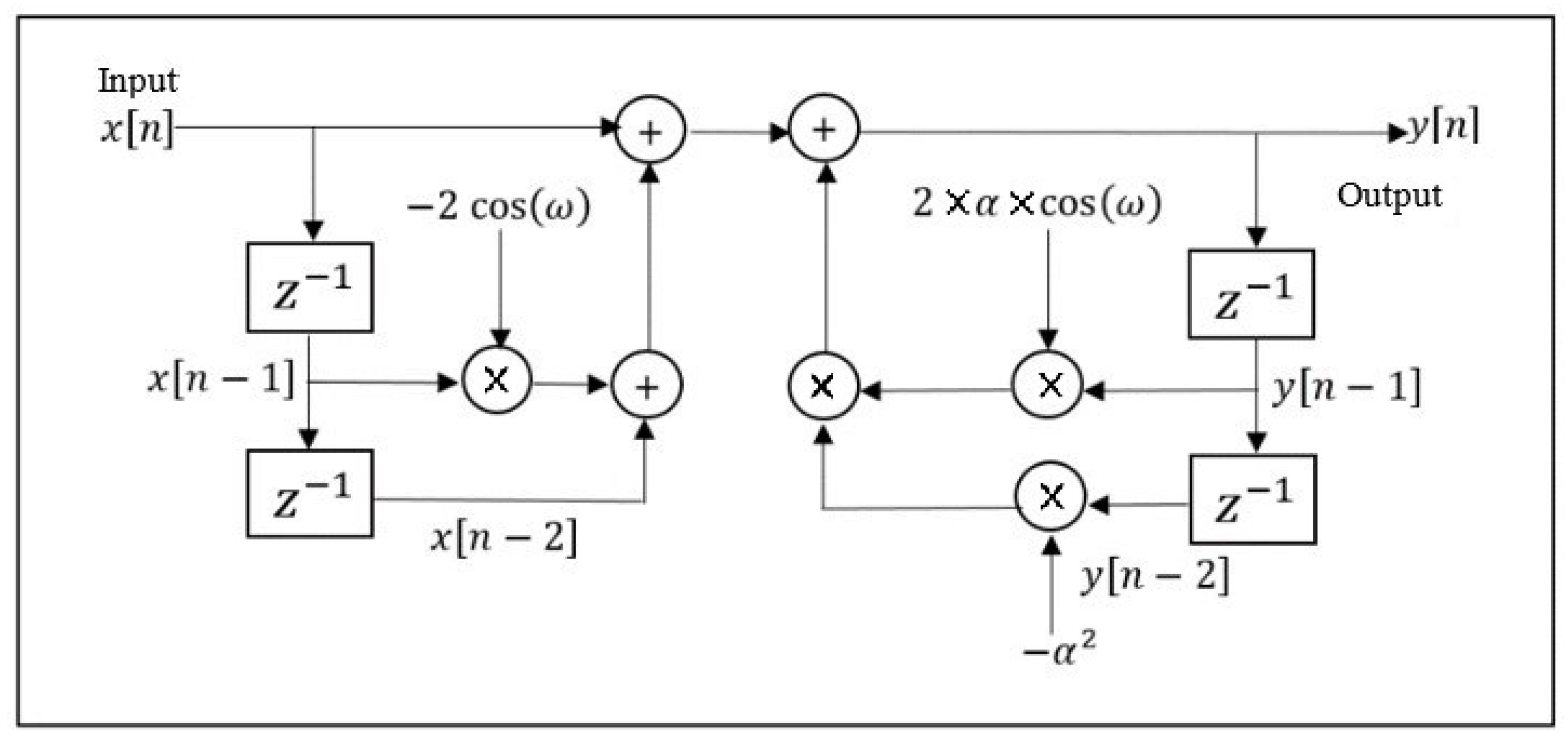
4.2. IIR Notch Filter
- (1)
- POSIT addition/subtraction,
- (2)
- POSIT multiplication,
- (3)
- POSIT division,
- (4)
- Cosine function for POSIT.
4.2.1. POSIT Divider
4.2.2. POSIT Cosine Function
5. Results and Discussion
- (a)
- A comparison within POSIT (regular multiplier vs. radix-4 modified booth multiplier)
- (b)
- A detailed comparison between POSIT and floating point
5.1. Second-Order IIR Notch Filter
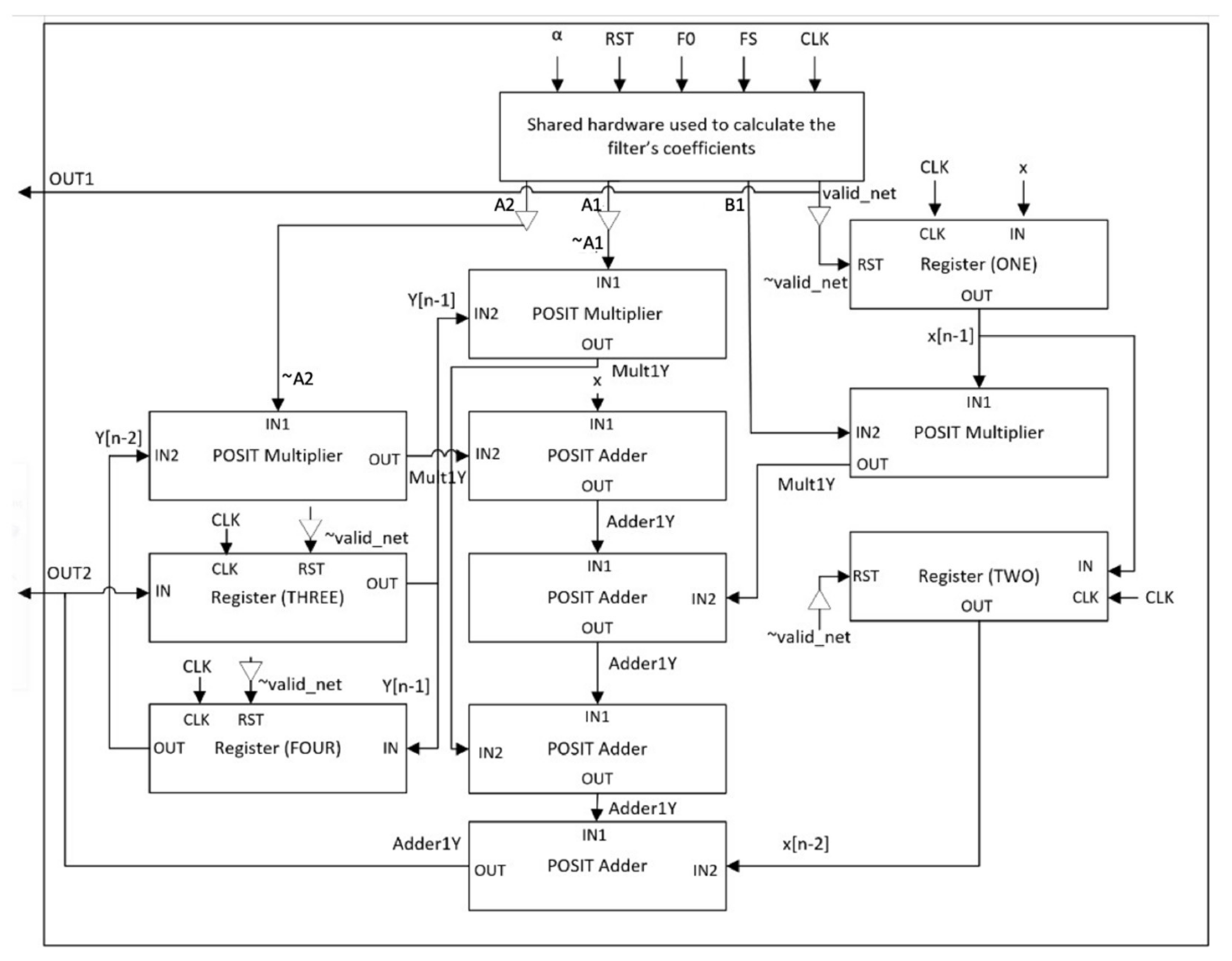
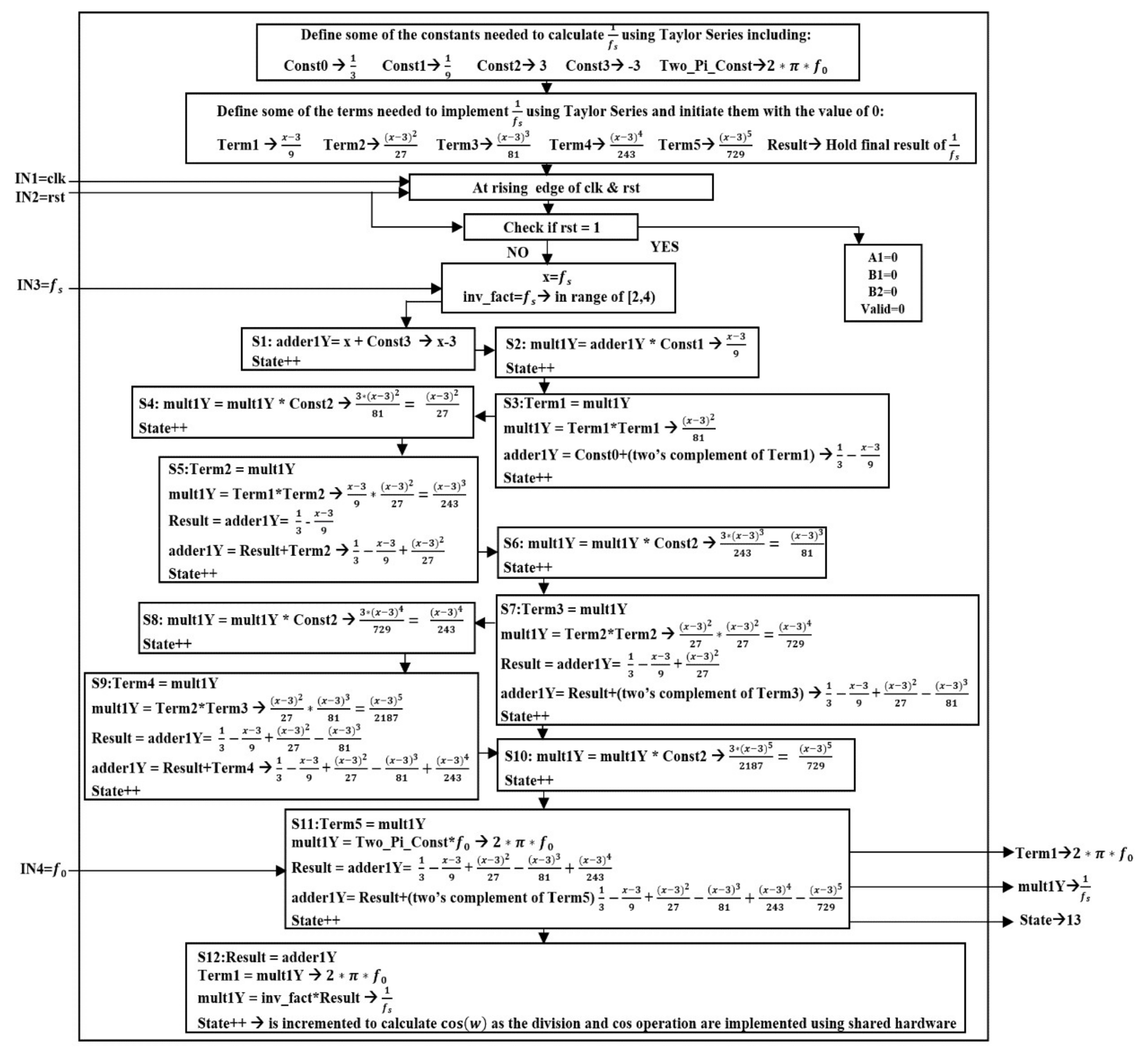
5.1.1. Calculating the Filter’s Coefficients
5.1.2. Generating the Output of the IIR Filter
5.2. Comparison
5.2.1. Radix-4 Modified Booth Multiplier vs. the Regular POSIT Multiplier
Accuracy
Area and Speed
Power and Energy
5.2.2. A Comparison between POSIT and Floating Point
Accuracy
Area and Speed
Power and Energy
5.3. Discussion
- (1)
- Using the Enhanced Radix-4 Modified Booth Multiplier (ERMBM) instead of a regular multiplier enhances the area, speed, power, and energy without affecting the accuracy of the output.
- (2)
- If the accuracy, area, and power are the main concern, then it is recommended to utilize the POSIT numbering system with a regular multiplier instead of floating point.
- (3)
- If the aim is to enhance all five performance metrics, then it is recommended to use POSIT units along with ERMBM instead of floating point, as POSIT optimizes area, speed, power, and energy by 35.68%, 20.66%, 31.49%, and 45.64%, respectively.
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hauser, J.R. Handling floating-point exceptions in numeric programs. ACM Trans. Program. Lang. Syst. 1996, 18, 139–174. [Google Scholar] [CrossRef]
- Lindstrom, P.; Lloyd, S.; Hittinger, J. Universal Coding of the Reals: Alternatives to IEEE Floating Point. In Proceedings of the Conference for Next Generation Arithmetic, Singapore, 28 March 2018; ACM Press: New York, NY, USA, 2018; p. 5. [Google Scholar]
- Gustafson, J.L. A Radical Approach to Computation with Real Numbers. Supercomput. Front. Innov. 2016, 3, 1–16. [Google Scholar] [CrossRef]
- Cook, J. Anatomy of a POSIT Number. 2018. Available online: https://www.johndcook.com/blog/2018/04/11/anatomy-of-a-POSIT-number/ (accessed on 3 April 2019).
- Jaiswal, M.; So, H. PA Cogen: A Hardware POSIT Arithmetic Core Generator. IEEE Access 2019, 7, 74586–74601. [Google Scholar] [CrossRef]
- Doable, R.; Chaturvedi, S. Implementation of 32 Bit Binary Floating Point Adder Using IEEE 754 Single Precision Format. VOSR J. VLSI Signal Processing (IOSR-JVSR-JVSP) 2015, 5, 2319–4197. [Google Scholar]
- Tejaswini, H.N.; Ravishankar, C.V. Single Precision Floating Point Numbers Multiplication using Standard IEEE 754. Int. J. Adv. Res. Electron. Commun. Eng. (IJARECE) 2015, 4, 1–5. [Google Scholar]
- Gustafson, J.; Yosemite, I. Beating Floating Point at its Own Game: POSIT Arithmetic. Supercomput. Front. Innov. Int. J. 2017, 4, 2409–6008. [Google Scholar]
- Montero, R.M. Study of the POSIT Number System: A Practical Approach. Bachelor’s Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2019; pp. 1–78. [Google Scholar]
- Carmichael, Z.; Langroudi, H.F.; Khazanov, C.; Lillie, J.; Gustafson, J.L.; Kudithipudi, D. Deep Positron: A Deep Neural Network Using the Posit Number System. arXiv, 2018; arXiv:1812.01762. [Google Scholar]
- Dam, L. Enabling High Performance POSIT Arithmetic Applications Using Hardware Acceleration. Master’s Thesis, TU Delft Electrical Engineering, Mathematics and Computer Science, Delft, The Netherlands, 2018; pp. 1–112. [Google Scholar]
- Ushanandhini, S.S. Designing of IIR Filter using Radix-4 Multiplier by Recharging Technique. Int. J. Trend Sci. Res. Dev. (IJTSRD) 2018, 2, 1100–1107. [Google Scholar]
- Wang, Y.; Li, B.; Li, Z. Fixed-point digital IIR filter design using multi-objective optimization evolutionary algorithm. In Proceedings of the 2010 IEEE Youth Conference on Information, Computing and Telecommunications, Beijing, China, 28–30 November 2010; pp. 174–177. [Google Scholar] [CrossRef]
- Chengliang, Z.; Lihong, W. IIR Digital Filter Research and Simulation on MATLAB. In Proceedings of the 4th International Conference on Signal Processing Systems (ICSPS), Kuala Lumpur, Malaysia, 21–22 December 2012; Volume 58, pp. 138–142. [Google Scholar]
- Bajwa, D.; Singh, K.; Chahal, N. Fixed Point digital IIR filter Design using two-stage ensemble evolutionary algorithm. Int. J. Adv. Res. Comput. Sci. Softw. Eng. (IJARCSSE) 2014, 4, 329–338. [Google Scholar]
- Stavrou, V.; Tsoulos, I.; Mastorakis, N. Transformations for FIR and IIR Filters’ Design. Symmetry 2021, 13, 533. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Stavrou, V.; Mastorakis, N.E.; Tsalikakis, D. GenConstraint: A programming tool for constraint optimization problems. SoftwareX 2019, 10, 100355. [Google Scholar] [CrossRef]
- Langroudi, S.H.F.; Pandit, T.; Kudithipudi, D. Deep Learning Inference on Embedded Devices: Fixed-Point vs Posit. In Proceedings of the 2018 1st Workshop on Energy Efficient Machine Learning and Cognitive Computing for Embedded Applications (EMC2), Williamsburg, VA, USA, 25 March 2018; Volume EMC2, pp. 19–23. [Google Scholar]
- Podobas, A.; Matsuoka, S. Hardware Implementation of POSITs and Their Application in FPGAs. In Proceedings of the 2018 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Vancouver, BC, Canada, 21–25 May 2018; pp. 138–145. [Google Scholar]
- Jaiswal, M.K.; So, H.K.-H. Architecture Generator for Type-3 Unum Posit Adder/Subtractor. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Jaiswal, M.K.; So, H.K.-H. Universal number posit arithmetic generator on FPGA. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 1159–1162. [Google Scholar]
- Lehóczky, Z.; Retzler, A.; Tóth, R.; Szabó, Á.; Farkas, B.; Somogyi, K. High-level. NET software implementations of unum type I and posit with simultaneous FPGA implementation using Hastlayer. In Proceedings of the Conference for Next Generation Arithmetic, Singapore, 28 March 2018; ACM Press: New York, NY, USA, 2018; p. 4. [Google Scholar]
- Hou, J.; Zhu, Y.; Shen, Y.; Li, M.; Wu, H.; Song, H. Tackling Gaps in Floating Point Arithmetic: Unum Arithmetic Implementaion on FPGA. In Proceedings of the IEEE 3rd International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Bangkok, Thailand, 18–20 December 2017; pp. 615–616. [Google Scholar]
- Glaser, F.; Mach, S.; Rahimi, A.; Gurkaynak, F.K.; Huang, Q.; Benini, L. An 826 MOPS, 210uW/MHz Unum ALU in 65 nm. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Chen, J.; Al-Ars, Z.; Hofstee, H.P. A matrix-multiply unit for posits in reconfigurable logic leveraging (open) CAPI. In Proceedings of the Conference for Next Generation Arithmetic, Singapore, 28 March 2018; ACM Press: New York, NY, USA, 2018; p. 1. [Google Scholar]
- Fadavi-Ardekani, J. M*N Booth encoded multiplier generator using optimized Wallace trees. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 1993, 1, 120–125. [Google Scholar] [CrossRef]
- Krushna, M.; Kumar, K. Modified Booth Encoding Multiplier for both Signed and Unsigned Radix Based Multi-Modulus Multiplier. Int. J. Mag. Eng. Technol. Manag. Res. (IJMETMR) 2015, 2, 1–6. [Google Scholar]
- Kang, J.-Y.; Gaudiot, J.-L. A fast and well-structured multiplier. Euromicro Symposium on Digital System Design, DSD, Rennes, France, 31 August–3 September 2004; pp. 508–515. [Google Scholar] [CrossRef]
- Tripathi, R.; Prakash, S. Comparative Design of Regular Structured Modified Booth Multiplier. Int. J. VLSI Des. Commun. Syst. (VLSICS) 2016, 7, 21–30. [Google Scholar] [CrossRef]
- Kshirsagar, R.; Aishwarya, E.; Vishwanath, A.; Jayakrishnan, P. Implementation of pipelined Booth Encoded Wallace tree Multiplier architecture. In Proceedings of the 2013 International Conference on Green Computing, Communication and Conservation of Energy (ICGCE), Chennai, India, 12–14 December 2013; pp. 199–204. [Google Scholar]
- Ramteke, S.; Khandagre, Y.; Dubey, A. Implementation of Low Power Booth’s Multiplier by Utilizing Ripple Carry Adder. Int. J. Sci. Eng. Res. (IJSER) 2014, 5, 2229–5518. [Google Scholar]
- Kaur, S.; Manna, M. Implementation of Modified Booth Algorithm (Radix-4) and its Comparison with Booth Algorithm (Radix-2). Res. India Publ. Adv. Electron. Electr. Eng. 2013, 3, 683–690. [Google Scholar]
- Wang, C.M.; Xiao, W.C. Second-order IIR Notch Filter Design and implementation of digital signal processing system. In Proceedings of the 2nd International Symposium on Computer, Communication, Control and Automation, Singapore, 1–2 December 2013; Atlantis Press: Paris, France, 2013; pp. 0576–0578. [Google Scholar]
- Lavanya, K.; Savidhan, S.; Akshatha, D. Computing Non-Restoring and Newton Raphson’s Method for Division. IOSR J. Electron. Commun. Eng. (IOSR-JECE) 2017, 12, 57–60. [Google Scholar]
- Oberman, S.; Flynn, M. An Analysis of Division Algorithms and Implementations; Departments of Electrical Engineering and Computer Science, Stanford University: Stanford, CA, USA, 1995; Volume 46, pp. 833–854. [Google Scholar]
- Malepati, H. Digital Media Processing DSP Algorithms Using C; Elsevier: Newnes, Australia, 2010; pp. 1–768. [Google Scholar]




| Finite Impulse Response Filter (FIR Filter) | Infinite Impulse Response Filter (IIR Filter) |
|---|---|
| Depend on current input only, no feedback is required (only zeros) | Depend on previous output, feedback is required (poles and zeros) |
| Uses more number of terms to achieve same result-more computations–slower | Uses less number of terms to achieve same result-less computations–faster. |
| Require more memory | Require less memory space |
| Can be easily designed with a linear phase | Non-linear phase |
| Always stable | Has stability issues–Not always stable |
| Has constant delay at all frequencies | Has unequal delays at each frequency |
| No analog history | Derived from analog filters |
| Used with high order tapping (20–2000) | Used with fewer order tapping type < 1/10th order of FIR filter (4–20) |
| Yi | Yi−1 | Yi−2 | Required Operation on the Multiplicand | Acquired Output |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 × MD | Zero |
| 0 | 0 | 1 | +1 × MD | Value of the multiplicand |
| 0 | 1 | 0 | +1 × MD | Value of the multiplicand |
| 0 | 1 | 1 | +2 × MD | Shifting the MD 1 bit to the left |
| 1 | 0 | 0 | −2 × MD | Finding 2′s complement of the MD and then shifting 1 bit to the left |
| 1 | 0 | 1 | −1 × MD | Finding 2′s complement of MD |
| 1 | 1 | 0 | −1 × MD | Finding 2′s complement of MD |
| 1 | 1 | 1 | 0 × MD | Zero |
| Term | Multiplication | Addition | Cycle Number |
|---|---|---|---|
| 10 | 6 | 12 | |
| 2 | - | 14 | |
| 6 | 3 | 21 | |
| A2 | 1 | - | 21 |
| B1 | 1 | - | 22 |
| A1 | 1 | - | 23 |
| Equation (13) Result | 3 | 4 | 27 |
| ERMBM | Output in POSIT = 01011011101000111001111111011000 Output in decimal = 14905.99023 | |
| Regular POSIT multiplier proposed by [5] | Output in POSIT = 01011011101000111001111111011000 Output in decimal = 14905.99023 | |
| MATLAB | 14905.990399999998771818354725838 | |
| ERMBM | Output in POSIT = 11010011010010100110100011100110 | |
| Regular POSIT multiplier proposed by [5] | 11010011010010100110100011100110 | |
| MATLAB | −0.0013229183999999998867791450862796 | |
| ERMBM | Output in POSIT = 01100101100010110011110000000010 | ERMBM error = 99.99999748 |
| Regular POSIT multiplier proposed by [5] | Output in POSIT = 01100101100010110011110000000010 | Regular multiplier error = 99.99999748 |
| MATLAB | 3237760.3303999998606741428375244 | |
| Bit Configuration | Slice LUTS | DSP48Es | Datapath Delay (ns) | Total Gate Delay (ns Logic) | Total Net Delay (ns Route) |
|---|---|---|---|---|---|
| Regular POSIT multiplier [5] (Exp = 7 & Regime = 2) | 2634 | 0 | 48.440 | 21.657 | 26.783 |
| Enhanced Radix-4 Modified Booth Multiplier (ERMBM) (Exp = 7 & Regime = 2) | 1928 | 0 | 23.268 | 11.698 | 11.570 |
| Percentage of area enhancement for ERMBM 26.80% | Percentage of speed enhancement for ERMBM 51.97% | ||||
| Bit configuration | Power (mW) | Energy (pJ) |
|---|---|---|
| Regular POSIT multiplier [5] (Exp = 7 & Regime = 2) | 1117 | 54,107.48 |
| Enhanced Radix-4 Modified Booth Multiplier (ERMBM) (Exp = 7 & Regime = 2) | 1111 | 25,850.748 |
| Percentage of power enhancement for ERMBM 0.54% | Percentage of energy enhancement for ERMBM 52.22% | |
| Calculation Source | Generated Output | Calculated Error |
|---|---|---|
| B1 (POSIT is More Accurate) | ||
| B1 from MATLAB | −1.763842361931102233771193617584 | |
| B1 from POSIT | 10111110011110001110100110101000 → −1.763842344 | |
| B1 from FP proposed in [6,7] | bfe1c598 → −1.7638425827026367 | |
| A1 (POSIT is more accurate) | ||
| A1 from MATLAB | −1.7087222881207552889658438170345 | |
| A1 from POSIT | 10111110100101010010001001011011 → −1.708722264 | |
| A1 from FP proposed in [6,7] | bfdab76b → −1.708722472190857 | |
| A2 (same precision) | ||
| A2 from MATLAB | 0.9384765625 | |
| A2 from POSIT | 00111111110000010000000000000000 → 0.9384765625 | POSIT error = 0 |
| A2 from FP proposed in [6,7] | 3f704000 → 0.9384765625 | FP error = 0 |
| Sample = 67 (same precision) | ||
| Y1 from MATLAB | 67.0 | |
| Y1 from POSIT | 0100110000011000000000000000000 → 67.0 | POSIT error = 0 |
| Y1 from FP proposed in [6,7] | 42860000 → 67.0 | FP error = 0 |
| Sample = −456 (POSIT is more accurate) | ||
| Y2 from MATLAB | −459.69304494529324530195843663682 | |
| Y2 from POSIT | 10101110011010001001110100101000 → −459.6930466 | |
| Y2 from FP proposed in [6,7] | c3e5d8b6 → −459.69305419921875 | |
| Sample = 19 (POSIT is more accurate) | ||
| Y3 from MATLAB | 41.946435760963943178399103612273 | |
| Y3 from POSIT | 01001010100111110010010010000000 → 41.9464111328125 | |
| Y3 from FP proposed in [6,7] | 4227c930 → 41.94647216796875 | |
| Sample = 28 (POSIT is More Accurate) | ||
| Y4 from MATLAB | 41.572953440710447008497063642695 | |
| Y4 from POSIT | 01001010100110010010101010101000 → 41.57291412 | . |
| Y4 from FP proposed in [6,7] | 42264ac0 → 41.572998046875 | |
| Sample = 160 (POSIT is more accurate) | ||
| Y5 from MATLAB | 161.28329915100100573765568271504 | |
| Y5 from POSIT | 01001110100001010010001000001101 → 161.2832546 | |
| Y5 from FP proposed in [6,7] | 4321488a → 161.28335571289062 | |
| Sample = 39 (POSIT is more accurate) | ||
| Y6 from MATLAB | 21.358347613975862138928193744926 | |
| Y6 from POSIT | 01001000101010110111011100110000 → 21.35829926 | |
| Y6 from FP proposed in [6,7] | 41aade00 → 21.3583984375 | |
| Sample = 142 (POSIT is more accurate) | ||
| Y7 from MATLAB | 118.34503631422772995296612011743 | |
| Y7 from POSIT | 01001101101100101100001010001101 → 118.3449955 | |
| Y7 from FP Proposed in [6,7] | 42ecb0ae → 118.34507751464844 | |
| Sample = 151 (POSIT is more accurate) | ||
| Y8 from MATLAB | 121.70887719492042148245152838541 | |
| Y8 from POSIT | 01001101110011011010101110111000 → 121.70887402 | |
| Y8 from FP proposed in [6,7] | 42f36af6 → 121.70890808105469 | |
| Sample = 117 (FP is more accurate) | ||
| Y9 from MATLAB | 89.562431604401888060911774239986 | |
| Y9 from POSIT | 01001100110011000111111111010100 → 86.56241608 | |
| Y9 from FP proposed in [6,7] | 42b31ff8 → 89.56243896484375 | |
| Sample = 294 (POSIT is more accurate) | ||
| Y10 from MATLAB | 277.44683801916972138270230542038 | |
| Y10 from POSIT | 01010000001010101110010011001000 → 277.4468384 | |
| Y10 from FP proposed in [6,7] | 43687263 → 277.4468231201172 | |
| Bit Configuration | Slice LUTS | DSP48Es | Datapath Delay (ns) | Total Gate Delay (ns Logic) | Total Net Delay (ns Route) |
|---|---|---|---|---|---|
| 32-bit POSIT utilizing regular multiplier in implementing IIR notch filter (Exp = 7 & Regime = 2) | 5729 | 8 | 58.070 | 28.799 | 29.271 |
| 32-bit FP IIR notch filter using the proposed FP adder/subtractor & the proposed multiplier | 7323 | 8 | 41.918 | 14.744 | 27.174 |
| Percentage of area enhancement for POSIT 21.77% | Percentage of speed enhancement for FP 27.81% | ||||
| Bit Configuration | Slice LUTS | DSP48Es | Datapath Delay (ns) | Total Gate Delay (ns Logic) | Total Net Delay (ns Route) |
|---|---|---|---|---|---|
| 32-bit POSIT utilizing ERMBM in implementing IIR notch filter (Exp = 7 & Regime = 2) | 12,270 | 0 | 58.014 | 28.844 | 29.17 |
| 32-bit FP IIR notch filter using the proposed FP adder/subtractor & the proposed multiplier | 19,077 | 0 | 73.125 | 32.918 | 40.207 |
| Percentage of area enhancement for POSIT 35.68% | Percentage of speed enhancement for POSIT 20.66% | ||||
| Bit Configuration | Power (mW) | Energy (pJ) |
|---|---|---|
| 32-bit POSIT utilizing regular multiplier in implementing IIR notch filter (Exp = 7 & Regime = 2) | 1630 | 94,654.1 |
| 32-bit FP IIR notch filter using the proposed FP adder/subtractor & the proposed multiplier | 2671 | 111,962.98 |
| Percentage of power enhancement for POSIT 38.98% | Percentage of energy enhancement for POSIT 15.46% | |
| Bit Configuration | Power (mW) | Energy (pJ) |
|---|---|---|
| 32-bit POSIT utilizing ERMBM in implementing IIR notch filter (Exp = 7 & Regime = 2) | 1619 | 93,924.67 |
| 32-bit FP IIR notch filter using the proposed FP adder/subtractor & the proposed multiplier | 2363 | 172,794.38 |
| Percentage of power enhancement of POSIT 31.49% | Percentage of energy enhancement of POSIT 45.64% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmaeel, A.A.; Abed, S.; Mohd, B.J.; Fairouz, A.A. POSIT vs. Floating Point in Implementing IIR Notch Filter by Enhancing Radix-4 Modified Booth Multiplier. Electronics 2022, 11, 163. https://doi.org/10.3390/electronics11010163
Esmaeel AA, Abed S, Mohd BJ, Fairouz AA. POSIT vs. Floating Point in Implementing IIR Notch Filter by Enhancing Radix-4 Modified Booth Multiplier. Electronics. 2022; 11(1):163. https://doi.org/10.3390/electronics11010163
Chicago/Turabian StyleEsmaeel, Anwar A., Sa’ed Abed, Bassam J. Mohd, and Abbas A. Fairouz. 2022. "POSIT vs. Floating Point in Implementing IIR Notch Filter by Enhancing Radix-4 Modified Booth Multiplier" Electronics 11, no. 1: 163. https://doi.org/10.3390/electronics11010163
APA StyleEsmaeel, A. A., Abed, S., Mohd, B. J., & Fairouz, A. A. (2022). POSIT vs. Floating Point in Implementing IIR Notch Filter by Enhancing Radix-4 Modified Booth Multiplier. Electronics, 11(1), 163. https://doi.org/10.3390/electronics11010163






