Robust Circuit and System Design for General-Purpose Computational Resistive Memories
Abstract
1. Introduction
2. Memory Array Topology and In-Memory Logic Schemes
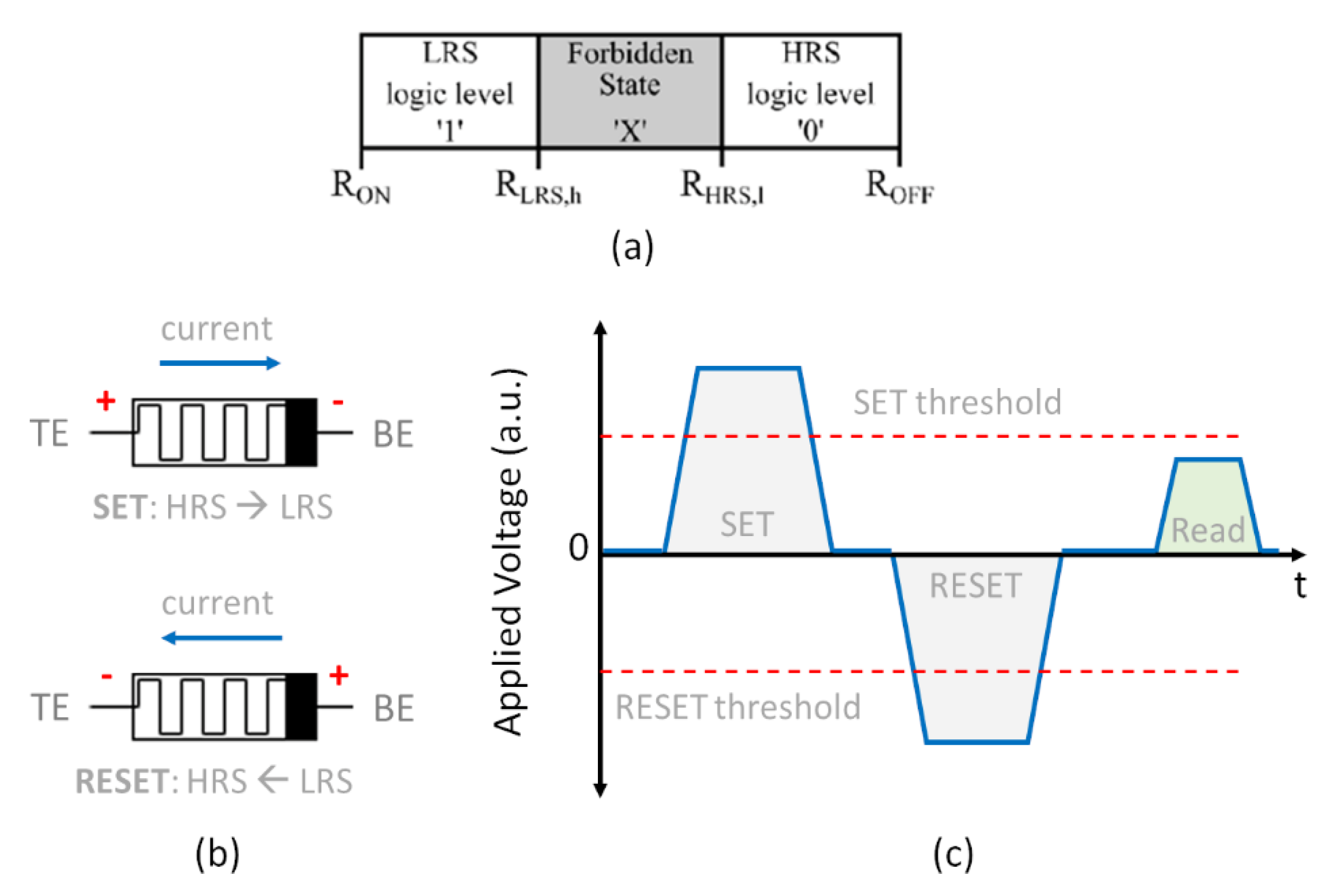
2.1. Definitions and Assumptions for Memristors
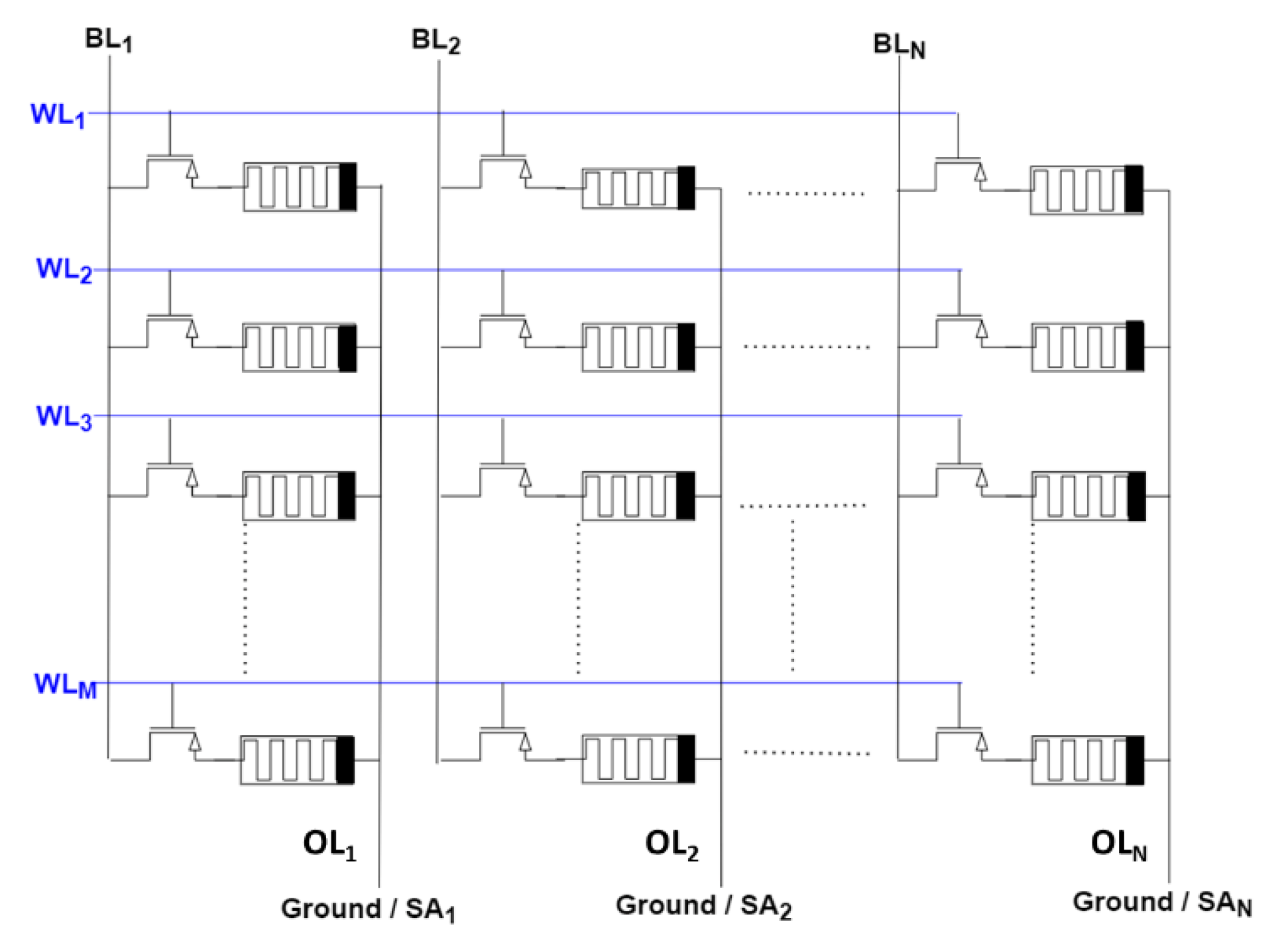
2.2. One Transistor One Memristor (1T1R) Crossbar Array
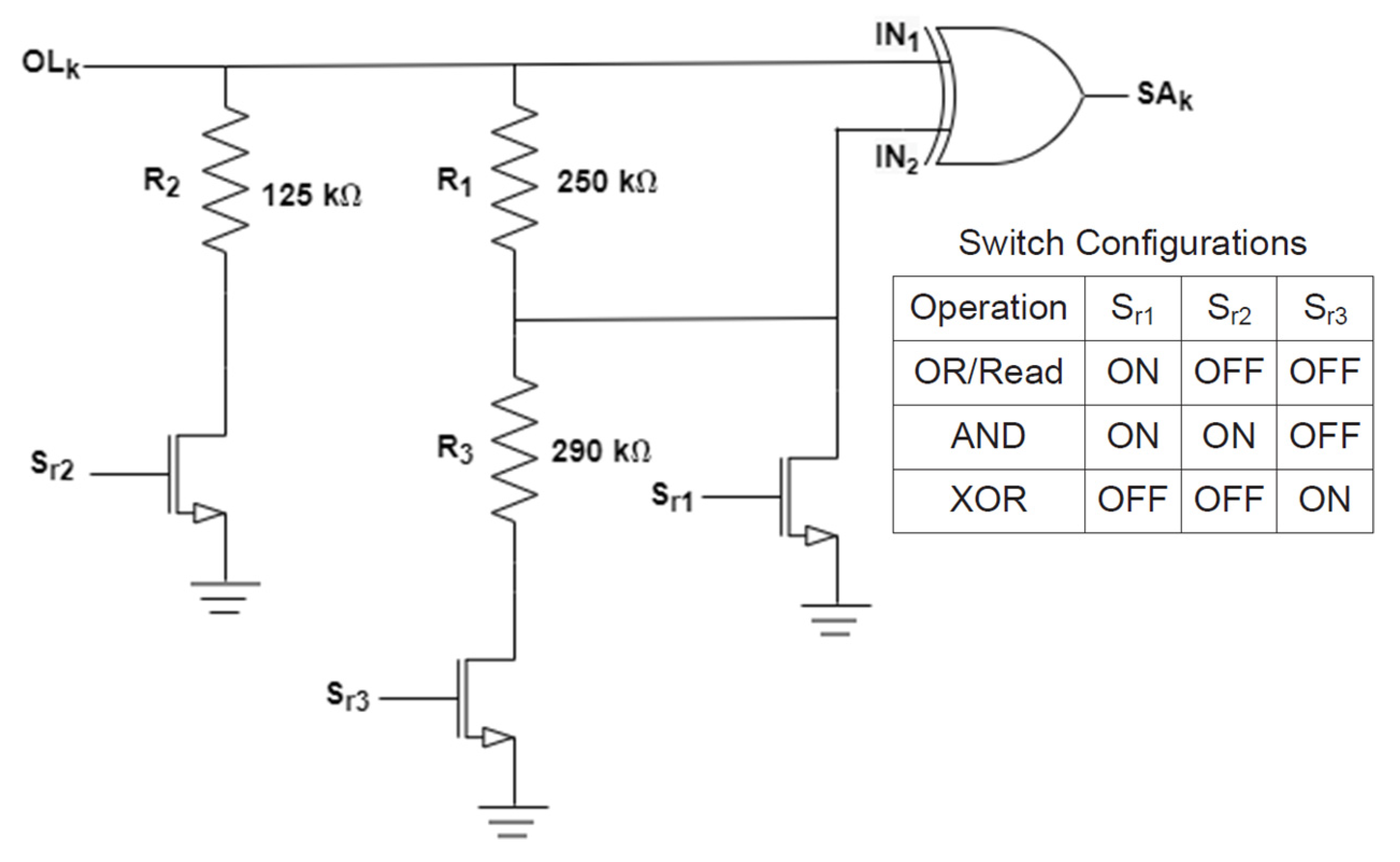
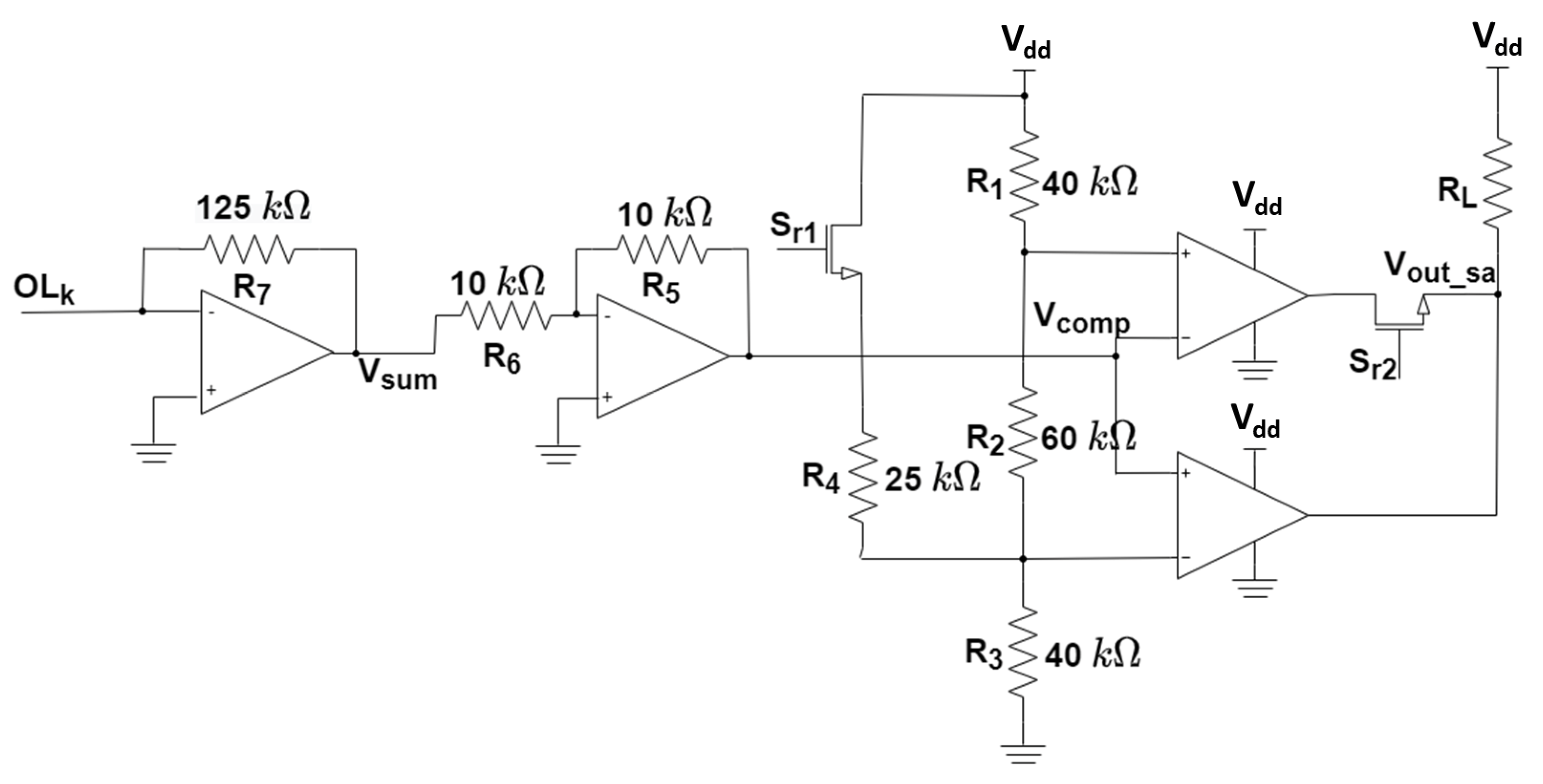
2.3. Sensing Circuit Implementations That Enable Memristor-Based Logic Operations
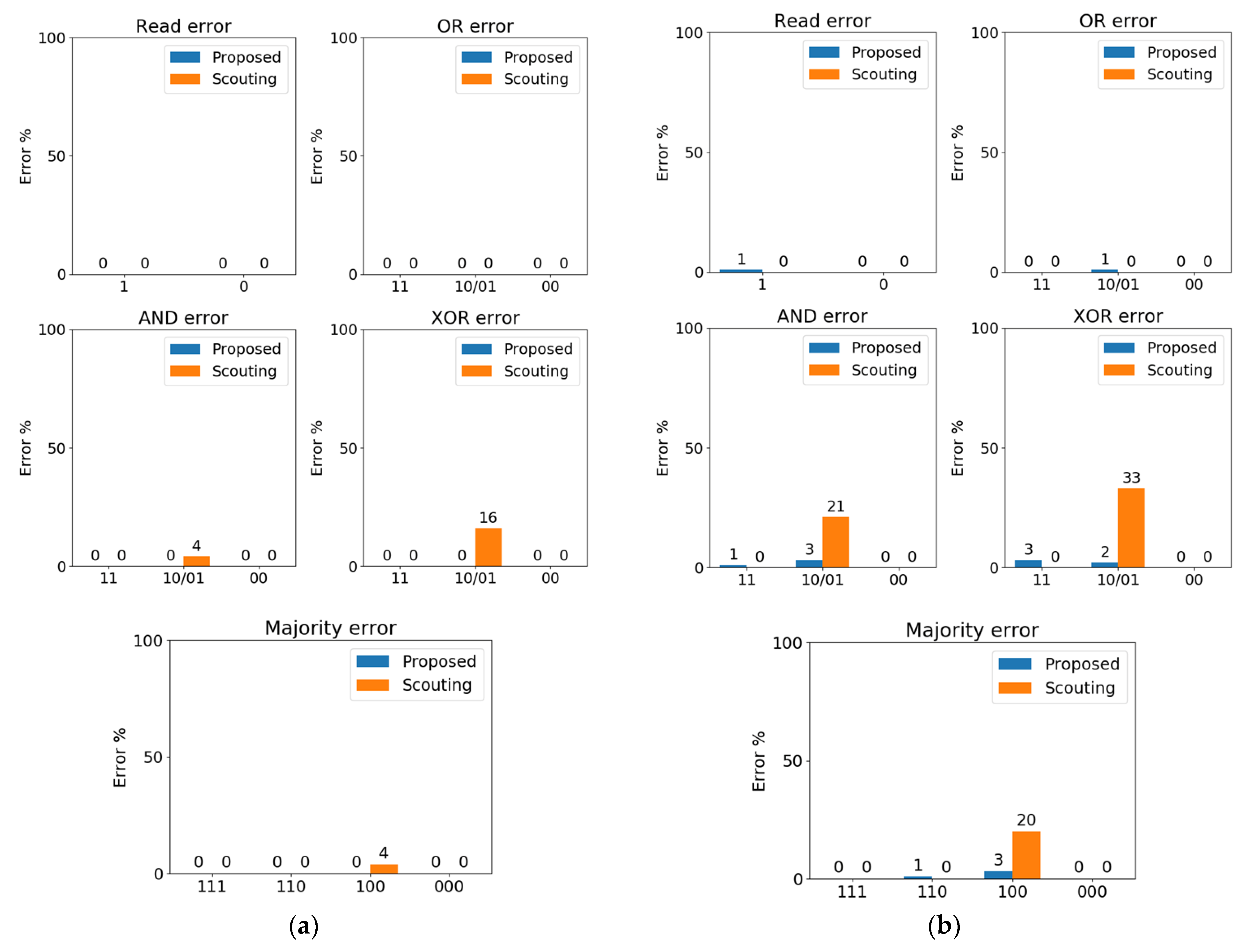
2.4. Performance Comparison in Presence of HRS and LRS Variability
- Both circuits are robust for memory read and OR logic operations.
- The original scouting SA presents an increasing error percentage up to 20% in MAJ operations when we apply input combinations with only one logic “1” (i.e., “001”, “010”, and “100”). This is attributed to the fact that the VIN1 value for nominal HRS and LRS values (0.36 V in Table 1) is very close to the threshold of the CMOS XOR gate. On the contrary, observed errors in the proposed circuit reach up to 3% for the same input combination when 20% SD is considered.
- The original scouting SA presents an increasing error percentage for the AND operation up to 21% when we apply input combinations with only one logic “1” (i.e., “01” and “10”), whereas the observed error in the proposed alternative circuit generally does not exceed 3% when 20% SD is considered.
- The most error-prone logic operation is XOR, for which the original scouting SA presents errors up to 33% when we apply input combinations with only one logic “1” (i.e., “01” and “10”). On the contrary, the observed errors in the proposed alternative SA topology generally do not exceed 2% when 20% SD is considered.
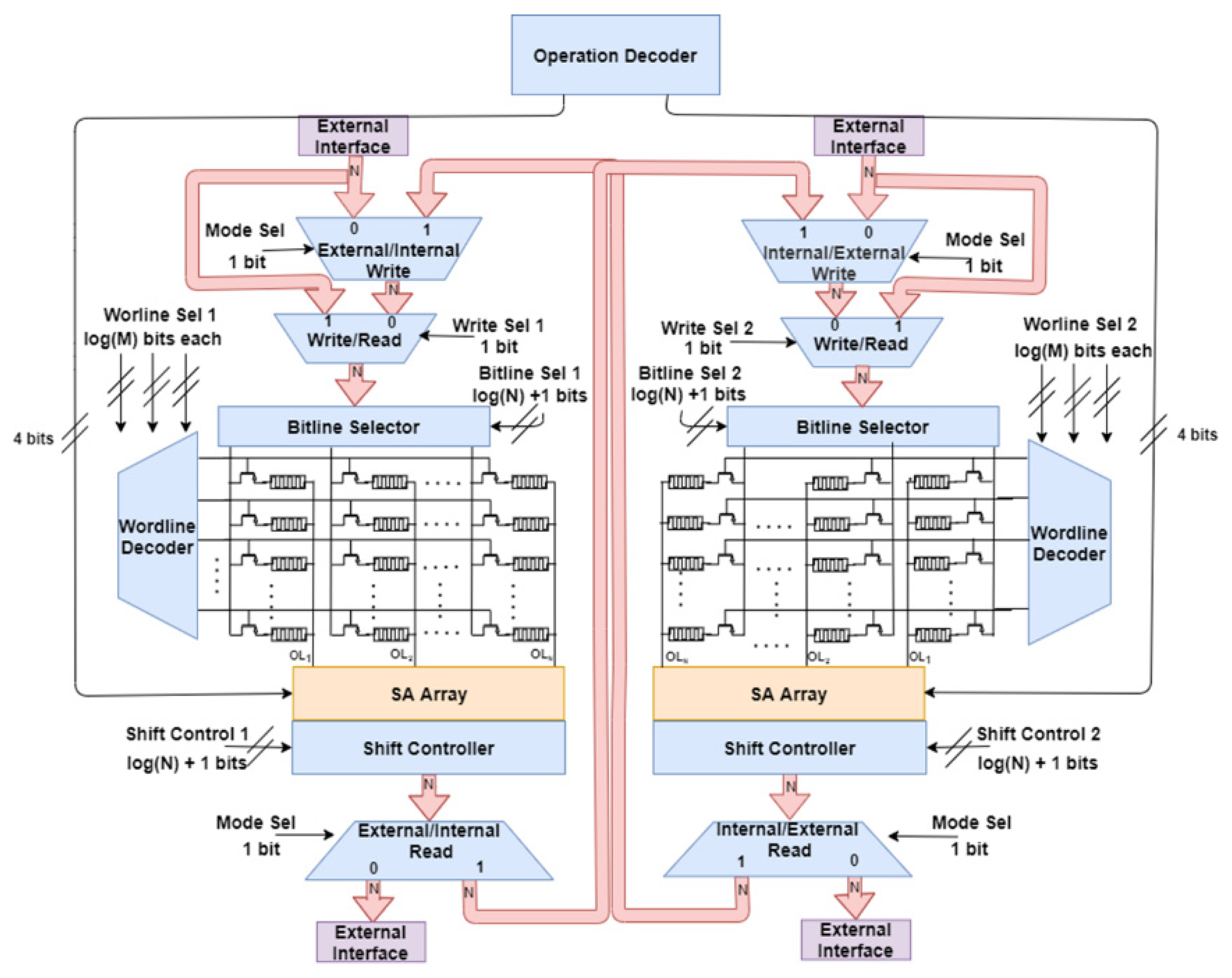
3. The “Twin” Computational ReRAM Architecture
3.1. Overall Design Description
3.2. Hardware Modules for Bit/Word-Wise Memory and Logic Operations
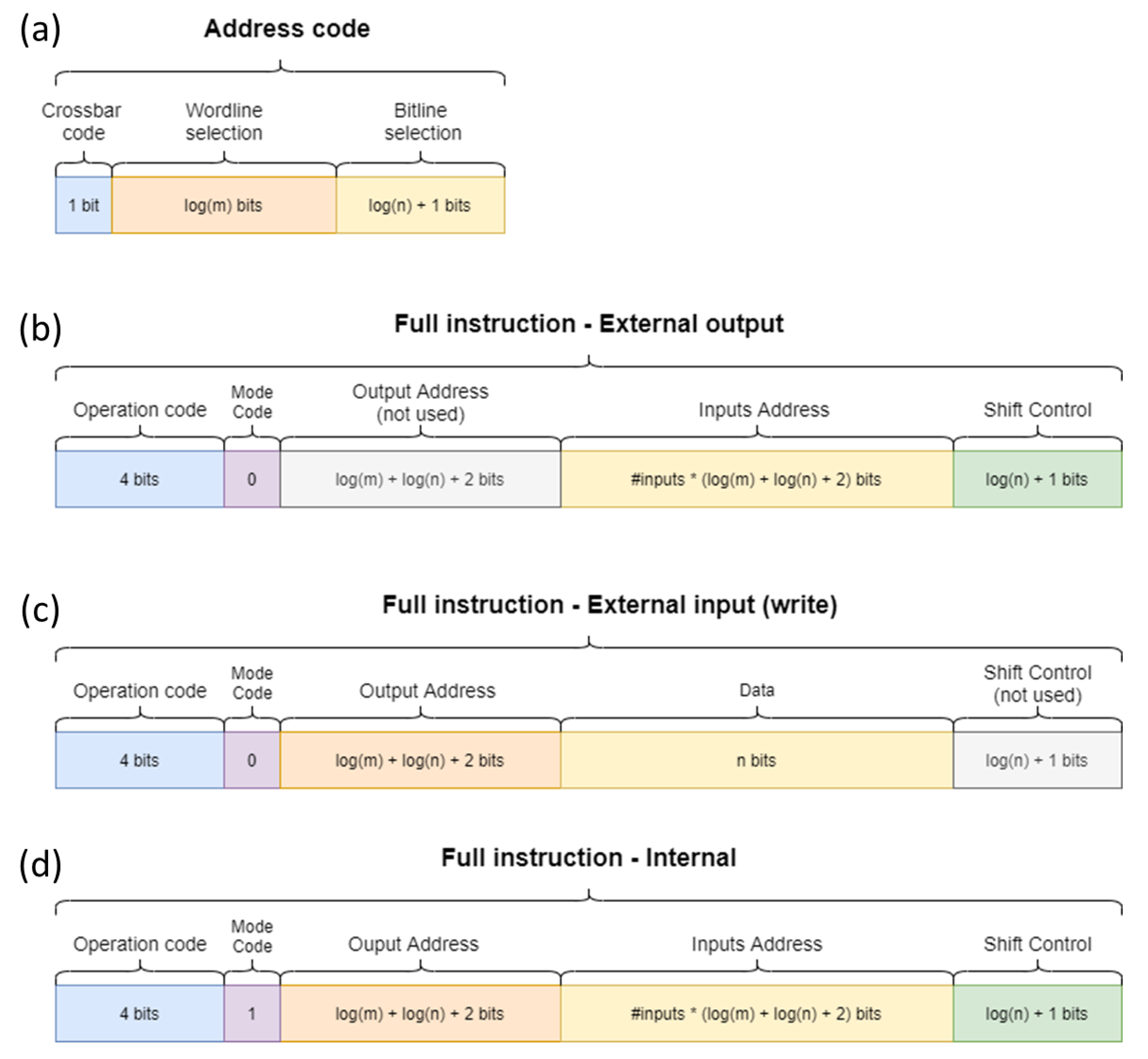
3.3. Supported Set of Instructions/Operations
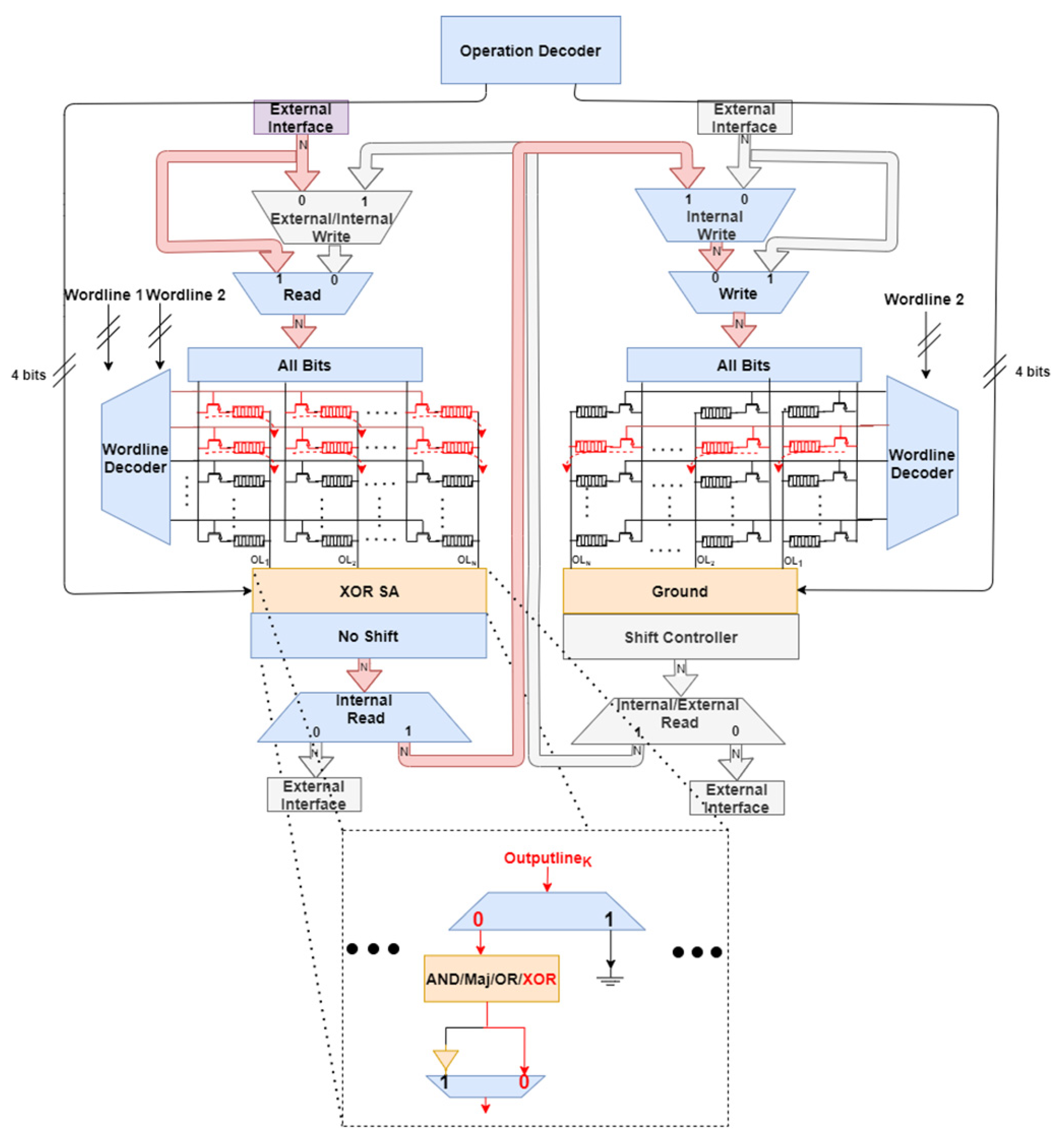
4. Examples of Memory and Logic Operations
4.1. System-Level Configuration Example
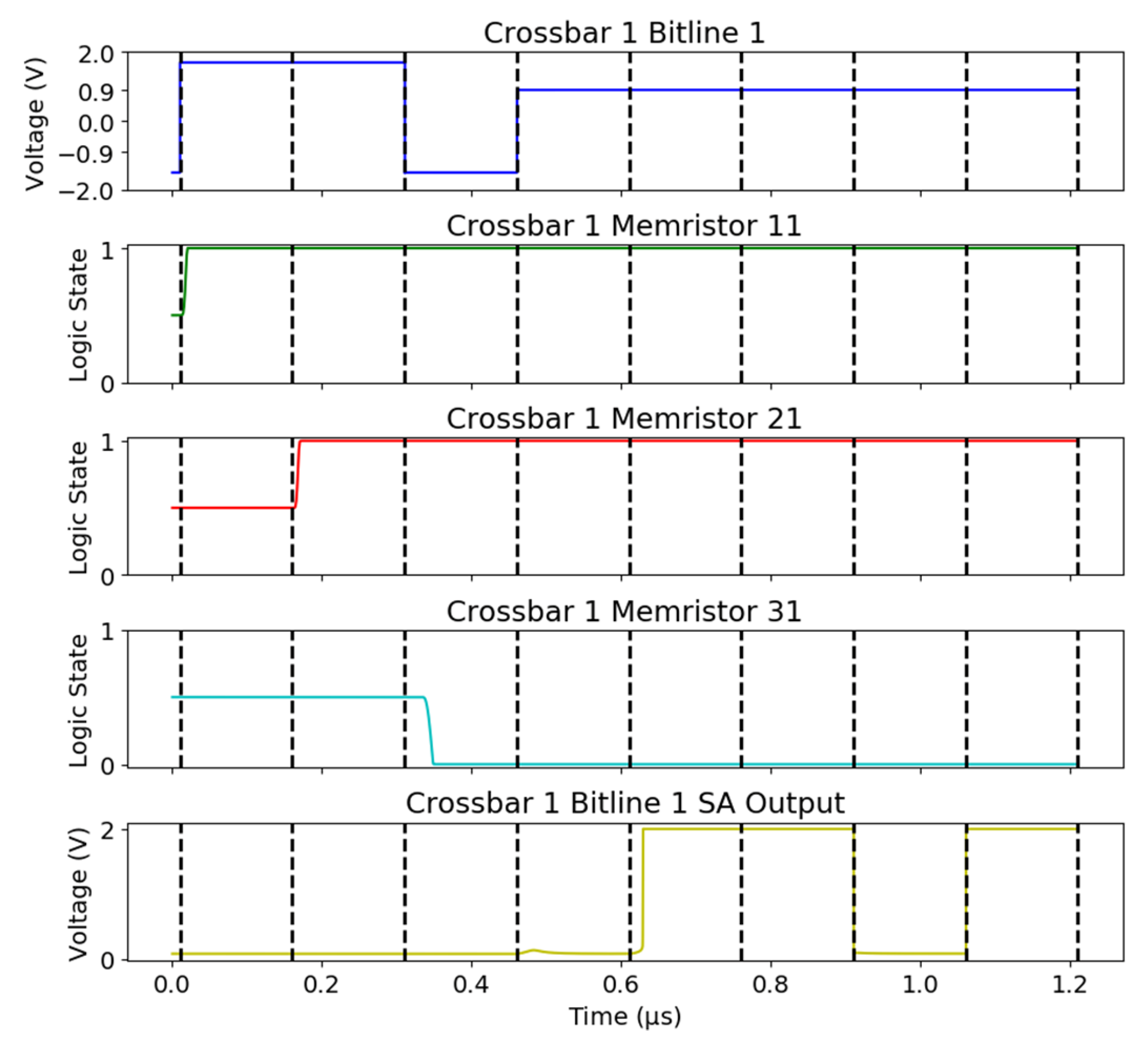
4.2. Simulation Results for Individual Memory and Logic Operations
4.3. Simulation Results for n-Bit Binary Addition
4.4. Performance Comparison Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| SA Operation | Equivalent Circuit |
|---|---|
| Read | 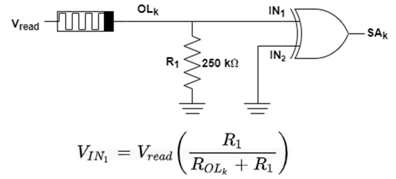 |
| OR | 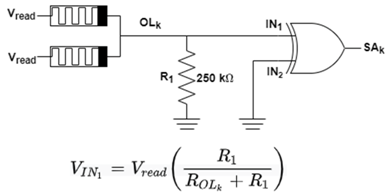 |
| XOR |  |
| AND | 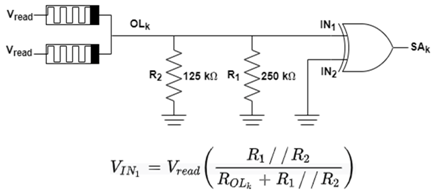 |
| MAJ | 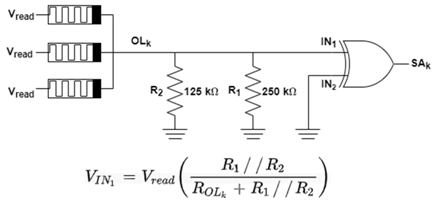 |
| SA Operation | Equivalent Circuit |
|---|---|
| Read |  |
| OR | 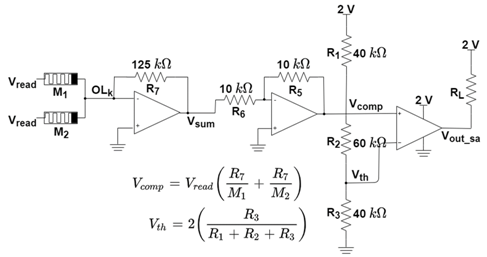 |
| XOR | 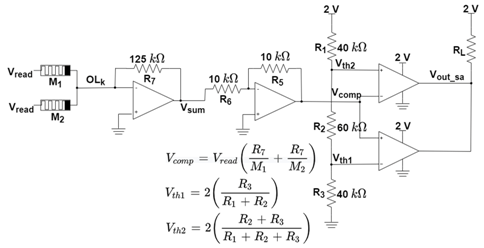 |
| AND | 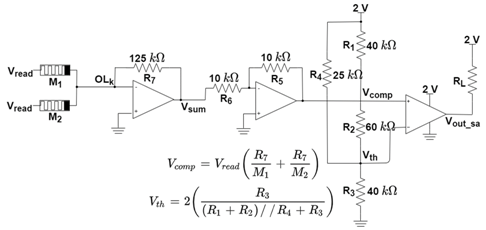 |
| MAJ | 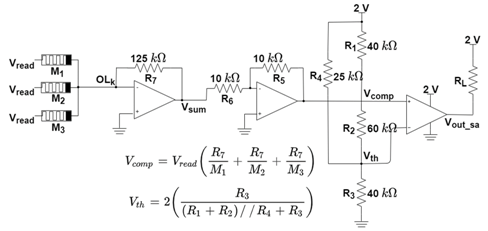 |
References
- Aly, M.M.S.; Wu, T.F.; Bartolo, A.; Malviya, Y.H.; Hwang, W.; Hills, G.; Markov, I.; Wootters, M.; Shulaker, M.M.; Wong, H.-S.P.; et al. The N3XT Approach to Energy-Efficient Abundant-Data Computing. Proc. IEEE 2018, 107, 19–48. [Google Scholar] [CrossRef]
- Sebastian, A.; Tuma, T.; Papandreou, N.; Le Gallo, M.; Kull, L.; Parnell, T.P.; Eleftheriou, E. Temporal correlation detection using computational phase-change memory. Nat. Commun. 2017, 8, 1115. [Google Scholar] [CrossRef] [PubMed]
- Crossbar Inc. Available online: https://www.crossbar-inc.com (accessed on 30 April 2021).
- Liu, C.; Wu, T. ReRAM-based Circuit and System Design for Future Storage and Computing. In Proceedings of the 2018 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Chengdu, China, 26–30 October 2018. [Google Scholar]
- Im, I.H.; Kim, S.J.; Jang, H.W. Memristive Devices for New Computing Paradigms. Adv. Intell. Syst. 2020, 2. [Google Scholar] [CrossRef]
- Govoreanu, B.; Kar, G.; Chen, Y.-Y.; Paraschiv, V.; Kubicek, S.; Fantini, A.; Radu, I.; Goux, L.; Clima, S.; Degraeve, R.; et al. 10 × 10 nm2 Hf/HfOx crossbar resistive RAM with excellent performance, reliability and low-energy operation. In Proceedings of the 2011 IEEE International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011; pp. 31.6.1–31.6.4. [Google Scholar]
- Li, C.; Belkin, D.; Li, Y.; Yan, P.; Hu, M.; Ge, N.; Jiang, H.; Montgomery, E.; Lin, P.; Wang, Z.; et al. In-Memory Computing with Memristor Arrays. In Proceedings of the 2018 IEEE International Memory Workshop (IMW), Kyoto, Japan, 13–16 May 2018; pp. 1–4. [Google Scholar]
- Vourkas, I.; Sirakoulis, G.C. Emerging Memristor-Based Logic Circuit Design Approaches: A Review. IEEE Circuits Syst. Mag. 2016, 16, 15–30. [Google Scholar] [CrossRef]
- Yadav, D.N.; Thangkhiew, P.L.; Datta, K. Look-ahead mapping of Boolean functions in memristive crossbar array. Integr. VLSI J. 2019, 64, 152–162. [Google Scholar] [CrossRef]
- Ye, W.; Cui, X.; Ma, Y.; Wei, F. An Improved Synthesis Method of Logic Circuits based on the NMOS-like RRAM Gates. In Proceedings of the 2020 IEEE 15th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Kunming, China, 3–6 November 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Cheng, L.; Li, Y.; Yin, K.; Hu, S.; Su, Y.; Jin, M.; Wang, Z.; Chang, T.; Miao, X. Functional Demonstration of a Memristive Arithmetic Logic Unit (MemALU) for In-Memory Computing. Adv. Funct. Mater. 2019, 29, 1905660. [Google Scholar] [CrossRef]
- Rohani, S.G.; Taherinejad, N.; Radakovits, D. A Semiparallel Full-Adder in IMPLY Logic. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 297–301. [Google Scholar] [CrossRef]
- Escudero, M.; Vourkas, I.; Rubio, A.; Moll, F. Memristive Logic in Crossbar Memory Arrays: Variability-Aware Design for Higher Reliability. IEEE Trans. Nanotechnol. 2019, 18, 635–646. [Google Scholar] [CrossRef]
- Zhu, X.; Long, H.; Li, Z.; Diao, J.; Liu, H.; Li, N.; Xu, H. Implication of unsafe writing on the MAGIC NOR gate. Microelectron. J. 2020, 103, 104866. [Google Scholar] [CrossRef]
- Gaillardon, P.E.; Amarú, L.; Siemon, A.; Linn, E.; Waser, R.; Chattopadhyay, A.; Micheli, G.D. The programmable logic-in-memory (plim) computer. In Proceedings of the 2016 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 14–18 March 2016; pp. 427–432. [Google Scholar]
- Bhattacharjee, D.; Devadoss, R.; Chattopadhyay, A. ReVAMP: ReRAM based VLIW architecture for in-memory computing. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 27–31. [Google Scholar]
- Xie, L.; Du Nguyen, H.; Yu, J.; Kaichouhi, A.; Taouil, M.; AlFailakawi, M.; Hamdioui, S. Scouting Logic: A Novel Memristor-Based Logic Design for Resistive Computing. In Proceedings of the 2017 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Bochum, Germany, 3–5 July 2017; pp. 176–181. [Google Scholar]
- Reuben, J. Binary Addition in Resistance Switching Memory Array by Sensing Majority. Micromachines 2020, 11, 496. [Google Scholar] [CrossRef] [PubMed]
- Pinto, F.; Vourkas, I. Design Considerations for the Development of Computational Resistive Memories. In Proceedings of the 2021 IEEE Latin American Symp. Circuits and Systems (LASCAS), Arequipa, Perú, 21–25 February 2021. in press. [Google Scholar]
- Vourkas, I.; Sirakoulis, G.C. Memristor-Based Nanoelectronic Computing Circuits and Architectures. In Emergence, Complexity and Computation; Springer International Publishing: Cham, Germany, 2016; Volume 19. [Google Scholar]
- Yakopcic, C.; Taha, T.M.; Subramanyam, G.; Pino, R.E. Generalized Memristive Device SPICE Model and its Application in Circuit Design. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2013, 32, 1201–1214. [Google Scholar] [CrossRef]
- Lu, W.; Kim, K.-H.; Chang, T.; Gaba, S. Two-terminal resistive switches (memristors) for memory and logic applications. In Proceedings of the 16th IEEE Asia and South Pacific Design Automation Conference (ASP-DAC 2011), Yokohama, Japan, 25–28 January 2011; pp. 217–223. [Google Scholar]
- Flocke, A.; Noll, T.G. Fundamental analysis of resistive nano-crossbars for the use in hybrid Nano/CMOS-memory. In Proceedings of the2006 Proceedings of the 32nd IEEE European Solid-State Circuits Conference, Montreux, Switzerland, 19–21 September 2006; pp. 328–331. [Google Scholar]
- Seok, J.Y.; Song, S.J.; Yoon, J.H.; Yoon, K.J.; Park, T.H.; Kwon, D.E.; Lim, H.; Kim, G.H.; Jeong, D.S.; Hwang, C.S. A review of three-dimensional resistive switching crossbar array memories from the integration and materials property points of view. Adv. Funct. Mater. 2014, 24, 5316–5339. [Google Scholar] [CrossRef]
- Fernandez, C.; Vourkas, I. ReRAM-based Ratioed Combinational Circuit Design: A Solution for in-Memory Computing. In Proceedings of the 2020 International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 7–9 September 2020. [Google Scholar]
- Yu, J.; Du Nguyen, H.A.; Abu Lebdeh, M.; Taouil, M.; Hamdioui, S. Enhanced Scouting Logic: A Robust Memristive Logic Design Scheme. In Proceedings of the 2019 IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), Qingdao, China, 17–19 July 2019; pp. 1–6. [Google Scholar]
- Papandroulidakis, G.; Vourkas, I.; Abusleme, A.; Sirakoulis, G.C.; Rubio, A. Crossbar-Based Memristive Logic-in-Memory Architecture. IEEE Trans. Nanotechnol. 2017, 16, 491–501. [Google Scholar] [CrossRef]
- Ali, K.A.; Rizk, M.; Baghdadi, A.; Diguet, J.-P.; Jomaah, J.; Onizawa, N.; Hanyu, T. Memristive Computational Memory Using Memristor Overwrite Logic (MOL). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 2370–2382. [Google Scholar] [CrossRef]
- Kalkur, T.S.; Pawlikiewicz, M. Verilog-A modeling of filamentary-based complementary resistance switching devices. In Proceedings of the 2018 IEEE 18th International Conference on Nanotechnology (IEEE-NANO), Cork, Ireland, 23–26 July 2018; pp. 1–4. [Google Scholar]
- Lehtonen, E.; Laiho, M. Stateful implication logic with memristors. In Proceedings of the 2009 IEEE/ACM International Symposium on Nanoscale Architectures, San Francisco, CA, USA, 30–31 July 2009; pp. 33–36. [Google Scholar]
- Kvatinsky, S.; Satat, G.; Wald, N.; Friedman, E.G.; Kolodny, A.; Weiser, U.C. Memristor-Based Material Implication (IMPLY) Logic: Design Principles and Methodologies. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2014, 22, 2054–2066. [Google Scholar] [CrossRef]
- Talati, N.; Gupta, S.; Mane, P.; Kvatinsky, S. Logic Design Within Memristive Memories Using Memristor-Aided loGIC (MAGIC). IEEE Trans. Nanotechnol. 2016, 15, 635–650. [Google Scholar] [CrossRef]
- Huang, P.; Kang, J.; Zhao, Y.; Chen, S.; Han, R.; Zhou, Z.; Chen, Z.; Ma, W.; Lifeng, L.; Liu, L.; et al. Reconfigurable Nonvolatile Logic Operations in Resistance Switching Crossbar Array for Large-Scale Circuits. Adv. Mater. 2016, 28, 9758–9764. [Google Scholar] [CrossRef] [PubMed]
- Rohani, S.G.; Taherinejad, N. An improved algorithm for IMPLY logic based memristive Full-adder. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–4. [Google Scholar]
- Siemon, A.; Drabinski, R.; Schultis, M.J.; Hu, X.; Linn, E.; Heittmann, A.; Waser, R.; Querlioz, D.; Menzel, S.; Friedman, J.S. Stateful Three-Input Logic with Memristive Switches. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Reuben, J.; Pechmann, S. Accelerated Addition in Resistive RAM Array Using Parallel-Friendly Majority Gates. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, in press. [Google Scholar] [CrossRef]



| Operation | Input Resistance | Original SA | Alternative SA | Logic Output | |||||
|---|---|---|---|---|---|---|---|---|---|
| R1 (KΩ) | R2 (KΩ) | R3 (KΩ) | VIN1 (V) | VIN2 (V) | Vcomp (V) | Vth1 (V) | Vth2 (V) | ||
| Read | 125 | X | X | 0.6 | 0 | 0.9 | 0.571 | X | 1 |
| Read | 125 × 106 | X | X | 1.8 × 10−6 | 0 | 9 × 10−7 | 0.571 | X | 0 |
| OR | 125 | 125 | X | 0.72 | 0 | 1.8 | 0.571 | X | 1 |
| OR | 125 | 125 × 106 | X | 0.6 | 0 | 0.9 | 0.571 | X | 1 |
| OR | 125 × 106 | 125 × 106 | X | 3.6 × 10−6 | 0 | 1.8 × 10−6 | 0.571 | X | 0 |
| AND | 125 | 125 | X | 0.514 | 0 | 1.8 | 1.333 | X | 1 |
| AND | 125 | 125 × 106 | X | 0.36 | 0 | 0.9 | 1.333 | X | 0 |
| AND | 125 × 106 | 125 × 106 | X | 1.2 × 10−6 | 0 | 1.8 × 10−6 | 1.333 | X | 0 |
| XOR | 125 | 125 | X | 0.8 | 0.433 | 1.8 | 0.571 | 1.429 | 0 |
| XOR | 125 | 125 × 106 | X | 0.73 | 0.37 | 0.9 | 0.571 | 1.429 | 1 |
| XOR | 125 × 106 | 125 × 106 | X | 7.8 × 10−6 | 4.17 × 10−6 | 1.8 × 10−6 | 0.571 | 1.429 | 0 |
| MAJ | 125 | 125 | 125 | 0.6 | 0 | 2.7 | 1.333 | X | 1 |
| MAJ | 125 | 125 | 125 × 106 | 0.514 | 0 | 1.8 | 1.333 | X | 1 |
| MAJ | 125 | 125 × 106 | 125 × 106 | 0.36 | 0 | 0.9 | 1.333 | X | 0 |
| MAJ | 125 × 106 | 125 × 106 | 125 × 106 | 1.8 × 10−6 | 0 | 2.7 × 10−6 | 1.333 | X | 0 |
| Operation | Description | SA Ctrl Bits b3b2b1b0 | Mode Sel Bit |
|---|---|---|---|
| Copy | Copy data to adjacent crossbar | 0000 | 1 |
| Inv | Inversion of the value in the SA output | XXX1 | X |
| OR | 2-input logic OR for two words in the same sub-array | 0000 | X |
| AND | 2-input logic AND for two words in the same sub-array | 0010 | X |
| XOR | 2-input logic XOR for two words in the same sub-array | 0100 | X |
| MAJ | 3-input MAJORITY for three words in the same sub-array | 0010 | X |
| Write | Write external input data to a memory word | 1XXX | 0 |
| Read | Read data stored in a memory word, to the external output | 0000 | 0 |
| Bit shift | Apply left/right logical shift to the SA output through the Shift Controller | N/A | X |
| Bit selection | Activate one target bitline through the Bitline Selector | N/A | X |
| Cycle | Operation | Output/Destination | Input | Schematic Guide |
|---|---|---|---|---|
| 1 | Write | word 11 | 011 | 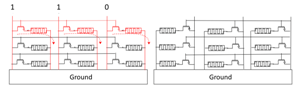 |
| 2 | Write | word 12 | 010 | 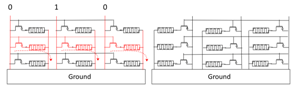 |
| 3 | Write | word 22 | 000 |  |
| Write | word 13 | 000 | ||
| 4 | XOR | word 21 | word 11 word 12 |  |
| 5 | MAJ | bit 222 | bit 111 bit 121 bit 131 |  |
| 6 | Copy | bit 132 | bit 222 |  |
| 7 | MAJ | bit 223 | bit 112 bit 122 bit 132 |  |
| 8 | XOR | word 13 | word 21 word 22 |  |
| Cycle | Opcode | Mode | Output | Input(s) | Shift |
|---|---|---|---|---|---|
| 1 | 1XXX | 0 | 001000 | 011 | XXX |
| 2 | 1XXX | 0 | 010000 | 010 | XXX |
| 3 | 1XXX | 0 | 011000 | 000 | XXX |
| 1XXX | 0 | 110000 | 000 | XXX | |
| 4 | 0100 | 1 | 101000 | 001000 010000 | 000 |
| 5 | 0010 | 1 | 110101 | 001011 010011 011011 | 001 |
| 6 | 0000 | 1 | 011101 | 110101 | 000 |
| 7 | 0010 | 1 | 110111 | 001101 010101 011101 | 001 |
| 8 | 0100 | 1 | 011000 | 101000 110000 | 000 |
| IMPLY [30,31] | MAGIC [32] | NAND [33] | MAJ+NOT [18] | Proposed | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Steps | Area | Steps | Area | Steps | Area | Steps | Area | Steps | Area | |
| OR | 2 | 3 | 2 | 4 | 2 | 6 | 3 | 3 | 1 | 2 |
| AND | 3 | 3 | 2 | 5 | 1 | 3 | 1 | 3 | 1 | 2 |
| NOR | 3 | 3 | 1 | 3 | 3 | 6 | 3 | 3 | 1 | 2 |
| NAND | 2 | 3 | 3 | 5 | 1 | 3 | 1 | 3 | 1 | 2 |
| XOR | 4 | 5 | 3 | 6 | 3 | 6 | 5 | 6 | 1 | 2 |
| MAJ | 26 | 5 | 6 | 6 | 7 | 7 | 1 | 3 | 1 | 3 |
| Description | Latency (Steps) | Circuit Area (N° of Memristors) | Reference |
|---|---|---|---|
| MAGIC (NOR, area optimized) | 15n | 5 | Talati et al. [32] |
| MAGIC (lNOR, latency optimized) | 12n + 1 | 11n − 1 | Talati et al. [32] |
| IMPLY (parallel) | 5n + 18 | 6n − 1 | Kvatinsky et al. [31] |
| IMPLY (serial) | 22n | 2 | Rohani et al. [34] |
| IMPLY (semi-serial) | 17n | 2 | Rohani et al. [12] |
| NAND | 10n | 9 | Huang et al. [33] |
| ORNOR | 2n + 15 | 6n + 6 | Siemon et al. [35] |
| MAJ + NOT | 4log2n + 6 | 6(6n + 16) | Reuben et al. [36] |
| Enhanced Scouting (XOR and MAJ) | 2n + 2 | 3n | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinto, F.; Vourkas, I. Robust Circuit and System Design for General-Purpose Computational Resistive Memories. Electronics 2021, 10, 1074. https://doi.org/10.3390/electronics10091074
Pinto F, Vourkas I. Robust Circuit and System Design for General-Purpose Computational Resistive Memories. Electronics. 2021; 10(9):1074. https://doi.org/10.3390/electronics10091074
Chicago/Turabian StylePinto, Felipe, and Ioannis Vourkas. 2021. "Robust Circuit and System Design for General-Purpose Computational Resistive Memories" Electronics 10, no. 9: 1074. https://doi.org/10.3390/electronics10091074
APA StylePinto, F., & Vourkas, I. (2021). Robust Circuit and System Design for General-Purpose Computational Resistive Memories. Electronics, 10(9), 1074. https://doi.org/10.3390/electronics10091074







