Integral Sliding Mode Anti-Disturbance Control for Markovian Jump Systems with Mismatched Disturbances
Abstract
1. Introduction
2. System Description
3. Design of Disturbance Observer
4. Design of ISS and ISM Controller
5. Dynamical Performance Analysis
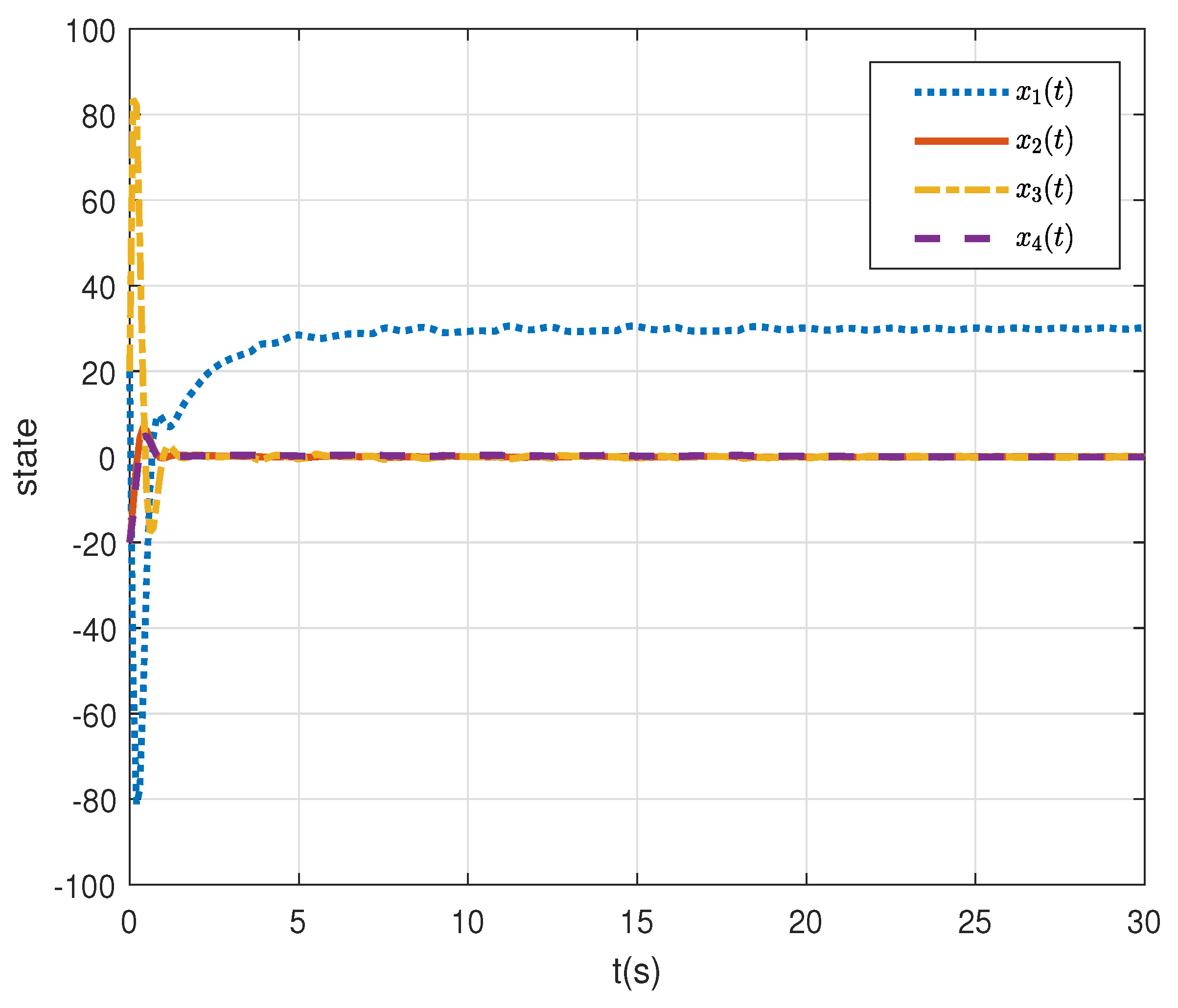
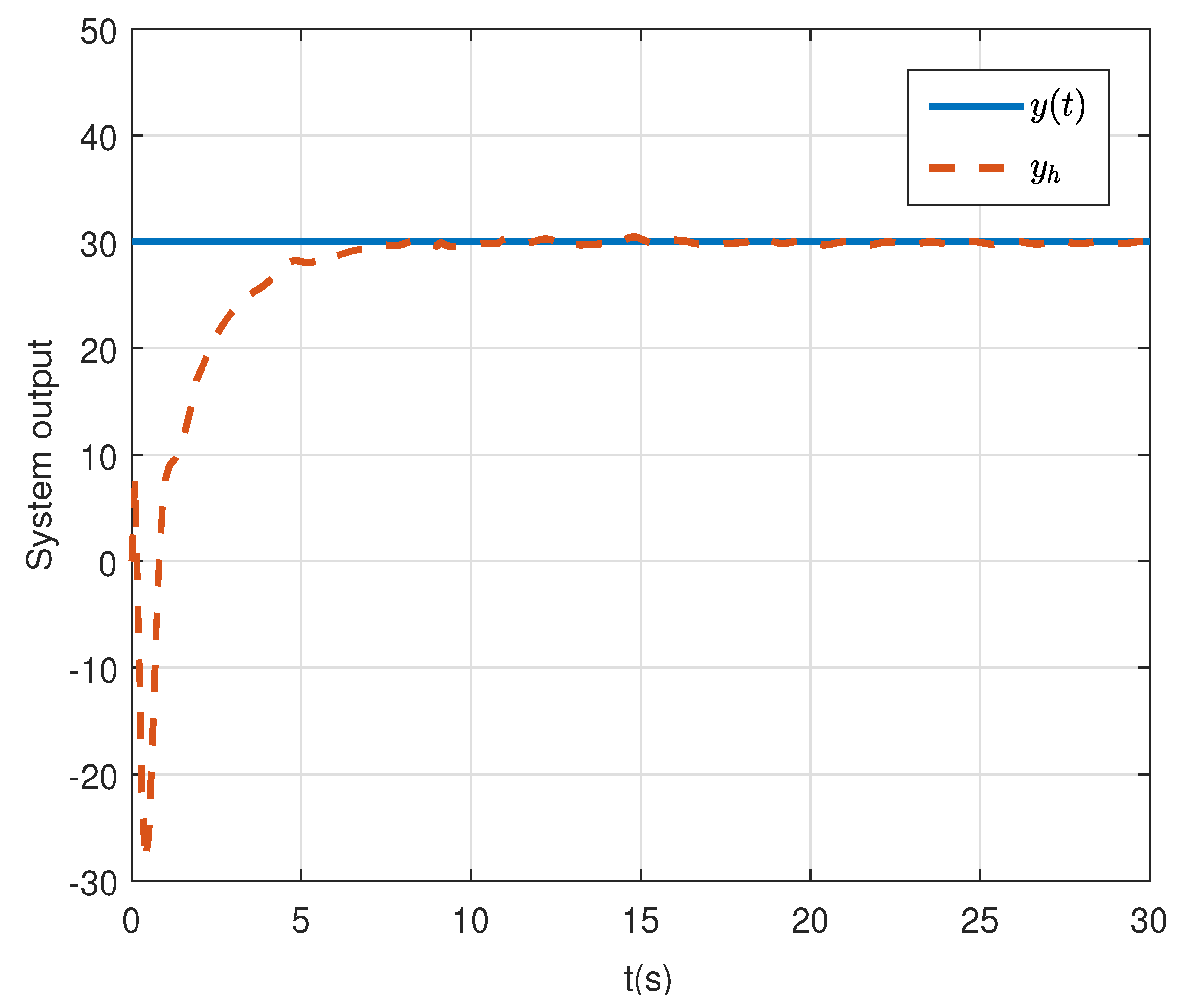
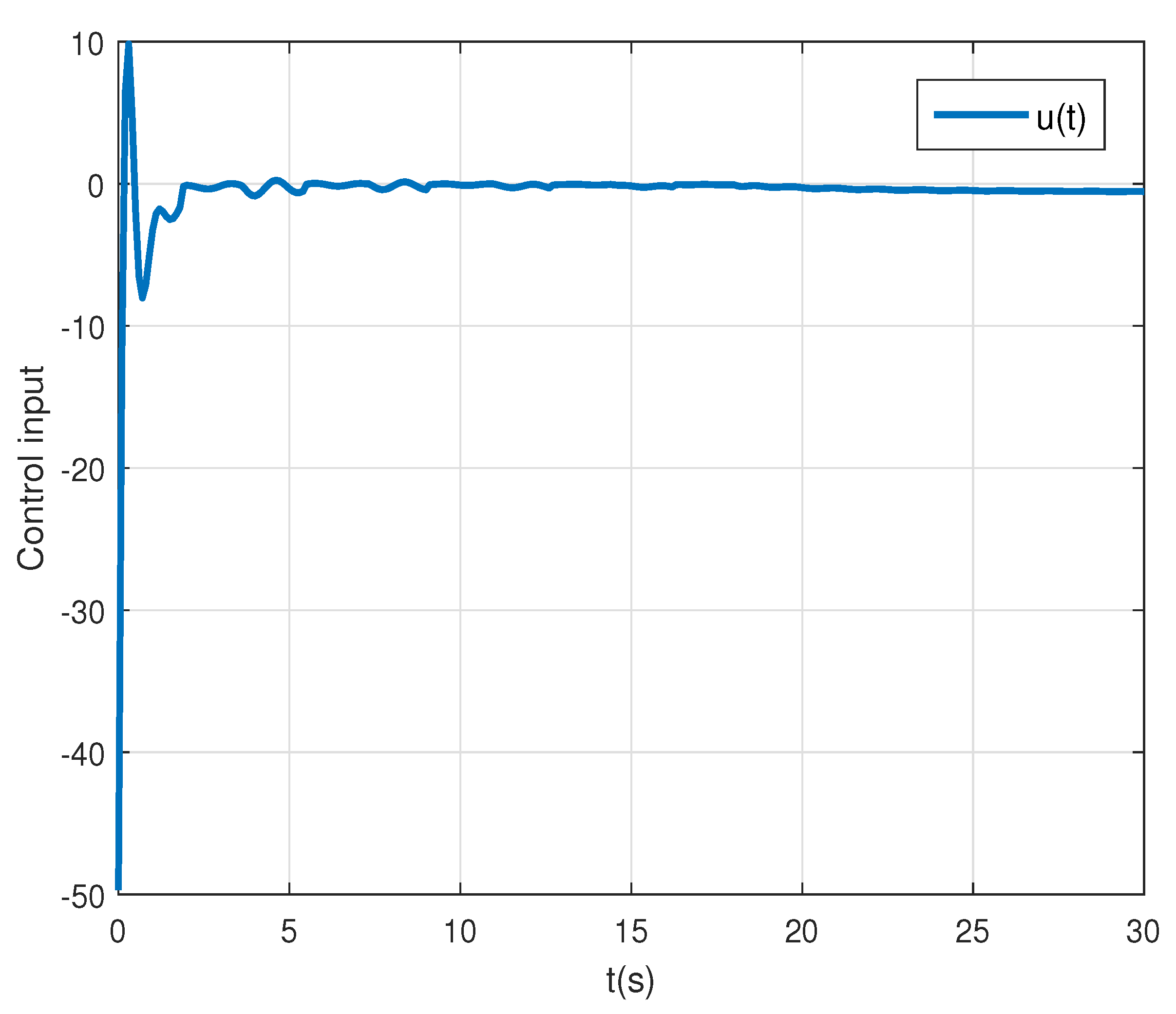
6. An Simulation Example
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Costa, O.L.V.; Fragoso, M.D.; Todorow, M.G. Continuous-Time Markov Jump Linear System; Springer: London, UK, 2013. [Google Scholar]
- Kawka, P.A.; Alleyne, A.G. Robust wireless servo control using a discrete-time uncertain Markovian jump linear model. IEEE Trans. Autom. Control 2019, 17, 733–742. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, L.P.; Spiryagin, M. Control and decision strategy for a class of Markovian jump systems in failure prone manufacturing process. IET Control Theory Appl. 2012, 6, 1803–1811. [Google Scholar] [CrossRef]
- Al-Azzawi, W.; Al-Akaidi, M. Robust stability of solar-power wireless network control system with stochastic time delays based on H∞ norm. Int. J. Syst. Sci. 2015, 46, 896–907. [Google Scholar] [CrossRef]
- Ding, D.R.; Wang, Z.D.; Han, Q.L. Neural-network-based output-feedback control with stochastic communication protocols. Automatica 2019, 106, 221–229. [Google Scholar] [CrossRef]
- Wu, L.G.; Shi, P.; Gao, H.J. State estimation and sliding-mode control of Markovian jump singular systems. IEEE Trans. Autom. Control 2010, 55, 1213–1219. [Google Scholar]
- Nogueira, S.L.; Siqueira, A.A.G.; Inoue, R.S.; Terra, M.H. Markov jump linear systems-based position estimation for lower limb exoskeletons. Sensors 2014, 14, 1835–1849. [Google Scholar] [CrossRef]
- Shi, P.; Liu, M.; Zhang, L.X. Fault-tolerant sliding-mode-observer synthesis of Markovian jump systems using quantized measurements. IEEE Trans. Ind. Electron. 2015, 62, 5910–5918. [Google Scholar] [CrossRef]
- Qi, W.H.; Zong, G.D.; Karimi, H.R. Sliding mode control for nonlinear stochastic singular semi-Markov jump systems. IEEE Trans. Autom. Control 2020, 65, 361–368. [Google Scholar] [CrossRef]
- Wu, Z.G.; Dong, S.L.; Shi, P.; Su, H.Y.; Huang, T.W. Reliable filtering of nonlinear Markovian jump systems: The continuous-time case. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 386–394. [Google Scholar] [CrossRef]
- Aberkane, S. Bounded real lemma for nonhomogeneous Markovian jump linear systems. IEEE Trans. Autom. Control 2013, 58, 797–801. [Google Scholar] [CrossRef]
- Shen, H.; Men, Y.Z.; Wu, Z.G.; Park, J.H. Nonfragile H∞ control for fuzzy markovian jump systems under fast sampling singular perturbation. IEEE Trans. Fuzzy Syst. 2018, 48, 2058–2069. [Google Scholar]
- Shen, M.Q.; Ma, Y.S.; Park, J.H.; Wang, Q.G. Fuzzy tracking control for Markov jump systems with mismatched faults by iterative proportional-integral observers. IEEE Trans. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Xia, Y.Q.; Shen, H.; Zhou, P.F. SMC design for robust stabilization of nonlinear Markovian jump singular systems. IEEE Trans. Autom. Control 2018, 63, 219–224. [Google Scholar] [CrossRef]
- Guo., L.; Cao, S.Y. Anti-Disturbance Control for Systems with Multiple Disturbances; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Zhang, Y.L.; Zhu, M.; Li, D.; Wang, J.M. ADRC dynamic stabilizabtion of an unstable heat equation. IEEE Trans. Autom. Control 2020, 65, 4424–4429. [Google Scholar] [CrossRef]
- Xia, Y.Q.; Pu, F.; Li, S.F.; Gao, Y. Lateral path tracking control of autonomous land vehicle based on ADRC and differential flatness. IEEE Trans. Ind. Electron. 2016, 63, 3091–3099. [Google Scholar] [CrossRef]
- Yu, P.; Liu, K.Z.; Wu, M.; She, J. Improved equivalent-inputbdisturbance approach based on H∞ control. IEEE Trans. Ind. Electron. 2020, 67, 8670–8679. [Google Scholar] [CrossRef]
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mech. 2020, 9, 706–710. [Google Scholar] [CrossRef]
- Sun, H.B.; Guo, L. Neural network-based DOBC for a class of nonlinear systems with unmatched disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 482–489. [Google Scholar] [CrossRef]
- Chen, W.H.; Ballanceand, D.J.; Gawthrop, P.J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Elect. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Sun, L.; Huo, W.; Jiao, Z.X. Disturbance-observer-based robust relative pose control for spacecraft rendezvous and proximity operations under input saturation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1605–1617. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, Y.; He, W.; Hui, Q. Modeling and observer-based vibration control of a flexible spacecraft with external disturbances. IEEE Trans. Ind. Electron. 2019, 66, 8648–8658. [Google Scholar] [CrossRef]
- Zhang, X.G.; Li, Z.X. Sliding-mode observer-based mechanical parameter estimation for permanent magnet synchronous motor. IEEE Trans. Power Electron. 2016, 31, 5732–5745. [Google Scholar] [CrossRef]
- Yang, J.; Cui, H.Y.; Li, S.H.; Zolotas, A. Optimized active disturbance rejection control for DC-DC buck converters with uncertainties using a reduced-order GPI observer. IEEE Trans. Circuits Syst. I Reg. Pap. 2018, 65, 832–841. [Google Scholar] [CrossRef]
- Yi, Y.; Zheng, W.X.; Sun, C.Y.; Guo, L. DOB fuzzy controller design for non-Gaussian stochastic distribution systems using two-step fuzzy identification. IEEE Trans. Fuzzy Syst. 2016, 24, 401–418. [Google Scholar] [CrossRef]
- Yi, Y.; Zheng, W.X.; Liu, B. Adaptive anti-disturbance control for systems with saturating input via dynamic neural network disturbance modeling. IEEE Trans. Cybern. 2020. [Google Scholar] [CrossRef]
- Kim, K.S.; Rew, K.H.; Kim, S. Disturbance observer for estimating higher order disturbances in time series expansion. IEEE Trans. Autom. Control 2010, 55, 1905–1911. [Google Scholar]
- Yao, X.M.; Park, J.H.; Wu, L.G.; Guo, L. Disturbance-observer-based composite hierarchical anti-disturbance control for singular Markovian jump systems. IEEE Trans. Autom. Control 2019, 64, 2875–2882. [Google Scholar] [CrossRef]
- Freidovich, L.B.; Khalil, H.K. Performance recovery of feedback-linearization-based designs. IEEE Trans. Autom. Control 2008, 53, 2324–2334. [Google Scholar] [CrossRef]
- Chowdhury, D.; Khalil, H.K. Practical synchronization in networks of nonlinear heterogeneous agents with application to power systems. IEEE Trans. Autom. Control 2020, 66, 184–198. [Google Scholar] [CrossRef]
- Utkin, V. Variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Application; Taylor and Francis: London, UK, 1998. [Google Scholar]
- Ding, S.H.; Mei, K.Q.; Li, S.H. A new second-order sliding mode and its application to nonlinear constrained systems. IEEE Trans. Autom. Control 2019, 64, 2545–2552. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, X.; Liu, L.; Dai, T. Adaptive sliding mode neural network control and flexible vibration suppression of a flexible spatial parallel robot. Electronics 2021, 10, 212. [Google Scholar] [CrossRef]
- Huynh, V.V.; Minh, B.L.N.; Amaefule, E.N.; Tran, A.T.; Tran, P.T. Highly robust observer sliding mode based frequency control for multi area power systems with renewable power plants. Electronics 2021, 10, 274. [Google Scholar] [CrossRef]
- Xu, S.S.; Chen, C.; Wu, Z. Study of nonsingular fast terminal sliding-mode fault-tolerant control. IEEE Trans. Ind. Electron. 2015, 62, 3906–3913. [Google Scholar] [CrossRef]
- Wang, J.H.; Xu, Y.L.; Xu., Y.; Yang, D.D. Time-varying formation for high-order multi-agent systems with external disturbances by event-triggered integral sliding mode control. Appl. Math. Comput. 2019, 359, 333–343. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Shen, H.; Karimi, H.R.; Duan, D. Dissipativity-based fuzzy integral sliding mode control of continuous-time T-S fuzzy systems. IEEE Trans. Fuzzy Syst. 2018, 26, 1164–1176. [Google Scholar] [CrossRef]
- Lee, J.; Chang, P.H.; Jin, M. Adaptive integral sliding mode control with time-delay estimation for robot manipulators. IEEE Trans. Ind. Electron. 2017, 64, 6796–6804. [Google Scholar] [CrossRef]
- Yang, C.Y.; Che, Z.Y.; Fu, J.; Zhou, L.N. Passivity-based integral sliding mode control and ε-bound estimation for uncertain singularly perturbed systems with disturbances. IEEE Trans. Circuits Syst. II Exp. Briefs 2019, 66, 3906–3913. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, H.; Zhang, X.; Yi, Y. Integral Sliding Mode Anti-Disturbance Control for Markovian Jump Systems with Mismatched Disturbances. Electronics 2021, 10, 1075. https://doi.org/10.3390/electronics10091075
Shen H, Zhang X, Yi Y. Integral Sliding Mode Anti-Disturbance Control for Markovian Jump Systems with Mismatched Disturbances. Electronics. 2021; 10(9):1075. https://doi.org/10.3390/electronics10091075
Chicago/Turabian StyleShen, Hong, Xiaoli Zhang, and Yang Yi. 2021. "Integral Sliding Mode Anti-Disturbance Control for Markovian Jump Systems with Mismatched Disturbances" Electronics 10, no. 9: 1075. https://doi.org/10.3390/electronics10091075
APA StyleShen, H., Zhang, X., & Yi, Y. (2021). Integral Sliding Mode Anti-Disturbance Control for Markovian Jump Systems with Mismatched Disturbances. Electronics, 10(9), 1075. https://doi.org/10.3390/electronics10091075




