Abstract
Chronic diseases, such as coronary artery disease and diabetes, are caused by inadequate physical activity and are the leading cause of increasing mortality and morbidity rates. Direct calorimetry by calorie production and indirect calorimetry by energy expenditure (EE) has been regarded as the best method for estimating the physical activity and EE. However, this method is inconvenient, owing to the use of an oxygen respiration measurement mask. In this study, we propose a model that estimates physical activity EE using an ensemble model that combines artificial neural networks and genetic algorithms using the data acquired from patch-type sensors. The proposed ensemble model achieved an accuracy of more than 92% (Root Mean Squared Error (RMSE) = 0.1893, = 0.91, Mean Squared Error (MSE) = 0.014213, Mean Absolute Error (MAE) = 0.14020) by testing various structures through repeated experiments.
1. Introduction
Physical inactivity is one of the leading causes of health problems worldwide [1]. Obesity rates have increased considerably in recent decades and is considered a global health challenge following industrialization [2]. Furthermore, diabetes is another disease that is increasingly prevalent [3]. A precise quantitative analysis and evaluation of habitual physical activities are essential to draw accurate and important correlations among key factors, such as sedentary time, physical activity, and health [4]. Diseases such as diabetes are usually caused by an inactive lifestyle; hence, a systematic health care is required. Furthermore, it is also necessary to design a suitable exercise program based on the energy expenditure (EE) required for health improvement.
Many studies have been reported on systems that evaluate EE based on the amount of exercise [5]; these systems generally aim to enhance the health and strength of patients using wireless healthcare monitoring devices [6,7]. Furthermore, in the wake of ubiquitous healthcare systems [8], calorie trackers, heart rate (HR) monitors, and motion detectors have been used to measure EE on exercise indexes. However, existing EE estimation tests and algorithms can be employed only to limited exercises, such as walking and running [9,10,11]. To enhance the basal metabolic rate, it is suggested that bone density and muscular strength through aerobics; tests on different weight training methods should be conducted; and an effective algorithm must be developed. The movement abilities of individuals vary for different exercises. Moreover, it is difficult for individuals to maintain a consistent movement intensity (MI).
Recently, to improve the accuracy of EE measurements, many studies have been conducted using pattern recognition and machine learning. One study improved the EE measurement accuracy using wearable multi-sensors, artificial neural networks, and linear regression line structures to measure the characteristics of different physical activities [12]. To acquire the physical activity data, in this study, three nonlinear regression equation methods that can improve the accuracy of EE prediction using waist-wearing sensors [13] and a linguistic model that can be activated by context-based fuzzy c-means were proposed [14]. A portable accelerometer and an electrocardiogram (ECG) sensor based on a machine-learning model for measuring EE has also been proposed [15]. In other studies, the daily EE was evaluated using a wearable sensor module with a neural network based on a physical activity layer algorithm and a radial basic function neural network [16,17]. Furthermore, a prediction model based on a feed-forward neural network was proposed to represent the effects of physical activity on HR. The model uses data on HR and physical activities and demonstrates a probable prediction with experimental results that are close to the actual data [18,19,20]. In addition, in the medical field, technical data analyses, such as machine learning and data mining, are widely used for early diagnosis. In other recent studies, a hybrid method to improve the reliability of the prediction model for experimental medical treatments has been proposed [21,22]. However, these studies are limited to reliability improvement of the prediction model of existing experimental medical treatments; additionally, technical analyses to estimate the measurement accuracy of energy consumed by various physical activities do not exist. Therefore, in this study, an ensemble model that can estimate the optimal evaluation of EE for various physical activities was developed. The proposed ensemble model achieved an optimization of more than 92%. This model was realized by incorporating probability-based optimized searchable genetic algorithms (GAs) into artificial neural networks (ANNs) to linearly readjust the value of the objective function. The proposed system can reduce accidents in which a fitness person or a sports player is injured due to excessive exercise by accurately grasping the level of physical activity; it is also expected to contribute to improving the sports performance.
2. Materials and Methods
2.1. Overview of Wireless Sensor System
Table 1 shows the physical characteristics of the participants. In this study, 53 applicants (43 males and 10 females) of various age groups were recruited to confirm that the algorithm proposed in this study was applicable to everyone and showed consistent performance. Figure 1 shows a patch-type sensor (AirBeat) [7] that can measure the energy consumption wirelessly. In the past, it was bulky and difficult to use; however, the patch-type sensor used in this study can be easily measured by attaching it to the chest.

Table 1.
Description of subjects.
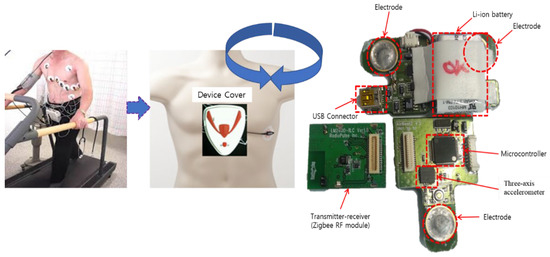
Figure 1.
Proposed design for energy expenditure (EE) measurement.
The wireless sensor system has a built-in patch-type sensor module for wireless monitoring of HR and exercise index. This system module consists of a sensor board, rubber board, and communication module [14]. The sensor board includes a Li-ion battery, universal serial bus (USB) interface connector, Zigbee radio frequency module, ECG acquisition module, microcontroller, voltage regulator, voltage converter, and three-axial acceleration motion detector. The microcontroller used a MSP 430 chip (Texas Instruments, Dallas, TX, USA) with built-in 60 Kb flash memory, 2048 B SRAM memory, and an 8 MHz clock frequency. It incorporates an 8-bit microprocessor and operates in a low-power mode. An ECG measurement device that measures the ECG using three electrodes is attached to the left chest of the user. The ECG measurement process was assessed using a commercial ECG monitor (CASE system, GE Medical, Chicago, IL, USA).
The acquired data were sent to the central monitor through the Zigbee telecommunication module [23] to enable wireless exercise control.
The AirBeat system is a sensor that can be attached to the body in an inverted triangle shape. The proposed system comprises a flexible printed circuit board that contains an analog, a digital electrical network, and sensors. As shown in Table 2, the device enables up to eight people within 400 m radius to perform multi-communication in real time [4,6].

Table 2.
Specifications of the AirBeat system.
The EE estimation model of a wireless sensor system designed to evaluate the EE is presented in Figure 2. During the data collection process, the exercise indexes and HRs of the participants were measured using a patch-type sensor (AirBeat system). The collected data were stored in the sensor modules and transmitted to a central computer through Zigbee modules. Using data processing, ECG signals obtained over 3 s were converted into digital ECG signals and filtered using a low-pass filter (LPF) and high-pass filter (HPF). The filtered output signals underwent pre-processing in three stages: differentiation, squaring, moving averages, dynamic noise removal, and error calibration to detect the HR. The acceleration signals were digitalized using a 12-bit analog-to-digital converter with a 100 MHz sampling rate. Furthermore, a robust zero-crossing detection technique was applied in real time by filtering each channel. The basic feature values for the conversion of exercise indexes were calculated through a two-step zero-crossing detection for noise removal to accurately detect the feature points of complex exercise patterns.
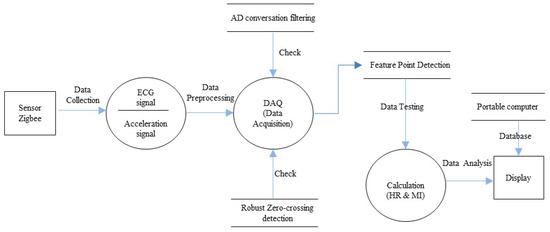
Figure 2.
Data flow diagram of wireless sensor system.
Through the moving window process, the exercise indexes and HRs were separated into consecutive windows for active analysis of the data. In this process, regressions between acceleration signals and exercise data obtained from the ECG signal were analyzed and used to build modules for the EE measurement. Finally, the EE prediction algorithm analyzed the HR and MI to estimate EE [11].
2.2. Optimal Method of EE
The design goal of the optimization method is to minimize the costs or maximize the efficiency. A naive optimal design can be obtained by comparing randomly generated alternative solutions using prior problem knowledge. In this method, the viability of each design was first investigated. Subsequently, our estimates for each solution’s primary objectives (cost and benefit) were compared and the best solution was adopted. The performance of the wireless sensor system and associated equipment can be effectively improved by determining an optimal strategy.
ANNs are widely being used in simulations. Research on ANN-based EE measurement emphasizes the importance of self-learning in process control and energy-use prediction in complex systems without the need for a data-acquisition system and energy management. However, GAs belong to a class of probabilistic search methods that strike a remarkable balance between the EE measurements and estimation of the search space. They significantly differ from random algorithms because they combine the elements of directed and stochastic search methods [24].
A hybrid method has been proposed to optimize the prediction model to minimize the cost of production or maximize production efficiency [25,26,27]. However, to date, the application of this method has been limited to the improvement of experimental medical prediction models or engineering design problems; methods for measuring the optimization of EE for various physical activities have not been developed. In this study, we propose a new hybrid method as an evaluation ensemble model (ANN and GA). The experimental data of various physical activities, including aerobic and anaerobic exercises, were obtained using a wireless sensor system.
The proposed model, a “hybrid neural network-GA EE estimation model,” can predict the evaluation of EE on various physical activities, regardless of the exercise intensity and position of the motion sensor. Accordingly, the EE estimation of a wireless sensor system can be improved.
2.3. Optimization Plan of GA and ANN
A brief outline of the optimization plan is presented in Figure 3. The process begins with the identification of the system input variables and their constraints. The system input variables comprise the measurement and prediction variables. The measurement variables are the targets (such as maximal oxygen uptake, maximum HR, and movement index), that is, the data required to achieve a specific fitness function (FF), such as EE minimization. The prediction variables are measurable quantities that may be controlled by the data; however, they may affect the system performance. The constraints of the input variables define the boundaries of the search space [24]. They are set based on real-life operating experience and knowledge of the system and component features/characteristics.

Figure 3.
Optimization using artificial neural networks–genetic algorithms (ANN-GA).
The next step involves developing the GA population of the input variables for use in a probabilistic optimum search. Subsequently, the system outputs were predicted based on the ANN modeling of the system. For EE estimation employing a wireless sensor system, the FF, beyond the function implied by the name, usually addresses the EE. Once the outputs are available through the ANN computation, the relevant outputs are passed to the cost function routine to determine the latest values and compare them. As the fitness requirements are updated periodically, a new generation is produced and subjected to the same evaluation process. This process continues until the maximum number of generations is reached [23]. The population of the final generated group was designated the final generation of FF.
The GA uses the FF, which is the basis for evaluating the fitness of each individual and the function to be optimized. This function calculates the fitness of each individual in the population. Because the displacement of the FF varies according to the problem, a standardized positive value between the fixed sections is typically used as the fitness value. One standardization method is to linearly readjust the value of the objective function according to the following equation:
where F and F′ denote the FF before standardization and the value of the standardized FF, respectively. Constants a and b may have fixed values from the start to the finish or may be adjusted for each generation.
F′ = aF + b
3. Proposed Method
The EE estimation of a wireless sensor system was studied using 320 data pairs as the learning data. The nominal system parameters are presented in Table 3. In the system model, the parameters were used to verify the nonlinear features of the input variables (training data: VO₂max, HR max, BMI) and output responses (measured data) in Equation (1), along with the EE estimation. FF is the basis for evaluating the fitness of each individual and a function to be optimized; it can be used to compare the performance of individual cases to the standard design case.

Table 3.
Nominal system parameters with different numbers of EE estimation.
3.1. ANN System Representation
The available test data must be optimally represented to train an ANN system model effectively. In the current study, 320 sets of test data and a mixture of field-measured and training data were used. The training was executed systematically with different numbers of nodes in each hidden layer. There are many methods for minimizing errors, such as training the network and changing the weights. Among these methods, the most frequently used is the error back propagation algorithm, which learns the connection load of the forward connection lines used in the activation process of pattern learning. The learning process was performed using the input and output datasets obtained from the system [25,26]. As shown in Figure 4, in this study, we used an error back propagation algorithm in an ANN with a multilayer perceptron, which is a feed-forward-network hierarchical neural network in which the signals are forwarded only from the previous layer to the next layer and an ANN with a sigmoid exponential function.
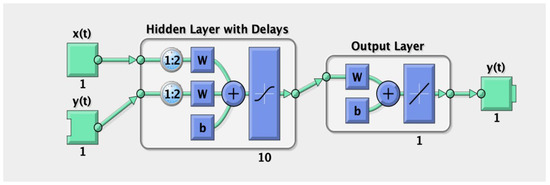
Figure 4.
ANN Structure of a wireless sensor system.
In the neural network, we had ten neurons in the hidden layer, and one output represented the measurement data of the anaerobic and aerobic exercises. As shown in Table 4, six hidden neurons were selected because this proved to be the most optimal method for our learning data.

Table 4.
Neural network performance based on training results.
3.2. Basic Operations of GA
First developed by Holland in 1975, the GA is a calculation model that solves complex real-world problems by simulating the evolution of the natural world on computers. It is a parallel and global search algorithm based on the principle of natural selection and the basic theories of biology of nature [27,28]. In the proposed EE estimation scheme, the outputs of GA optimization should be the optimal set of measurement variables to minimize the FF at a specific value of the prediction variable. The flowchart in Figure 3 outlines the key features of the selected GA evolution program. To solve the optimization problem, we used the steady state GA (SSGA), which uses the elitist uniform crossover, wherein individuals with a high fitness are selected to constitute the next generation, and the roulette wheel (RW) selection method. The SSGA consists of the following steps.
Step 1: Create the initial population, which is a trade-off between an efficient search process and the avoidance of premature convergence. The size of the initial population was 100. For the initial generation, the connection probability of the neurons in the neural network, , was set to 0.3.
Step 2: Select two individuals with the highest fitness in the population.
Step 3: Conduct uniform crossover for the two selected parents; crossover was performed in three steps. First, two parent individuals were selected from the population by the selection operator. Next, the crossover position for chromosome exchange between them was determined randomly. Finally, two new child individuals were created by exchanging the gene values between the two chromosomes based on the crossover position. In this study, the crossover probability, was set to 1.0, it varied adaptively according to the fitness value, as follows:
Step 4: Run the mutation operator to the created children. In the case of the GA that uses binary strings as chromosomes, the mutation operator changes from 0 to 1 and 1 to 0, depending on the mutation probability of each bit. In this study, the mutation probability, was set to 1.0; it changed adaptively, depending on the fitness value, and is expressed as follows:
Step 5: Exclude the two individuals with the lowest fitness from the population.
Step 6: Insert the created children into the population.
Step 7: Repeat Steps 2–6 until the specified number of generations or target value is attained. The algorithm was terminated after a fixed number of iterations. In this study, FF was set to 0.05 [23].
The initial weights of the neural network were confirmed using a GA. Subsequently, the neural network was learned using the training data. Seventy pairs of data were used as learning data in the neural network generation algorithm through the genetic-neuro system. The parameters used in the generation was the maximum hidden layer neuron number Hmax 12, 2000 repetition number, and 300 initial generated individuals; the RW method was used to determine the choice of maternal line. Further, we substituted 10% of the best individuals from this generation for the worst individuals in the next generation.
By comparing the early generations of the 300 individuals using test and verification data, it was confirmed that the mean absolute percentage error improved. We used a one-point crossover for the recombination and set the mating probability, Pc = 1, as shown in Figure 5, to adjust the conformity value. A Gaussian operator was used for the crossover, as shown in Figure 6. The probability of connection of the early generation nerve network neuron was Plink = 0.3, the probability of mutation was Pm = 0.1, and the goodness-of-fit function was F′ = 0.05.
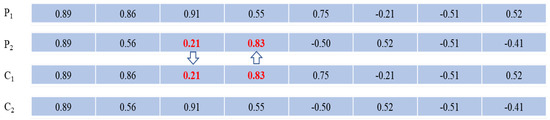
Figure 5.
Recombination, two-point crossover. P1 and P2 were chosen randomly from within the genes in the parents. C1 and C2 are the generated children.

Figure 6.
Mutation, Gaussian operator. P is the elected parent, Pm is the mutation probability, and C is the generated child.
4. Discussion
The energy expenditure prediction algorithm using the ensemble model proposed in this study was optimized for 53 healthy adults. Performance evaluation was performed according to the number of neurons, to improve the performance of the ensemble model. The best results were obtained when six neurons were held.
A comparison of the performance of previous studies and the proposed algorithm is provided in Table 5. In previous studies, energy expenditure was measured with the subject wearing an oxygen mask and a device on the chest. Eight parameters were extracted from the data, including heart rate, breath rate, acceleration counts, and chest skin temperature. These parameters were learned through a multiple regression model, and thus, energy expenditure was measured. Another study measured energy consumption by measuring heart rate, respiration, and motion information in both arms, thighs, and chest. Eleven subjects participated in an experiment in which pre-designated protocols such as sitting, office work, and treadmill tests were conducted for 3 h. In addition, this study measured energy consumption by extracting the HR from 20 subjects with spinal cord injury. The algorithm proposed in this study uses a multiple linear model and an artificial neural network. Seven feature points, such as standard deviation, coefficient of variation, and HR index, were extracted from the HR, and energy consumption was extracted through data fitting and model evaluation. The disadvantage of the aforementioned studies was the requirement to wear an oxygen mask and a sensor on the chest. However, the energy consumption extraction method proposed in this study enables accurate energy consumption measurement using a probabilistic method by simply attaching a wireless sensor system with a built-in HR monitor and accelerometer.

Table 5.
Performance comparison table with previous studies.
5. Results
The following three optimal control cases were studied for a range of EE estimations [31]:
- Case 1: General physical activity and exercise
- Case 2: Four exercises (walking, fast walking, running, and slow running)
- Case 3: Variable anaerobic exercise
- Case 4: Results from the proposed algorithm
The results of these three optimal control cases were compared with those of the normalized (standard design) case. In the normalized case, the input variables were maintained at their nominal values, that is, 70% training data, 20% validation data, and 10% test data.
A comparison of the EE (kcal) under the general physical activity/exercise condition is shown in Figure 7. As can be observed, over the entire range of EE, most of the exercise energy was consumed in the normalized case. The excess in EE was generally +2 kcal and −3 kcal than that of case +1.5 kcal and −2 kcal greater than that of Case 2, and 1 kcal greater than that of Case 3.
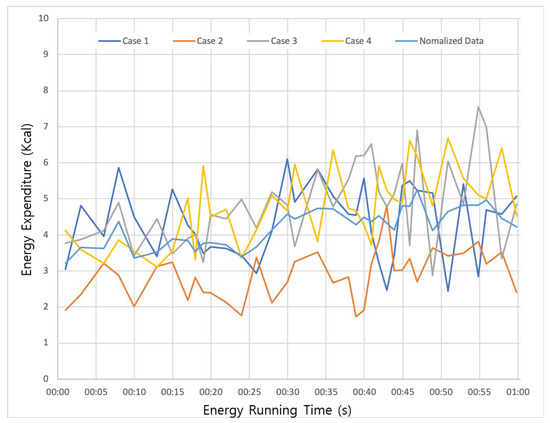
Figure 7.
Approximation of EE (kcal) for general physical activity/exercise conditions.
The drops in the MSE, along with the epochs, during the training and validation processes are illustrated in Figure 8. It can be observed that the training and test curves are very close. In these processes, the auto-stop function was imposed, and the best results were obtained in approximately 112 epochs for both cases. The final results of the simulation, including the MSE and correlation coefficients, R2, were less than 9% for the output variables, and the MSE was 0.01664. This is significantly better than those of the single-hidden-layer configurations, where the MSE values exceeded 0.01. A comparison of the EE MSE for the general physical activity/exercise condition is shown in Figure 8, where it can be seen that the EE reached a nearly MSE of the exercise running time. This applies to all four cases. It was also found that although the MSE values appeared close for all four cases at exercise time, there were considerable improvements in the three optimal cases in which EE was estimated to be above 5%.
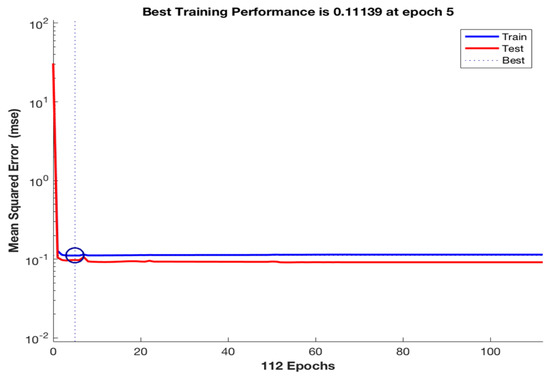
Figure 8.
Distribution of EE Mean Squared Error (MSE) for general physical activity exercise conditions.
Across all these comparisons, the EE estimation provides a successful optimization of a general physical activity/exercise case. This demonstrates the potential of achieving a higher EE when using more control variables in the optimal control strategy. In a previous study, the accuracy was 92% when we used an ANN for the optimal prediction of EE [32]. Therefore, the energy consumption prediction using the hybrid ANN and GA model proposed in this study can perform more than 5% optimization compared to the ANN model. This study also illustrates the potential of applying ANN modeling and GA search techniques for EE estimation using wireless sensor systems.
6. Conclusions
We propose a new hybrid method to improve EE prediction performance. The optimal utilization of EE estimation in wireless sensor systems is important for achieving accurate EE predictions. To customize the performance of the neural network, an optimal neural network was constructed. The hybrid neural network GA exhibited excellent accuracy in EE prediction optimization. The proposed model, which is an ensemble of a GA and a neural network used to automatically design a neural network, can increase the performance of the optimal neural network by up to 5%. Both neural networks and GAs are particularly suitable for investigating the complex nonlinear EE estimation, considering the ability of the ANN to learn complex nonlinear mapping and that of the GA to search for the global optimum in a limited parametric space. This method can be applied to predict the EE of various activities to verify high accuracy and optimization performance. New data for other features related to EE must be verified using this algorithm. The aim of this study was to develop a mobile solution application that suggests a customized exercise after the user completes one round of running with AirBeat, based on the algorithm acquired from the current exercise. This is expected to provide an optimized exercise method tailored to each individual to maximize energy consumption by learning existing health data.
Author Contributions
K.H.K. constructed the energy expenditure model and suggested the concepts for the work; M.K. and S.S. analyzed the data and performed the experiments; J.J. reviewed the firmware and analyzed the data for the research; M.L. supervised the writing of the article, gave suggestions. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
This research was supported by the Mid-career Researcher Program (No. 2016R1A2B3009423) through NRF grant funded by the MSIT (Ministry of Science and ICT) and the Basic Science Research Program through the NRF funded by the Ministry of Education of Korea (No. 2018R1A6A1A 030 15496), and the Jilin Education Program (JJKH20201015KJ) of China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cordain, L.; Gotshalla, R.W.; Eatonb, S.B. Evolutionary Aspects of Exercise. World Rev. Nutr. Diet. 1997, 1, 49–60. [Google Scholar]
- World Health Organization. Obesity: Preventing and managing the global epidemic. In Report of a WHO Consultation; WHO Technical Report Series 894; World Health Organization: Geneva, Switzerland, 2000. [Google Scholar]
- Sarah, W.; Roglic, G.; Green, A.; Sicree, R.; King, H. Global prevalence of diabetes: Estimates for the year 2000 and projections for 2030. Diabetes Care 2004, 27, 1047–1053. [Google Scholar] [CrossRef]
- Simon, M.; Ramirez, E. Reducing sedentary behavior: A new paradigm in physical activity promotion. Am. J. Lifestyle Med. 2011, 5, 518–530. [Google Scholar]
- Kim, Y.T.; Park, D.G.; Kang, J.; Seo, K.S. Development of patch type sensor module for real-time monitoring of heart rate and agility index. In Proceedings of the 7th IEEE Conference on Sensors (SENSORS 2008), Lecce, Italy, 26–29 October 2008; pp. 1151–1154. [Google Scholar]
- Meina, L.; Byun, K.H.; Kim, H.J.; Kang, J.; Kim, Y.T. Patch type sensor module for estimating the energy expenditure. In Proceedings of the 8th IEEE Conference on Sensors (SENSORS 2009), Christchurch, New Zealand, 25–28 October 2009; pp. 1455–1458. [Google Scholar]
- Li, M.; Kim, Y.T. Development of patch-type sensor module for wireless monitoring of heart rate and movement index. Sens. Actuators A Phys. 2012, 173, 277–283. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Lee, D.-S.; Mukhopadhyay, S.; Chung, W.-Y. Ubiquitous healthcare data analysis and monitoring using multiple wireless sensors for elderly person. Sens. Transducer J. 2008, 90, 87–99. [Google Scholar]
- Lin, C.-W.; Yang, Y.-T.; Wang, J.-S.; Yang, Y.-C. A wearable sensor module with a neural-network-based activity classification algorithm for daily energy expenditure estimation. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 991–998. [Google Scholar]
- Twomey, N.; Faul, S.; Marnane, W.P. In Comparison of accelerometer-based energy expenditure estimation algorithms. In Proceedings of the 4th International Conference on Pervasive Computing Technologies for Healthcare, Munchen, Germany, 22–25 March 2010; pp. 1–8. [Google Scholar]
- Kang, K.H.; Kim, Y.T. Energy expenditure prediction algorithm based on correlation analysis of exercise indexes. In Proceedings of the International Conference on Information Science and Applications (ICISA 2014), Seoul, Korea, 6–9 May 2014; pp. 1–4. [Google Scholar]
- Dong, B.; Biswas, S.; Montoye, A.; Pfeiffer, K. Comparing metabolic energy expenditure estimation using wearable multi-sensor network and single accelerometer. In Proceedings of the 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC 2013), Osaka, Japan, 3–7 July 2013; pp. 2866–2869. [Google Scholar]
- Vathsangam, H.; Emken, A.; Schroeder, E.T.; Spruijt-Metz, D.; Sukhatme, G.S. Determining energy expenditure from treadmill walking using hip-worn inertial sensors: An experimental study. IEEE Trans. Biomed. Eng. 2011, 10, 2804–2815. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Kwak, K.C.; Kim, Y.T. Intelligent predictor of energy expenditure with the use of patch-type sensor module. Sensors 2012, 12, 14382–14396. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.S.; Lin, C.W.; Yang, Y.T.; Kao, T.P.; Wang, W.H.; Chen, Y.S. A Pace sensor system with machine learning-based energy expenditure regression algorithm. In Proceedings of the 7th International Conference on Intelligent Computing (ICIC 2011), Zhengzhou, China, 11–14 August 2011; pp. 529–536. [Google Scholar]
- Ng, W.W.; Xu, S.; Wang, T.; Zhang, S.; Nugent, C. Radial Basis Function Neural Network with Localized Stochastic-Sensitive Autoencoder for Home-Based Activity Recognition. Sensors 2020, 5, 1479–1495. [Google Scholar] [CrossRef] [PubMed]
- Meina, L.; Kwak, K.-C.; Kim, Y.T. Estimation of Energy Expenditure Using a Patch-Type Sensor Module with an Incremental Radial Basis Function Neural Network. Sensors 2016, 16, 1566. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, Y.M.; Yuchi, M.; Ding, M.Y. Heart Rate Prediction Model Based on Physical Activities Using Evolutionary Neural Network. In Proceedings of the International Conference on Genetic and Evolutionary Computing (ICGEC 2010), Shenzhen, China, 13–15 December 2010; pp. 198–201. [Google Scholar]
- Yuchi, M.; Jo, J. Heart Rate Prediction Based on Physical Activity Using Feedforward Neural Network. In Proceedings of the International Conference on Convergence and Hybrid Information Technology (ICHIT 2008), Busan, Korea, 11–13 November 2008; pp. 344–350. [Google Scholar]
- Xiao, F.; Yuchi, M.; Jo, J.; Ding, M.Y.; Hou, W.G. A Research of Physical Activity’s Influence on Heart Rate Using Feedforward Neural Network. In Proceedings of the 6th International Symposium on Neural Networks (ISNN 2009), Wuhan, China, 26–29 May 2009; pp. 1089–1096. [Google Scholar]
- Mitchell, T.M. Genetic Algorithms; Machine Learning: Boston, MA, USA, 1997; pp. 249–270. [Google Scholar]
- Simon, H. Neural networks: A comprehensive foundation. Knowl. Eng. Rev. 1994, 13, 409–412. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Genetic Algorithms. In Introduction to Evolutionary Computing; Springer: New York, NY, USA, 2003; pp. 37–69. [Google Scholar]
- Zakeria, M.; Bahramib, A.; Anijdanb, S.H.M. Using genetic algorithm in heat treatment optimization of 17-4PH stainless steel. Mater. Des. 2007, 28, 2034–2039. [Google Scholar] [CrossRef]
- Arabasadi, Z.; Alizadehsani, R.; Roshanzamir, M.; Moosaei, H.; Yarifard, A.A. Computer aided decision making for heart disease detection using hybrid neural network-Genetic algorithm. Comput. Methods Programs Biomed. 2017, 141, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Pappu, S.M.J.; Gummadi, S.N. Artificial neural network and regression coupled genetic algorithm to optimize parameters for enhanced xylitol production by Debaryomyces nepalensis in bioreactor. Biochem. Eng. J. 2017, 120, 136–145. [Google Scholar] [CrossRef]
- Chow, T.T. Global optimization of absorption chiller system by genetic algorithm and neural network. Energy Build. 2002, 34, 103–109. [Google Scholar] [CrossRef]
- Gjoreski, H.; Kaluža, B.; Gams, M.; Milić, R.; Luštrek, M. Context-based ensemble method for human energy expenditure estimation. Appl. Soft Comput. 2015, 37, 960–970. [Google Scholar] [CrossRef]
- Lu, K.; Yang, L.; Seoane, F.; Abtahi, F.; Forsman, M.; Lindecrantz, K. Fusion of heart rate, respiration and motion measurements from a wearable sensor system to enhance energy expenditure estimation. Sensors 2018, 18, 3092. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Masso, X.; Serra-Ano, P.; Garcia-Raffi, L.; Sanchez-Perez, E.; Giner-Pascual, M.; Gonzalez, L.M. Neural network for estimating energy expenditure in paraplegics from heart rate. Int. J. Sports Med. 2014, 35, 1037–1043. [Google Scholar] [CrossRef] [PubMed]
- Anderson, C.; Christine, M. Practical genetic algorithms. J. Am. Stat. Assoc. 2005, 100, 1099. [Google Scholar] [CrossRef]
- Kang, K.H.; Shin, S.H.; Jung, J.; Kim, Y.T. Estimation of a physical activity energy expenditure with a patch-type sensor module using artificial neural network. Concurr. Comput. Pract. Exp. 2021, 33, e5455. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).