A Generic Interface Enabling Combinations of State-of-the-Art Path Planning and Tracking Algorithms
Abstract
1. Introduction
2. The Path Tracking Problem
3. Tracking Error Classification
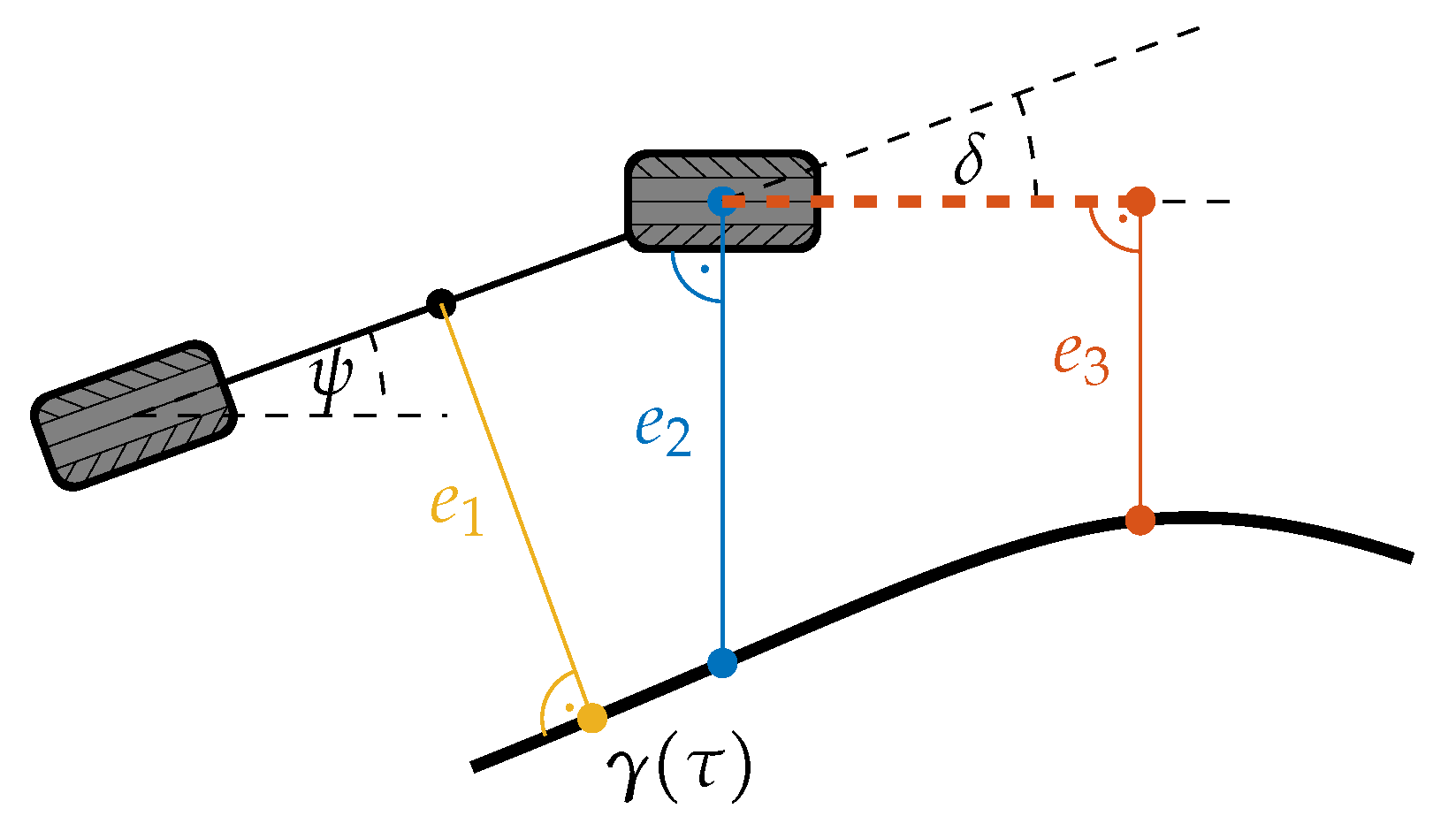
3.1. Vehicle Reference Point
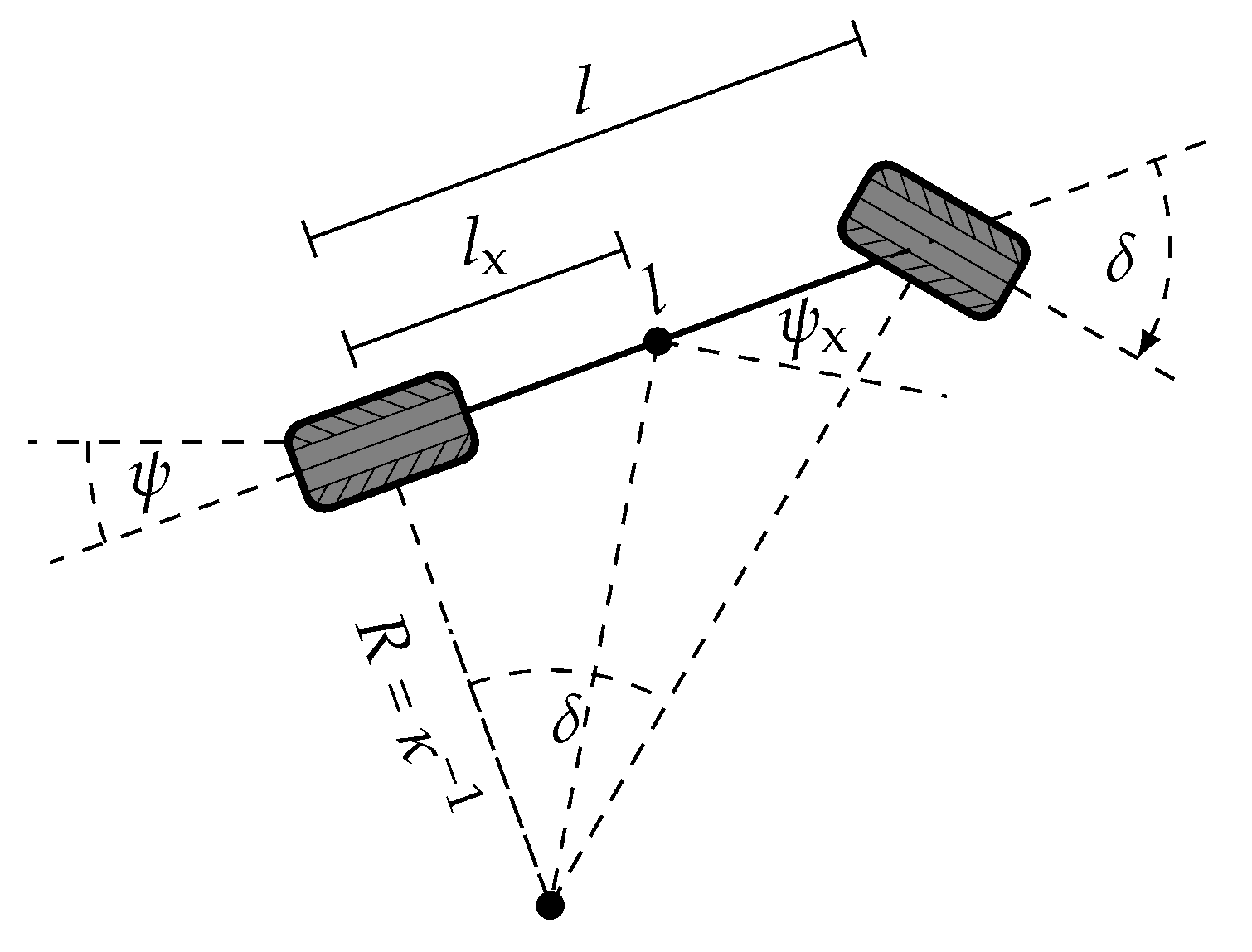
- Rear axle: A vehicle, in general, features non-holonomic dynamics. The rear axle is the point of the vehicle with the "most constrained" motion. Assuming zero lateral slip, the motion of the rear axle is aligned with the vehicle heading. Therefore, a constant zero tracking implies that also the vehicle heading is aligned to the reference path, which is a favorable tracking property. From control system theory the center of the rear axle is of interest, as it is a flat output of the system restricting on slip-free vehicle kinematics (see for example [11,16]). The turning radius of the rear axle in cornering is smaller than the turning radius of the front axle (see Figure 4). Therefore, the choice of the rear axle as a vehicle reference point, in general, implies potential undesired overshooting of the vehicle’s front.
- Front axle: If the vehicle reference point is set to the center of the front axle, the non-holonomic vehicle kinematics in principle do not have to be considered in the control design, as stopping and adjustment of the steering angle enables tracking of arbitrary reference paths within the limited turning radius. This enables a simplified control design, especially for low dynamic driving tasks as parking. A drawback of this reference point is the smaller turning radius of the rear axle in cornering (cf. rear axle reference point), which implies potentially undesired curve cutting.
- Center of gravity: The choice of the center of gravity as a vehicle reference, simplifies the setup of the vehicle’s equations of motion. Therefore, it is used in many control system design approaches. From tracking perspective its position, somewhere in the middle of the car is of interest, in order to minimize the total distance of all points with respect to the reference path.
- Center of oscillations/percussion: In the center of oscillation or percussion, the translation and rotation impact of a lateral tire slip at the rear axle are in balance. Consequently, this point is of special interest in order to design control laws, which are robust with respect to lateral rear axle tires slip. The choice of this reference point is popular in tracking controllers designed for limit-handling, as racing applications (see for example [17,18]). For front-wheel-steered vehicles the position of the center of percussion with respect to the rear axle is:where is the distance of rear axle and center of gravity, m the vehicle mass and the vehicle’s inertia in the center of gravity with respect to the vertical vehicle axis.
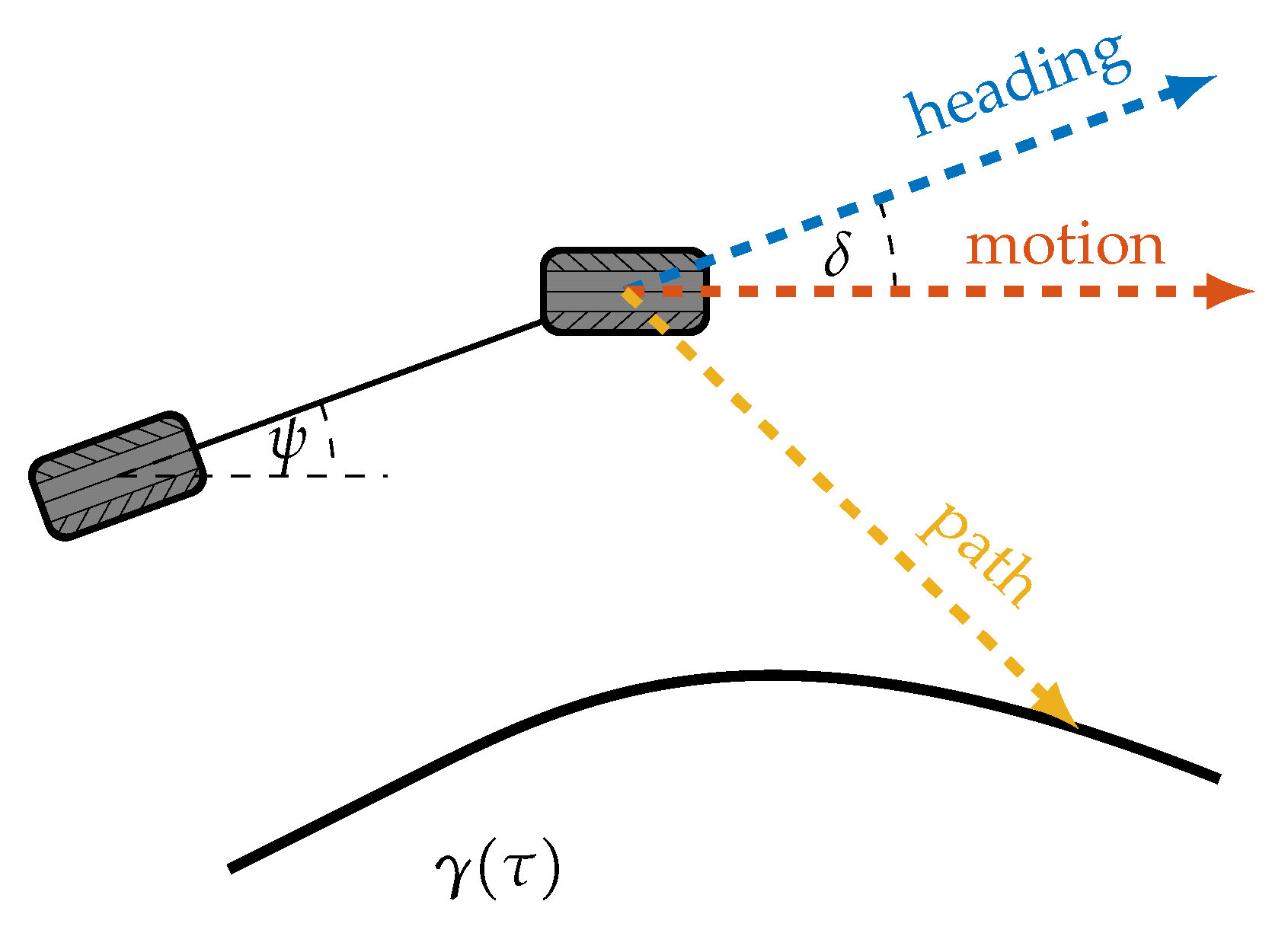
3.2. Look-Ahead
- look-ahead towards the vehicle heading,
- look-ahead towards the direction of motion in vehicle reference point,
- and look-ahead towards the reference path in a certain distance.
3.3. Error Orientation
- perpendicular to the vehicle heading,
- perpendicular to the direction of vehicle motion in the vehicle reference point,
- perpendicular to the path.
3.4. Application to State-of-the-Art Tracking Controller
4. Tracking Error Computation
4.1. Intersection of Reference Path and a Straight Line
4.2. Intersection of Reference Path and a Circle
4.3. Point Projection Onto the Reference Path
5. Summary of Interface Requirements from Tracking Control Perspective
6. Interface Requirements from Path Planning Perspective
- Global: Identification for the respective path segment.
- Local: Application of the actual error computation within the path segment (see Section 4).
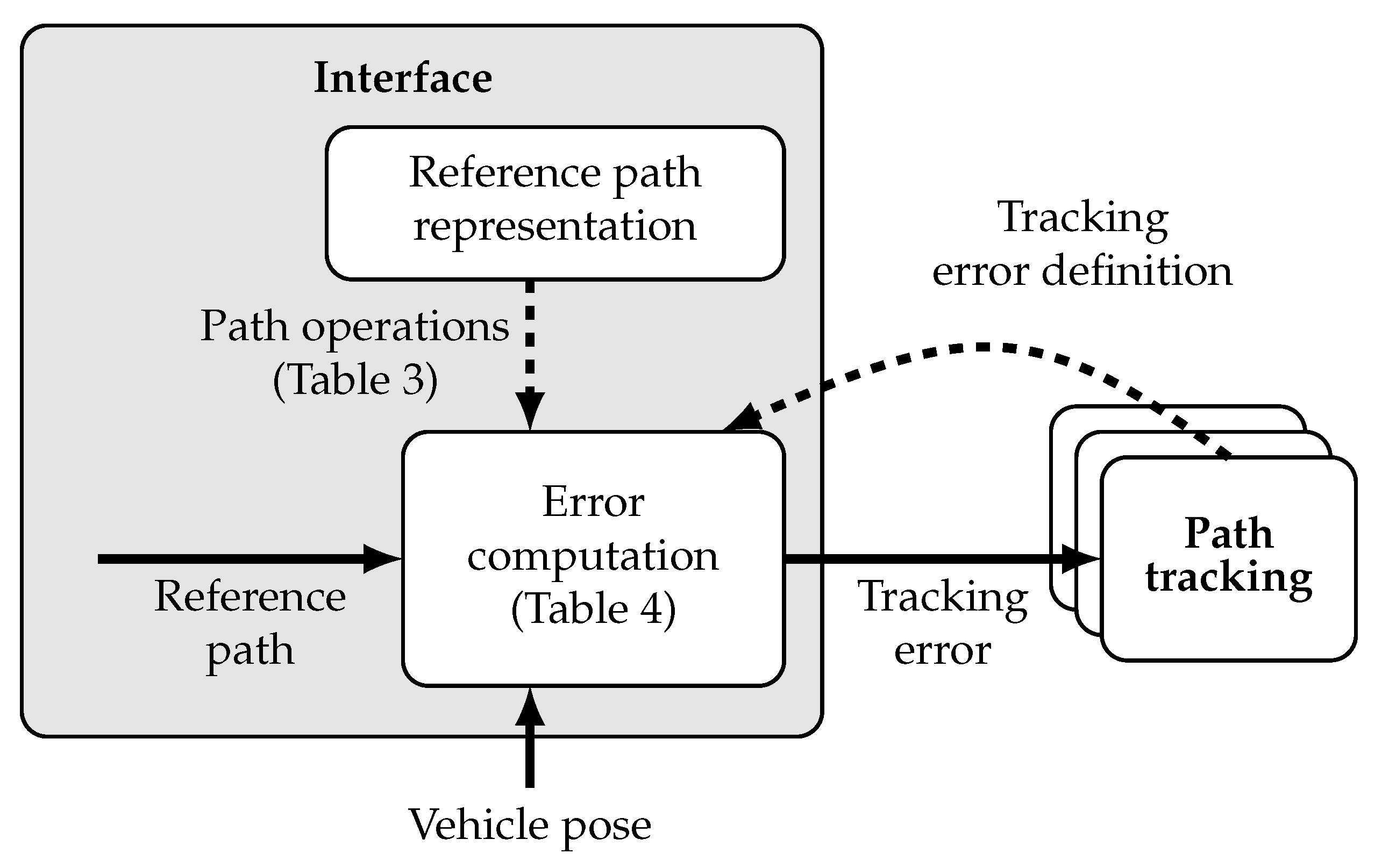
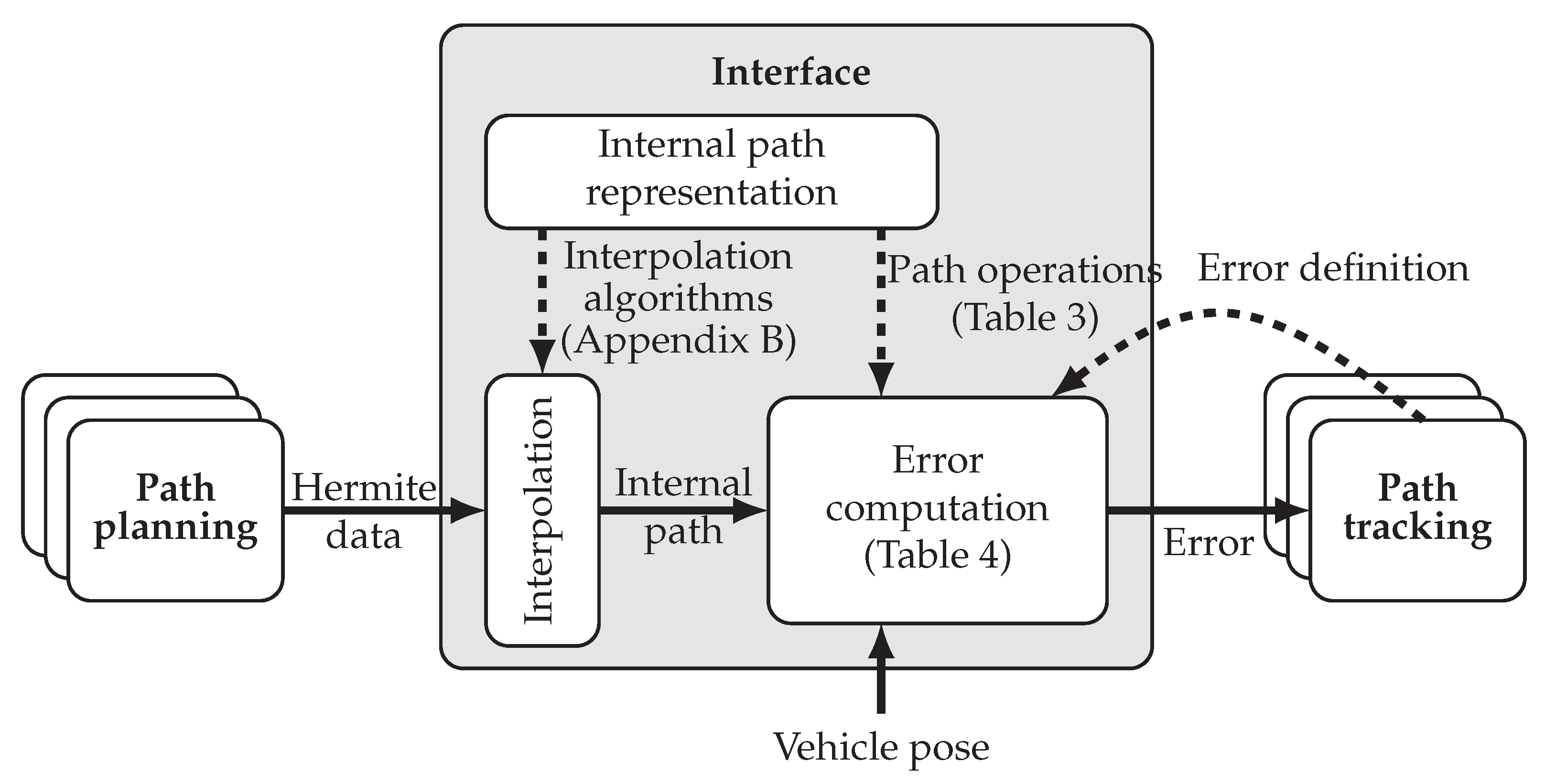
7. A Generic Path Planning and Tracking Interface
- Decision for an internal path representation.
- Implementation of corresponding Hermite waypoint data interpolation algorithms (see Appendix B), in order to accomplish input (planning) modularity with respect to different data types (G0, G1, ⋯).
- Implementation of corresponding error computation, based on the path operations discussed in Section 4 (path-line intersection, path-circle intersection and point projection), in order to accomplish output modularity (control).
- In simulation, it supports a straight-forward identification of an appropriate component set, based on iterative combination, simulation and evaluation, considering specific scenarios and corresponding KPIs. This is an important aspect of ODD-based AD function assembly. Furthermore, a specific error definition can be applied as common evaluation measure for a set of tracking controllers, which could not be compared on a quantitatively based on their different native error definition on a fair basis (cf. the example in Section 8).
- In operation, it enables the simultaneous execution of different software components as well as switching between different components. This on the one hand supports the design of AD-functions, for a set of varying ODDs extending the application range of Level 4 driving functions. On the other hand, it supports the application of redundant and fail-operational software in order to increase safety of an AD function.
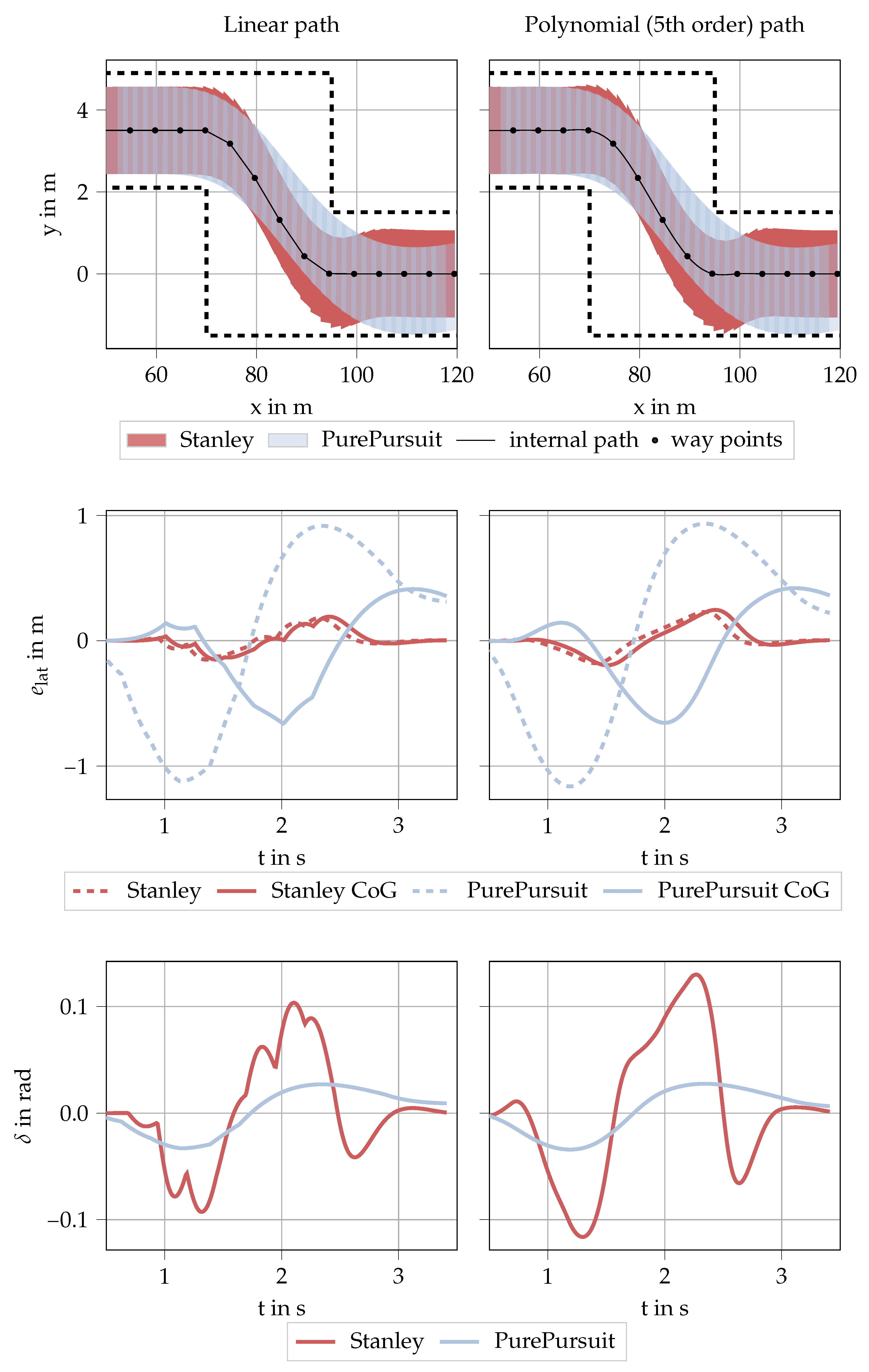
8. Exemplary Interface Application
Discussion
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
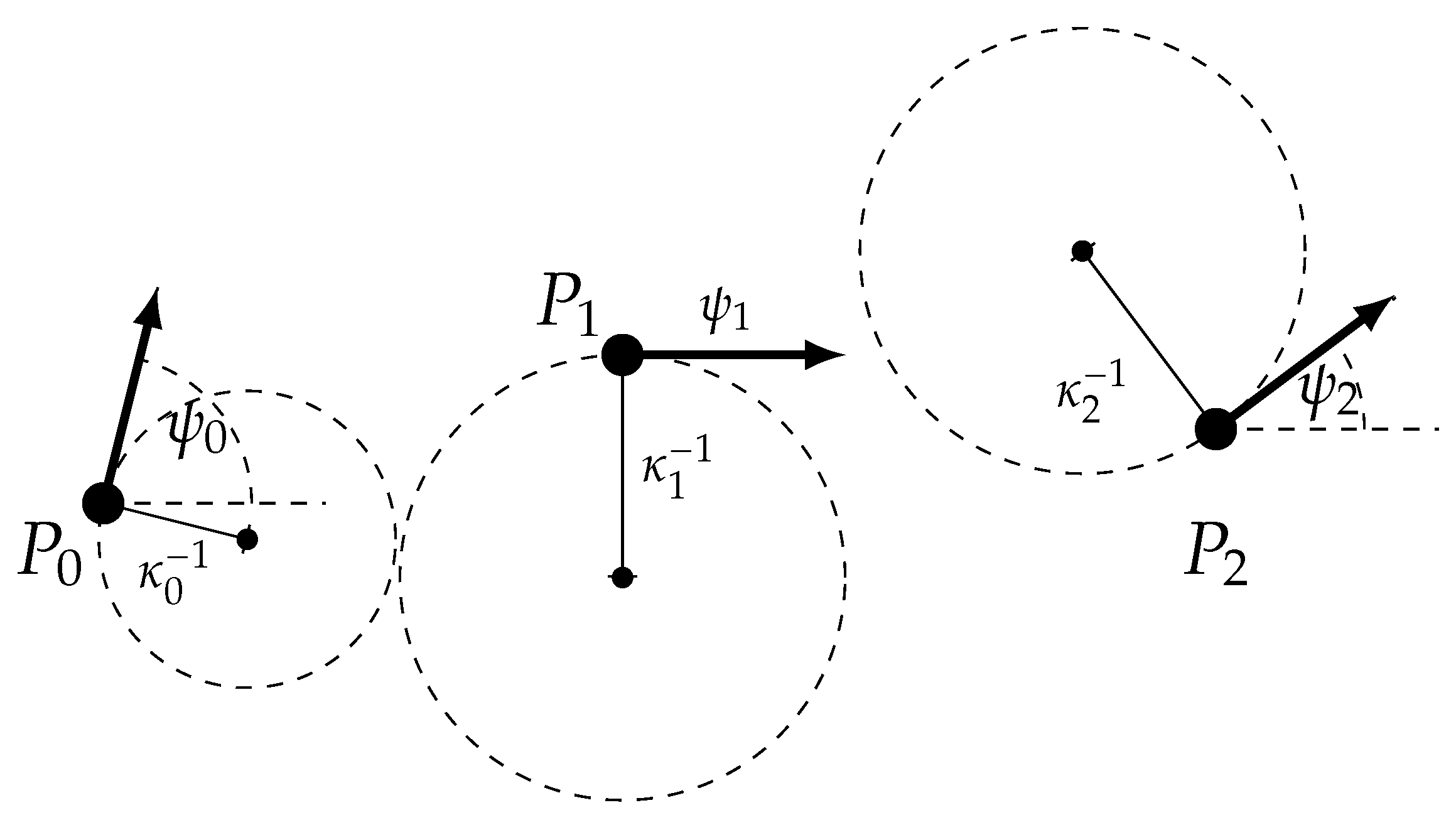
Appendix A. Parametric Path
Appendix A.1. Basics
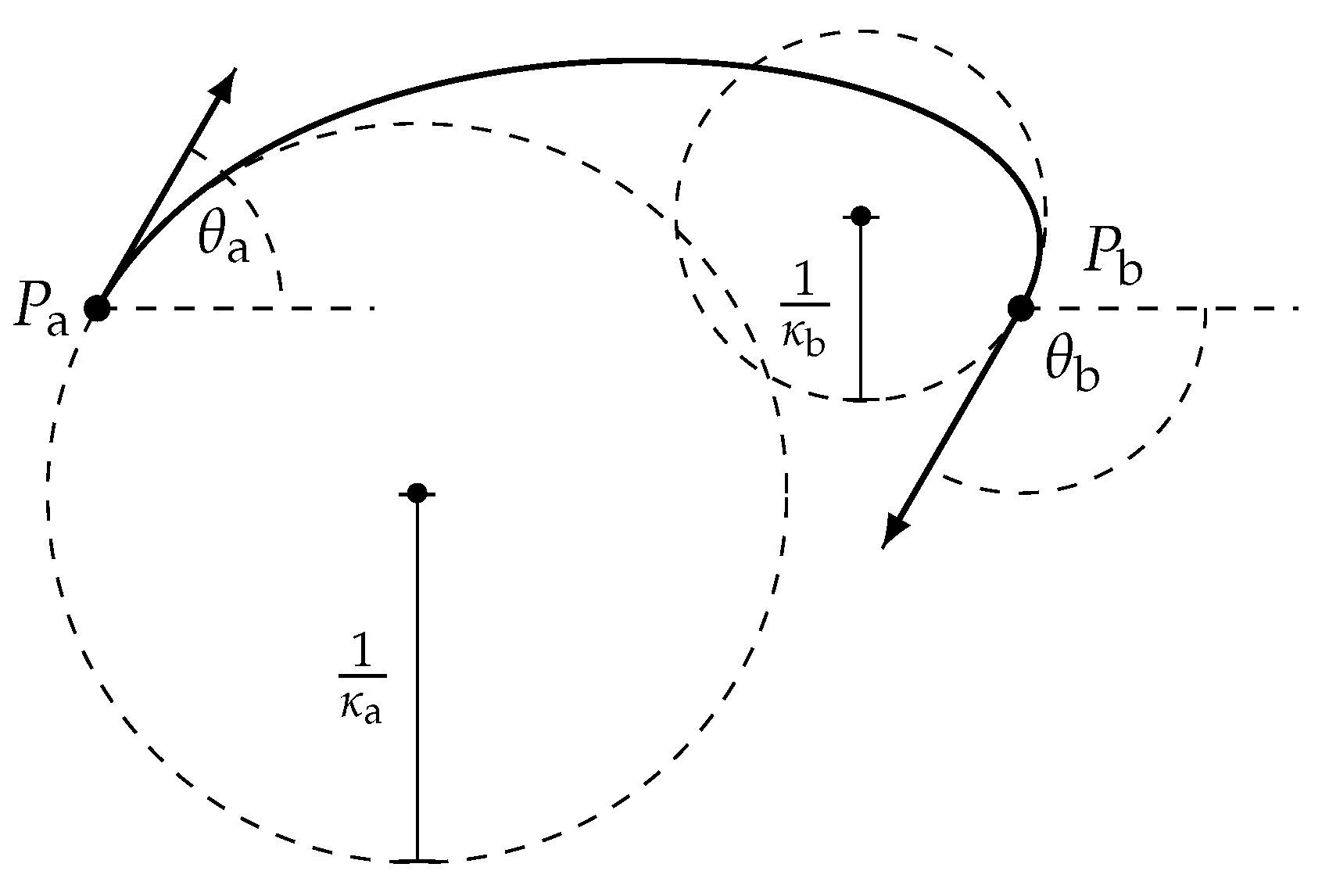
Appendix A.2. Clothoidal Path
Appendix A.3. Polynomial Path
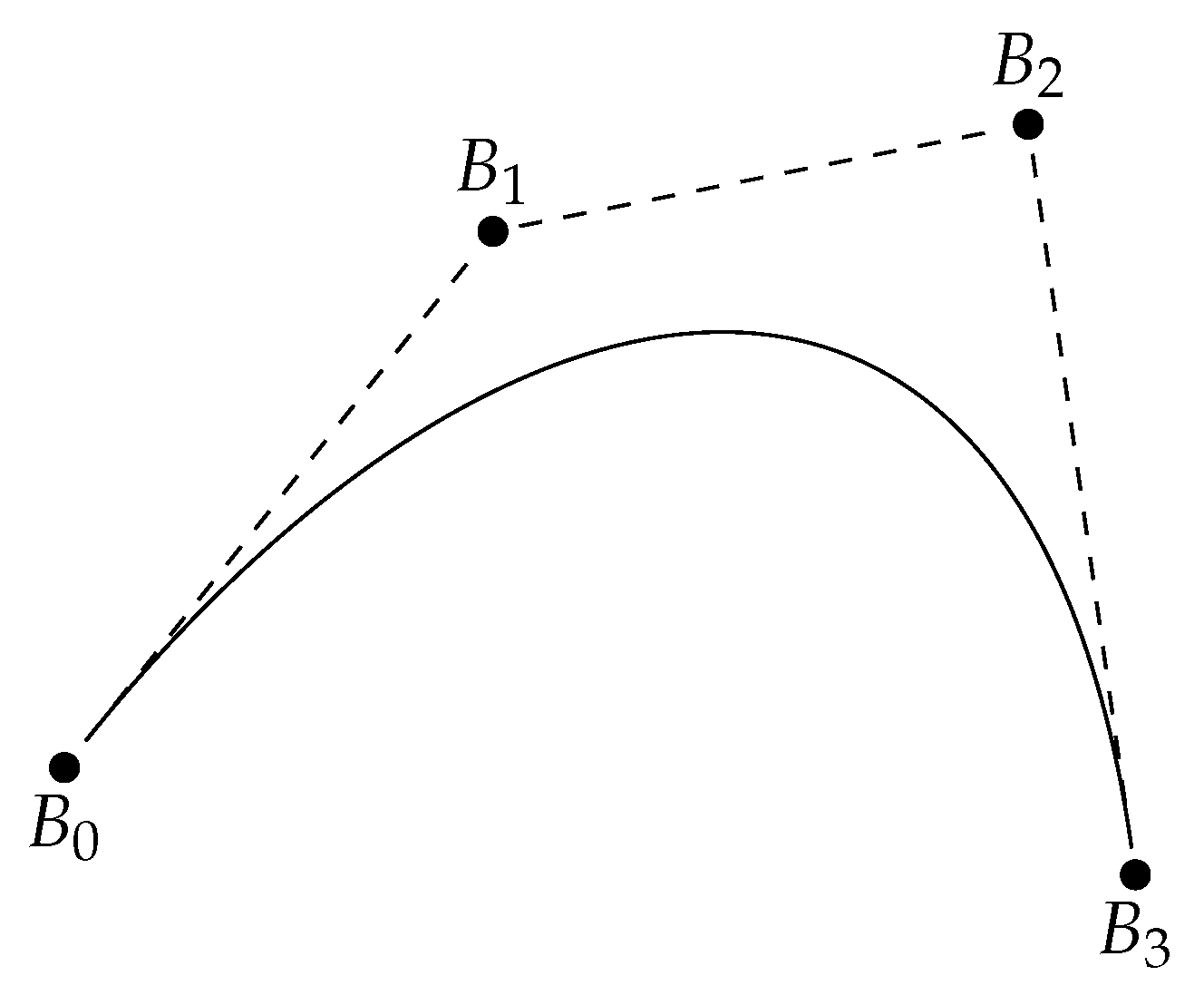
Appendix B. Hermite Data Interpolation
| Data | Continuity | Spline Order | Boundary Conditions |
|---|---|---|---|
| C0 | C2 | 3 | 4 |
| C1 | C2 | 4 | 2 |
| C0 | C3 | 4 | 6 |
| C1 | C3 | 5 | 4 |
References
- SAE. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles; SAE: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A Survey of Autonomous Driving: Common Practices and Emerging Technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Ulbrich, S.; Reschka, A.; Rieken, J.; Ernst, S.; Bagschik, G.; Dierkes, F.; Nolte, M.; Maurer, M. Towards a functional system architecture for automated vehicles. arXiv 2017, arXiv:1703.08557. [Google Scholar]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Paden, B.; Cap, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Sorniotti, A.; Barber, P.; De Pinto, S. Path Tracking for Automated Driving: A Tutorial on Control System Formulations and Ongoing Research. In Automated Driving; Watzenig, D., Horn, M., Eds.; Springer: Cham, Switzerland, 2017; Chapter 5; pp. 71–140. [Google Scholar]
- You, D.; Wang, H.; Yang, K. State-of-the-art and trends of autonomous driving technology. In Proceedings of the TEMS-ISIE 2018-1st Annual International Symposium on Innovation and Entrepreneurship of the IEEE Technology and Engineering Management Society, Beijing, China, 30 March–1 April 2018. [Google Scholar] [CrossRef]
- Kato, S.; Tokunaga, S.; Maruyama, Y.; Maeda, S.; Hirabayashi, M.; Kitsukawa, Y.; Monrroy, A.; Ando, T.; Fujii, Y.; Azumi, T. Autoware on board: Enabling autonomous vehicles with embedded systems. In Proceedings of the 9th ACM/IEEE International Conference on Cyber-Physical Systems (ICCPS), Porto, Portugal, 11–13 April 2018; pp. 287–296. [Google Scholar]
- Hamid, U.Z.A.; Saito, Y.; Rahman, M.A.A.; Zamzuri, H.; Raksincharoensak, P. A review on threat assessment, path planning and path tracking strategies for collision avoidance systems of autonomous vehicles. Int. J. Veh. Auton. Syst. 2018, 14, 134. [Google Scholar] [CrossRef]
- Tang, J. Review: Analysis and Improvement of Traffic Alert and Collision Avoidance System. IEEE Access 2017, 5, 21419–21429. [Google Scholar] [CrossRef]
- Werling, M.; Gröll, L. From flatness-based trajectory tracking to path following. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 271–1275. [Google Scholar] [CrossRef]
- De Luca, A.; Oriolo, G.; Samson, C. Feedback control of a nonholonomic car-like robot. In Robot Motion Planning and Control; Laumond, J.-P., Ed.; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 1998; Volume 229, Chapter 4; pp. 171–253. [Google Scholar]
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking. In Technical Report CMU-RI-TR-09-08; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Chatzikomis, C.; Sorniotti, A.; Gruber, P.; Zanchetta, M.; Willans, D.; Balcombe, B. Comparison of Path Tracking and Torque-Vectoring Controllers for Autonomous Electric Vehicles. IEEE Trans. Intell. Veh. 2018, 3, 559–570. [Google Scholar] [CrossRef]
- Calzolari, D.; Schurmann, B.; Althoff, M. Comparison of trajectory tracking controllers for autonomous vehicles. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, Yokohama, Japan, 16–19 October 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Rouchon, P.; Fliess, M.; Levine, J.; Martin, P. Flatness, motion planning and trailer systems. In Proceedings of the 32nd Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; pp. 2700–2705. [Google Scholar]
- Kritayakirana, K.; Gerdes, J.C. Using the centre of percussion to design a steering controller for an autonomous race car. Veh. Syst. Dyn. 2012, 50, 33–51. [Google Scholar] [CrossRef]
- Peters, S.C.; Frazzoli, E.; Iagnemma, K. Differential flatness of a front-steered vehicle with tire force control. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 298–304. [Google Scholar] [CrossRef]
- Xu, S.; Peng, H. Design, Analysis, and Experiments of Preview Path Tracking Control for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 21, 48–58. [Google Scholar] [CrossRef]
- Nestlinger, G.; Stolz, M. Bumpless Transfer for Convenient Lateral Car Control Handover. IFAC-PapersOnLine 2016, 49, 132–138. [Google Scholar] [CrossRef]
- Broggi, A.; Bertozzi, M.; Fascioli, A.; Bianco, C.G.L.; Piazzi, A. The ARGO Autonomous Vehicle’s Vision and Control Systems. Int. J. Intell. Control Syst. 1999, 3, 409–441. [Google Scholar]
- Yuan, X.; Huang, G.; Shi, K. Improved Adaptive Path Following Control System for Autonomous Vehicle in Different Velocities. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3247–3256. [Google Scholar] [CrossRef]
- Guldner, J.; Sienel, W.; Tan, H.S.; Ackermann, J.; Patwardhan, S.; Bünte, T. Robust automatic steering control for look-down reference systems with front and rear sensors. IEEE Trans. Control Syst. Technol. 1999, 7, 2–11. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F.; Chen, N. Should the Desired Heading in Path Following of Autonomous Vehicles be the Tangent Direction of the Desired Path? IEEE Trans. Intell. Transp. Syst. 2015, 16, 3084–3094. [Google Scholar] [CrossRef]
- Hoffmann, G.M.; Tomlin, C.J.; Montemerlo, M.; Thrun, S. Autonomous automobile trajectory tracking for off-road driving: Controller design, experimental validation and racing. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 2296–2301. [Google Scholar] [CrossRef]
- Kolb, J.K.; Nitzsche, G.; Wagner, S. A simple yet efficient Path Tracking Controller for Autonomous Trucks. IFAC-PapersOnLine 2019, 52, 307–312. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Xi, L.; Tian, Y. Design of a path-tracking steering controller for autonomous vehicles. Energies 2018, 11, 1451. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Zhou, Q.; Tian, Y. A Model Predictive Controller with Switched Tracking Error for Autonomous Vehicle Path Tracking. IEEE Access 2019, 7, 53103–53114. [Google Scholar] [CrossRef]
- Chen, C.; Jia, Y.; Shu, M.; Wang, Y. Hierarchical Adaptive Path-Tracking Control for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2900–2912. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Y.; Wang, J.; Member, S. Fuzzy Observer-Based Transitional Path-Tracking Control for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 1–11. [Google Scholar] [CrossRef]
- Bruschetta, M.; Picotti, E.; Mion, E.; Chen, Y.; Beghi, A.; Minen, D. A Nonlinear Model Predictive Control based Virtual Driver for high performance driving. In Proceedings of the CCTA 2019-3rd IEEE Conference on Control Technology and Applications, Hong Kong, China, 19–21 August 2019; pp. 9–14. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, J.; Qiu, J.; Yang, W.; Sun, H.; Chen, Q. A Novel Fuzzy Observer-Based Steering Control Approach for Path Tracking in Autonomous Vehicles. IEEE Trans. Fuzzy Syst. 2019, 27, 278–290. [Google Scholar] [CrossRef]
- Hiraoka, T.; Nishihara, O.; Kumamoto, H. Automatic path-tracking controller of a four-wheel steering vehicle. Veh. Syst. Dyn. 2009, 47, 1205–1227. [Google Scholar] [CrossRef]
- Tieber, K. Motion planning and control of a people mover. Master’s Thesis, Graz University of Technology, Graz, Austria, 2019. [Google Scholar]
- Samson, C. Path Following And Time-Varying Feedback Stabilization of a Wheeled Mobile Robot. In Proceedings of the Second International Conference on Automation, Robotics and Computer Vision, Singapore, 16–18 September 1992; Volume 3. [Google Scholar]
- Dominguez, S.; Ali, A.; Garcia, G.; Martinet, P. Comparison of lateral controllers for autonomous vehicle: Experimental results. In Proceedings of the IEEE Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1418–1423. [Google Scholar] [CrossRef]
- Solea, R.; Nunes, U. Trajectory planning with velocity planner for fully-automated passenger vehicles. In Proceedings of the IEEE Conference on Intelligent Transportation Systems (ITSC), Toronto, ON, Canada, 17–20 September 2006; pp. 474–480. [Google Scholar] [CrossRef]
- Ackermann, J.; Guldner, J.; Sienel, W.; Steinhauser, R. Linear and Nonlinear Controller Design for Robust Automatic Steering. IEEE Trans. Control Syst. Technol. 1995, 3, 132–143. [Google Scholar] [CrossRef]
- Elkaim, G.H.; Connors, J.; Nagle, J. The overbot: An off-road autonomous ground vehicle testbed. In Proceedings of the Institute of Navigation-19th International Technical Meeting of the Satellite Division (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006; Volume 3, pp. 1449–1456. [Google Scholar]
- Sentouh, C.; Chevrel, P.; Mars, F.; Claveau, F. A sensorimotor driver model for steering control. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 2462–2467. [Google Scholar] [CrossRef]
- Coulter, R.C. Implementation of the Pure Pursuit Path Tracking Algorithm. In Technical Report CMU-RI-TR-92-01; Carnegie Mellon University: Pittsburgh, PA, USA, 1992. [Google Scholar]
- Cibooglu, M.; Karapinar, U.; Soylemez, M.T. Hybrid controller approach for an autonomous ground vehicle path tracking problem. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED 2017), Valletta, Malta, 3–6 July 2017; Volume 8, pp. 583–588. [Google Scholar] [CrossRef]
- Spencer, M.R. Polynomial Real Root Finding in Bernstein Form Polynomial Real Root Finding in Bernstein Form. Ph.D Thesis, Birgham Young University-Provo, Provo, UT, USA, 1994. [Google Scholar]
- McNamee, J.M.; Pan, V.Y. Efficient polynomial root-refiners: A survey and new record efficiency estimates. Comput. Math. Appl. 2012, 63, 239–254. [Google Scholar] [CrossRef][Green Version]
- Meek, D.S.; Walton, D.J. A note on finding clothoids. J. Comput. Appl. Math. 2004, 170, 433–453. [Google Scholar] [CrossRef][Green Version]
- Ma, Y.L.; Hewitt, W.T. Point inversion and projection for NURBS curve: Control polygon approach. In Proceedings of the Theory and Practice of Computer Graphics (TPCG), Birmingham, UK, 5 June 2003; Volume 20, pp. 113–120. [Google Scholar] [CrossRef]
- Chen, X.D.; Zhou, Y.; Shu, Z.; Su, H.; Paul, J.C. Improved Algebraic Algorithm On Point Projection For Bézier Curves. In Proceedings of the Second International Multi-Symposiums on Computer and Computational Sciences (IMSCCS 2007), Iowa City, IA, USA, 13–15 August 2007. [Google Scholar]
- Song, H.C.; Xu, X.; Shi, K.L.; Yong, J.H. Projecting points onto planar parametric curves by local biarc approximation. Comput. Graph. 2014, 38, 183–190. [Google Scholar] [CrossRef]
- Hu, S.M.; Wallner, J. A second order algorithm for orthogonal projection onto curves and surfaces. Comput. Aided Geom. Des. 2005, 22, 251–260. [Google Scholar] [CrossRef]
- Latombe, J.C. Robot Motion Planning; Springer: Boston, MA, USA, 1991. [Google Scholar]
- Lavalle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.; Morys, B.; Pan, S.; Wang, J.; Li, K. Threat Assessment Techniques in Intelligent Vehicles: A Comparative Survey. IEEE Intell. Transp. Syst. Mag. 2020. [Google Scholar] [CrossRef]
- Lefèvre, S.; Vasquez, D.; Laugier, C. A survey on motion prediction and risk assessment for intelligent vehicles. ROBOMECH J. 2014, 1, 1–14. [Google Scholar] [CrossRef]
- Choe, R.; Puig-Navarro, J.; Cichella, V.; Xargay, E.; Hovakimyan, N. Trajectory Generation Using Spatial Pythagorean Hodograph Bézier Curves. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimee, FL, USA, 5–9 January 2015; pp. 1–32. [Google Scholar] [CrossRef]
- Scheuer, A.; Laugier, C. Planning Sub-Optimal and Continuous-Curvature Paths for Car-Like Robots. In Proceedings of the 1998 IEEE/RSJ International Conference on Intelligent Robots and Systems. Innovations in Theory, Practice and Applications (Cat. No.98CH36190), Victoria, BC, Canada, 17 October 1998; Volume 1, pp. 25–31. [Google Scholar] [CrossRef]
- Gim, S.; Adouane, L.; Lee, S.; Dérutin, J.P. Clothoids Composition Method for Smooth Path Generation of Car-Like Vehicle Navigation. J. Intell. Robot. Syst. Theory Appl. 2017, 88, 129–146. [Google Scholar] [CrossRef]
- Bertolazzi, E.; Frego, M. On the G 2 Hermite Interpolation Problem with clothoids. J. Comput. Appl. Math. 2018, 341, 99–116. [Google Scholar] [CrossRef]
- Meek, D.S.; Walton, D.J. Clothoid Spline Transition Spirals. Math. Comput. 1992, 59, 117. [Google Scholar] [CrossRef]
- Vázquez-Méndez, M.E.; Casal, G. Clothoid computation: A simple and efficient numerical algorithm. J. Surv. Eng. 2016, 142, 1–9. [Google Scholar] [CrossRef]
- Chen, Y.; Cai, Y.; Zheng, J.; Thalmann, D. Accurate and Efficient Approximation of Clothoids Using Bézier Curves for Path Planning. IEEE Trans. Robot. 2017, 33, 1242–1247. [Google Scholar] [CrossRef]
- Montés, N.; Herraez, A.; Armesto, L.; Tornero, J. Real-time clothoid approximation by rational bezier curves. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 2246–2251. [Google Scholar] [CrossRef]
- Horner, W.G. A new method of solving numerical equations of all orders, by continuous approximation. Philos. Trans. R. Soc. Lond. 1819, 109, 308–335. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS Book; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.C. Path smoothing techniques in robot navigation: State-of-the-art, current and future challenges. Sensors 2018, 18, 3170. [Google Scholar] [CrossRef]
- Bojanov, B.D. Spline Functions and Multivariate Interpolations; Springer Netherlands Imprint Springer: Dordrecht, The Newtherland, 1993. [Google Scholar]
- Schaback, R. Optimal Geometric Hermite Interpolation of Curves. In Mathematical Methods for Curves and Surfaces II; Daehlen, M., Lyche, T., Schumaker, L.L., Eds.; Vanderbilt University Press: Nashville, TN, USA, 1998; pp. 1–12. [Google Scholar]
- Krajnc, M. Interpolation scheme for planar cubic G 2 spline curves. Acta Appl. Math. 2011, 113, 129–143. [Google Scholar] [CrossRef]
- Piazzi, A.; Guarino Lo Bianco, C. Quintic G/sup 2/-splines for trajectory planning of autonomous vehicles. In Proceedings of the IEEE Intelligent Vehicles Symposium 2000, Dearborn, MI, USA, 3–5 October 2000; pp. 198–203. [Google Scholar] [CrossRef]
- Piazzi, A.; Lo Bianco, C.G.; Bertozzi, M.; Fascioli, A.; Broggi, A. Quintic G2-Splines for the Iterative Steering of Vision-Based Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2002, 3, 27–36. [Google Scholar] [CrossRef]
- Piazzi, A.; Romano, M.; Lo Bianco, C.G. G3-splines for the path planning of wheeled mobile robots. In Proceedings of the European Control Conference (ECC 2003), Cambridge, UK, 1–4 September 2003; pp. 1845–1850. [Google Scholar] [CrossRef]
- Piazzi, A.; Lo Bianco, C.; Romano, M. n3-Splines for the Smooth Path Generation of Wheeled Mobile Robots. IEEE Trans. Robot. 2007, 23, 1089–1095. [Google Scholar] [CrossRef]
- Manocha, D.; Canny, J.F. Detecting cusps and inflection points in curves. Comput. Aided Geom. Des. 1992, 9, 1–24. [Google Scholar] [CrossRef]
- Walton, D.J.; Meek, D.S. Cubic Bezier Spiral Segments for Planar G2 Curve Design. In Proceedings of the 7th International Conference on Computer Graphics, Virtual Reality, Visualisation and Interaction in Africa, Franschhoek, South Africa, 21–23 June 2010; pp. 21–26. [Google Scholar] [CrossRef]


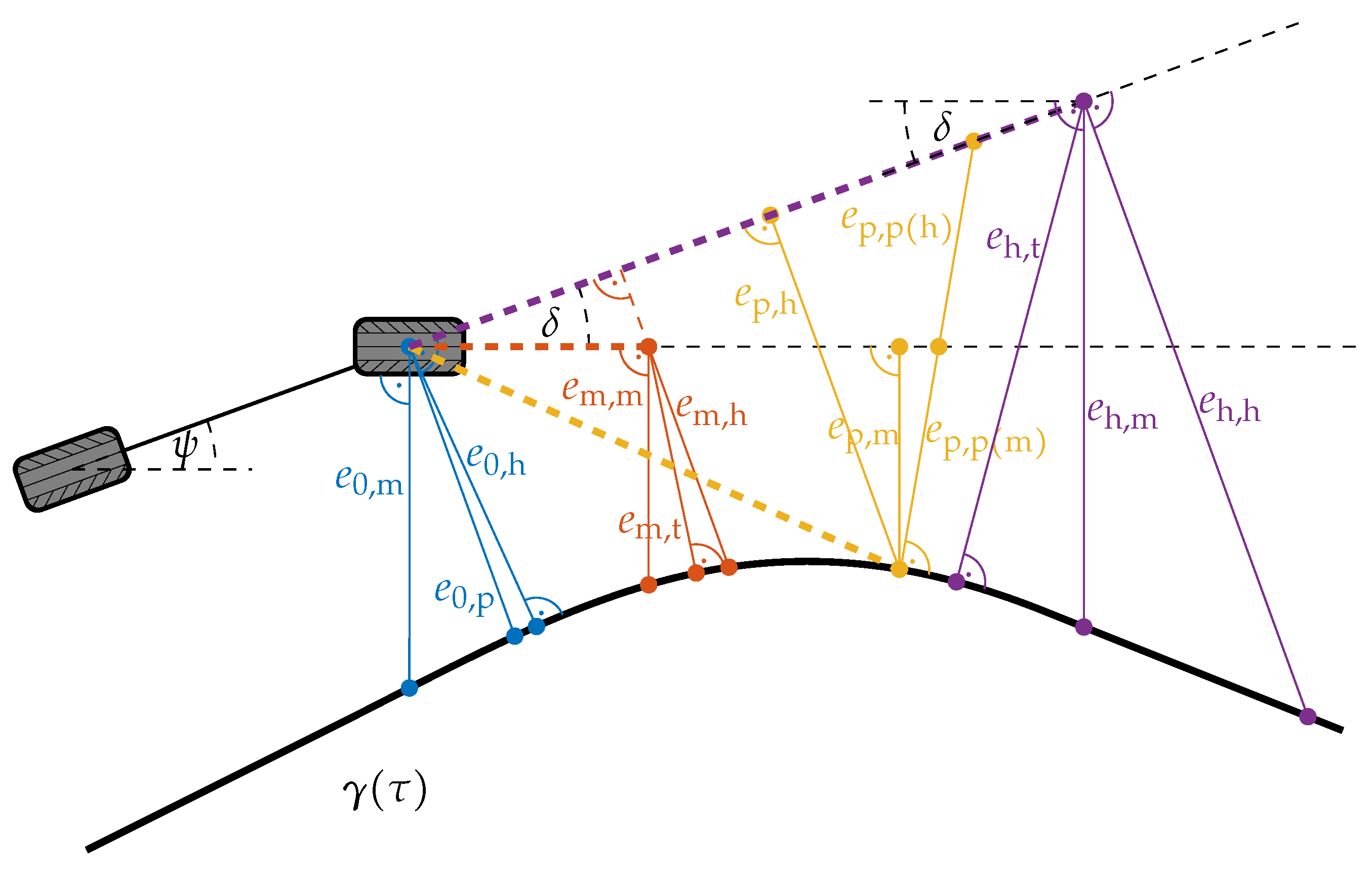


| Look-Ahead | Error Orientation | |
|---|---|---|
| no | heading | |
| no | motion | |
| no | path | |
| heading | heading | |
| heading | motion | |
| heading | path | |
| motion | heading | |
| motion | motion | |
| motion | path | |
| path | heading | |
| path | motion | |
| path | path (heading) | |
| path | path (motion) |
| Controller | Vehicle Ref. | Look-Ahead | Error Orient. |
|---|---|---|---|
| Hoffmann (Stanley) [25], Kolb [26] | front | no | path |
| Sun [27,28], Kritayakirane [17], | CG | no | path |
| Chen [29], Hu [30] Bruschetta [31] | |||
| Chatzikomis [14], Xu [19], Zhang [32] | CG | no | heading |
| Hiraoka [33] | CP | no | path |
| Tieber [34], Samson [35], | rear | no | path |
| Dominguez [36], Solea [37] | |||
| Nestlinger [20], Ackermann [38], | CG | heading | heading |
| ARGO [21], Guldner [23], Yuan [22] | |||
| Elkaim [39] | CG | heading | path |
| Solea [37] | rear | motion | path |
| Sentouh [40] | CG | motion | motion |
| Coulter (Pure-pursuit) [41] | rear | path | heading |
| Operation | |
|---|---|
| A | intersection line/path |
| B | intersection circle/path |
| C | point projection on path |
| a | intersection line/line |
| c | point projection on line |
| Error Orientation | ||||
|---|---|---|---|---|
| Path | Heading | Motion | ||
| look-ahead | no | C | A | A |
| path | B+a | B+c | B+c | |
| heading | C | A | A | |
| motion | C | A | A | |
| Parameter | Value |
|---|---|
| k | 19 |
| 1 | |
| 0.013 | |
| vehicle reference | front |
| look-ahead | no |
| error orientation | path |
| Parameter | Value |
|---|---|
| l | 2.68 m |
| 10 m | |
| vehicle reference | rear |
| look-ahead | path |
| error orientation | heading |
| Approach |
|
| Concept |
|
| Benefits |
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rumetshofer, J.; Stolz, M.; Watzenig, D. A Generic Interface Enabling Combinations of State-of-the-Art Path Planning and Tracking Algorithms. Electronics 2021, 10, 788. https://doi.org/10.3390/electronics10070788
Rumetshofer J, Stolz M, Watzenig D. A Generic Interface Enabling Combinations of State-of-the-Art Path Planning and Tracking Algorithms. Electronics. 2021; 10(7):788. https://doi.org/10.3390/electronics10070788
Chicago/Turabian StyleRumetshofer, Johannes, Michael Stolz, and Daniel Watzenig. 2021. "A Generic Interface Enabling Combinations of State-of-the-Art Path Planning and Tracking Algorithms" Electronics 10, no. 7: 788. https://doi.org/10.3390/electronics10070788
APA StyleRumetshofer, J., Stolz, M., & Watzenig, D. (2021). A Generic Interface Enabling Combinations of State-of-the-Art Path Planning and Tracking Algorithms. Electronics, 10(7), 788. https://doi.org/10.3390/electronics10070788






