Abstract
This manuscript deals with the situation in which the different agents or buses in a power network have access to local renewable resources and must manage its use in a distributed fashion. The buses distributedly decide the amount of power to be generated using their local renewable power plants, and that to be demanded from the grid. The decisions are made according to the optimization of a cost function that considers both economic and technical factors. The problem is approached resorting to a game-theoretical framework that requires a negotiation process among the neighboring buses. An iterative algorithm is proposed in order to solve this problem, providing existence and convergence conditions under which the buses reach a suitable equilibrium. The algorithm performance is tested in simulations over a modification of the IEEE 14-bus system, in which the lines are modeled as resistances and distributed generation is considered. Simulations on a network of 44 buses are also included to show the scalability of the method.
1. Introduction
The electric power system is defined as a network of electrical components deployed to supply, transfer, store, and use electric power. Traditional power systems have a top-down operated architecture in which their components can be broadly classified as generators that supply the electric power; the transmission system that carries the power to the load centers; and the distribution system that feeds the loads. This paradigm is now being altered by the creation of real-time electricity markets and the integration of the so-called prosumers, that is, agents at the electricity grid that can both consume and produce power. This new situation, on the one hand, creates new opportunities for a better network regulation and penetration of renewable energy and, on the other hand, introduces new needs for real-time communication and control algorithms.
Although there is a controversial debate about the current effects of the electricity liberalization on electricity prices, it is clear that the real implementation of competitive markets should lead to efficiency gains in the economy, thus reducing electricity prices. More importantly, this paradigm allows the system to integrate distributed renewable generation plants, reducing wholesale prices [1] and fulfilling the environmental objectives. As an example, in Europe, the goal is to double the production of energy from renewable sources in only 10 years, which, given the distributed and variable nature of renewable energy plants, represents a tremendous challenge for the grid and introduces the need of new distributed algorithms to preserve network stability [2].
This manuscript considers a liberalized market in which each bus or agent is capable of making real-time decisions according to economical and technical factors. The problem is formulated for DC grids, which, in comparison to conventional AC networks, provide certain advantages, as, for example, the absence of reactive power or an efficient integration with small distributed generation units, whose power is obtained in DC, and with common appliances, which operate using a DC voltage [3]. In addition, DC networks do not have synchronization requirements, which drastically reduce the complexity in the control of the system [4].
On the other hand, DC networks have some associated disadvantages over the traditional AC transmission system. Perhaps the main one is that, due to commutation problems, electrical power cannot be produced with a high DC voltage, and the voltage cannot be increased by using a power transformer. In addition, circuit breakers for DC systems are more expensive than those for AC systems. Anyway, the proposed approach can be extended to AC networks under the hypothesis of near-zero angles in the different voltage buses (see, for instance, [5]).
Obviously, the decisions taken by the different buses, if acting purely as selfish agents minimizing their costs, can dramatically affect the voltage regulation of the grid, making the power flow unfeasible or extremely inefficient. This way, coordination and negotiation algorithms become crucial for the real implementation of these paradigms. In this context of competition, many authors have resorted to Game Theory, which is a branch of mathematics that study the interaction and decision of rational players or agents whose goals can be in opposition (non-cooperative games), see reference [6]. This mathematical modeling has been used to cope with this kind of problems in electric systems ([7]). In [8], a problem in which a set of generators must choose the price of selling of the energy generated is introduced. A bid adjustment algorithm is presented for the resulting Bertrand competition game, which is a rather well-known non-cooperative game in which, at each iteration, the sellers (generators) change their bids and the system operator decides how much production to allocate to each of them. In [9,10], the authors propose a non-cooperative game-theoretic framework to study the strategic behavior of distributed microgrids that generate renewable energies. The former is based on a sequence of linearized games; meanwhile, the latter extends the previous work to a distributed and resilient fashion. Another similar approach can be found in [10], where the game is stated over an AC microgrid using an approximation to DC considering that the angle of the different voltage buses are near zero [5]. Furthermore, in [11] a non-cooperative game-theoretic framework for optimally controlling energy storage systems (ESSs) in power distribution networks is proposed. In that context, the work not only takes into consideration economic factors but also grid stability aspects, including the power flow constraints. Game Theory has also been applied to the demand-side management problem in which the users intend to reduce their monetary expenses by producing or storing rather than just purchasing their energy needs from the grid [12,13]. Finally, in [14], several distributed schemes to solve the optimal power flow problem in power systems are presented. However, none of them model and solve the problem in a realistic non-cooperative fashion, modeling the selfish nature of involved actors.
This manuscript studies a situation in which (all of some of) the grid buses or agents are capable of making decisions according to local interests (cost functions). These decisions are encapsulated through the voltage levels at each bus, which can be controlled using the converter interfaces of the distributed generators. In these cost functions, both economical and stability factors are considered. Each bus is able to manage a limited renewable generation unit, whose generated power affects the bus costs/revenues, to its voltage level, and to the losses in the lines. In order to reach a suitable equilibrium, the article proposes a new algorithm based on a negotiation process that can be formulated as a non-cooperative game. The algorithm has the following features:
- The decisions can be taken in a distributed and negotiated manner.
- The algorithm ensures both the consideration of local (economic) objectives and the fulfillment of physical and operational limitations of the grid.
- The privacy of the different buses is preserved, and therefore there is no sensible information, as locally produced and demanded power, operation costs or local power generation limits is shared.
- An analysis of the negotiation algorithm is developed when the decisions of the buses are subjected to constraints that evolve during the negotiation. This constitutes a mayor theoretical extension compared to other preliminary results obtained by the authors in [15,16].
- Local conditions to ensure the convergence to a suitable equilibrium are provided.
The above-mentioned dynamical evolution of the constraints appears as a result of the explicit consideration of limitations in the power lines, which depends on the decisions made by the agents or buses. To the best of the authors’ knowledge, this is the first time that this problem is tackled explicitly including these limitations, which involves a relevant difficulty to the convergence analysis, and it has been typically neglected (see, for instance, [10]) or approximated by a fixed value. For instance, Ref. [11] considers a fixed bound in the active power transference; however, this bound physically evolves with the voltage level at the line extremes. Related to this, another main contribution of the article is the development of conditions to ensure the existence and convergence of the negotiation algorithm that can be locally checked. Differently from other negotiation algorithms such as [9], here each bus can distributedly modify the weights in its local cost function without exchanging critical information with the rest of the network. Finally, the proposed algorithm preserves buses privacy and does not share any critical information during the negotiation and, differently from [10], each bus only requires knowledge about the parameters of adjacent power lines.
This manuscript is organized as follows: Section 2 presents the problem setup and the grid model. In Section 3, the problem is formally stated together with the assumption needed. Section 4 introduces a game-theoretical-based algorithm in order to solve the problem. The conditions under which the problem can be solved are presented in Section 5. Finally, some simulation examples are drawn in Section 6 and conclusions are exposed in Section 7.
Notation 1.
A graph is an ordered pair comprising a set of vertices or buses, and a set of edges or power lines. An undirected graph is a graph in which edges have no orientation, so that, if , then . The neighborhood of i, is defined as the set of vertices with edges connected to vertex i. denotes the element in the i-th row and j-th of the matrix A. Finally, denotes the i-th element of the vector x.
2. Problem Set up and Grid Modeling
Consider a direct-current power network comprising a set of buses connected according to a given undirected graph , where represents the set of power lines between the buses. Consider also that each bus is endowed with a smart device able to measure and process the electric variables of the bus, and to communicate with neighboring buses through the power lines (see, for instance, [17]). Moreover, each bus must feed a local load that demands a power, , and may have access and control a local renewable energy plant to generate power .
Let denote the current incoming from bus j to bus i (), the current demanded by the load of bus i, and the current injected by bus i through its local renewable plant. Finally, let be the voltage level at bus i. The power line from bus i to j is modeled as a resistor (please note that ). The resistance of the parallel of all resistors connected to bus i is denoted by .
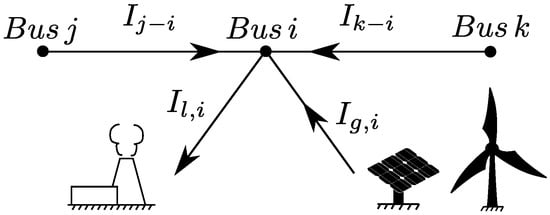
Figure 1.
Current balance at bus i.
Analogously, applying the Ohm’s law to all the lines incoming to bus i, and substituting the current value in the above equation, it yields that:
Finally, taking into account that the power demanded by the local load is and that the generated power can be expressed as , the above equation can be rewritten as follows:
It is worth pointing out that the generated power is quadratic on the bus voltage, , and depends linearly on , for . Thus, , where stands for a vector composed by all the buses’ voltages except that of bus i.
We consider the following constraints due to physical and operational limitations:
Constraint 1.
The buses voltages are upper and lower bounded by and , in such a way that:
Constraint 2.
The current carried by the power line connecting any pair of buses i and j is upper bounded by :
Constraint 3.
The amount of power generated with renewable resources at each bus is upper bounded by :
Finally, we introduce two assumptions related to the capabilities of the buses required to implement the distributed voltage regulation proposed in this article.
Assumption 1.
Each bus can control the power generated by its renewable energy plant within the bounds defined in (5).
Assumption 2.
Each bus knows of the parameters of the adjacent power lines, and , for all , and the power demanded by its local load, .
The parameters of power transmission lines, such as resistance and reactance, are often known by the electrical system operator. Thus, since we are considering a smart real-time power electric market seems logical to assume that this knowledge is available by each of the generators. Note that this assumption is weaker than the one in [10], where the whole set of parameters were known by all the agents of the microgrid.
3. Problem Formulation
This section introduces the problem under consideration. As it will be formally stated, the goal of every bus i in the grid will be to optimally decide the power generated with renewable resources, , by communicating and negotiating with neighboring nodes to minimize its local costs and fulfill the physical and operational constraints of the grid. Furthermore, to preserve privacy of its operation, each bus i does not share information about locally produced and demanded power, operation costs or local power generation limits. Instead, taking into account the direct relation between and in (2) (for fixed ), they only communicate proposals for the buses voltages, and reformulate the problem as choosing .
In order to model the local costs, we propose a cost function that takes into consideration multiple factors:
- The expenses (revenue) for consuming (injecting) energy from (to) the grid, given by:where model the marginal cost (revenue).
- The contribution of the bus to the voltage stability of the grid, penalizing the difference between the bus voltage level and its reference value:where is a fixed weight and is the reference voltage of the grid.
- The minimization of the electric losses in the adjacent lines of each bus, which are penalized by:where is a fixed weight.
- The cost of operation and maintenance (O&M) of the renewable resource that is given by [18]:where is a fixed cost and is the marginal cost of O&M (). There are in the literature other ways of modeling the O&M cost (for a broader study on this topic, the author is referred to [19]).
Taking into account the above-described factors, the following cost function can be defined:
where is given in (2).
Current flowing from bus i to j directly depends on voltages and through Ohm’s law. In addition, the power generated by agent i, , depends on the local voltage and the voltages of the neighboring buses through Equation (2). Hence, and and therefore all Constraints 1, 2, and 3, can be written in terms of the local and neighboring voltages .
Let us define as the sets:
In order to meet all the constraints, the voltage of bus i must belong to the feasible set . The complete feasible voltage set is defined as .
We are now in the position to formally state the distributed voltage regulation problem.
Problem 1.
The objective of each bus involved in the power network is to optimally choose the voltage such that:
| = | arg | |
| s.t. |
A last assumption concerning the feasibility of the problem is introduced.
Assumption 3.
There exists a set of voltages such that .
Please note that this assumption is directly fulfilled if the power flow has at least one feasible solution, which is obviously required.
4. Distributed Voltage Regulation
Observe that Problem 1 cannot be locally solved, since the buses ignore and cannot select the voltages of their neighbors, which are required to compute the terms (6), (8) and (9) of the cost function and to check the current and power constraints (4) and (5). In order to overcome this difficulty and find a solution for the optimization problem described above, an iterative algorithm based on non-cooperative Game Theory is proposed.
4.1. Description of the Problem as a Non-Cooperative Game
Let us consider each bus of the grid as a player in a non-cooperative game framework and assume, continuing with the arguments presented in the previous section that the buses or players have individual or local objectives and, hence, they do not fully cooperate. Therefore, consider a non-cooperative game-theoretical scenario defined over:
- The set of players or buses .
- The payoff or cost function associated with every player .
- The set of feasible decisions for every player .
Considering competitive buses, it is assumed that a Nash equilibrium is a desirable set of decisions.
Definition 1.
A Nash equilibrium of the game is a situation in which no player (bus) changes its decision (bus voltage) as long as the rest of the buses keeps the same decision as well. Mathematically, a Nash equilibrium is defined by a set of decisions such that
Please note that Assumption 3 does not directly imply that the game admits a Nash equilibrium. Although the feasible set is non-empty, it is possible that none of the feasible solutions is adequate for all the players at the same time. Therefore, we have to deal with the existence of a Nash equilibrium for the proposed game. However, prior to that, it is convenient to introduce the next results.
Proposition 1.
Proposition 2.
The set can be written as , where is composed by every such that
Proposition 3.
The set is composed by every such that
with:
The proof of Propositions 1, 2, and 3 can be obtained by substituting the Voltage Kirchhoff law and (2) into (10), (12) and (13) and after some mathematical manipulations.
Concerning the existence of a Nash equilibrium, firstly observe that the game is not an standard one, but a Generalized Nash Equilibrium Problem [20], since each player’s feasible set depends on the rival players’ strategies . The existence of a Nash equilibrum for generalized games is not easy to establish. Recently, some existence Theorems have been reported in [21]. In particular, the next result is based on [21] (Theorem 3.1). The proof can be easily deduced from that reference.
Lemma 1.
Consider that Assumption 3 holds. If the weights of the cost function are chosen in such a way that , then there exists a generalized Nash equilibrium for the game.
For the developments to come, it is convenient to analyze a simplified version of this game, the so-called unconstrained game, in which the decisions of the players are not subject to constraints. In other words, a game in which . In this case, a necessary and sufficient condition can be given for the existence and uniqueness of a Nash equilibrium.
Let us introduce the following notation:
where if buses i and j are not connected.
Lemma 2.
The unconstrained game admits a unique Nash equilibrium , given by , if and only if matrix is non-singular.
Lemma 2 is a particularization of a result previously obtained by the authors in [15], and its proof can be found in that reference. Please observe that the condition established in Lemma 2 must be evaluated using global information. Therefore, it is interesting to provide a way to distributedly ensure the existence and uniqueness of a Nash equilibrium for the unconstrained game. The next property states a condition for the weights that will help in this purpose and that will be used as well in subsequent results.
Property 1.
Property 1 is local, that is, every agent can enforce its fulfillment by suitably choosing its local weights. If Property 1 is fulfilled, matrix is a strictly diagonally dominant matrix and, then, it is a non-singular matrix through the Levy–Desplanques Theorem.
Note that, on the one hand, the existence of a Nash equilibrium does not imply that the player’s decision converges to it, and, on the other hand, the computation of this equilibrium requires global information, so the Nash equilibrium cannot be locally computed. The next section presents an iterative algorithm that makes the players’ decisions converge to the Nash equilibrium.
4.2. Iterative Algorithm
This algorithm assumes that each player shares only their decisions on the voltage associated with its local buses, and do not reveal any other local information, such as the power generated and demanded , their power generation limit , or their weighting factors .
Let us denote k as the iteration step, so that is the local voltage decided by player i at time k, and is the voltage decided by the rest of the players. We consider that the players exchange their decisions at the end of every iteration, in such a way that at instant k player i knows for all .
Then, let us reformulate cost function (14) with the voltage variables and (all the ) in terms of k as .
In a similar way, the feasible set for the decision taken at instant k is now , which can be rewritten using available information as:
where
and have an equivalent expression that but considering the voltage .
Consider now the following optimization problem, which is a reformulation of Problem 1 to be iteratively solved by each player.
Problem 2.
The objective of each bus involved in the power network at iteration step k is to find the voltage such that:
| = | arg | |
| s.t. |
The complete algorithm implemented by each player is described in Algorithm 1. After an initialization phase, each player iteratively solves Problem 2 and communicates its decision to neighboring players until a final agreement is reached. At that point, the Nash equilibrium of the game will be finally attained, and the power generated can be obtained from the voltage at the equilibrium, .
The following section analyzes the convergence of this iterative algorithm to the Nash equilibrium of the game.
| Algorithm 1: Iterative algorithm. | |
| 1: | Initialization: |
| 2: | Set s.t. and (17) |
| 3: | Specify power loads |
| 4: | Set |
| 5: | Set tolerance |
| 6: | Set and exchange with neighbors |
| 7: | Set |
| 8: | Iterative update: |
| 9: | While . |
| 11: | Find according to Problem 2 |
| 10: | Exchange with neighbors |
| 12: | End while |
| 13: | Find from using (2). |
5. Convergence Analysis
This section presents conditions for the convergence of the above-described algorithm to the Nash equilibrium of the game. As an introduction for the analysis, the next subsection studies the situation in which the decisions of every player are not subject to any constraints. In other words, for the unconstrained scenario, Problem 2 will be solved without considering the feasible sets in such a way that may take any possible real number. Then, the constrained scenario will be considered.
Let us define as the difference between the actual decision vector, , and the equilibrium of the unconstrained game, , defined in Lemma 2, that is, . Moreover, the next definition will be used.
Definition 2.
[22] Consider a linear discrete-time system , with M a constant square matrix. The next sentences are equivalent:
- Matrix M is Schur.
- The eigenvalues of matrix M belong to the unit circle.
- The discrete-time system is asymptotically stable.
- The discrete-time system admits a quadratic Lyapunov function (QLF) , beginning with P as a positive definite matrix that satisfies the Stein inequality; this is .
Furthermore, the next sentences are also equivalent:
- Matrix M is diagonally Schur stable.
- The discrete-time system admits a diagonal quadratic Lyapunov function (DQLF) , beginning with P as a diagonal positive definite matrix that satisfies the Stein inequality; this is .
5.1. Unconstrained Scenario
In this case, a necessary and sufficient condition can be established for the convergence.
Theorem 1.
Assume the existence of a unique Nash equilibrium of the unconstrained game, given by in Lemma 2. Then, the decisions , obtained with the execution of the algorithm described in Algorithm 1, converge to if and only if matrix is Schur. Otherwise, the decisions diverge from the Nash equilibrium.
Proof.
Under the unconstrained scenario, the solution for Problem 2 is the voltage such that , since cost function is convex in . Then,
The complete vector of decisions can be jointly written for all the players as . By using this expression and the definition of , the following linear relation is obtained:
Hence, the convergence of the algorithm is ensured if and only if matrix is Schur. □
The convergence condition required on matrix can only be evaluated with global information. In other words, some kind of agreement between the agents is needed to prevent the divergence of the negotiation algorithm. In this scenario, Property 1 can be very helpful in defining this agreement. If each agent individually sets the weights according to Property 1, matrix will have all its eigenvalues contained in the unit circle. The proof is direct by using the Gershgorin circle Theorem, which allows for bounding the spectrum of a square matrix. Then, if this is the case, Theorem 1 ensures the convergence of the negotiation to a unique Nash equilibrium. It is worth remembering that the fulfillment of Property 1 can be locally ensured without global information.
5.2. Constrained Scenario
Consider now the algorithm with the original formulation of Problem 2, in which must belong to the constrained feasible sets .
This section presents two convergence analyses for two different cases: when the unconstrained Nash equilibrium given in Lemma 2 belongs to the feasible set for every iteration step and the opposite situation.
Theorem 2.
Assume the existence of a unique Nash equilibrium for the unconstrained game, given by in Lemma 2. Assume also that , . Then, the decisions obtained with the execution of the algorithm described in Algorithm 1 converge to if matrix is diagonally Schur stable.
Proof.
Recall the definition of , whose evolution for the unconstrained game is linear and would be given by . However, the evolution of is different when the constraints come into play, and it cannot be expressed in a compact form, but component by component, as follows:
According to Definition 2, if matrix is diagonally Schur stable, the linear evolution of the error for the unconstrained game, , admits a diagonal quadratic Lyapunov function (DQLF) , that is, a quadratic Lyapunov function whose Lyapunov matrix P is diagonal. Hence, from Definition 2, there exists a positive definite diagonal matrix P such that:
Then, according to the diagonal structure of P, there exists a scalar such that:
Next, it is proved that the same function, , is also a DQLF for the evolution of in the constrained game. First, observe that the increment of the Lyapunov function can be written as
where according to (20).
Next, consider that, as the inequalities and are satisfied, it holds that the second and third addends in the previous equation are both less than zero, and thus:
ϵ being a positive scalar. Hence, is a valid Lyapunov function for the constrained case, ensuring the stabilization of , that is, , as . Therefore, the decisions of the players eventually reach the Nash equilibrium. In other words, . □
The condition in Theorem 2 requires to be diagonally Schur stable, which is a stronger condition than the one in Theorem 1, where matrix is simply required to be Schur. However, it will be shown that, if all the agents set the weights meeting Property 1, matrix is ensured to be diagonally Schur stable.
First of all, notice that, if Property 1 is fulfilled, matrix is a diagonally quasi-dominant matrix. The reader is referred to [23] for a formal definition of diagonally quasi-dominance. Now, according to Proposition 2.7.9 in [24], if matrix is a diagonally quasi-dominant matrix, then matrix is diagonally Schur stable.
Therefore, Property 1 is the key to ensuring the convergence of the algorithm to the Nash equilibrium for the constrained game as well.
Next, the problem when the equilibrium of the unconstrained game remains outside of the feasible region will be addressed.
Theorem 3.
Assume the existence of a Nash equilibrium for the constrained game, given by . Assume that the feasible set for Problem 2 is static and non-empty for every iteration, that is, . Furthermore, assume the existence of a unique Nash equilibrium for the unconstrained game, given by in Lemma 2, such that . Then, the decisions , obtained with the execution of the algorithm described in Algorithm 1, will converge to if matrix is diagonally Schur stable.
Proof.
The proof of Theorem 3 is based on the Banach fixed-point theorem, which is a powerful tool to ensure the existence and uniqueness of fixed points of a map that are applied in an iterative way. Then, a map is called a contraction map if there exists such that , , being any distance in the metric space. The Banach fixed-point theorem ensures in those cases the existence and uniqueness of a fixed point , that is, .
In order to use this result, it will be shown that the evolution of for the constrained game given in (20) is a contractive mapping over the feasible set of decisions. This implies that the evolution of the iterations admits a unique fixed point in the feasible set that is , and the decision vector converges to a unique Nash equilibrium, given by .
If matrix is diagonally Schur stable, the evolution of without constraints, i.e., , admits a DQLF in the form , P being diagonally positive definite.
Take two arbitrary feasible decisions at any negotiation step k, namely, . Using the aforementioned error between the actual decision vector and the Nash equilibrium, it is possible to define and .
Then, the distance between both errors induced by matrix P can be obtained as:
Next, it will be demonstrated that , or equivalently , where can be computed component by component using (20). After some mathematical manipulations, similar to those in Theorem 2, one can derive that:
ϵ being a positive scalar.
Now, consider that ; this is the difference of two consecutive decisions with respect to the Nash equilibrium of the unconstrained system. Then, the above inequality proves that the mapping , with in (20), is contractive, this implying the convergence of to a fixed point . Once the fixed point is reached, the agents won’t change their decisions, so the Nash equilibrium of the constrained game is found. By using the definition of , it is clear that the value of the Nash equilibrium for the constrained game is related with the value of the Nash equilibrium of the unconstrained game through . This ends the proof. □
The convergence to the Nash equilibrium of the constrained game requires that, at each iteration k, the feasible set of Problem 2 is non-empty and static. On the other hand, Assumption 3 just ensures the existence of a static non-empty feasible set for Problem 1. Remember that Assumption 3 directly satisfes if the power flow has, at least, one feasible solution.
However, it is not clear that Assumption 3 is, in general, enough to meet the requirements of Theorem 3. If Constraints 2 and 3 are removed, that is, if only the voltage constraint is considered, then the feasible set for the voltages will be static and non-empty, so Assumption 3 will be enough to ensure the convergence to the Nash equilibrium. Thus, in order to provide a convergence proof for the constrained game, an assumption on the definition of the feasible set might be required.
It must be mentioned that, notwithstanding, the simulations show that the Nash equilibrium is reached with constraints that change with time. Therefore, it is possible that Assumption 3 is enough to ensure the feasibility of the problem and no further assumptions are required. Anyway, the feasibility analysis and, if necessary, the additional assumptions required are left for future research.
6. Simulation Results
This section presents some simulations to show the performance of the proposed distributed voltage regulation algorithm. Some illustrative examples on a modification of the IEEE 14-bus system will be shown in this section. This network has been selected due to its wide use to study voltage regulation problems (see, for instance, [25]). After that, additional simulations are conducted on a larger network in order to show the scalability of the proposed method.
6.1. Simulations on a Modification of the IEEE 14-Bus System
The simulations carried out within this section are performed on a modification of the IEEE 14-bus system, considering three generators at the buses 3, 7, and 12. In order to adapt the corresponding network to a DC framework, the lines are characterized by their resistances. A schematic of the network and the values of the lines resistances are illustrated in Figure 2 and Table 1, respectively. Moreover, the values of the installed loads are included in Table 2 (there are no loads for nodes that do not appear in the table).
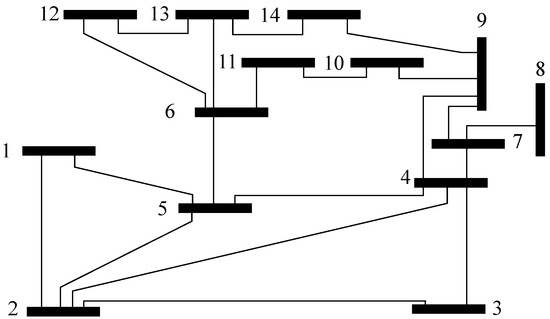
Figure 2.
Schematic of the IEEE-14 bus system.

Table 1.
IEEE 14-bus network lines resistance (p.u.).

Table 2.
IEEE 14-bus power loads (p.u.).
A possible solution for the power flow of the grid is given by a generation of MW, MW and MW. In this scenario, the voltage levels at each bus of the grid are shown in Table 3 (expressed in per unit). In the next examples, these voltages levels are considered as the references .

Table 3.
Initial voltage levels in per unit.
Example 1.
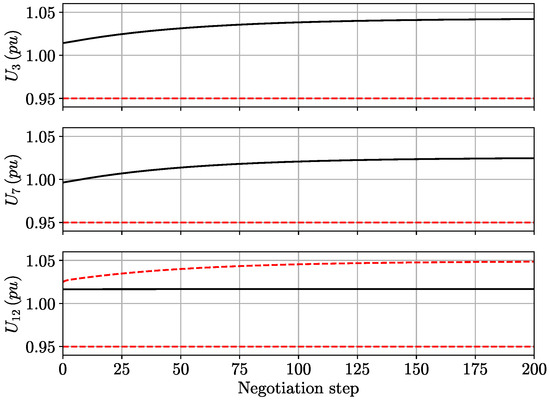

Let us consider a scenario in which buses 3, 7, and 12 have additional renewable power installed. For instance, let’s assume that MW, MW and MW are the power limits of the corresponding generators. Moreover, let us consider Constraint 1 with and . This example does not introduce any current constraint. Hence, observe that belongs to the feasible set , allowing at least one feasible solution for the problem and therefore satisfying Assumption 3. Finally, the cost functions (14) of buses 3, 7, and 12 are characterized by the weighting costs , , , and for .
The iterative algorithm described in Algorithm 1 is executed in buses 3, 7, and 12, whereas the rest of the buses choose the voltage satisfying the power flow at each iteration.
The results are shown in Figure 3. Observe that, after some iterations, the buses agree with a voltage level that is different to the reference voltage, considering their local cost functions and constraints. The exact voltage levels at the equilibrium are shown in Table 4.

Figure 3.
Buses 3, 7, and 12 negotiation and the associated constraints (dashed lines).

Table 4.
Voltage level at the equilibrium for Example 1.
Additionally, Figure 3 presents the upper and lower voltage limits at each iteration in dashed lines (the lower limits are never met in this example). It can be observed that agents 3 and 7 saturate in their decisions due to Constraint 3, while agent 12 reaches the Nash equilibrium far from its local bounds.
Example 2.
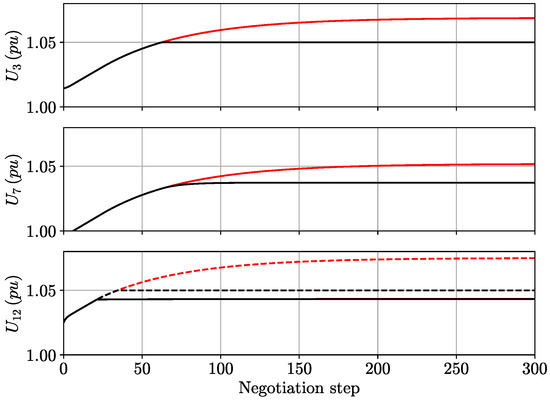

Consider the situation of the previous example but with modified weighting costs: , , , and for . In this case, more profit is given to the buses for their generated power and less costs are associated with voltage levels different from the references.
Black lines in Figure 4 show the decisions at each iteration of the negotiation process and the corresponding limits (dashed lines). Note that, as a consequence of the new cost functions, the voltages at the equilibrium are higher than those obtained in the previous example. In fact, is constrained by Constraint 1 reaching the upper bound . The exact voltage levels at the equilibrium are shown in Table 5. In addition, red lines in Figure 4 depict the evolution of the negotiation when Constraint 1 is not taken into consideration. As it can be seen, both buses 3 and 7 reach a higher value than in the equilibrium prioritizing the power injection rather than the voltage deviations.

Figure 4.
Buses 3, 7, and 12 negotiation and the associated constraints (dashed lines) for: (i) original problem of Example 2 (black ink); (ii) problem stated in Example 2 when Constraint 1 is not taken into account (red ink).

Table 5.
Voltage level at the equilibrium for Example 2.
Example 3.

Finally, let us introduce a current constraint in one of the lines. In particular, a current limit is established at the power line connecting buses 4 and 7, which with the weighting costs fixed in Example 2 and without current constraints carried Now, consider that due to physical limitations. By running again the distributed voltage regulation algorithm, different voltage levels are reached at the Nash equilibrium of the game (see Table 6).

Table 6.
Voltage level at the equilibrium for Example 3.
In particular, note that bus 7 decreases its voltage level, reducing the difference with and, consequently, the current flowing through the line connecting both.
6.2. Algorithm Performance on a Large-Scale Network
In this section, a larger network is considered in order to show the scalability of the proposed algorithm. In particular, the network is the one depicted in Figure 5. The nominal voltage of the grid is 20 kV and a base power of 20 MW is considered in all the results. Again, the power lines will be modeled only considering the real part of the impedance. A list with the installed loads can be found in Table 7. For further details regarding the technical characteristic of the network, the reader is referred to [26].
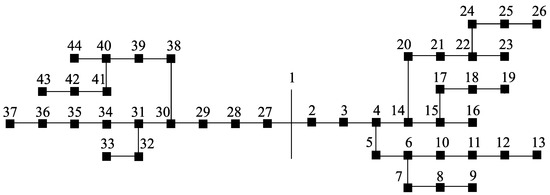
Figure 5.
Schematic of a large scale system conformed by 44 buses [26].

Table 7.
Rated power of loads in p.u.
In this case, let us consider a scenario in which there are ten buses with additional 2 MW of renewable power installed. These buses are the ones defined by set . The voltage references are fixed as for every Now, let us consider two different examples that are analogous to those presented in Examples 1 and 2 in previous section.
Example 4.
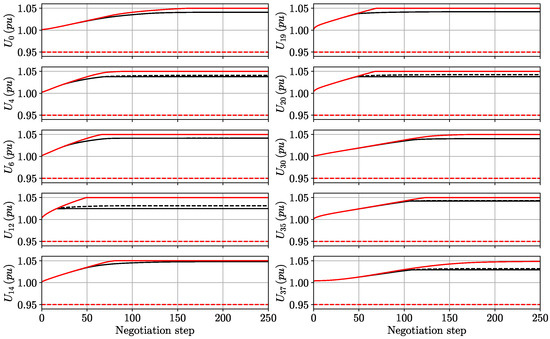
Consider the sequel weighting parameters that characterize the cost functions (14): , , , and for every . Note that these weights are the same as those chosen for Example 1. Figure 6 shows in black lines the decisions on the voltage at each negotiation step until reaching the equilibrium.

Figure 6.
Evolution of the decisions on the voltage at each negotiation step for examples 4 (black) and 5 (red) and the corresponding constraints (in dashed lines).
Example 5.
In this example, let us consider the following weighting parameters: , , , and for every . Recall that these weights are the same that those chosen for Example 2. Figure 6 shows in red lines the decisions on the voltage at each negotiation together with the corresponding constraints (dashed lines). It can be seen that, in this case, the voltage deviations with respect to the reference values are less penalized than in the previous example, reaching higher voltages.
It is worth pointing out that, as a consequence of the variations in the weighting parameters, the voltages at the equilibrium in Example 5 are higher than those obtained in Example 4. This fact not only has an impact on the voltages of buses in , but it also raises the voltages of all the network buses.
Furthermore, Figure 6 shows the capabilities of the algorithm when it deals with a large network. Although more iterations are required to reach the Nash equilibrium, in comparison with the network of 14 buses, it can be seen that the number is still low (less than 250). This result illustrates that the proposed distributed regulation method is a good candidate to be implemented in larger networks. The formal study of the impact of the number of buses, and the number of buses capable of making decisions, in the convergence time is left for future work.
7. Conclusions
This manuscript has presented a game-theoretical framework for the voltage regulation problem over DC grids. Each bus of the grid negotiates to minimize a local cost without revealing private information as the costs or the power generated by renewable power sources. An iterative negotiation algorithm has been proposed, analyzing its convergence to the Nash equilibrium of the game when the decisions are constrained according to the physical and operational limitations of the grid. It has been shown that a certain property (Property 1) is key to ensuring convergence to a Nash equilibrium, and also that this property can be distributedly ensured by suitably setting the weights of the cost functions.
Finally, some simulation examples have been included in order to illustrate the effectiveness of the method. The simulations show that the algorithm is robust even for the situation in which the theoretical results fail to prove its convergence. Then, looking for relaxed conditions for the convergence is one of the most promising lines of future research. In addition, the application of the algorithm to AC grids will be tackled in the future.
Author Contributions
L.O.: Conceptualization, Formal analysis, Writing—original draft, funding acquisition; P.M.: Conceptualization, Formal analysis, Supervision, Writing—review and editing; Á.R.d.N.: Conceptualization, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by AEI/FEDER Grant No. TEC2016-80242-P through the Laboratorio de Simulación Hardware-in-the-loop de Sistemas Ciberfísicos (LaSSiC).
Acknowledgments
Research was partially supported by grants TEC2016-80242-P (through the Laboratorio de simulación hardware-in-the-loop de sistemas ciberfísicos (LaSSiC)) and DPI-75294-C2-2-R by AEI/FEDER.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moreno, B.; López, A.J.; García-Álvarez, M.T. The electricity prices in the European Union. The role of renewable energies and regulatory electric market reforms. Energy 2012, 48, 307–313. [Google Scholar] [CrossRef]
- Newhouse, S.E. Introduction to Matrix Generalized Inverses and Their Application; Technical Report GSFC X-643-66-34; NASA Goddard Space Flight Center: Greenbelt, MD, USA, January 1966. [Google Scholar]
- Engelen, K.; Shun, E.L.; Vermeyen, P.; Pardon, I.; D’hulst, R.; Driesen, J.; Belmans, R. The Feasibility of Small-Scale Residential DC Distribution Systems. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 2618–2623. [Google Scholar] [CrossRef]
- Kumar, M.; Srivastava, S.C.; Singh, S.N. Control Strategies of a DC Microgrid for Grid Connected and Islanded Operations. IEEE Trans. Smart Grid 2015, 6, 1588–1601. [Google Scholar] [CrossRef]
- Glover, J.D.; Sarma, M.S.; Overbye, T. Power System Analysis and Design; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Başar, T.; Olsder, G.J. Dynamic Noncooperative Game theory; SIAM: Philadelphia, PA, USA, 1999; Volume 23. [Google Scholar]
- Saad, W.; Han, Z.; Poor, H.V.; Başar, T. Game-theoretic methods for the smart grid: An overview of microgrid systems, demand-side management, and smart grid communications. IEEE Signal Process. Mag. 2012, 29, 86–105. [Google Scholar] [CrossRef]
- Cherukuri, A.; Cortés, J. Decentralized Nash equilibrium seeking by strategic generators for DC optimal power flow. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, J.; Sauer, P.W.; Domínguez-García, A.; Başar, T. A game-theoretic framework for control of distributed renewable-based energy resources in smart grids. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3623–3628. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Q. A Game-Theoretic Framework for Resilient and Distributed Generation Control of Renewable Energies in Microgrids. IEEE Trans. Smart Grid 2017, 8, 285–295. [Google Scholar] [CrossRef]
- Scarabaggio, P.; Carli, R.; Dotoli, M. A game-theoretic control approach for the optimal energy storage under power flow constraints in distribution networks. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1281–1286. [Google Scholar] [CrossRef]
- Atzeni, I.; Ordóñez, L.G.; Scutari, G.; Palomar, D.P.; Fonollosa, J.R. Demand-Side Management via Distributed Energy Generation and Storage Optimization. IEEE Trans. Smart Grid 2013, 4, 866–876. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M.; Palmisano, V. A Distributed Control Approach Based on Game Theory for the Optimal Energy Scheduling of a Residential Microgrid with Shared Generation and Storage. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 960–965. [Google Scholar] [CrossRef]
- Kargarian, A.; Mohammadi, J.; Guo, J.; Chakrabarti, S.; Barati, M.; Hug, G.; Kar, S.; Baldick, R. Toward Distributed/Decentralized DC Optimal Power Flow Implementation in Future Electric Power Systems. IEEE Trans. Smart Grid 2018, 9, 2574–2594. [Google Scholar] [CrossRef]
- Orihuela, L.; Millán, P.; Carbonell-Márquez, J.F. Distributed Negotiation with a Class of Quadratic Cost Functions. IFAC PapersOnLine 2017, 50, 12285–12290. [Google Scholar] [CrossRef]
- del Nozal, A.R.; Orihuela, L.; Millán, P. A Game-Theoretic Framework for Distributed Voltage Regulation over HVDC grids. In Proceedings of the IEEE European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018. [Google Scholar]
- Dostert, K. Telecommunications over the power distribution grid–possibilities and limitations. IIR Powerline 1997, 6, 97. [Google Scholar]
- Baziar, A.; Kavousi-Fard, A. Considering uncertainty in the optimal energy management of renewable micro-grids including storage devices. Renew. Energy 2013, 59, 158–166. [Google Scholar] [CrossRef]
- Abdi, H.; Beigvand, S.D.; Scala, M.L. A review of optimal power flow studies applied to smart grids and microgrids. Renew. Sustain. Energy Rev. 2017, 71, 742–766. [Google Scholar] [CrossRef]
- Facchinei, F.; Kanzow, C. Generalized Nash equilibrium problems. Ann. Oper. Res. 2010, 175, 177–211. [Google Scholar] [CrossRef]
- Dutang, C. Existence theorems for generalized Nash equilibrium problems: An analysis of assumptions. J. Nonlinear Anal. Optim. 2013, 4, 115–126. [Google Scholar]
- Akyar, H. On Schur diagonal stability. Appl. Math. 2010, 2, 1–13. [Google Scholar] [CrossRef]
- McKenzie, L. Matrices with dominant diagonals and economic theory. In Mathematical Methods in the Social Sciences; Kenneth, A., Samuel, K., Patrick, S., Eds.; Stanford University Press: Stanford, CA, USA, 1960. [Google Scholar]
- Kaszkurewicz, E.; Bhaya, A. Matrix Diagonal Stability in Systems and Computation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Reis, C.; Barbosa, F. A comparison of voltage stability indices. In Proceedings of the MELECON 2006-2006 IEEE Mediterranean Electrotechnical Conference, Baltimore, MD, USA, 22–24 March 2006; pp. 1007–1010. [Google Scholar]
- Kryonidis, G.C.; Demoulias, C.S.; Papagiannis, G.K. A new voltage control scheme for active medium-voltage (MV) networks. Electr. Power Syst. Res. 2019, 169, 53–64. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).