Fractional Order Graph Filters: Design and Implementation
Abstract
1. Introduction
2. Preliminaries
2.1. Graph and Graph Signal
2.2. Graph Shift
2.3. Graph Filtering
3. Design of Fractional Order Graph Filter
3.1. Definition of Fractional Order Graph Filter
3.2. Design Method
- Set the number of population. With population increasing, the optimization result may be better, but the speed may be slower. We use feasible population function to create a random initial population that satisfies the bounds and linear constraints.
- Use roulette strategy to determine the fitness of individuals, and judge whether they meet the optimization criteria. If they do, output the best individuals and their optimal solutions. Otherwise, proceed to the next step.
- According to the fitness, the individuals with high fitness are selected with high probability and the individuals with low fitness are eliminated.
- Generate new individuals according to crossover probability . The crossover function is an arithmetic function.
- Generate new individuals according to the mutation function, which is adaptive feasible function.
- Generate new population by crossover and mutation.
- Repeat the following steps until we get the optimal results or implement it for enough number of times.
3.3. Filter Performance
3.4. Stability Analysis
4. Distributed Implementation
4.1. Continued Fraction Equation Method
| Algorithm 1: The Matrix Version of Modified Lentz’s Algorithm |
|
| Algorithm 2: Distributed Implementation of Fractional Order GSO Approximated by CFE |
|
4.2. Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The Emerging Field of Signal Processing on Graphs: Extending High-dimensional Data Analysis to Networks and Other Irregular Domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Stankovic, L.; Mandic, D.; Dakovic, M.; Brajovic, M.; Scalzo, B.; Constantinides, T. Graph Signal Processing—Part I: Graphs, Graph Spectra, and Spectral Clustering. arXiv 2019, arXiv:1907.03467v2. [Google Scholar]
- Stankovic, L.; Mandic, D.; Dakovic, M.; Brajovic, M.; Scalzo, B.; Constantinides, A.G. Graph Signal Processing—Part II: Processing and Analyzing Signals on Graphs. arXiv 2019, arXiv:1909.10325v1. [Google Scholar]
- Stankovic, L.; Mandic, D.; Dakovic, M.; Brajovic, M.; Scalzo, B.; Li, S.; Constantinides, A.G. Graph Signal Processing—Part III: Machine Learning on Graphs, from Graph Topology to Applications. arXiv 2020, arXiv:2001.00426v1. [Google Scholar]
- Grady, L.J.; Polimeni, J.R. Discrete Calculus; Springer London: London, UK, 2010. [Google Scholar] [CrossRef]
- Krim, H.; Hamza, A.B. Geometric and differential topology of manifolds. In Geometric Methods in Signal and Image Analysis; Cambridge University Press: Cambridge, UK, 2015; pp. 168–237. [Google Scholar] [CrossRef]
- Škrjanc, I. Pitch Angle Control of Unmanned Air Vehicle with Uncertain System Parameters. J. Intell. Robot. Syst. 2006, 47, 285–297. [Google Scholar] [CrossRef]
- Ma, J.; Huang, W.; Segarra, S.; Ribeiro, A. Diffusion Filtering of Graph Signals and Its Use in Recommendation Systems. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 20–25 March 2016. [Google Scholar] [CrossRef]
- Cheung, M.; Shi, J.; Wright, O.; Jiang, L.Y.; Liu, X.; Moura, J.M.F. Graph Signal Processing and Deep Learning: Convolution, Pooling, and Topology. IEEE Signal Process. Mag. 2020, 37, 139–149. [Google Scholar] [CrossRef]
- Isufi, E.; Lorenzo, P.D.; Banelli, P.; Leus, G. Distributed Wiener-Based Reconstruction of Graph Signals. In Proceedings of the 2018 IEEE Statistical Signal Processing Workshop, Breisgau, Germany, 1 June 2018; pp. 21–25. [Google Scholar] [CrossRef]
- Isufi, E.; Loukas, A.; Simonetto, A.; Leus, G. Autoregressive Moving Average Graph Filtering. IEEE Trans. Signal Process. 2017, 65, 274–288. [Google Scholar] [CrossRef]
- Saad, L.B.; Isufi, E.; Beferull-Lozano, B. Graph Filtering with Quantization over Random Time-varying Graphs. In Proceedings of the 2019 IEEE Global Conference on Signal and Information Processing, Ottawa, ON, Canada, 11–14 November 2019. [Google Scholar] [CrossRef]
- Gavili, A.; Zhang, X.P. On the Shift Operator, Graph Frequency, and Optimal Filtering in Graph Signal Processing. IEEE Trans. Signal Process. 2017, 65, 6303–6318. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Li, B.Z.; Cheng, Q.Y. The fractional Fourier transform on graphs. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference, Kuala Lumpur, Malaysia, 12–15 December 2017. [Google Scholar]
- Wang, Y.; Li, B. The Fractional Fourier Transform on Graphs: Sampling and Recovery. In Proceedings of the 2018 14th IEEE International Conference on Signal Processing, Beijing, China, 12–16 August 2018. [Google Scholar]
- Sandryhaila, A.; Moura, J.M. Discrete Signal Processing on Graphs: Frequency Analysis. IEEE Trans. Signal Process. 2014, 62, 3042–3054. [Google Scholar] [CrossRef]
- Shuman, D.I.; Ricaud, B.; Vandergheynst, P. Vertex-frequency Analysis on Graphs. Appl. Comput. Harmon. Anal. 2016, 40, 260–291. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold Regularization: A Geometric Framework for Learning from Labeled and Unlabeled Examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Girault, B.; Gonçalves, P.; Fleury, E.; Mor, A.S. Semi-supervised Learning for Graph to Signal Mapping: A Graph Signal Wiener Filter Interpretation. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 1115–1119. [Google Scholar] [CrossRef]
- Zhang, F.; Hancock, E.R. Graph Spectral Image Smoothing Using the Heat Kernel. Pattern Recognit. 2008, 41, 3328–3342. [Google Scholar] [CrossRef]
- Isufi, E.; Leus, G. Distributed Sparsified Graph Filters for Denoising and Diffusion Tasks. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 5865–5869. [Google Scholar]
- Tremblay, N.; Puy, G.; Gribonval, R.; Vandergheynst, P. Compressive Spectral Clustering. In Proceedings of The 33rd International Conference on Machine Learning; Balcan, M.F., Weinberger, K.Q., Eds.; PMLR: New York, NY, USA, 2016; Volume 48, pp. 1002–1011. [Google Scholar]
- Natali, A.; Coutino, M.; Leus, G. Topology-Aware Joint Graph Filter and Edge Weight Identification for Network Processes. In Proceedings of the 2020 IEEE 30th International Workshop on Machine Learning for Signal Processing, Espoo, Finland, 21–24 September 2020. [Google Scholar] [CrossRef]
- Sandryhaila, A.; Moura, J.M.F. Discrete Signal Processing on Graphs. IEEE Trans. Signal Process. 2013, 61, 1644–1656. [Google Scholar] [CrossRef]
- Segarra, S.; Marques, A.G.; Ribeiro, A. Optimal Graph-Filter Design and Applications to Distributed Linear Network Operators. IEEE Trans. Signal Process. 2017, 65, 4117–4131. [Google Scholar] [CrossRef]
- Shi, X.; Feng, H.; Zhai, M.; Yang, T.; Hu, B. Infinite Impulse Response Graph Filters in Wireless Sensor Networks. IEEE Signal Process. Lett. 2015, 22, 1113–1117. [Google Scholar] [CrossRef]
- Shuman, D.I.; Vandergheynst, P.; Kressner, D.; Frossard, P. Distributed Signal Processing via Chebyshev Polynomial Approximation. IEEE Trans. Signal Inf. Process. Netw. 2018, 4, 736–751. [Google Scholar] [CrossRef]
- Freeborn, T.; Maundy, B.; Elwakil, A. Field Programmable Analogue Array Implementation of Fractional Step Filters. IET Circ. Devices Syst. 2010, 4, 514. [Google Scholar] [CrossRef]
- Radwan, A.; Soliman, A.; Elwakil, A.; Sedeek, A. On the Stability of Linear Systems with Fractional-order Elements. Chaos Solitons Fractals 2009, 40, 2317–2328. [Google Scholar] [CrossRef]
- Radwan, A.G.; Elwakil, A.S.; Soliman, A.M. On The Generalization Of Second-order Filters To The Fractional-order Domain. J. Circ. Syst. Comput. 2009, 18, 361–386. [Google Scholar] [CrossRef]
- Ali, A.S.; Radwan, A.G.; Soliman, A.M. Fractional Order Butterworth Filter: Active and Passive Realizations. IEEE J. Emerg. Sel. Top. Circ. Syst. 2013, 3, 346–354. [Google Scholar] [CrossRef]
- Said, L.A.; Ismail, S.M.; Radwan, A.G.; Madian, A.H.; El-Yazeed, M.F.A.; Soliman, A.M. On the Optimization of Fractional Order Low-pass Filters. Circ. Syst. Signal Process. 2016, 35, 2017–2039. [Google Scholar] [CrossRef]
- Shuman, D.I.; Vandergheynst, P.; Frossard, P. Chebyshev Polynomial Approximation for Distributed Signal Processing. In Proceedings of the 2011 International Conference on Distributed Computing in Sensor Systems and Workshops (DCOSS), Barcelona, Spain, 27–29 June 2011. [Google Scholar] [CrossRef]
- Oppenheim, A.V. Discrete-time Signal Processing; Pearson Education India: Delhi, India, 1999. [Google Scholar]
- Ribeiro, G.B.; Lima, J.B. Deslocamento Fracionário De Sinais Sobre Grafos. In Proceedings of the XXXV Simpósio Brasileiro de Telecomunicaçoes e Processamento de Sinais, São Pedro, Brazil, 3–6 September 2017; pp. 871–875. [Google Scholar]
- Riascos, A.P.; Mateos, J.L. Fractional dynamics on networks: Emergence of anomalous diffusion and Lévy flights. Phys. Rev. E 2014, 90. [Google Scholar] [CrossRef]
- Euler, L. A Commentary on The Continued Fraction by Which The Illustrious La Grange Has Expressed The Binomial Powers. Available online: http://xxx.lanl.gov/abs/math/0507459v1 (accessed on 22 July 2005).
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar] [CrossRef]
- Coutino, M.; Isufi, E.; Leus, G. Advances in Distributed Graph Filtering. IEEE Trans. Signal Process. 2019, 67, 2320–2333. [Google Scholar] [CrossRef]
- von Luxburg, U. A Tutorial on Spectral Clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Valimaki, V.; Laakso, T. Fractional Delay Digital Filters. In Proceedings of the IEEE International Symposium on Circuits and Systems, Chicago, IL, USA, 3–6 May 1993. [Google Scholar] [CrossRef]
- Acharya, A.; Das, S.; Pan, I.; Das, S. Extending the Concept of Analog Butterworth Filter for Fractional Order Systems. Signal Process. 2014, 94, 409–420. [Google Scholar] [CrossRef]
- Aittomaki, T.; Leus, G. Graph Filter Design Using Sum-of-squares Representation. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 2–6 September 2019. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms In Search, Optimization, and Machine Learning; Addison-Wesley: San Francisco, CA, USA, 1989. [Google Scholar]
- Perraudin, N.; Paratte, J.; Shuman, D.; Martin, L.; Kalofolias, V.; Vandergheynst, P.; Hammond, D.K. GSPBOX: A toolbox for signal processing on graphs. arXiv 2014, arXiv:1408.5781v2. [Google Scholar]
- Kenlay, H.; Thanou, D.; Dong, X. On The Stability of Polynomial Spectral Graph Filters. In Proceedings of the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 5350–5354. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Podlubny, I.; Feliu, V. Some Approximations of Fractional Order Operators Used in Control Theory and Applications. J. Fract. Calc. Appl. Anal. 2000, 3, 231–248. [Google Scholar]
- Lentz, W.J. Continued Fraction Calculation of Spherical Bessel Functions. Comput. Phys. 1990, 4, 403. [Google Scholar] [CrossRef]

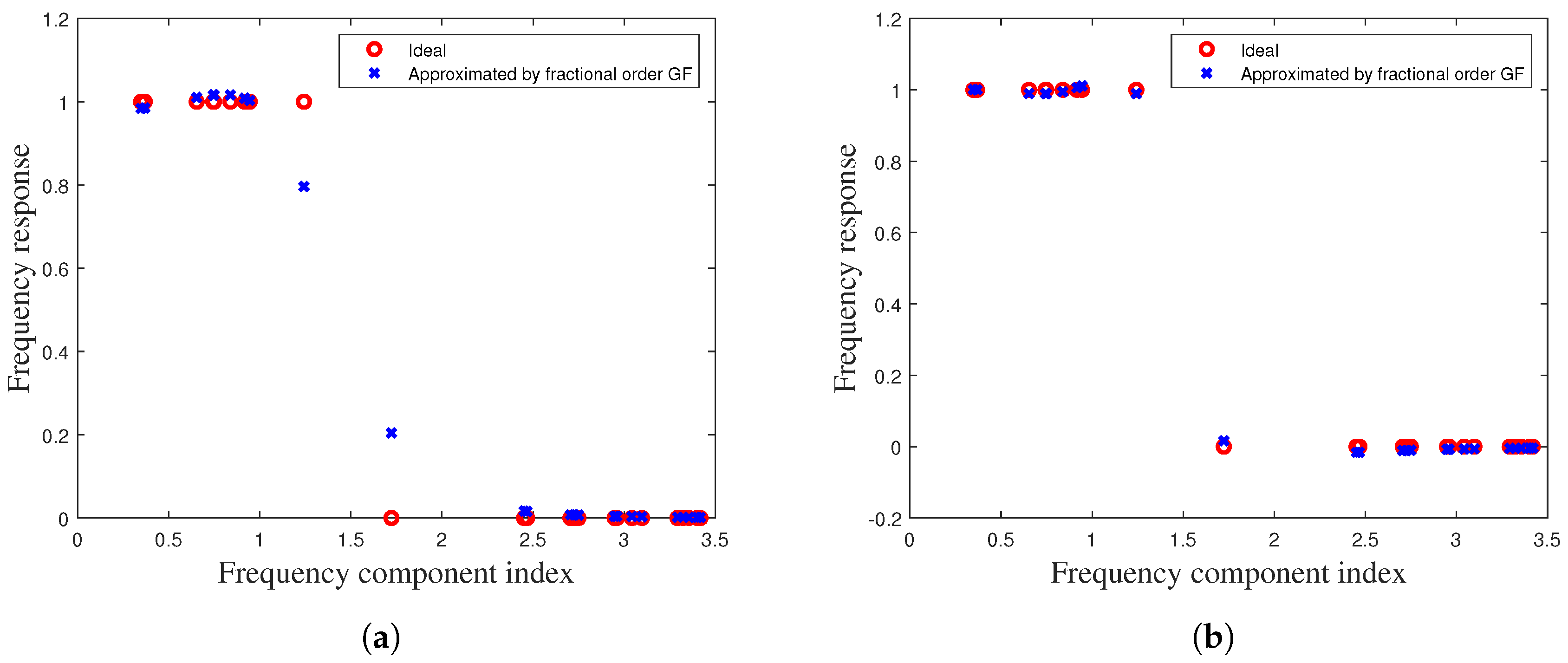
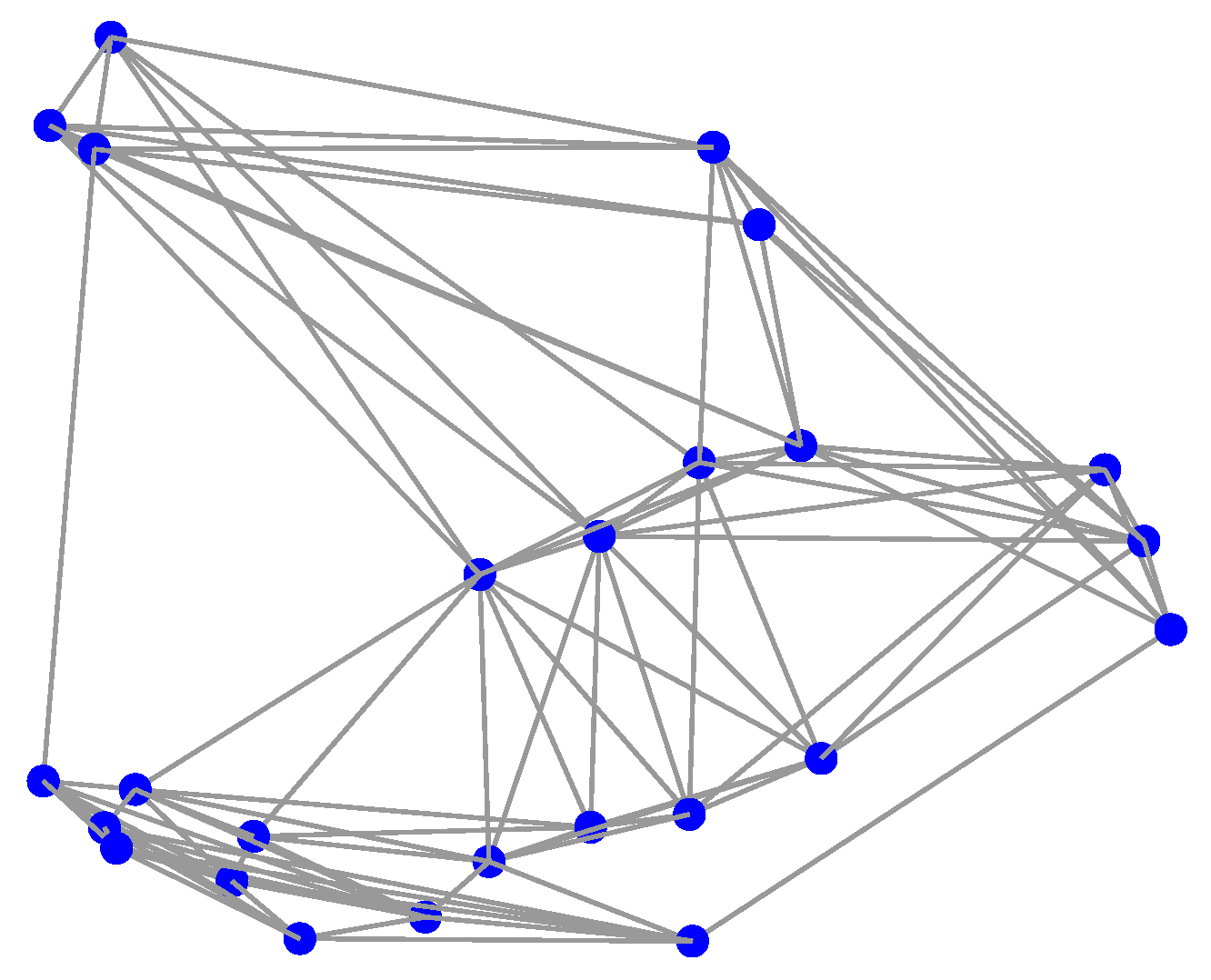


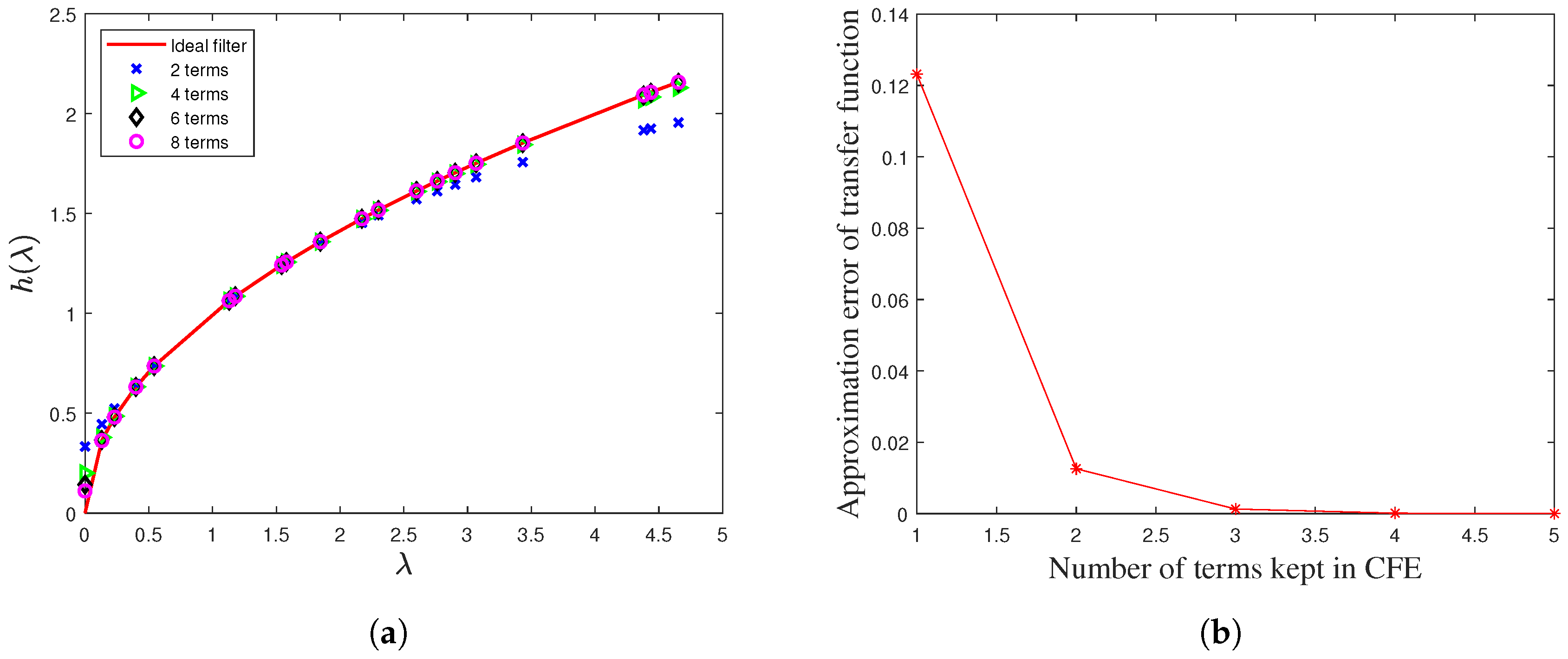

| Frequency Response | J | |||
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, X.; Feng, H.; Hu, B. Fractional Order Graph Filters: Design and Implementation. Electronics 2021, 10, 437. https://doi.org/10.3390/electronics10040437
Qiu X, Feng H, Hu B. Fractional Order Graph Filters: Design and Implementation. Electronics. 2021; 10(4):437. https://doi.org/10.3390/electronics10040437
Chicago/Turabian StyleQiu, Xinyi, Hui Feng, and Bo Hu. 2021. "Fractional Order Graph Filters: Design and Implementation" Electronics 10, no. 4: 437. https://doi.org/10.3390/electronics10040437
APA StyleQiu, X., Feng, H., & Hu, B. (2021). Fractional Order Graph Filters: Design and Implementation. Electronics, 10(4), 437. https://doi.org/10.3390/electronics10040437






