Understanding the Thermal Time Constants of GaN HEMTs through Model Order Reduction Technique
Abstract
1. Introduction
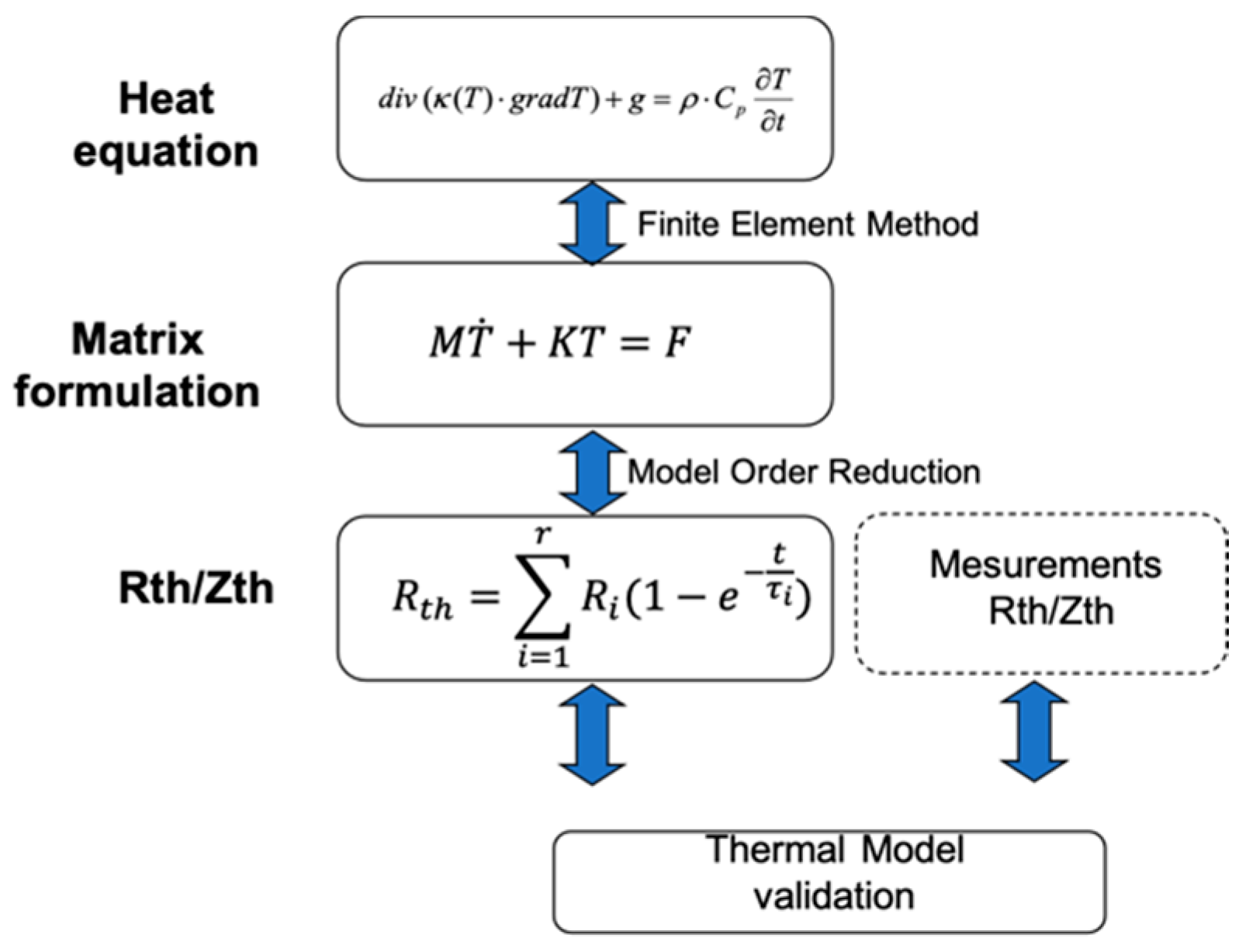
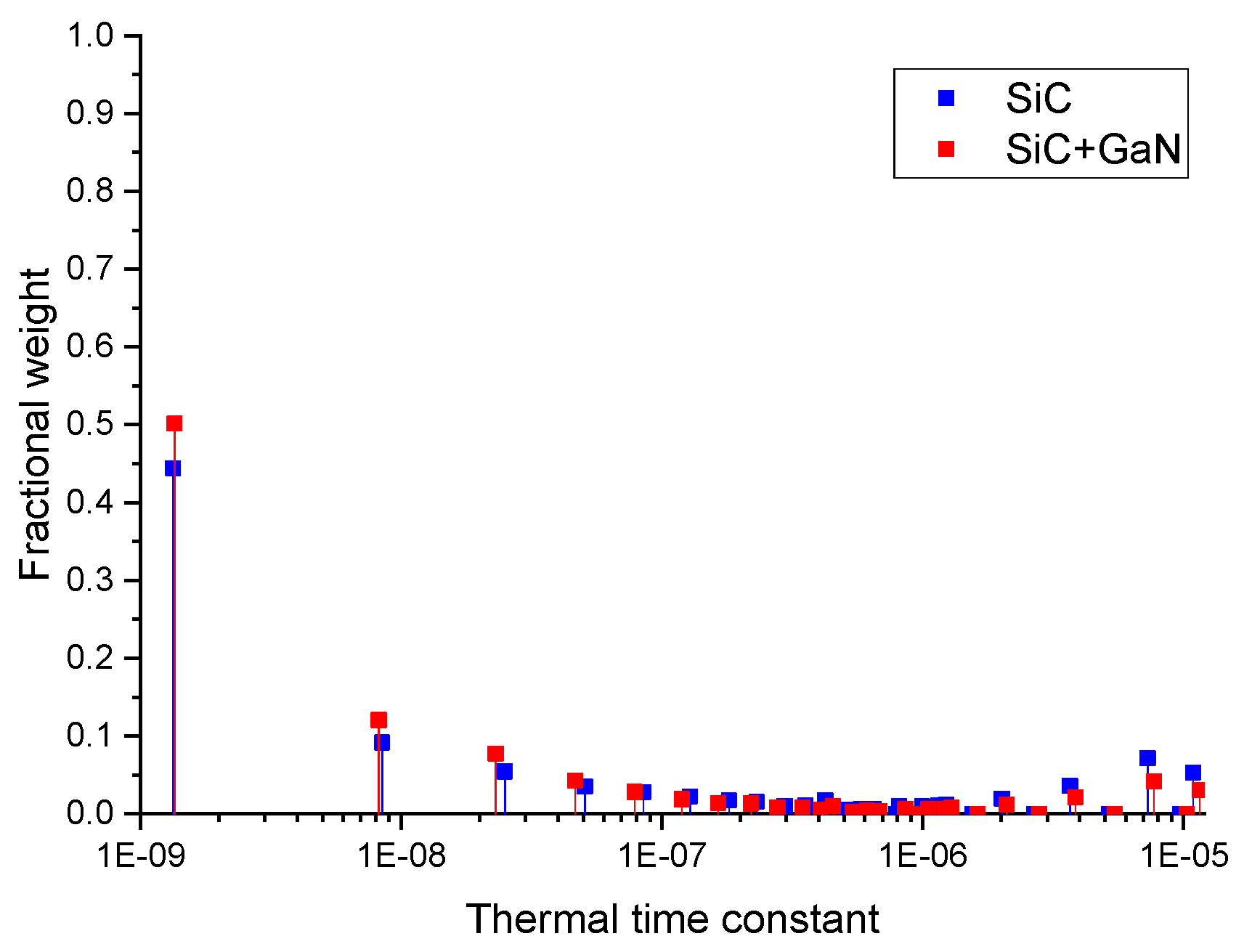
2. Extraction of Real Thermal Time Constants with Ritz Model Order Reduction Technique
Finite Element Linear Formulation of the Heat Equation
- –
- The number n of numerical equations is very large (few 100,000), so it is very difficult to compute all the eigenvalues and the eigenvectors;
- –
- The second difficulty involves selecting the main eigenvalues;
- –
- The steady state is not reached if all the eigenvalues are not considered.
3. One Dimensional (1-D) Analysis
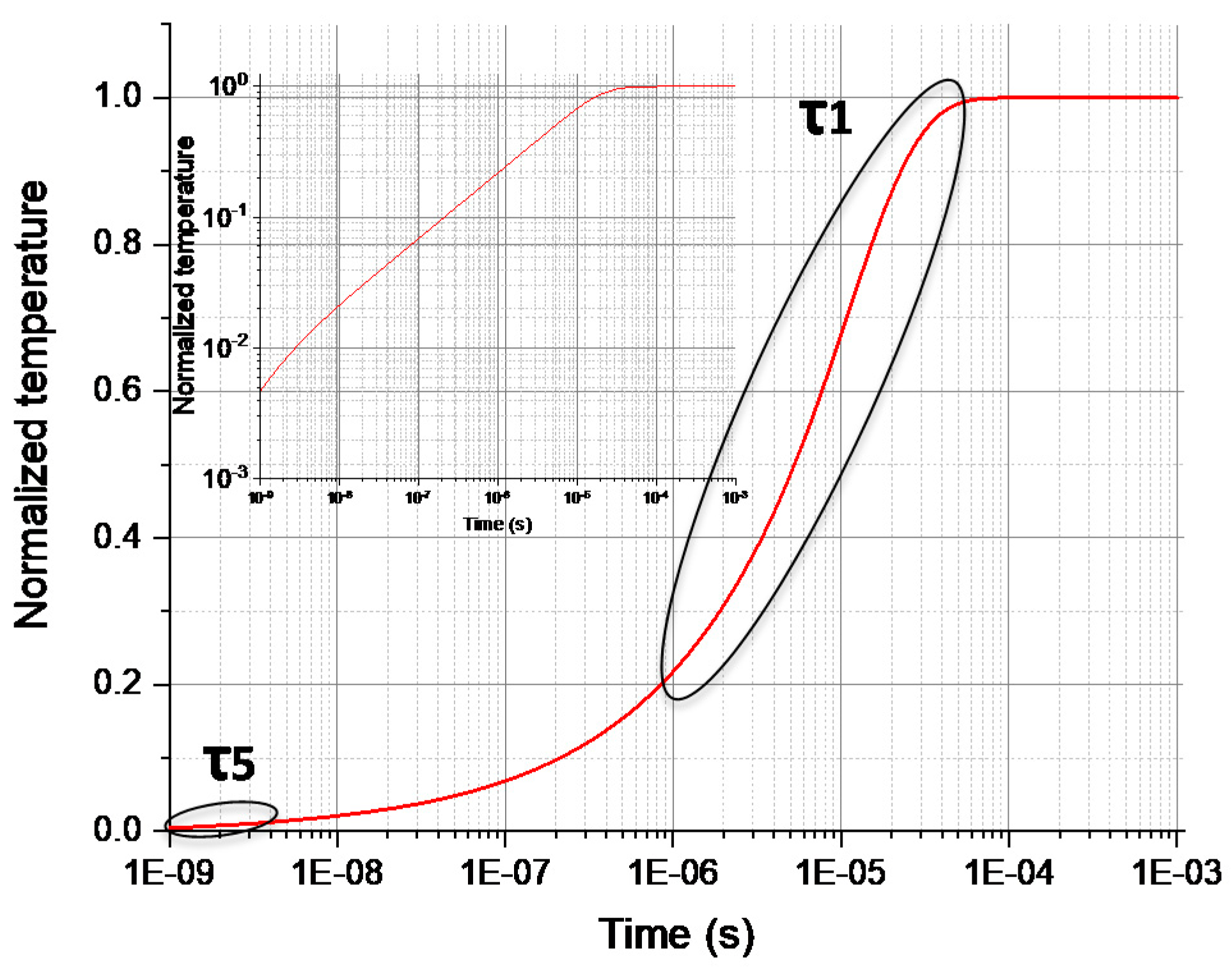
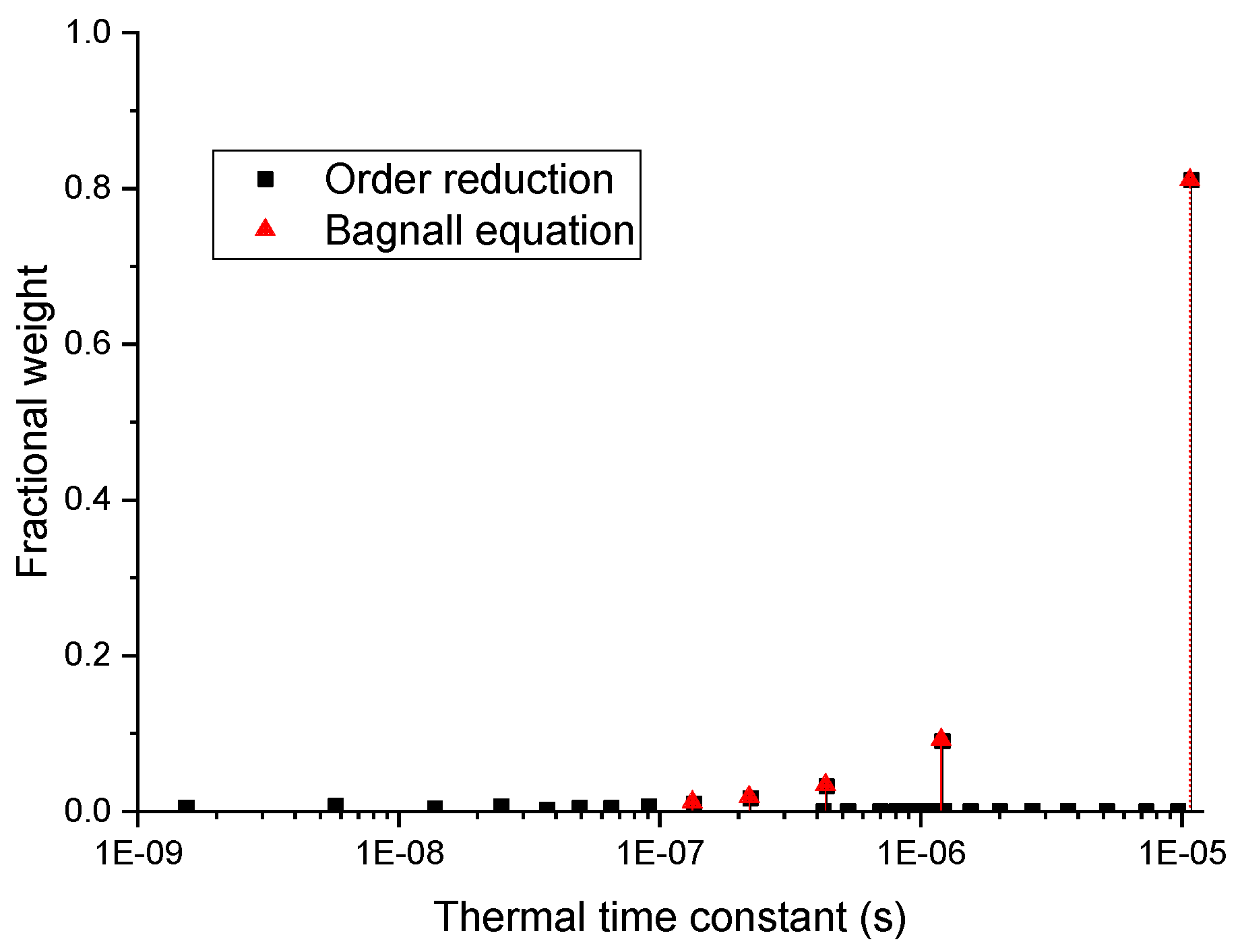
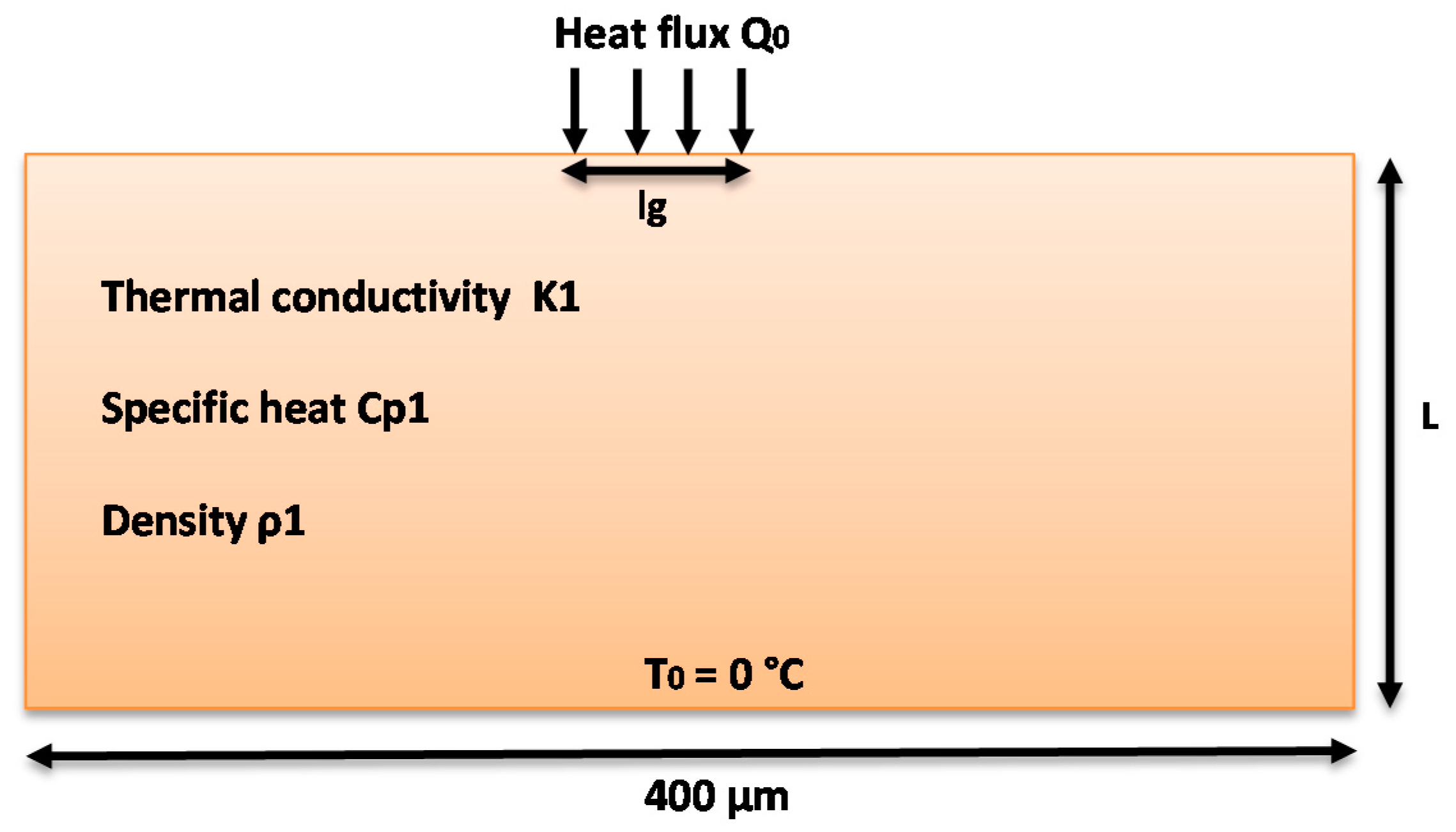
3.1. 1-D, Single-Layer Simulation
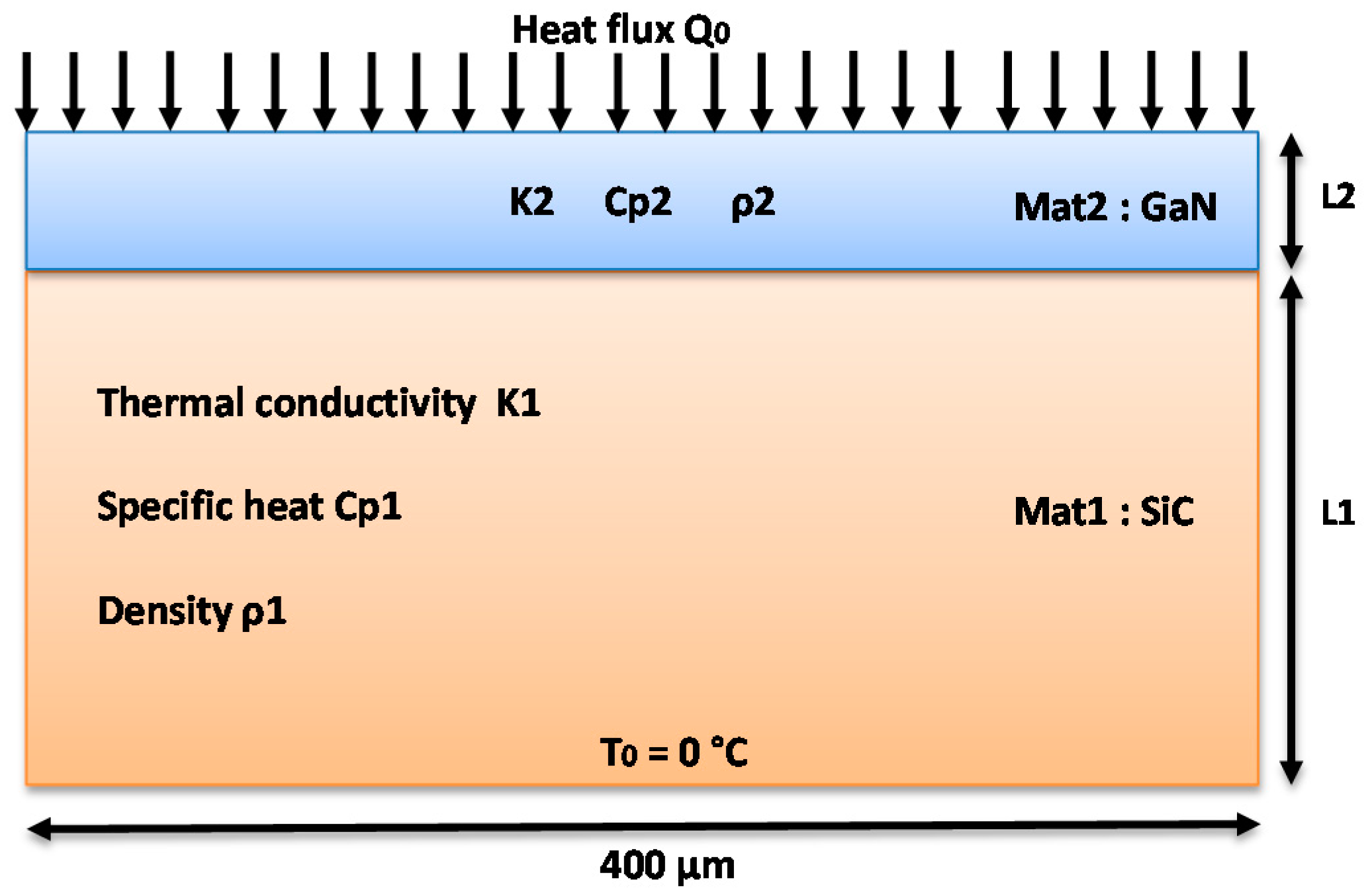
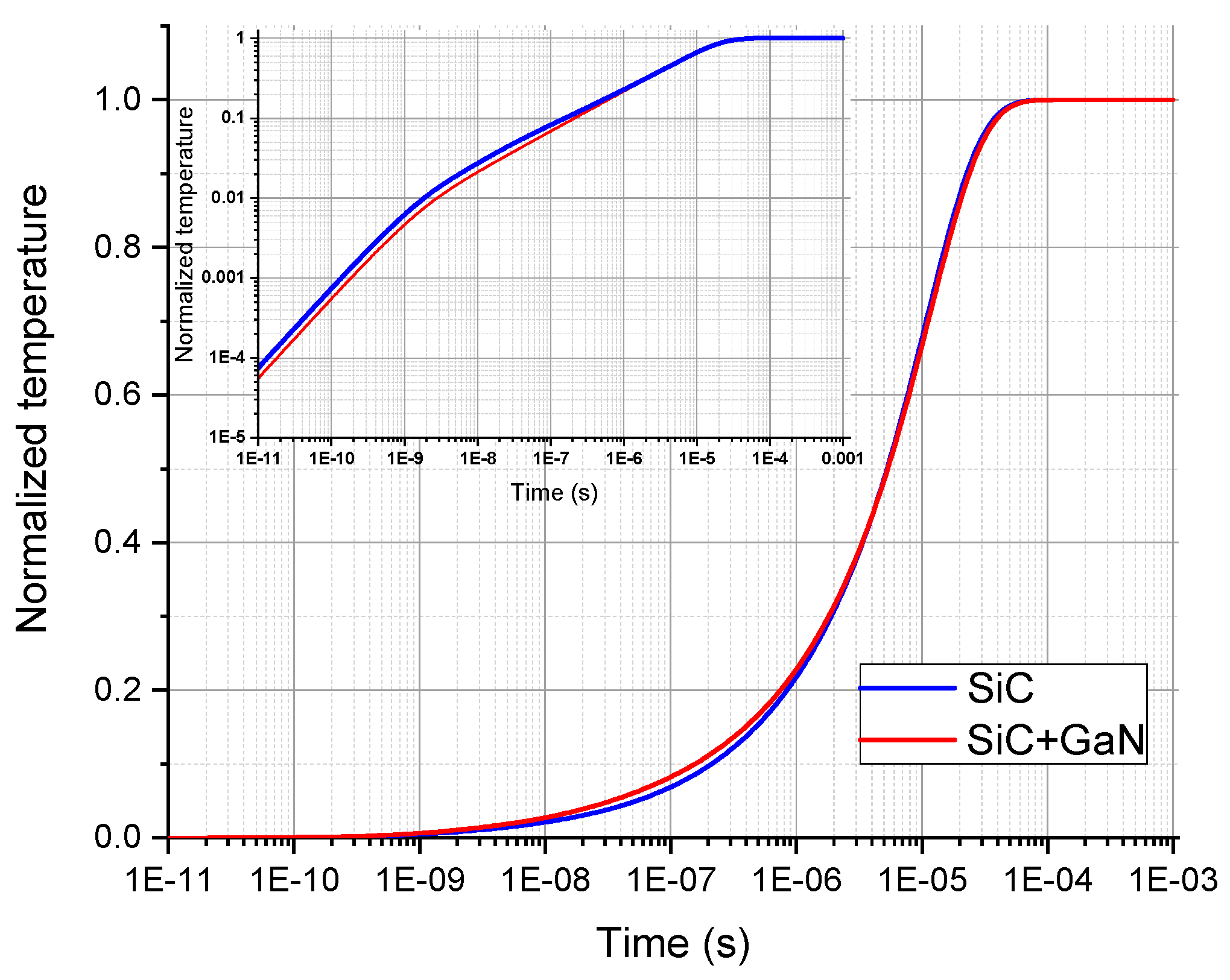
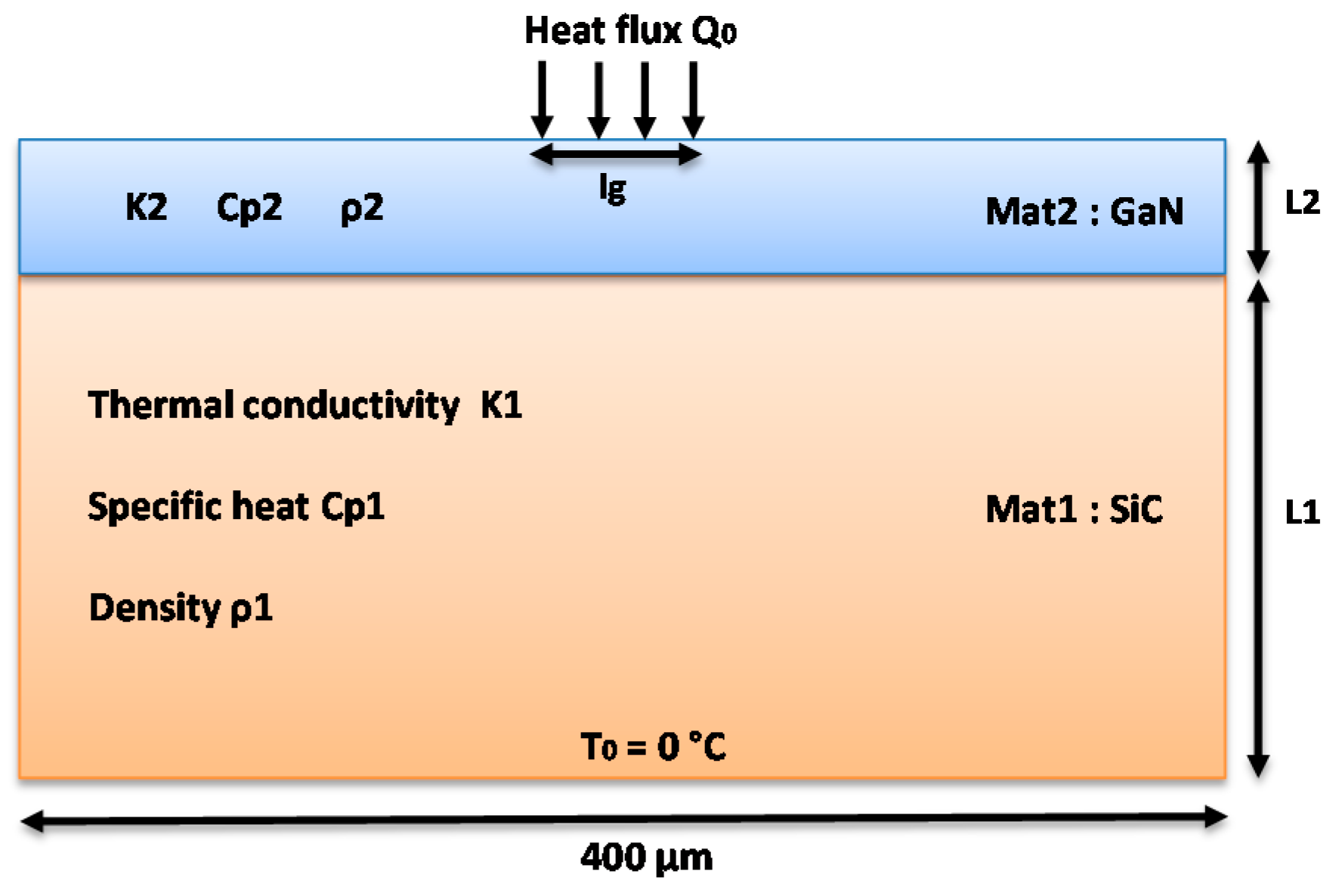
3.2. One-Dimension, Two-Layers Simulation
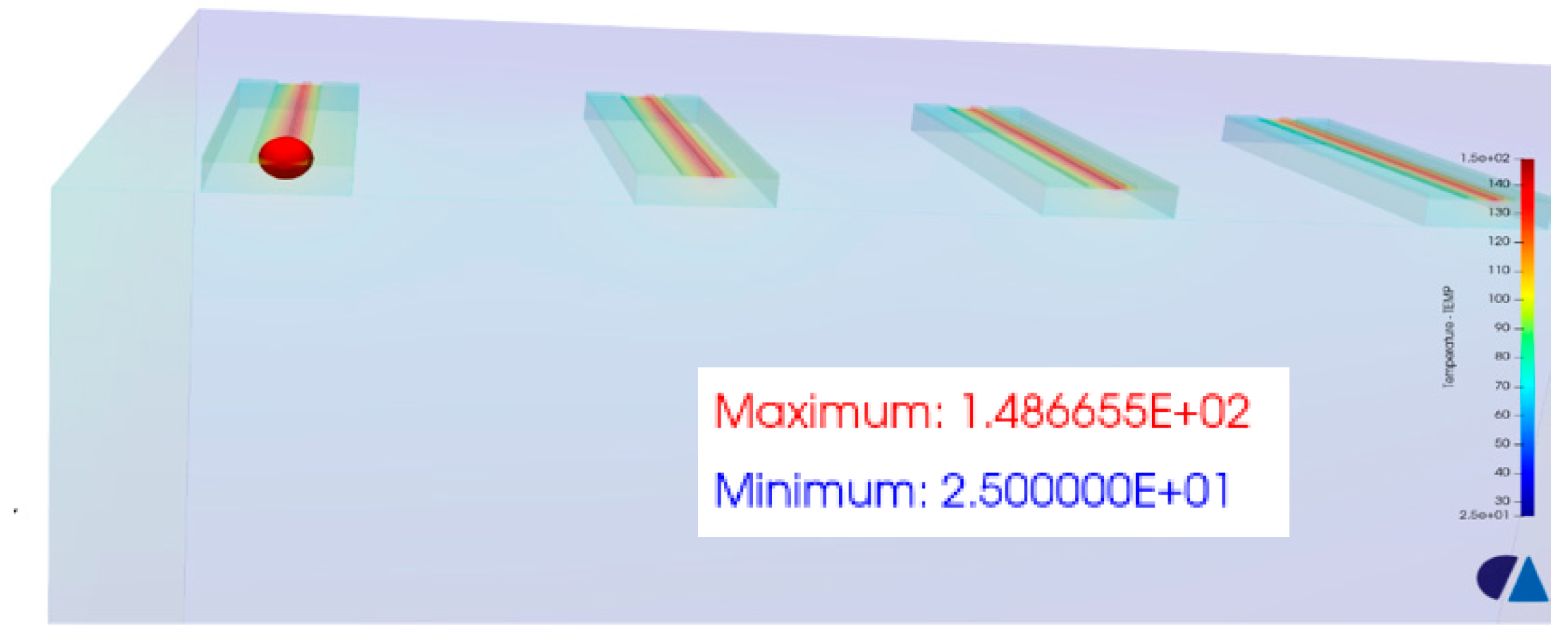
4. Two-Dimensional (2-D) Analysis
4.1. 2-D, One-Layer Simulation
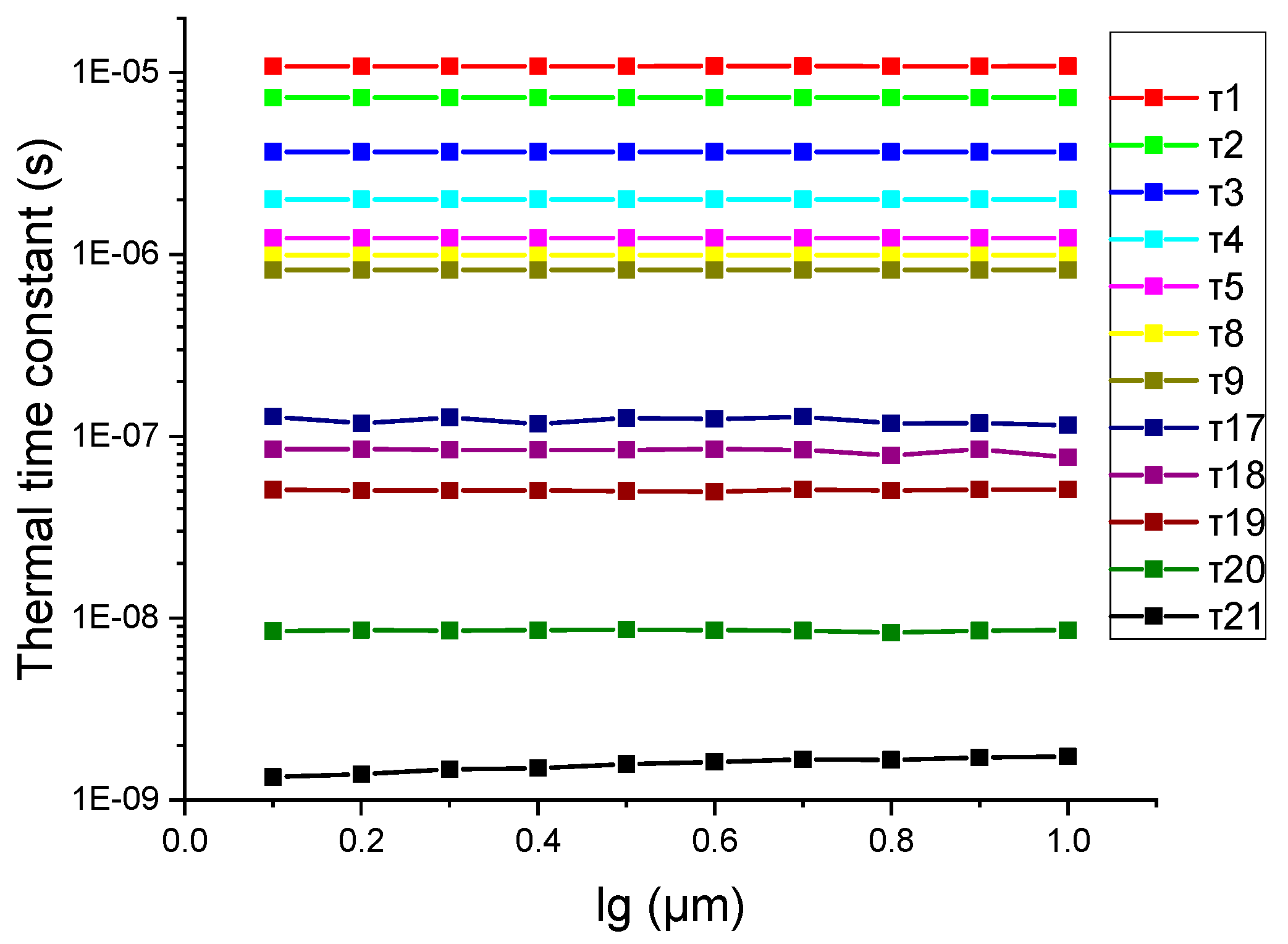
4.2. 2-D, Two-Layer Simulation
5. Calibration between Simulation Results and Measurements
6. Conclusions
- –
- that there are several thermal time constants in a HEMT, even with a 1-D, single layer;
- –
- the influence of the GaN layer on the thermal time constants;
- –
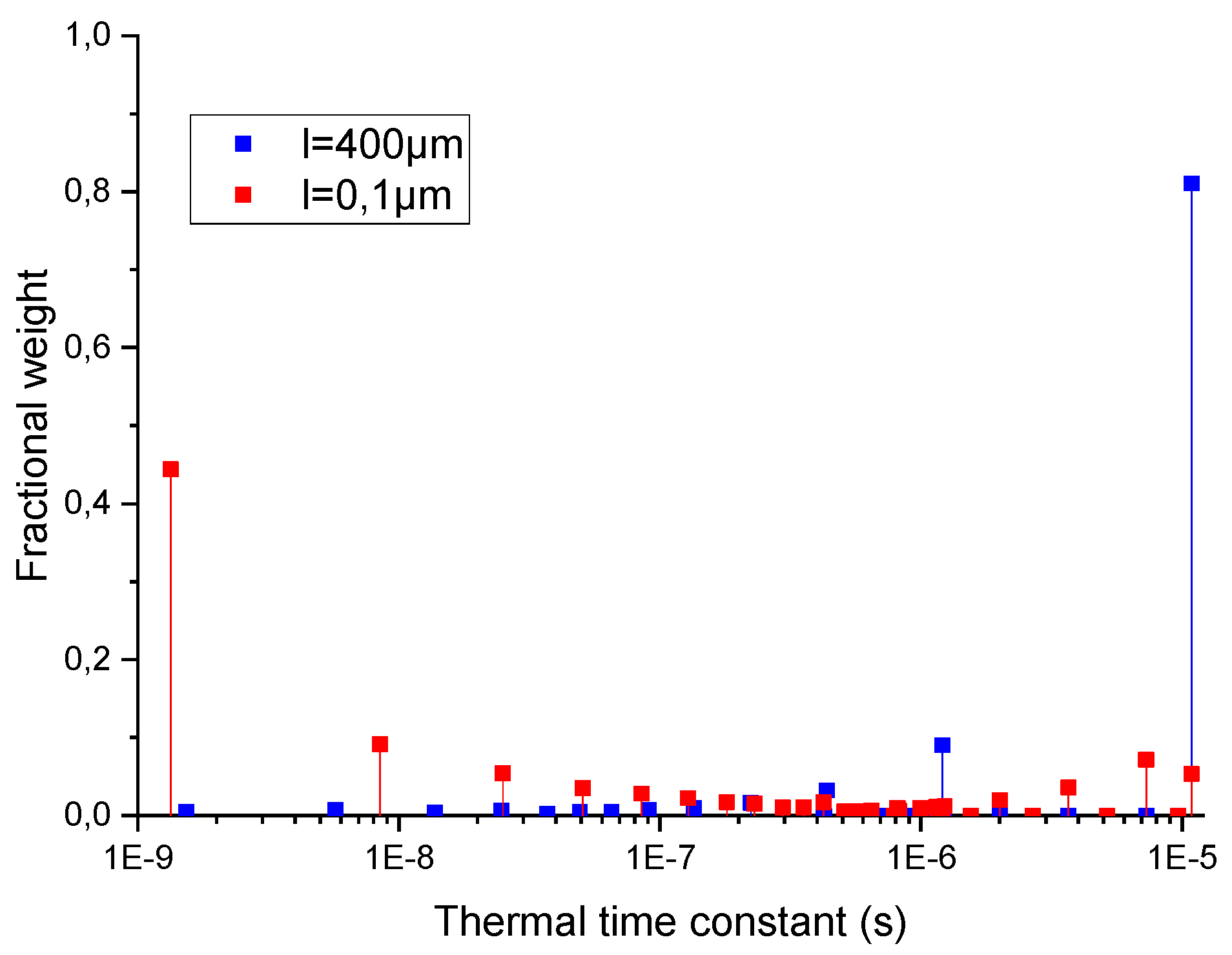
- the evolution of the thermal time constants with the dimensions of the devices, and in particular with the gate length, which is one of the key points to address in high-frequency applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chowdhury, S.; Mishra, U.K. Lateral and Vertical Transistors Using the AlGaN/GaN Heterostructure. IEEE Trans. Electron. Devices 2013, 60, 3060–3066. [Google Scholar] [CrossRef]
- Albers, J. An exact recursion relation solution for the steady-state surface temperature of a general multilayer structure. IEEE Trans. Compon. Packag. Manuf. Technol. Part A 1995, 18, 31–38. [Google Scholar] [CrossRef][Green Version]
- Yovanovich, M.M.; Muzychka, Y.S.; Culham, J.R. Spreading Resistance of Isoflux Rectangles and Strips on Compound Flux Channels. J. Thermophys. Heat Transf. 1999, 13, 495–500. [Google Scholar] [CrossRef]
- Geer, J.; Desai, A.; Sammakia, B. Heat Conduction in Multilayered Rectangular Domains. J. Electron. Packag. 2007, 129, 440–451. [Google Scholar] [CrossRef]
- Masana, F. A closed form solution of junction to substrate thermal resistance in semiconductor chips. IEEE Trans. Compon. Packag. Manuf. Technol. Part A 1996, 19, 539–545. [Google Scholar] [CrossRef]
- Darwish, A.; Bayba, A.; Hung, H. Thermal Resistance Calculation of AlGaN–GaN Devices. IEEE Trans. Microw. Theory Tech. 2004, 52, 2611–2620. [Google Scholar] [CrossRef]
- Bagnall, K.R.; Wang, E.N. Transient thermal dynamics of GaN HEMTs. In Proceedings of the 2016 15th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 31 May–3 June 2016; pp. 1551–1557. [Google Scholar]
- Bagnall, K.R.; Wang, E.N. Theory of Thermal Time Constants in GaN High-Electron-Mobility Transistors. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 8, 606–620. [Google Scholar] [CrossRef]
- Cahill, D.G.; Ford, W.K.; Goodson, K.E.; Mahan, G.D.; Majumdar, A.; Maris, H.J.; Merlin, R.; Phillpot, S.R. Nanoscale thermal transport. J. Appl. Phys. 2003, 93, 793–818. [Google Scholar] [CrossRef]
- Lacroix, D.; Joulain, K.; Lemonnier, D. Monte Carlo transient phonon transport in silicon and germanium at nanoscales. Phys. Rev. B 2005, 72, 064305. [Google Scholar] [CrossRef]
- Sommet, R.; Chang, C.; Quere, R.; Dueme, P. Model order reduction of linear and nonlinear 3D thermal finite-element description of microwave devices for circuit analysis. Int. J. RF Microwawe Comput.-Aided Eng. 2005, 15, 398–411. [Google Scholar] [CrossRef]
- Jobert, N. Working Wonders with ADPL Math Illustrated: Thermal Modal Analysis. Available online: https://www.padtinc.com/blog/author/nicolas-jobert/ (accessed on 12 September 2017).
- Wilson, E.L.; Yuan, M.W. Dynamic analysis bydirect superposition of Ritz vectors. Earthq. Eng. Struct. Dyn. 1982, 10, 813–821. [Google Scholar] [CrossRef]
- Cahill, D.G.; Braun, P.V.; Chen, G.; Clarke, D.R.; Fan, S.; Goodson, K.E.; Keblinski, P.; King, W.P.; Mahan, G.D.; Majumdar, A.; et al. Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 2014, 1, 011305. [Google Scholar] [CrossRef]
- Jakani, A.; Sommet, R.; Gaillard, F.; Nallatamby, J.-C. Comparison of GaN HEMTs Thermal Re-sults through Different Measurements Methodologies: Validation with 3D Simulation. In Proceedings of the International Workshop on Integrated Nonlinear Microwave and Millimetre-Wave Circuits, Berlin, Germany, 23 September 2021. [Google Scholar]
- Shakouri, A.; Ziabari, A.; Kendig, D.; Bahk, J.-H.; Xuan, Y.; Ye, P.D.; Yazawa, K.; Shakouri, A. Stable thermoreflectance thermal imaging microscopy with piezoelectric position control. In Proceedings of the 2016 32nd Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 14–17 March 2016; pp. 128–132. [Google Scholar] [CrossRef]
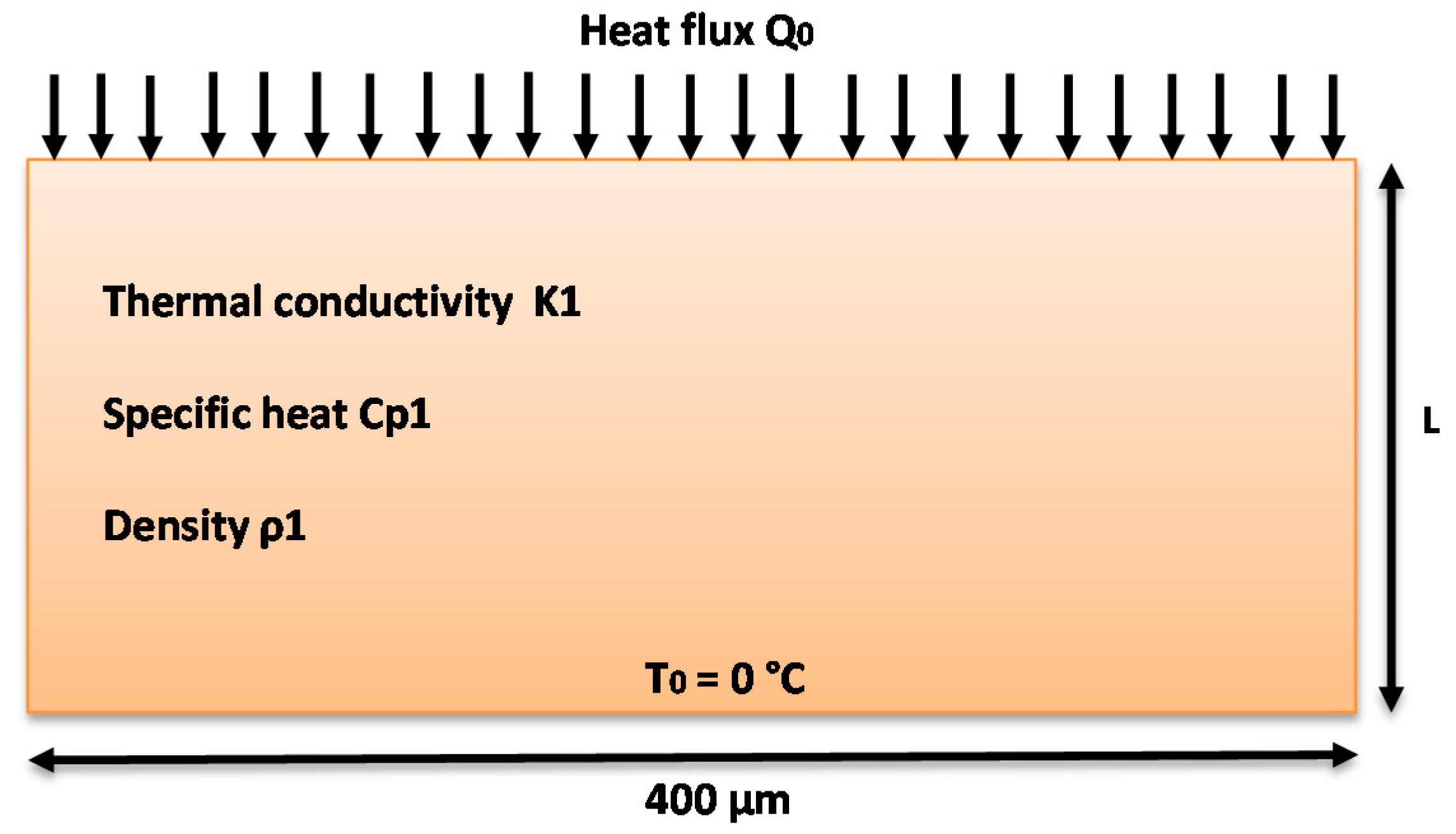






| ρ (Kg.m−3) | Cp (J. Kg−1. K−1) | K (W.m−1. K−1) | L (m) |
|---|---|---|---|
| 3210 | 665 | 390 | 70 × 10−6 |
| Thermal Time Constant (s) | Order Reduction | Ref. [7] |
|---|---|---|
| τ1 | 1.087 × 10−5 | 1.087 × 10−5 |
| τ2 | 1.208 × 10−6 | 1.208 × 10−6 |
| τ3 | 4.358 × 10−7 | 4.348 × 10−7 |
| τ4 | 2.228 × 10−7 | 2.218 × 10−7 |
| τ5 | 1.352 × 10−7 | 1.342 × 10−7 |
| Example | α1 (W.m2.J−1) | α2 | L1 (µm) | L2 (µm) |
|---|---|---|---|---|
| 1 | 1.827 10−4 | 6.414 × 10−5 | 70 | 2 |
| 2 | 1.827 10−4 | 6.414 10−5 | 70 | 8 |
| 3 | 8.696 10−5 | 6.414 10−5 | 70 | 2 |
| Thermal Time Constant (s) | Order Reduction | Equation (14) | Equation (15) |
|---|---|---|---|
| Example 1 (GaN 2 µm/SiC) | |||
| Example 2 (GaN 8 µm /SiC) | |||
| Example 3 (GaN 2 µm/Si) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakani, A.; Sommet, R.; Simbélie, F.; Nallatamby, J.-C. Understanding the Thermal Time Constants of GaN HEMTs through Model Order Reduction Technique. Electronics 2021, 10, 3138. https://doi.org/10.3390/electronics10243138
Jakani A, Sommet R, Simbélie F, Nallatamby J-C. Understanding the Thermal Time Constants of GaN HEMTs through Model Order Reduction Technique. Electronics. 2021; 10(24):3138. https://doi.org/10.3390/electronics10243138
Chicago/Turabian StyleJakani, Anass, Raphael Sommet, Frédérique Simbélie, and Jean-Christophe Nallatamby. 2021. "Understanding the Thermal Time Constants of GaN HEMTs through Model Order Reduction Technique" Electronics 10, no. 24: 3138. https://doi.org/10.3390/electronics10243138
APA StyleJakani, A., Sommet, R., Simbélie, F., & Nallatamby, J.-C. (2021). Understanding the Thermal Time Constants of GaN HEMTs through Model Order Reduction Technique. Electronics, 10(24), 3138. https://doi.org/10.3390/electronics10243138






