Abstract
This paper presents an energy-management strategy based on a recently introduced Political Optimizer (PO) for a microgrid installation at Wroclaw University of Science and Technology. The aim of the study is to check the effectiveness of two recently introduced meta-heuristic algorithms at power-system-operations planning. The optimization algorithms were compared with other conventional meta-heuristics wherein performance tests were carried out by minimizing costs in an IEEE 30-bus system. The best performing algorithm was then used to minimize the Levelized Cost of Energy (LCOE) in a microgrid consisting of renewable energy sources such as solar PV panels, a micro-hydro power plant, a fuel cell with a hydrogen storage tank and a Li-ion storage unit.
1. Introduction
The current topology of the power system is being modified by a host of factors including increasing energy consumption, penetration of renewable energy sources, decentralization and significant control-system implementation in order to satisfy the community-determined objectives such as cost or emissions minimization [1]. These changes are driven by a shift in the energy policies of both national and international governing bodies, as well as by the attitude of the people themselves, and are evidenced by the numerous binding agreements that have been signed, such as the Paris agreement [2] and the European green deal [3]. Both of these agreements promote sustainable development.
A fitting solution to the sustainable-development conundrum is the microgrid. It can also be seen as a concept that is partly responsible for the changes in the topology of the power system. The definition of a microgrid is varied and depends upon the organization defining it. Nevertheless, the common attributes between the definitions provided by the US Department of Energy [4] and CIGRE [5] are that microgrids represent a group of interconnected loads and generating sources, they have well-defined electrical boundaries, they are controllable, they are decentralized power systems, they are equipped with robust communication and smart-grid technologies, and they can work in tandem with the grid or in a standalone mode. Finally, they are seen as a single entity by the Distribution System Operator (DSO).
An integral part of the modern microgrid is the Energy-Management System (EMS) which according to the International Electrotechnical Commission (IEC) standard 61970 is defined as a computer system consisting of various applications and support services that enable the effective operation of the power system so that the adequate security of the energy supply is maintained and is provided at a minimum cost. In general, from review articles found in the literature [6,7,8], the EMS of a microgrid has a host of functions which are shown in Figure 1. They include data acquisition, which involves the collection of data from various elements present in the microgrid such as generators, loads, storage devices, the main grid and weather forecasts. The acquired data is then appropriately processed according to the needs of the central computer of the microgrid, which could involve operations such as sampling, normalization, etc. Then comes forecasting, which involves predicting the time-dependent variables present in the microgrid such as the outputs of the weather-dependent renewable energy sources and the load demand. Forecasting in the long term (day ahead, week ahead and year ahead) is a process that is not performed online, and the forecasting referred to in Figure 1 is in the very short term (15 min ahead). This is because the short-term forecasts are more accurate than the long-term forecasts, and the plan for dispatch created 15 min before is much more accurate than the one created over a longer term. This process is succeeded by optimization which involves the creation of a schedule that balances power supply and demand over a period of time, which results in the Economic Dispatch (ED). This step is also the focus of this article. The final step involves the real-time control of the operation of the microgrid.
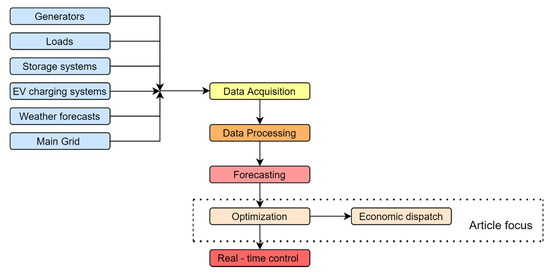
Figure 1.
Functions of the EMS of the microgrid.
A few examples of EMSs found in the literature are described further on. A hierarchical multi-agent approach using Particle Swarm Optimization (PSO) [9] for the energy management of a microgrid consisting of storage devices, renewable energy sources and electrical vehicles is presented in [10]. The objective function used in the study was the minimization of the operational cost and the innovativeness of the study comes from the low-computational-burden models that were created in order to simulate both the electrical and thermal characteristics of the system under consideration. The performance of the approach was evaluated over 3 different scenarios which considered the normal operation of the microgrid, the normal operation with autonomous capability and the analysis of the prosumer operations of the consumers under normal operating conditions. Overall, the implementation of the EMS was shown to reduce the costs by 11% in comparison with a business-as-usual approach. A multi-objective optimization approach considering cost minimization, PV-system-utilization rate and power fluctuations in a microgrid is presented in [11]. The study investigated the influence of demand-side response and Electrical Vehicle (EV) charging and discharging on the functioning of the microgrid under four different scenarios. The scenarios involved cases where both the controlled and uncontrolled charging of EVs were each considered with and without transferrable loads. For the purposes of optimization, a multi-objective seeker optimization algorithm was considered [12]. The microgrid model used consisted of elements such as PV panels, storage systems, EV charging ports, diesel engines and residential loads. The results showed an improvement in cost minimization, efficiency and security in the operation of the microgrid when controlled charging and demand-side response were considered together in comparison with the other explored scenarios. A mixed-integer, non-linear-programming approach to the optimization of an islanded water-energy-based microgrid is presented in [13]. The main purpose of the optimization model was to manage the demand for water within the water-distribution network, along with the smart management of electrical chillers for temperature moderation and, additionally, the management of electrical power generators. The study made an attempt to solve the ED problem on a day-ahead time horizon. The microgrid under consideration had numerous elements such as PV panels, energy-storage systems, conventional sources of power, both commercial and residential loads, and a comprehensive water-distribution network. In order to verify the performance of the proposed approach, a comparison was made between the cases wherein the ED was made with and without water-demand management and/or thermal management. The results indicated that hourly savings up to $150 can be made by including the water-distribution network within the ED problem, and that thermal management can additionally lower the hourly costs. While a few studies regarding EMSs of various microgrids have been described above, a more comprehensive description of the various microgrid architectures and EMSs are provided in detail in the following review papers [6,8].
- The examples provided above used different optimization algorithms in order to carry out the ED or energy management in diverse microgrids. In fact, new optimization algorithms are always being developed and it is not clear which optimization algorithm would serve as the best for the EMSs of microgrids. The question is quite relevant given the rapid adoption and development of microgrids. In this regard, the contributions of this paper are summarized as follows:
- The investigation of two recently developed optimization algorithms for carrying out Optimal-Power-Flow (OPF) studies in electrical networks. This step is essential since it is important to test any new approach on a standard, well-known system before it is used for energy management in highly localized and diverse microgrids. The tested algorithms include the Political Optimizer (PO) and the Lichtenberg Algorithm (LA). The OPF studies were carried out by the cost minimization of the IEEE 30-bus system.
- The comparison of the performance of the newly developed approaches with existing conventional approaches. In this regard, a comprehensive comparison of the values of all the decision variables as a result of applying the PO and LA were compared with the results from applying the Particle Swarm Optimization (PSO) and Genetic Algorithm (GA). Furthermore, a small comparison of the results taken from the well-known literature was also made.
- The best performing optimization algorithm was then selected to carry out ED studies in a microgrid that consisted of numerous sources of energy such as Li-ion storage systems, fuel cells (FCs), solar PV panels, micro-hydro power plants and diesel generators (DGs). The LCOE of all the sources of energy were calculated and it was found to be minimized during the operation of the microgrid. The microgrid was connected and hourly grid prices were used in the study.
- Finally, in order to understand the cost implications year round, clustering was used to identify representative days of the year with which comparisons were made regarding the microgrid operation. The microgrid model was based on the existing elements present at Wroclaw University of Science and Technology.
- The novelty of the study comes from the fact that the Political Optimizer and the Lichtenberg Algorithm have not yet been used for OPF studies. Moreover, the study shows that the Political Optimizer is an effective option for an energy-management system of microgrids, which, to the best of our knowledge, has not yet been explored. The study presents an energy-management approach that analyzes the behavior of the microgrid and the LCOE cost for an entire year, which is valuable to microgrid planners in the region.
The rest of the paper is organized as follows. Section 2 provides a comprehensive description of the PO, which was the main optimization algorithm chosen to carry out the ED for the microgrid. It also presents brief descriptions of other optimization algorithms that were considered. This is followed by a comparison of the results of applying the optimization algorithms to OPF studies. Section 3 provides the microgrid model, the mathematical model and the LCOE calculations. Section 4 describes the generators and their mathematical models. Section 5 presents the results and analysis of the microgrid operation while considering the changing weather during a calendar year. This is followed by the conclusions that were made from the study.
2. Investigated Optimization Algorithms
2.1. Political Optimizer
The PO is a socio-inspired, human-behavior-based, meta-heuristic optimization algorithm. It is based on the workings of political institutions and the electoral procedure. It is modeled on the steps that are usually followed in setting up a government, such as elections, the affairs of the parliament, the elections for constituencies, members defecting from one party to another, and in general the campaigns held by all of the stakeholders in the elections [14]. The effectiveness of this algorithm in locating the final global minimum solution comes from its dual-sided approach. The first approach involves every individual that represents a solution candidate trying to win an election, and the second approach involves every contesting political party trying to form a government by gaining a majority of the seats in the parliament.
The solution-searching process of the algorithm is as follows: it begins with a declaration of the population size that is then divided into n political parties that consist of n members. Every member of every party represents a candidate solution and is a vector of the decision variables of the problem. During this step the algorithm calculates the number of constituencies, which aids in locating the best party member at a particular index within a party, and is equal to the number of parties and members n. This concept is explained further with an explanation and is illustrated in Figure 2.
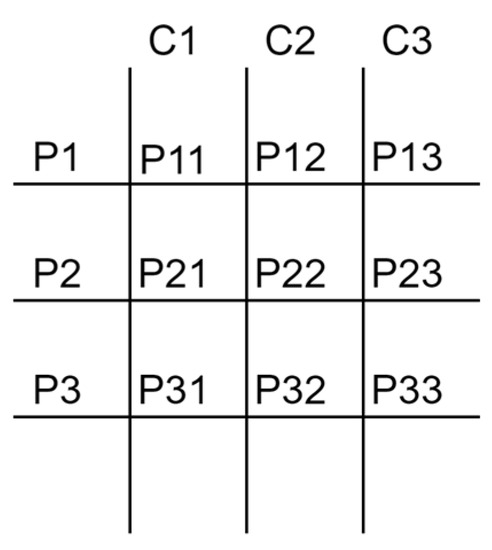
Figure 2.
Constituency allocation.
It can be seen from the figure that for a population of nine individual candidates, three parties with three individuals are created. The political parties are represented by P1, P2 and P3 and every candidate has an index representing their party number and their position within the party. For example, P22 represents a member from party two and is located at the second position within the party. As mentioned previously, the algorithm creates as many constituencies as there are parties. Hence, from the figure it can be seen that three constituencies are created, which are C1, C2 and C3. Now the members (solution candidates) from each party that have the same position number within each constituency are compared with each other and the member with the best fitness is selected as that constituent’s winner. For example, in the case of constituent C1, the members at position 1 of every party (P11, P21 and P31) are compared and the best candidate solution is chosen as the constituent’s winner.
Apart from the constituency winners, all of the party members are also compared with one another within the same party and the solution candidate with the best fitness is chosen as the party leader. The constituency winners go on further to form the parliament, at which point a new phase of the solution-searching process is initiated wherein the existing solutions are further improved.
The process during which the existing solutions are improved is the exploratory and exploitation phase of the algorithm. This helps in the identification of the global minimum solution. The fitness of each candidate is improved by changing their position on the solution-search space wherein this change is guided by their past position, the position of the constituency winner and the position of the party leader. In addition to this process, party switching is also performed wherein members are moved from one party to another, and in doing so the member with the lowest fitness in a party is replaced by the newly arriving member. Once these two processes are complete, the new objective function values (fitness) are re-calculated and new constituency winners and party leaders are determined once again. A step called parliamentary affairs is then initiated, during which random position changes are introduced, and if this results in an improvement in the fitness value then the new location replaces the old one. The process is then repeated until the stopping criteria defined by the user are met. The algorithm is illustrated in Figure 3.
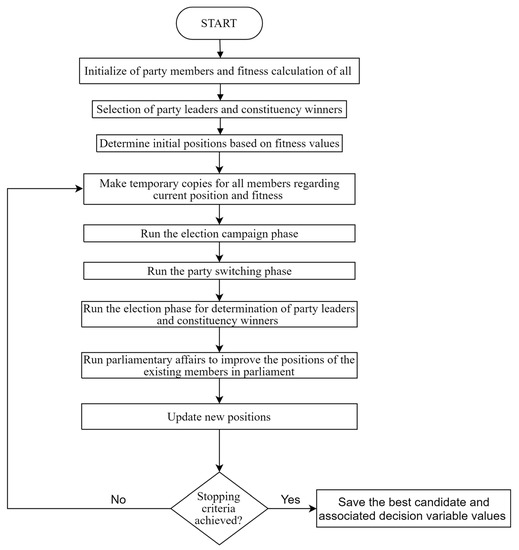
Figure 3.
Political Optimizer.
2.2. Lichtenberg Algorithm
The Lichtenberg Algorithm (LA) is a nature-inspired, meta-heuristic approach based on the exploitation of fractal power. It takes advantage of the randomness involved in the Lichtenberg-Figure (LF) formation and incorporates it into the solution-searching process. A well-known example of an LF is lightning formation in clouds.
In fact, lightning formation is the real-world phenomenon upon which the LA is based. Lightning is formed as a result of an electrical discharge from electrical fields that are formed due to the relative movement of clouds amongst one another and the resulting friction. They can be categorized into many different types, such as ground-to-cloud, inter-cloud and intra-cloud, cloud-to-ground and cloud-to-atmosphere. Amongst all the types of lightning propagation, the intra-cloud phenomenon is the most apt for an optimization algorithm due to its area coverage, which is considerably higher than in the case of the other lightning types. This propagation creates an LF that can be recreated in a laboratory by witnessing an electric discharge on di-electric materials [15].
A well-known approach for creating LFs is the Diffusion Limited Aggregation (DLA) which creates them via cluster formation [16]. Two inputs are needed for this approach, which are the cluster size and number of particles. Once these two parameters are defined, a random figure is generated by utilizing fractal geometry. Two such figures that were created on different runs of the algorithm are shown in Figure 4, and it can be seen that they are quite different despite being created from the same parameters. This randomness in formation aids in the exploration of the solution-search space for the optimization algorithm.

Figure 4.
Lichtenberg figure.
The algorithm, while using the DLA and the LF to solve optimization problems, has introduced certain improvements, which are as follows. The first improvement, called measure 1, enables the efficient exploration of the solution-search space by reducing the space between branches. This is achieved by introducing a value between 0 and 1 at every iteration and multiplying it by the size of the LF. In measure 2, instead of altering the size of the LF it is rotated randomly, which has shown an improvement in the performance of the algorithm with respect to the problems associated with a large number of decision variables [17]. Measure 3 is introduced in order to solve local optimization problems and it is also known as as the refinement parameter. This is done by creating an entirely new LF for the local optimization problem, which is obtained by multiplying the size of the original LF by the refinement parameter that takes a value between 0 and 1. The final measure is introduced in order to keep the solution-search space continuous and not discrete. It has 3 possible inputs which are 0, 1 and 2. A value of 0 maintains one LF throughout the iterative process, 1 creates a new LF at every iteration and 2 loads a previously saved LF from the archives. The algorithm is initiated by the declaration of the population size and the number of particles, which are two independent parameters. The number of particles in this case is used for LF creation. During the creation of the figure, the particles are distributed throughout the solution-search space, during which time the objective function value is calculated for certain locations depending upon the population size. The algorithms continues to explore new areas of the solution-search space until the stopping criteria that were defined have been satisfied. The algorithm is shown in Figure 5.
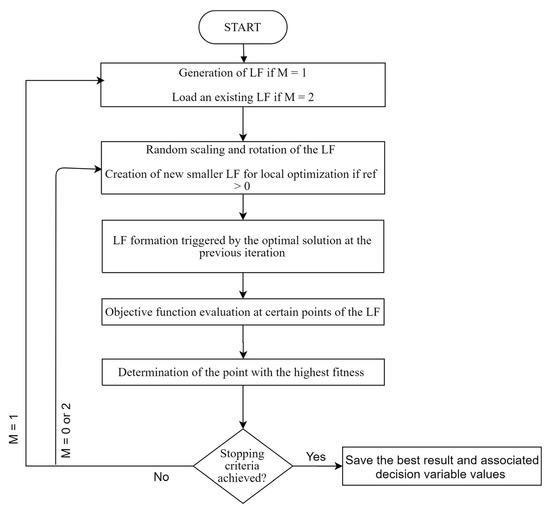
Figure 5.
Lichtenberg algorithm.
Apart from the two optimization algorithms mentioned, this study has also decided to compare the performance of the newly introduced algorithms with two conventional optimization algorithms which are the Genetic Algorithm (GA) and PSO. The literature on the two approaches and their applications to OPF studies is widely available. A few of them can be found in [18,19,20,21].
2.3. Performance Evaluation of the Investigated Algorithms
The PO, LA, GA and PSO were implemented in the IEEE 30-bus system since it is a well-known power system in the literature with which to compare the performance of optimization approaches. In this study, the proposed approaches were first evaluated in this standard system and then the best algorithm was chosen for ED in microgrids.
Modeled based on a part of an existing transmission system, the IEEE 30-bus system had a total of 6 generators located at bus numbers 1, 2, 5, 8, 11 and 13. The tap settings for the transformers could only be adjusted for a few within the system and they were located between 6 and 9, 28 and 27, 4 and 12, and finally 6 and 10. The reactive power injection was made at buses 10, 12, 15, 17, 20, 21, 23, 24 and 29.
Table 1 provides information regarding the decision variables as set by the optimization algorithms when they were run on the IEEE 30-bus system. The decision variables included the active power from five generators, except for the largest one since it served as the slack generator and included the voltage magnitude at all of the generating buses and the supply from the reactive power compensators. It can be seen from the table that the PO and GA both had the best result when it comes to cost minimization ($801.6/h) but the PO was quicker at arriving at the same result with a run time of 4.09 s, which is more than 3 s faster than that of PSO and was the quickest of the compared algorithms. With regard to the other algorithms, the GA performed slower than both the PO and PSO and had a good final solution, and the LA was the worst with the longest run time and the worst solution.

Table 1.
Control variables, cost and computation time comparison of meta-heuristics applied to OPF.
3. Microgrid Layout, Mathematical Model and LCOE Calculations
3.1. Microgrid Layout
The layout of the microgrid is presented in the Figure 6 and was partially modeled on the setup at Wroclaw University of Technology. In total, the number of generators is 10 (including storage) and the number of loads is 13 (including storage). Amongst the generators were four PV panels with peak powers of 13 kW, 12.5 kW, 8 kW and 16.5 kW, two diesel generators with a rating of 4.8 kW/6 kVA, a Li-ion battery system (BESS) with a capacity of 9.8 kWh, a fuel cell (FC), a hydrogen storage tank (HST) with a capacity of 4.2 kWh, and finally a micro-hydro power plant with a peak power of 10.46 kW. The loads were modeled according to the values provided in Figure 6.
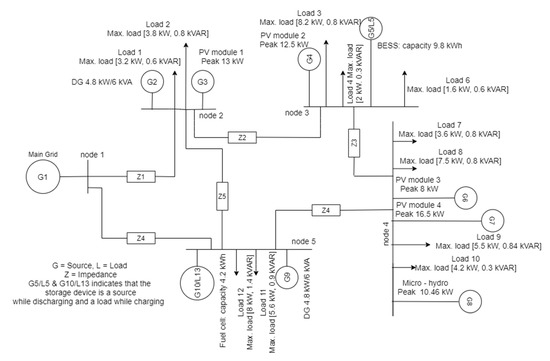
Figure 6.
Microgrid layout.
The nodes of the microgrid were interconnected by aluminum cables that were XLPE insulated and had an outer sheath composed of PVC. The electrical characteristics of the cable are summarized in Table 2.

Table 2.
Cable data.
3.2. Mathematical Model
The optimization process carried out by the EMS in this study was dependent upon an objective function that attempted to minimize the LCOE associated with the generators in the microgrid. The LCOE is a metric that takes into account numerous costs such as the capital cost, operational and maintenance costs and initial installation costs. Moreover, the model accounted for the import/export of power from the main grid for which the hourly prices were downloaded from the website for the European Network of Transmission System Operators for Electricity (ENTSO-E). The objective function is shown below where Tc is the overall cost function that is minimized during the microgrid operation. Pi is the generated power of every generator i in the microgrid and their corresponding LCOE is represented using Ci. The power exchange with the main grid is represented by PEX and the cost for doing so is represented by CEX. ng represents the total generators present within the microgrid.
During microgrid operation, the EMS ensures that the parameters such as voltage magnitude and voltage angle, amongst others, are maintained within the limits defined by the DSO. It also ensures that the active and reactive powers produced by the generators stay within their respective minimum and maximum generating capabilities. In general, the above-mentioned functions of the EMS are represented by means of equality and inequality constraints and in this study, they follow the constraints that are typical for AC-OPF studies. The equations are shown from (2) to (7).
3.3. LCOE Calculations
Any microgrid is inherently diverse with regard to the multiple sources of renewable energy that are present within its energy mix. In order to compare the cost-effectiveness of all the different generators available and aid in investment planning, the LCOE is used [22,23]. The calculations result in the assertion of price per unit of energy produced for every generator type in the microgrid, and take into account the total investment costs such as the capital cost and the cost of installation. Additionally, it considers the operational and maintenance costs and any other costs one may encounter during the lifetime of the generator. The total energy produced by a generator type over its lifetime is also assumed. It is important to mention here that the LCOE is a static metric and not a dynamic one since it remains unchanged during the project lifetime. It is also a metric that is spatially dependent since the lifetime performance of renewable-energy-based generators is very much region specific. The LCOE also does not consider any financial benefits that might be associated with the project, such as tax rebates. In conclusion, it is a metric that is best representative of the costs when it is calculated by the project proponents that take into account the local availability of various sources of energy. The metric is calculated as per (9)
where Ct represents the yearly total costs and Et represents the yearly total energy outputs. Both the terms are discounted over the generator lifetime by where, r is the discounted rate and t is the year under consideration. The total lifetime is T. A more comprehensive version of (8) is shown in (9).
where:
- Cc: Initial capital cost (assumed as a single payment in the study)
- Ic: Installation costs
- Fc: Fuel costs
- : Operation and maintenance costs discounted by
The rest of the variables have the same meaning as those used in Equation (9).
4. Generator Models
4.1. Solar PV Panels
The solar panels that were used in the microgrid layout derive their characteristics from the curves obtained from the real panels that are installed on the roof of the electrical engineering building at Wroclaw University of Science and Technology. The obtained data was normalized and then the peak power was set according to the models in the layout. The cost associated with the panels can be calculated by Equation (10)
where the total capital cost of the solar panels is represented by Ccpv, the cost of one solar panel is Cpv and the total number of such panels is Npv. For the purposes of the calculation of the LCOE, the cost of installation was set at 20% of the capital cost [24]. The lifetime of the panels is around 25 years, which is equal to the project lifetime in this study; therefore, it was decided that no replacement would be involved. The yearly maintenance associated with the panels, which includes both cleaning and inspection, was set at $6.5/yr [24]. The inverters, which typically last around 10–11 years, had to be replaced two times during the project lifetime. All of the costs associated with the LCOE calculations are summarized in Table 3 at the end of the section.

Table 3.
Parameters and values for calculating the LCOE for every generator type.
4.2. Li-Ion Storage System (BESS)
The BESS was modeled according to the approach presented in [24,25]. The equations related to BESS charging and discharging are as follows.
The charging process is represented by Equation (11) where the BESS energy level at a given time step t is represented by Es(t) and at step t−1 it is represented by Es(t − 1). The self-discharge rate of the BESS is represented by . Eg(t) and El(t) represent the energy produced and the load demand in the microgrid at the time step t, whereas , represent the converter efficiency, charge controller efficiency and round-trip efficiency, respectively.
The BESS discharging was modeled according to (12).
where all the parameters are defined in the same manner as in (11).
The total cost (Ccbss) associated with the BESS is presented in (13) where the capital cost associated with each unit is represented by Cbss and the total number of such units is represented by Nbss.
The installation cost for BESS was determined at 5% of Ccbss [24]. The O&M costs were not considered for this energy source since it needs little to no maintenance and has no moving parts. A standard Li-ion battery system has a lifespan of 5,000 cycles. Based on simulations of the microgrid model that was run on data from the past 5 years, it was found that the average cycles per year are 671.5. This puts the lifespan of the BESS in this project at 7.4 years, which indicates that it has to be replaced three times over the entire project lifespan. This replacement cost has been included in the LCOE calculations in a discounted fashion. Furthermore, the fuel costs for the BESS were calculated based on the energy consumed during charging.
4.3. Fuel Cell + Hydrogen Storage Tank
The hydrogen-fuel-based generating system was the most expensive system of all the generators in the microgrid and had numerous components to it. In general, the working of the system was modeled according to Equations (14) and (15), where (14) represents the process of energy production by the fuel cell. In this case, the H2 stored in the hydrogen storage tank was combined with oxygen to produce electrical energy, heat and water. This process took place when the load demand in the microgrid was greater than the energy produced.
Ehs(t) is the energy equivalent of the hydrogen stored during time step t and Ehs(t − 1) represents the same during time step t − 1. Eg, El and have the same definitions as before, whereas is the fuel-cell efficiency. The process of excess-energy conversion to hydrogen within the microgrid is represented by Equation (15), in which case the electrolyzer utilized this energy to split water into hydrogen and oxygen and the hydrogen was stored in the tanks.
In (15), represents the electrolyzer efficiency, whereas the other variables have the same definitions as before. More information on the fuel cell and hydrogen storage apparatus can be obtained from [24].
The total cost associated with this system is as follows. The total capital cost (Ccfc) is defined as a product of the capital cost of one unit (Cfc) multiplied by the total number of units (Nfc). In this case, the capital cost included the cost of purchasing the fuel cell, the hydrogen storage tank and the electrolyzer. The total installation cost was set at 3% of the total capital cost. The O&M costs were considered for the fuel cell, the electrolyzer and the hydrogen storage tank, which were set at $120/kW/yr, $12/kW/yr and $5/kW/yr, respectively [24]. During the entire lifetime of the project, the fuel cell did not need replacement due to its high lifespan of 40,000 h. The electrolyzer had a shorter lifespan of 15 years and was replaced once. The fuel cost in this case included the energy that was consumed by producing hydrogen from water.
4.4. Diesel Generators (DGs)
The only non-renewable sources of energy in this microgrid were the DGs. They also represented a steady and stable source of energy within the microgrid. There were two units, both identical to one another with a rating of 4.8 kW/6 kVA. The fuel consumption of the DG was modeled as per (16),
where FDG(t) is the total consumed fuel, aDG and bDG are consumption coefficients, PDGgen is the power produced by the DG and its rated power is represented by PDGrat. The total capital cost is calculated by (17),
where the total cost is Ccdg, the cost per DG unit is Cdg and the total number of units is Ndg. The installation cost in this study was set at 3.5% of the Ccdg. The O&M costs were set at $510/kW/yr. The DG units had lifespans close to 20,000 h and since they operated regularly throughout the project lifespan, they were replaced every two years. The costs associated with the replacement were accounted for in the LCOE after being appropriately discounted.
4.5. Micro-Hydro Power Plant
Micro-hydro power plants usually refer to water-based generators that have a rating lower than 0.5 MW. The advantages of considering such miniature versions of hydro power plants are that they require less capital, they have a lower impact on the surrounding environment, they can work on smaller streams, and they are easy to operate [26]. Despite the advantages, the output power from the plant is variable and is seasonally dependent since the water levels are also seasonally dependent. In this study, the following equations were utilized to model the behavior of micro-hydro plants.
where represents the turbine efficiency at 80% [26]. represents the water density at a value of 998 kg/m3. g has a value of 9.8 m/s2 and represents the acceleration associated with gravity. The head of the water source feeding the power plant is represented by h with a value of 12 m in this study. The water discharge represented by Q is calculated using Equation (19) and the units are m3/s. The stream is characterized by its velocity (V) in m/s and cross-sectional area (A) in m2. For this study, it was assumed that the plant was controllable and that the discharge was kept within a range of 0.7 m3/s and 0.11 m3/s.
Equation (20) provides the capital cost that was associated with the project, where the total number of water turbines that were incorporated within the project is represented by , and represents the cost of an individual turbine. represents the capital cost of the entire setup. The installation cost was set at 10% of the . In this study, the considered turbine was a Francis turbine and the O&M costs per year for such a turbine were set at 8% [26]. The lifespan of such a turbine was set at 32 years, but it was a very cautious estimate since the turbines can work much longer. Hence, no replacement was considered during the project lifetime.
Table 3 presents the values of all the variables needed to calculate the LCOE of each generator.
5. Results
In order to understand the operation of the microgrid from a yearly standpoint, clustering was employed in order to split the yearly load data. In this case, the optimal number of clusters was determined using the elbow method and the clustering algorithm used was k-means clustering [27,28]. Both of these methods are quite popular and can be found in numerous references such as in [29].
Figure 7 provides figures with respect to the clustering of the yearly load data and the yearly power output of the microgrid. The Within Cluster Sum of Squares (WCSS) process was used in order to determine the optimal number of clusters, which was three. From each cluster, a representative day was chosen. In general, they can be correlated with the seasonal changes in Poland. Cluster 1 in Figure 7a has a load demand between those of clusters 2 and 3, which represent the spring/autumn months. Cluster 2 in Figure 7a had the highest load demand and is typical of winter, whereas cluster 3 in Figure 7a had the lowest load demand and is typical of the summer months.
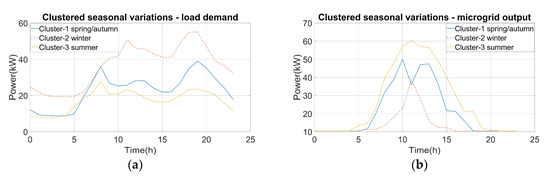
Figure 7.
Clustered seasonal load variations (a) and clustered seasonal variations in microgrid output (b).
There are also generation data that corresponding to the load data of the days that represent the different clusters. This information is provided in Figure 7b, wherein cluster 1 is typical of the microgrid generation during the spring. Cluster 2 is characteristic of the winter, during which the microgrid energy generated was low throughout the day, and cluster 3 is characteristic of the summer when the microgrid energy production is at its maximum.
The microgrid storage devices operations are presented in Figure 8a,b. In Figure 8a for cluster 1, it can be seen that the Li-ion storage device was charged around mid-day. This is when the microgrid power generation exceeded the load demand, and it began discharging in the evening when the load demand exceeded the power that was generated in the microgrid. A similar characteristic is seen with the hydrogen storage device in Figure 8b for cluster 1. The microgrid operation for cluster 2 shows that the Li-ion storage device was charged to full capacity at mid-day, but it discharged immediately. In fact, on certain winter days the Li-ion storage device did not charge at all. This was because on most winter days, the load demand was greater than the microgrid power generation for much of the day. The hydrogen storage tank for cluster 2 was filled only up to 27% of its capacity due to the lack of excess net energy in the microgrid. The microgrid operation for cluster 3 shows that the Li-ion storage device was charged to full capacity in the morning and did not discharge until the evening. This was because of the high microgrid power generation during the day compared to the load demand. The hydrogen storage device also reached its maximum capacity due to an excess of net energy in the microgrid.
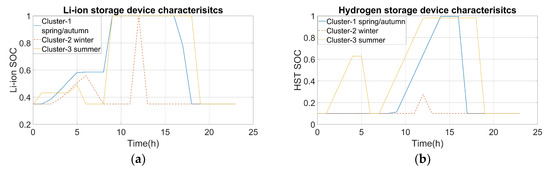
Figure 8.
Charging/discharging: battery storage system (a) and hydrogen storage system (b).
Figure 9a represents the dynamic microgrid interaction with the main grid. It can be deduced that for cluster 1 during mid-day, when the power generated within the microgrid was higher than the load demand, the power was exported to the main grid, whereas during the evening when the load demand was higher than the energy produced, it was imported. Figure 9b provides the price signal as a result of LCOE minimization by the optimizer, and it can be seen that the price signal remained below 0.1 USD/kWh for most parts of the day except when the fuel cell discharged. This is because the LCOE of the hydrogen-based generator is much higher when compared to the others. For cluster 2, it can be seen that, unlike in the case of cluster 1, where power was exported to the main grid during mid-day, there was only the importation of power from the main grid due to the high load demand and the low energy supply in the microgrid. The price signal for cluster 2 stayed below 0.1 (USD/kWh) with the exception of two small spikes. In comparison to cluster 1, the spike is lower in magnitude because in the earlier case the hydrogen storage reached full capacity and the fuel cell ran longer, and in this cluster the fuel cell ran for a shorter time. For cluster 3, it can be inferred that for much of the day the power was being exported to the main grid due to the high generation in the microgrid. This fact is also reflected in the price signal, where it can be seen that the price stayed close 0.02 USD/kWh, which is the lowest for all three seasonal clusters, and that there are two spikes in this case, which strictly point to the fuel-cell operation due to its high LCOE.
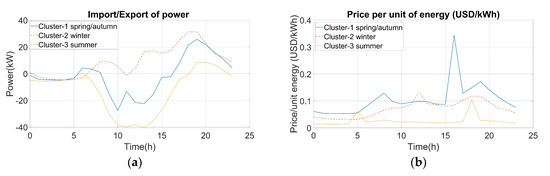
Figure 9.
Microgrid interaction with the main grid (a) price signal (b).
6. Conclusions
This paper presents the application of a recently introduced PO for the energy management of microgrids. This particular algorithm was chosen based on the analysis of its performance against numerous well-known optimization algorithms for optimal power flow in a standard IEEE 30-bus system. During the analysis, another recently introduced algorithm called the LA was also tested for its performance, and it was noticed that the LA performed poorly, whereas the PO showed promise.
A comprehensive microgrid model was chosen wherein the generators were modeled partly based on real data available from the generating sources at Wroclaw University of Science and Technology, and partly based on studies in the literature. The LCOE was calculated for all of the generators based on their lifetime, the project lifetime, and the expected energy returns and costs involved with their purchase and operation. The objective function for the EMS was to minimize the LCOE cost.
In order to carry out the analysis of the microgrid operation over an entire year, clustering was employed in order to select representative days and investigate the functioning of the storage devices, the price signal and the power exchange with the main grid during these days. It was observed that the microgrid operation was most profitable during the summer season.
This study can be improved in several ways. Among the goals of future works should be the consideration of the multi-objective functions with the inclusion of the emission coefficients of all the generating sources, the stochastic optimization considering the unpredictable nature of renewable energy generators in the microgrid, the addition of other renewable sources of energy such as wind turbines, bio gas generators and geo thermal generators, the exploration of the possibility of multi-agent optimization and also the exploration of possible new optimization algorithms that have been developed, which could potentially lead to more efficient energy management.
Author Contributions
Conceptualization, V.S.; methodology, V.S.; software, V.S.; validation, M.J. and J.J.; formal analysis, V.S.; investigation, V.S.; resources, M.J. and H.R.K.; data curation, D.K.; writing—original draft preparation, V.S.; writing—review and editing, J.J. and H.R.K.; visualization, V.S.; supervision, Z.L. and J.J.; project administration, M.J. and Z.L.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by K38W05D02 of Wroclaw University of Science and Technology.
Data Availability Statement
The data are available on request from corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mosa, M.A.; Ali, A.A. Energy management system of low voltage dc microgrid using mixed-integer nonlinear programing and a global optimization technique. Electr. Power Syst. Res. 2021, 192, 106971. [Google Scholar] [CrossRef]
- Paris Agreement. United Nations Paris Agreement. 2015. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 8 September 2021).
- European Comission. The European Green Deal; European Comission: Brussels, Belgium, 2019. [Google Scholar]
- Ton, D.T.; Smith, M.A. The U.S. Department of Energy’s Microgrid Initiative. Electr. J. 2012, 25, 84–94. [Google Scholar] [CrossRef]
- Marnay, C.; Chatzivasileiadis, S.; Abbey, C.; Iravani, R.; Joos, G.; Lombardi, P.; Mancarella, P.; Von Appen, J. Microgrid evolution roadmap. In Proceedings of the 2015 International Symposium on Smart Electric Distribution Systems and Technologies (EDST), Vienna, Austria, 7–11 September 2015; pp. 139–144. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Suresh, V.; Janik, P.; Guerrero, J.M.; Leonowicz, Z.; Sikorski, T. Microgrid Energy Management System with Embedded Deep Learning Forecaster and Combined Optimizer. IEEE Access 2020, 8, 202225–202239. [Google Scholar] [CrossRef]
- Vera, Y.E.G.; Dufo-López, R.; Bernal-Agustín, J.L. Energy management in microgrids with renewable energy sources: A literature review. Appl. Sci. 2019, 9, 3854. [Google Scholar] [CrossRef] [Green Version]
- Kaczorowska, D.; Rezmer, J.; Sikorski, T.; Janik, P. Application of PSO algorithms for VPP operation optimization. Renew. Energy Power Qual. J. 2019, 17, 91–96. [Google Scholar] [CrossRef]
- Farinis, G.Κ.; Kanellos, F.D. Integrated energy management system for Microgrids of building prosumers. Electr. Power Syst. Res. 2021, 198, 107357. [Google Scholar] [CrossRef]
- Hou, H.; Xue, M.; Xu, Y.; Xiao, Z.; Deng, X.; Xu, T.; Liu, P.; Cui, R. Multi-objective economic dispatch of a microgrid considering electric vehicle and transferable load. Appl. Energy 2020, 262, 114489. [Google Scholar] [CrossRef]
- Shafik, M.B.; Chen, H.; Rashed, G.I.; El-Sehiemy, R.A. Adaptive multi objective parallel seeker optimization algorithm for incorporating TCSC devices into optimal power flow framework. IEEE Access 2019, 7, 36934–36947. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J. Dynamic economic dispatch of islanded water-energy microgrids with smart building thermal energy management system. Appl. Energy 2020, 276, 115422. [Google Scholar] [CrossRef]
- Askari, Q.; Younas, I.; Saeed, M. Political Optimizer: A novel socio-inspired meta-heuristic for global. Knowl.-Based Syst. 2020, 195, 105709. [Google Scholar] [CrossRef]
- Niemeyer, L.; Pietronero, L.; Wiesmann, H.J. Fractal Dimension of Dielectric Breakdown. Phys. Rev. Lett. 1984, 52, 1033–1036. [Google Scholar] [CrossRef]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B. 1983, 27, 5686. [Google Scholar] [CrossRef] [Green Version]
- Pereira, J.L.J.; Francisco, M.B.; Diniz, C.A.; Oliver, G.A.; Cunha, S.S.; Gomes, G.F. Lichtenberg Algorithm: A Novel Hybrid PHYSICS-Based Meta-Heuristic for Global Optimization. Expert Syst. Appl. 2020, 170, 114522. [Google Scholar] [CrossRef]
- Gomez-Gonzalez, M.; López, A.; Jurado, F. Optimization of distributed generation systems using a new discrete PSO and OPF. Electr. Power Syst. Res. 2012, 84, 174–180. [Google Scholar] [CrossRef]
- Kim, J.Y.; Mun, K.J.; Kim, H.S.; Park, J.H. Optimal power system operation using parallel processing system and PSO algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 1457–1461. [Google Scholar] [CrossRef]
- Foltyn, L.; Vysocký, J.; Prettico, G.; Běloch, M.; Praks, P.; Fulli, G. OPF solution for a real Czech urban meshed distribution network using a genetic algorithm. Sustain. Energy, Grids Netw. 2021, 26, 100437. [Google Scholar] [CrossRef]
- García-Muñoz, F.; Díaz-González, F.; Corchero-García, C. A novel algorithm based on the combination of AC-OPF and GA for the optimal sizing and location of DERs into distribution networks. Sustain. Energy Grids Netw. 2021, 27, 100497. [Google Scholar] [CrossRef]
- Branker, K.; Pathak, M.J.M.; Pearce, J.M. A review of solar photovoltaic levelized cost of electricity. Renew. Sustain. Energy Rev. 2011, 15, 4470–4482. [Google Scholar] [CrossRef] [Green Version]
- Jones-albertus, R.; Feldman, D.; Fu, R.; Horowitz, K.; Woodhouse, M. Technology advances needed for photovoltaics to achieve widespread grid price parity. Prog. Photovolt. Res. Appl. 2016, 24, 1272–1283. [Google Scholar] [CrossRef]
- Kumar, P.P.; Saini, R.P. Optimization of an off-grid integrated hybrid renewable energy system with various energy storage technologies using different dispatch strategies. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 32, 1–30. [Google Scholar] [CrossRef]
- Levron, Y.; Guerrero, J.M.; Beck, Y. Optimal Power Flow in Microgrids with Energy Storage. IEEE Trans. Power Syst. 2013, 28, 3226–3234. [Google Scholar] [CrossRef] [Green Version]
- Roque, A.; Sousa, D.M.; Casimiro, C.; Margato, E. Technical and economic analysis of a micro hydro plant—A case study. In Proceedings of the 2010 7th International Conference on the European Energy Market EEM 2010, Madrid, Spain, 23–25 June 2010; pp. 10–15. [Google Scholar] [CrossRef]
- Jasiński, M.; Sikorski, T.; Borkowski, K. Clustering as a tool to support the assessment of power quality in electrical power networks with distributed generation in the mining industry. Electr. Power Syst. Res. 2019, 166, 52–60. [Google Scholar] [CrossRef]
- Jasiński, M.; Sikorski, T.; Kostyła, P.; Leonowicz, Z.; Borkowski, K. Combined Cluster Analysis and Global Power Quality Indices for the Qualitative Assessment of the Time-Varying Condition of Power Quality in an Electrical Power Network with Distributed Generation. Energies 2020, 13, 2050. [Google Scholar] [CrossRef] [Green Version]
- Andrew, N. Machine Learning Yearning, Technical Strategy for AI Engineers in the Era of Deep Learning. 2018. Available online: https://storage.googleapis.com/kaggle-forum-message-attachments/693524/14574/ML_book.pdf (accessed on 8 September 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).