1. Introduction
Coastal water quality monitoring is an important activity for retrieving information about the state of a marine ecosystem. In the Republic of Croatia, the degree of sea bathing water quality is regulated by the Regulation on Sea bathing water quality (OG 73/08) and the EU Directive on management of bathing water quality No 2006/7/EC. Consequently, it is necessary to constantly monitor the quality of the sea and the cleanliness of the coast, primarily because of human and animal health, fishing, and also because of tourism as one of the main economic incomes and activities of people on the Adriatic coast, especially in the summer season [
1]. This is why responsible authorities schedule in situ measurements of various water quality indicators for continuous, albeit sparse, monitoring.
One of the indicators that depicts the quality of marine and freshwater is the concentration of Chlorophyll-a (Chl-a). Besides merely showing the quality of the water, Chl-a can also be used as a proxy for phytoplankton biomass and that is why it is an indicator of water quality and trophic status [
2]. This is why it is important to continuously monitor Chl-a in a body of water.
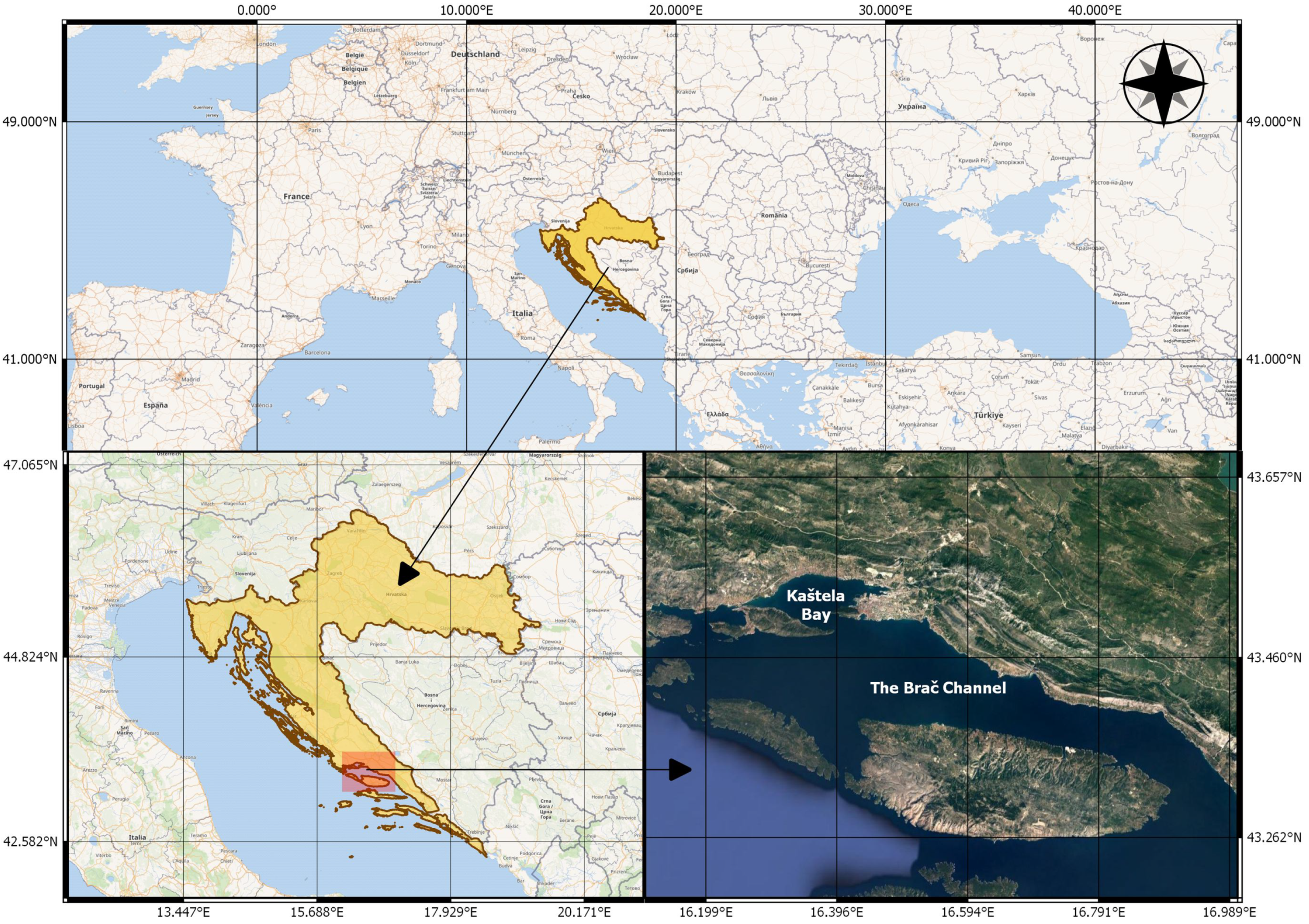
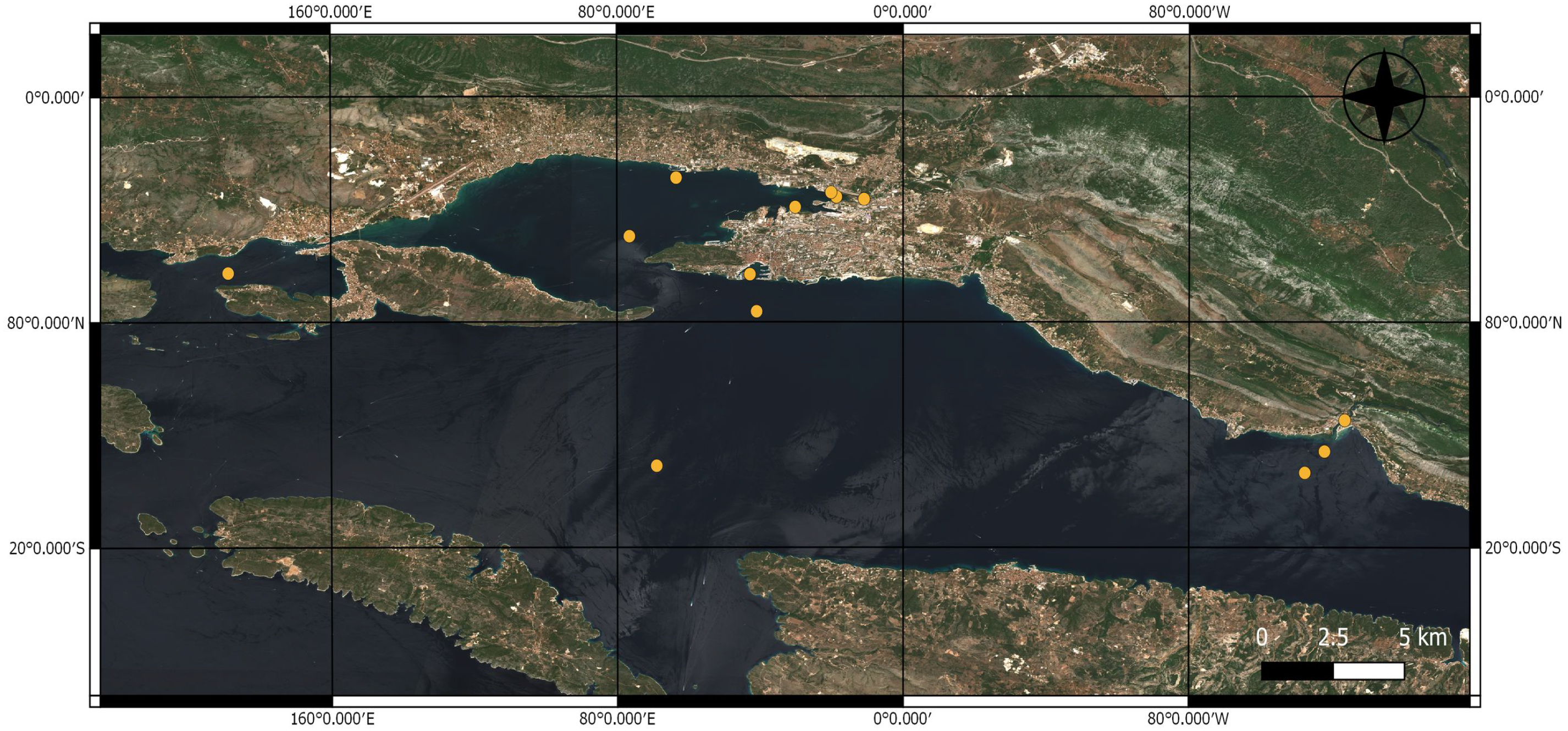
In this study, we analyzed the possibility of estimating Chl-a in coastal environments, specifically in the Kaštela Bay and the Brač Channel in Croatia, by using satellite remote sensing to complement the existing in situ monitoring with continuous and more frequent assessment.
Characteristics of the coastal environment result in the complexity of the marine ecosystem and pose challenges to the monitoring of water quality indices. Increases in natural or anthropogenic nutrients result in higher concentrations of phytoplankton and marine organisms, which we measure as a concentration of Chl-a [
3]. The concentration of Chl-a is usually measured by taking samples of water and making laboratory analysis of collected samples. This way, we can establish the concentration level for only a limited number of points of the research area, which makes this approach not only expensive and weather-dependent but also does not provide a broader picture of the distribution of Chl-a concentration [
4].
Thus, in this paper, we offer an approach to calculate Chl-a concentration using the images obtained by Sentinel-2 satellite instruments. With this approach, we can obtain a broader picture of Chl-a distribution and concentrations because Chl-a is an optically active component that has a characteristic spectral signature allowing its detection with optical sensors onboard satellites. Moreover, Chl-a is connected with important processes in the sea (e.g., eutrophication and algae blooms); so, with remote sensing, continuous monitoring of changes in the sea becomes possible.
1.1. Related Work
Water quality monitoring using multispectral or hyperspectral remote sensing represents a great challenge in order to find the relationship between in situ data and reflectances obtained by various sensors. There are many optical and nonoptical parameters that affect water quality and can be estimated using satellite data [
5,
6]. The main research focus is on the optical properties of water such as chlorophyll [
7], turbidity [
8], total suspended matters [
9], and colored dissolved organic matters [
10], which affect the reflected radiation of the sea and, thus, can be measured remotely.
Many studies show a different usage of observations and methods for retrieving the concentration of Chl-a for different types of monitored waters. The widely used Ocean color (OC3) algorithm for the calculation of Chl-a concentration based on three bands (B01, B02, and B03), representing blue to green ratios, was proposed in [
11]. This algorithm is an empirical, with parameters trained on data originating from ocean and coastal waters. Fitted parameters are published for various satellites. Sentinel-2 parameters are published in [
12]. Case-2 Regional/Coast Colour (C2RCC) [
13] is a physics-based processor for the calculation of various water parameters (such as Chl-a, total suspended matter (TSM), and colored dissolved organic matter (CDOM)). This algorithm utilizes a neural network trained on a large amount of data for inverting top-of-atmosphere (TOA) radiance to water-leaving reflectance. Implementation for various satellites is available as a part of ESA’s Sentinel Toolbox SNAP [
14]. Types of water studied by various researches are lakes, rivers, oceans, estuaries, and coastal waters. Studies focus on certain study areas and use only certain satellite data. Methods for estimating parameters vary from fitting a formula parameter to machine learning algorithms. In [
15], authors compared Sentinel-2A and Earth Observing-1 (EO1) for estimation of Chl-a and turbidity, where Sentinel-2A showed better results in retrieving concentration for both parameters (Chl
: 0.72 vs. 0.57 and TU
: 0.7 vs. 0.63). Further, the authors used reflectance ratio for mapping Chl-a, which can be seen in several other studies using different reflectance values for developing algorithms [
2,
16,
17]. Sentinel-2 and Landsat-8 have good spatial resolution, which makes them suitable for monitoring the water quality along the coast [
12,
18,
19,
20,
21], as opposed to Sentinel-3, SeaWiFS (Sea-Viewing Wide Field-of-View Sensor), and MODIS (Moderate Resolution Imaging Spectroradiometer), which have large spatial resolutions better for monitoring the open sea [
22,
23,
24].
Several studies show that using regression models can have a big potential for retrieving the concentration of Chl-a in coastal environments and lakes [
15,
25,
26,
27,
28]. For example, the authors in [
3] compared predictive performance on three different regression models (Simple Linear Regression—SLR, Multiple Linear Regression—MLR, and Generalized Additive Models—GAMs) and Landsat-8 imagery. The results showed that GAM outperformed SLR and MLR, while the MLR performed better in predicting log-transformed Chl-a values. Furthermore, in [
29], the authors compared Ordinary Least Square (OLS) with Ridge Regression (OPT) to estimate Chl-a, turbidity, and suspended sediment based on relationship with Landsat reflectance. Ridge Regression estimation showed better results compared with Ordinary Least Square analysis.
1.2. Proposed Method
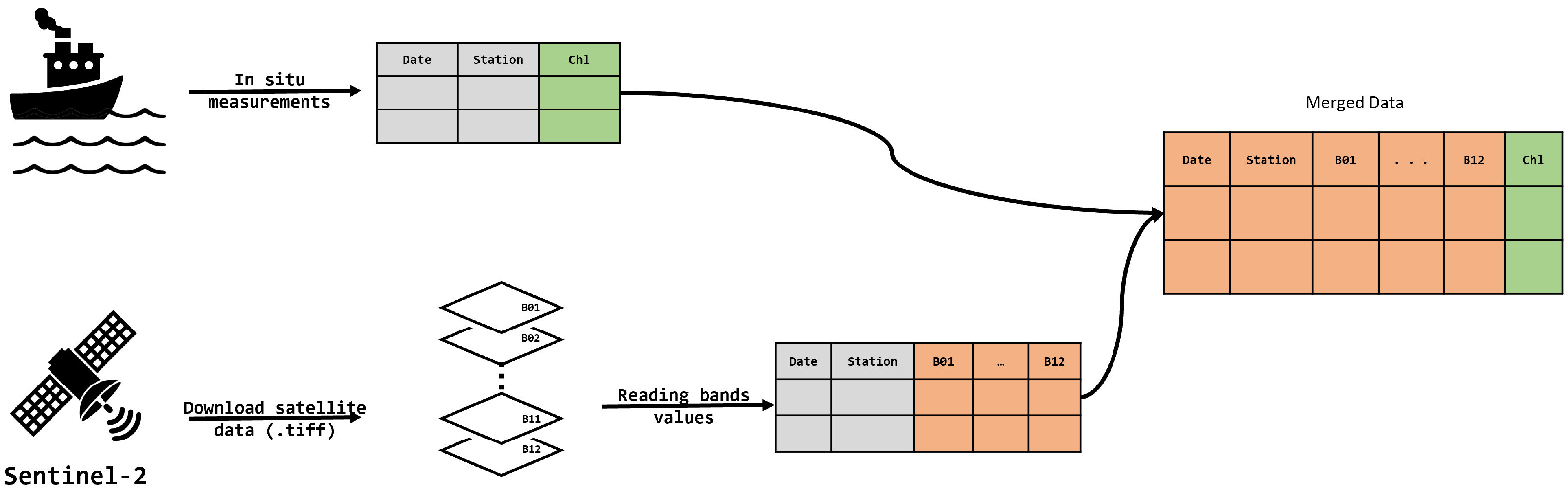
The aim of this paper is to reveal the correlation between in situ Chl-a data and Sentinel-2 satellite band reflectance data using Ridge Regression for estimating the coefficients of Multiple Linear Regression to retrieve Chl-a concentration. The aforementioned studies used only predefined formulas and bands to develop a predictive model, while we present a regression model that takes all of the Sentinel-2 band reflectance data into account. Our modeling approach is purely data-oriented and aimed towards discovering the formula from the available data. The implemented regression model provided coefficients to create a formula used to estimate Chl-a concentration, which will be presented as a map of Chl-a distribution in the area of the Kaštela Bay and the Brač Channel revealing the spatial distribution of the Chl-a parameter and overall state of the aquatorium.
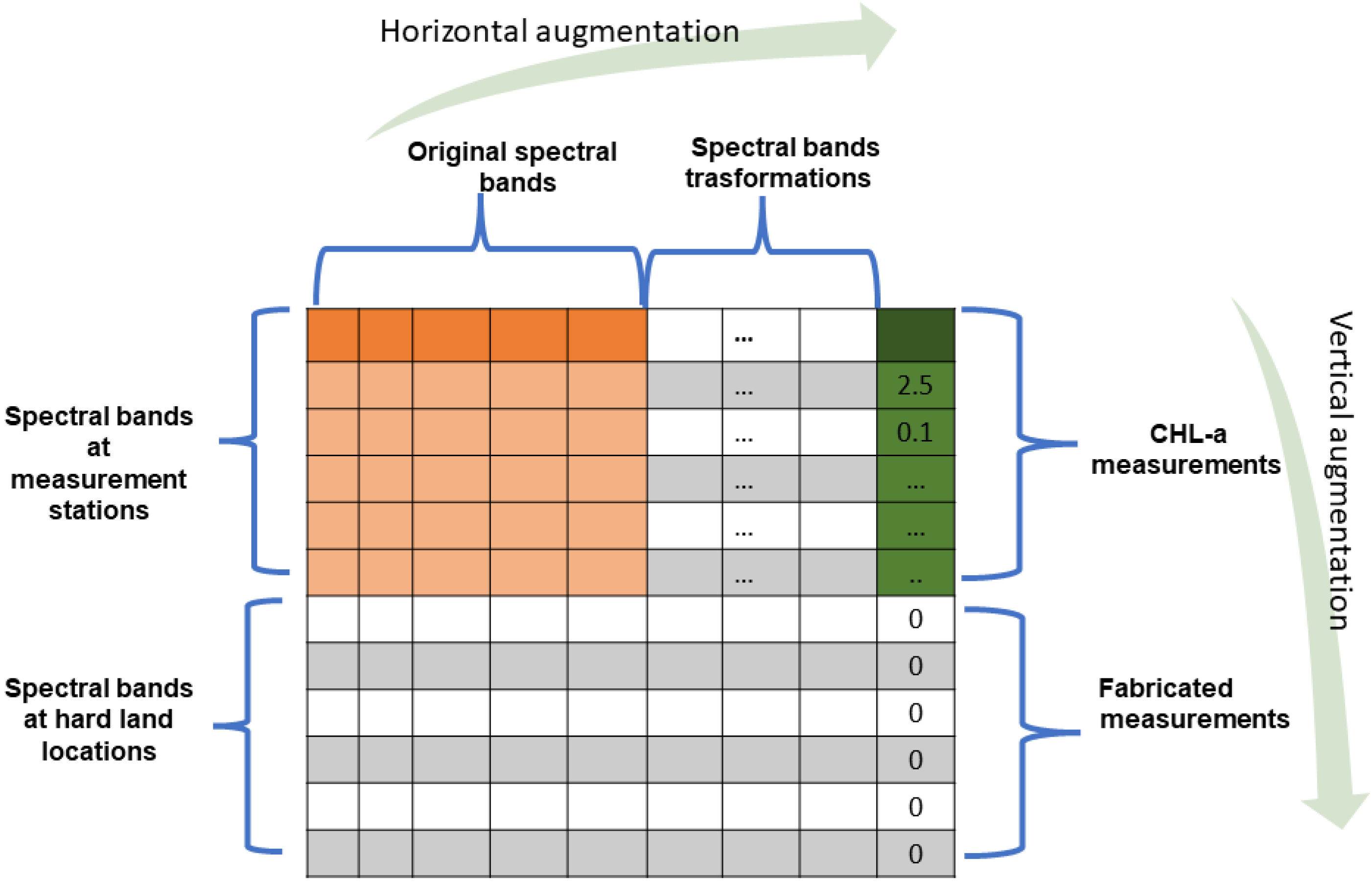
The main contribution of this paper is a novel method for developing a sophisticated and reliable model for predicting Chl-a from Sentinel-2. The developed model is tailored specifically for the study area. This is achieved by augmenting the original data set in two dimensions—horizontally (by performing feature augmentation by transforming the feature values) and vertically (by adding value 0 to the Chl-a measurements for the locations on land without Chl-a). The horizontal augmentation improved the correlation of predicted and measured Chl-a concentrations by providing a more sophisticated model with nonlinear dependencies on the spectral reflectances. The vertical augmentation enriched the data set with new data items. In this way, the regression algorithm receives not only the features of locations with Chl-a concentration but the locations without the Chl-a as well, making the data set more balanced. This method enabled creation of a model that is sophisticated and fitted to the features of the study area. Although the model is precisely fitted for the case study area and past measurements, the evaluation of the model shows that our model does not overfit. The reliability of the model is qualitatively validated on the algae bloom incident. Finally, the two novel contributions of the paper can be summed up as follows:
A method for developing a sophisticated formula for estimation of Chl-a values in coastal waters where we have a limited number of measurements.
A new regression formula for estimating Chl-a concentrations in coastal waters of study area.
3. Results
Ridge Regression model was developed on the constructed data set in a way of training the model on 80% of the data set, and testing and validating the model on the remaining 20% of the data set. Train set and Test set were constructed by randomly shuffling and splitting items into 80% and 20% of items, respectively. Further, we evaluated the constructed model and results using two approaches:
Quantitative evaluation was performed on training and testing portions of the data set;
Qualitative evaluation was performed by inspecting resulting images of Chl-a distribution for certain dates and discussing in the scope of the known events.
First, we wanted to make sure that the vertical augmentation we used on our data set is a valid approach and will yield better results. We developed a model on the original data set of 12 features and evaluated the model score. Then, we developed a model trained on the 80% of the vertically augmented data set including fabricated chlorophyll-free stations, and evaluated the model score. The results shown in
Table 4 indeed show better values of evaluation measures for both train and test portions of the data set for the model trained with vertically augmented data set. The percentage of data taken for training (80%) and testing (20%) is the same for each constructed data set.
Furthermore, in order to objectively verify that the horizontal augmentation is a valid approach to our problem, we trained the Ridge Regression model and observed the results for five different variations of features, from original bands to bands with all four data transformations applied.
This way, we ensured that the Ridge Regression model is not overfitted with additional features.
Table 5 shows combinations of bands and transformations that we used for incremental Ridge Regression model testing. The model shows the most accurate results by taking into account all of the transformed features and original band values. The
metric for train data is 0.685 and for test data is 0.6599, while RMSE metric is 0.2254 for train and 0.2051 for test data. This shows that Chl-a is quite correlated with transformed reflectance values of Sentinel-2 bands.
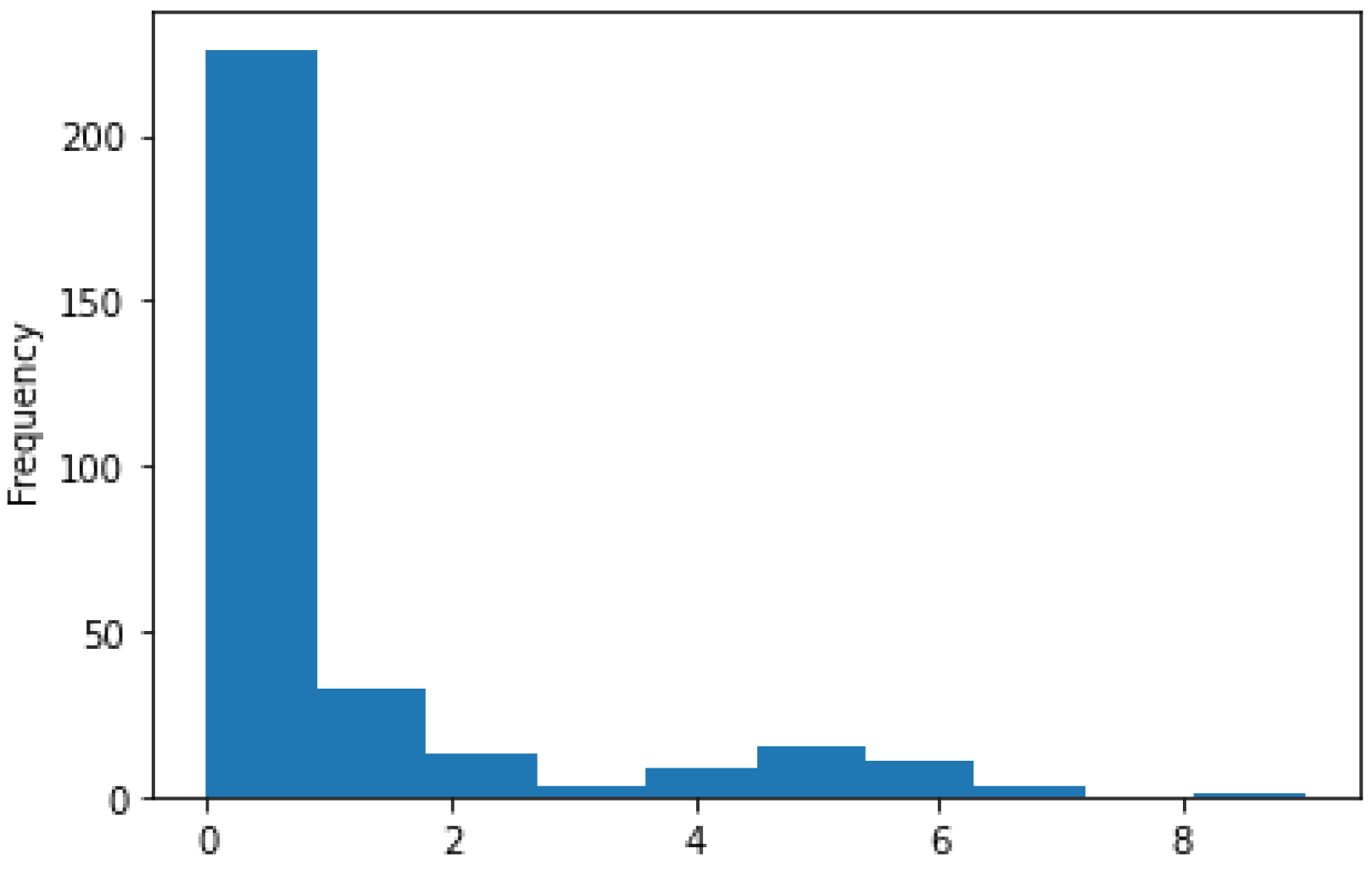
Figure 6 shows the relationship between values of in situ and predicted Chl-a values in the form of an error plot. From the error plot, we can notice that for both the test and the train data, the predicted values of Chl-a follow the same trend. Although the prediction is not perfectly accurate, for measurements with higher values of Chl-a, predicted values are higher, while for measurements with low Chl-a, predicted values are lower. For a certain number of measurements denoted as zero Chl-a, we have low predicted Chl-a but not exactly zero since for these points’ reflectances are measured on land, which has different behavior than the sea.
The predictions are made using a formula based on Equation (
10).
where
Equation (
10) is constructed as a Multiple Linear Regression for estimating Chl-a concentration, where the coefficients are obtained by training the Ridge Regression model. Every feature represents either original or transformed band where every feature shows different correlation with in situ Chl-a. The coefficients can be considered as weights showing what influence the feature has on final output. For original band values (
), the most correlated bands are B01, B8A, and B12, while transformed features show the best correlation as follows:
Squared features () for bands B04, B06, B07, and B8A;
Squared root features () for bands B04, B11, and B12;
Reciprocal transformed features () for band B02;
Logarithmic transformed features () for bands B04, B05, and B8A.
Among selected features, we noticed that three of the transformed features of band B04 (
,
, and
) have higher coefficients. B04 is usually used in combination with vegetation red edge. Values of bands B05 or B8A are often proposed for retrieving Chl-a in coastal waters [
21] or lakes [
49]. Further, there is a correlation with bands B06 and B8A in two different features, which are vegetation red edge bands usually used for retrieving various vegetation indices (e.g., NDVI—Normalized difference vegetation index).
As a result, we can conclude that the Ridge Regression gives bias to bands B01, B02, B04, B05, B06, B8A, B11, and B12, which makes them important features in detecting Chl-a concentration in the area of Kaštela Bay and the Brač Channel.
In order to further investigate the validity of the obtained formula, we observed the spatial distribution of the predicted Chl-a value for the whole water body of the study area. Estimated Formula (
10) is applied to
.tiff band images by using the raster calculator in the free and open-source GIS (Geographic Information System) software—QGIS [
50].
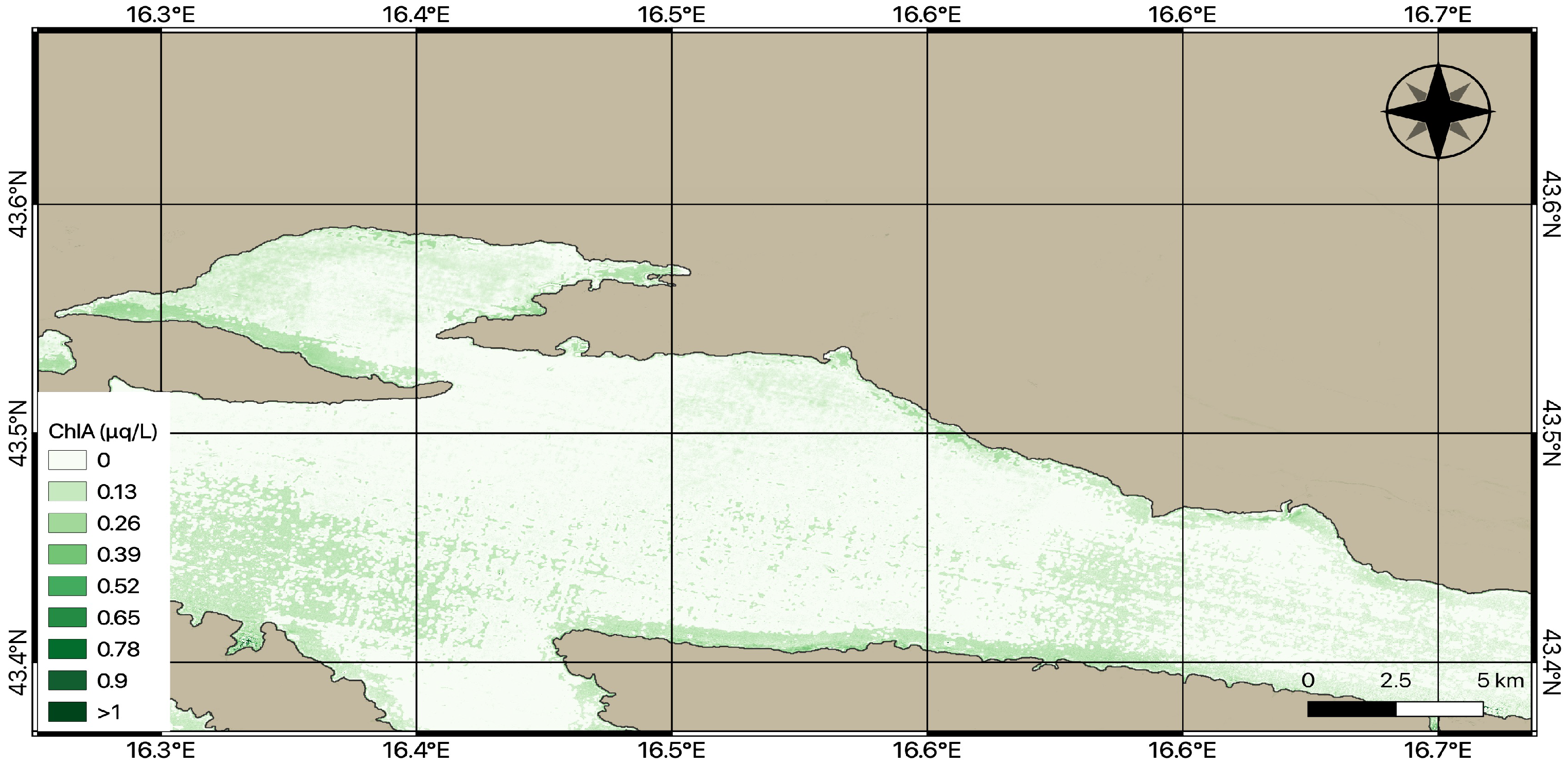
Figure 7 shows mapped Chl-a in the Kaštela Bay and the Brač Channel using the newly proposed formula and Sentinel Level-2A satellite data from 30 September 2017. Higher concentration of Chl-a can be spotted at the coastline where the circulation of water is lower. The obtained map confirms our assumptions that Chl-a is higher in the nearby vicinity of the rivers Jadro and Cetina and along the coast.
Furthermore, in
Figure 7, it is possible to see how the applied formula separates the land from the sea quite well, as well as the identification of other water surfaces and the concentrations of Chl-a in them (the example of the river Cetina).
Estimated formula assigns negative values to land and objects without chlorophyll, such as boats in the sea. We assume that this is the effect of vertical augmentation since the algorithm has learned that the features of the hard objects on land have low values of Chl-a. Of course, there are some pixels that are classified as Chl-a on land, but this is a model error that can be ignored.
3.1. Comparison with Other Methods for Chl-a Estimation
As we stressed in the related work section, many scientists have already developed different algorithms for the assessment of Chl-a concentration that are based on remote sensing. In this paper, we selected the two most common algorithms for implementation in order to check the performance of these algorithms over our data set, and to compare them to our algorithm. These two algorithms are as follows:
Ocean color (OC3) algorithm, as proposed in [
11], and coefficients adopted from the study in [
12]. OC3 was implemented as a function to calculate the Chl-a value having the same band values as our algorithm. The resulting value was evaluated having in situ measurement as ground truth.
Case-2 Regional/Coast Colour (C2RCC) algorithm [
13]. We used the C2RCC processor provided in the SNAP processing toolbox from ESA. We collected the Sentinel-2 images from
https://scihub.copernicus.eu/ (accessed on 12 October 2021) for several dates of the in situ measurements, processed the whole data set using C2RCC S2-MSI processor, and created a Chl-a map of the area. The processor used default parameters since other algorithms we compared did not use any external data or information. Predicted values of Chl-a concentration were further extracted only on the coordinates of measurement and compared with the in situ measurements.
The results of the evaluation are shown in
Table 7. By comparing the shown values, we can conclude that according to both evaluation measures, our model results in better predictions compared with in situ measurement. This is not surprising, since our model is trained with in situ measurement data and tested on a portion of the data set that was not used for training but originated from the same source. However, what surprised us is that the correlation coefficient
was negative for both OC3 and C2RCC. This shows that predictions of these two models are not correlated at all with in situ measurements. Negative
score values means that the model does not follow the trend of the data. Both the OC3 and C2RCC algorithms predict the values of Chl-a that are not correlated at all with the in situ measurements. This means that Chl-a in our study area cannot be predicted with commonly used algorithms but needs a more suitable model, such as the one we developed in this research.
3.2. Qualitative Validation
In this section, we will demonstrate the usefulness of mapping Chl-a concentrations. First, we will show the resulting Chl-a map in case of occurrence of unwanted phenomenon related to Chl-a—Algae blooms. Algae blooms occur under certain weather conditions such as changes in temperature and higher rainfall in the spring; moreover, algal blooms are affected by an increased intake of nutrient salts of nitrogen and phosphorus that serve as food for phytoplankton [
51].
Some algae can release toxins that negatively affect human health, but also lead to the extinction of fish and negative impacts on all seafood-dependent animals [
52]. With algae blooms where the sea is bacteriologically clean, there is no danger to human health but it is an inconvenience to bathers during the summer season.
Detecting algae blooms is challenging, due to the different cell sizes and types of phytoplankton [
53]. Chl-a can indicate a potential increase in algae, so maps of Chl-a concentrations calculated from satellite images can provide information on the possible spatial distribution of algae.
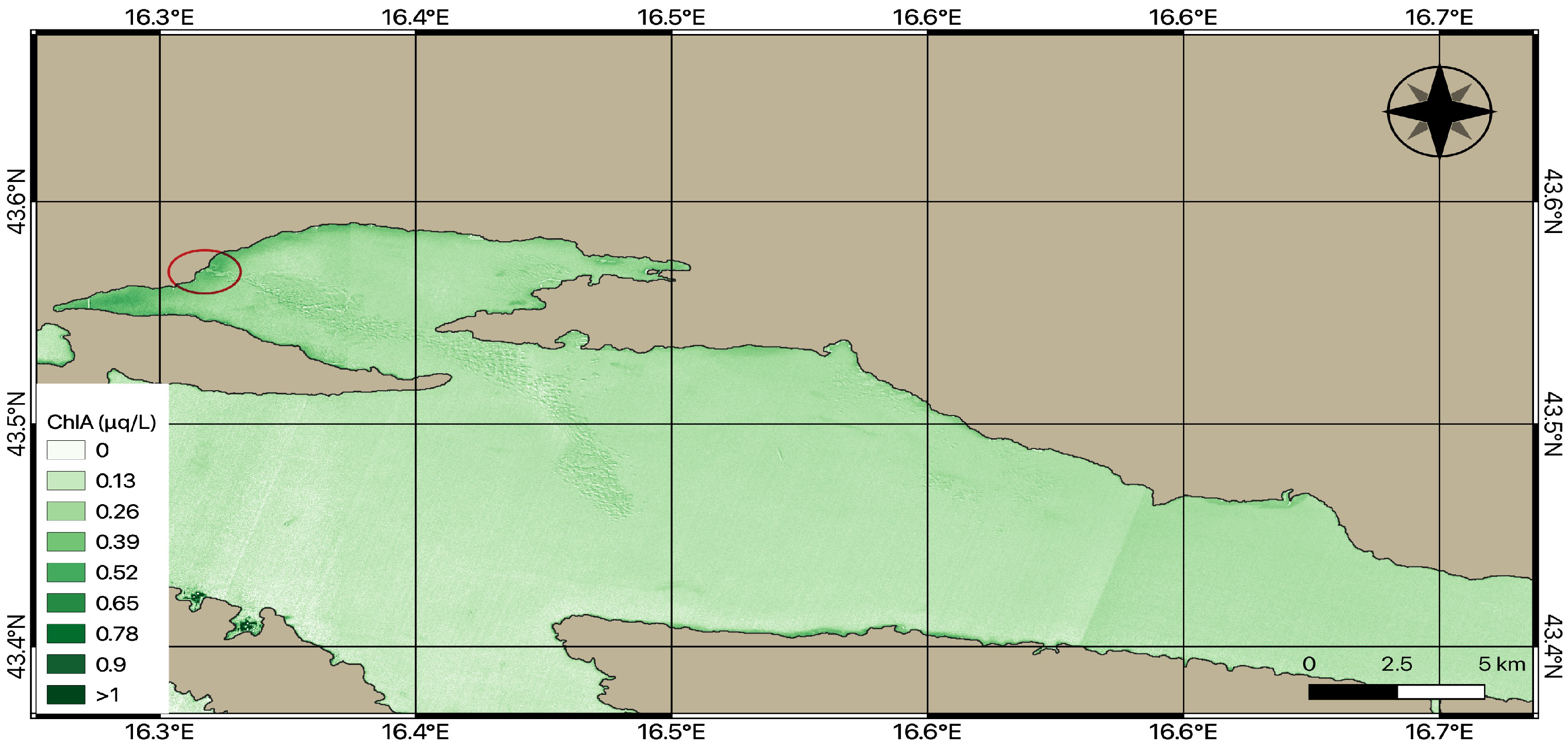
Figure 8 shows a photo of the beach in Kaštela Bay on 1 April 2021, where the algae blooms can be seen. This incident was reported in the media and discussed on social media. To see if our method for retrieving Chl-a can be used to detect changes in the sea during the algae blooms, we downloaded the first available satellite image taken on 2 April 2021 and applied Formula (
10) on image bands (
Figure 9).
In
Figure 9, the same scale of Chl-a concentration range is applied as in
Figure 7. The Sentinel Level-2A image (
Figure 7) was taken in the period when there were no reported algae blooms in media for our study area. Based on the publicly available data published by the Ministry of Environmental Protection and Energy [
54], which is a legal entity of the Republic of Croatia, in the summer and autumn months, the phytoplankton algae Dinophysis caudata from the Dinoflagellata group were recorded in relatively high abundance in almost all areas of the Adriatic sea. Dinophysis caudata algae produces toxic metabolites such as okadaic acid and DTX toxin. Based on these facts, the abundance of the algae population is potentially captured in the image (
Figure 7), but we cannot claim this with certainty.
First, we can notice that the green color, which represents a higher concentration of Chl-a, is more pronounced at the time of algae blooms in
Figure 9 compared with
Figure 7 when there were no algae blooms in the sea. Comparing scenes with and without algae blooms can be the first indicator that changes are happening in the sea.
On
Figure 9, we marked the location where the image (
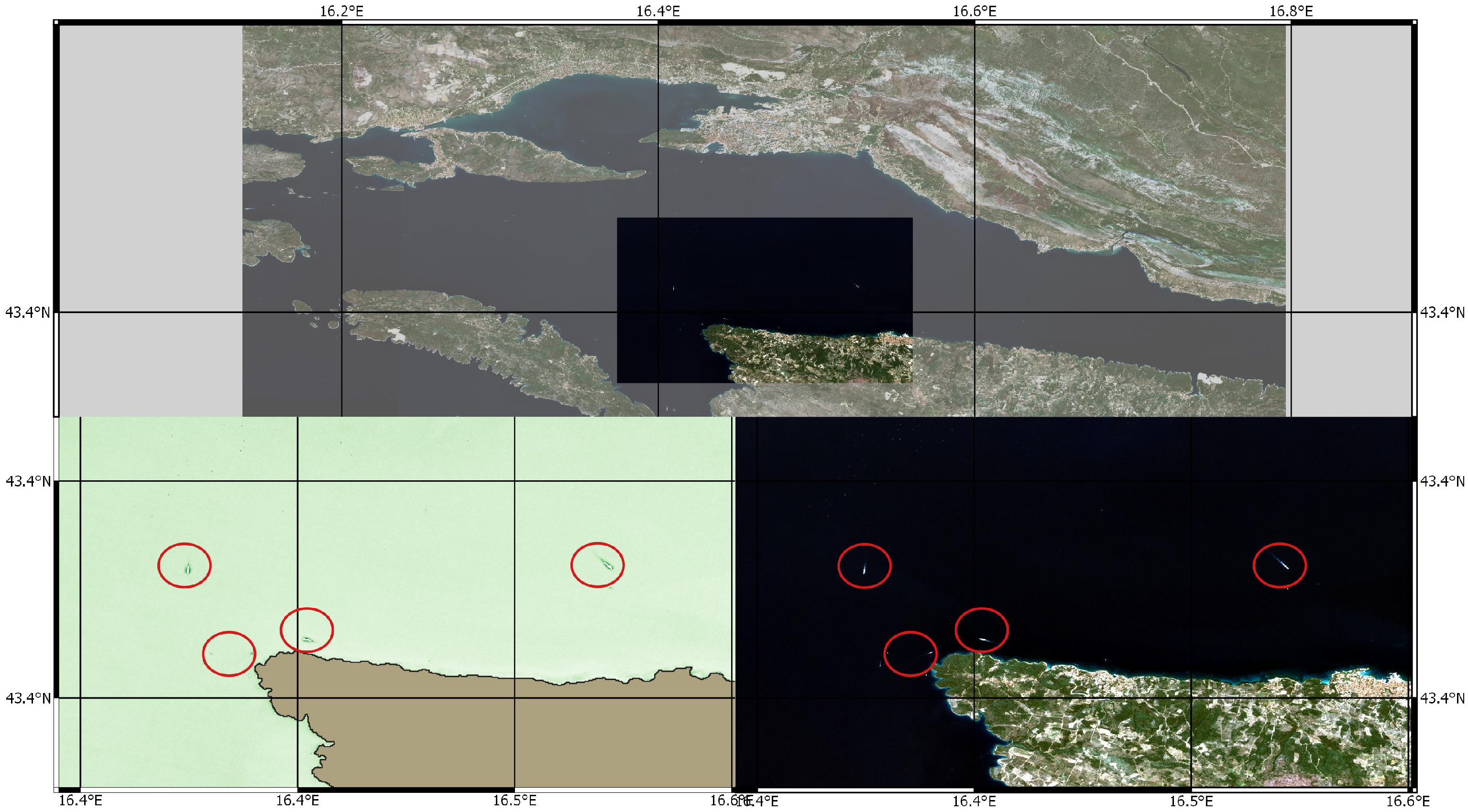
Figure 8) was taken with the ellipse. It is visible that the whole coast shows the highest concentration of Chl-a when the algae bloom incident occurred. This does not mean that any increase of Chl-a indicates the algae bloom incident but shows that our model detects the Chl-a of algae on the water surface. Nevertheless, our model also excludes objects in the sea such as boats, as shown in
Figure 10. In this figure, we can clearly see boats in the sea near the shore at the time the satellite image was taken.
4. Conclusions and Future Work
This study describes a method for obtaining the Ridge Regression model applied to in situ and Sentinel Level-2A satellite data and discusses the obtained results. The data set is constructed by making feature augmentation and adding arbitrary points representing stations with zero concentration of Chl-a. The best results in the application of Ridge regression had a combination that included all of the transformed features of the bands, both for train ( and ) and test data ( and ). Obtained coefficients of applied Ridge Regression model are used for the implementation of MLR formula in order to estimate and map Chl-a distribution in the Adriatic sea for the areas of Kaštela Bay and the Brač Channel situated in the Republic of Croatia. In the estimated formula for Chl-a prediction, bands B01, B02, B04, B05, B06, B8A, B11, and B12 in different transformations showed the best correlation with in situ Chl-a data. Predicted concentration of Chl-a is high at the coast and nearby rivers, which are areas usually classified as places with a high Chl-a trend.
One of the undesirable sea phenomena that can be unpleasant and dangerous for human and animal health is algae blooms. They can cause discomfort to bathers in the summer; so, it is useful to monitor and predict changes in the sea. We applied a formula for predicting Chl-a on Sentinel-2 images taken on the date of the incident of algae blooms that occurred in April 2021 in our study area. This showed larger deviations in Chl-a concentration during algae blooms, compared with when there was no algae bloom in this area. Thus, prediction of Chl-a concentration using remote sensing gives us the opportunity to monitor the water quality in an inexpensive way and gives us a broader picture of distribution of Chl-a.
Statistical evaluation of our algorithm shows that it is possible to find correlations of band values and transformations of those values with measured Chl-a concentration for oligotrophic waters with relatively small values of Chl-a concentration. Our model output is more correlated with measurement values than the prediction of OC3 and C2RCC algorithms.
In the future, in addition to chlorophyll, other optical parameters such as turbidity, total suspended matter (TSM), and colored dissolved organic matter (CDOM) can be used to predict water quality. Therefore, to improve the existing model, we could include the listed parameters in order to achieve higher accuracy for water quality prediction. Additionally, for better results, it is necessary to further enrich the data set for training and testing, so we plan to include data from other satellites in our future work, such as Sentinel-3 or Landsat-8. In this way, the data set will be enriched with measurements for which we excluded the data from the Sentinel-2 satellite.