1. Introduction
War trauma data are the core elements of wargaming, military medical service training, and medical decision-making [
1]. With the continuous development of modern warfare, the analysis and research of physical war trauma data have become more and more important. However, the amount of existing data is not sufficient to support large-scale analysis and evaluation, and the confidential nature of war trauma data makes them hard to collect and obtain from public channels. Therefore, efficient and credible data augmentation of war trauma data has become a research work with great practical significance. To the best of our knowledge, research on this topic has been limited. In the currently used method, the additional physical trauma data are still artificially generated by well-trained experts or doctors based on their professional knowledge and experience. However, this method is not only inefficient, time-consuming, and labor cost-intensive, but also inherently biased due to its dependence on personal subjective cognition, which is difficult to overcome. In addition, different experts have no unified standard for assessing injury consequences. Furthermore, the amount of artificially generated war trauma data is too small to meet the actual needs. Therefore, we developed a standardized evaluation algorithm to improve the quality of assessment of injury consequences and find an automatic, efficient, and credible approach for small-sample augmentation of war trauma data.
More than half a century since the concept of artificial intelligence (AI) was first formally proposed at the Dartmouth Conference [
2], the AI technology has empowered amazing developments in many fields. Meanwhile, the external environment and challenges faced by the development of AI have also undergone profound changes [
3]. These changes are especially prominent in certain fields, such as big data, virtual reality, super-computing, and mobile payment. Therefore, under the trend that the overall environment is getting closer to big data, deep learning (DL), which is based on machine learning, has become the core element of the application of AI [
4] and has led to satisfactory application results in many fields, such as cloud computing [
5], image identification [
6], sports training [
7], and AlphaGo [
8]. Recently, AI technologies such as DL started to be gradually applied in the field of medical research, including in promoting disease management [
9], computer-aided diagnosis [
10], biomedical information processing [
11], medical image recognition [
12], and disease prediction [
13]. Especially in disease prediction, AI has been recognized as one of the key elements of an accurate and robust prediction system [
14]. For example, deep neural networks (DNNS), which are AI tools, are now used to assist physicians and for automatic diagnosis. Specific application cases include early detection of cardiovascular disease [
15], cancer diagnosis [
16], survival prediction [
17], and injury severity assessment [
18].
Compared with machine-learning methodologies and shallow neural networks, DL, which is now the core of the AI method, overcomes the research drawbacks of limited samples and low generalizability by training large-scale annotated sample data to automatically extract complex sample features and fully optimize the model parameters layer by layer. Thus, DL can carry out a more essential characterization of the data and demonstrates a superior feature-learning ability [
19]. In other words, with the existing technology level, the larger the scale and the higher the quality of the annotated data are, the better the performance of the model will be. Therefore, DL can effectively solve many complex problems in the medical field [
20,
21]. In the prediction and diagnosis of some diseases, the accuracy and efficiency of predictive DL models have surpassed those of professional doctors and experts [
22] and have thus made outstanding contributions to the development of the medical field.
2. Related Work
Currently, there are two main methods of data augmentation: oversampling and generative adversarial network (GAN). The principle of oversampling is as follows: if the samples of different classes are imbalanced, the training data can be expanded by copying the training samples of the minority class or adding noises to create new ones [
23]. To solve the imbalanced dataset learning problem, in 2002, Bowyer et al. [
24] created a synthetic minority oversampling technique (SMOTE), which generated synthetic minority class samples. In 2005, Han et al. [
25] proposed a borderline SMOTE algorithm, which considered the minority instances near the borderline and the neighboring instances. The following year, David et al. [
26] proposed a cluster SMOTE; Bai et al. [
27] proposed an adaptive synthetic sampling approach (ADASYN) for imbalanced learning in 2008; Barua et al. [
28] suggested a MWMOTE in 2014; Douzas et al. [
29] proposed a SOMO method in 2017. Most of these methods focused on imbalanced learning by adding oversampling examples to the imbalanced datasets. However, physical war trauma data are not imbalanced but insufficient in every class. Therefore, the abovementioned oversampling techniques are not suitable for the augmentation of physical war trauma data.
A GAN is a data augmentation model based on DL, which can be used to learn the potential distribution of complex data, generate large-scale and high-quality synthetic samples, effectively solve the problem of insufficient data due to factors such as difficulty and cost of sample acquisition [
30]. Thus, the GAN has become one of the most promising data augmentation approaches in recent years. A GAN is intrinsically a generation model [
31] that does not depend on a priori hypotheses but on the internal confrontation between the data and the model itself to achieve unsupervised learning. To solve the inadequate problem of real data, a GAN can generate synthetic samples of the existing data with the same distribution [
32]. A GAN’s structure consists of two feedforward neural networks: a generator G and a discriminator D. In the learning process, G continuously generates new synthetic samples while D discriminates between the synthetic samples and the real samples as accurately as possible, then gives feedback. In this way, the GAN has created a game similar to “counterfeit currency identification” in which both sides of the game continue to improve their abilities through confrontation.
However, the samples processed by a GAN are mainly two-dimensional data such as pictures and voice signals. A GAN generates virtual images by rotating, scaling, cropping, and changing the brightness, contrast, hue, saturation and adding random noise to image data. However, the GAN is not a good choice for augmenting physical war trauma data.
In the medical field, the application of medical scoring is increasingly maturing, especially in medical treatment, early diagnosis, trauma assessment, and other aspects to the point that it now plays an important auxiliary role. For example, Gabriele Canzi et al. introduced the comprehensive facial injury (CFI) score for comprehensively evaluating severity of facial injuries [
33]. Hasanka Ratnayake et al. used a laboratory-derived early warning score to predict in-hospital mortality and admission to the intensive care unit (ICU) [
34]. Konlawij Trongtrakul et al. created the acute kidney injury (AKI) risk prediction score for early prediction of the condition among critically ill surgical patients [
35].
The trauma score is a common type of medical score that predicts severity of an injury. It uses scientific scoring to quantitatively or semi-quantitatively assess injury severity and its consequences to the injured [
36]. The scoring standard was developed by a panel of experts in the field who will continue to improve and optimize it based on feedback from the application of the trauma score as well as from related research progress. Recently, several improved injury severity score (ISS) methods have been proposed. Cristiane et al. created a novel trauma and injury severity score (TRISS) for survival prediction [
37]; Yang et al. used a revised injury severity score (RISS) to evaluate the severity of injuries of patients hospitalized due to an accident [
38]; Shi et al. developed a weighted injury severity score (WISS) to improve adult trauma mortality prediction [
39]. For example, RISS divides the human body into six public parts: the head, the face, the chest, the abdomen, the limbs, and the body surface. Then, it squares the standard ISS for each of the most serious injuries of the three most serious body parts of the patient and puts them together. As for the second most serious injuries, only their ISS values are put together. If there are more than four injured parts, the standard injury severity score of the most serious injuries of the fourth part is added. The RISS equation is as follows:
where
A1,
B1, and
C1 mean the most serious injuries of the three most serious body parts;
A2,
B2, and
C2 mean the second most serious injuries of the three most serious body parts;
D means the standard injury severity score of the most serious injuries of the fourth part.
Taken together, various novel scientific scoring methods have gradually become doctors’ helping hands in evaluating patients’ injuries. Medical scoring belongs to the category of predictive science. Because different scoring mechanisms have different limitations, it is impossible to achieve 100% accuracy in prediction. However, with the continuous advancements in medicine and with the revision, expansion, and improvement of the scoring mechanisms by researchers in the related domains, medical scoring approaches are expected to become more scientific, practical, and in line with objective reality [
40].
On the other hand, the DL technology combined with knowledge from different disciplines for interdisciplinary field research is an emerging trend. For example, Yang et al. enhanced PIR-based multiperson localization by combining DL with the domain knowledge [
41], and Ding et al. combined the domain knowledge and DL for domain adaptation in machine translation [
42]. Therefore, combining DL with the domain knowledge of medical experts according to the characteristics of war trauma data is key to the successful application of DL to the augmentation of war trauma data.
Based on the above research, to solve the data augmentation problems with small-sample war trauma data by studying the GAN’s idea and the medical trauma scoring method, this article proposes an approach that combines a WTSS with a DNN [
43]. The WTSS–DNN integrated model simulates the generative model in thought, including sample generation and discrimination. The injuries are generated through random sampling and evaluated with WTSS, and then marked with an injury consequence label; this is the sample generation link. The assessment of the prediction accuracy of the DNN classifier is combined with the discrimination of unreasonable injuries by the expert panel; this is the discrimination link. After the accuracy and plausibility of the synthetic samples have been judged, the expert panel provides feedback, based on which, on the one hand, the characteristics of the synthetic samples are further investigated while the necessary optimization and adjustments to the WTSS algorithm are made; and on the other hand, the unreasonable synthetic samples are filtered out to improve data rationality. Eventually, the accuracy and plausibility of the augmented data are expected to stabilize and be optimized to generate credible samples.
This data augmentation approach is the first attempt to combine war trauma assessment in the medical field with DL in the AI field. The WTSS–DNN integrated model can automatically generate large-scale and credible virtual war trauma data, making it possible to carry out related data-based military research, which has great practical significance. In addition, this approach not only helps to solve the war trauma data augmentation problem, but the WTSS algorithm we have proposed also provides a practical auxiliary tool for quickly evaluating soldiers’ injuries and formulating treatment strategies.
3. Materials and Methods
In this section, we first explain the overall process of the research, then introduce the WTSS algorithm in detail. Next, we introduce the structure of our DNN classifier, and then determine the multiclassification metrics used in the algorithm to evaluate the performance of the classifier. Finally, the method of judging the plausibility of the generated synthetic samples is introduced.
3.1. Workflow of the Study
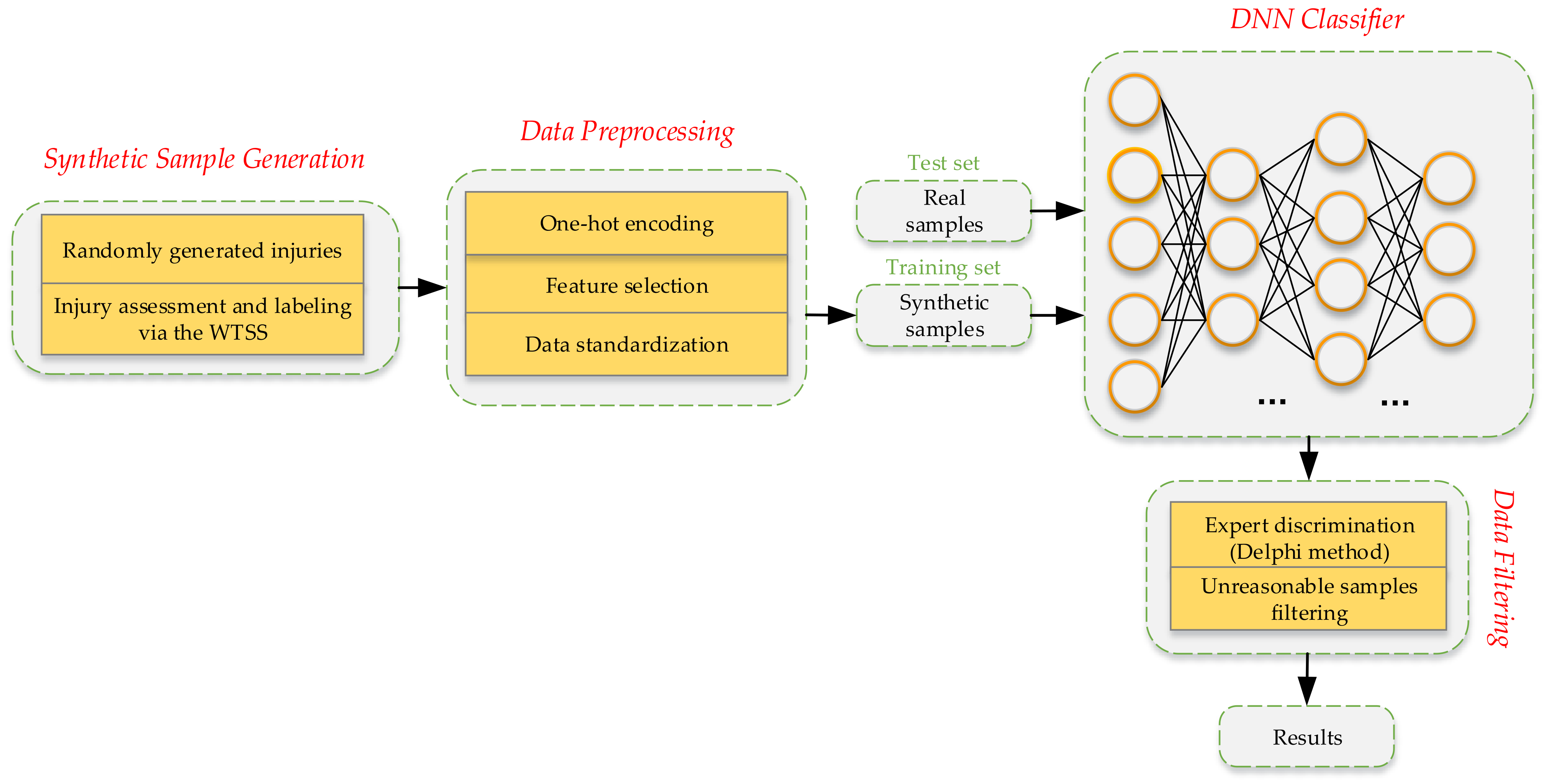
To solve the data augmentation problem and the supervised learning problem, an integrated modeling approach that incorporates the war trauma severity scoring algorithm (WTSS) and a DNN model was proposed. This approach’s workflow is summarized as follows (
Figure 1).
Based on the known probability distributions, the injured parts, injury types, and complications were randomly sampled and then combined to form a complete war trauma injury condition. Next, we used the WTSS algorithm to calculate the severity score and evaluate the consequences, after which the injury consequence label was marked.
After the data preprocessing, to test the accuracy of the injury consequence prediction, we trained a DNN classifier with the generated data and tested it with real data.
Through the Delphi method, the expert panel reached a consensus on unreasonable multiple injuries based on the domain knowledge [
44] and then filtered out the unreasonable synthetic samples after the data generation.
After the predicted accuracy was evaluated and the unreasonable synthetic samples were filtered out, credible virtual war trauma data were finally output.
Figure 1.
Workflow of the WTSS–DNN integrated approach.
Figure 1.
Workflow of the WTSS–DNN integrated approach.
3.2. Random Injury Generation
In the injury generation process, we first randomly sampled the injured part according to the probability of occurrence; then, we randomly selected the possible injury types according to the injured part; finally, we randomly sampled whether it is accompanied by complications; if there were complications, we randomly selected the possible complications.
3.3. WTSS Algorithm
After injuries were randomly generated, the focus of the research was on how to conduct standardized and accurate injury assessments. To solve this problem, we conducted multiple rounds of discussions and communication with the expert panel and finally decided to carry out a standardized quantitative assessment of various injuries by proposing a war trauma severity scoring algorithm.
Via in-depth summary of the various existing trauma scoring algorithms and based on the idea of multiple nonlinear regression and the key factors that affect severity of an injury (injured part, injury type, complications, and whether there are multiple injuries), after several rounds of testing and optimization, the equation for WTSS was finally determined as follows:
where
F represents the severity score;
Pi represents the weight coefficient of injury severity for each of the seven body parts;
Xi shows whether the corresponding body part was injured (if not injured, the corresponding
Xi value equals 0; otherwise, it equals the injury severity standard score for the corresponding body part);
Ci shows whether the injury was accompanied by complications (if there were no complications,
Ci equals 0; otherwise, it equals the corresponding severity score); the bias
a is the correction value for multiple injuries (if there were multiple injuries,
a equals −20; otherwise, it equals 0).
Next, we calculated
F according to the predictive factors
Pi,
Xi,
Ci, and
a, then selected the corresponding score interval according to the magnitude of
F. Finally, we labeled the synthetic samples with the consequences of the injury. The pseudocode of WTSS is provided in Algorithm 1.
| Algorithm 1. War trauma severity score (WTSS).
|
| Input: Weight coefficient of injury parts: Pi = {P0, P1, ..., P6}. |
| Injury type score: Xi = {X0, X1, ..., X6}. |
| Complication score: Ci = {C0, C1, ..., C6}. |
| Correction value for multiple injuries: a = −20. |
| Output: Severity score: F(P, X, C). |
| 1: n = 0 |
| 2: for i = 0 to 6 do |
| 3: if Pi 0 and Xi 0 then |
| 4: xA0; F(P, X, C) += Pi*Xi |
| 5: xA0; n += 1 |
| 6: end if |
| 7: if Ci 0 then |
| 8: F(P, X, C) += Ci |
| 9: end if |
| 10: end for |
| 11: if n > 1 then |
| 12: F(P, X, C) += a |
| 13: end if |
| 14: return F(P, X, C) |
The WTSS algorithm is a nonlinear model which ignores complicated details of the injury and uses a good correlation between the injuries’ consequences and the severity of the injured parts and the injury types [
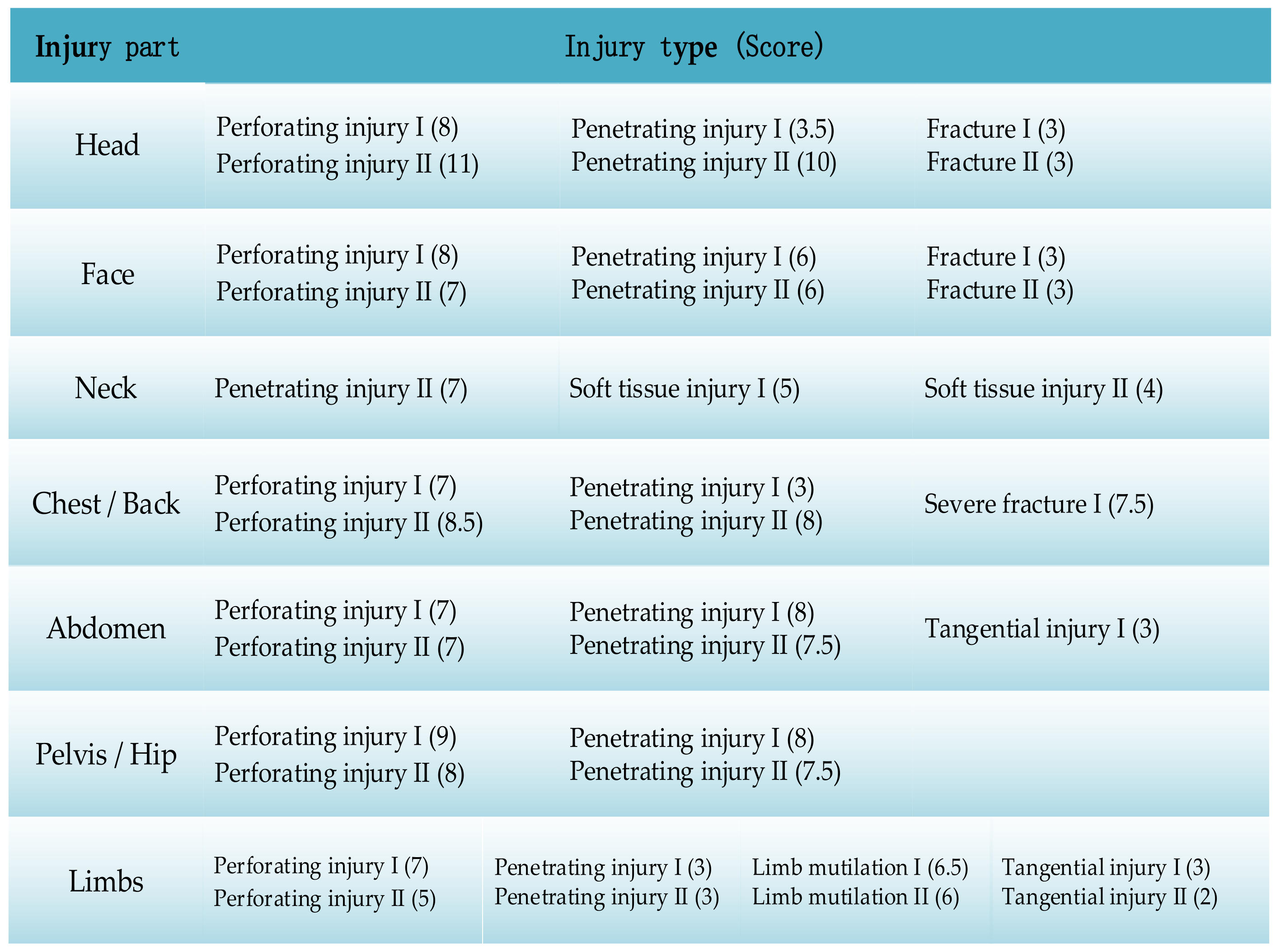
45]. The weight coefficients of injuries in different body parts are shown in
Table 1, and the example of the standard severity score for injury types and complications are shown in
Figure 2 and
Figure 3. The score intervals for the injury consequences are listed in
Table 2.
In a situation wherein different injury types or complications have the same standard injury severity score in a certain injured part, we coded them to distinguish. Taking the abdomen as an example, the coding method is shown in
Figure 4.
As an independent scoring algorithm to determine severity of war trauma, WTSS does not perform an extremely accurate diagnosis of a specific injury. Instead, it performs standardized assessment and prediction of the most probable consequences of injuries from an objective perspective to ensure accuracy of the injury consequence assessment. Additionally, WTSS is not only the core of our WTSS–DNN integrated model that contributes to large-scale analysis and evaluation of war trauma data, but it also helps to quickly evaluate and diagnose soldiers’ injuries on the battlefield and determine the treatment strategy. Furthermore, in complex battlefield environments, the soldier’s age, physical constitution, and other factors may cause different consequences of the same trauma. Consequently, WTSS only objectively assesses the injury without considering the age and other physiological indicators to meet the requirements of the ideal scoring method that is “easy to implement, objective, and accurate” [
38].
3.4. Deep Neural Network
Because the WTSS algorithm is a complicated nonlinear model, this article used a DNN as a classifier model to test the accuracy of injury consequences. The DNN classifier consists of an input layer, an output layer, and several hidden layers. It uses multilayer nonlinear information processing, which can be widely and flexibly used to solve problems such as classification, regression, dimensionality reduction, feature extraction, and clustering. First, we built a suitable DNN classifier network structure according to the actual needs, and the network structure was determined to be 22–16–16–16–4 after the experiment. Next, to test whether such a classifier has excellent generalization ability, we trained it with synthetic samples and tested it with real samples. To verify its performance, we used four multiclassification metrics based on a confusion matrix: accuracy, precision, recall, and the F
1 score [
46]. Among these metrics, the F
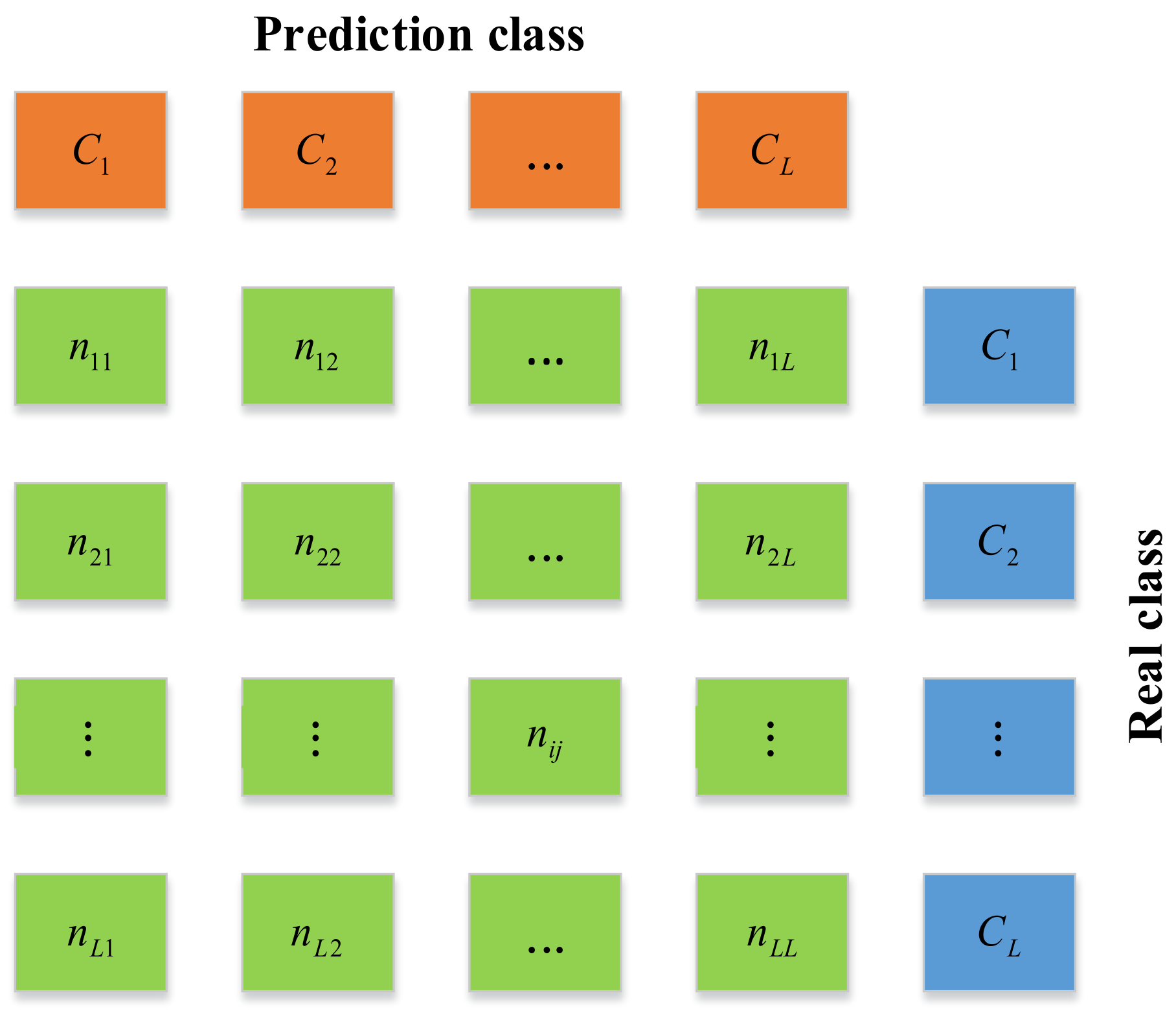
1 score is the harmonic average of precision and recall. Finally, we adjusted and optimized the hyperparameters and then determined the best learning rate and the training sample size. The confusion matrix is shown in
Figure 5.
In
Figure 5,
L represents the class number,
nii and
nij—the number of class
Ci samples correctly predicted as class
Ci and incorrectly predicted as class
Ci, respectively;
Ri and
Pi indicate the recall and the precision of class
Ci, defined in Equations (3) and (4), and the accuracy and the F
1 score are defined in Equations (5) and (6).
3.5. Discrimination of Unreasonable Injuries Based on the Delphi Method
After data generation, to improve the data plausibility of the synthetic samples, the expert panel reached a consensus on multiple unreasonable injuries based on the domain knowledge and provided feedback. Based on this feedback, we analyzed the law of unreasonable injury combinations and filtered out the unreasonable synthetic samples to improve data plausibility. Finally, we outputted the credible synthetic samples.
4. Empirical Analysis
Due to the high confidentiality and difficulty of access to war trauma data, it is gradually attracting greater attention from the army, military academies, and related hospitals. To eliminate obstacles to related research, an efficient and credible data augmentation approach is urgently needed in order to support large-scale war trauma data research and war game deduction. Our proposed integrated model provides a new and feasible way to meet the real need for large-scale and automated generation of credible war trauma data.
4.1. Data Collection
In this study, we collected and organized two types of real war trauma data at a certain scale: data on gunshot wounds and blast injuries. We selected 338 cases (minor injury, 114 cases; moderate injury, 82 cases; serious injury, 74 cases; and critical injury and death, 68 cases) complete with the available data to form the test set. After the preprocessing operations such as one-hot encoding, data standardization, and feature reduction, our war trauma data had a total of 22 features.
4.2. Results Analysis
We implemented our proposed WTSS–DNN integrated model in Python 3.7.7 and conducted experiments on a personal computer with a Windows 64-bit operating system. After a series of tests on the DNN, the optimal values of all the hyperparameters were determined. The classifier’s input dimension was 22, equal to the feature dimension of the war trauma samples. The number of hidden layers of the classifier was set at 4, with each using ReLUs as the activation function. The softmax function was used as the output layer, and categorical cross-entropy was used as the loss function. We used TensorFlow 2.0.0 and GPU to train our DNN classifier; the epoch was set at 1000 and the batch size was set at 256. We chose Adam as our optimization algorithm as it performed best compared to SGD and RMSProp3 [
47].
After determining the best network structure of the DNN classifier (22–16–16–16–16–4), we conducted contrast experiments at different learning rates [
48]. Specifically, we kept the network structure and other hyperparameters unchanged, then set the values of the learning rate to be 0.05, 0.02, 0.01, 0.005, 0.002, 0.001, 0.0005, and 0.0001, respectively.
Table 3 shows accuracy, precision, recall, and the F
1 score at different learning rates on the same training set with a sample size of 10,000. The results show that the 0.001 learning rate led to the best overall model performance and thus was selected and used.
Next, we explored the best training sample size (
n). On the one hand, low numbers of training samples cannot fully teach sample features and meet the requirements of model accuracy; and on the other hand, too high numbers of training samples can increase the calculation costs and time costs and are not conducive to optimizing the hyperparameters. Therefore, we sought to determine the best training sample size in the range of 1000–20,000 through the trial and error method [
49]. In the search process, to avoid the impact of class imbalance on the experimental results, synthetic samples of the four classes were extracted at the same proportion to form a training set for the experiment and test. The overall performance results of the multiclassification metrics at different training sample sizes are shown in
Table 4.
The experimental results showed that the small-scale training set did not meet the requirements for model accuracy. As the training sample size continued to increase, the predicted accuracy gradually increased. When the training sample size was 8000, the accuracy reached 80.88%; and when the training scale increased to 12,000, the accuracy increased to 84.33%. However, model performance became deteriorated when the training scale was greater than 12,000, which indicates that blindly increasing the training scale could not guarantee a consistently higher classification accuracy. Besides, when the training scale was increased, as the harmonic average of precision and recall, the trend of the F1 score was basically consistent with that of accuracy. Therefore, we supposed that selecting a training sample size of 12,000 can achieve the best compromise between the training cost and the classification performance.
Finally, our DNN classifier achieved the best overall performance with 84.33% accuracy, 90.07% precision, 88.44% recall, and an 89.25% F1 score.
4.3. Evaluation of WTSS Combined with a DNN
In this section, we first explored the accuracy of injury assessment of different classifier models. Subsequently, to evaluate the respective contributions of the WTSS algorithm and the DNN classifier in the WTSS–DNN data augmentation method, we set up an ablation experiment. Finally, we provided the prediction results of the DNN for real data through the confusion matrix.
First, we compared our DNN model with three classic machine-learning classifiers: random forest (RF) [
50], XGBoost [
51], and naïve Bayes (NB) [
52].
The RF, XGBoost, and NB models and our DNN model were trained with the same training set and then tested with the same real samples. As shown in
Figure 6, our DNN classifier performed better than the three classic machine-learning models. The NB model showed the weakest performance in comparison with the other classifier models because when the number of features is large or when the correlation between the features is high, the NB classification effect is poor. These results indicate that classic machine-learning models cannot be effectively trained when there are few samples and verified that a DNN classifier trained with a large amount of data has better classification performance.
Next, to evaluate the respective contributions of the WTSS algorithm and the DNN classifier in the WTSS–DNN integrated model, we set up an ablation experiment. Specifically, we combined different injury assessment methods with different classifier models to observe performance of various combinations. Injury assessment methods include the WTSS algorithm and the manual assessment method (MA); classification models include DNN, RF, XGBoost, and NB. The results of the ablation experiment are shown in
Table 5.
From the results of the ablation experiment, we can see that the WTSS algorithm is better than the traditional manual evaluation method, the prediction performance of the DNN classifier is better than that of the machine-learning model, and the combination of WTSS and the DNN performs best. Therefore, the combination of WTSS and the DNN can effectively solve the data augmentation problem of war trauma data and shows superiority compared with artificial generation methods.
Finally, we provided the prediction results of the DNN for real data through the confusion matrix.
From
Table 6, we can see that the prediction accuracy for minor injuries and moderate injuries is very high, but the prediction accuracy for critical injuries is only about 60%, which is caused by the complexity of critical injuries.
4.4. Data Filtering
The Delphi method, also known as the “expert investigation method”, was invented in 1946 by RAND Corporation in the United States. The Delphi method is based on the key assumption that predictions from groups are usually more accurate than predictions from individuals. The goal of this method is to use a structured iterative approach to obtain consensual opinions from an expert panel [
44].
For the multiple injuries data generated, some injury combinations are unreasonable—they are almost impossible to appear in a real war. To improve plausibility and usability of the synthetic samples in our experiment, we decided to use the Delphi method to evaluate unreasonable multiple injuries and filter them out. After several rounds of identification and discussions, the expert panel reached a consensus on the unreasonable multiple injuries based on the domain knowledge. We analyzed the experts’ feedback and then filtered out the unreasonable synthetic samples to improve data plausibility to output credible samples. Next, to verify whether the data plausibility improved or not, we randomly selected 300 original multiple-injury synthetic samples and 300 filtered ones, put them into three groups, and conducted contrast experiments. Then, we counted the number of reasonable samples before and after filtering. The experimental results are shown in
Figure 7.
The experimental results showed that data plausibility of the synthetic samples filtered out was significantly improved in comparison with that of the original ones and came close to 100%.
5. Discussion
For the WTSS–DNN integrated model, plausibility and effectiveness of the WTSS algorithm play a crucial role in the performance of WTSS–DNN. Therefore, we evaluated plausibility and effectiveness of the WTSS algorithm through the two methods described below. First, the expert panel intervention and assistance. The parameter setting and the scoring standard of the algorithm were determined after multiple rounds of discussions and evaluations with the expert panel, which is highly reasonable and professional. Second, we tested plausibility and effectiveness of the algorithm through ablation experiments. In the ablation experiments, on the one hand, we used the DNN classifier to verify accuracy and plausibility of the algorithm in injury assessment. The experimental results show that the prediction accuracy rate reached 84.43%, which is a satisfactory result. On the other hand, we compared the WTSS algorithm with the traditional manual assessment method, further verified plausibility and superiority of the WTSS algorithm in injury assessment. Therefore, compared with the artificially generated methods, the performance of the proposed WTSS algorithm combined with a DNN in war trauma data augmentation is superior, can ensure high data quality, and automatically generates large-scale war trauma data on demand.
However, the experiment also showed that the prediction accuracy of the severity of multiple injuries was lower than that for a single injury due to the complexity of multiple injuries. Furthermore, after determining the WTSS standards, the proposed approach no longer relies on additional professional knowledge due to the characteristics of DL. Thus, for nonprofessionals, the proposed approach has a low barrier to successful application. Although we were able to generate credible virtual trauma data only for blast injuries and gunshot wounds in this study, with the continuous real data collection, the types of war trauma we can generate will become more abundant. Finally, the combination of DL with medical scoring algorithms can be used for other types of injury data augmentation, such as for surgical injuries and emergency injuries.