Abstract
Greenhouse gas emissions are the cause of climate change, which in turn has a negative impact on people and the environment. Reducing the fuel consumption of conventional engines reduces climate-damaging emissions and can, thus, contribute to achieving climate protection goals. In addition, fuel costs are a major cost factor for long-haul trucking. Eco-driving helps to reduce fuel costs when driving on inclines and declines. Due to the high mass and, therefore, high kinetic and potential energy of heavy trucks, fuel can be saved by coasting before slopes and before speed limits. However, energy-efficient and non-cooperative driving, i.e., without considering other road users, can lead to increased fuel consumption as vehicles impede each other. To resolve conflicts in road traffic, a variety of methods that enable cooperative driving exist. In general, vehicles communicate with vehicle-to-everything (V2X) and negotiate a joint driving strategy. This paper presents a method that combines cooperative and energy-efficient driving and examines the impact on fuel consumption during uphill driving. The method relies on the exchange of trajectories for cooperative maneuver coordination. By computing a strategic trajectory, energy-efficient driving with long coasting maneuvers is enabled. In the simulative evaluation, travel over hills with two and three trucks is investigated. It is shown that the combination of cooperative and eco-driving reduces the fuel costs for traffic.
1. Introduction
Greenhouse gases are a driver of climate change and it has a negative impact on the environment and humans. This also affects Central European countries such as Germany, where the climate is relatively mild and, here, for example, an increase in extreme weather events is assumed [1]. In addition to the direct influence of these weather events, indirect consequences are expected, for example, the increase of health problems among people is mentioned in [2]. In the IPCC report [3], the target for temperature increase is 1.5 degrees Celsius to limit the negative effects. To realize this, the European Union, adopted the Green Deal. In the report [4], actions are proposed and the goal to make European climate neutral by the year 2050 has been given. As a first milestone, at least 50% of greenhouse gases should already be reduced in 2030 compared to 1990. To achieve this, all sectors, including the transport sector, must make their contribution. In addition to the electrification of the powertrain, reducing fuel consumption is one way of making a contribution.
Furthermore, one of the main cost factors, besides driver costs for long-distance trucking companies, are fuel costs. Depending on the cost estimate, they amount to between 30 and 41% of the total cost of ownership (TCO) [5,6]. Many factors influence fuel consumption such as weather, but also the driving behavior of truck drivers [7,8]. For this reason, there is eco-driving training that teaches energy-efficient driving. According to [9], for example, this saves 7% fuel. However, the effect wears off over time [7,10,11]. In order to achieve long-lasting fuel reductions, many truck manufacturers, therefore, offer in-vehicle systems, which have the advantage over humans that they still function equally well years later. Such systems are also called GPS cruise control and are offered by most European manufacturers under company-specific names, e.g., EfficientCruise from MAN Truck & Bus [12], Predictive Powertrain Control from Daimler [13], Opticruise from Scania [14], I-See from Volvo [15], Optivision from Renault Trucks [16], Predictive Cruise Control from DAF Trucks [17], or HI-CRUISE from IVECO Magirus [18]. With information of the topology through a digital map and the current position, energy-efficient coasting maneuvers can be performed. For example, a coasting maneuver can be performed instead of a constant run over a hilltop. Before reaching the top, the vehicle initiates a coasting maneuver: the vehicle first slows down due to the driving resistance, and on the subsequent downhill slope, the vehicle accelerates again due to the gradient force without using fuel. This is also referred to as look-ahead control (LAC) or eco-driving [19,20]. It should be noted that there are different definitions of eco-driving in the literature. Fafoutellis et al. [21] and Huang et al. [10], define eco-driving as measures to reduce fuel consumption, which is why they include, for example, the selection of a fuel-efficient route, also known as eco-routing. On the other hand, Zavalko [11] and Saerens [22], for example, only refer to energy-efficient driving as eco-driving and represent the original and more accurate definition, which is why it is used here. According to Nordström [14], fuel savings of 4–5% can be achieved. However, eco-driving is not only used in trucks, but also in passenger cars. For example, the Porsche InnoDrive research project showed that eco-driving can save fuel by approximately 10% on a defined route [23]. Furthermore, car manufacturers are now also offering eco-driving as a driver assistance system, e.g., Route-Ahead Assist from BMW [24] or Predictive Efficiency Assist from Audi [25]. While the positive effect on fuel consumption of eco-driving is often mentioned in the literature and by manufacturers, Samaras et al. [26] has shown that at very high traffic density, eco-driving leads to increased fuel consumption instead of fuel savings. This means that vehicles with eco-driving can obstruct other traffic participants. However, it is unclear in which situations this occurs. Alam [27], on the other hand, states that uphill driving is a critical situation for trucks, especially for driving in string formation. By rolling out in front of downhill slopes, another truck can be forced to reduce its speed on the uphill slope. It may then have to accelerate again on the uphill slope to reach its desired speed or on strong inclines where acceleration is not possible due to the mass, therefore, driving in an energy-inefficient engine operating point is necessary to maintain the speed.
In addition to the described scenario on a hill, there are many other conflict situations in road traffic in which vehicles can obstruct each other [28]. One example is merging onto a highway. Vehicles on the highway have the right-of-way and may block a vehicle from entering the highway. In order to manage such situations, methods for cooperative driving have been developed, e.g., Eiermann et al. [29], show a role-based concept which can be used to realize merging on highways with heavy traffic. Other methods, however, such as in [30] or [31], use only trajectories for coordination to solve such situations and do not have a distributed state machine. In addition, machine learning algorithms are used to realize autonomous driving. Tami et al. [32], for example, uses this to make decisions for lane changes. However, the presented methods mostly refer to short-term planning horizons, which are not sufficient for energy-efficient driving and, therefore, do not include eco-driving.
To solve conflict situations in energy-efficient driving, it is, therefore, important to combine energy-efficient and cooperative driving in one method. The idea of combining both areas has already been published in [33]. However, the present publication describes in detail the method and the algorithm, respectively. In addition, the concept is extended, e.g., for the consideration of non-V2X vehicles. Furthermore, the effectiveness is quantified for the first time for a hill driving scenario, since this is considered critical for eco-driving in the literature. Different variants such as eco-driving without V2X or cooperative and eco-driving are compared. Finally, the results are discussed in-depth.
2. Related Work
2.1. Eco-Driving
Eco-driving is an optimization problem [19,22,34,35]. The goal is to cover as much distance as possible over a certain time horizon while consuming as little fuel as possible or to reach a given route between the starting point and the end point with as few fuel consumptions and in as less time as possible. From this follows the cost function J, which must be minimized [19]:
where is the terminal cost, the running cost, the trajectory to be driven or the vehicle states, the controller inputs, the end time, and the time. The terminal costs include all the distance covered in the given time. On the other hand, the running costs mainly describe the fuel costs and, thus, the energy input. The energy input depends on the driving forces. The driving forces or driving resistance can be described in different degrees of detail, in-depth descriptions can be found in [36,37,38]. Without considering inertial forces due to rotating masses such as wheels, the following relationship results:
with
where denotes engine force, the rolling resistance, the drag resistance, the gradient force, the mass, the longitudinal coordinate, the acceleration, the gravitational acceleration, rolling resistance coefficient, drag coefficient, the frontal area, the air density, the velocity, and the gradient of the road.
Thus, cruising with constant speed, the following equation results:
It must be considered that is not equal to the fuel consumption since the efficiency losses of the engine and transmission are added to the fuel consumption. However, it is obvious from Equation (6), without consideration of the terminal state, that the optimization problem results in a velocity close to 0 because depends on the velocity through and the lower the velocity is the smaller is and, thus, . A velocity close to 0 increases driving times for non-autonomous or automated vehicles, which in turn results in increased costs for forwarding companies, since the driver must be paid for a longer period of time. The highest velocity permitted by law on the road section serves as the upper limit for the velocity. For trucks over 3.5 t on German highways, for example, the highest velocity is 80 km/h [39].
The optimization problem can be solved with different methods. Due to the limited computing capacity, optimization is usually not performed over the entire route, but only over a certain horizon. For a distance without gradients an analytical solution can still be found [34], otherwise numerical solution methods must be used. In many works, such as [20] or [35], Dynamic Programming (DP) is used, but Sequential Quadratic Programming (SQP) is also possible as used in [40]. As a rule, the numerical solution methods are very computationally expensive, especially DP. Further, the computational effort for DP depends, for instance, on the number of states and the discretization. For energy-efficient driving, therefore, the velocity range, for example, must often be severely restricted to achieve real-time solutions in vehicle applications [19,35]. In addition, when the system is simplified in a strong way, e.g., by linearization and discretization, the optimal driving strategy may no longer be found [41]. Furthermore, heuristic methods are also used, for instance in [42], a coasting maneuver is always computed from the current state. If, for example, the coasting maneuver at a hill first reduces the velocity and then builds it up again by the downslope force, then the optimal rollout time is reached. Compared to numerical methods, heuristic methods are usually more computationally efficient and are very robust against disturbances. The disadvantage, however, is that no optimum driving strategy can be guaranteed.
2.2. Cooperative Driving
Cooperative behavior is defined by Düring and Pascheka [43]: “We call an agent ’s behavior cooperative behavior with respect to agent and with respect to a total utility function , if by choosing this behavior agent knowingly and willingly increases the total utility in a coupled situation, compared to a reference utility.” In this context, cooperative driving can take different forms with the purpose of maximizing the total utility. Burger et al. [44] first distinguished between explicit and implicit communication. In explicit communication, messages are exchanged between vehicles or infrastructure via V2X. In implicit communication, messages are indirectly communicated through cooperative behavior, e.g., initiating a slight delay to create a gap so that someone can make a lane change. To further increase the benefits of cooperative driving, however, explicit communication is necessary. In the simplest case, an enlarged environment model can be built up by communicating information, e.g., one’s own environment data. This is also called a cooperative environment model. In addition, cooperative prediction can be used to communicate one’s own schedule to other road users. This has the advantage that it eliminates the need to predict other road users, which minimizes uncertainty. The highest benefit from cooperative driving is achieved by coordinating a joint driving maneuver through negotiation or collaborative planning. In collaborative planning, the best global plan is executed. This means that the optimization problem from Section 2.1 must be solved for all vehicles.
However, a global optimization is often not feasible. For example, Okoso et al. [45], show that in path-finding for vehicles with optimal parking, also called automated valet parking, no solution is found with an optimal solver for 25 vehicles or more within 300 s. Knies et al. [46], performed a global optimization for only three vehicles in a highway scenario. Despite the small number of vehicles, due to the large number of possible driving actions, it was stated that it is not feasible to perform an optimization in a reasonable amount of time. This means the solution algorithm is not real-time capable and that there is a possibility that no optimal solution can be found with many vehicles.
Therefore, various local concepts exist for joint maneuver coordination, for example, Sawade et al. [47], proposed a distributed state machine. If a cooperative situation is detected, a vehicle can communicate its desired state to other vehicles. The maneuver is only executed if all vehicles change to the same state. This eliminates misunderstandings, but each situation requires its own state machine. In addition, a situation analysis is necessary to recognize a cooperative situation. Furthermore, this does not implement eco-driving.
Lehmann et al. [30] proposed a generic method by exchanging planned and desired trajectories. The planned trajectory is the current schedule, which can be executed according to the valid traffic rules. This is always communicated to other vehicles via V2X. If, for example, a road user wants to change lanes, but it cannot be performed because another road user is occupying the lane and has the right-of-way, then a desired trajectory can be sent. A desired trajectory always collides with a planned trajectory of another road user. Hereby, the vehicle with right-of-way recognizes the cooperation request. By adjusting the trajectory so that it is collision-free with the desired trajectory, the cooperation can be executed. The trajectories are calculated by polynomials in Freenet coordinates of the road. There are several extensions of the concept, for example, Llaster et al. [31] has extended this with alternative trajectories and explicit costs to the trajectories. Alternative trajectories are trajectories that a vehicle is potentially willing to drive, but do not represent the optimal driving strategy. This should allow faster maneuver coordination. The disadvantage is that every vehicle needs the same road model. There is no information on how far the vehicle can deviate from trajectories, which can negatively influence the robustness or lead to unsafe situations. Due to the limited computing capacity in vehicles and the requirement for real-time, only relatively short trajectories can be calculated which, therefore, cannot represent energy-efficient driving with long coasting maneuvers.
With the method presented by Heß et al. [48], coordination is not realized with trajectories but with occupied space at a time. This space is communicated to other road users when there is a need for cooperation, e.g., when changing lanes. This should allow robust cooperation to take place. This was also demonstrated in real experiments on a test track [49]. However, the disadvantage is that a situation analysis is necessary and, thus, is not a generic approach. In addition, it does not represent eco-driving.
2.3. Vehicle-to-Everything Communication
In the previous section, methods for cooperative driving were shown, which rely on explicit communication. Essentially, there are two ways to realize V2X, one via ad-hoc networks and one via cellular networks. Ad-hoc network such as ITS-G5 or IEEE 802.11p do not require any other infrastructure and send messages via broadcast to all surrounding participants [50,51,52,53]. The more messages that are sent or the larger the message packets are and, thus, the more data is sent per second, the greater the channel load becomes, and packet loss may occur [54]. In order not to overload the channel, Decentralized Congestion Control (DCC) [55] has, therefore, been introduced in Europe, in which accesses to the channel are dynamically controlled [56].
In cellular networks, such as V2X-LTE or 5G NR mode 1 messages are sent over a cell tower. Cellular networks have the advantage of a theoretically infinite range and better channel load control by the infrastructure, but will require network coverage [51,52,53,57].
In addition to packet loss, latency also occurs in the real world due to message transmission. In a real-world experiment, the latency was between 88 and 125 ms for IEEE 802.11p and always over 2500 ms for V2X-LTE. In this context, the latency increased for both transmission techniques at higher speeds [58]. However, the deployment of 5G in cellular networks is expected to bring significant improvements over LTE technology and enable latencies of about 4 to 1 ms [59]. In the following, an ad-hoc network such as IEEE 802.11p is assumed, first because no further infrastructure is required and second because this technology is already used in a series, e.g., in the VW Golf 8 [60].
As already mentioned, ad-hoc networks send messages via broadcast to all surrounding participants, making this an open network. However, to prevent anyone from arbitrarily disrupting the network, a certification procedure according to IEEE 1609.2 is used in Europe [61]. Only authenticated participants can, thus, join the network, which should send reliable data.
Moreover, in Europe, two messages have already been standardized. One is the Cooperative Awareness Message (CAM) [62] and the other is the Decentralized Environmental Notification Message (DENM) [63]. The CAM contains information about the current vehicle state, e.g., the current position or the current speed. This message is sent cyclically. In contrast, the DENM is event and position related and is only sent when an event occurs, e.g., emergency braking. In this case, the message can be forwarded from one vehicle to more distant vehicles using the multi-hop mechanism [50]. For cooperative maneuver coordination, the Maneuver Coordination Message (MCM) [64], is currently under development, but no standardization has been published yet.
2.4. Summary
Cooperative and energy-efficient driving is an optimization problem that cannot be solved in real-time using state-of-the-art methods. The methods for cooperative maneuver coordination are not designed for eco-driving. On the other hand, the methods for eco-driving do not consider other road users. For practical use, it is, therefore, desirable to have a method that is generic and combines both areas. In addition, the computational capacity should be as small as possible to enable an application in real vehicles with real-time requirements. Furthermore, the message size should be as small as possible so that the communication channel is loaded as little as possible and, thus, the risk of packet loss is minimized. Additionally, a method for use in real vehicles must be robust against uncertainties.
3. Method
In order to enable short-term cooperative maneuver coordination, there are different procedures as explained in Section 2.2. The method of Lehmann et al. [30] has the advantage that it is a generic method, which does not require a situation analysis. Another advantage is that the cooperation is occurs with only two trajectories, planned and desired trajectories. This is to keep the channel load as low as possible and, thus, for example, to minimize packet loss during communication. For this reason, the concept for short-term coordination is adopted here. However, in deviation from the original concept, trajectories in this approach are transmitted in UTM coordinates to achieve independence from a road map. Algorithm 1 shows the definition of the MCM used for the investigations. The definition was created in the platform and language independent description of data structures Protocol Buffers [65].
| Algorithm 1 Definition of MCM in the Protocol Buffers notation. |
| syntax = “proto3”; |
| message MCM { |
| uint32 v2xId = 1;//V2X station ID |
| int64 timestamp = 2;//time in us |
| Trajectory planTra = 3;//planed trajectory |
| optional Trajectory desireTra = 4;//desired trajectory |
| message Trajectory { |
| repeated PolySection longPos = 1;//UTM-easting |
| repeated PolySection latPos = 2;//UTM-northing |
| message PolySection { |
| repeated float coefficients = 1;//coefficients of polynomial a_0, a_1, … |
| float start = 2;//start time in s, real start time = start time + timestamp |
| float end = 3;//end time in s, real end time = start time + timestamp |
| float xOffset = 4;//UTM-Offset, whole number because of accuracy float32 |
| } |
| } |
| } |
The calculation of UTM positions from the MCM is performed according to Equation (7):
with and the corresponding UTM coordinate. To achieve the necessary accuracy of Float64 for UTM coordians, the Float32 values in Equation (7) must be converted to Float64. It is assumed that vehicles are located in the same UTM zone. If necessary, the heading and the velocity are also required, e.g., for collision checks. These can be determined by deriving the position. For stationary vehicles, the heading can be determined from the CAM. Likewise, the current height can be determined from the reference position [66] of the CAM; this could be necessary information for bridges with stationary objects, for example.
For energy-efficient driving a strategic trajectory is computed, which can represent long coasting maneuvers. Thereby, it is important to get a continuous trajectory to each computation step. An overview of the components of the algorithm is given in the following figure (Figure 1):
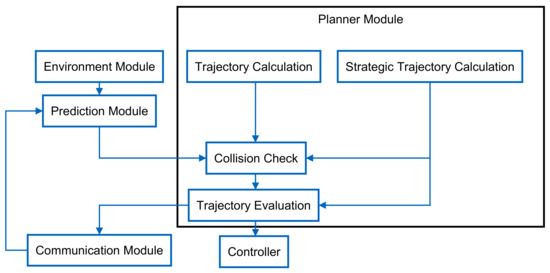
Figure 1.
Overview system architecture.
The environment model provides an object list with all surrounding objects. The object list is passed to the prediction module. Objects that are V2X-capable are assigned the planned and, if necessary, desired trajectory by the MCM. For these, no prediction is necessary. For non-V2X objects, the planned trajectory is predicted. Schubert et al. [67] compared methods for predicting vehicles, but the models are only valid for short time horizons. For the maneuver planner, however, longer planning horizons of, e.g., 10 s are needed. For this reason, prediction is performed as in [68]. The assumption is made that objects move along the current lane with constant velocity. The object information with the trajectories is passed to the planner module.
The planner in itself contains several components. In the trajectory calculation it is assumed that the ego vehicle moves along a route on the right lane. This is also the most frequently used lane for trucks on multi-lane highways and often the only permitted lane. Overtaking or evasive maneuvers are not calculated in this paper. There are different ways to calculate trajectories. Gonzalez et al. [69], gives an overview. For the concept it is not crucial which method is used for the trajectory calculation. However, it is important that different trajectories are computed that cover the maneuver space as well as possible and are feasible to drive. For this reason, a graph or search tree method was selected. Starting from the initial state, a partial trajectory to the next node is calculated using the driving forces and possible driving actions. The possible driving actions are accelerating, maintaining speed, coasting, smooth braking, and braking. From each individual node, the trajectory with the driving actions is in turn extended to the planned time horizon or end node. By calculating the trajectories with driving forces, the drive ability is guaranteed, since unrealistic accelerations do not occur. If a driving action cannot be carried out, e.g., because the permissible speed is exceeded, then this trajectory is discarded.
In Section 2.1 different methods were presented on how to calculate trajectories for energy-efficient trajectories. Again, it is not crucial which method is chosen, as long as a continuous trajectory can be computed over the given horizon for each computation cycle. Due to the low computational capacity and robustness, a heuristic method was chosen, which is described in detail in [33]. This method combines locally optimal trajectories, such as coasting before a speed limit or maintaining maximum allowed speed between two speed limits, into a continuous trajectory. The local trajectories are generated according to fixed rules and computed using driving resistance models. The use of driving resistances ensures feasibility of driving.
The collision check is performed with the calculated trajectories of the ego vehicle and the planned and desired trajectories of the other road users. Ego trajectories are the calculated trajectories from the graph methods and up to the same time horizon as the strategic trajectory. This ensures that the optimal energy-efficient trajectory is always included. A collision is initially understood as a violation of the safety distance according to the German Road Traffic Act (StVO). Due to inaccuracies of, e.g., the measurement data acquisition or determination of the position or the trajectory traversal, a multi-stage collision check is performed. The trajectories are assigned tolerances. At any time of the trajectory, the position may deviate by a previously defined value. The value is velocity-dependent and increases linearly from 0 to 50 km/h. The maximum tolerance value is, thus, set at speed of 50 km/h and above. The maximum tolerance value is therefore set from 50 km/h. The speed limit comes from StVO §4 [39]. The law prescribes a distance of at least 50 m on German highways for trucks from a velocity of 50 km/h, which is why the safety distance is constant from this velocity. If the tolerance value is exceeded when the trajectory is traversed, a reset to the current position is performed, otherwise trajectories are always calculated from the planned point of the last planned trajectory at the given time. This means that the actual distance can deviate by a factor of two from the tolerance for trajectories, and during resets this changes abruptly. In addition, numerical inaccuracies in the calculation from one calculation cycle to another can result in a changed distance dimension, i.e., for a safety distance of, for example, 50 m, the calculated distance changes from 50.0000000001 m to 49.9999999998 m. If this is the initial distance, no calculation of collision-free trajectories is possible in this example. For these reasons, there are three collision checks with different distances:
- Stage 1: Safety distance according to StVO + double tolerances of the trajectory.
- Stage 2: Safety distance according to StVO in first, e.g., three seconds, otherwise like Stage 1.
- Stage 3: Safety distance according to StVO.
The trajectories are then evaluated. For this purpose, the costs of a trajectory are determined. It is assumed that the trajectories are in sampled form with fixed time steps and points. First, the costs for the own vehicle are determined:
with
where and are weighting factors. describes how energy efficiently a trajectory can be executed. For this purpose, the costs for the execution of individual trajectories are added up, also called driving costs and the average is calculated. compares the velocity profiles of the trajectory and the strategic trajectory. Therefore, the amount of the velocity differences of the two trajectories at a given time is determined and nominated with . The maximum value is 1. On the one hand, this is to ensure an appropriate velocity and, on the other hand, to enable the detection of coasting maneuvers that are far ahead. Subsequently, the cooperation costs are calculated:
where is the number of detected collisions of Stage 1 with desired trajectories of other road users. describes a factor in how far cooperative trajectories should be preferred.
In general, the trajectories with the best cooperative costs are selected which are collision-free with other trajectories. As a rule, only trajectories that meet the Stage 1 collision check are considered. If there are no trajectories that satisfy Stage 1, then Stage 2 is considered. The aim is that at least towards the end of the trajectory the distance for Stage 1 is reached again. If there are also no trajectories that fulfill Stage 2, then Stage 3 trajectories are considered. In the next calculation cycle, an attempt is made again to find trajectories of Stage 1 or 2. If no collision-free trajectory can be found, then an emergency trajectory is calculated, which performs braking.
If the wish of other road users is fulfilled, then the desired trajectory is stored, and this is treated in the next calculation cycles as a right-of-way planned trajectory.
If a trajectory is available whose is significantly below the cooperative costs, then this is set as the desired trajectory.
The planned and desired trajectories are forwarded to the communication module and transmitted to other road users via MCM. However, with the trajectory calculation at hand, these must be converted into polynomials beforehand. The planned trajectory is also passed on to the controller. The planned trajectory also contains information about the driving action, such as speed hold or coasting. The controller calculates a target acceleration from this which is passed on to the ACC interface. In addition, an explicit gear setting is made for coasting and shifting to gear 0.
4. Evaluation
4.1. Simulation Environment
The commercial program for vehicle simulations TruckMaker 9.1.1 from IPG was used as the simulation tool. TruckMaker Release 9 offers, among other things, the possibility to simulate several detailed eco vehicles with SimNet [70]. Within the IMAGinE project an additional interface for Robot Operating System (ROS) was created, called CMRosIF. Furthermore, the possibility of a simplified V2X simulation with ROS and a topic-based synchronization between ROS and TruckMaker was implemented [71]. The program code was written in C++ and integrated in ROS framework. Ubuntu 16.04 was used as the operating system and the corresponding ROS version Kinetic [72], was used for the functional code.
The truck used was a semi-tractor with trailer typical of long-distance transport. As in [68], a demo truck is used for the investigations, in which the 8-speed was replaced by a 12-speed transmission according to Fries [73] and Wolf [74], since these are typical for long-distance transport. The truck used had an output of 353.0 kW with a maximum engine torque of 2250 Nm. The lateral control was controlled by IPG-Driver along the route, i.e., the vehicle drives in the right lane. The control for the longitudinal control is conducted via the ACC interface. For gear selection, a separate transmission logic was used to skip gears and to shift in neutral gear when coasting was requested by the planned trajectory.
4.2. Scenarios
In Section 1, uphill driving was identified as a problem with eco-driving. For this reason, a road with a hill of 2% incline and 6% decline was selected. On inclines at more than 2%, trucks may experience a drop in speed due to their heavy weight or from being underpowered [75]. Koy and Spacek [76] have shown that even with high engine power and large gradients between 4% and 8%, constant cruising at 80 km/h is not possible. At a gradient of 2%, the selected truck with 40 t can still drive over the hill at 80 km/h. According to §18 of the German Road Traffic Regulations (StVO) [39], 80 km/h corresponds to the maximum permitted speed for trucks on German highways. 40 t corresponds to the permissible total mass for trucks in Germany according to Road Traffic Licensing Regulations (StVZO) §34 [77]. At a gradient of −2%, using Equation (2) and parameters from Fries [73], a 40 t truck is accelerated by the downslope force with only 0.097 m/s2 at 80 km/h, while a 13 t truck is decelerated even with −0.002 m/s2. In order not to avoid an excessively long coasting process, a slope of −6% gradient was chosen. Figure 2 shows the elevation profile of the track. It should be noted that without driving resistances, the truck would absorb energy when passing through the track because the potential energy at the end is lower. However, this is not important for the investigations since individual variants are compared with the same route profile.
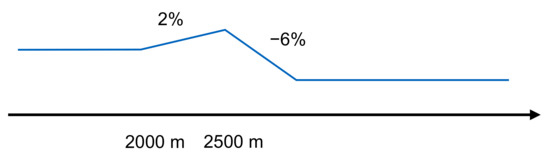
Figure 2.
Road elevation profile.
The first truck always started at 1500 m. Two or three trucks drove at the maximum velocity of 80 km/h permitted on German highways. The initial distance was selected depending on the safety distance and the tolerance for driving the trajectories. As already mentioned, the safety distance for trucks on German highways at speeds of 50 km/h and above is 50 m according to StVO §4 [39]. To fulfill the collision check of Stage 1, at least two times the tolerance had to be added up as described in Section 3. If the distance was too large, no cooperation was necessary, which is why the initial distance was chosen as close as possible to the minimum distance for the collision check of Stage 1. With a tolerance of 10 m for traversing the trajectories and an addition of approximately 0.5 m to compensate for small deviations, an initial distance of 70.5 m is obtained. The scenario always lasted 80 s. In order to avoid additional effects due to an energy-efficient driving strategy such as pulse and glide [19], no trajectories with coasting were calculated in the study except for the strategic trajectory. Table 1 shows selected parameters. With the specified parameter set, all simulations could be reliably executed. The parameters themselves were determined during the development of the concept. Five variants were run and are summarized in Table 2. Variant 1 simulates non-V2X vehicles that are not driving in an energy-efficient manner and, thus, represents the baseline scenario. Variant 2 represents non-V2X vehicles that do drive energy efficiently, unlike Variant 1. Variants 3 and 4 represent V2X vehicles that use cooperative prediction but no maneuver coordination. Variant 3, unlike Variant 4, does not use an energy-efficient driving strategy. Variant 5 represents an energy-efficient and cooperative vehicle.

Table 1.
Parameter Planner Algorithms.

Table 2.
Overview variants of driving strategy.
4.3. Results
4.3.1. Two Trucks
Table 3 shows the absolute, and Figure 3 the relative average fuel consumption and the average speed per vehicle for the respective variant. Two trucks, each with a total weight of 40 t, travel the route described in Figure 2. Two test runs were performed in each case to minimize uncertainties due to incomplete determinism in the simulation. The mean value was calculated from the test runs.

Table 3.
Two heavy trucks driving over a hill. Average fuel consumption and velocity per truck.
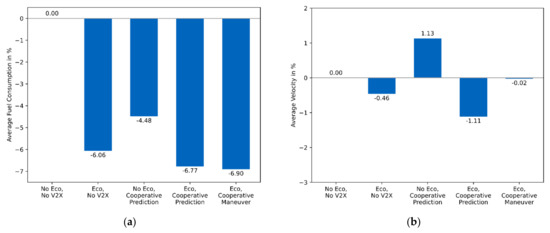
Figure 3.
Two heavy trucks driving over a hill. (a) Relative average fuel consumption. (b) Relative average velocity.
The worst consumption is achieved with no energy-efficient driving and no communication, while the best consumption is achieved with eco-driving and cooperative maneuver coordination with planned and desired trajectories. It can also be seen that besides cooperative maneuver planning, cooperative prediction achieves an advantage in eco-driving. The improved fuel consumption is due to coasting, where hardly any fuel is consumed. However, coasting increases the travel time, which is evident from the lower average speed. The highest average velocity in eco-driving is achieved by cooperative maneuver planning, although the lowest fuel consumption is achieved here. This can be explained by the fact that the deceleration of the second vehicle is minimized by a later coasting maneuver of the first vehicle.
4.3.2. Three Trucks
In contrast to Section 4.3.1, three trucks were considered instead of two in the otherwise same scenario. Table 4 shows the absolute, and Figure 4 the relative average fuel consumption per vehicle and the average velocity.

Table 4.
Three heavy trucks driving over a hill. Average fuel consumption and velocity per truck.
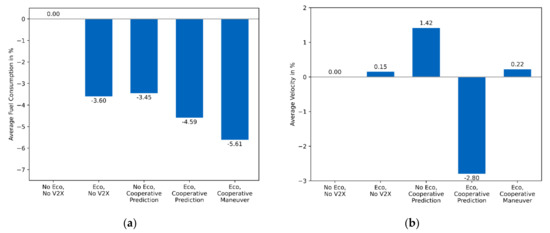
Figure 4.
Three heavy trucks driving over a hill. (a) Relative average fuel consumption. (b) Relative average velocity.
Again, it is shown that eco-driving in combination with cooperative maneuver planning achieves the best consumption. In addition, the average velocity for eco-driving with cooperative maneuver planning is in second place. While the order in fuel consumption has remained the same, the average consumption has increased. This can be explained by the fact that now, instead of one vehicle foregoing its optimal driving maneuver, two vehicles forego their optimal driving maneuver through cooperation.
5. Discussion
In the previous section, it was shown that for a scenario considered critical in the literature for trucks, eco-driving in combination with cooperative maneuver planning has the lowest fuel consumption in sum of all vehicles. The implementation has many parameters such as weighting factors for the trajectory cost or the time horizon for the trajectory length. Different parameters change the behavior. Due to the infinite number of possible combinations no parameter optimization was performed over all variations, and only one working set was selected. Therefore, a global optimum cannot be assumed. Additionally, the choice of parameters must distinguish between the potential for improvement in individual situations and computation time. For example, a longer time horizon of the trajectories could improve the result but would also significantly increase the computation time. The goal should be an implementation that can also be used in vehicles.
In the present code, a simulation with a HP ZBook 17 G3 32 GB RAM and Intel Core i7-6820HQ processor with the clock frequency 2.70 GHz *4 achieved a real-time of about 0.6 times with the vehicle simulation TruckMaker for two vehicles. With three vehicles this has already dropped to approx. 0.3. This does not prove the real-time capability, but the numbers show that with more vehicles the speed in the simulation is clearly reduced. On the one hand, one more vehicle must be calculated, and on the other hand, more trajectories are exchanged, which increases the effort for collision checking, for example. In real applications, however, only one algorithm for one vehicle has to be calculated on one computer, which means that less computing capacity is required compared to the simulation. A measurement of the computational effort for the planning algorithm in the simulation is not possible due to the coupling of the framework ROS and the simulation tool TruckMaker, because here the synchronization slows down the time. However, initial tests in a real vehicle have shown that the implementation can in principle also be run on a vehicle.
In the simulation, an optimal V2X simulation was used; latencies were only caused by the chain of ROS nodes but not by the air interface. Since the planner worked with a frequency of 10 Hz, the latency is hereby at least one cycle and, thus, 100 ms. In order not to get any additional latency for the prediction, here the frequency of the ROS node is 20 Hz. Packet losses due to communication were not considered due to the ideal air interface. Therefore, no statements can be made about the channel load and any necessary adjustments to the authorization of channel access by, for example, DCC in Europe.
Furthermore, no safety-critical aspects were investigated with regard to communication. In Section 2.3 it was mentioned that messages are sent and received with authentication, but a vehicle with an authenticated system could knowingly send false information to harm other road users. For this reason, it is still necessary to drive with a distance greater than the safety distance, as in the described approach. Other systems that work independently of the presented planner, such as emergency brake assistants, can act as an additional safety instance.
All vehicles were always considered in the evaluation. For the first vehicle, however, eco-driving without cooperation is always the best driving strategy. Thus, the overall traffic is improved with cooperation; for an individual vehicle, there may be an increase in consumption in individual situations. According to the definition of cooperation from Section 2.2, however, everyone should benefit over a long time horizon, since the same vehicle does not always have to forego an advantage, but benefits from cooperation in other situations. For forwarding companies that may have a larger fleet of vehicles, the total consumption over a longer period of time is decisive, therefore, the short-term disadvantage of a vehicle is not decisive. In addition, according to German law StVO §1 [39], other road users may not be obstructed more than is avoidable. However, it is unclear how often this situation occurs in the everyday life of vehicle fleets. Beyond this, however, other scenarios can be made more energy efficient through cooperation, which also has a positive impact on fuel consumption. However, an analysis of the number of potential situations in everyday trucking operations is very time consuming since the environmental data must be recorded and evaluated in addition to the vehicle’s own data.
In the present investigations, the calculation of trajectories with coasting, with the exception of the strategic trajectory, was omitted. With coasting trajectories and the correct choice of parameters, consumption could be further reduced, e.g., by displaying pulse and glide. According to Scania [78], approximately 0.5% fuel can be saved here on flat routes. However, preliminary tests have shown that vehicles increase the distance under certain circumstances, e.g., before climbing a slope or by performing a coasting maneuver. This makes sense, but a higher distance means that cooperation on the uphill slope is no longer necessary, which is why the optimum configuration has not been selected here. A comparison of the different variants would be distorted by this because the fuel consumption is no longer attributable to driving over the hill.
In the concept, it is intended to treat accepted desired trajectories as right-of-way planned trajectories in further calculations. Under certain circumstances, however, it is possible that collision-free trajectories can no longer be found, e.g., because a vehicle with the right-of-way suddenly changes its driving strategy and initiates a gentle braking maneuver. In this case, an emergency trajectory is then calculated, which is a less than optimal solution for subsequent driving due to inappropriate braking. The concept can be further extended here, in that in some circumstances the accepted desired trajectory is discarded. In the present implementation this is not considered. In addition, further improvement in the implementation, e.g., calculation of the strategic trajectory instead of using the heuristic method with Dynamic Programming, are conceivable. The effect of implementation changes on fuel consumption would have to be investigated on a case-by-case basis.
A maximum of three vehicles were examined in the simulations. In Section 1, it was described that vehicles with eco-driving interfere with each other when there is a lot of traffic. In the studies, however, eco-driving was always better than non-energy efficient driving. This can be due to different reasons, e.g., that the number of vehicles was still too small or that the presented trajectory-based algorithm shows a better behavior with non- V2X vehicles than vehicles with ACC system. For the exact statements further investigations must be carried out.
6. Conclusions
In this publication, a concept was presented in detail that combines eco- and cooperative driving. In addition, the concept can include non-V2X vehicles through prediction. Thereby, the eco-driving was ensured by calculating a strategic trajectory. Short-term coordination was performed with planned and desired trajectories via V2X. Without the need for cooperation, the strategic trajectory was followed. With the help of a vehicle simulation, different possibilities of driving over a hill were presented. The impact of eco-driving, cooperative perception, and cooperative maneuver planning on fuel consumption was investigated. Eco-driving with cooperative maneuver planning resulted in the lowest fuel consumption. In addition, it was shown that using this concept does not lower the average velocity compared to eco-driving and not using V2X.
In future work, the concept will be combined with a collective perception. The collective or cooperative perception allows building a common enlarged environment model. With this it is possible to detect more objects than only with the individual board sensors. Furthermore, the algorithm will be tested in real vehicles. For this purpose, two trucks have been equipped for cooperative driving.
Author Contributions
Conceptualization, J.H.; methodology, J.H.; software, J.H.; investigation, J.H.; writing—original draft preparation, J.H.; writing—review and editing, J.H., J.C.M., F.D. and A.Z.; supervision, F.D. and A.Z.; project administration, F.D. and A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by MAN Truck & Bus SE and the IMAGinE (Intelligent Maneuver Automation—cooperative hazard avoidance in realtime) project. IMAGinE is founded by the German Federal Ministry for Economic Affairs and Energy (BMWi).
Data Availability Statement
The database is not currently open to the public for free. However, it may be obtained for academic purposes only by contacting the corresponding author.
Acknowledgments
The authors would like to thank all the editors and anonymous reviewers for their careful reading and insightful remarks.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bundesministerium für Umwelt, Naturschutz und Nukleare Sicherheit. Klimaschutz in Zahlen: Fakten, Trends und Impulse Deutscher Klimapolitik. Available online: https://www.bmu.de/fileadmin/Daten_BMU/Pools/Broschueren/klimaschutz_zahlen_2019_broschuere_bf.pdf (accessed on 17 February 2021).
- Bunz, M.; Mücke, H.-G. Klimawandel—physische und psychische Folgen. Bundesgesundh. Gesundh. Gesundh. 2017, 60, 632–639. [Google Scholar] [CrossRef] [PubMed]
- Masson-Delmotte, V. Global Warming of 1.5 °C: An IPCC Special Report on the Impacts of Global Warming of 1.5 °C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty. Available online: https://www.ipcc.ch/sr15/ (accessed on 17 February 2021).
- European Commission. The European Green Deal. Available online: https://eur-lex.europa.eu/legal-content/DE/TXT/?qid=1576150542719&uri=COM%3A2019%3A640%3AFIN (accessed on 15 September 2021).
- Nowak, G.; Maluck, J.; Stürmer, C.; Pasemann, J. The Era of Digitized Trucking: Transforming the Logistics Value Chain. Available online: https://www.strategyand.pwc.com/media/file/The-era-of-digitized-trucking.pdf (accessed on 23 June 2019).
- Esch, T.; Dahlhaus, U. Antrieb. In Nutzfahrzeugtechnik: Grundlagen, Systeme, Komponenten, 8; Überarbeitete und Erweiterte Auflage, Hoepke, E., Breuer, S., Eds.; Springer Vieweg: Wiesbaden, Germany, 2016; pp. 403–540. ISBN 978-3-658-09537-6. [Google Scholar]
- Walnum, H.J.; Simonsen, M. Does driving behavior matter? An analysis of fuel consumption data from heavy-duty trucks. Transp. Res. Part D Transp. Environ. 2015, 36, 107–120. [Google Scholar] [CrossRef]
- Zhou, M.; Jin, H.; Wang, W. A review of vehicle fuel consumption models to evaluate eco-driving and eco-routing. Transp. Res. Part D Transp. Environ. 2016, 49, 203–218. [Google Scholar] [CrossRef]
- International Council on Clean Transportation. Truck Eco-Driving Programs: Current Status in Latin America and International Best Practicies. Available online: https://theicct.org/sites/default/files/publications/eco-driving-latam-EN-apr2021.pdf (accessed on 13 September 2021).
- Huang, Y.; Ng, E.C.; Zhou, J.L.; Surawski, N.C.; Chan, E.F.; Hong, G. Eco-driving technology for sustainable road transport: A review. Renew. Sustain. Energy Rev. 2018, 93, 596–609. [Google Scholar] [CrossRef]
- Zavalko, A. Applying energy approach in the evaluation of eco-driving skill and eco-driving training of truck drivers. Transp. Res. Part D Transp. Environ. 2018, 62, 672–684. [Google Scholar] [CrossRef]
- MAN Truck & Bus, A.G. MAN EfficientCruise®—GPS-Gesteuerter Tempomat|MAN Lkw. Available online: https://www.truck.man.eu/de/de/man-welt/technologie-und-kompetenz/effizienzsysteme/gps-gestuetzter-tempomat/GPS-gestuetzter-Tempomat.html (accessed on 23 August 2017).
- Daimler, A.G. Predictive Powertrain Control—Schlauer Tempomat Spart Sprit. Available online: http://media.daimler.com/marsMediaSite/de/instance/ko/Predictive-Powertrain-Control---Schlauer-Tempomat-spart-Sprit.xhtml?oid=9917205 (accessed on 29 March 2018).
- Nordström, P.-E. Spectacular Fuel Savings—Scania Opticruise with Performance Modes. Available online: https://www.scania.com/group/en/spectacular-fuel-savings-scania-opticruise-with-performance-modes/ (accessed on 30 March 2018).
- Pudenz, K. Bei Steigung und Gefälle: I-See von Volvo Trucks Hilft Beim Kraftstoffsparen. Available online: https://www.springerprofessional.de/automobil---motoren/fahrerassistenz/bei-steigung-und-gefaelle-i-see-von-volvo-trucks-hilft-beim-kraf/6578176?searchResult=1.bei%20steigung%20gef%C3%A4lle%20i%20see%20von%20volvo%20trucks%20hilft&searchBackButton=true (accessed on 29 March 2018).
- Renault Trucks. Optivision. Available online: http://www.renault-trucks.de/aktuelles/optivision-k4z.html (accessed on 30 March 2018).
- DAF Trucks, N.V. Predictive Cruise Control. Available online: http://www.daftrucks.de/de-de/trucks/comfort-and-safety-systems-euro-6/predictive-cruise-control (accessed on 30 March 2018).
- Iveco Magirus, A.G. Der neue STRALIS: TCO2 Champion. Available online: https://www.iveco.com/austria/neufahrzeuge/pages/tco2-champion-stralis-truck-aspx.aspx (accessed on 3 March 2018).
- Sciarretta, A.; Vahidi, A. Energy-Efficient Driving of Road Vehicles; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-030-24126-1. [Google Scholar]
- Hellström, E. Look-Ahead Control of Heavy Vehicles; Department of Electrical Engineering, Linköping University: Linköping, Switzerland, 2010; ISBN 978-91-7393-389-6. [Google Scholar]
- Fafoutellis, P.; Mantouka, E.G.; Vlahogianni, E.I. Eco-Driving and Its Impacts on Fuel Efficiency: An Overview of Technologies and Data-Driven Methods. Sustainability 2021, 13, 226. [Google Scholar] [CrossRef]
- Saerens, B. Optimal Control Based Eco-Driving: Theoretical Approach and Practical Applications. Ph.D. Thesis, Katholieke Universiteit Leuven, Heverlee, Belgium, 2012. [Google Scholar]
- Roth, M.; Radke, T.; Lederer, M.; Gauterin, F.; Frey, M.; Steinbrecher, C.; Schröter, J.; Goslar, M. Porsche InnoDrive—An Innovative Approach for the Future of Driving. In Proceedings of the 20th Aachen Colloquium Automobile and Engine Technology, Aachen, Germany, 10 October–12 November 2011; pp. 1453–1467. [Google Scholar]
- BMW, A.G. Efficient Driving: Lower Consumption and Increase Range with BWM Efficient Dynamics. Available online: https://www.bmw.cc/en/topics/fascination-bmw/efficient-dynamics/energy-management.html (accessed on 5 August 2021).
- Audi, A.G. Driver Assistance Systems. Available online: https://www.audi-mediacenter.com/en/technology-lexicon-7180/driver-assistance-systems-7184 (accessed on 5 August 2021).
- Samaras, Z.; Ntziachristos, L.; Toffolo, S.; Magra, G.; Garcia-Castro, A.; Valdes, C.; Vock, C.; Maier, W. Quantification of the Effect of ITS on CO2 Emissions from Road Transportation. Transp. Res. Procedia 2016, 14, 3139–3148. [Google Scholar] [CrossRef] [Green Version]
- Alam, A. Fuel-Efficient Heavy-Duty Vehicle Platooning. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- Ulbrich, S.; Grossjohann, S.; Appelt, C.; Homeier, K.; Rieken, J.; Maurer, M. Structuring Cooperative Behavior Planning Implementations for Automated Driving. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems (ITSC 2015), Gran Canaria, Spain, 15–18 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2159–2165, ISBN 978-1-4673-6596-3. [Google Scholar]
- Eiermann, L.; Sawade, O.; Bunk, S.; Breuel, G.; Radusch, I. Cooperative automated lane merge with role-based negotiation. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 20–23 October 2020. [Google Scholar]
- Lehmann, B.; Gunther, H.-J.; Wolf, L. A Generic Approach towards Maneuver Coordination for Automated Vehicles. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3333–3339, ISBN 978-1-7281-0322-8. [Google Scholar]
- Llatser, I.; Michalke, T.; Dolgov, M.; Wildschuette, F.; Fuchs, H. Cooperative Automated Driving Use Cases for 5G V2X Communication. In Proceedings of the 2019 IEEE 2nd 5G World Forum (5GWF), Dresden, Germany, 30 September–2 October 2019; pp. 120–125. [Google Scholar]
- Tami, R.; Soualmi, B.; Doufene, A.; Ibanez, J.; Dauwels, J. Machine learning method to ensure robust decision-making of AVs. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1217–1222, ISBN 978-1-5386-7023-1. [Google Scholar]
- Hauenstein, J.; Diermeyer, F. Cooperative Longitudinal Control for Commercial Vehicles. In 9. Tagung Automatisiertes Fahren. 9; Tagung Automatisiertes Fahren: Munich, Germany, 2019. [Google Scholar]
- Sciarretta, A.; Nunzio, G.D.; Ojeda, L.L. Optimal Ecodriving Control: Energy-Efficient Driving of Road Vehicles as an Optimal Control Problem. IEEE Control Syst. 2015, 35, 71–90. [Google Scholar] [CrossRef] [Green Version]
- Radke, T. Energieoptimale Längsführung von Kraftfahrzeugen Durch Einsatz Vorausschauender Fahrstrategien; Karlsruher Institut für Technologie: Karlsruhe, Germany, 2013. [Google Scholar]
- Haken, K.-L. Grundlagen der Kraftfahrzeugtechnik, 2., Akualisierte und Erw. Aufl.; Hanser: München, Germany, 2011; ISBN 978-3-446-42849-2. [Google Scholar]
- Ayoubi, M.; Eilemann, A.; Mankau, H.; Pantow, E.; Repmann, C.; Seiffert, U.; Wawzyniak, M.; Wiebelt, A. Fahrzeugphysik. In Vieweg Handbuch Kraftfahrzeugtechnik; Pischinger, S., Seiffert, U., Eds.; Springer: Wiesbaden, Germany, 2016; pp. 57–130. ISBN 978-3-658-09527-7. [Google Scholar]
- Breuer, S.; Kopp, S. Fahrmechanik. In Nutzfahrzeugtechnik: Grundlagen, Systeme, Komponenten, 8; Überarbeitete und Erweiterte Auflage, Hoepke, E., Breuer, S., Eds.; Springer Vieweg: Wiesbaden, Germany, 2016; pp. 37–122. ISBN 978-3-658-09537-6. [Google Scholar]
- Grundgedanken, G. Straßenverkehrs-Ordnung (StVO). Available online: https://www.gesetze-im-internet.de/stvo_2013/ (accessed on 21 July 2018).
- Khalik, Z.; Padilla, G.P.; Romijn, T.; Donkers, M. Vehicle Energy Management with Ecodriving: A Sequential Quadratic Programming Approach with Dual Decomposition. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 4002–4007, ISBN 978-1-5386-5428-6. [Google Scholar]
- Bauer, K.-L. Echtzeit-Strategieplanung für Vorausschauendes Automatisiertes Fahren; Karlsruher Institut für Technologie: Karlsruhe, Germany, 2019. [Google Scholar]
- Huber, M. Verfahren zum Betreiben Eines Fahrzeuges, Insbesondere Eines Nutzfahrzeuges, Steuer- und/oder Auswerteeinrichtung, Fahrerassistenzsystem für ein Nutzfahrzeug Sowie Nutzfahrzeug. DE102008023135B4, 12 November 2009. [Google Scholar]
- Düring, M.; Pascheka, P. Cooperative decentralized decision making for conflict resolution among autonomous agents. In Proceedings of the 2014 IEEE International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Alberobello, Italy, 23–25 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 154–161, ISBN 978-1-4799-3020-3. [Google Scholar]
- Burger, C.; Orzechowski, P.F.; Tas, O.S.; Stiller, C. Rating cooperative driving: A scheme for behavior assessment. In Proceedings of the IEEE ITSC 2017, 20th International Conference on Intelligent Transportation Systems: Mielparque Yokohama in Yokohama, Kanagawa, Japan, 16–19 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6, ISBN 978-1-5386-1526-3. [Google Scholar]
- Okoso, A.; Otaki, K.; Nishi, T. Multi-Agent Path Finding with Priority for Cooperative Automated Valet Parking. In Proceedings of the IEEE ITSC 2019, 2019 22st International Conference on Intelligent Transportation Systems (ITSC) Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2135–2140, ISBN 978-1-5386-7023-1. [Google Scholar]
- Knies, C.; Hermansdorfer, L.; Diermeyer, F. Cooperative Maneuver Planning for Highway Traffic Scenarios based on Monte-Carlo Tree Search. AAET Automatisiertes und Vernetztes Fahren: Beiträge zum gleichnamigen 20. Braunschweiger Symposium am 6. und 7. Februar 2019, Stadthalle, Braunschweig, 1. Auflage; ITS mobility e.V: Braunschweig, Germany, 2019; pp. 10–25. ISBN 978-3-937655-46-8. [Google Scholar]
- Sawade, O.; Schulze, M.; Radusch, I. Robust Communication for Cooperative Driving Maneuvers. IEEE Intell. Transport. Syst. Mag. 2018, 10, 159–169. [Google Scholar] [CrossRef]
- Heß, D.; Lattarulo, R.; Pérez, J.; Schindler, J.; Hesse, T.; Köster, F. Fast Maneuver Planning for Cooperative Automated Vehicles. In Proceedings of the IEEE ITSC 2018, 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1625–1632, ISBN 978-1-7281-0322-8. [Google Scholar]
- Heß, D.; Lattarulo, R.; Perez, J.; Hesse, T.; Köster, F. Negotiation of Cooperative Maneuvers for Automated Vehicles: Experimental Results. In Proceedings of the IEEE ITSC 2019, 2019 22st International Conference on Intelligent Transportation Systems (ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1545–1551, ISBN 978-1-5386-7023-1. [Google Scholar]
- Festag, A. Standards for vehicular communication—From IEEE 802.11p to 5G. Elektrotech. Inftech. 2015, 132, 409–416. [Google Scholar] [CrossRef]
- Weber, R.; Misener, J.; Park, V. C-V2X—A Communication Technology for Cooperative, Connected and Automated Mobility. In Proceedings of the Mobile Communication Technologies and Applications; 24. ITG-Symposium, Osnabrueck, Germany, 15–16 May 2019; pp. 111–116, ISBN 3800749610. [Google Scholar]
- Molina-Masegosa, R.; Gozalvez, J.; Sepulcre, M. Comparison of IEEE 802.11p and LTE-V2X: An Evaluation with Periodic and Aperiodic Messages of Constant and Variable Size. IEEE Access. 2020, 8, 121526–121548. [Google Scholar] [CrossRef]
- Naik, G.; Choudhury, B.; Park, J.-M. IEEE 802.11bd & 5G NR V2X: Evolution of Radio Access Technologies for V2X Communications. IEEE Access 2019, 7, 70169–70184. [Google Scholar] [CrossRef]
- Almeida, T.T.; de Gomes, C.L.; Ortiz, F.M.; Junior, J.G.R.; Costa, L.H.M.K. IEEE 802.11p Performance Evaluation: Simulations vs. Real Experiments. In Proceedings of the IEEE ITSC 2018, 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3840–3845, ISBN 978-1-7281-0322-8. [Google Scholar]
- European Telecommunications Standards Institute. Intelligent Transport Systems (ITS); Decentralized Congestion Control Mechanisms for Intelligent Transport Systems Operating in the 5 GHz Range; Access Layer Part, V1.2.1, 2018 (ETSI TS 102 687). Available online: https://www.etsi.org/deliver/etsi_ts/102600_102699/102687/01.02.01_60/ts_102687v010201p.pdf (accessed on 30 July 2021).
- Eckhoff, D.; Sofra, N.; German, R. A performance study of cooperative awareness in ETSI ITS G5 and IEEE WAVE. In Proceedings of the 2013 10th Annual Conference on Wireless On-Demand Network Systems and Services (WONS 2013), Banff, AB, Canada, 18–20 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 196–200, ISBN 978-1-4799-0749-6. [Google Scholar]
- Molina-Masegosa, R.; Gozalvez, J. LTE-V for Sidelink 5G V2X Vehicular Communications: A New 5G Technology for Short-Range Vehicle-to-Everything Communications. IEEE Veh. Technol. Mag. 2017, 12, 30–39. [Google Scholar] [CrossRef]
- Dey, K.C.; Rayamajhi, A.; Chowdhury, M.; Bhavsar, P.; Martin, J. Vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communication in a heterogeneous wireless network—Performance evaluation. Transp. Res. Part C Emerg. Technol. 2016, 68, 168–184. [Google Scholar] [CrossRef] [Green Version]
- Ganesan, K.; Lohr, J.; Mallick, P.B.; Kunz, A.; Kuchibhotla, R. NR Sidelink Design Overview for Advanced V2X Service. IEEE Internet. Things M 2020, 3, 26–30. [Google Scholar] [CrossRef]
- Rudschies, W. C2X im VW Golf 8: Erster ADAC Test. Available online: https://www.adac.de/rund-ums-fahrzeug/tests/assistenzsysteme/c2x-im-vw-golf-8/ (accessed on 5 October 2020).
- European Telecommunications Standards Institute. Intelligent Transport Systems (ITS); Security; Security Header and Certificate Formats, V1.4.1, 2020 (ETSI TS 103 097). Available online: https://www.etsi.org/deliver/etsi_ts/103000_103099/103097/01.04.01_60/ts_103097v010401p.pdf (accessed on 24 November 2020).
- European Telecommunications Standards Institute. Intelligent Transport Systems (ITS); Vehicular Communications; Basic Set of Applications; Part 2: Specification of Cooperative Awareness Basic Service, V1.3.2, 2014 (ETSI EN 302 637-2). Available online: http://www.etsi.org (accessed on 16 September 2018).
- European Telecommunications Standards Institute. Intelligent Transport Systems (ITS); Vehicular Communications; Basic Set of Applications; Part 3: Specifications of Decentralized Environmental Notification Basic Service, V1.2.2, 2014 (ETSI EN 302 637-3). Available online: http://www.etsi.org (accessed on 16 September 2018).
- European Telecommunications Standards Institute. Work Programme: Details of ‘DTS/ITS-00184’ Work Item. Available online: https://portal.etsi.org/webapp/WorkProgram/Report_WorkItem.asp?WKI_ID=53496&curItemNr=1&totalNrItems=1&optDisplay=10&qSORT=HIGHVERSION&qETSI_ALL=&SearchPage=TRUE&qETSI_NUMBER=103+561&qINCLUDE_SUB_TB=True&qINCLUDE_MOVED_ON=&qSTOP_FLG=&qKEYWORD_BOOLEAN=&qCLUSTER_BOOLEAN=&qFREQUENCIES_BOOLEAN=&qSTOPPING_OUTDATED=&butSimple=Search&includeNonActiveTB=FALSE&includeSubProjectCode=&qREPORT_TYPE=SUMMARY (accessed on 4 November 2020).
- Google LLC. Protocol Buffers. Available online: https://developers.google.com/protocol-buffers (accessed on 5 August 2021).
- European Telecommunications Standards Institute. Intelligent Transport Systems (ITS); Users and Applications Requirements; Part 2: Applications and Facilities Layer Common Data Dictionary, V1.2.1, 2014 (ETSI TS 102 894-2). Available online: https://www.etsi.org/deliver/etsi_ts/102800_102899/10289402/01.02.01_60/ts_10289402v010201p.pdf (accessed on 30 July 2021).
- Schubert, R.; Richter, E.; Wanielik, G. Comparison and evaluation of advanced motion models for vehicle tracking. In Proceedings of the 2008 IEEE 11th International Conference on Information Fusion, Cologne, Germany, 30 January–3 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 730–735, ISBN 9783000248832. [Google Scholar]
- Hauenstein, J.; Gromer, J.; Mertens, J.C.; Diermeyer, F.; Kraus, S. Collective Perception: Impact on Fuel Consumption for Heavy Trucks. In Proceedings of the VEHITS 2021—7th International Conference on Vehicle Technology and Intelligent Transport Systems, Online Streaming, 28–30 April 2021; pp. 350–361, ISBN 978-989-758-513-5. [Google Scholar]
- Gonzalez, D.; Perez, J.; Milanes, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transport. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- IPG Automotive GmbH. CarMaker 9: Improved Versatility, Efficiency and Scalability. Available online: https://ipg-automotive.com/products-services/simulation-software/carmaker-release-90/ (accessed on 30 July 2021).
- Ahn, N.; Specka, F. Development and Test of Cooperative Driving Functions in a Virtual Environment. In Proceedings of the 38th FISITA World Congress, Virtual Congress, Prague, Czech Republic, 14–16 September 2021. [Google Scholar]
- Open Source Robotics Foundation, Inc. ROS Kinetic Kame. Available online: http://wiki.ros.org/kinetic (accessed on 15 July 2019).
- Fries, M.J. Maschinelle Optimierung der Antriebsauslegung zur Reduktion von CO2-Emissionen und Kosten im Nutzfahrzeug; Technische Universität München: München, Germany, 2019. [Google Scholar]
- Wolff, S. Mehrzieloptimierung von schweren Nutzfahrzeuggetrieben zur Verbesserung der Transporteffizienz und der TCO. In Semesterarbeit; Technische Universität München: München, Germany, 2016. [Google Scholar]
- Ellinghaus, D.; Steinbrecher, J. Lkw im Straßenverkehr: Eine Untersuchung über die Beziehungen Zwischen Lkw- und Pkw-Fahrern. Available online: https://www.bau.uni-siegen.de/subdomains/verkehrsplanung/publikationen/uniroyal/buch27.pdf (accessed on 6 August 2021).
- Koy, T.; Spacek, P. Geschwindigkeiten in Steigungen und Gefällen. Available online: http://archiv.ivt.ethz.ch/iv/research/v_in_steigungen/vss1998079.pdf (accessed on 6 August 2021).
- Der Straßenverkehrs-Zulassungs, V.Ä. Straßenverkehrs-Zulassungs-Ordnung (StVZO). Available online: https://www.gesetze-im-internet.de/stvzo_2012/ (accessed on 21 July 2017).
- Scania Deutschland GmbH. Scania gewinnt Europäischen Transport. Preis für Nachhaltigkeit 2018. Available online: https://www.scania.com/ (accessed on 30 March 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).