A New Analytical Design Methodology for a Three-Section Wideband Wilkinson Power Divider

Abstract

In this paper, a new analytical design technique for a three-section wideband Wilkinson power divider is presented. The proposed design technique utilizes the dual-frequency behavior of commensurate transmission lines for the even-mode analysis and contributes a set of completely new and rigorous design equations for the odd-mode analysis. Measurement of a fabricated prototype utilizing the proposed technique shows an excellent return-loss (>16 dB), insertion loss (<3.35 dB), and excellent isolation (>22.7 dB) over 104% fractional bandwidth extending beyond the minimum requirements.

1. Introduction

Power dividers are indispensable and ubiquitous components in radio-frequency (RF)/microwave systems [1,2]. For example, they are frequently used in antenna feeding networks, multistage and Doherty power amplifiers, mixers, and in RF/microwave measurements. Owing to their ability to provide decent matching and isolation in a simpler structure, the three-port Wilkinson power divider (WPD) has become one of the most widely used power divider types [3]. Due to their importance, there is an abundance of reports in the literature on the design and development of WPDs. Recent advancements in high-data-rate wireless communication systems have refueled significant interest in the development of power dividers with a major research focus on wideband, harmonic-suppressed, and multi-band topologies [2,4,5,6].

The conventional multi-section WPD was designed by using the theory reported in [3], which is a fully analytical technique applied only to a two-section WPD. For three or more sections, the reported technique is actually a table-based design and is therefore less computer-friendly. In addition, for this conventional design for a bandwidth, BW = $f_2-f_1$, the reflection profile appears as the one shown in Figure 1a, with $f_0$ being the mid-band frequency and $-|S_{11m}|$ is the minimum return-loss in dB. In this paper, a fully analytical design approach is presented for a three-section WPD that can be easily implemented using a computational tool, such as MATLAB/Octave. In addition, as depicted in Figure 1b, the proposed design methodology utilizes a dual-band design concept [7] to arrive at a wideband design. This dual-band design approach guarantees that the resonance frequencies are always located at $f_1$ and $f_2$, and therefore, the achieved BW $=f_H-f_L=(f_2-f_1)+2f_{ex}$, where $2f_{ex}$ is the extra bandwidth that provides a margin for process/component variations. This approach is the usual choice for a commercial development setup, where the minimum bandwidth requirement $f_2-f_1$ will always be met, and $2f_{ex}$ will allow flexibility to meet design goal requirements.

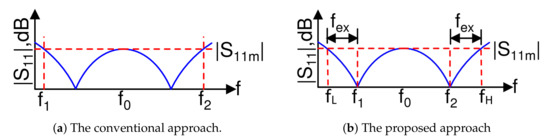
Figure 1. The conventional vs. the proposed design methodologies.

2. The Three-Section WPD and the Proposed Design Equations

The classic three-section 3 dB WPD is depicted in Figure 2. P1 refers to the input port, whereas P2 and P3 are the two output ports. Each port has a termination impedance of $Z_0$. Further, $Z_3$, $Z_2$, and $Z_1$ are the characteristic impedances of three transmission lines, while $\theta$ refers to their electrical length. Finally, $2R_3$, $2R_2$, and $2R_1$ are the isolation resistors connected as shown in the Figure. Since the structure is fully symmetric about a horizontal axis passing through P1, the widely known even-odd mode analysis technique is utilized to perform its analysis.

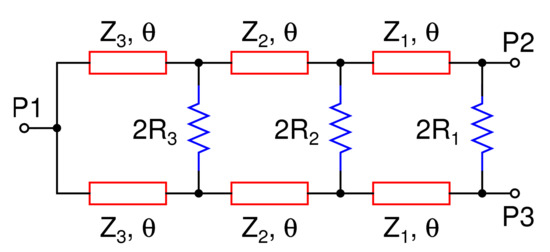
Figure 2. The three-section WPD.

2.1. Even-Mode Analysis

The even-mode equivalent circuit is shown in Figure 3a which has been obtained after bisecting the network of Figure 2. In the even mode excitation, two equal voltage generators with the same polarity are connected to P2 and P3, hence no current flows through the resistors, and thus the plane of symmetry becomes a virtual open. It is apparent that this equivalent circuit is in fact a special case of multi-section commensurate transmission lines discussed in [7]. To formulate the expression of $Z_2$ and $Z_3$, we can refer to similar equations as shown in [7], which were derived for the three-section transmission line. Now, by considering a source impedance of $2Z_0$ and a load impedance of $Z_0$, we can obtain the following:

$$Z_2=\frac{2Z_0{R}_{1}a{Z}_3+X_1(1+a^2)Z_3^2-\frac{R_{1}a}{2Z_0}{Z}_3^3}{p_1{Z}_3^2-2Z_0{R}_{1}a},$$

(1)

where $p_1=a+\frac{1}{a}(1-\frac{R_1}{2Z_0})$ and a = tan$\theta .$

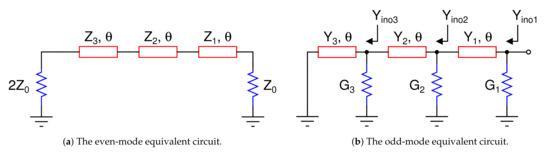
Figure 3. The even- and odd-mode equivalent circuits of the three-section WPD.

The value of $Z_3$ is obtained by solving the fourth-order equation in $Z_3$ given by:

$$A{Z}_3^4+B{Z}_3^3+C{Z}_3^2+D{Z}_3+E=0,$$

(2)

where

$$\begin{array}{cc}\hfill A& =\frac{R_1^2{a}^4}{2Z_0}-p_1(R_1-2Z_0)\frac{R_{1}a}{2Z_0}-R_1{p}_1^2{a}^2\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill B& =p_1{X}_1(R_1-2Z_0)(1+a^2)+2p_1^2{Z}_0{X}_{1}a-p_1{X}_1{R}_1{a}^2-2X_1{R}_1{a}^3(1+a^2)\hfill \end{array}$$

(4)

$$\begin{array}{c}C=2Z_0{X}_1^2{a}^2{(1+a^2)}^2-4Z_{0}X{R}_1^2{a}^4+4p_1{Z}_0{R}_1^2{a}^3+R_1^2(R_1-2Z_0)a^2+\hfill \\ \hfill 2p_1{Z}_0{X}_1^{2}a(1+a^2)+2p_1{R}_1{Z}_0(R_1-2Z_0)a\end{array}$$

(5)

$$\begin{array}{cc}\hfill D& =8Z_0^2{R}_1{X}_1{a}^3(1+a^2)+2Z_0{R}_1^2{X}_1{a}^3-2Z_0{R}_1{X}_1(R_1-2Z_0)a(1+a^2)-4p_1{Z}_0^2{R}_1{X}_1{a}^2\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill E& =8Z_0^3{R}_1^2{a}^4-4Z_0^2{R}_1{X}_1^2{a}^2(1+a^2)-4Z_0^2{R}_1^2(R_1-2Z_0)a^2-4Z_0^2{R}_1^3{a}^4.\hfill \end{array}$$

(7)

Out of the four roots of $Z_3$ obtained from (2) using MATLAB, only the positive real roots will be considered, which in turn will be used to find $Z_2$ from (1). The design consideration for choosing $Z_1$ is outlined in Section 3. Finally, as explained in [7], $\theta$ at $f_1$ for a dual-band design is chosen as:

$$\theta =\pi /(1+f_2/f_1).$$

(8)

2.2. Odd-Mode Analysis

The odd-mode equivalent circuit is shown in Figure 3b, which has been obtained after bisecting the network of Figure 2. In the odd-mode excitation, two equal voltage generators with opposite polarity are connected to P2 and P3; hence, the resistors’ mid-points are at zero potential, and the plane of symmetry becomes a virtual short. Due to the presence of shunt resistors, it is easier to work in terms of admittance, therefore, all the Z variables mentioned earlier have been replaced with $Y=1/Z$, for example, $Y_3=1/Z_3$. As shown in the Figure, $Y_{inoi}$, $i=\{1,2,3\}$ is the input admittance looking towards the left at the $i^{th}$ section, including the conductance $G_i=1/R_i$ at that node. Applying the formula of input admittance for a terminated transmission line section from [8], we have:

$$Y_{ino3}=G_3+j{B}_3$$

(9)

where $B_3=-Y_3/a$.

$$\begin{array}{cc}\hfill Y_{ino2}& =G_2+Y_2\frac{Y_{ino3}+j{Y}_{2}a}{Y_2+j{Y}_{ino3}a}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & =\frac{(G_2{Y}_2-G_2{B}_{3}a+Y_2{G}_3)+j(G_2{G}_{3}a+Y_2{B}_3+Y_2^{2}a)}{(Y_2-B_{3}a)+j{G}_{3}a}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill Y_{ino1}& =G_1+Y_1\frac{Y_{ino2}+j{Y}_{1}a}{Y_1+j{Y}_{ino2}a}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & =\frac{(G_1{Y}_1-Y_{in1}{Y}_1)+j{Y}_1^{2}a}{-Y_1+ja(Y_{ino1}-G_1)}\hfill \end{array}$$

(13)

By equating the right-hand sides of (11) and (13), we get:

$$\begin{array}{c}{G}_2(Y_1{Y}_2-Y_1{B}_{3}a)+G_3(Y_1{Y}_2-Y_1^2{a}^2)+(Y_0{a}^2-G_1{a}^2)G_2{G}_3+\hfill \\ \hfill G_1(Y_1{Y}_2-Y_1{B}_{3}a-Y_2{B}_{3}a-Y_2^2{a}^2)-Y_0{Y}_1{Y}_2+Y_1{Y}_0{B}_{3}a+Y_0{Y}_2{B}_{3}a+Y_0{Y}_2^2{a}^2=0\end{array}$$

(14)

$$\begin{array}{c}{G}_2(Y_0{B}_3{a}^2-Y_0{Y}_{2}a+G_1{Y}_{2}a-G_1{B}_3{a}^2)+G_3(G_1{Y}_{1}a-Y_0{Y}_{1}a-Y_0{Y}_{2}a+G_1{Y}_{2}a)+\hfill \\ \hfill G_2{G}_3{Y}_{1}a+Y_1^2{Y}_{2}a-Y_1^2{B}_3{a}^2+Y_1{Y}_2{B}_3+Y_1{Y}_2^{2}a=0\end{array}$$

(15)

We solve (14) and (15) simultaneously to find the expressions of $G_2$ and $G_3$ as follows:

$$G_2=\frac{-N\pm \sqrt{N^2-4MO}}{2M}$$

(16)

$$G_3=\frac{A_{1}S-P{D}_1}{(P{B}_1-A_{1}Q)+(P{C}_1-A_{1}R)G_2}$$

(17)

where,

$$\begin{array}{cc}\hfill M& =P(P{C}_1-A_{1}R)\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill N& =[P(P{B}_1-A_{1}Q)+R(A_{1}S-P{D}_1)+S(P{C}_1-A_{1}R)]\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill O& =Q(A_{1}S-P{D}_1)+(P{B}_1-A_{1}Q)S\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill P& =Y_0{B}_3{a}^2-Y_0{Y}_{2}a+G_1{Y}_{2}a-G_1{B}_3{a}^2\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill Q& =G_1{Y}_{1}a-Y_0{Y}_{1}a-Y_0{Y}_{2}a+G_1{Y}_{2}a\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill R& =Y_{1}a\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill S& =Y_1^2{Y}_{2}a-Y_1^2{B}_3{a}^2+Y_1{Y}_2{B}_3+Y_1{Y}_2^{2}a\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill A_1& =Y_1{Y}_2-Y_1{B}_{3}a\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill B_1& =Y_1{Y}_2-Y_1^2{a}^2\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill C_1& =Y_0{a}^2-G_1{a}^2\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill D_1& =G_1(Y_1{Y}_2-Y_1{B}_{3}a-Y_2{B}_{3}a-Y_2^2{a}^2)-Y_0{Y}_1{Y}_2+Y_1{Y}_0{B}_{3}a+Y_0{Y}_2{B}_{3}a+Y_0{Y}_2^2{a}^2\hfill \end{array}$$

(28)

Out of the two roots of $G_2$ obtained from (16), only the positive real roots will be considered, which will be used to find $G_3$ from (17). The criteria for choosing $G_1$ is outlined in the following section.

3. The Proposed Design Methodology

Based on the new design equations obtained in the previous section, the proposed analytical design methodology is as follows.

• $\theta$ is calculated from (8), where $f_1$ and $f_2$ refer to the band edge frequencies for the minimum bandwidth requirement.
• $Z_2$ and $Z_3$ are calculated as per the even-mode Equation (1) through (8). The value of $Z_1$ can be chosen as any value between $20\mathsf{\Omega }$ and $120\mathsf{\Omega }$ such that the resulting values of $Z_2$ and $Z_3$ also lie within this range for a practical microstrip implementation, and such that the mid-band $|S_{11e}|<|S_{11em}|$ as $S_{11}=S_{11e}$, where $S_{11e}$ is the even-mode $S_{11}$ and $S_{11em}$ is the desired $S_{11}$ value between the resonance frequencies $f_1$ and $f_2$ to ensure the bandwidth requirement. This calculation is conveniently done using a numerical tool, such as MATLAB/Octave, by using the following steps:

  i.

  Choose $Z_1$ such that $20\mathsf{\Omega }<Z_1<120\mathsf{\Omega }$.

  ii.

  Find $Z_2$ and $Z_3$ from (1) and (2) such that $20\mathsf{\Omega }<Z_2,Z_3<120\mathsf{\Omega }$.

  iii.

  From a set of $Z_1$, $Z_2$, and $Z_3$, verify $|S_{11e}|=0$ at $f_1$ and $f_2$.

  iv.

  Check whether $|S_{11e}|<|S_{11em}|$ from the selected set of $Z_1$, $Z_2$, and $Z_3$. If not, repeat from Step (1).

• The Y values for the odd-mode equations are found by inverting the Z values obtained in the previous step, for example, $Y_2=1/Z_2$.
• $G_2$ and $G_3$ are calculated using (16)–(28). While evaluating these expressions, $G_1$ is chosen as a free variable so as to satisfy $|S_{22}|<|S_{22m}|$ at $f_0$. It may be noted that $S_{22}=S_{33}=(S_{22e}+S_{22o})/2$, where $S_{22e}$ is the even-mode $S_{22}$, $S_{22o}$ is the odd-mode $S_{22}$, and $S_{22m}$ is the desired $S_{22}$ value between the resonance frequencies $f_1$ and $f_2$ to ensure the bandwidth requirement. $S_{22e}$ can be easily calculated using the parameters found in the previous step. The port isolation need not be separately analyzed as $S_{23}=(S_{22e}-S_{22o})/2$. It is apparent that while the expressions of $Z_2$, $Z_3$, $G_2$, and $G_3$ guarantees a dual-band profile, $Z_1$ and $G_1$ are chosen to define the midband behavior resulting in a wideband design. This completes the design process.

Utilizing the above-mentioned design methodology, the simulated results of a few design examples are shown in Figure 4, and the resulting numerical values of the important parameters are listed in Table 1. It is apparent from Figure 4 and Table 1 that the proposed WPD can be theoretically designed for a frequency ratio ($r=f_2/f_1$) in the range of 1–4.75 considering a 10 dB reference for the return loss and isolation parameters. However, since an additional bandwidth can be obtained in the proposed scheme, as explained earlier with the help of Figure 1b, the maximum frequency ratio ($r_f=f_H/f_L$) is equal to 12, which is equivalent to a $169\%$ fractional bandwidth.

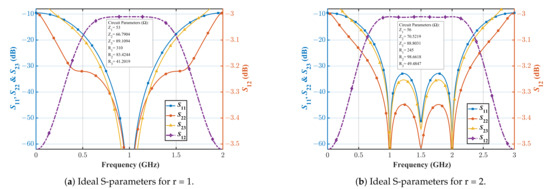
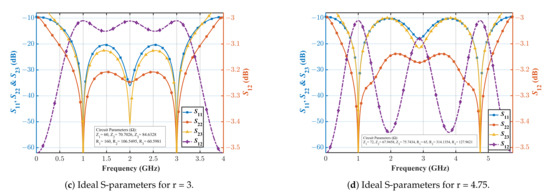
Figure 4. Ideal S-parameters with variation of the frequency ratio.

Table 1. Realizable frequency ratio.

Frequency Ratio, r	Band Edge Frequencies		Minimum Return Loss & Isolation Loss (dB)	Maximum Band Edge Frequencies		Maximum Frequency Ratio, ${\mathit{r}}_{\mathit{f}}$	% FBW
	${\mathit{f}}_1$ (GHz)	${\mathit{f}}_2$ (GHz)		${\mathit{f}}_{\mathit{L}}$ (GHz)	${\mathit{f}}_{\mathit{H}}$ (GHz)
4.75	1.00	4.75	10.00	0.44	5.31	12.07	169.39
4.00	1.00	4.00	10.00	0.41	4.59	11.20	167.20
			13.60	0.58	4.42	7.62	153.60
3.50	1.00	3.50	10.00	0.38	4.12	10.84	166.22
			16.60	0.69	3.81	5.52	138.65
3.00	1.00	3.00	10.00	0.35	3.65	10.43	165.00
			20.20	0.78	3.22	4.13	122.00
2.00	1.00	2.00	10.00	0.28	2.72	9.71	162.60
			30.00	0.88	2.12	2.41	82.70
1.50	1.00	1.50	10.00	0.24	2.26	9.42	161.61
			30.00	0.83	1.67	2.01	67.11

4. The Prototype and Measurement Results

The proposed analytical design methodology is used to calculate the design parameters of a three-section WPD with $f_1=$1 GHz, $f_2=2$ GHz, $|S_{11em}|<-20$ dB, and $|S_{22m}|<-20$ dB as an example. The calculated ideal design parameters using MATLAB are found to be as follows: $Z_3=94.8\mathsf{\Omega },Z_2=75.2\mathsf{\Omega },Z_1=59.8\mathsf{\Omega },R_3=18.2\mathsf{\Omega },R_2=66.5\mathsf{\Omega },$$R_1=114.8\mathsf{\Omega }$. Subsequently, these values are used to implement and optimize the WPD in microstrip technology using a Cadence AWR design environment. All these values are optimized to balance the effects of junction discontinuity and component parasitics. The optimized design parameters are listed in Figure 5. The Roger’s RO4003C substrate parameters are as follows: ${ϵ}_r=3.55$, substrate height = 1.524 mm, and copper cladding = 1 oz/1 oz. The fabricated prototype is depicted in Figure 5a, whereas the measurement setup is shown in Figure 5b.

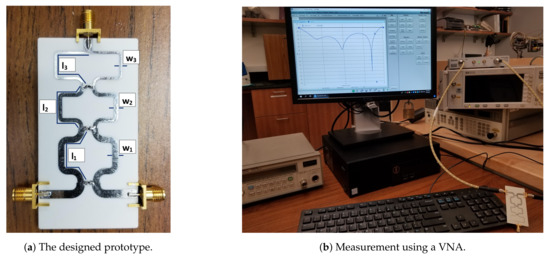
Figure 5. The designed prototype using the proposed analytical design methodology and its measurement using a Tektronix TT506A VNA. The VNA display on the computer screen shows the measured isolation. Dimension (mm): l₃ = 35, w₃ = 1, l₂ = 31.3, w₂ = 1.65, l₁ = 31.83, w₁ = 2.54. Resistors (Ω) optimized to the closest commercially available values: 2R₃ = 499, 2R₂ = 232, 2R₁ = 118.

The prototype is measured using a Tektronix TTR506A vector network analyzer (VNA) with a full two-port SOLT calibration. The electromagnetic simulation (EM) and the measured results in the range of 0.5–2.5 GHz are compared in Figure 6 and Figure 7.

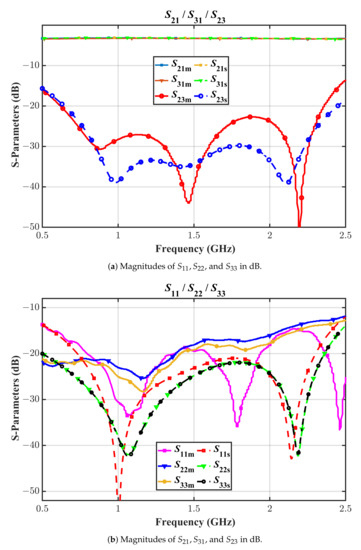
Figure 6. The simulated and the measured s-parameters in dBs. S_ijm stands for measured data and S_ijs stands for simulated data.

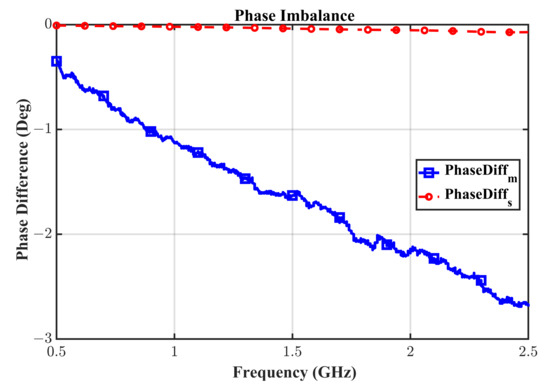
Figure 7. The simulated and measured phase difference in degrees.

It is apparent from Figure 6a,b that the designed prototype has excellent transmission parameters maintaining an insertion-loss of lesser than $3.35$ dB (not very far from the ideal 3 dB value) throughout the band from 0.635 GHz to 2 GHz. A clear frequency shift is evident for the return-loss parameter $-|S_{11}|$, and its value is still better than 16 dB in the band from 0.635 GHz to 2 GHz, thanks to the over-design guaranteed by the proposed technique. There is some mismatch between the simulated and measured EM values which normally occur in any high-frequency design. In our case, it was possibly due to the Panasonic isolation resistor non-idealities at high frequencies. Unfortunately, the model of these resistors is not available, so it is not possible to include their impact in the simulation. Another potential reason for the mismatch can be the fabrication errors originating from limited milling accuracy. Nevertheless, the measured results show an outstanding performance of the proposed WPD, as it meets all the goals that a practical WPD will be required to meet during their deployment in the field, and we therefore accepted this result. Specifically, the measured isolation is excellent throughout the band with a minimum value of 22.7 dB. The measured phase imbalance is decent, remaining within 3 degrees, as shown in Figure 7.

Although the main advantage of the proposed design is its novel, fully analytical, and computer-friendly design methodology, to highlight the novelty of this work further, a comparison table is presented in Table 2. From this table, the %FBW enhancement is also discernible as compared to other previous notable works.

Table 2. Comparison of the proposed design methodology and previous works.

Reference	Techniques/Topology	Center freq. (GHz)	Minimum Reflection/Isolation (dB)	FBW (%)	Operational Frequency Ratio, (${\mathit{f}}_{\mathit{H}}$/${\mathit{f}}_{\mathit{L}}$)
[2]	Single Section Optimized Isolation Network	1.00	20.00	68.00	2.03
[9]	Two stubs and three coupled-line sections	2.05	10.00	62.00	1.90
[10]	Complex isolation network	1.00	20.00	15.00	1.16
[11]	Transversal filters with series RLC network	2.84	15.00	90.00	2.64
[12]	Parallel coupled filters	2.02	10.00	53.70	1.73
[13]	Port-to-Port Isolation Structure	2.50	10.00	78.00	2.28
This Work	Three-section TL Lines & three resistors	1.32	16.00	103.60	3.15

5. Conclusions

A completely new analytical design methodology for a three-section WPD was presented in this paper. The methodology mixed the rigorous design equations with a dual-band design technique to arrive at a robust design that is more immune to process/component variations. The design methodology has been validated through several examples which dictate the capabilities of the proposed technique. Even though there was a slight mismatch between the simulated and measured results, they are still in good harmony, as all the design goals have been achieved with the fabricated prototype. In particular, the demonstration of a 104% fractional bandwidth ensuring a maximum 3.35 dB insertion loss and a minimum 16 dB of return loss and isolation is remarkable compared to other state-of-the-art techniques. Therefore, this novel approach has excellent potential to serve as a starting point for designing any ultra-wideband WPD in a very simple yet compact structure.