Stray Flux Multi-Sensor for Stator Fault Detection in Synchronous Machines
Abstract
:1. Introduction
2. Magnetic Field Measurement
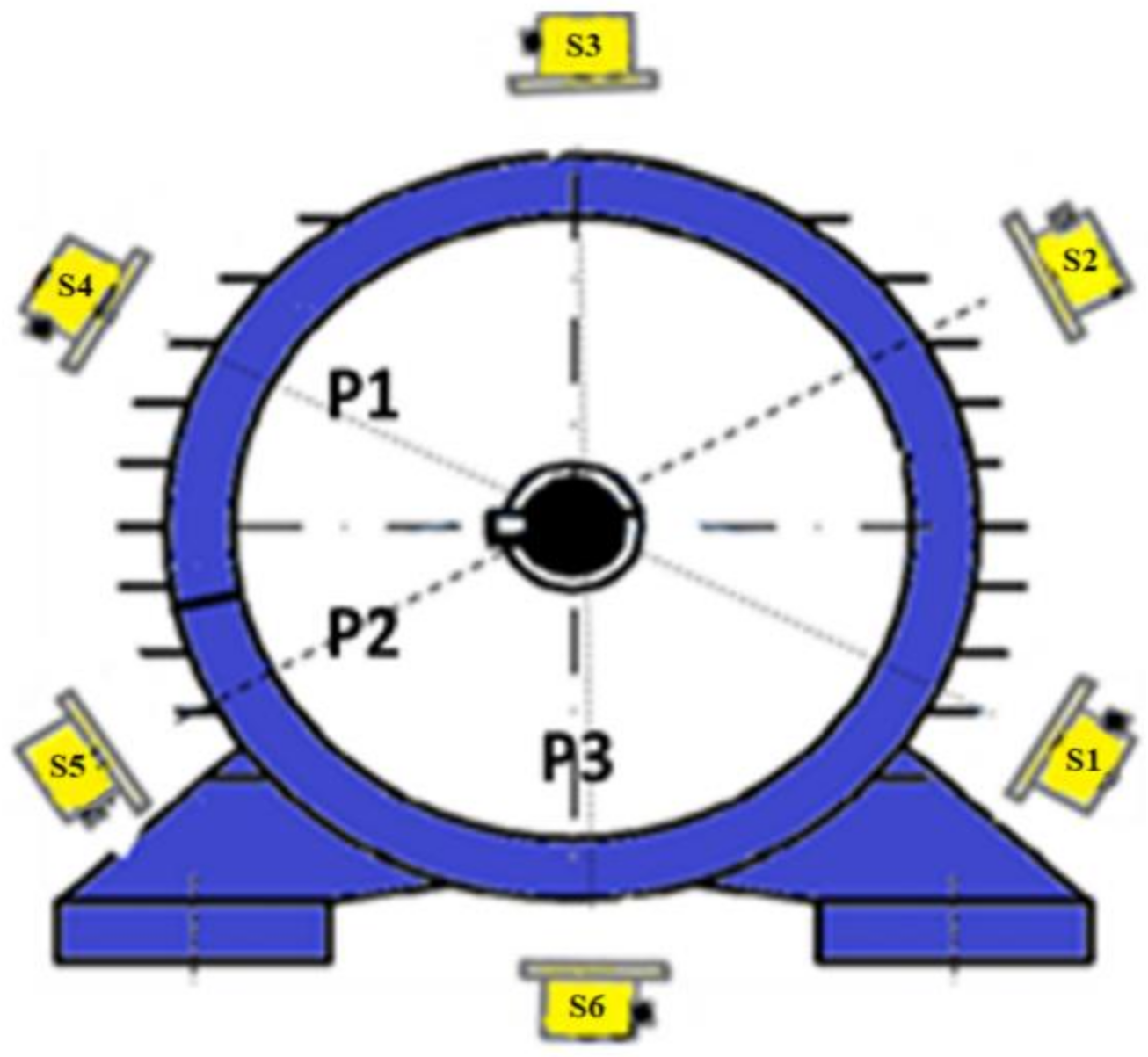
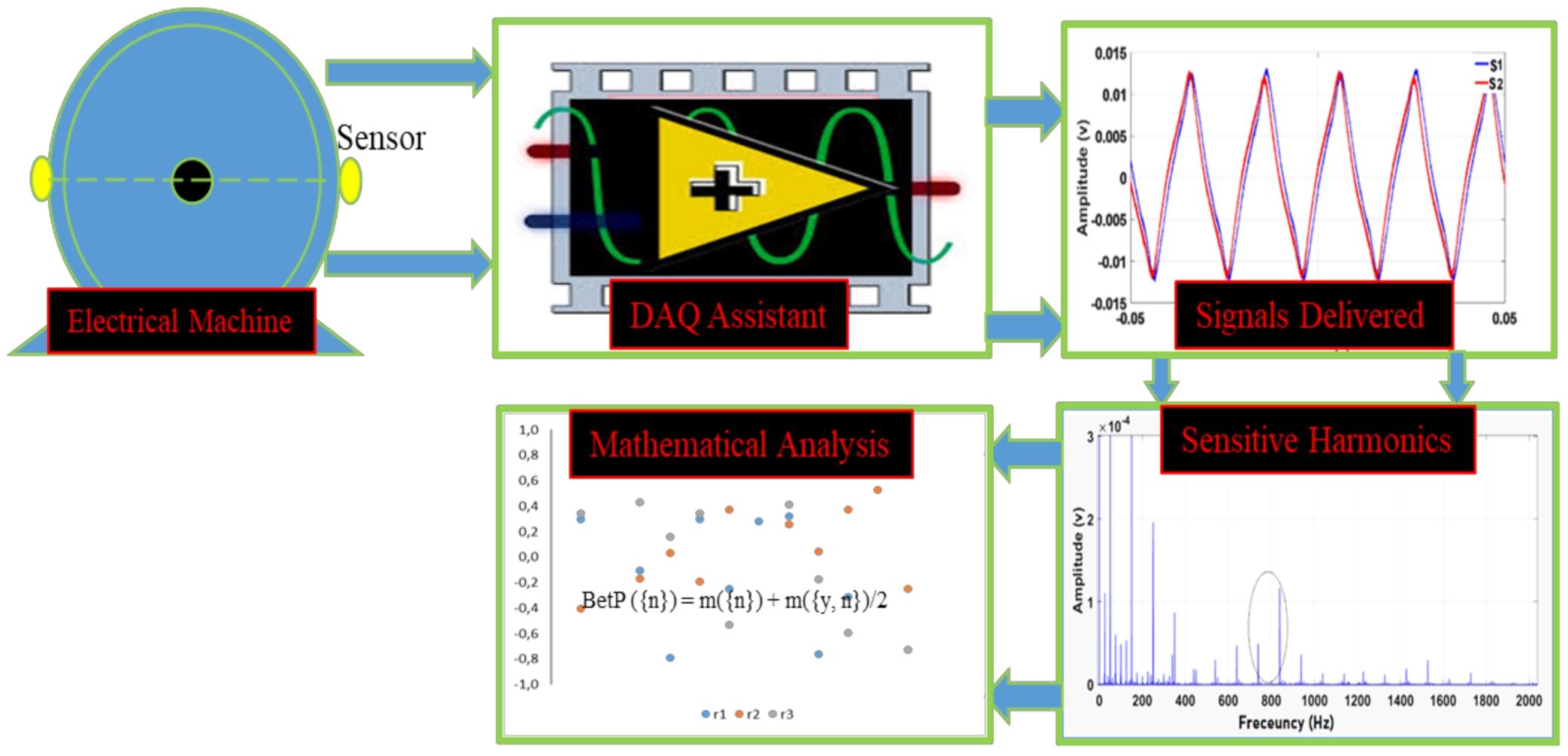
2.1. Principle of the Methodology
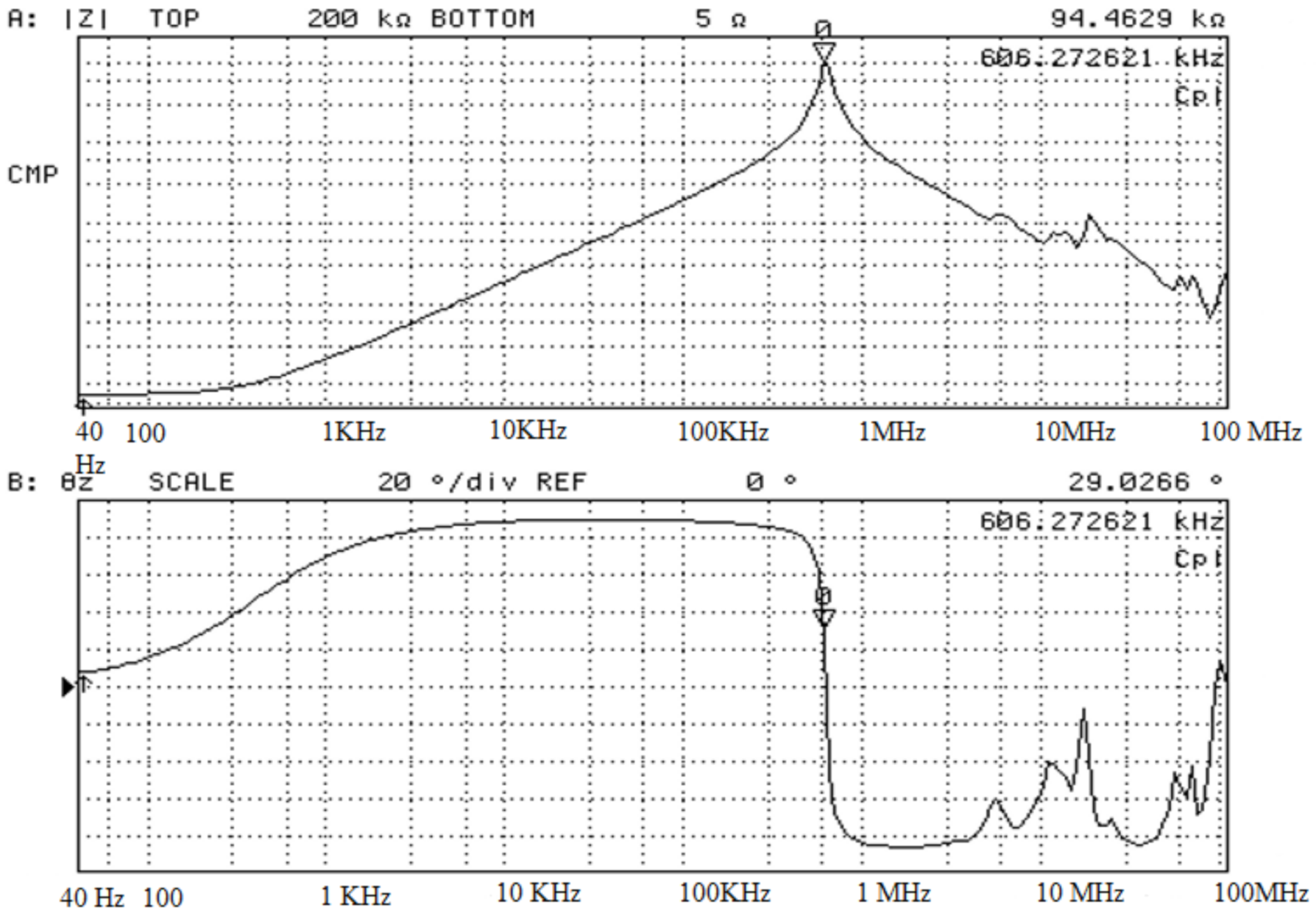
2.2. Sensor and Acquisition Characterization
3. Diagnostic Method
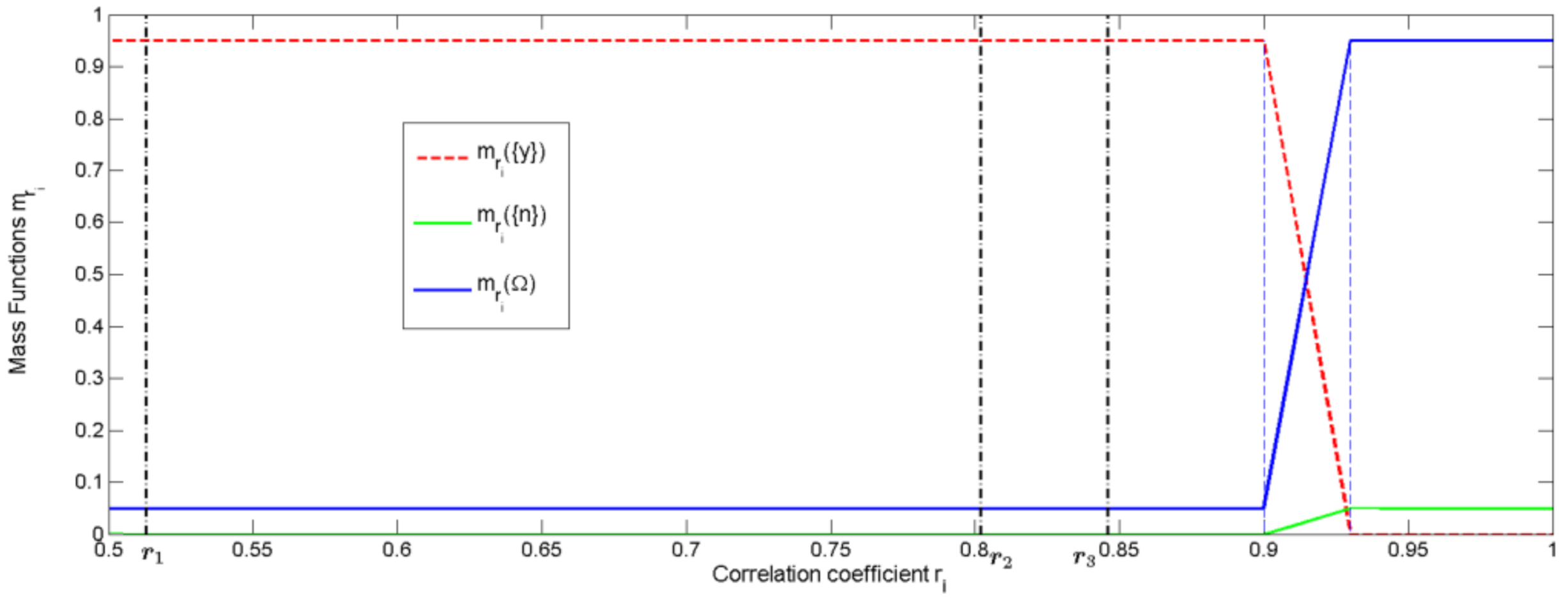
- If ri is close to 0, there is no linear relationship between and when k varies. Therefore, the amplitudes of the harmonics vary in a different way, which indicates the presence of an inter-turn short-circuit fault in the stator.
- If ri is close to −1, and vary strictly in opposite direction and linearly in case of load variation. In this case, there is also a stator fault in the machine.
- On the contrary, when ri is close to 1, and vary together linearly according to load variations. This means that the external magnetic field around the machine keeps a good symmetry. The machine may be in good condition, but this could be confirmed for other positions because the position of the sensors from the faulty turn has also an influence on the Pearson coefficient [20].
4. Experimental Results
4.1. Presentation of the Test Bench
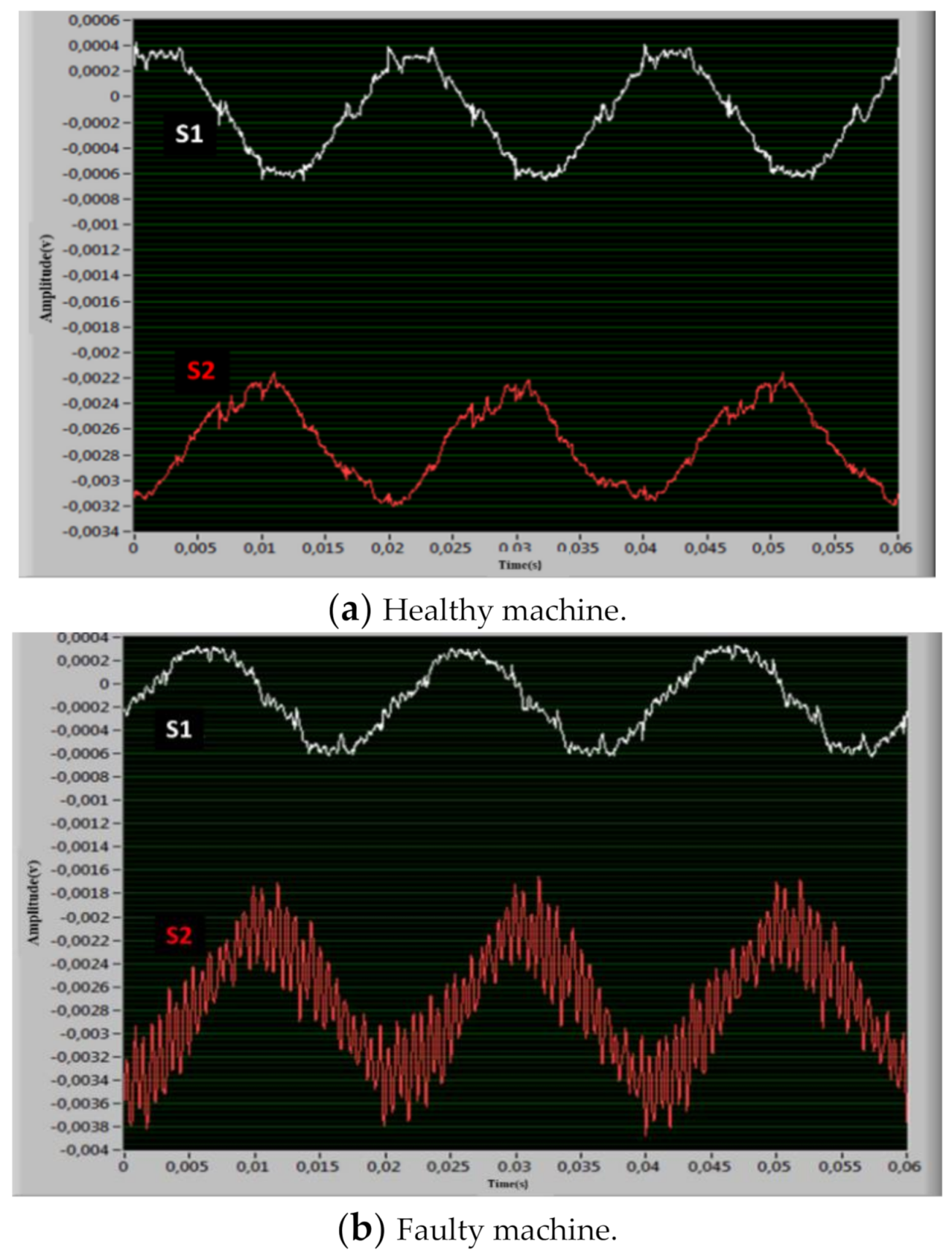
4.2. Measurement Analysis
- −
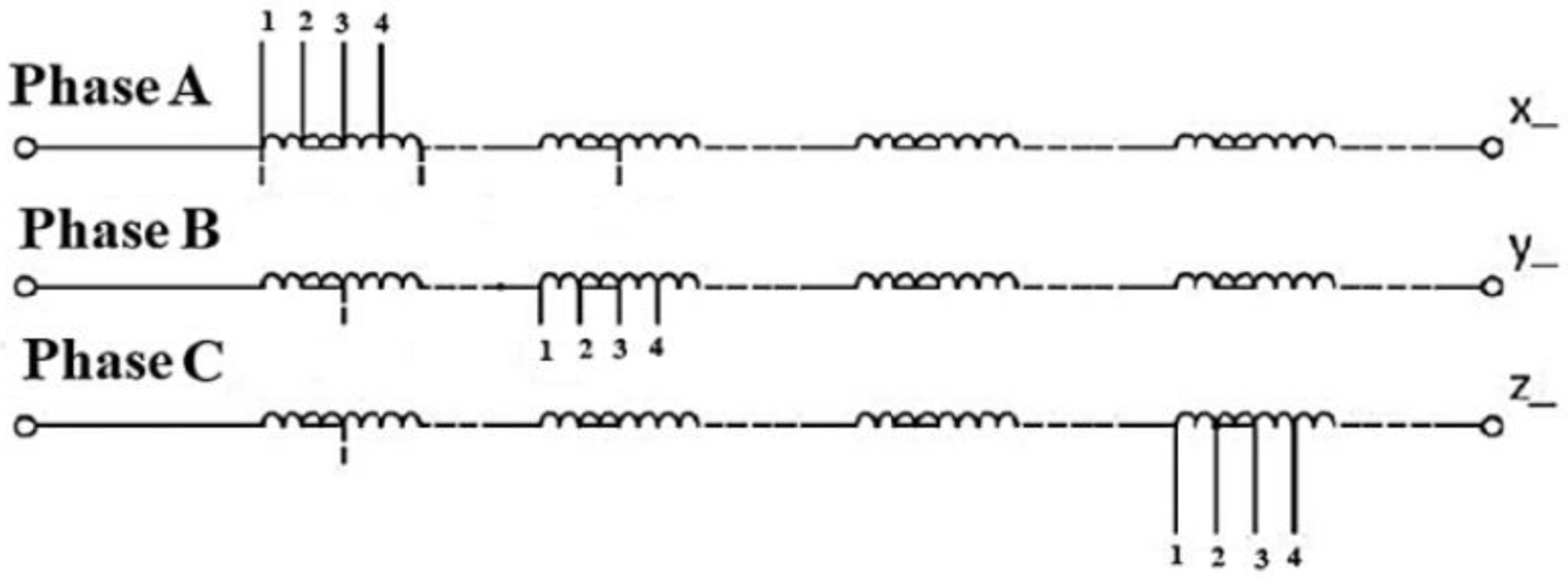
- Without short circuit;
- −
- Short circuits between 1–2, 2–3, and 1–4, for the three phases;
- −
- Isc = 3A for short circuits on coil ‘1–2’, one turn short circuit;
- −
- Isc = 9A for short circuits on coil ‘2–3’, three turns in short circuit;
- −
- Isc = 15A for short circuits on coil ‘1–4’, five turns in short circuit.
- (1)
- Example of calculation of belief functions, fusion, and probability of fault
- (2)
- Results obtained for global tests
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bramerdorfer, G.; Silber, S.; Weidenholzer, G.; Amrhein, W. Comprehensive cost optimization study of high-efficiency brushless synchronous machines. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 1126–1131. [Google Scholar]
- Petrov, A.; Plokhov, I.; Rassõlkin, A.; Vaimann, T.; Kallaste, A.; Belahcen, A. Adjusted electrical equivalent circuit model of induction motor with broken rotor bars and eccentricity faults. In Proceedings of the 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 58–64. [Google Scholar]
- Hamadache, M.; Lee, D.; Veluvolu, K.C. Rotor speed-based bearing fault diagnosis (rsb-bfd) under variable speed and constant load. IEEE Trans. Ind. Electron. 2015, 62, 6486–6495. [Google Scholar] [CrossRef]
- Fournier, E.; Picot, A.; Régnier, J.; Yamdeu, M.T.; Andréjak, J.-M.; Maussion, P. Current-based detection of mechanical unbalance in an induction machine using spectral kurtosis with reference. IEEE Trans. Ind. Electron. 2015, 62, 1879–1887. [Google Scholar] [CrossRef] [Green Version]
- Tong, Z.; Li, W.; Zhang, B.; Jiang, F.; Zhou, G. Online Bearing Fault Diagnosis Based on a Novel Multiple Data Streams Transmission Scheme. IEEE Access 2019, 7, 66644–66654. [Google Scholar] [CrossRef]
- Perisse, F.; Mercier, D.; Lefevre, E.; Roger, D. Robust diagnostics of stator insulation based on high frequency resonances measurements. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 1496–1502. [Google Scholar] [CrossRef]
- Torregrossa, D.; Khoobroo, A.; Fahimi, B. Prediction of acoustic noise and torque pulsation in pm synchronous machines with static eccentricity and partial demagnetization using field reconstruction method. IEEE Trans. Ind. Electron. 2012, 59, 934–944. [Google Scholar] [CrossRef]
- Thomson, W.T.; Fenger, M. Current signature analysis to detect induction motor faults. IEEE Ind. Appl. Mag. 2001, 7, 26–34. [Google Scholar] [CrossRef]
- Lim, W.Q.; Zhang, D.H.; Zhou, J.H.; Belgi, P.H.; Chan, H.L. Vibration-based fault Diagnosis platform for rotary machines. In Proceedings of the 36th Annual Conference on IEEE Industrial Electronics Society (IECON 2010), Glendale, AZ, USA, 7–10 November 2010; pp. 1404–1409. [Google Scholar]
- Younsi, M.O.; Lecointe, J.; Ninet, O.; Morganti, F.; Brudny, J.; Zidat, F. A noninvasive external flux based method for in-service induction motors torque estimation. IEEE Trans. Energy Convers. 2018, 34, 782–788. [Google Scholar] [CrossRef]
- Frosini, L.; Borin, A.; Girometta, L.; Venchi, G. A novel approach to detect short circuits in low voltage induction motor by stray flux measurement. In Proceedings of the 20th International Conference on Electrical Machines (ICEM ’12), Marseille, France, 2–5 September 2012; pp. 1536–1542. [Google Scholar]
- Sun, L.; Wang, X.; Xu, B. A detection method for broken rotor bar fault in induction motors based on SVD and SFOC-ESPRIT. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2015, 30, 147–156. [Google Scholar]
- Gritli, Y.; Rossi, C.; Casadei, D.; Filippetti, F. Square current spacevector signature analysis for rotor fault detection in wound-rotor induction machine. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 2894–2898. [Google Scholar]
- Briz, F.; Degner, M.W.; Garcia, P.; Diez, A.B. High-frequency carrier-signal voltage selection for stator winding fault diagnosis in inverter-fed ac machines. IEEE Trans. Ind. Electron. 2008, 55, 4181–4190. [Google Scholar] [CrossRef]
- Chernyavska, I.; Vítek, O. Analysis of air-gap eccentricity in inverter fed induction motor by means of motor current signature analysis and stray flux of motor. In Proceedings of the IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 72–76. [Google Scholar]
- Bessous, N.; Pusca, R.; Romary, R.; Saba, S. Rolling Bearing Failure Detection in Induction Motors using Stator Current, Vibration and Stray Flux Analysis Techniques. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Marina Bay Sands Expo, Singapore, 18–21 October 2020; pp. 1088–1095. [Google Scholar]
- Irhoumah, M.; Pusca, R.; Lefevre, E.; Mercier, D.; Rromary, R. Evaluation of the voltage supply unbalance and detection of the short-circuit faults in induction machine through the neighboring magnetic field. In Proceedings of the 2021 International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 27–29 May 2021. [Google Scholar]
- Pusca, R.; Romary, R.; Ceban, A.; Brudny, J.F. An online universal diagnosis procedure using two external flux sensors applied to the AC electrical rotating machines. Sensors 2010, 10, 10448–10466. [Google Scholar] [CrossRef] [PubMed]
- Irhoumah, M.; Pusca, R.; Lefevre, E.; Mercier, D.; Romary, R.; Demian, C. Information Fusion with Belief Functions for Detection of Interturn Short-Circuit Faults in Electrical Machines Using External Flux Sensors. IEEE Trans. Ind. Electron. 2018, 65, 2642–2652. [Google Scholar] [CrossRef]
- Irhoumah, M.; Pusca, R.; Lefevre, E.; Mercier, D.; Romary, R. Detection of the Stator Winding Inter-Turn Faults in Asynchronous and Synchronous Machines Through the Correlation Between Harmonics of the Voltage of Two Magnetic Flux Sensors. IEEE Trans. Ind. Appl. 2019, 55, 2682–2689. [Google Scholar] [CrossRef]
- Irhoumah, M.; Pusca, R.; Lefèvre, E.; Mercier, D.; Romary, R. Information fusion with Correlation Coefficient for detecting inter-turn short circuit faults in asynchronous machines. In Proceedings of the 2019 IEEE 12th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Toulouse, France, 27–30 August 2019; pp. 232–237. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Smets, P. Decision making in the TBM: The necessity of the pignistic transformation. Int. J. Approx. Reason. 2005, 38, 133–147. [Google Scholar] [CrossRef] [Green Version]
- Denoeux, T. Decision-making with belief functions: A review. Int. J. Approx. Reason. 2019, 109, 87–110. [Google Scholar] [CrossRef] [Green Version]


| P1 | P2 | P3 | ||||
|---|---|---|---|---|---|---|
| loads | S1 (μV) | S4(μV) | S2(μV) | S5 (μV) | S3 (μV) | S6 (μV) |
| no load | 5.06 | 1.52 | 5.04 | 3.08 | 4.14 | 2.93 |
| load 1 | 7.06 | 3.18 | 6.89 | 5.10 | 5.80 | 4.77 |
| load 2 | 8.39 | 3.56 | 8.11 | 5.95 | 6.85 | 4.84 |
| load 3 | 9.17 | 3.61 | 8.97 | 6.48 | 7.35 | 5.08 |
| load 4 | 9.69 | 4.14 | 9.44 | 7.18 | 7.96 | 5.30 |
| P1 | P2 | P3 | ||||
|---|---|---|---|---|---|---|
| loads | S1 (μV) | S4 (μV) | S2 (μV) | S5 (μV) | S3 (μV) | S6 (μV) |
| no load | 9.52 | 13.80 | 4.77 | 5.87 | 6.75 | 4.18 |
| load 1 | 9.32 | 16.09 | 5.55 | 6.00 | 6.11 | 5.08 |
| load 2 | 11.45 | 15.75 | 6.84 | 8.50 | 7.98 | 5.49 |
| load 3 | 12.88 | 16.04 | 7.63 | 9.65 | 9.31 | 5.16 |
| load 4 | 12.97 | 16.11 | 7.17 | 9.45 | 9.38 | 4.54 |
| P1 | P2 | P3 | |
|---|---|---|---|
| No fault | 0.964 | 0.993 | 0.937 |
| A–3A | 0.542 | 0.973 | 0.129 |
| B–3A | 0.802 | 0.846 | 0.513 |
| C–3A | −0.692 | 0.960 | 0.821 |
| A–6A | 0.984 | 0.992 | −0.032 |
| A–15A | 0.989 | 0.952 | 0.960 |
| B–15A | 0.986 | 0.948 | −0.649 |
| C–15A | 0.996 | 0.972 | 0.015 |
| A–18A | 0.886 | 0.997 | 0.988 |
| In Case of the Faulty Machine B–3A | ||
|---|---|---|
| Position P1 () | Position P2 () | Position P3 () |
| Step 1 | |||
| ) | |||
0.95 × 0.95 = 0.9025 | 0.95 × 0.05 = 0.0475 | ||
0.05 × 0.95 = 0.0475 | 0.05 × 0.05 = 0.0025 | ||
| , | |||
| Step 2 | |||
0.9975 × 0.95 = 0.9476 | 0.9975 × 0.05 = 0.0499 | ||
0.0025 × 0.95 = 0.0024 | 0.0025 × 0.05 = 0.0001 | ||
| , | |||
| P1 | P2 | P3 | Fusion of the Three Positions |
|---|---|---|---|
| 55.56% (4) | 22.22% (7) | 77.78% (2) | 88.89% (1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irhoumah, M.; Pusca, R.; Lefèvre, E.; Mercier, D.; Romary, R. Stray Flux Multi-Sensor for Stator Fault Detection in Synchronous Machines. Electronics 2021, 10, 2313. https://doi.org/10.3390/electronics10182313
Irhoumah M, Pusca R, Lefèvre E, Mercier D, Romary R. Stray Flux Multi-Sensor for Stator Fault Detection in Synchronous Machines. Electronics. 2021; 10(18):2313. https://doi.org/10.3390/electronics10182313
Chicago/Turabian StyleIrhoumah, Miftah, Remus Pusca, Eric Lefèvre, David Mercier, and Raphael Romary. 2021. "Stray Flux Multi-Sensor for Stator Fault Detection in Synchronous Machines" Electronics 10, no. 18: 2313. https://doi.org/10.3390/electronics10182313
APA StyleIrhoumah, M., Pusca, R., Lefèvre, E., Mercier, D., & Romary, R. (2021). Stray Flux Multi-Sensor for Stator Fault Detection in Synchronous Machines. Electronics, 10(18), 2313. https://doi.org/10.3390/electronics10182313






