Learning-Rate Annealing Methods for Deep Neural Networks
Abstract
:1. Introduction
2. Backgrounds
- Progress and application of DNNs: Deep neural networks have made significant progress in a variety of applications for understanding visual scenes [6,7,8], sound information [9,10,11,12], physical motions [13,14,15,16], graph-based data representation [17], and other decision processes [18,19,20,21]. Their optimization algorithms related to our work are reviewed in the following.
- Variance reduction: The variance of stochastic gradients is detrimental to SGD, motivating variance reduction techniques [22,23,24,25,26,27,28] that aim to reduce the variance incurred due to their stochastic process of estimation, and improve the convergence rate mainly for convex optimization, while some are extended to non-convex problems [29,30,31]. One of the most practical algorithms for better convergence rates includes momentum [32], modified momentum for accelerated gradient [33], and stochastic estimation of accelerated gradient descent [34]. These algorithms are more focused on the efficiency in convergence than the generalization of models for accuracy. We focus on the baseline SGD with learning rate annealing.
- Energy landscape: The understanding of energy surface geometry is significant in deep optimization of highly complex non-convex problems. It is preferred to drive a solution toward a plateau in order to yield better generalization [35,36,37]. Entropy-SGD [36] is an optimization algorithm biased toward such a wide flat local minimum. In our approach, we do not attempt to explicitly measure geometric properties of the loss landscape with extra computational cost, but instead implicitly consider the variance determined by the learning rate annealing.Batch size selection: There is a trade-off between the computational efficiency and the stability of gradient estimation leading to the selection of their compromise with, generally, a constant, while the learning rate is scheduled to decrease for convergence. The generalization effect of stochastic gradient methods has been analyzed with constant batch size [38,39]. On the other hand, increasing the batch size per iteration with a fixed learning rate has been proposed in [40], where the equivalence of increasing the batch size to learning rate decay is demonstrated. A variety of varying batch size algorithms have been proposed by variance of gradients [41,42,43,44]. However, the batch size is usually fixed in practice, since increasing the batch size results in a huge computational cost.
3. Learning-Rate Annealing Methods
3.1. Preliminary
3.2. Related Works
3.2.1. Adaptive Learning Rate
3.2.2. Learning-Rate Decay
3.2.3. Learning-Rate Warmup
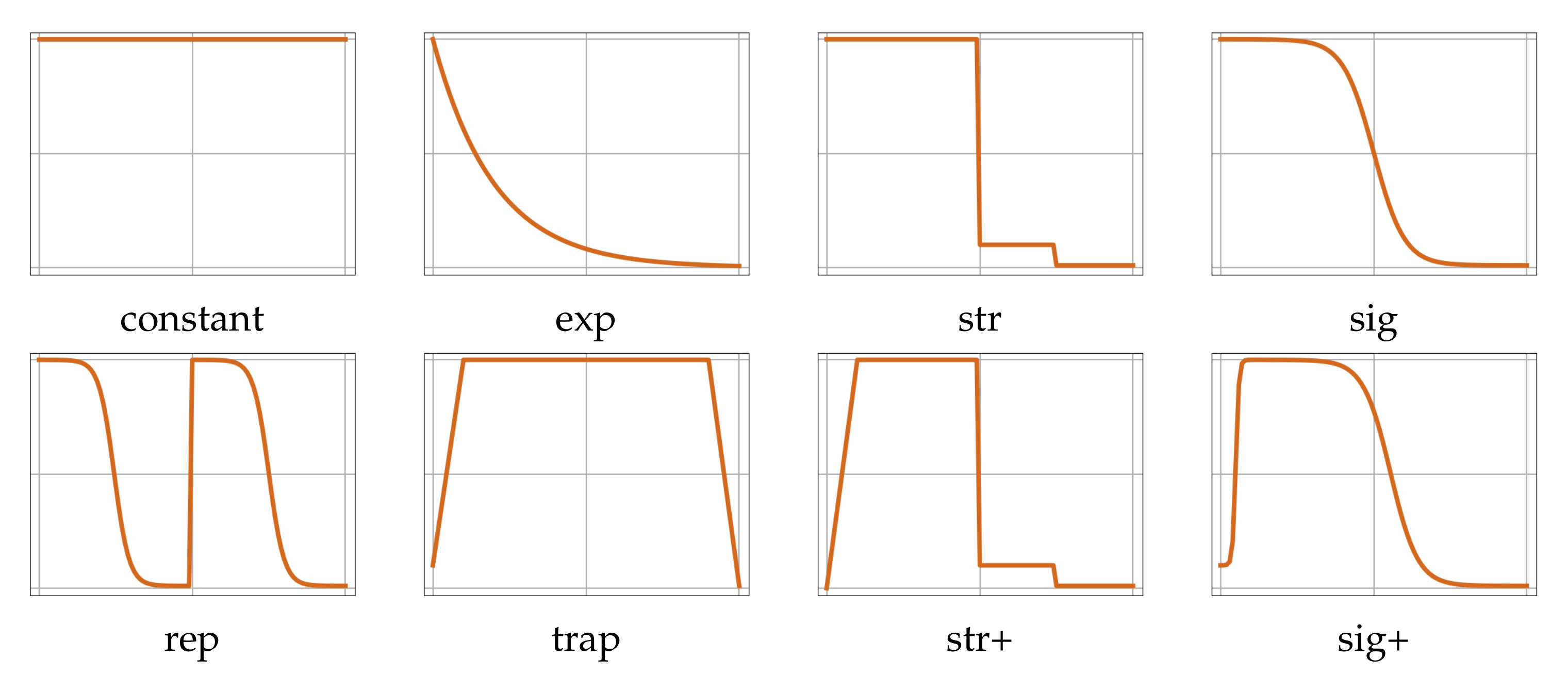
3.3. Proposed Sigmoid Decay with Warmup
4. Experimental Results and Discussion
4.1. Experimental Set-Up
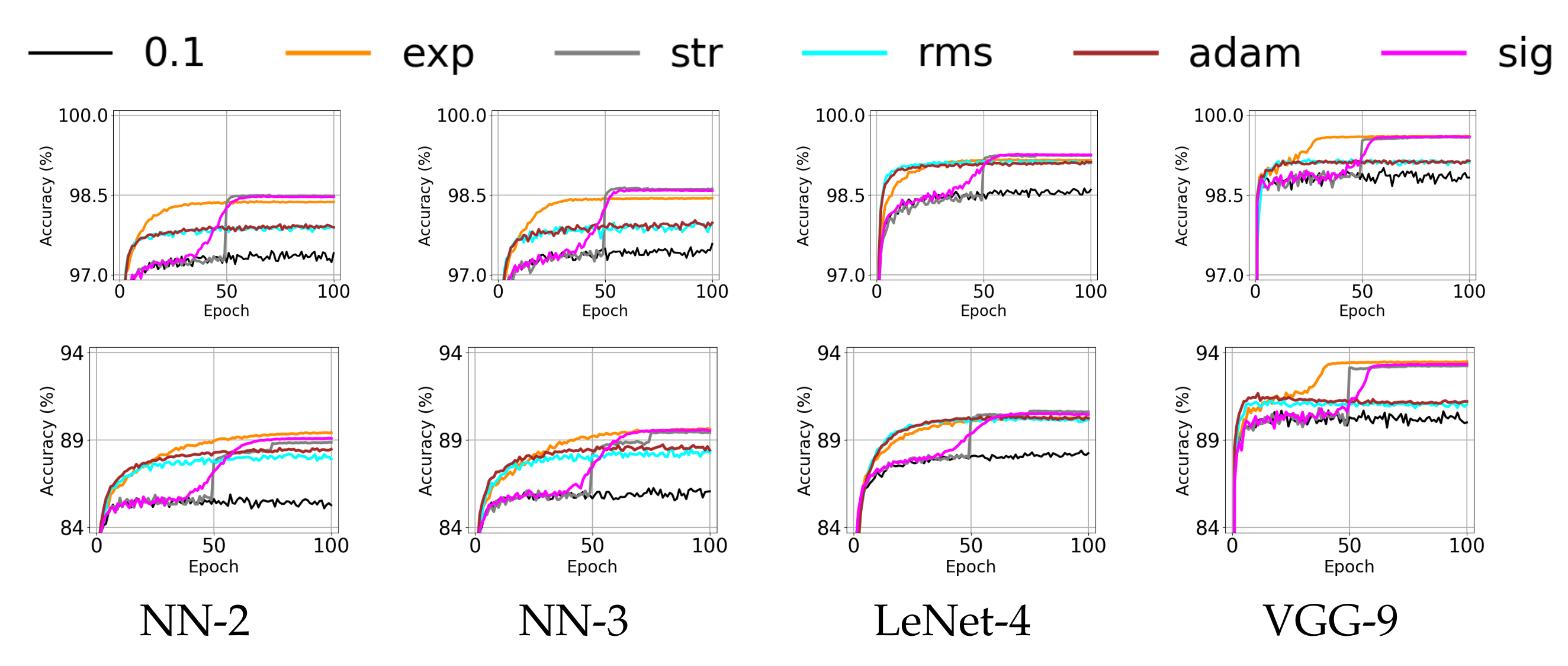
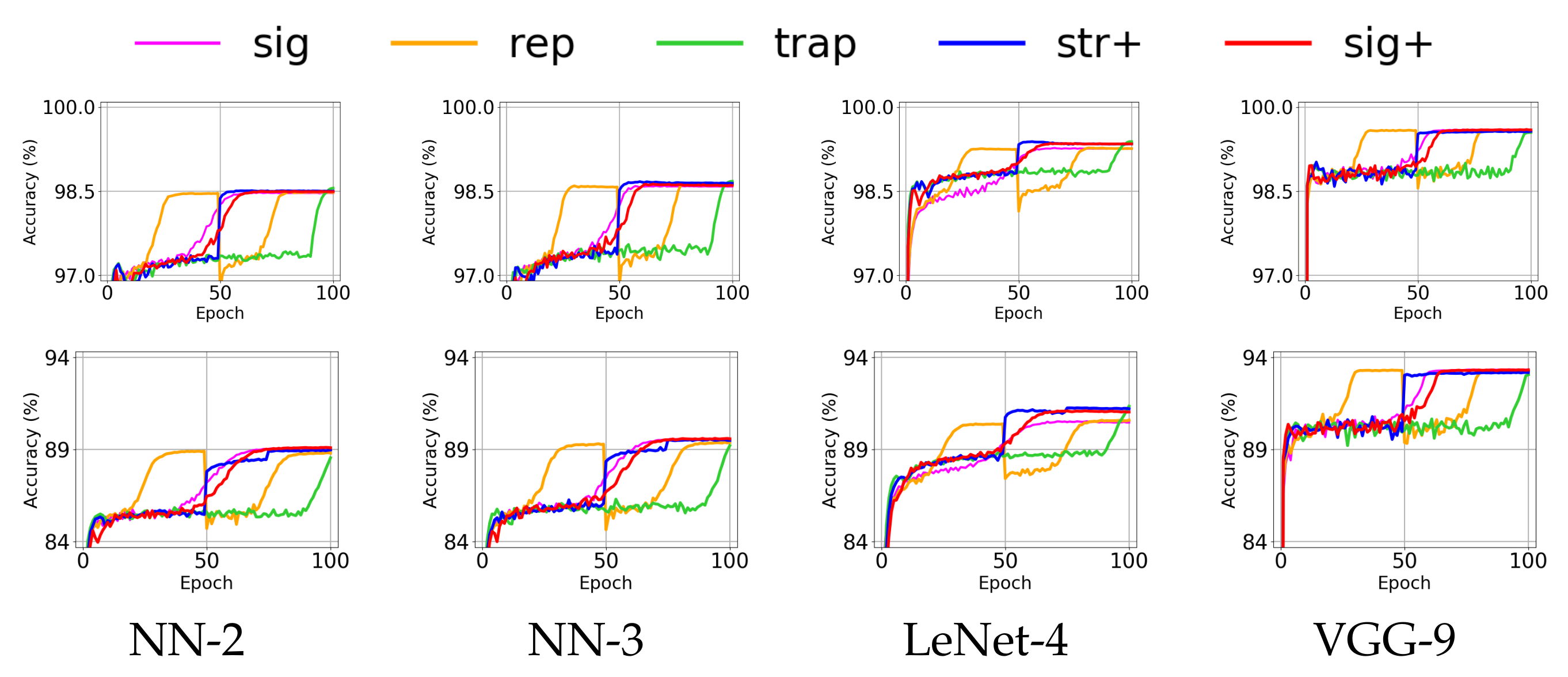
4.2. Effect of Annealing Methods for Shallow Networks
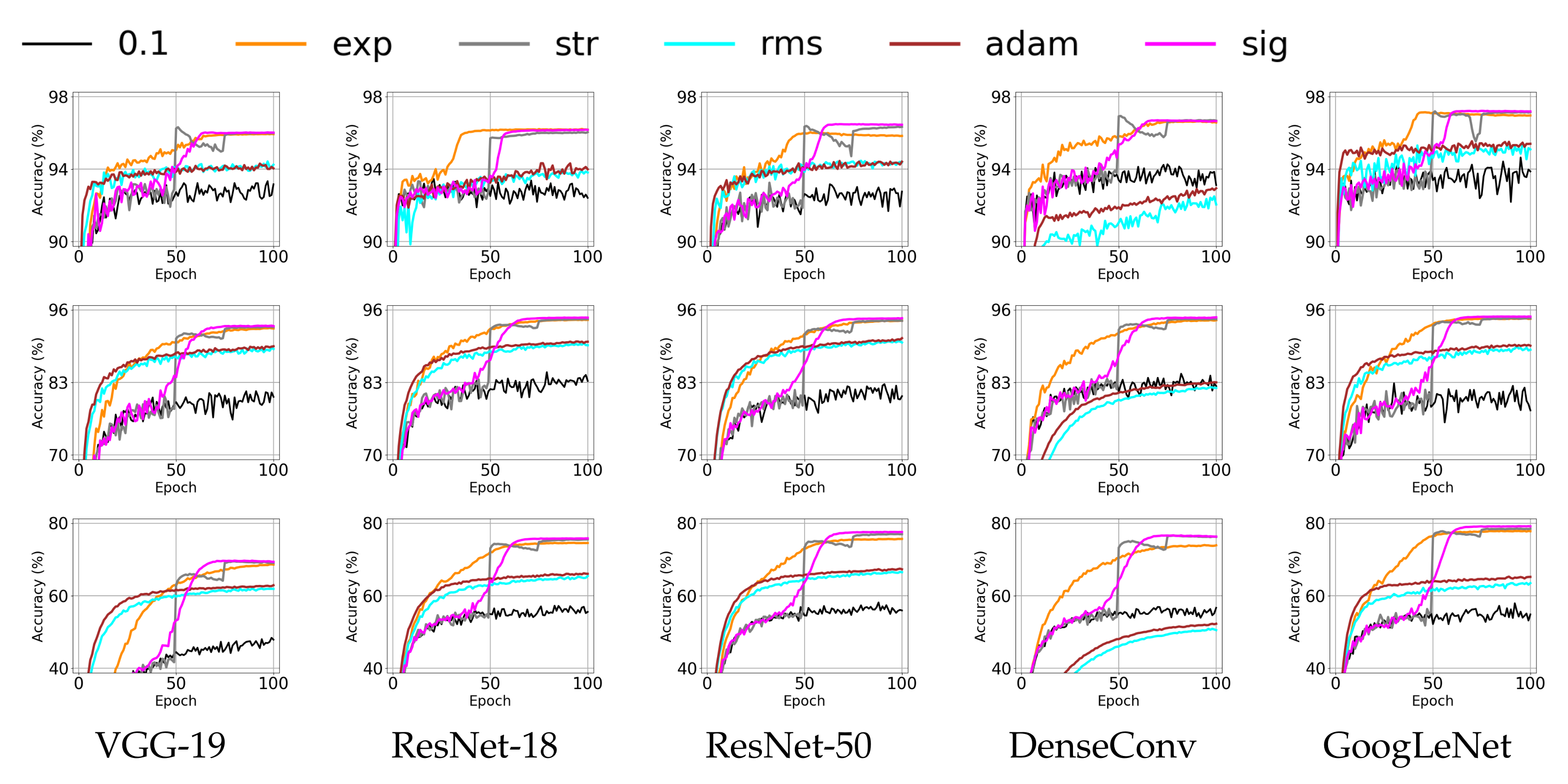
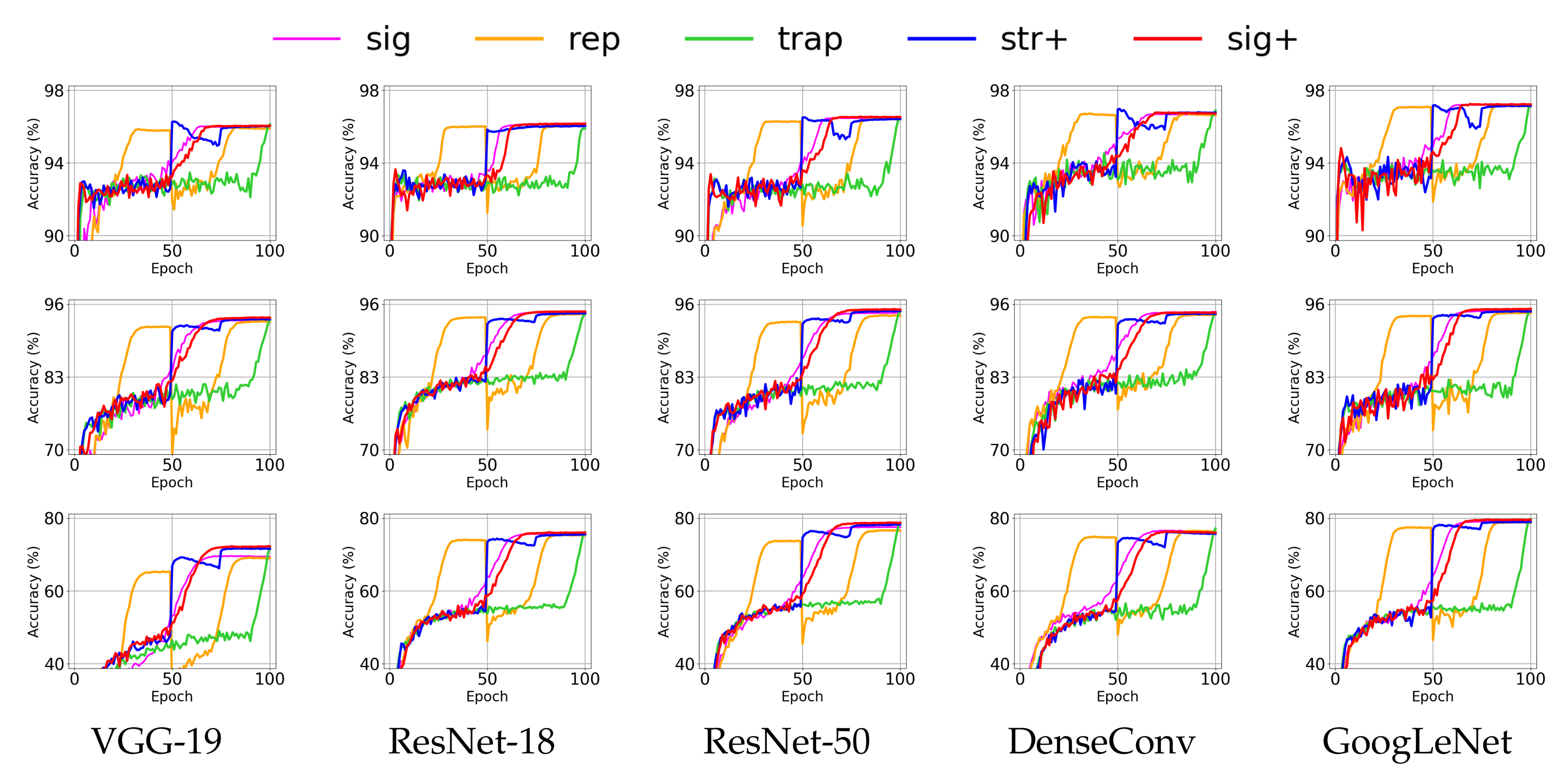
4.3. Effect of Annealing Methods for Deep Neural Networks
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Cogn. Model. 1988, 5, 1. [Google Scholar] [CrossRef]
- Zhang, T. Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 116. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of COMPSTAT’2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Bottou, L.; Curtis, F.E.; Nocedal, J. Optimization methods for large-scale machine learning. SIAM Rev. 2018, 60, 223–311. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015; pp. 3431–3440. [Google Scholar]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep Convolutional Neural Network for Inverse Problems in Imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, J.; Gu, S.; Zhang, L. Learning a deep single image contrast enhancer from multi-exposure images. IEEE Trans. Image Process. 2018, 27, 2049–2062. [Google Scholar] [CrossRef]
- Aytar, Y.; Vondrick, C.; Torralba, A. Soundnet: Learning sound representations from unlabeled video. Adv. Neural Inf. Process. Syst. 2016, 29, 892–900. [Google Scholar]
- Li, J.; Dai, W.P.; Metze, F.; Qu, S.; Das, S. A comparison of Deep Learning methods for environmental sound detection. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 126–130. [Google Scholar]
- Mesaros, A.; Heittola, T.; Benetos, E.; Foster, P.; Lagrange, M.; Virtanen, T.; Plumbley, M.D. Detection and classification of acoustic scenes and events: Outcome of the dcase 2016 challenge. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 379–393. [Google Scholar] [CrossRef] [Green Version]
- Van den Oord, A.; Dieleman, S.; Schrauwen, B. Deep content-based music recommendation. Adv. Neural Inf. Process. Syst. 2013, 2643–2651. [Google Scholar]
- Dosovitskiy, A.; Fischer, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; van der Smagt, P.; Cremers, D.; Brox, T. Flownet: Learning optical flow with convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 2758–2766. [Google Scholar]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. DeepDriving: Learning Affordance for Direct Perception in Autonomous Driving. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015. [Google Scholar]
- Finn, C.; Levine, S. Deep visual foresight for planning robot motion. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2786–2793. [Google Scholar]
- Shahroudy, A.; Ng, T.T.; Gong, Y.; Wang, G. Deep multimodal feature analysis for action recognition in rgb+ d videos. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1045–1058. [Google Scholar] [CrossRef] [Green Version]
- Ullah, I.; Manzo, M.; Shah, M.; Madden, M. Graph Convolutional Networks: Analysis, improvements and results. arXiv 2019, arXiv:1912.09592. [Google Scholar]
- Owens, A.; Efros, A.A. Audio-visual scene analysis with self-supervised multisensory features. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 631–648. [Google Scholar]
- Ahmad, K.; Conci, N. How Deep Features Have Improved Event Recognition in Multimedia: A Survey. In ACM Transactions on Multimedia Computing Communications and Applications; ACM: New York, NY, USA, 2019. [Google Scholar]
- Wang, H.; Wang, N.; Yeung, D.Y. Collaborative deep learning for recommender systems. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1235–1244. [Google Scholar]
- Cheng, H.T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.; et al. Wide & deep learning for recommender systems. In Proceedings of the First Workshop on Deep Learning for Recommender Systems, Boston, MA, USA, 15 September 2016; pp. 7–10. [Google Scholar]
- Roux, N.L.; Schmidt, M.; Bach, F. A Stochastic Gradient Method with an Exponential Convergence Rate for Finite Training Sets. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 2, pp. 2663–2671. [Google Scholar]
- Johnson, R.; Zhang, T. Accelerating stochastic gradient descent using predictive variance reduction. Adv. Neural Inf. Process. Syst. 2013, 26, 315–323. [Google Scholar]
- Chatterji, N.S.; Flammarion, N.; Ma, Y.A.; Bartlett, P.L.; Jordan, M.I. On the Theory of Variance Reduction for Stochastic Gradient Monte Carlo. In Proceedings of the 3rd International Conference on Machine Learning (ICML-2018), Stockholm, Sweden, 11–13 July 2018; pp. 764–773. [Google Scholar]
- Zhong, W.; Kwok, J. Fast stochastic alternating direction method of multipliers. In Proceedings of the 31st International Conference on Machine Learning (ICML-14), Beijing, China, 21–26 June 2014; pp. 46–54. [Google Scholar]
- Shen, Z.; Qian, H.; Zhou, T.; Mu, T. Adaptive Variance Reducing for Stochastic Gradient Descent. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI-2016), New York, NY, USA, 9 July 2016; pp. 1990–1996. [Google Scholar]
- Zou, D.; Xu, P.; Gu, Q. Stochastic Variance-Reduced Hamilton Monte Carlo Methods. In Proceedings of the 35th International Conference on Machine Learning, Stockholm Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; PMLR: Stockholm Sweden, 2018; Volume 80, pp. 6028–6037. [Google Scholar]
- Zhou, K.; Shang, F.; Cheng, J. A Simple Stochastic Variance Reduced Algorithm with Fast Convergence Rates. In Proceedings of the 35th International Conference on Machine Learning, Stockholm Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; PMLR: Stockholm, Sweden, 2018; Volume 80, pp. 5980–5989. [Google Scholar]
- Allen-Zhu, Z.; Hazan, E. Variance reduction for faster non-convex optimization. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 699–707. [Google Scholar]
- Huo, Z.; Huang, H. Asynchronous mini-batch gradient descent with variance reduction for non-convex optimization. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Liu, S.; Kailkhura, B.; Chen, P.Y.; Ting, P.; Chang, S.; Amini, L. Zeroth-order stochastic variance reduction for nonconvex optimization. Adv. Neural Inf. Process. Syst. 2018, 31, 3731–3741. [Google Scholar]
- Sutton, R. Two problems with back propagation and other steepest descent learning procedures for networks. In Proceedings of the Eighth Annual Conference of the Cognitive Science Society, Amherst, MA, USA, 15–17 August 1986; pp. 823–832. [Google Scholar]
- Nesterov, Y. A method for unconstrained convex minimization problem with the rate of convergence O (1/k2). Doklady AN USSR 1983, 269, 543–547. [Google Scholar]
- Kidambi, R.; Netrapalli, P.; Jain, P.; Kakade, S. On the Insufficiency of Existing Momentum Schemes for Stochastic Optimization. In Proceedings of the 2018 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 11–16 February 2018; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Flat minima. Neural Comput. 1997, 9, 1–42. [Google Scholar] [CrossRef] [PubMed]
- Chaudhari, P.; Choromanska, A.; Soatto, S.; LeCun, Y.; Baldassi, C.; Borgs, C.; Chayes, J.; Sagun, L.; Zecchina, R. Entropy-SGD: Biasing Gradient Descent Into Wide Valleys. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Dinh, L.; Pascanu, R.; Bengio, S.; Bengio, Y. Sharp minima can generalize for deep nets. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 7–9 August 2017; Volume 70, pp. 1019–1028. [Google Scholar]
- Hardt, M.; Recht, B.; Singer, Y. Train faster, generalize better: Stability of stochastic gradient descent. In Proceedings of the 3rd International Conference on Machine Learning; Balcan, M.F., Weinberger, K.Q., Eds.; PMLR: New York, NY, USA, 2016; Volume 48, pp. 1225–1234. [Google Scholar]
- He, F.; Liu, T.; Tao, D. Control Batch Size and Learning Rate to Generalize Well: Theoretical and Empirical Evidence. Adv. Neural Inf. Process. Syst. 2019, 32, 1141–1150. [Google Scholar]
- Smith, S.L.; Kindermans, P.J.; Ying, C.; Le, Q.V. Don’t decay the learning rate, increase the batch size. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Balles, L.; Romero, J.; Hennig, P. Coupling adaptive batch sizes with learning rates. arXiv 2016, arXiv:1612.05086. [Google Scholar]
- Levy, K. Online to Offline Conversions, Universality and Adaptive Minibatch Sizes. Adv. Neural Inf. Process. Syst. 2017, 30, 1613–1622. [Google Scholar]
- De, S.; Yadav, A.; Jacobs, D.; Goldstein, T. Automated inference with adaptive batches. Artif. Intell. Stat. 2017, 54, 1504–1513. [Google Scholar]
- Liu, X.; Hsieh, C.J. Fast Variance Reduction Method with Stochastic Batch Size. In Proceedings of the Thirty-Fifth International Conference on Machine Learning (ICML-2018), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Schaul, T.; Zhang, S.; LeCun, Y. No more pesky learning rates. In Proceedings of the International Conference on Machine Learning (ICML-2013), Atlanta, GA, USA, 16–21 June 2013; pp. 343–351. [Google Scholar]
- Zeiler, M.D. ADADELTA: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. Coursera Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Landro, N.; Gallo, I.; La Grassa, R. Combining Optimization Methods Using an Adaptive Meta Optimizer. Algorithms 2021, 14, 186. [Google Scholar] [CrossRef]
- Carvalho, P.; Lourencco, N.; Machado, P. Evolving Learning Rate Optimizers for Deep Neural Networks. arXiv 2021, arXiv:2103.12623. [Google Scholar]
- Pouyanfar, S.; Chen, S.C. T-LRA: Trend-based learning rate annealing for deep neural networks. In Proceedings of the 2017 IEEE Third International Conference on Multimedia Big Data (BigMM), Laguna Hills, CA, USA, 19–21 April 2017; pp. 50–57. [Google Scholar]
- Wilson, A.C.; Roelofs, R.; Stern, M.; Srebro, N.; Recht, B. The marginal value of adaptive gradient methods in machine learning. Adv. Neural Inf. Process. Syst. 2017, 30, 4148–4158. [Google Scholar]
- Li, Y.; Wei, C.; Ma, T. Towards explaining the regularization effect of initial large learning rate in training neural networks. arXiv 2019, arXiv:1907.04595. [Google Scholar]
- George, A.P.; Powell, W.B. Adaptive stepsizes for recursive estimation with applications in approximate dynamic programming. Mach. Learn. 2006, 65, 167–198. [Google Scholar] [CrossRef] [Green Version]
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. In Proceedings of the International Conference on Learning Representations (ICLR-2017), Toulon, France, 24–26 April 2017. [Google Scholar]
- Goyal, P.; Dollár, P.; Girshick, R.; Noordhuis, P.; Wesolowski, L.; Kyrola, A.; Tulloch, A.; Jia, Y.; He, K. Accurate, large minibatch sgd: Training imagenet in 1 hour. arXiv 2017, arXiv:1706.02677. [Google Scholar]
- He, T.; Zhang, Z.; Zhang, H.; Zhang, Z.; Xie, J.; Li, M. Bag of tricks for image classification with convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 558–567. [Google Scholar]
- Xing, C.; Arpit, D.; Tsirigotis, C.; Bengio, Y. A walk with sgd. arXiv 2018, arXiv:1802.08770. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images with Unsupervised Feature Learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning 2011, Granada, Spain, 12–17 December 2011. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Citeseer: Princeton, NJ, USA, 2009. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
| Data-Set | Content | #Class | Pixel Size | Channel | #Training Data | #Test Data |
|---|---|---|---|---|---|---|
| MNIST [61] | handwritten digits | 10 | gray | 60,000 | 10,000 | |
| Fashion-MNIST [62] | fashion items | 10 | gray | 60,000 | 10,000 | |
| SVHN [63] | digits in street | 10 | color | 73,257 | 26,032 | |
| CIFAR-10 [64] | natural photo | 10 | color | 60,000 | 10,000 | |
| CIFAR-100 [64] | natural photo | 100 | color | 60,000 | 10,000 |
| (1) Average (Upper Part) and Maximum (Lower Part) of Validation Accuracy for MNIST | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ave | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| NN-2 | 97.87 | 98.26 | 97.90 | 98.44 | 98.55 | 98.52 | 98.20 | 98.19 | 98.53 | 98.57 | 98.58 | 98.55 |
| NN-3 | 97.97 | 98.27 | 97.97 | 98.51 | 98.69 | 98.65 | 98.28 | 98.25 | 98.69 | 98.70 | 98.72 | 98.67 |
| LeNet-4 | 98.97 | 99.23 | 99.05 | 99.22 | 99.30 | 99.31 | 99.30 | 99.27 | 99.33 | 99.40 | 99.42 | 99.40 |
| VGG-9 | 99.32 | 99.62 | 99.33 | 99.64 | 99.62 | 99.62 | 99.38 | 99.37 | 99.63 | 99.56 | 99.60 | 99.62 |
| max | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| NN-2 | 98.06 | 98.38 | 98.01 | 98.59 | 98.65 | 98.65 | 98.33 | 98.33 | 98.63 | 98.67 | 98.68 | 98.65 |
| NN-3 | 98.18 | 98.39 | 98.09 | 98.65 | 98.81 | 98.79 | 98.39 | 98.41 | 98.80 | 98.84 | 98.83 | 98.73 |
| LeNet-4 | 99.20 | 99.39 | 99.18 | 99.40 | 99.45 | 99.48 | 99.41 | 99.37 | 99.48 | 99.52 | 99.53 | 99.51 |
| VGG-9 | 99.43 | 99.66 | 99.42 | 99.71 | 99.66 | 99.69 | 99.50 | 99.43 | 99.69 | 99.62 | 99.65 | 99.68 |
| (2) Average and Maximum of Validation Accuracy for Fashion-MNIST | ||||||||||||
| ave | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| NN-2 | 86.93 | 89.19 | 86.89 | 89.54 | 88.97 | 89.23 | 88.87 | 89.00 | 89.03 | 88.54 | 89.07 | 89.23 |
| NN-3 | 87.28 | 89.42 | 87.67 | 89.80 | 89.58 | 89.71 | 89.16 | 89.22 | 89.49 | 89.20 | 89.66 | 89.72 |
| LeNet-4 | 89.16 | 90.68 | 89.33 | 90.45 | 90.77 | 90.65 | 90.79 | 90.76 | 90.68 | 91.34 | 91.39 | 91.22 |
| VGG-9 | 91.83 | 93.14 | 91.79 | 93.56 | 93.33 | 93.38 | 91.97 | 92.07 | 93.42 | 93.06 | 93.27 | 93.36 |
| max | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| NN-2 | 87.25 | 89.55 | 87.08 | 89.72 | 89.28 | 89.48 | 89.21 | 89.40 | 89.43 | 88.84 | 89.36 | 89.47 |
| NN-3 | 87.52 | 89.83 | 87.90 | 90.02 | 89.88 | 90.11 | 89.49 | 89.52 | 89.78 | 89.42 | 89.93 | 90.05 |
| LeNet-4 | 89.78 | 91.08 | 89.86 | 91.16 | 91.40 | 91.36 | 91.30 | 91.08 | 91.46 | 91.69 | 91.72 | 91.56 |
| VGG-9 | 92.10 | 93.65 | 92.33 | 93.82 | 93.55 | 93.67 | 92.36 | 92.46 | 93.80 | 93.37 | 93.64 | 93.61 |
| (1) Average (Upper Part) and Maximum (Lower Part) of Validation Accuracy for SVHN | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ave | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| VGG-19 | 87.01 | 94.98 | 94.65 | 95.94 | 96.33 | 96.06 | 94.68 | 94.61 | 96.02 | 96.11 | 96.31 | 96.08 |
| ResNet-18 | 94.31 | 96.04 | 94.19 | 96.23 | 96.06 | 96.20 | 94.33 | 95.05 | 96.10 | 95.90 | 96.08 | 96.20 |
| ResNet-50 | 94.14 | 94.98 | 93.77 | 96.10 | 96.34 | 96.51 | 94.91 | 94.84 | 96.43 | 96.41 | 96.56 | 96.57 |
| DenseConv | 95.29 | 95.36 | 90.80 | 96.68 | 96.97 | 96.76 | 92.82 | 93.22 | 96.84 | 96.89 | 97.01 | 96.82 |
| GoogLeNet | 95.43 | 95.88 | 95.91 | 97.17 | 97.22 | 97.25 | 95.80 | 95.93 | 97.18 | 97.14 | 97.22 | 97.27 |
| max | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| VGG-19 | 94.67 | 95.14 | 94.83 | 96.07 | 96.49 | 96.25 | 94.78 | 94.74 | 96.12 | 96.17 | 96.38 | 96.23 |
| ResNet-18 | 94.49 | 96.29 | 94.56 | 96.33 | 96.19 | 96.34 | 94.54 | 95.19 | 96.28 | 96.05 | 96.22 | 96.36 |
| ResNet-50 | 94.68 | 95.24 | 94.03 | 96.38 | 96.59 | 96.65 | 95.04 | 95.08 | 96.68 | 96.56 | 96.72 | 96.65 |
| DenseConv | 95.61 | 95.80 | 91.06 | 96.78 | 97.08 | 96.90 | 93.03 | 93.48 | 96.92 | 97.00 | 97.12 | 96.91 |
| GoogLeNet | 95.72 | 96.30 | 96.10 | 97.29 | 97.36 | 97.39 | 95.97 | 96.14 | 97.26 | 97.27 | 97.36 | 97.40 |
| (2) Average and Maximum of Validation Accuracy for CIFAR-10 | ||||||||||||
| ave | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| VGG-19 | 84.37 | 90.56 | 89.72 | 92.80 | 93.04 | 93.26 | 89.67 | 89.89 | 92.98 | 93.15 | 93.46 | 93.72 |
| ResNet-18 | 86.73 | 91.59 | 90.15 | 94.32 | 94.37 | 94.69 | 90.73 | 90.91 | 94.30 | 94.35 | 94.48 | 94.81 |
| ResNet-50 | 85.29 | 91.81 | 90.05 | 94.13 | 94.17 | 94.61 | 91.24 | 91.28 | 94.10 | 94.64 | 94.87 | 95.20 |
| DenseConv | 86.79 | 88.91 | 75.85 | 94.24 | 94.46 | 94.72 | 82.97 | 83.64 | 94.22 | 94.35 | 94.41 | 94.65 |
| GoogLeNet | 86.30 | 91.64 | 89.61 | 94.54 | 94.57 | 94.93 | 90.46 | 90.59 | 94.57 | 94.85 | 94.83 | 95.23 |
| max | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| VGG-19 | 85.80 | 91.07 | 90.02 | 92.99 | 93.46 | 93.43 | 89.92 | 90.07 | 93.13 | 93.35 | 93.68 | 93.87 |
| ResNet-18 | 87.52 | 91.81 | 90.34 | 94.57 | 94.50 | 94.98 | 91.25 | 91.36 | 94.43 | 94.62 | 94.77 | 95.09 |
| ResNet-50 | 87.01 | 92.09 | 90.36 | 94.77 | 94.40 | 95.16 | 91.82 | 91.73 | 94.44 | 94.80 | 95.04 | 95.33 |
| DenseConv | 87.57 | 89.43 | 76.54 | 94.57 | 94.74 | 94.93 | 83.60 | 84.25 | 94.40 | 94.64 | 94.81 | 94.92 |
| GoogLeNet | 87.31 | 91.95 | 89.80 | 94.91 | 95.04 | 95.43 | 90.94 | 90.97 | 94.94 | 95.19 | 94.96 | 95.41 |
| (3) Average and Maximum of Validation Accuracy for CIFAR-100 | ||||||||||||
| ave | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| VGG-19 | 51.04 | 65.09 | 64.05 | 68.75 | 69.65 | 69.92 | 63.10 | 63.49 | 69.31 | 71.88 | 71.86 | 72.43 |
| ResNet-18 | 60.00 | 68.02 | 65.35 | 74.67 | 75.65 | 75.99 | 66.36 | 66.90 | 75.55 | 76.14 | 75.66 | 76.17 |
| ResNet-50 | 60.36 | 69.67 | 66.06 | 75.68 | 77.05 | 77.68 | 67.77 | 68.11 | 76.86 | 78.69 | 78.42 | 78.92 |
| DenseConv | 60.02 | 62.71 | 36.21 | 74.10 | 76.63 | 76.83 | 51.36 | 52.69 | 76.65 | 77.15 | 76.23 | 76.55 |
| GoogLeNet | 60.45 | 69.05 | 63.98 | 78.04 | 78.69 | 79.35 | 65.49 | 66.37 | 78.97 | 79.74 | 79.15 | 79.73 |
| max | 0.1 | 0.01 | 0.001 | exp | str | sig | rms | adam | rep | trap | str+ | sig+ |
| VGG-19 | 52.60 | 66.02 | 64.65 | 69.10 | 70.50 | 70.33 | 64.37 | 63.97 | 70.21 | 72.52 | 72.33 | 72.70 |
| ResNet-18 | 60.79 | 68.62 | 65.86 | 74.83 | 76.11 | 76.69 | 67.10 | 67.59 | 75.79 | 76.66 | 75.82 | 76.55 |
| ResNet-50 | 62.00 | 70.15 | 67.09 | 76.32 | 77.58 | 78.19 | 68.71 | 68.62 | 77.81 | 79.18 | 78.86 | 79.38 |
| DenseConv | 60.92 | 63.48 | 37.06 | 74.78 | 76.84 | 77.20 | 52.69 | 53.54 | 76.89 | 77.55 | 76.62 | 76.99 |
| GoogLeNet | 61.66 | 69.50 | 64.46 | 78.38 | 79.20 | 79.97 | 66.96 | 67.86 | 79.58 | 80.18 | 79.70 | 80.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, K.; Derbel, B.; Won, K.-J.; Hong, B.-W. Learning-Rate Annealing Methods for Deep Neural Networks. Electronics 2021, 10, 2029. https://doi.org/10.3390/electronics10162029
Nakamura K, Derbel B, Won K-J, Hong B-W. Learning-Rate Annealing Methods for Deep Neural Networks. Electronics. 2021; 10(16):2029. https://doi.org/10.3390/electronics10162029
Chicago/Turabian StyleNakamura, Kensuke, Bilel Derbel, Kyoung-Jae Won, and Byung-Woo Hong. 2021. "Learning-Rate Annealing Methods for Deep Neural Networks" Electronics 10, no. 16: 2029. https://doi.org/10.3390/electronics10162029
APA StyleNakamura, K., Derbel, B., Won, K.-J., & Hong, B.-W. (2021). Learning-Rate Annealing Methods for Deep Neural Networks. Electronics, 10(16), 2029. https://doi.org/10.3390/electronics10162029







