Miller Plateau Corrected with Displacement Currents and Its Use in Analyzing the Switching Process and Switching Loss
Abstract
1. Introduction
2. Miller Plateau Corrected with Displacement Currents
3. Analyzing the Switching Process and Switching Loss with the New Miller Plateau
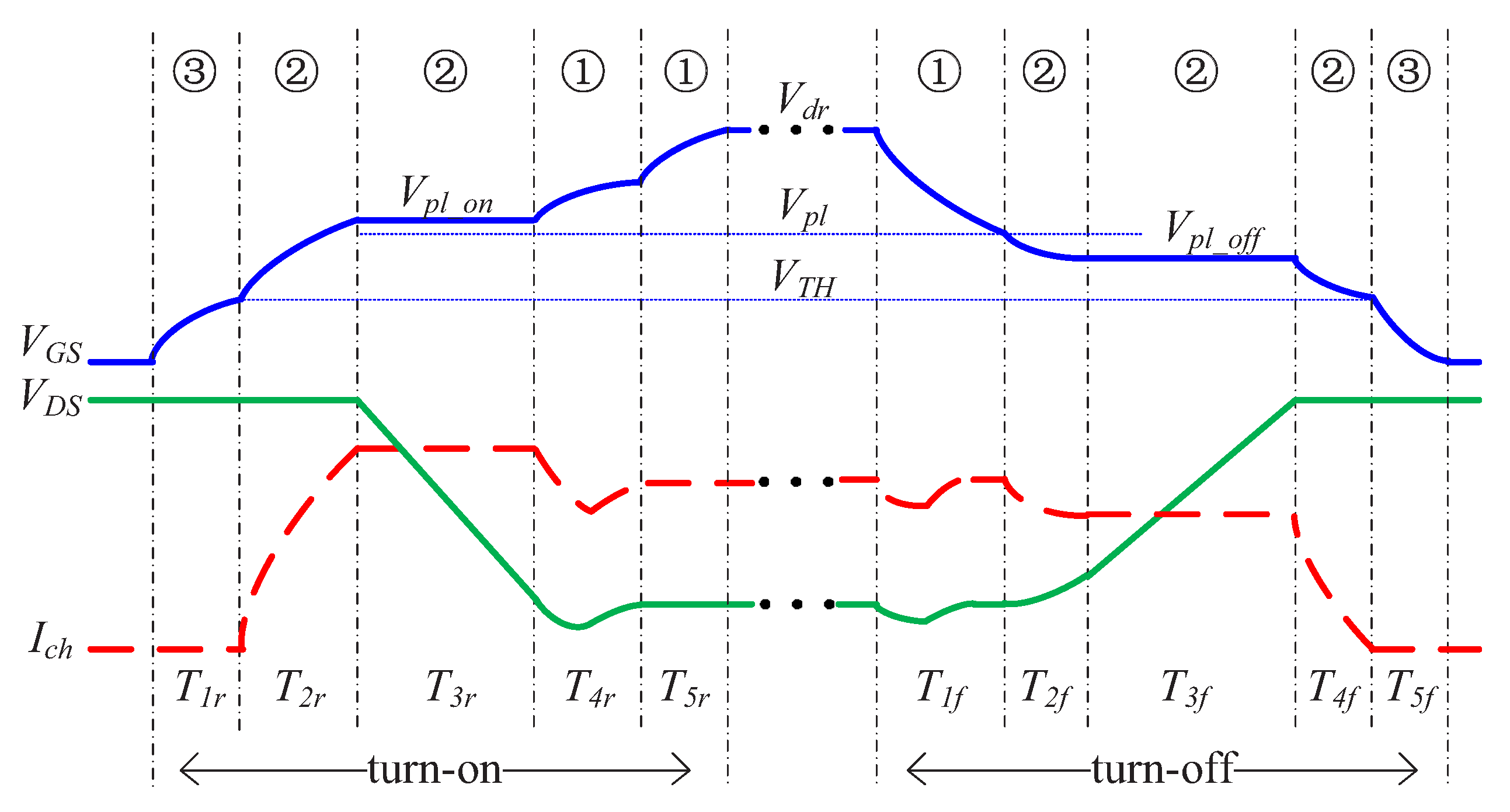
3.1. Switching Waveform Analysis Using the New Miller Plateau
3.2. Switching Loss Analysis Using the New Miller Plateau
4. Experimental and Simulation Verification
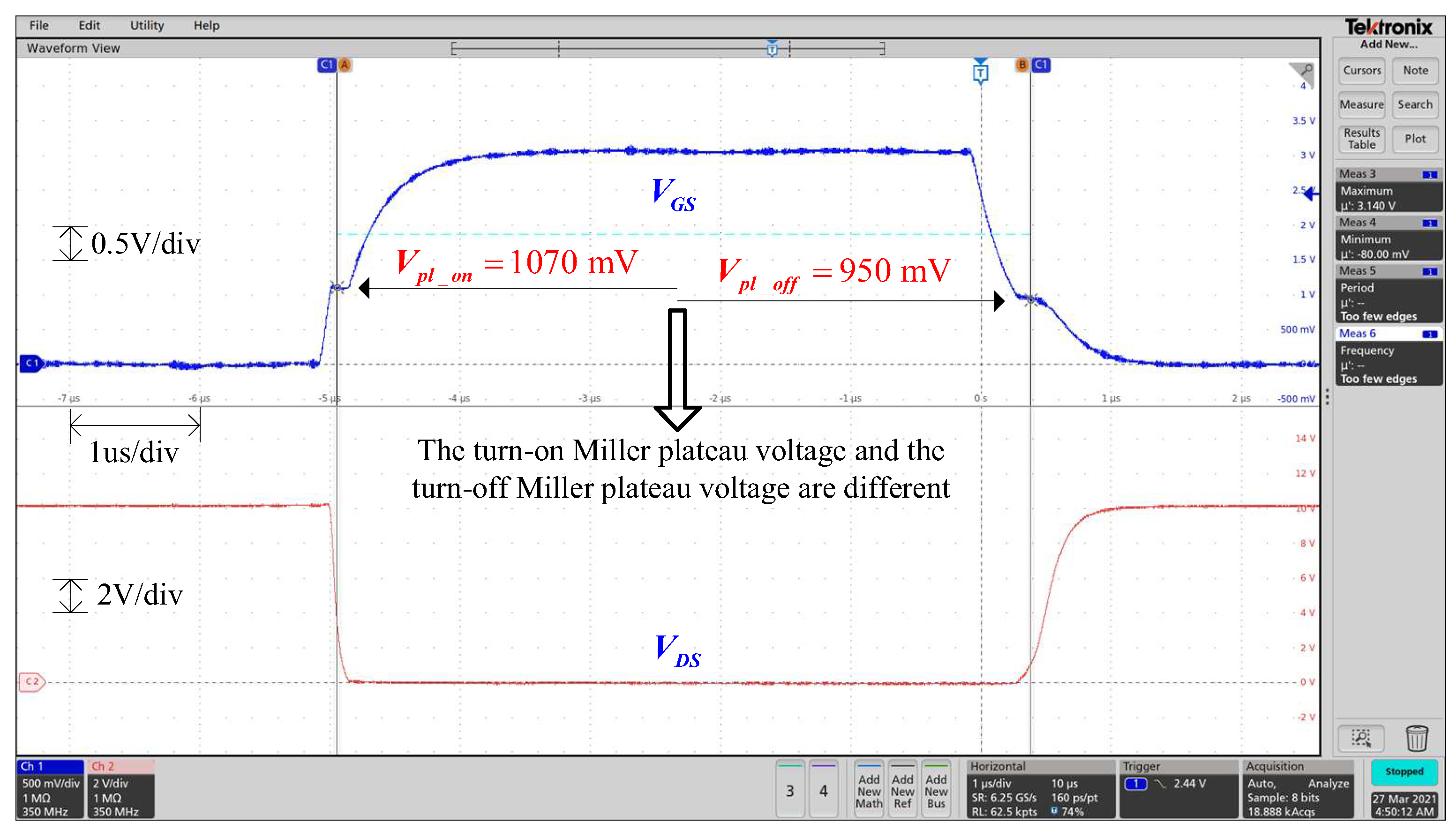
4.1. Experimental Test Result of the Miller Plateau
4.2. Verification of Analyzing the Switching Waveform
| Algorithm 1 |
|
if (vov < 0) begin mosfet_state = ‘OFF; end else if (gfs * vov < V(vd, vs)/ron) begin mosfet_state = ‘ACTIVE; end else begin mosfet_state = ‘ON; end if (mosfet_state == ‘OFF) begin I(vd,vs) <+ 0.0; end else if (mosfet_state == ‘ACTIVE) begin I(vd,vs) <+ gfs * vov; end else begin I(vd,vs) <+ V(vd, vs)/ron; end |
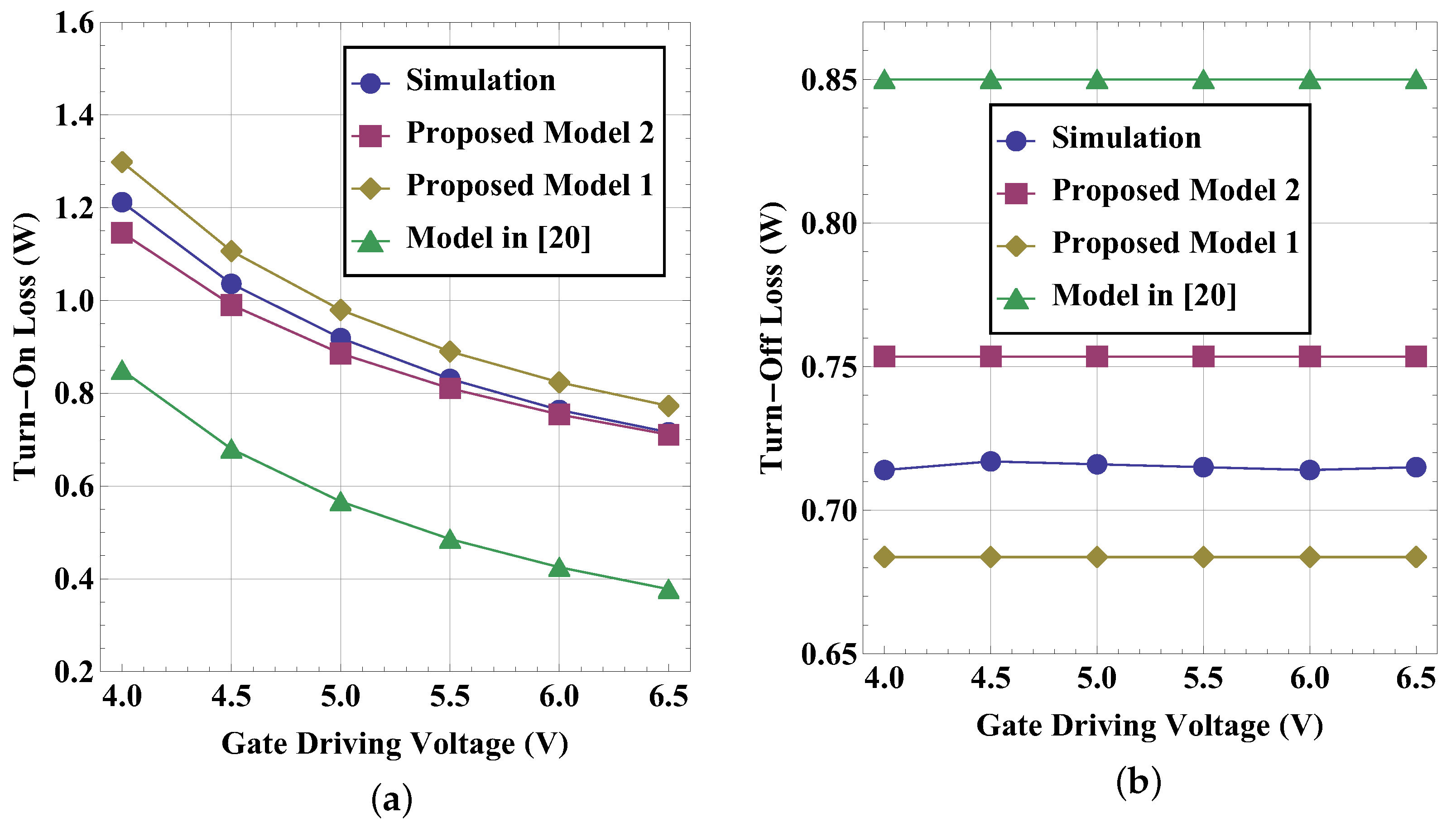
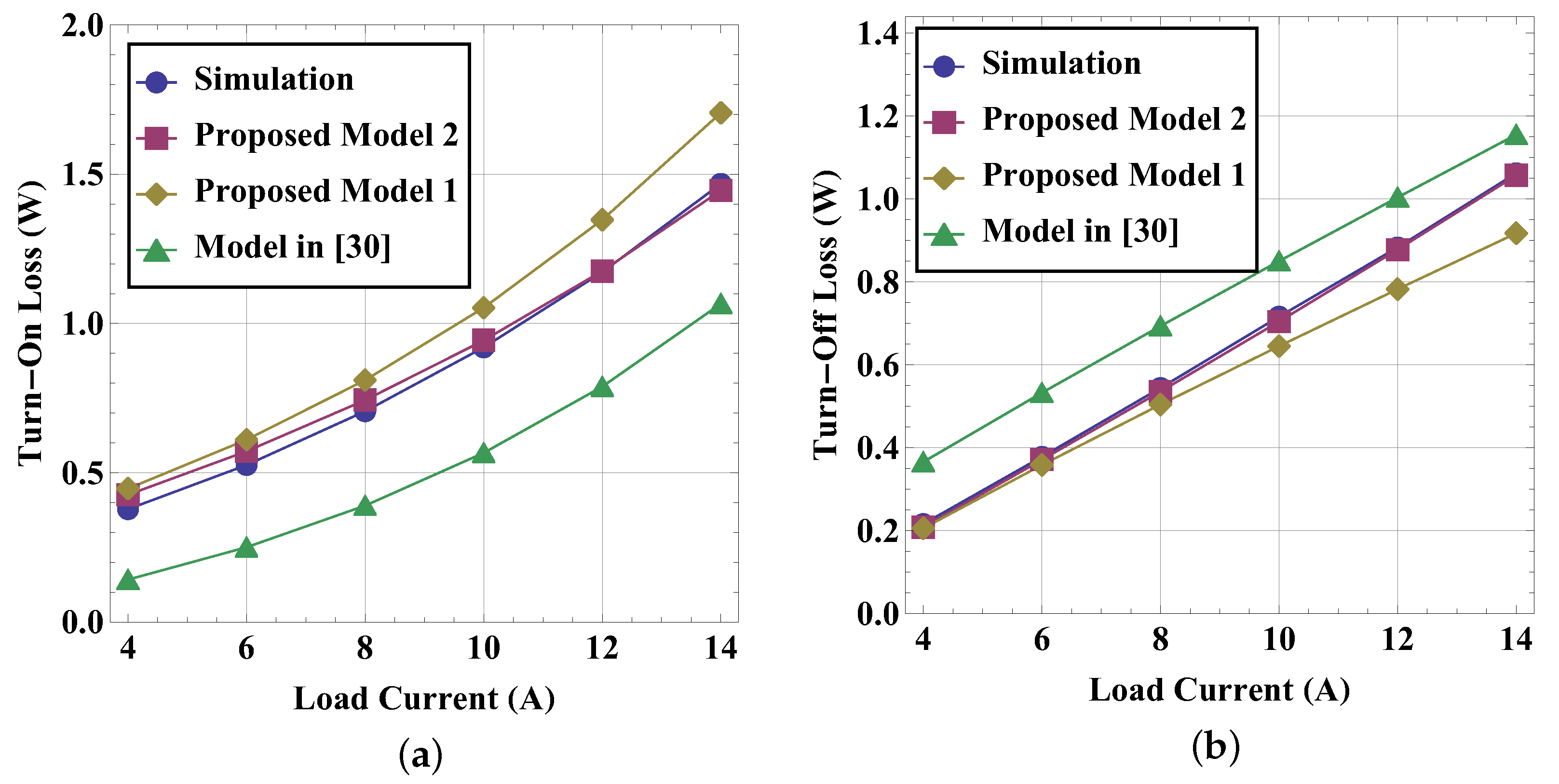
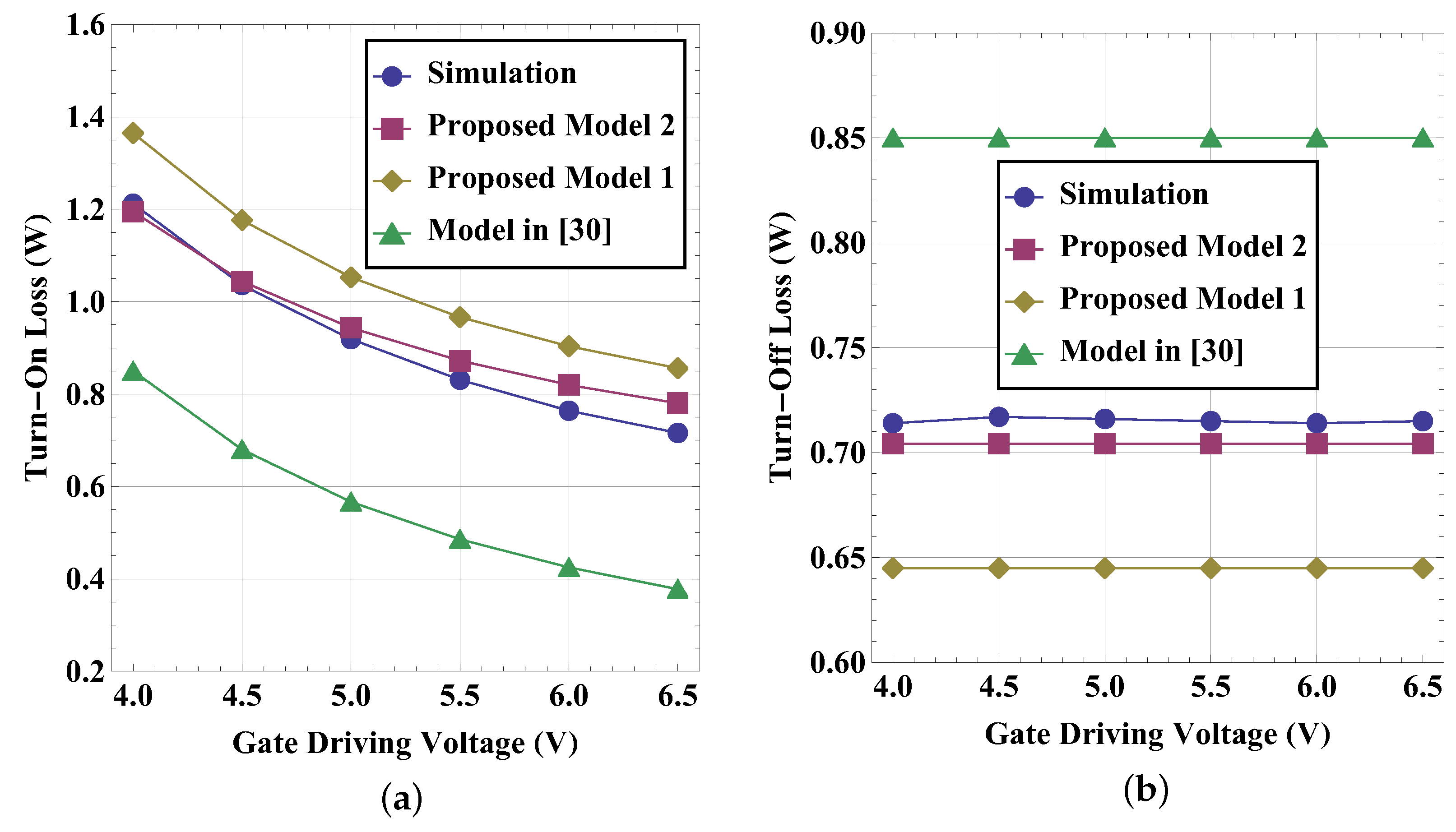
4.3. Verification of Analyzing Switching Loss
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMOS | Complementary metal-oxide semiconductor |
| DC | Direct current |
| EMI | Electromagnetic interference |
| FOM | Figures of merit |
| KCL | Kirchhoff’s current law |
| IoT | Internet of Things |
| MOSFET | Metal-oxide-semiconductor field-effect transistor |
| SMPS | Switching mode power supply |
| SPICE | Simulation Program with Integrated Circuit Emphasis |
Nomenclature
| , , | Parasitic interelectrode (gate, drain, and source) capacitances |
| External capacitance connected between the gate and source electrodes | |
| External capacitance connected between the drain and source electrodes | |
| Input capacitance. Equals | |
| Reverse transfer capacitance. Equals | |
| Output capacitance. Equals | |
| Switching frequency of an SMPS | |
| Power MOSFET’s transconductance in the ACTIVE state | |
| , , | Channel current, drain current, and load current |
| , | Miller plateau currents in the turn-on and turn-off processes |
| Average gate current when changes from to during turn-on | |
| Average gate current when changes from to during turn-off | |
| The constant rate when falls linearly from to zero during turn-on | |
| The constant rate when rises linearly from zero to during turn-off | |
| , | Parasitic inductances of the drain and source leads |
| , | Turn-on and turn-off switching power losses |
| Drain–source on-state resistance | |
| Gate resistance | |
| Switching period of an SMPS | |
| , | Turn-off time and turn-on time |
| to | Each interval of the turn-off sequence |
| to | Each interval of the turn-on sequence |
| The time constant related to and | |
| The time constant related to and | |
| , , | Gate–source voltage, gate–drain voltage, and drain–source voltage |
| Gate driving voltage | |
| Traditional Miller plateau voltage | |
| , | Miller plateau voltages in the turn-on and turn-off processes |
| Power MOSFET’s threshold voltage |
References
- Minoli, D.; Sohraby, K.; Occhiogrosso, B. IoT Considerations, Requirements, and Architectures for Smart Buildings—Energy Optimization and Next-Generation Building Management Systems. IEEE J. Internet Things 2017, 4, 269–283. [Google Scholar] [CrossRef]
- Chettri, L.; Bera, R. A Comprehensive Survey on Internet of Things (IoT) Toward 5G Wireless Systems. IEEE J. Internet Things 2020, 7, 16–32. [Google Scholar] [CrossRef]
- Shousha, M.; Dinulovic, D.; Haug, M.; Petrovic, T.; Mahgoub, A. A Power Management System for Electromagnetic Energy Harvesters in Battery/Batteryless Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3644–3657. [Google Scholar] [CrossRef]
- Ruan, T.; Chew, Z.J.; Zhu, M. Energy-Aware Approaches for Energy Harvesting Powered Wireless Sensor Nodes. IEEE J. Sens. 2017, 17, 2165–2173. [Google Scholar] [CrossRef]
- Perreault, D.J.; Hu, J.; Rivas, J.M.; Han, Y.; Leitermann, O.; Pilawa-Podgurski, R.C.N.; Sagneri, A.; Sullivan, C.R. Opportunities and Challenges in Very High Frequency Power Conversion. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Washington, DC, USA, 15–19 February 2009; pp. 1–14. [Google Scholar]
- Huang, C.; Mok, P.K.T. An 84.7% Efficiency 100-MHz Package Bondwire-Based Fully Integrated Buck Converter with Precise DCM Operation and Enhanced Light-Load Efficiency. IEEE J. Solid-State Circuits 2013, 48, 2595–2607. [Google Scholar] [CrossRef]
- Lee, B.; Song, M.K.; Maity, A.; Ma, D.B. A 25-MHz Four-Phase SAW Hysteretic Control DC-DC Converter with 1-Cycle Active Phase Count. IEEE J. Solid-State Circuits 2019, 54, 1755–1763. [Google Scholar] [CrossRef]
- Liu, X.; Huang, C.; Mok, P.K.T. A High-Frequency Three-Level Buck Converter with Real-Time Calibration and Wide Output Range for Fast-DVS. IEEE J. Solid-State Circuits 2018, 53, 582–595. [Google Scholar] [CrossRef]
- Dai, J.; Zhao, J.; Qu, K.; Lin, M. A Fast Hysteresis Control Strategy Based on Capacitor Charging and Discharging. IEICE Electron. Express 2014, 11, 1–6. [Google Scholar] [CrossRef][Green Version]
- Shenoy, P.S.; Amaro, M.; Morroni, J.; Freeman, D. Comparison of a Buck Converter and a Series Capacitor Buck Converter for High-Frequency, High-Conversion-Ratio Voltage Regulators. IEEE Trans. Power Electron. 2016, 31, 7006–7015. [Google Scholar] [CrossRef]
- Xu, D.; Guan, Y.; Wang, Y.; Wang, W. Topologies and Control Strategies of Very High Frequency Converters: A Survey. CPSS Trans. Power Electron. Appl. 2017, 2, 28–38. [Google Scholar] [CrossRef]
- Cheng, X.; Shao, W.; Zhang, Y.; Zeng, J.; Zhang, Z. High Frequency and High Efficiency DC-DC Converter with Sensorless Adaptive-Sizing Technique. IEICE Electron. Express 2020, 17, 1–4. [Google Scholar] [CrossRef]
- Zhao, Q.; Stojcic, G. Characterization of Cdv/dt Induced Power Loss in Synchronous Buck DC-DC Converters. IEEE Trans. Power Electron. 2007, 22, 1508–1513. [Google Scholar] [CrossRef]
- Wang, Q. The Impact of Parasitic Elements on Spurious Turn-on in Phase-Shifted Full-Bridge Converters. J. Power Electron. 2016, 16, 883–893. [Google Scholar] [CrossRef]
- Wang, J.; Chung, H.S. Impact of Parasitic Elements on the Spurious Triggering Pulse in Synchronous Buck Converter. IEEE Trans. Power Electron. 2014, 29, 6672–6685. [Google Scholar] [CrossRef]
- Li, R.; Zhu, J.; Xie, M. Parasitic Parameter Effects on the dv/dt-Induced Low-Side MOSFET False Turn-on in Synchronous Buck Converters. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 2247–2254. [Google Scholar]
- Liu, T.; Wong, T.T.Y.; Shen, Z.J. A Survey on Switching Oscillations in Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 893–908. [Google Scholar] [CrossRef]
- Ren, Y.; Xu, M.; Zhou, J.; Lee, F.C. Analytical Loss Model of Power MOSFET. IEEE Trans. Power Electron. 2006, 21, 310–319. [Google Scholar]
- Funaki, T.; Arioka, H.; Hikihara, T. The Influence of Parasitic Components on Power MOSFET Switching Operation in Power Conversion Circuits. IEICE Electron. Express 2009, 6, 1697–1701. [Google Scholar] [CrossRef]
- Klein, J. Synchronous Buck MOSFET Loss Calculations with Excel Model; Application Note AN-6005; Fairchild Semiconductor. 2006. Available online: http://www.bdtic.com/DataSheet/FAIRCHILD/AN-6005.pdf (accessed on 18 August 2021).
- Depew, J. Efficiency Analysis of a Synchronous Buck Converter Using Microsoft Office Excel-Based Loss Calculator. Application Note AN-1471. Microchip Technology Inc. 2012. Available online: https://www.microchip.com/en-us/application-notes/an1471 (accessed on 18 August 2021).
- Lakkas, G. MOSFET Power Losses and How They Affect Power-Supply Efficiency. Application Note Slyt664. Texas Instruments. 2016. Available online: https://www.ti.com/lit/an/slyt664/slyt664.pdf (accessed on 18 August 2021).
- Rodriguez, M.; Rodriguez, A.; Miaja, P.F.; Sebastian, J. Analysis of the Switching Process of Power MOSFETs Using a New Analytical Losses Model. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition (ECCE), San Jose, CA, USA, 20–24 September 2009; pp. 3790–3797. [Google Scholar]
- Eberle, W.; Zhang, Z.; Liu, Y.; Sen, P.C. A Practical Switching Loss Model for Buck Voltage Regulators. IEEE Trans. Power Electron. 2009, 24, 700–713. [Google Scholar] [CrossRef]
- Xiong, Y.; Sun, S.; Jia, H.; Shea, P.; Shen, Z.J. New Physical Insights on Power MOSFET Switching Losses. IEEE Trans. Power Electron. 2009, 24, 525–531. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, J.; Liu, Y.; Sen, P.C. Switching Loss Analysis Considering Parasitic Loop Inductance with Current Source Drivers for Buck Converters. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 1482–1486. [Google Scholar]
- Castro, I.; Roig, J.; Gelagaev, R.; Vlachakis, B.; Bauwens, F.; Lamar, D.G.; Driesen, J. Analytical Switching Loss Model for Superjunction MOSFET with Capacitive Nonlinearities and Displacement Currents for DC-DC Power Converters. IEEE Trans. Power Electron. 2016, 31, 2485–2495. [Google Scholar] [CrossRef]
- Nikoo, M.S.; Jafari, A.; Perera, N.; Matioli, E. New Insights on Output Capacitance Losses in Wide-Band-Gap Transistors. IEEE Trans. Power Electron. 2020, 35, 6663–6667. [Google Scholar] [CrossRef]
- Yoo, A.; Chang, M.; Trescases, O.; Wang, H.; Ng, W.T. FOM (Figure of Merit) Analysis for Low Voltage Power MOSFETs in DC-DC Converter. In Proceedings of the 2007 IEEE Conference on Electron Devices and Solid-State Circuits (EDSSC), Tainan, Taiwan, 20–22 December 2007; pp. 1039–1042. [Google Scholar]
- Ying, Y. Device Selection Criteria Based on Loss Modeling and Figure of Merit. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2008. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Kluwer Academic Publishers: New York, NY, USA, 2004; pp. 93–94. [Google Scholar]
- Grant, D.A.; Gowar, J. Power MOSFETs: Theory and Applications; John Wiley & Sons: New York, NY, USA, 1989; pp. 97–132. [Google Scholar]
- Zhang, H.; Zhao, M.; Wu, X. Zero-Current Switching Method for DC-DC Buck Converter in Portable Application. Electron. Lett. 2015, 51, 1913–1914. [Google Scholar] [CrossRef]
- Razavi, B. Design of Analog CMOS Integrated Circuits, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2017; pp. 174–178. [Google Scholar]
- Baker, R.J. CMOS: Circuit Design, Layout, and Simulation, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 660–663. [Google Scholar]
- Sansen, W.M.C. Analog Design Essentials; Springer: Dordrecht, The Netherlands, 2006; pp. 214–215. [Google Scholar]
- NCE2030K. Datasheet: NCE N-Channel Enhanced Mode Power MOSFET (v1.0); NCE Power Co.: Wuxi, China; Available online: https://pdf1.alldatasheetcn.com/datasheet-pdf/view/982315/NCEPOWER/NCE2030K.html (accessed on 18 August 2021).





| Turn-On | Turn-Off | ||
|---|---|---|---|
| When | When | |||||
|---|---|---|---|---|---|---|
| Meas. | Exist. | Prop. | Meas. | Exist. | Prop. | |
| 1070 mV | 710 mV | 760 mV | 1230 mV | 710 mV | 922 mV | |
| 950 mV | 710 mV | 695 mV | 909 mV | 710 mV | 644 mV | |
| Measured | Existing | Proposed | |
|---|---|---|---|
| 160 mV | 0 mV | 162 mV | |
| 41 mV | 0 mV | 51 mV |
| Turn-On | Turn-Off | ||||||
|---|---|---|---|---|---|---|---|
| On | Cal. | Sim. | Error | Off | Cal. | Sim. | Error |
| 312 ps | 313 ps | 1.28 ns | 1.29 ns | ||||
| 598 ps | 577 ps | 195 ps | 240 ps | ||||
| 767 ps | 772 ps | 954 ps | 1.05 ns | ||||
| 20.0 ps | 22 ps | 775 ps | 785 ps | ||||
| 5.52 ns | 5.50 ns | 6.44 ns | 6.45 ns | ||||
| The Loss Calculation Method in [20] | The Loss Calculation Method in [30] | |||||
|---|---|---|---|---|---|---|
| Original Model in [20] | Proposed Model 1 | Proposed Model 2 | Original Model in [30] | Proposed Model 1 | Proposed Model 2 | |
| 42.1% | 09.9% | 8.0% | 43.0% | 15.8% | 5.2% | |
| 35.7% | 10.1% | 9.7% | 29.8% | 08.7% | 1.6% | |
| The Loss Calculation Method in [20] | The Loss Calculation Method in [30] | |||||
|---|---|---|---|---|---|---|
| Original Model in [20] | Proposed Model 1 | Proposed Model 2 | Original Model in [30] | Proposed Model 1 | Proposed Model 2 | |
| 39.3% | 7.2% | 2.9% | 39.3% | 15.8% | 4.3% | |
| 18.8% | 4.4% | 5.3% | 18.9% | 09.8% | 1.5% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Song, S.; Xie, N.; Chen, H.; Wu, X.; Zhao, M. Miller Plateau Corrected with Displacement Currents and Its Use in Analyzing the Switching Process and Switching Loss. Electronics 2021, 10, 2013. https://doi.org/10.3390/electronics10162013
Liu S, Song S, Xie N, Chen H, Wu X, Zhao M. Miller Plateau Corrected with Displacement Currents and Its Use in Analyzing the Switching Process and Switching Loss. Electronics. 2021; 10(16):2013. https://doi.org/10.3390/electronics10162013
Chicago/Turabian StyleLiu, Sheng, Shuang Song, Ning Xie, Hai Chen, Xiaobo Wu, and Menglian Zhao. 2021. "Miller Plateau Corrected with Displacement Currents and Its Use in Analyzing the Switching Process and Switching Loss" Electronics 10, no. 16: 2013. https://doi.org/10.3390/electronics10162013
APA StyleLiu, S., Song, S., Xie, N., Chen, H., Wu, X., & Zhao, M. (2021). Miller Plateau Corrected with Displacement Currents and Its Use in Analyzing the Switching Process and Switching Loss. Electronics, 10(16), 2013. https://doi.org/10.3390/electronics10162013







