Abstract
Conventionally, public key certificates bind one subject with one static public key so that the subject can facilitate the services of the public key infrastructure (PKI). In PKI, certificates need to be renewed (or revoked) for several practical reasons, including certificate expiration, private key breaches, condition changes, and possible risk reduction. The certificate renewal process is very costly, especially for those environments where online authorities are not available or the connection is not reliable. A dynamic public key certificate (DPKC) facilitates the dynamic changeover of the current public–private key pairs without renewing the certificate authority (CA). This paper extends the previous study in several aspects: (1) we formally define the DPKC; (2) we formally define the security properties; (3) we propose another implementation of the Krawczyk–Rabin chameleon-hash-based DPKC; (4) we propose two variants of DPKC, using the Ateniese–Medeiros key-exposure-free chameleon hash; (5) we detail two application scenarios.
1. Introduction
Certificates act as the critical tokens in conventional PKI systems. With the trust of the CA, a validated certificate allocates communicating partners the tasks of entity authentication, document signature verification, session key distribution and agreement, and other functions.
For several practical reasons, a subject’s public–private key pair will need to be renewed from time to time [1,2], for example because a private key has been compromised, to reduce the risks of services (such as session key generation) related to a specific private key, or to specify the different terms for different public keys; however, the certificate renewal process is very costly and is very difficult or even infeasible in some scenarios, for example if there is no reliable communication between different entities and their certificate authorities or it is infeasible to set up such an online authority for certain Internet of Things (IoT) networks, ad hoc networks, and Wireless Sensor Networks (WSN).
One possible solution to providing several public–private key pairs in one certificate is by specifying several public keys and delivering the private keys to the subject through a secure channel. This solution might help in some situations but it is not scalable and not secure in many scenarios. Firstly, the long list of private keys requires a larger tamper-resistant memory space. Secondly, all of the key pairs need to be generated when the certificate is issued. This creates a large burden on the CA or the requesters, limiting the scalability. Thirdly, if the entity is compromised, then all services related to the compromised private keys are discredited, while storing all the private keys simultaneously increases the risk of being compromised.
In our previous study [3] based on the Krawczyk–Rabin chameleon signature [4,5], we proposed the dynamic public key certificate (DPKC), whereby the subject of the certificate can dynamically coin new public–private key pairs on the spot, such that a verifier can validate the new public keys using the same certificate. Please note that this new approach does not totally exclude the certificate renewal process but facilitates the owner’s capacity to change the public key dynamically during the certificate validation period. This new approach has several advantages and potential new applications. It facilitates the change of the public key dynamically, thereby reducing both the client’s burden of maintaining several public–private key pairs and the authority’s burden of managing many certificates per client. The owner can eliminate obsoleted private keys from storage to reduce the risks while generating new keys for the same certificate. It dramatically reduces the costs related to communication with the CAs (or even eliminates the requirement for online CAs in some applications). Several applications for this new approach will be introduced in Section 5.
Related Work
Efficient key management is quite challenge in various networking environments. For symmetric-key-based systems, the challenges include the predistribution of keys, the redistribution of keys, or the generation of new keys via key agreements [6,7,8]. For networks with PKI [6,7,8,9,10,11,12,13,14], the challenge lies in designing efficient and reliable cryptographic algorithms, as well as methods to distribute, renew, and revoke certificates. We focus on key management for PKI systems in this paper.
Within the context of grid communications, Mohamed et al. [9] designed new certificate formats, CA hierarchies, and renewal processes to improve the efficiency of smart grid communications. Wu and Zhou [6] integrated elliptic curve cryptographies (ECC) and symmetric key techniques to improve the efficiency and accessibility of smart grid communications. Metke et al. [10] studied key management for smart grid communications and decided that PKI is the most effective solution for securing grids.
Regarding ad hoc networks, He et al. [7] proposed the combined integration of security keys, such that both communication overheads are reduced and lightweight key management is achieved. Other studies [11,12] focused on distributing the management of public keys. By utilizing user acquaintances and certificates, another previous study [13] proposed a public key management system with a self-organizing function. Another study [14] designed efficient key-management schemes to effectively deter active attacks, while in [8] secure key revocation and renewal schemes were designed using ECC and symmetric encryptions.
Conventional public key certificates facilitate authentication and non-repudiation services, prohibiting escrow of the corresponding private key; on the other hand, identity-based (ID-based) cryptosystems [15] inherently own the escrow key properties, while the authority that owns the escrow keys can naturally recover encrypted data when necessary. Conventionally, in order to implement the two kinds of public key services mentioned above, one needs to build two independent public key systems—one is the certificate-based PKI and the other is the ID-based cryptosystem. Lin et al. [16], based on chameleon hashes, proposed a novel key management infrastructure that integrates the “inherent key escrow” characteristic of ID-based encryption [15] into a PKI that can specify two public keys in one certificate, of which one public key is used for key escrow and the other is a conventional public key.
Krawczyk and Rabin [4,5] defined the notation of chameleon signatures and chameleon hashing functions. A chameleon hashing function allows the owner of the trapdoor function to easily find the collisions for a given input; regarding the collision-finding capacity, this is similar to a conventional cryptographic hashing function. Several other studies [16,17,18,19,20] have aimed to either extend the chameleon signatures and hashing functions or apply them in various contexts. One application involved secure vehicular ad hoc network (Vanet) communications. In [17,18,19,20,21], an onboard unit (OBU) in a car based on chameleon hashing was used to forge a new ephemeral public key in each session, then using the corresponding ephemeral private key to securely share a session key with its communicating partner. Such methods of dynamical ephemeral public key generation might seem to satisfy the goals of our study at first glance, but they cannot ensure the forward secrecy if the OBUs are compromised; that is, if an OBU is compromised, then all the previous communications would be compromised. In Vanet approaches, it is usually assumed that OBUs are tamper-resistant and that attackers cannot disclose secret values inside an OBU.
Ateniese et al. [22] outlined the requirements for modifying, deleting, or compressing blocks in blockchain applications; therefore, they proposed new types of blockchains, whereby the contents of some blocks can be edited by the designated entities when required. They integrated chameleon hashes into the design of the blockchains. There are some similarities between their schemes and ours; both approaches leverage the collision-finding capacities in chameleon hashes to allow the designated entities to properly modify the input contents of the hashes. A chameleon hash acts as the partial contents of a block in their scheme [22], while a chameleon hash acts as the partial content of a certificate in our schemes and the dynamic public keys are the inputs of the hashes. In [23], Bellare and Ristov proved that chameleon hash functions and Sigma protocols are equivalent and found new effective designs for chameleon hashes.
Pahl and Donini [24] proposed the use of public key certificates for authenticating IoT devices in order to strengthen DTLS services. Hewa et al. [25] applied Elliptic Curve Qu–Vanstone (ECQV) certificates in IoT scenarios and used the blockchain-based smart contracts to manage the certificates. In view of the heavy certificate validation overheads for IoT devices, [26] explored the distributed caching related to certificate validation among IoT devices; their results showed that the design can greatly reduce the validation time of a device. Another previous study [26] is complementary to ours in the sense that their design can be integrated with ours to reduce the computational overheads related to certificate validation; however, previous studies [24,25,26] did not address the fact that IoT devices are relatively easily compromised and that private keys inside the devices can be disclosed, endangering the security of the certificate-related services.
Unlike the tamper resistance assumption in OBU, devices in ad hoc networks, WSNs, and IoT networks are usually deployed in hostile environments, whereby once the device is captured, its internal secrets are disclosed. For such scenarios, assuming a device with a conventional certificate is compromised one day later, then the previous communications and session keys that are dependent on the private key of the certificate would be endangered too; that is, they cannot provide forward secrecy. This motivated us to propose the DPKC concept [3]; even if we assume a device with a certificate might be compromised one day later, the previous communications using the same certificate would still be secure, meaning it provides forward secrecy.
Even though the above mentioned papers have tackled some of the challenges related to public key certificates, none of them have addressed the challenges of dynamically changing a public key in a certificate and providing forward secrecy. In [3], Chien first formulated the concept of the dynamic public key certificate and then proposed a simple implementation using the Krawczyk–Rabin chameleon hash and signature approach. In this paper, we greatly extend the previous study [3] in several aspects: (1) we formally define the DPKC; (2) we formally define the security properties; (3) we propose another implementation of the Krawczyk–Rabin chameleon-hash-based DPKC; (4) we propose two variants of DPKC, using the Ateniese–Medeiros key-exposure-free chameleon hash [27]; (5) we detail two application scenarios.
2. Preliminaries
Before introducing our schemes, chameleon hashes and signatures and the proof of knowledge concept are reviewed below.
2.1. Chameleon Hash and Signatures
The notation for chameleon signatures and chameleon hashing functions was first introduced by Krawczyk and Rabin [4,5]. A chameleon hashing function allows the owner of the trapdoor function to easily find the collisions for a given input, except for the collision-finding capacity, which is similar to a conventional cryptographic hashing function. Chameleon signatures are secure digital signatures on the chameleon hashes of the messages. Both undeniable signatures [28] and chameleon signatures simultaneously provide non-transferability and non-repudiation; undeniable signatures achieve non-transferability in an interactive way, while chameleon signatures do this in a non-interactive way. The generation of a chameleon signature is computed by the signer alone and the verification of a chameleon signature is performed by the verifier alone. Because a chameleon signature is a signature on the chameleon hash of the message, the designated recipient can find the collisions of the chameleon hash. If the recipient delivers such a collision for a chameleon signature, then the signer repudiates the collisions by offering the original message–signature pair or by offering another collision.
Ateniese and Medeiros reported on the key exposure issue of the Krawczyk–Rabin chameleon hash construction [4,5], whereby the signer can recover the long-term private key of the designated receiver if the latter provides a collision. Later, Chen et al. [29] showed that the ID-based solutions [27] only partially solve the key exposure challenge, since the recipient needs to have new public–private key pairs for each transaction. Other studies such as [29,30,31] proposed several chameleon hash and signature schemes without the key exposure issue.
It is these properties of non-repudiation, non-forge-ability, and designated recipient collision-finding capability that we will twist to design our dynamic public key certificate (DPKC) schemes. Not all chameleon hash and signature schemes can be modified to meet the requirements of our dynamic public key certificate schemes.
In the following, we introduce the formal definition of a chameleon hash scheme given by Chen et al. 2009 [31].
Definition 1.
The chameleon hash scheme with key exposure freeness includes four efficient algorithms (SPG, KG, H, F) [31]:
- -
- System Parameter Generation SPG: Upon input of a security parameter k, a probabilistic polynomial time algorithm outputs the system parameters SP;
- -
- Key Generation KG: Upon input of the system parameters SP, a probabilistic polynomial time algorithm outputs a trapdoor–hash key pair (TK, HK);
- -
- Hashing Computation HC: Upon input of a message m, the hash key HK, a customized identity I, and a random string r, a probabilistic polynomial time algorithm outputs the hashed value l = CHash(I, HK, m, r). Note that l is independent on TK. A customized identity is a string extended from one’s identity with additional information (such as roles, transaction identities, etc.) to differentiate one instance from another. Note that I could be null in some implementations;
- -
- Collision Computation FC: Upon input of a message m, the trapdoor key TK, a random string r, and another message , a deterministic polynomial time algorithm outputs a string r’ that satisfies the following equation:
A secure chameleon hash scheme with key exposure freeness satisfies the following properties:
- -
- Collision resistance: For algorithms without the trapdoor key TK, on input of a message m, another message , and a random string r, they cannot output a string that satisfies CHash(I, HK, , ) = CHash(I, HK, m, r) with non-negligible probability;
- -
- Semantic security: The probability distributions of the random values CHash(I, HK, m, r) and CHash(I, HK, , ) are computationally indistinguishable for all pairs of messages m and ;
- -
- Key exposure freeness: Assume a designated receiver does not provide a collision under m, then no efficient adversary can find a collision for a given chameleon hash value CHash(I, HK, m, r). Even if the adversary has submitted many polynomial queries on triples () of the choice to the oracle, where does not equal the challenge I, the adversary still cannot find a collision.
A chameleon signature with key exposure freeness is a secure digital signature on the chameleon hash value of a message. The following definition is taken from [31].
Definition 2.
The chameleon signature scheme with key exposure freeness has a specific denial protocol and the following algorithms:
- -
- System Parameter Generation SPG: Upon input of a security parameter k, a probabilistic polynomial time algorithm outputs the system parameters, SP.
- -
- Key Generation KG: Upon input of the system parameters SP, a probabilistic polynomial time algorithm outputs a signing–verification key pair () and a trapdoor–hash key pair (TK, HK);
- -
- Signature Generation SG: Upon input of a customized identity I, the hash key HK, the signing key , a message m, and a random string r, a probabilistic polynomial time algorithm outputs a signature on the chameleon hash value l = CHash(I, HK, m, r);
- -
- Signature Verification SV: Upon input of a customized identity I, a message m, the hash key HK, the verification key , a random string r, and a signature , a deterministic polynomial time algorithm outputs a verification decision ;
- -
- Denial Protocol DP: The signer and the judge perform DP in a non-interactive way. The signer provides the judge with a valid collision () and some auxiliary information to prove the forgery of the given chameleon signature (, r) on the message m. If and only if is valid and , the judge concludes that the signature on the message m is a forgery;
- -
- A chameleon signature scheme satisfies the properties [30,31]:
- -
- Unforgeability: Only the signer can generate a valid chameleon signature, the designated receiver can only produce a forgery of a chameleon signature previously generated by the signer;
- -
- Non-transferability: The signature is not universal verifiable, whereby a designated receiver has no way to convince a third party that the signer really provided a signature on a certain message;
- -
- Non-repudiation: Legitimate signature claims could be denied by the signer;
- -
- Deniability: A forgery of a signature could be denied by the signer;
- -
- Message hiding: To deny the validity of a forgery, the signer does not have to reveal the original message.
Note that a general chameleon hash without an emphasis on the key exposure freeness property is similar to the above definition with the following exceptions. The hash key HK is the public key of the designated recipient, the TK is the private key, and the customized identity I is not mandatory in the corresponding algorithms. Additionally, the key exposure freeness property is not mandatory. Likewise, a general chameleon signature without an emphasis on the key exposure freeness is similar to the above example with the following exceptions. The hash key HK is the public key of the designated recipient, the TK is the private key, and the customized identity I is not mandatory in the corresponding algorithms. Additionally, the message recovery property and the message hiding property are not mandatory.
2.2. Proof of Knowledge
A prover who knows a secret number wants to convince a verifier of their knowledge without exposing the secret, which is called the proof of knowledge of a discrete logarithm. The implementation of the proof of knowledge, based on the Schnorr signature [32] on message (g, Y), is reviewed as follows. The prover chooses and computes and , whereby h() is a cryptographic hash function. The prover accepts the proof (c, s) if and only if . We refer to this requirement as ZK-proof () in the rest of this paper.
Similar constructions could be obtained to prove the knowledge without exposing x as follows [33]. The prover chooses and computes and . The prover accepts the proof if and only if (c, s) satisfies . We refer to this requirement as ZK-proof () in the rest of this paper.
3. The Proposed Dynamic Public Key Certificates
This section formally defines the dynamic public key certificate and proposes several implementations. The ADPKC scheme behaves similarly to a conventional public key certificate in PKI, except that the subject (the owner) of the certificate can choose the new public keys and any verifiers can check the validity of the dynamic public keys using the same certificate.
Definition 3.
The dynamic public key certificate (DPKC) scheme involves three kinds of entities, namely the CA, registered client (U), and verifier (V), whereby the CA is a trusted entity. The scheme has six efficient algorithms (SPG, KG, DPKCG, DPKCV, DPKF, DPKV):
- -
- System Parameter Generation SPG: Upon input of a security parameter k, a probabilistic polynomial time algorithm outputs the system parameters SP, which includes the public key of the CA, , which is trusted by all entities. The corresponding private key is securely owned by the CA;
- -
- Key Generation KG: Upon input of the system parameters SP, a probabilistic polynomial time algorithm outputs a public–private key pair () for each registered entity U;
- -
- Dynamic Public Key Certificate Generation DPKCG: To generate a dynamic public key certificate, the CA requires the information that an ordinary certificate has. The information includes the public key and the other necessary information, such as the identity of the issuer (the CA), the identity of the subject, the algorithms, the parameters, the valid period, and the application scopes; we denote these other data as . The CA generates a dynamic public key certificate, as defined in Equation (2), where is the CA’s signature on the data and the chameleon hash . Note that in could be null in some implementations (that is, = ):
- -
- Dynamic Public Key Certificate Verification DPKCV: Given the CA’s public key and a dynamic public key certificate , a decision is output;
- -
- Dynamic Public Key Finding DPKF: This algorithm consists of two sub-algorithms, whereby the first one randomly generates new public–private key pairs, while the second one, based on the new key pairs, generates the corresponding data, which satisfies ;
- -
- The 1st sub-algorithm. Upon input of (), a probabilistic polynomial time algorithm outputs two public–private key pairs () and (). Please note that could be the initial public key , while the second key pair () is the one that preserves forward secrecy in the applications;
- -
- The 2nd sub-algorithm. Given (which includes I, m, r, etc.), the long-term trapdoor key (or a related converted trapdoor), and the new key pairs, a deterministic (or probabilistic) algorithm outputs a string r′, such that it satisfies = . It may also generate an optional proof, which depends on the implementations;
- -
- Dynamic Public Key Verification DPKV: Given the CA’s public key and a dynamic public key certificate , two public keys and , , and the optional proof, a verification decision is output. The decision is based on the results of the verification of the certificate, the verification of which Equation (3) provides, and the validity of the optional proof:
A secure dynamic public key certificate scheme has the following properties specified below:
- -
- Collision resistance: No efficient algorithm without the long-term trapdoor key , upon input of a message m and a random string r, outputs another message and a string that satisfy = , with non-negligible probability;
- -
- Unforgeability: Only the CA can produce a valid dynamic public key certificate. Additionally, the subject of a certificate can only produce a collision of the chameleon hash specified in that certificate;
- -
- Public verifiability: The validity of a dynamic public key certificate and its corresponding public keys can be verified by any party;
- -
- Forward secrecy: Even if the subject of a dynamic public key certificate might be captured one day and all its current memories are compromised, all of the previous ephemeral private keys should still be secure.
We can see that even though dynamic public key certificates are based on chameleon hashes, they own different features. For examples, the semantic security of a message is not required in DPKCs, while forward secrecy is necessary in DPKCs. We now introduce some new implementations of DPKC schemes.
3.1. A New Implementation Using the Krawczyk–Rabin Chameleon Hash
The Krawczyk–Rabin chameleon hash is introduced as follows. Let the prime factors be and , such that , where is a large prime factor; is a generator for a subgroup of order in . Let be the long-term private key of a recipient U and be the long-term public key. The chameleon is defined as ;
The proposed DPKC scheme is defined as follows:
- -
- System Parameter Generation SPG, Key Generation KG: The parameter initialization and the private–public key generation are the same as that in the Krawczyk–Rabin scheme; however, in our scheme, each registered user U has two initial key pairs () and ().
- -
- Dynamic Public Key Certificate Generation DPKCG: The CA generates a DPKC for U, using DCHash_1 defined in Equation (4).where DCHash_1 is defined as:
- -
- Dynamic Public Key Certificate Verification DPKCV: Given a , a verifier validates the certificate by performing signature verification on the CA’s signature ;
- -
- Dynamic Public Key Finding DPKF: For ith () renewable public keys, the user U chooses two new key pairs () and () and then computes as defined in Equation (5). The new dynamic public key tuple is (, , , ZK-proof ()), where ZK-proof () is a zero-knowledge proof of the knowledge :(that is, = ).
Please note that the owner, instead of keeping the initial private keys (), can keep the last ephemeral private keys () only to find a valid public key tuple for the next session, since = = as long as the equation = = holds. This design has the advantage that the owner only keeps the last tuple to save space;
- -
- Dynamic Public Key Verification DPKV: Given the certificate and the new public key tuple (, , , ZK-proof ()), a verifier first checks the validity of and then checks whether holds and the validity of ZK-proof (). If U follows the DPKF, then the equation should hold, since = = = ;
- -
- Another variant of this construction is letting = , ZK-proof (). and ;
3.2. An Implementation Based on the Ateniese–Medeiros Key-Exposure-Free Chameleon Hash
The Ateniese–Medeiros key-exposure-free chameleon hash is based on the Nyberg–Rueppel signature [34], whereby p and q are two large prime factors, such that ; g is a generator of a subgroup of quadratic residues , while g is of order q. The recipient U selects a private key , while the public key is . The chameleon hash is defined as follows: , where , .
Now, we construct a DPKC scheme as follows:
- -
- System Parameter Generation SPG, Key Generation KG: The parameter initialization and the private–public key generation are the same as that in the Ateniese–Medeiros scheme; However, in our scheme, each registered user U has two key pairs () and ().
- -
- Dynamic Public Key Certificate Generation DPKCG: The CA generates a DPKC for U, using DCHash_2 as defined in Equation (6):where DCHash_2 is defined as:
- -
- Dynamic Public Key Certificate Verification DPKCV: Given , a verifier validates the certificate by performing signature verification on the CA’s signature ;
- -
- Dynamic Public Key Finding DPKF: For ith () renewable public keys, the user U chooses one new key pair () and the old one (), then executes the following steps:
- (1)
- The user chooses ;
- (2)
- The user computes , , and .
Then, the new public key tuple () satisfies Equation (7):
- -
- Dynamic Public Key Verification DPKV: Given the certificate and the new public key tuple (), a verifier first checks the validity of , then checks whether holds. If U follows the DPKF, then the equation should hold as shown in (1).
In [30], Ateniese and Medeiros showed another version of the chameleon hash as . Based on this chameleon, we can construct a DPKC scheme in a similar way. Here, we let C = in the certificate, choose a random number , the compute and . Then, we obtain .
4. Security Analysis
The security properties of the proposed dynamic chameleon hashes (DCHash) and the proposed DPKC schemes are analyzed here. Because our DPKC schemes apply a secure digital signature on the content of a DPKC and the chameleon hash value (DCHash) of the content, the unforgeability of the DPKC is assured when the corresponding chameleon hashes (DCHash) are collision-resistant to all entities (except the designated recipient, which here is the subject of the certificate); therefore, we only need to prove that the proposed DCHashs are collision-resistant to all except the designated recipient, which here is the subject of the certificate.
Theorem 1.
The proposed DCHash_1 is collision-resistant to all except the designated recipient, who is the subject of the certificate.
Proof.
We first assume that the attacker (not the subject) can forge another collision (, , , ZK-proof ()) for DCHash_1, then we show the contradiction whereby the attacker owns the private keys of the subject. Assume the attacker finds the collisions that satisfy = = = = ; this implies that the attacker who forges can derive the secret . This contradicts the security of the DLP problem. This proves the collision resistance to all except the designated recipient, who is the subject of the certificate. □
Theorem 2.
The proposed DCHash_2 is collision-resistant as long as the long-term private key is secure.
Proof.
This result is trivial, since we only substitute in the Ateniese–Medeiros chameleon hash , whereby , . The collision-resistant property of the Ateniese–Medeiros chameleon hash was proven in [27]. □
Now, the forward secrecy of the dynamic public keys is proven as follows.
Theorem 3.
All of the proposed DPKC schemes ensure the forward secrecy of the dynamicprivate keyswhen the subject eliminates all previous obsolete private keysfrom its storage and the DLP problem is difficult.
Proof.
In the calculations of the proposed CHash, only the ephemeral public keys are used, while the corresponding private keys are never used in the calculations. All pairs (,) are randomly and independently generated. So long as all of the previous obsolete private keys are deleted from storage and the DLP problem is hard, adversaries cannot derive the private keys. □
5. Applications
Public keys facilitate many security services, such as authentication, signatures, and encryption. A DPKC scheme allows a subject to dynamically change the public keys and provides the forward secrecy for the previous private keys, even if we assume that the subject might be compromised one day later. This could have several potential new applications, in addition to the conventional applications.
5.1. General Application Scenarios
One main application opportunity is applying the DPKC schemes in those scenarios where public key certificates are desirable but an online CA is not available or the connection is not reliable.
The CA only keeps the original signed DPKC certificates. In order for both the CA and any verifier to verify whether a new public key is valid, they need the original certificate and the new public key tuple, which is (), as shown in Section 3.2. A verifier should keep the new public key tuple if it requires a jurisdiction from a third party later; this requirement is just like that in a conventional digital signature where a verifier needs a signature and the message to validate its validity.
The verification of each new public key tuple is independent from other instances for the same DPKC certificate and there is no requirement to record the tuple history in order to verify any instance.
5.2. General Applications in WSN/IoT Scenarios
In IoT/WSN scenarios, nodes (things) are usually deployed in unprotected areas. Data are encrypted and then transmitted in a hop-to-hop manner back to their backend servers. The security of the source-to-destination path depends on the security of the encryption of each link along the path; therefore, any breaches from any links along the path back to the backend servers would compromise the whole system security. In many implementations, the encryption of each link is based on the public key of the nodes. With the DPKC schemes introduced in Section 3, applications with can use the dynamic public keys to generate public-key-based encryptions, periodically change the public keys, and delete the obsoleted ones. Even if a node might be compromised one day later, the encryptions that were based on previous public keys would still be secure.
Nodes in WSN/IoT can change (public key, private key) pairs on the spot without accessing one-line CA servers. This is very useful for those WSN/IoT scenarios where online CA services provided or reliable and-cost-effective connections cannot be ensured.
5.3. Integration with Non-Perfect Forward Secrecy Key Agreement Schemes to Provide Perfect Forward Secrecy
Many IoT devices and mobile devices are resource-limited, meaning the computational or communicational complexity of a protocol will significantly affect the performance of the devices in terms of battery life, delay, and other factors; therefore, even although both key agreement and forward secrecy are desirable properties in such applications, they are not enforced in several related standards and not implemented in many products [35,36,37,38,39,40].
To reduce the computational overhead for a client in adopting the Diffie–Hellman key agreement, Chien [41] formulated the modified computational Diffie–Hellman problem (MCDHP) and introduced an approach that can easily transform existent Diffie–Hellman key agreement schemes to their corresponding MCDHP-based variants, such that the computational cost to the clients can be reduced. This solution reduces the costs or concerns of adopting Diffie–Hellman session keys in resource-limited devices. The transformation maintains all of the security properties of the original key agreement schemes, except that forward secrecy is no longer preserved; if a device’s long-term private key is compromised, then all previous session key generations involved with the private key are also compromised.
Here, we show how we can simultaneously reduce a client’s computational overhead in the Diffie–Hellman keying process and achieve forward secrecy by integrating both our DPKC schemes with the MCDHP-based key agreement schemes.
Before detailing the integration process, Chien’s MCDHP-based schemes are briefly reviewed as follows.
Definition 4.
The modified computational Diffie–Hellman problem (the MCDHP) over group is formulated as follows. Given , , , and x + t, where y, , and t are random numbers and is a generator for , the task is to output .
Chien [41] proved that the MCDHP problem is as hard as the CDHP problem. Figure 1 depicts a general scheme for converting a CDHP keying process into a MCDHP keying process. The notation is introduced first and then followed by the explanation of the steps.
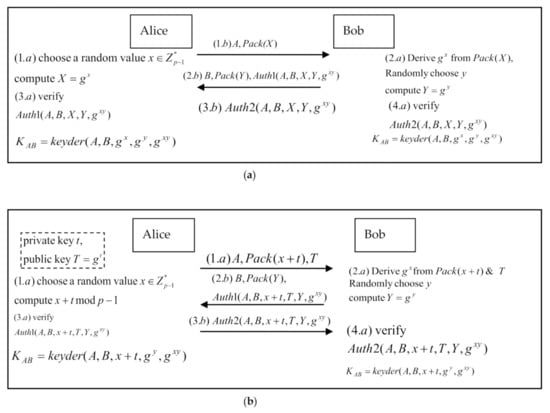
Figure 1.
(a) The conventional authenticated D-H key agreement. (b) The MCDHP-based authenticated D-H key agreement with enhanced client efficiency.
5.4. Notations
B, A: B and A denote the identities of the entities Bob and Alice. Here, Alice is the client.
KAB: Denotes the session key to be established between the two parties.
T = gt, t,: T = gt denotes the long-term public key for Alice, where t is the corresponding private key.
X, Y, x, y: X = gx and Y = gy denote the public keys, where x and y are the corresponding ephemeral private keys.
⊕, ||: ⊕/|| denotes exclusive-OR/concatenation operation.
Pack(X): The goal of this function is to deliver the value X to the receiver, which can be implemented as a plaintext or an encryption of the value X; its implementation depends on each specific protocol.
Auth1(.), Auth2(.), Auth3(.): These values denote the authentication codes applied on the inputs, while the designated receivers can verify the authenticity of the received data. The implementations depend on each specific protocol.
keyder (.): The derivation function for session keys.
Figure 1a depicts the general process for conventional CDHP-based key agreements. After exchanging the keying materials X = gx and Y = gy, the two entities compute the same key KAB = gxy. This simplified process may not include the authentication of the communicating parties.
Figure 1b depicts the general MCDHP-based D-H key agreement process. Instead of transmitting X = gx, the client transmits the vector (x + t, T = gt); Bob uses Alice’s public key T to derive X = gx+t/T = gx. After exchanging the keying materials, the two entities derive the key KAB = gxy. This MCDHP-based key agreement reduces the client’s one modular exponentiation at the extra cost of one exponentiation and one modular multiplication at the server. This arrangement fits many IoT/WSN scenarios, where the devices are very resource-limited and the servers are resource-abundant.
Now, we are ready to show how one can apply the DPKC in the MCDHP-based key agreement schemes such that the integrated solution both reduces the client’s computation costs and provides forward secrecy. The key idea is that a client with chooses the new public keys and notifies the server in the MCDHP-based key agreement schemes to use this new key to derive the keying material X and the session key KAB. This mechanism assures the forward secrecy of the session keys and the previous private keys , even if we assume the device might be compromised one day later. This integrated solution has several merits: (1) devices can dynamically change their public–private key pairs without accessing the online CA; (2) the potential benefits of hacking devices are greatly reduced, in turn greatly reducing the motives for hacking these devices; (3) the solution can conquer many obstacles that hinder PKI services in IoT applications.
6. Conclusions
In this paper, we have reviewed the dynamic public key certificate, formally formulated the DPKC, and proposed several efficient chameleon-hash-based implementations. The DPKC allows clients to dynamically choose new public–private key pairs without renewing their certificates. This could greatly reduce the costs of public key renewal and overcome many of the obstacles that hinder PKI services in mobile nodes and IoT devices. Several potential applications have been introduced. One application involves solving the forward secrecy issues related to link encryption in WSN/IoT scenarios. The security of the source-to-destination path depends on the security of the encryption of each link along the path. With the DPKC schemes, a node can use the next node’s dynamic public key to perform the public key encryption, such that the forward secrecy can be ensured, even if a node might be compromised later.
The other application involves integrating DPKC schemes with non-perfect forward secrecy key agreements to fill the void regarding secure key agreements in several mobile device/IoT security standards. The integrated solution reduces the client’s computational overhead in the Diffie–Hellman keying process and ensures the perfect forward secrecy of the session keys and the dynamic private keys. Interesting areas for further studies could include new efficient implementations of DPKC schemes and new applications.
Funding
This project is partially supported by the Ministry of Science and Technology of Taiwan, under the grant no. MOST 108-2221-E-260-009-MY3.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Iliadis, J.; Gritzalis, S.; Spinellis, D.; de Cock, D.; Preneel, B. Towards a framework for evaluating certificate status information mechanisms. Comput. Commun. 2003, 1–8. [Google Scholar] [CrossRef]
- Myers, M. Revocation: Options and Challenges. In Proceedings of the Third International Conference on Financial Cryptography, Anguilla, British West Indies, 1 February 1999; pp. 165–171. [Google Scholar]
- Chien, H.-Y. Dynamic Public Key Certificates for IoT and WSN Scenarios. In Proceedings of the 2018 IEEE 42nd Annual Computer Software and Applications Conference (COMPSAC), Tokyo, Japan, 23–27 July 2018; Volume 2, pp. 646–651. [Google Scholar]
- Krawczyk, H.; Rabin, T. Chameleon Signatures. In Proceedings of the Seventh ISOC Network and Distributed System Security Symposium, San Diego, CA, USA, 23–26 February 2000; pp. 42–53. [Google Scholar]
- Krawczyk, H.; Rabin, T. Chameleon Hashing and Signatures. In IACR Cryptology Eprint; CiteeSeer: Princeton, NJ, USA, 1998; Available online: https://eprint.iacr.org/1998/010.ps (accessed on 16 August 2021).
- Wu, D.; Zhou, C. Fault-Tolerant and Scalable Key Management for Smart Grid. IEEE Trans. Smart Grid 2011, 2, 375–381. [Google Scholar] [CrossRef]
- He, W.B.; Huang, Y.; Sathyam, R.; Nahrstedt, K.; Leem, W.C. SMOCK: A Scalable Method of Cryptographic Key Management for Mission-Critical Wireless Ad-Hoc Net-works. IEEE Trans. Inf. Forensics Secur. 2009, 4, 140–150. [Google Scholar]
- Mansour, I.; Chalhoub, G.; Lafourcade, P.; Delobel, F. Secure key renewal and revocation for Wireless Sensor Networks. In Proceedings of the 39th Annual IEEE Conference on Local Computer Networks, Edmonton, AB, USA, 8–11 September 2014; pp. 382–385. [Google Scholar]
- Mahmoud, M.M.E.A.; Mišić, J.; Shen, X. A scalable public key infrastructure for smart grid communications. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 784–789. [Google Scholar]
- Metke, A.R.; Ekl, R.L. Security Technology for Smart Grid Networks. IEEE Trans. Smart Grid 2010, 1, 99–107. [Google Scholar] [CrossRef]
- Zhou, L.; Haas, Z. Securing ad hoc networks. IEEE Netw. 1999, 13, 24–30. [Google Scholar] [CrossRef]
- Jiejun, K.; Petros, Z.; Luo, H.; Lu, S.; Zhang, L. Providing robust and ubiquitous security support for mobile ad-hoc networks. In Proceedings of the Ninth International Conference on Network Protocols, ICNP, Riverside, CA, USA, 11–14 November 2001; pp. 251–260. [Google Scholar]
- Capkun, S.; Buttyán, L.; Hubaux, J.-P. Self-organized public-key management for mobile ad hoc networks. IEEE Trans. Mob. Comput. 2003, 2, 52–64. [Google Scholar] [CrossRef]
- Zhu, B.; Bao, F.; Deng, R.H.; Kankanhalli, M.S.; Wang, G. Efficient and robust key management for large mobile ad hoc networks. Comput. Netw. 2005, 48, 657–682. [Google Scholar] [CrossRef]
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Workshop on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2000; pp. 47–53. [Google Scholar]
- Lin, J.; Zhu, W.; Wang, Q.; Zhang, N.; Jing, J.; Gao, N. RIKE+: Using revocable identities to support key escrow in public key infrastructures with flexibility. IET Inf. Secur. 2015, 9, 136–147. [Google Scholar] [CrossRef]
- Chen, C.Y.; Hsu, T.C.; Wu, H.T.; Chiang, J.Y.; Hsieh, W.S. Anonymous Authentication and Key-Agreement Schemes in Vehicular Ad-Hoc Networks. J. Internet Technol. 2014, 15, 893–902. [Google Scholar]
- Choi, J.; Jung, S. A handover authentication using credentials based on chameleon hashing. IEEE Commun. Lett. 2010, 14, 54–56. [Google Scholar] [CrossRef]
- Guo, S.; Zeng, D.; Xiang, Y. Chameleon Hashing for Secure and Privacy-Preserving Vehicular Communications. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2794–2803. [Google Scholar] [CrossRef]
- Shen, A.-N.; Guo, S.; Zeng, D.; Guizani, M. A lightweight privacy-preserving protocol using chameleon hashing for secure vehicular communications. In Proceedings of the 2012 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March 2012; pp. 2543–2548. [Google Scholar]
- Huang, Y.H.; Fan, K.H.; Hsieh, W.S. Message Authentication Scheme for Vehicular Ad—Hoc Wireless Networks without RSU. J. Inf. Hiding Multimed. Signal Process. 2015, 6, 113–122. [Google Scholar]
- Ateniese, G.; Magri, B.; Venturi, D.; Andrade, E. Redactable Blockchain—or—Rewriting History in Bitcoin and Friends. In Proceedings of the 2017 IEEE European Symposium on Security and Privacy (EuroS&P), Paris, France, 26–28 April 2017; pp. 111–126. [Google Scholar]
- Bellare, M.; Ristov, T. A Characterization of Chameleon Hash Functions and New, Efficient Designs. J. Cryptol. 2014, 27, 799–823. [Google Scholar] [CrossRef]
- Pahl, M.-O.; Donini, L. Securing IoT microservices with certificates. In Proceedings of the NOMS 2018—2018 IEEE/IFIP Network Operations and Management Symposium, Taipei, Taiwan, 23–27 April 2018; pp. 1–5. [Google Scholar]
- Hewa, T.; Bracken, A.; Ylianttila, M.; Liyanage, M. Blockchain-based Automated Certificate Revocation for 5G IoT. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar]
- Wang, M.; Qian, C.; Li, X.; Shi, S. Collaborative Validation of Public-Key Certificates for IoT by Distributed Caching. IEEE/ACM Trans. Netw. 2019, 29, 847–855. [Google Scholar] [CrossRef]
- Ateniese, G.; de Medeiros, B. Identity-Based Chameleon Hash and Applications; Springer: Berlin/Heidelberg, Germany, 2004; pp. 164–180. [Google Scholar]
- Chaum, D.; Antwerpen, H.V. Undeniable signatures. In Cryptology-Crypto; LNCS 435; Springer: Berlin/Heidelberg, Germany, 1989; pp. 212–216. [Google Scholar]
- Chen, X.; Zhang, F.; Kim, K. Chameleon Hashing Without Key Exposure. In Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2004; Volume 3225, pp. 87–98. [Google Scholar]
- Ateniese, G.; de Medeiros, B. On the Key Exposure Problem in Chameleon Hashes; Springer: Berlin/Heidelberg, Germany, 2005; pp. 165–179. [Google Scholar]
- Chen, X.F.; Zhang, F.; Tian, H.B.; Wei, B.D.; Kim, K. Key-Exposure Free Chameleon Hashing and Signatures Based on Discrete Logarithm Systems; Sun Yat-sen University: Guangzhou, China, 2009; Available online: https://eprint.iacr.org/2009/035.pdf (accessed on 16 August 2021).
- Schnorr, C.P. Efficient signature generation by smart cards. J. Cryptol. 1991, 4, 161–174. [Google Scholar] [CrossRef]
- Chaum, D.; Pedersen, T.P. Wallet Databases with Observers. In Advances in Cryptology—CRYPTO’ 92; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2001; pp. 89–105. [Google Scholar]
- Naccache, D.; Pointcheval, D.; Stern, J. Twin Signatures: An Alternative to The Hash-And-Sign Paradigm. In Proceedings of the 8th ACM Conference on Computer and Communication Security (ACM CCS), Philadelphia, PA, USA, 5–8 November 2001; pp. 20–27. [Google Scholar]
- EPC Gen2 Standard. EPC™ Radio-Frequency Identity Protocols Class-1 Generation-2 UHF RFID Protocol for Communications at 860 MHz—960 MHz Version 1.2.0; EPCglobal: Cambridge, MA, USA, 2008. [Google Scholar]
- ISO/IEC FCD 15693-3. Contactless Integrated Circuit(s) Cards—Vicinity Cards—Part 3: Anticollision and Transmission Protocol; International Organization for Standardization, International Electrotechnical Commission: Geneva, Switzerland, 2009. [Google Scholar]
- ISO/IEC 14443. Identification Cards—Contactless Integrated Circuit Cards—Proximity Cards—Part 4: Transmission Protocol; International Organization for Standardization, International Electrotechnical Commission: Geneva, Switzerland, 2008. [Google Scholar]
- NFC Forum Technical Specifications. NFC Simple NDEF Exchange Protocol (SNEP) Specification; NFC FORUM: Mountain View, CA, USA, 2014. [Google Scholar]
- NFC-SEC-01. NFC-SEC Cryptography Standard Using ECDH and AES, 2nd ed.; Ecma International: Geneva, Switzerland, 2010. [Google Scholar]
- ZigBee 3.0. The ZigBee Alliance. 2012. Available online: https://csa-iot.org/ (accessed on 16 August 2021).
- Chien, H.-Y. A Generic Approach to Improving Diffie–Hellman Key Agreement Efficiency for Thin Clients. Comput. J. 2015, 59, 592–601. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).