Design and Analysis of a Novel High-Gain DC-DC Boost Converter with Low Component Count
Abstract
:1. Introduction
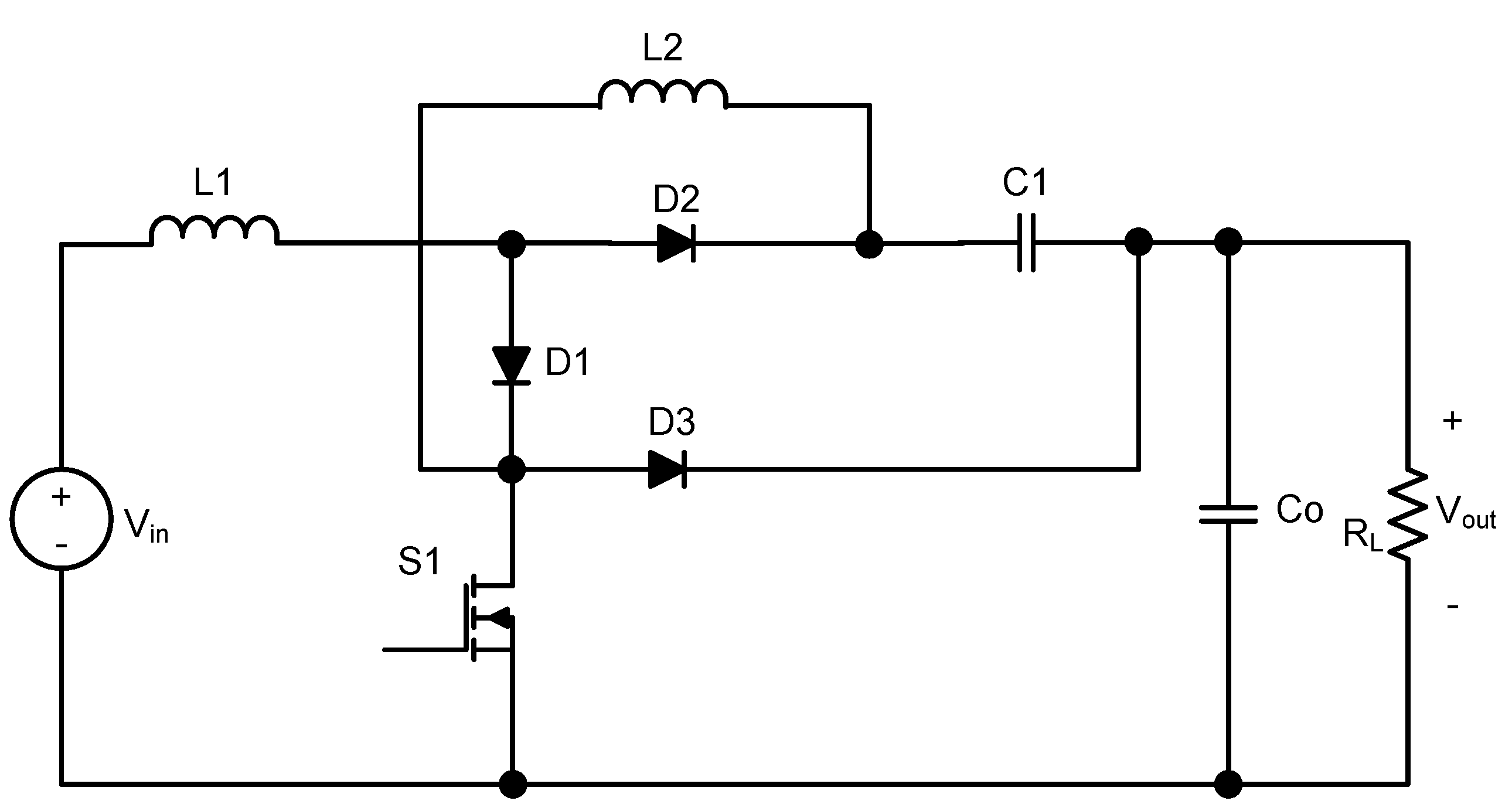
2. Operation and the Switching Modes
2.1. During M0
2.2. During M1
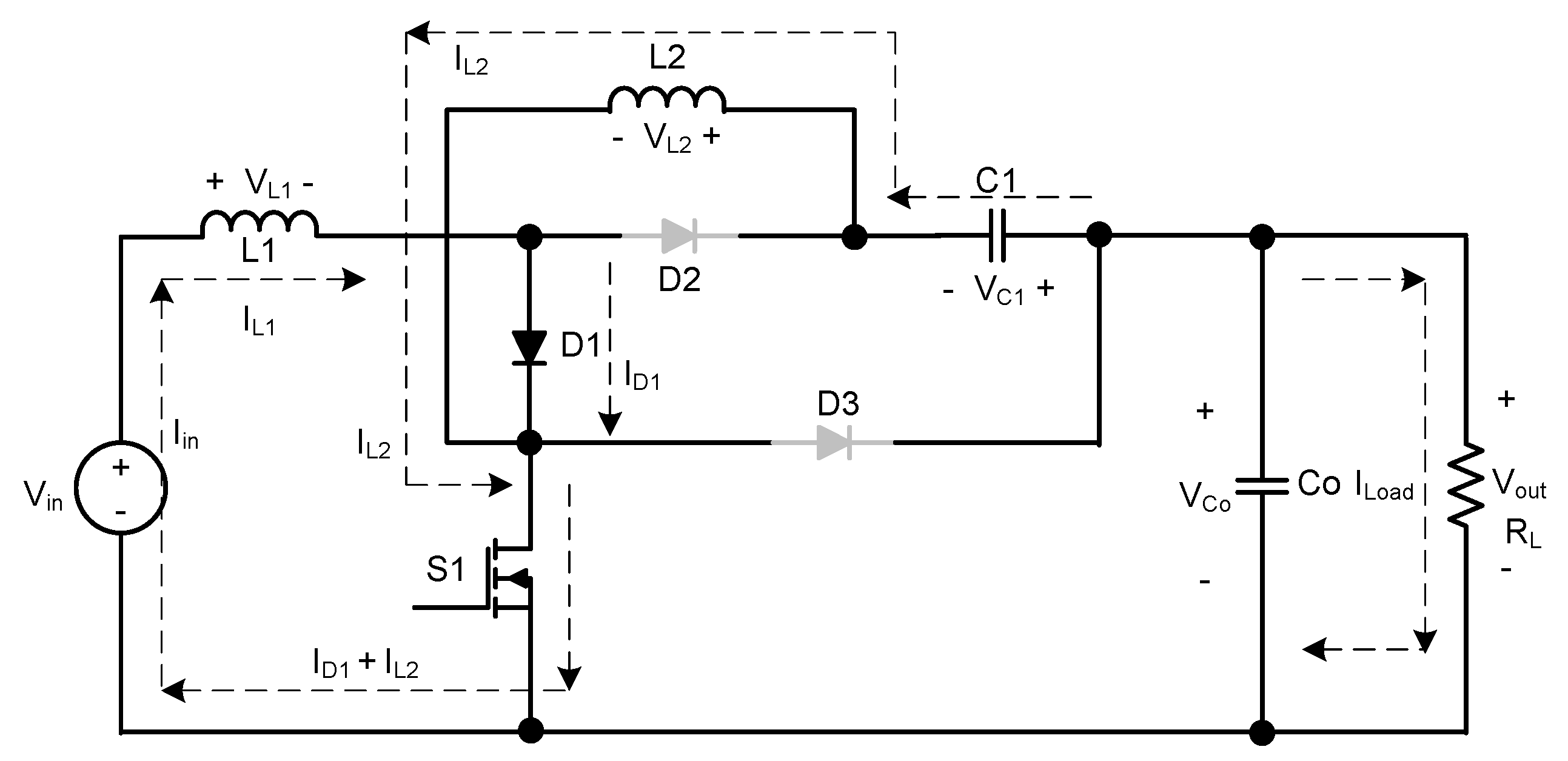
3. Steady-State Analysis
3.1. DC Voltage Gain
3.2. Voltage Stresses
3.3. Efficiency Analysis
4. Designing of the Passive Components
4.1. Design of Inductor L1
4.2. Design of Inductor L2
4.3. Design of Capacitor C1
4.4. Design of Capacitor Co
5. Results
5.1. Operating Modes of the Proposed Converter
5.2. Output DC Voltage
5.3. DC Voltage Stress
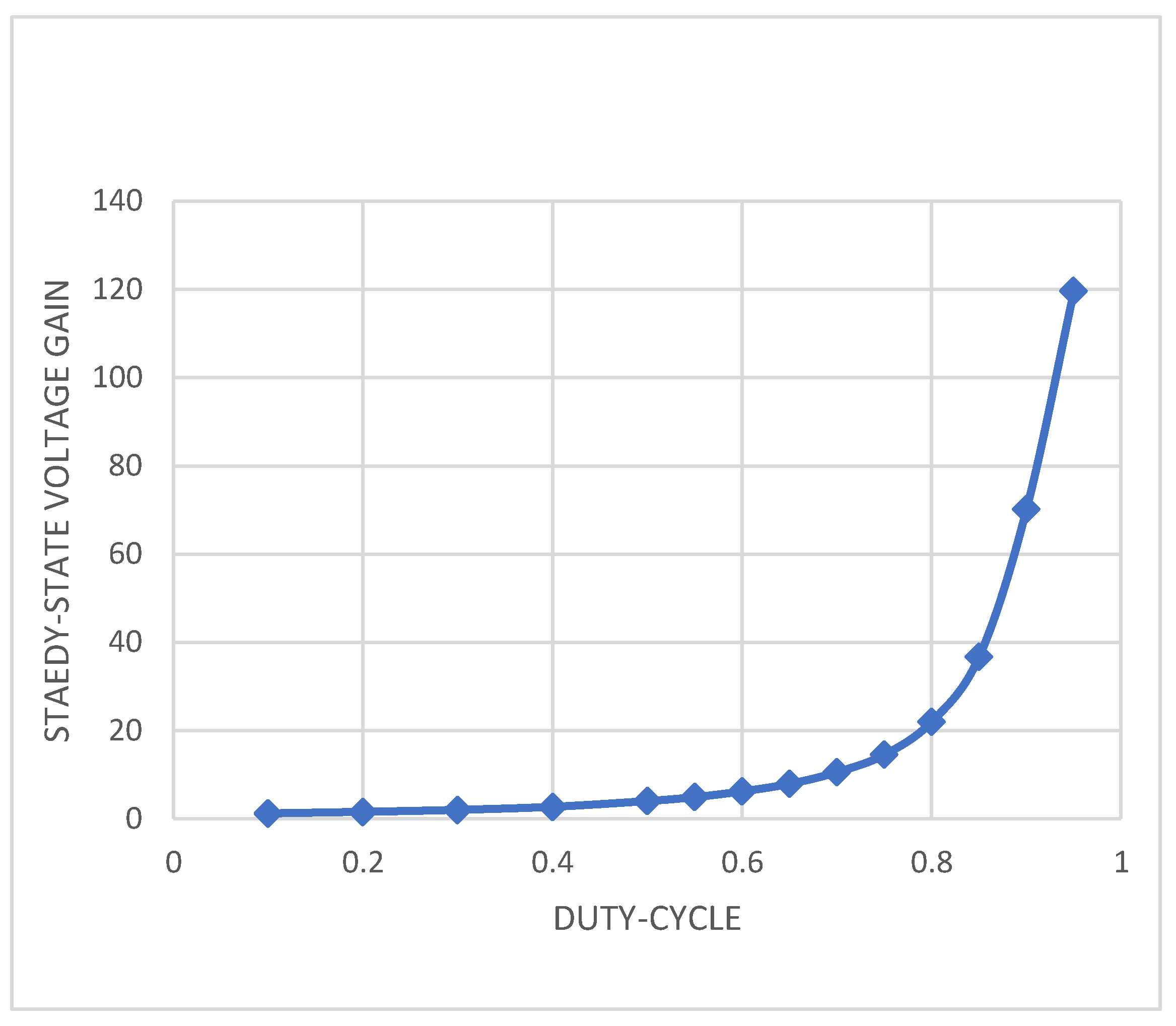
5.4. DC Voltage Gain vs. Duty-Cycle Response
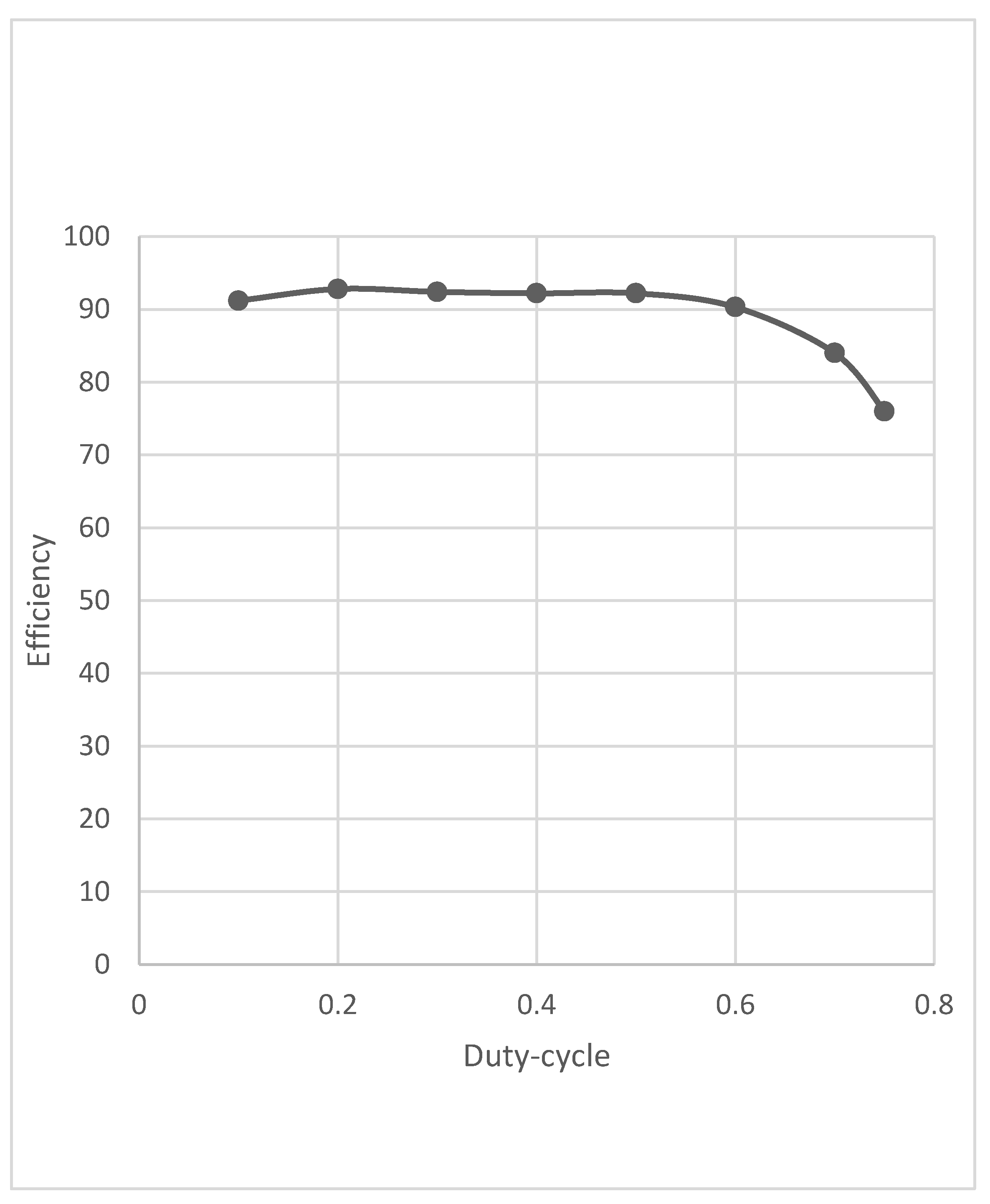
5.5. Efficiency vs. Duty-Cycle Response
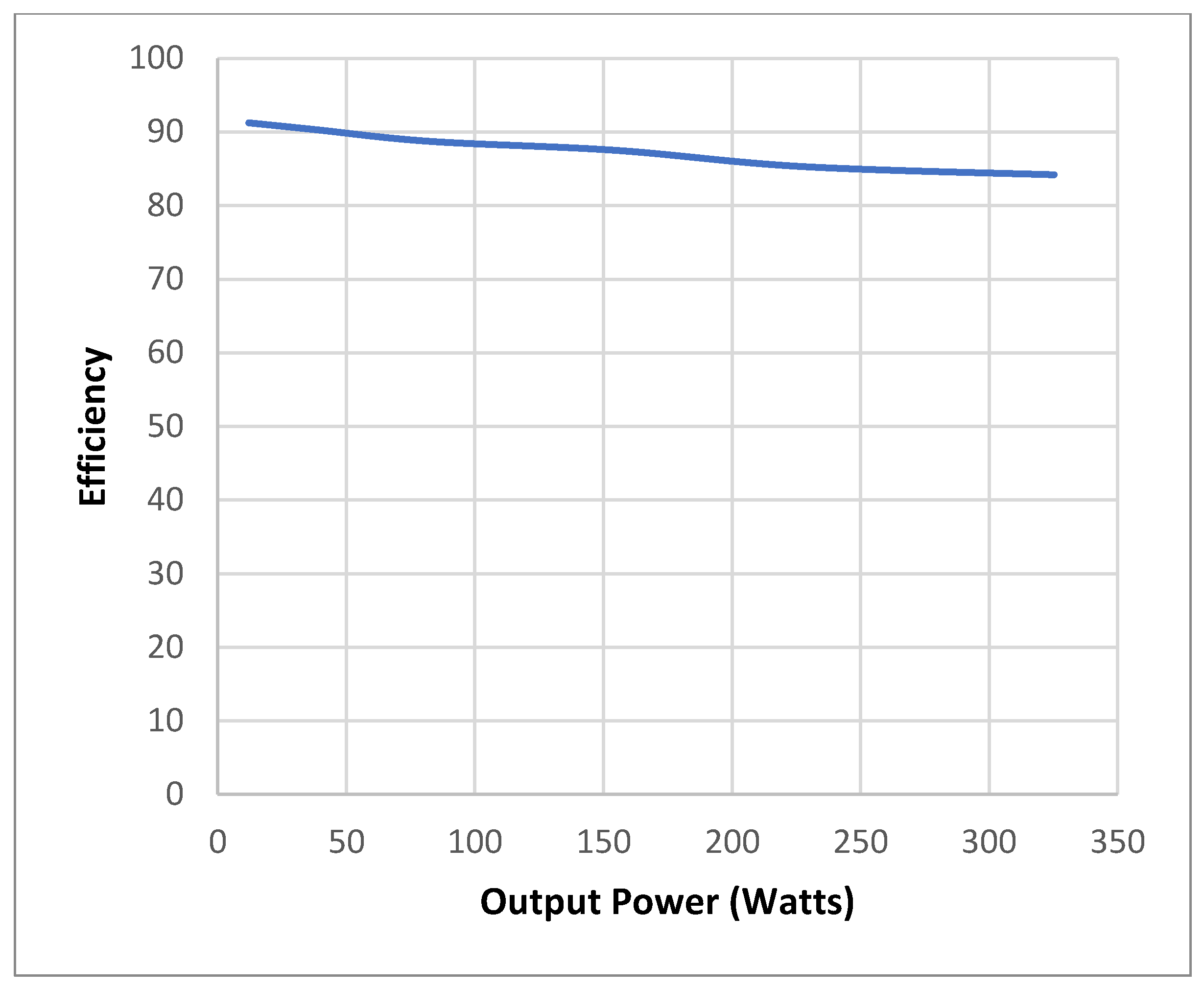
5.6. Efficiency vs. Output Power Response
5.7. Efficiency Comparison with Cascaded-Boost Converter
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shahir, F.M.; Babaei, E. Extended topology for a Boost DC-DC Converter. IEEE Trans. Power Electron. 2019, 34, 2375–2384. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Almakhles, D.J.; Padmanaban, S.; Blaabjerg, F.; Subramaniam, U.; Ionel, D.M. Analysis and Investigation of Hybrid DC–DC Non-Isolated and Non-Inverting Nx Interleaved Multilevel Boost Converter (Nx-IMBC) for High Voltage Step-Up Applications: Hardware Implementation. IEEE Access 2020, 8, 87309–87328. [Google Scholar] [CrossRef]
- Ferdowsi, A.M.; Shamsi, P. A Family of Scalable Non-Isolated Interleaved DC-DC Boost Converters with Voltage Multiplier Cells. IEEE Access 2019, 7, 11707–11721. [Google Scholar] [CrossRef]
- Jiang, W.; Chincholkar, S.H.; Chan, C.-Y. Investigation of a Voltage-Mode Controller for a dc-dc Multilevel Boost Converter. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 908–912. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Duong, T.-D.; Lim, Y.C. Switched-Capacitor-Based Dual-Switch High-Boost DC–DC Converter. IEEE Trans. Power Electron. 2018, 33, 4181–4189. [Google Scholar] [CrossRef]
- Khaligh, A.; Li, Z. Battery, Ultracapacitor, Fuel Cell, and Hybrid Energy Storage Systems for Electric, Hybrid Electric, Fuel Cell, and Plug-In Hybrid Electric Vehicles: State of the Art. IEEE Trans. Veh. Technol. 2010, 59, 2806–2814. [Google Scholar] [CrossRef]
- Lai, C.-M.; Cheng, Y.-H.; Hsieh, M.-H.; Lin, Y.-C. Development of a Bidirectional DC/DC Converter with Dual-Battery Energy Storage for Hybrid Electric Vehicle System. IEEE Trans. Veh. Technol. 2017, 67, 1036–1052. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Pires, V.F.; Cordeiro, A.; Foito, D.; Silva, J.F. High Step-Up DC-DC Converter for Fuel Cell Vehicles Based on Merged Quadratic Boost-Cuk. IEEE Trans. Veh. Technol. 2019, 68, 7521–7530. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Li, J.; Sumner, M.; Xia, C. DC–DC Boost Converter With a Wide Input Range and High Voltage Gain for Fuel Cell Vehicles. IEEE Trans. Power Electron. 2018, 34, 4100–4111. [Google Scholar] [CrossRef]
- Ferdowsi, A.A.M.; Shamsi, P. High-Voltage-Gain DC-DC Step-Up Converter with Bifold Dickson Voltage Multiplier Cells. IEEE Trans. Power Electron. 2019, 34, 9732–9742. [Google Scholar]





| D | S1 | D1 | D2 | D3 | ||||
|---|---|---|---|---|---|---|---|---|
| (13) | PSIM | (14) | PSIM | (15) | PSIM | (16) | PSIM | |
| 0.1 | 12.34 | 12.34 | 1.22 | 1.24 | 11.24 | 11.12 | 12.34 | 12.34 |
| 0.2 | 15.62 | 15.61 | 3.12 | 3.15 | 12.8 | 12.5 | 15.62 | 15.61 |
| 0.3 | 20.4 | 20.44 | 6.11 | 6.07 | 14.42 | 14.35 | 20.4 | 20.44 |
| 0.4 | 27.8 | 27.8 | 11.22 | 11.2 | 16.8 | 16.67 | 27.8 | 27.8 |
| 0.5 | 40 | 40.1 | 20.2 | 20.17 | 20.24 | 20.01 | 40 | 40.1 |
| 0.6 | 62.5 | 62.5 | 37.51 | 37.44 | 27.2 | 26.6 | 62.5 | 62.5 |
| 0.7 | 111.11 | 111.11 | 78.11 | 78.08 | 39.24 | 38.33 | 111.11 | 111.11 |
| 0.75 | 160 | 159.8 | 113.82 | 113.8 | 39.88 | 38.31 | 160 | 159.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafiq, U.; Murtaza, A.F.; Sher, H.A.; Gandini, D. Design and Analysis of a Novel High-Gain DC-DC Boost Converter with Low Component Count. Electronics 2021, 10, 1761. https://doi.org/10.3390/electronics10151761
Rafiq U, Murtaza AF, Sher HA, Gandini D. Design and Analysis of a Novel High-Gain DC-DC Boost Converter with Low Component Count. Electronics. 2021; 10(15):1761. https://doi.org/10.3390/electronics10151761
Chicago/Turabian StyleRafiq, Usman, Ali Faisal Murtaza, Hadeed A. Sher, and Dario Gandini. 2021. "Design and Analysis of a Novel High-Gain DC-DC Boost Converter with Low Component Count" Electronics 10, no. 15: 1761. https://doi.org/10.3390/electronics10151761
APA StyleRafiq, U., Murtaza, A. F., Sher, H. A., & Gandini, D. (2021). Design and Analysis of a Novel High-Gain DC-DC Boost Converter with Low Component Count. Electronics, 10(15), 1761. https://doi.org/10.3390/electronics10151761





