A Predictive Control Strategy for Energy Management in Micro-Grid Systems
Abstract
:1. Introduction
2. Related Work
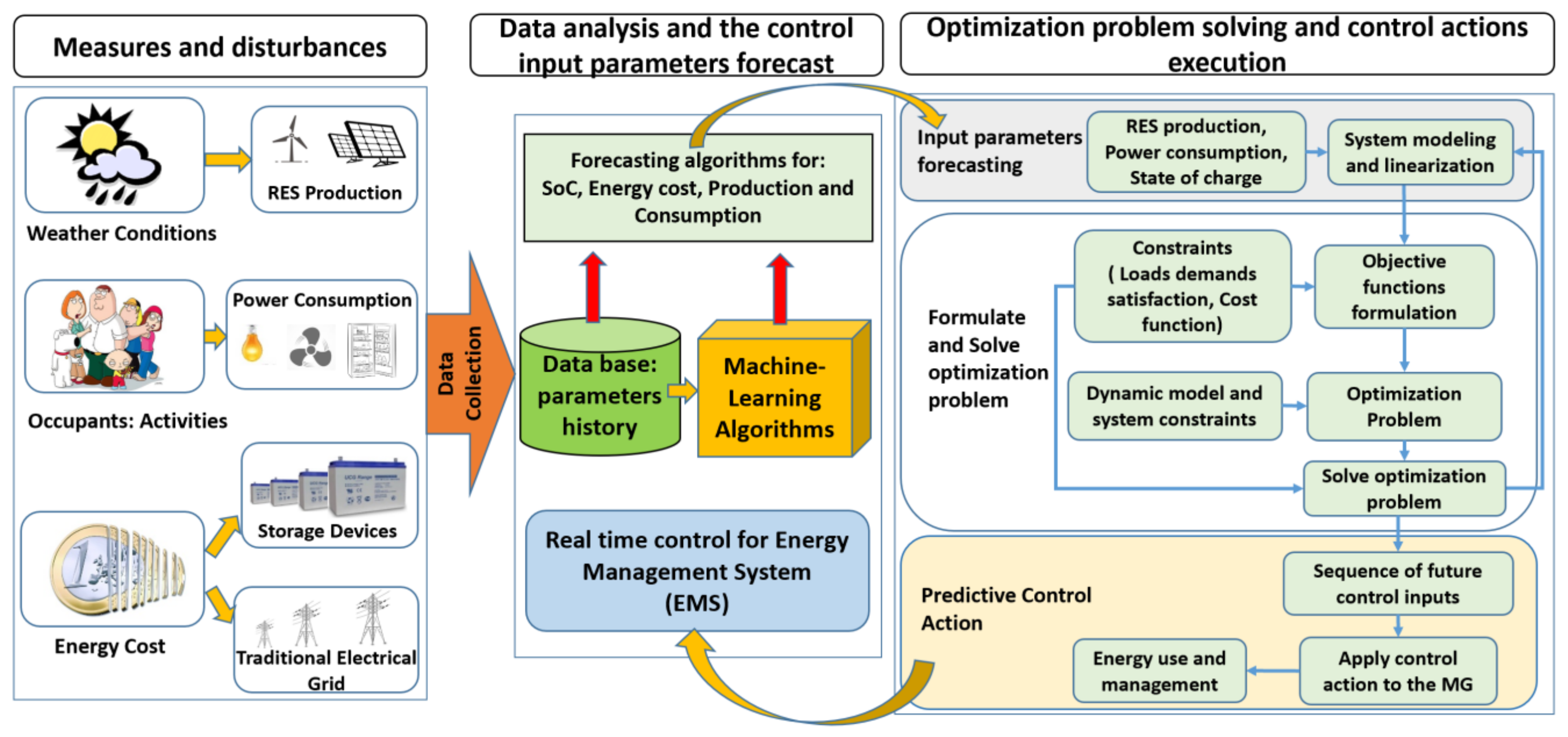
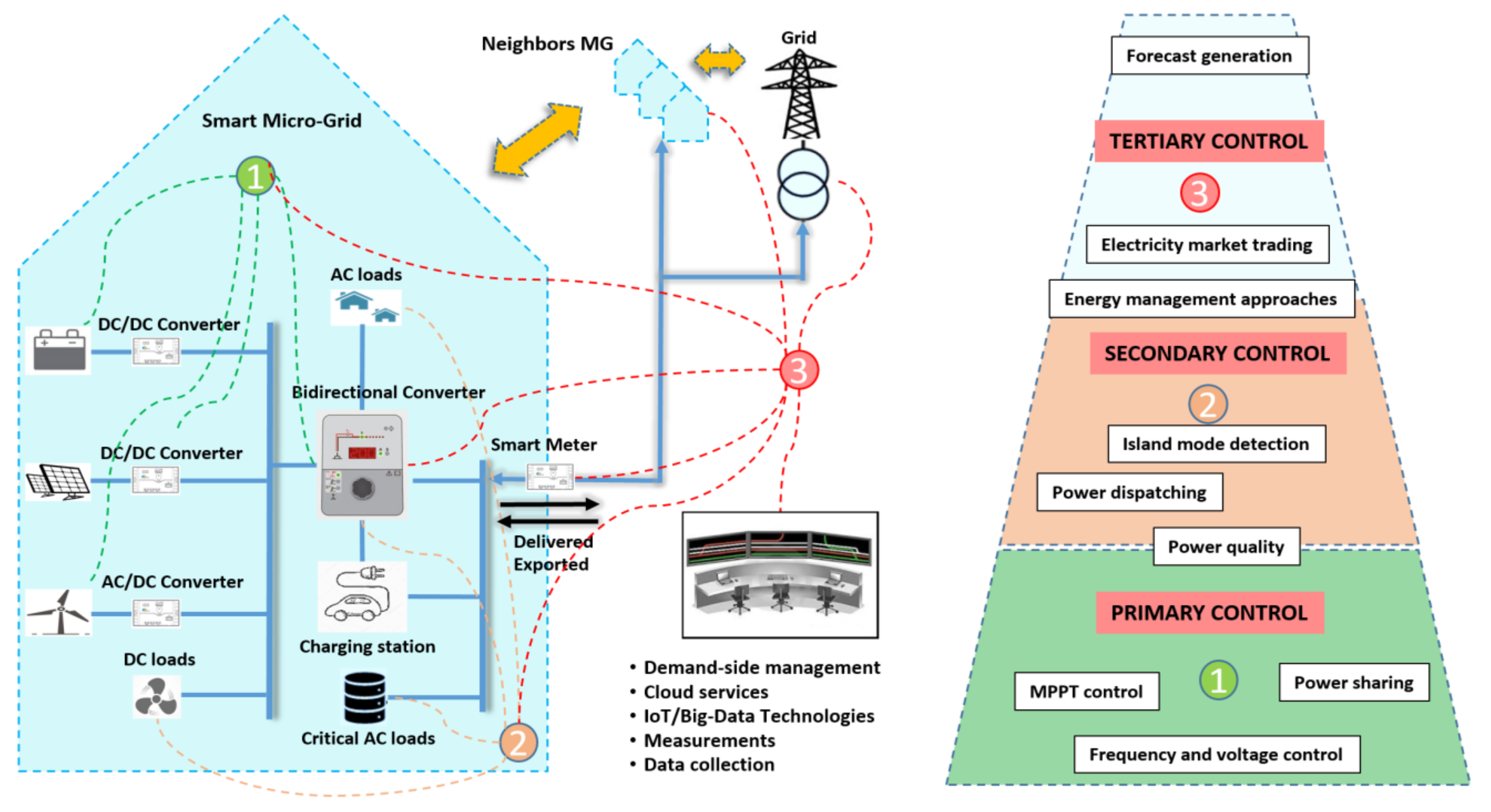
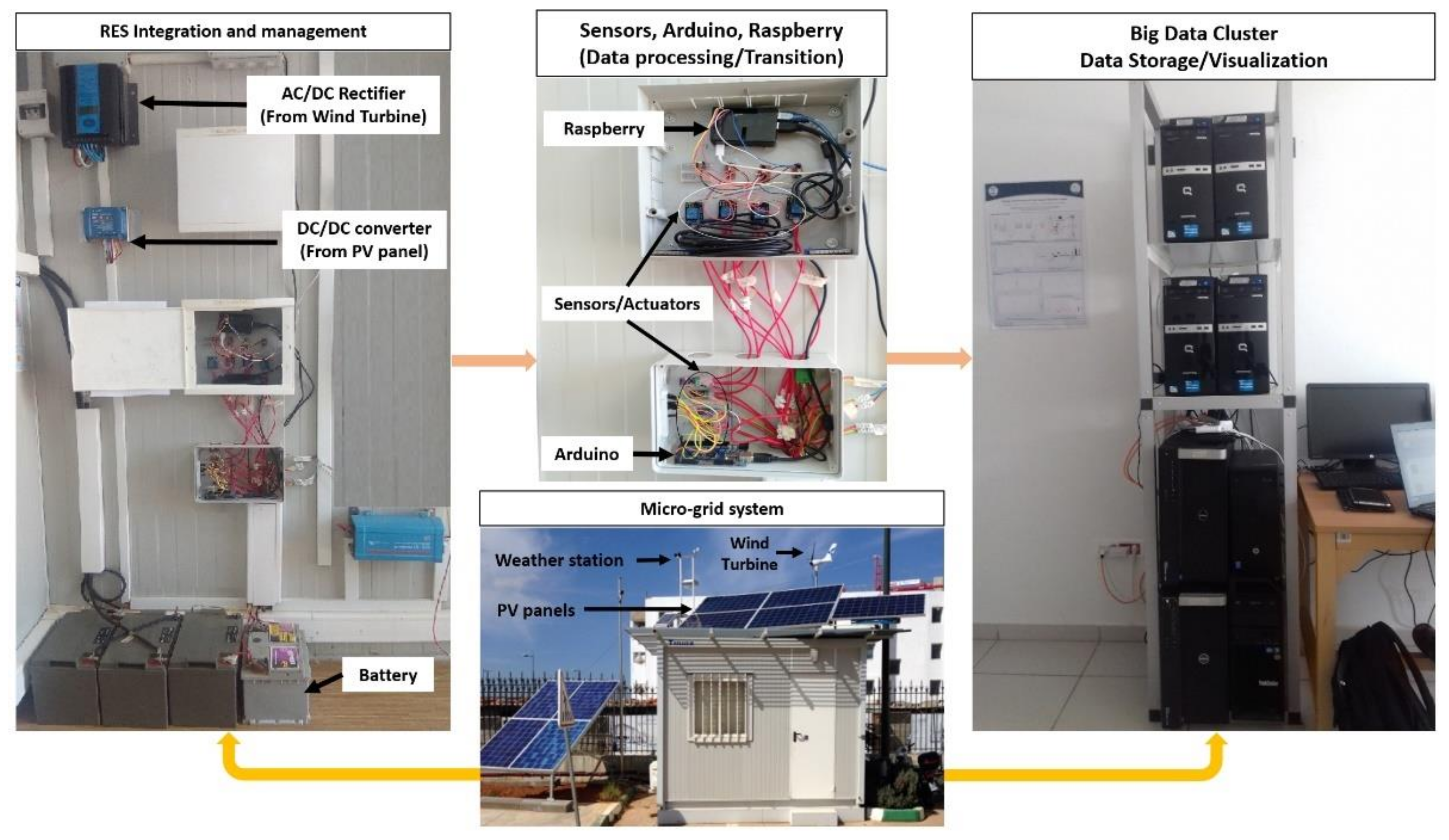
3. Materials and Methods
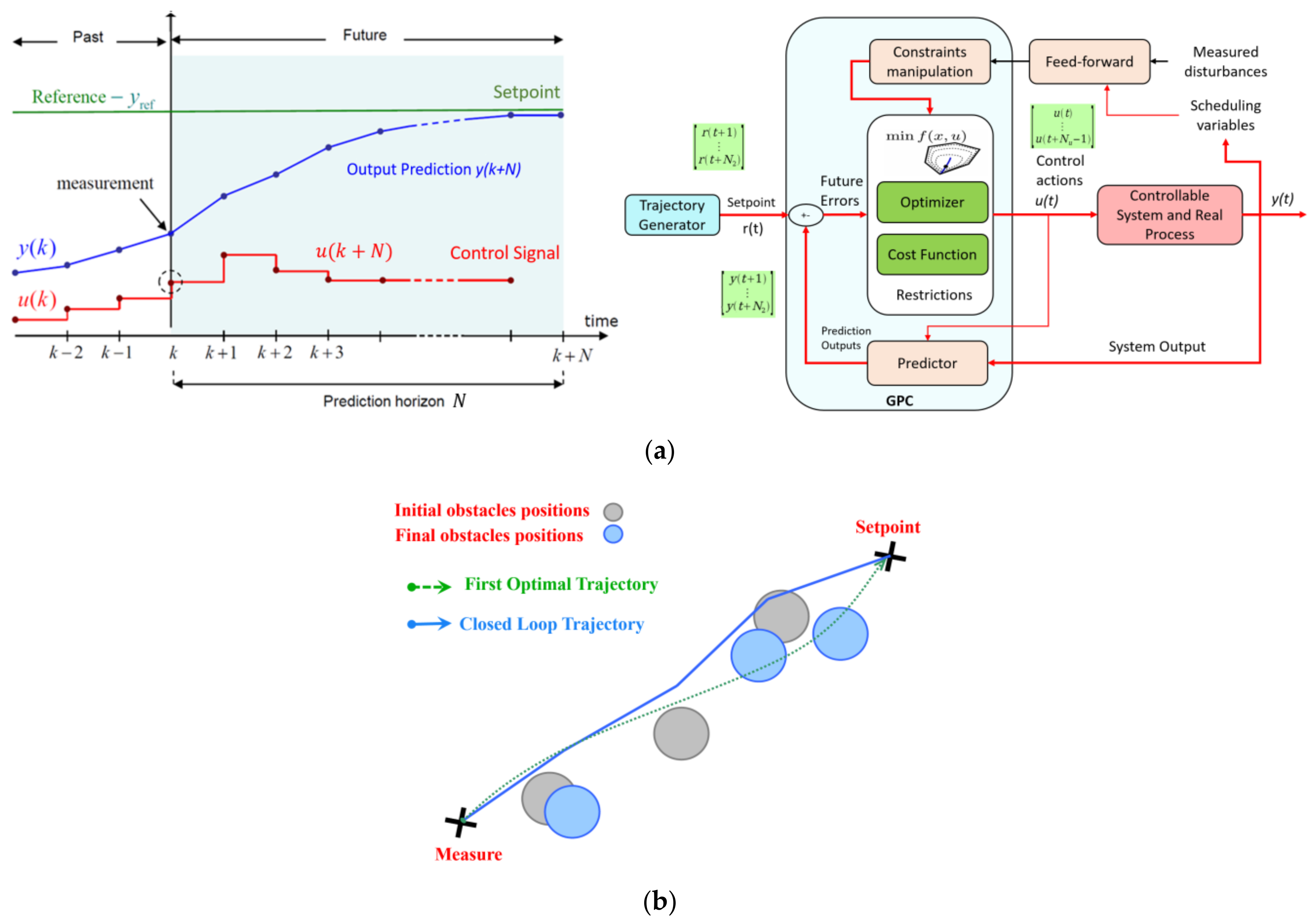
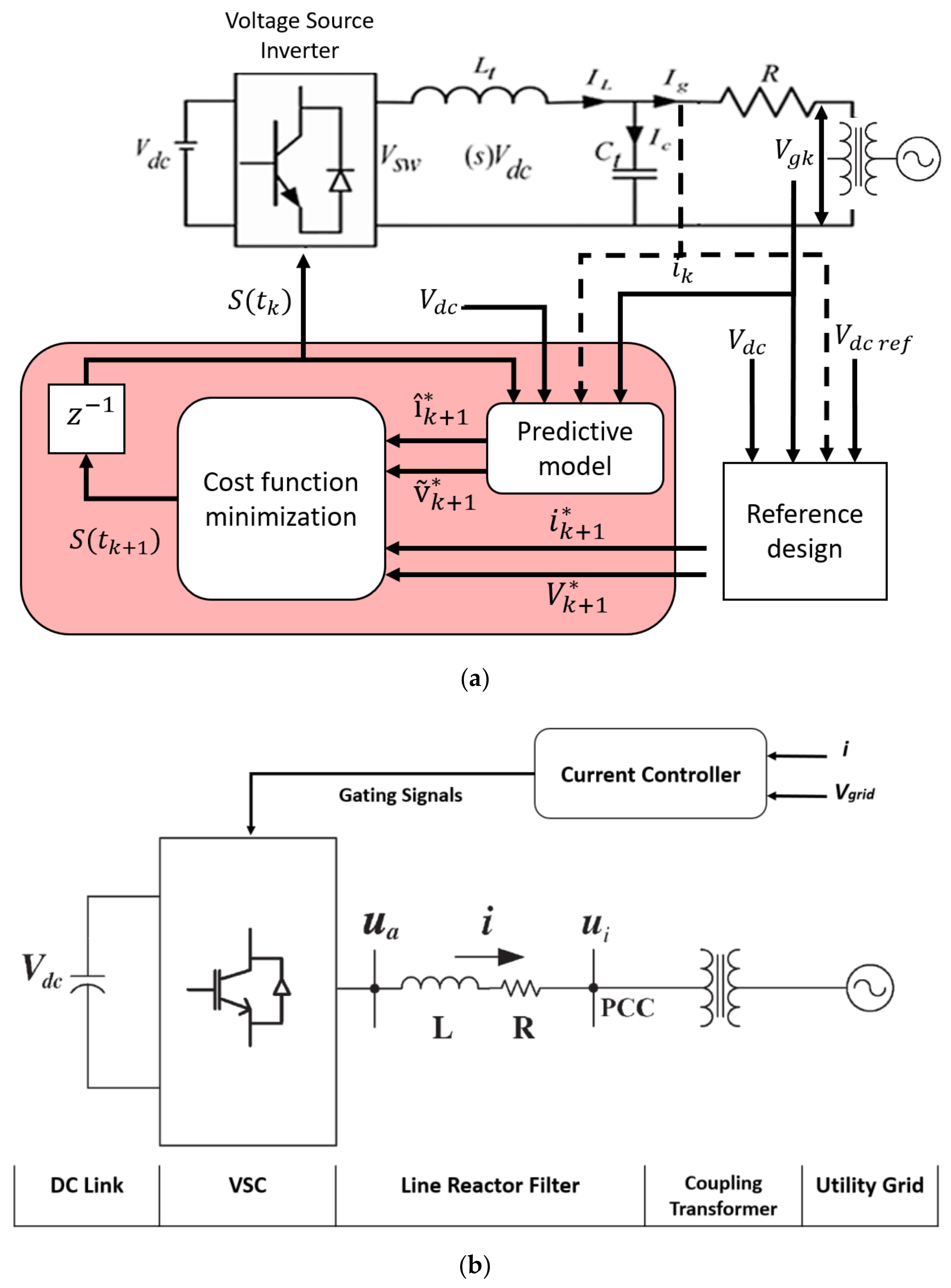
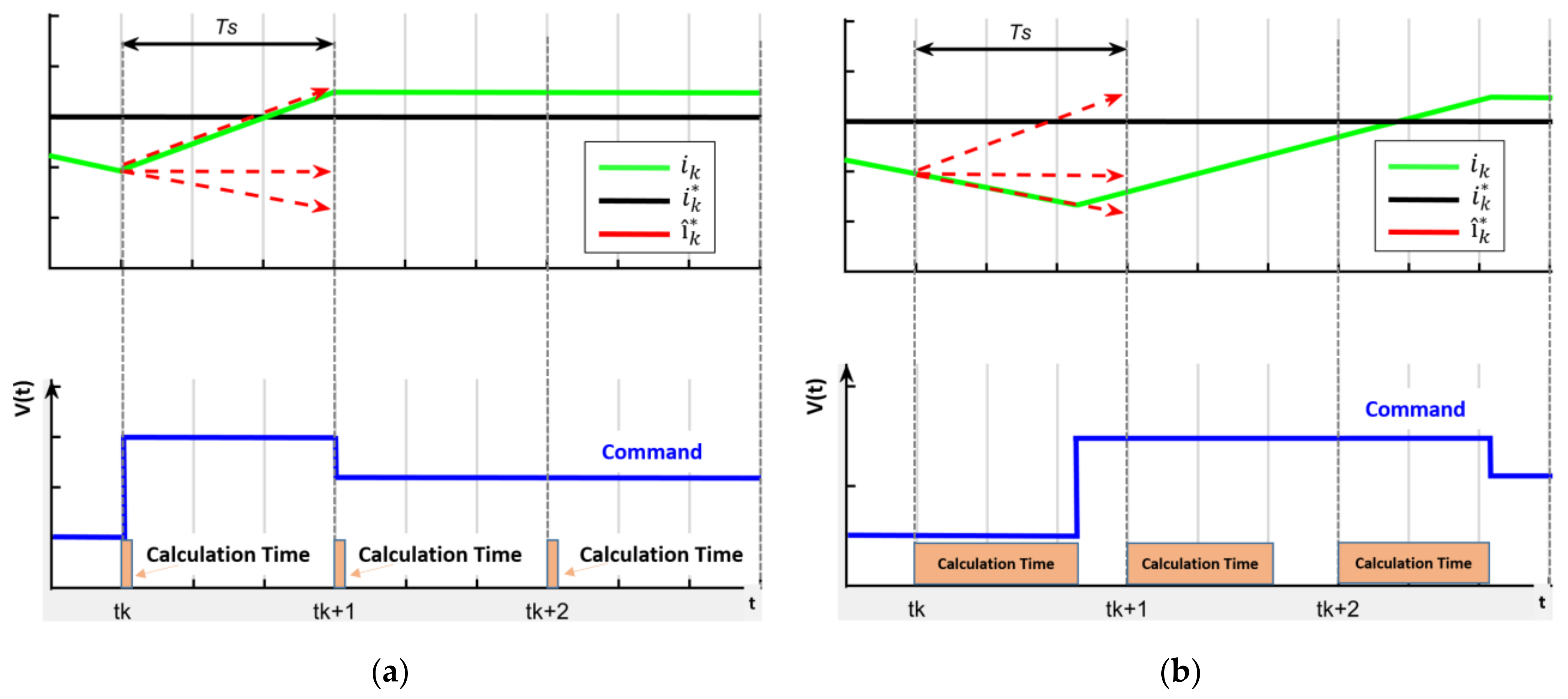
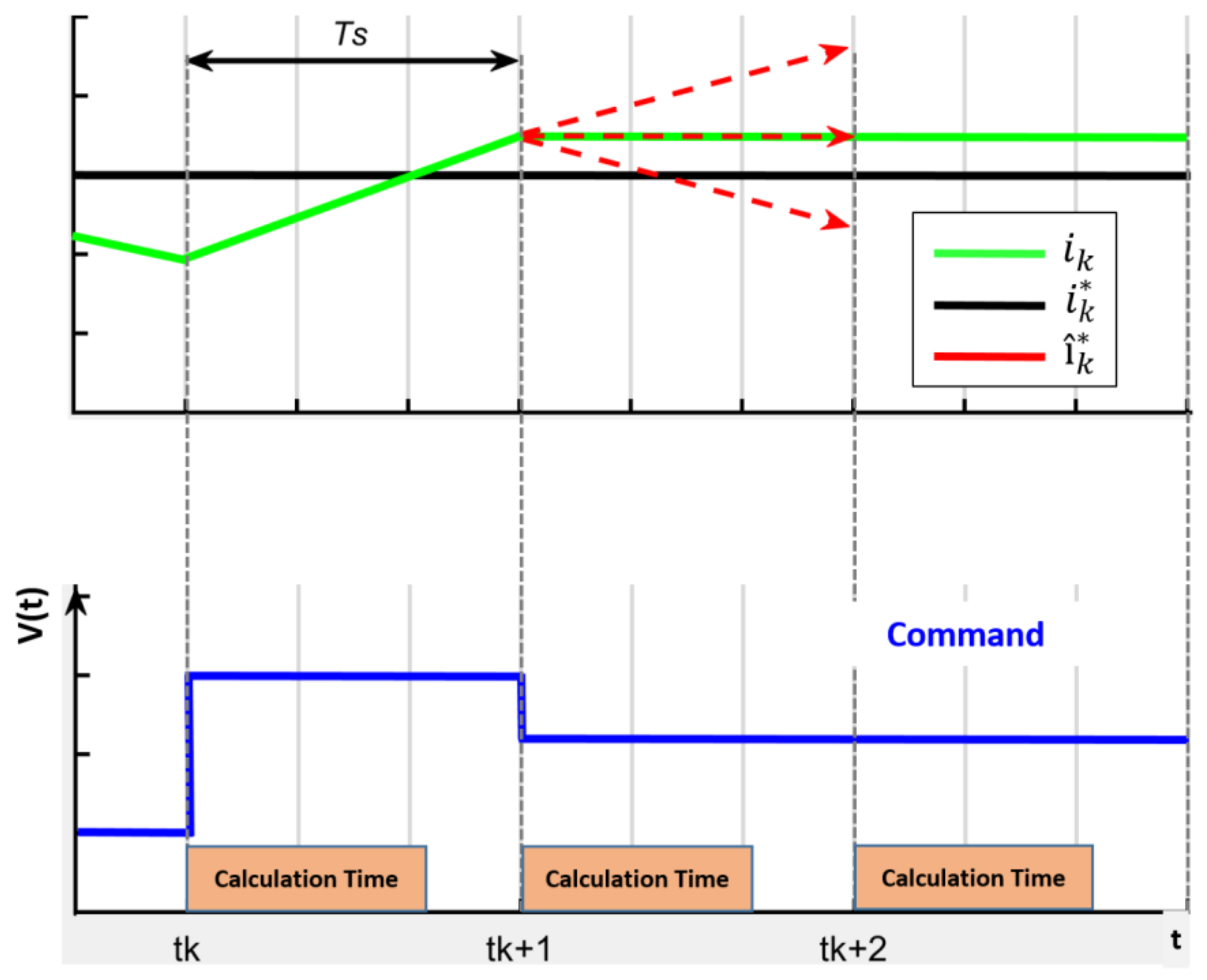
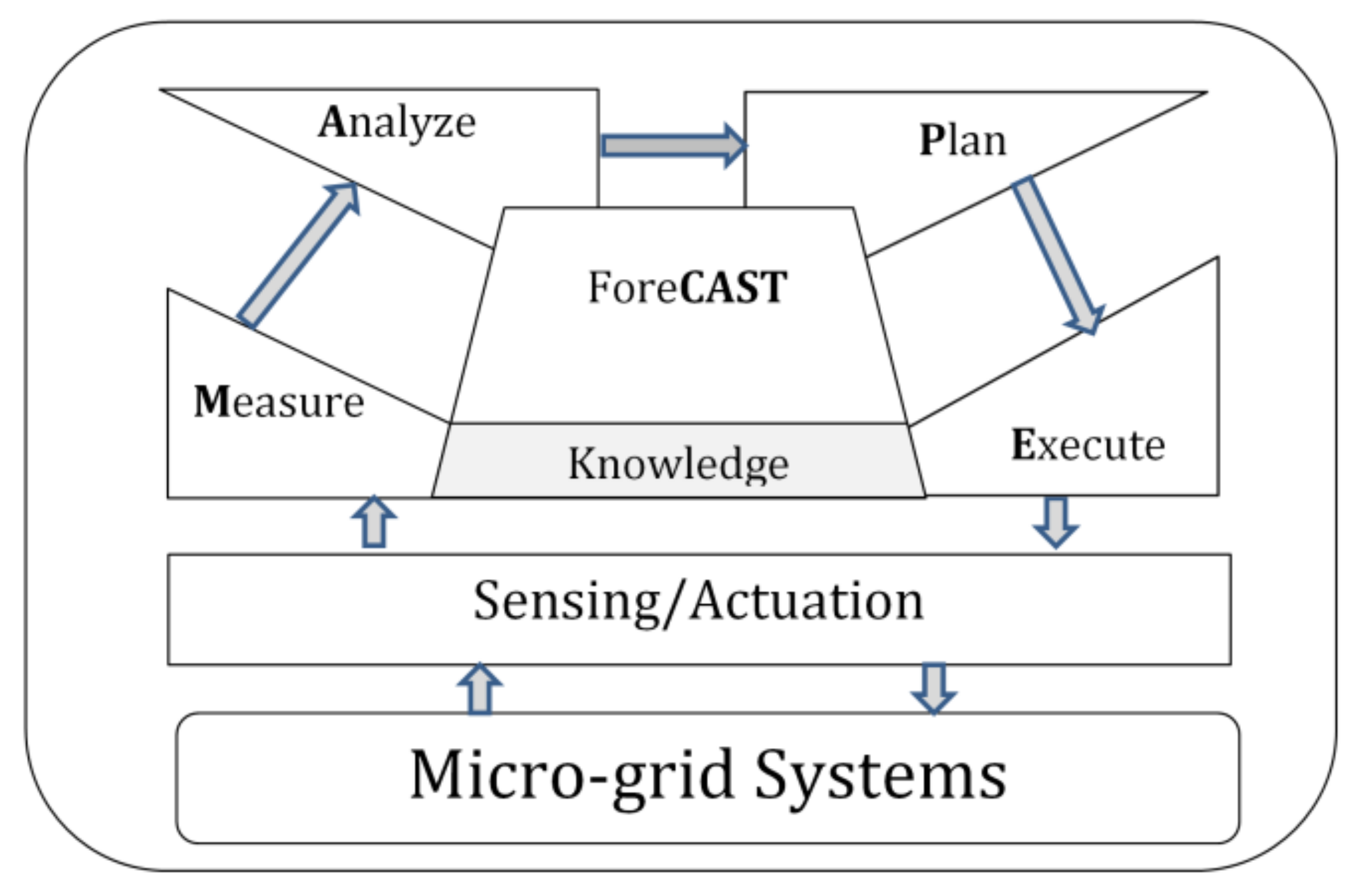
3.1. Control Strategy Design and GPC Integration
3.2. Single-Phase Modeling for MG Synchronization
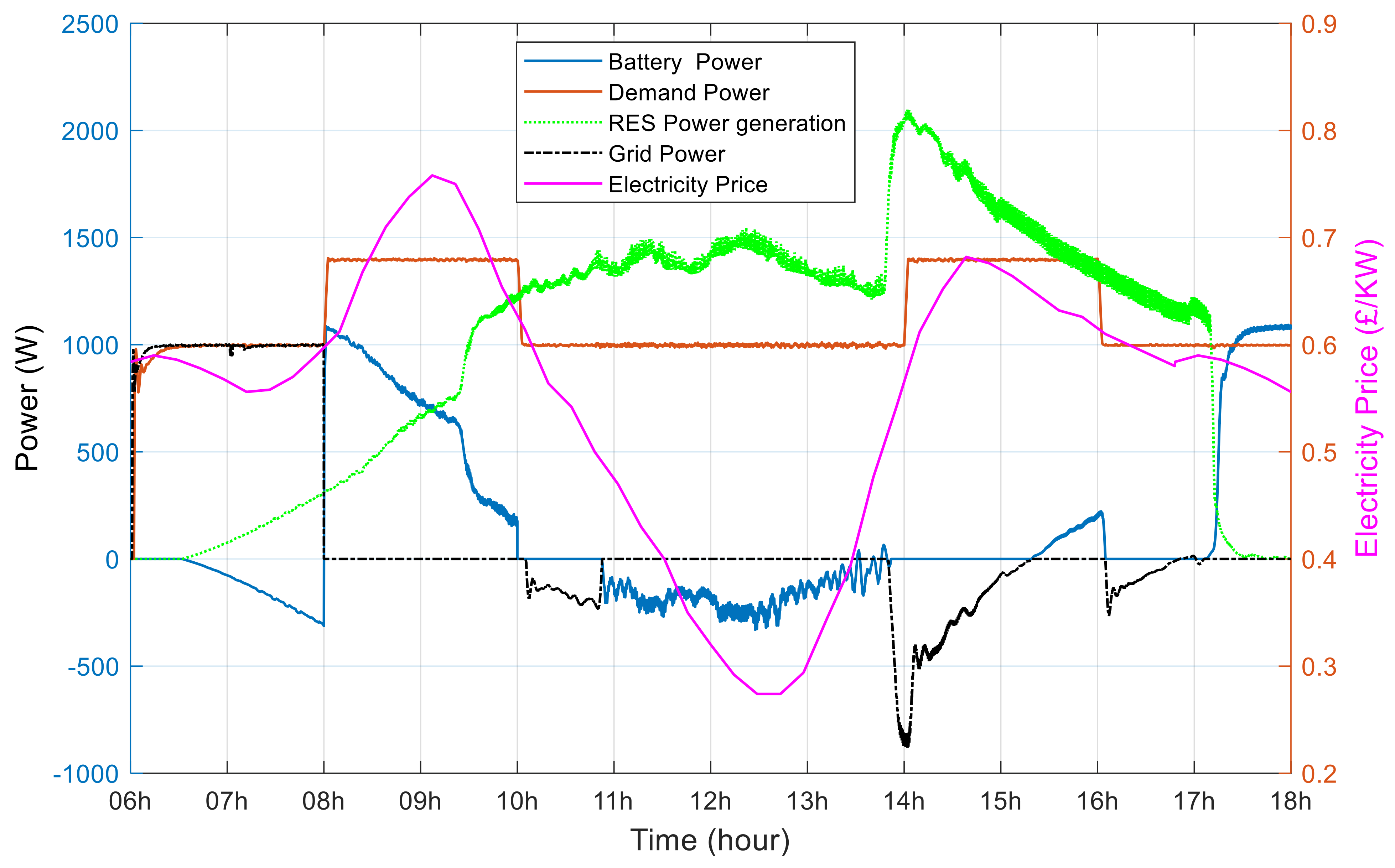
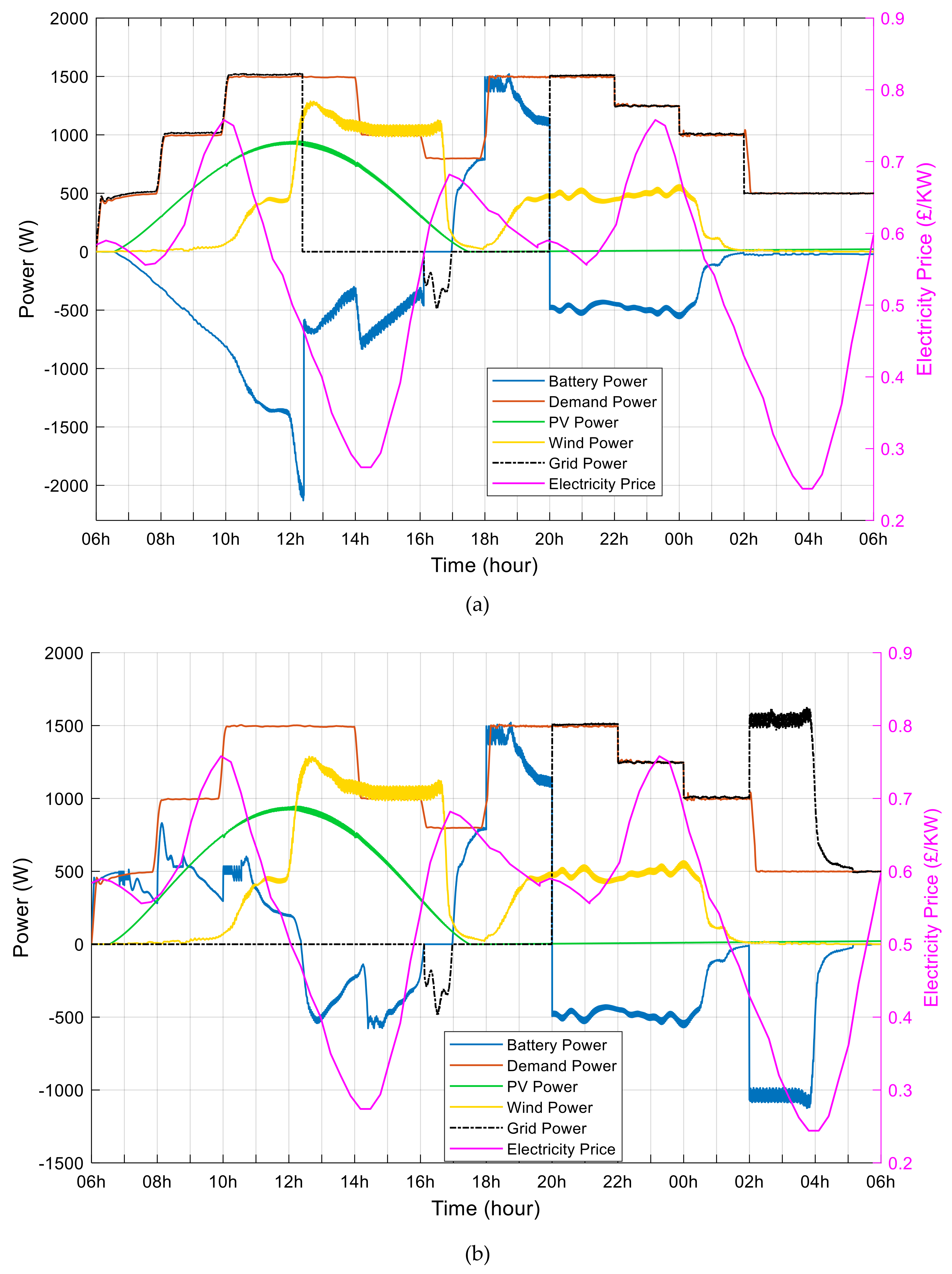
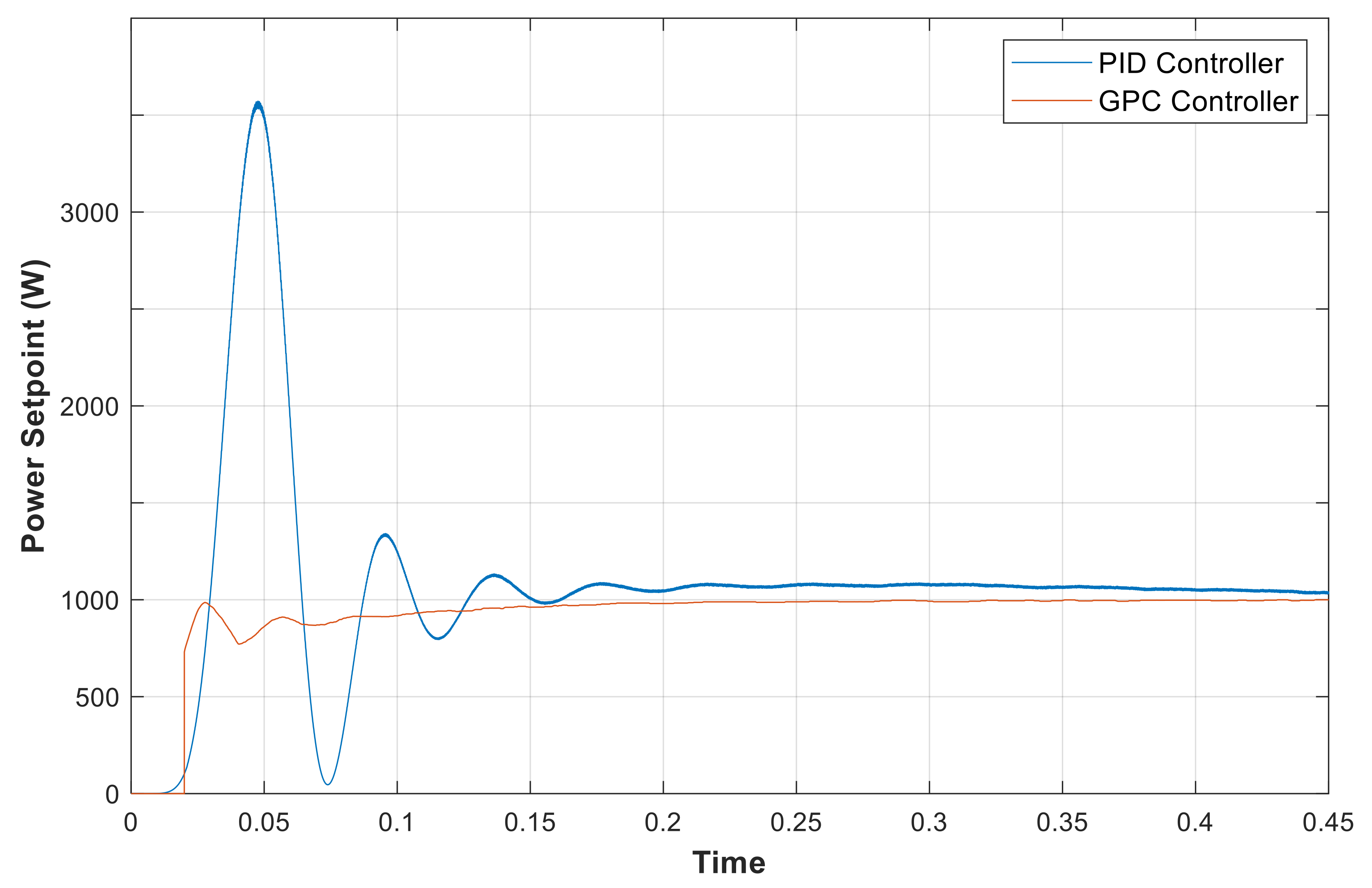
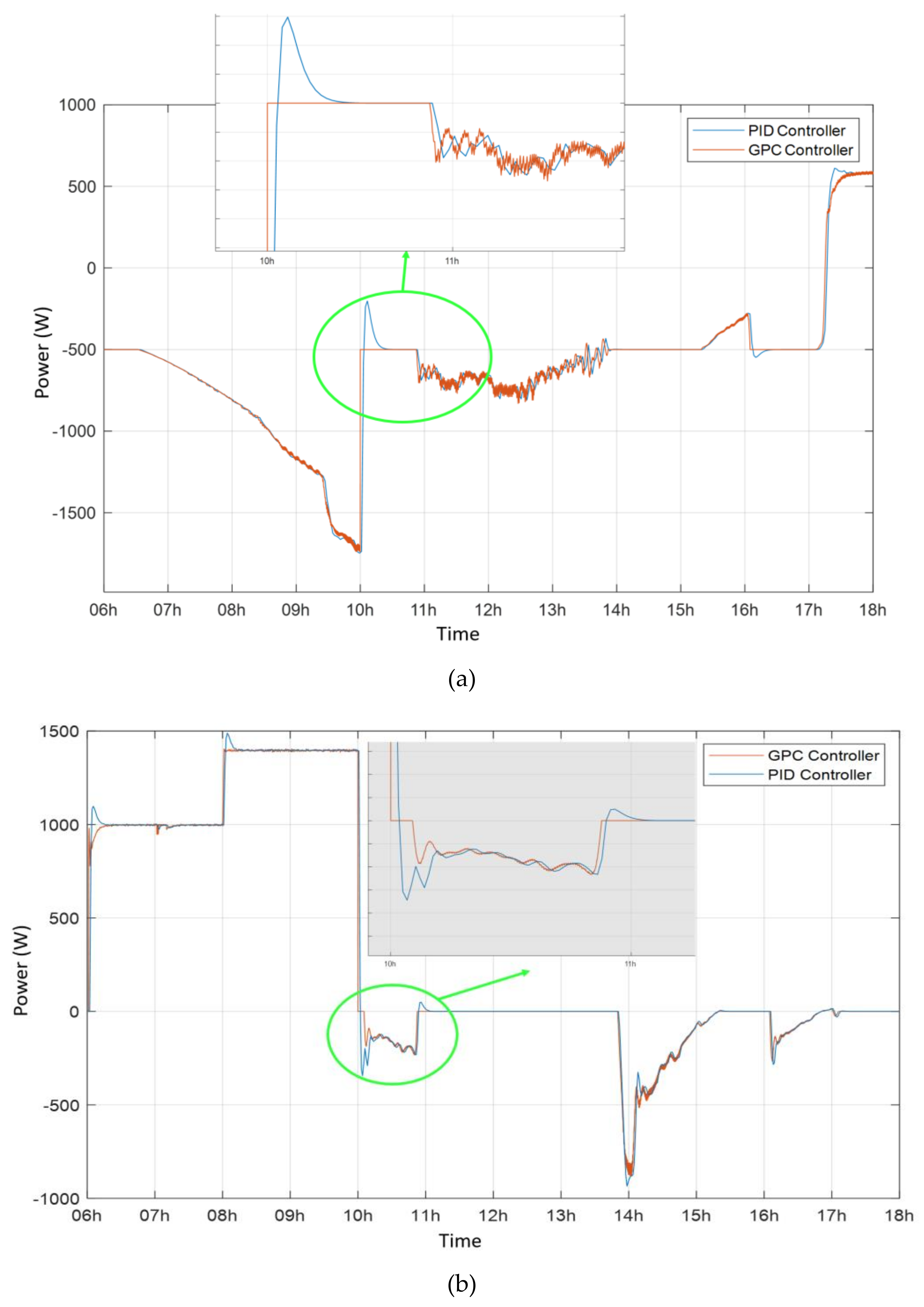
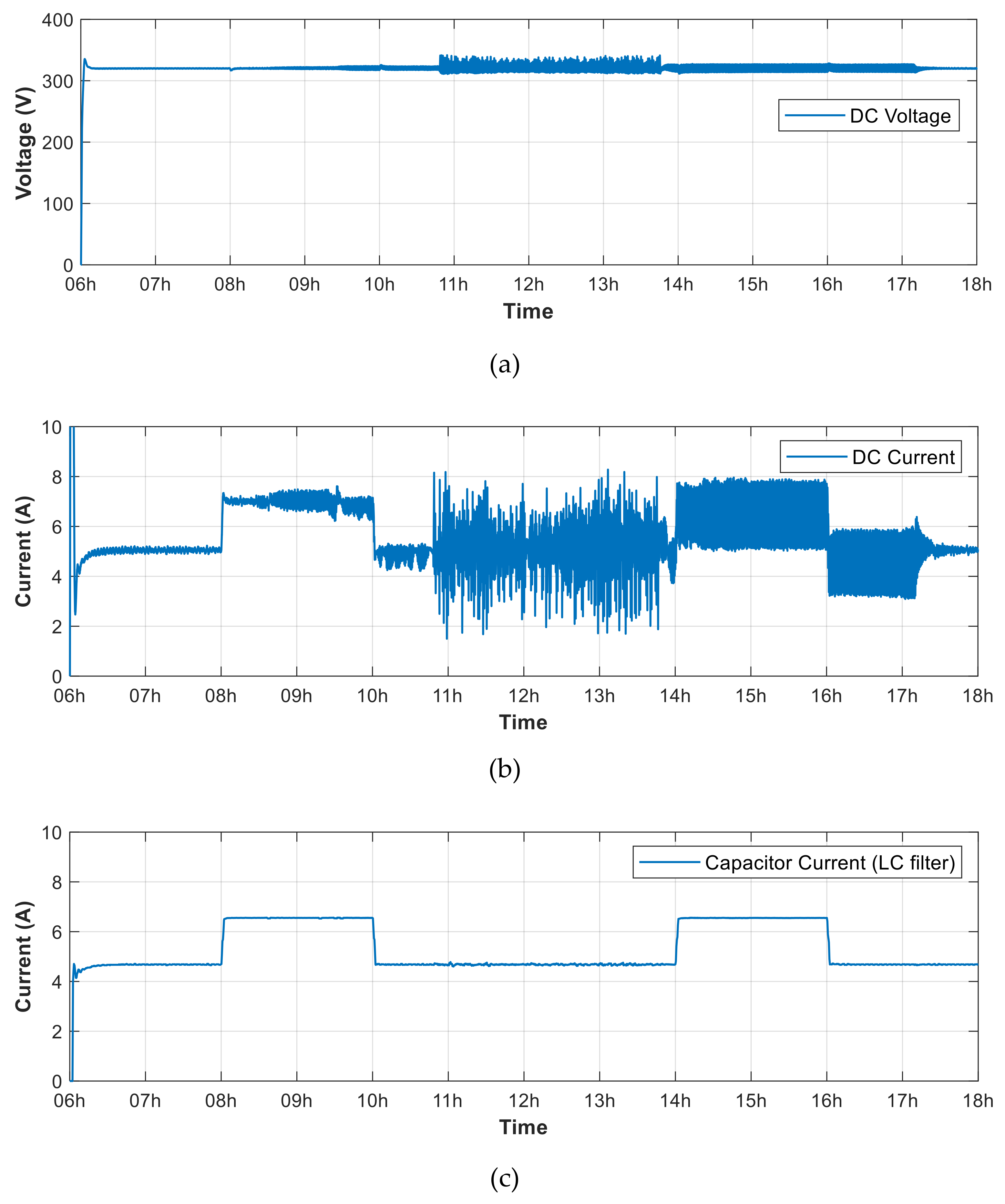
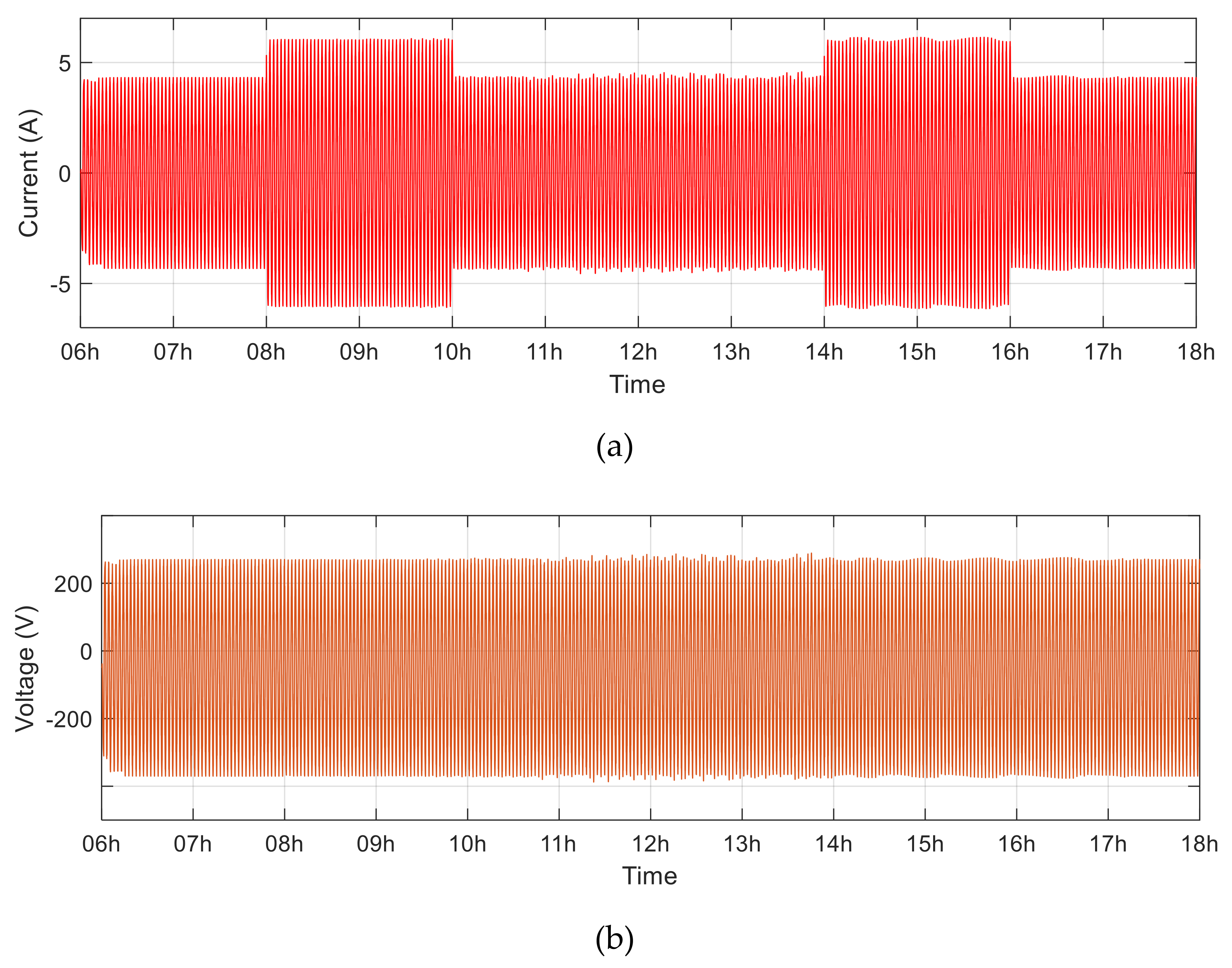
4. Results and Performance Evaluation
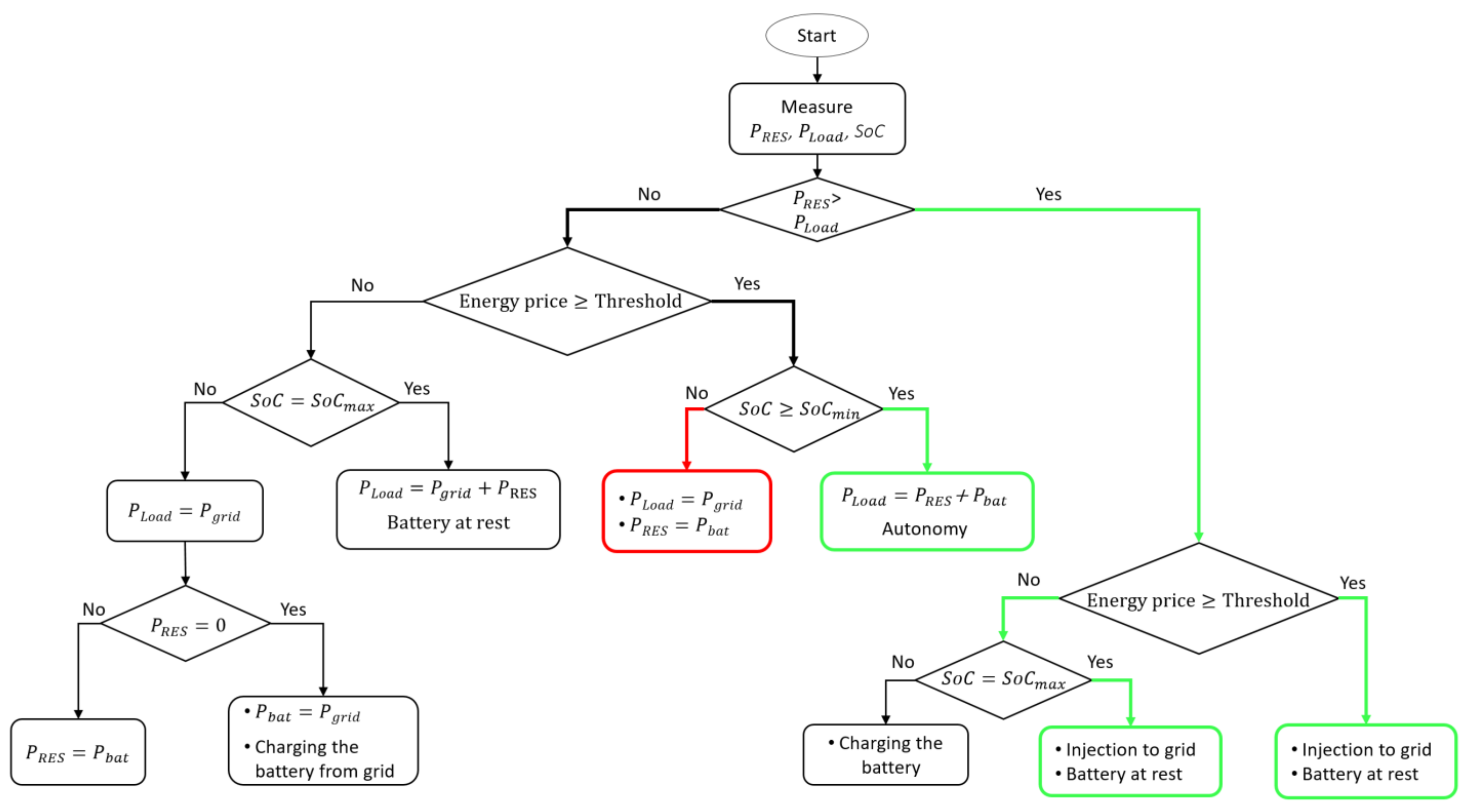
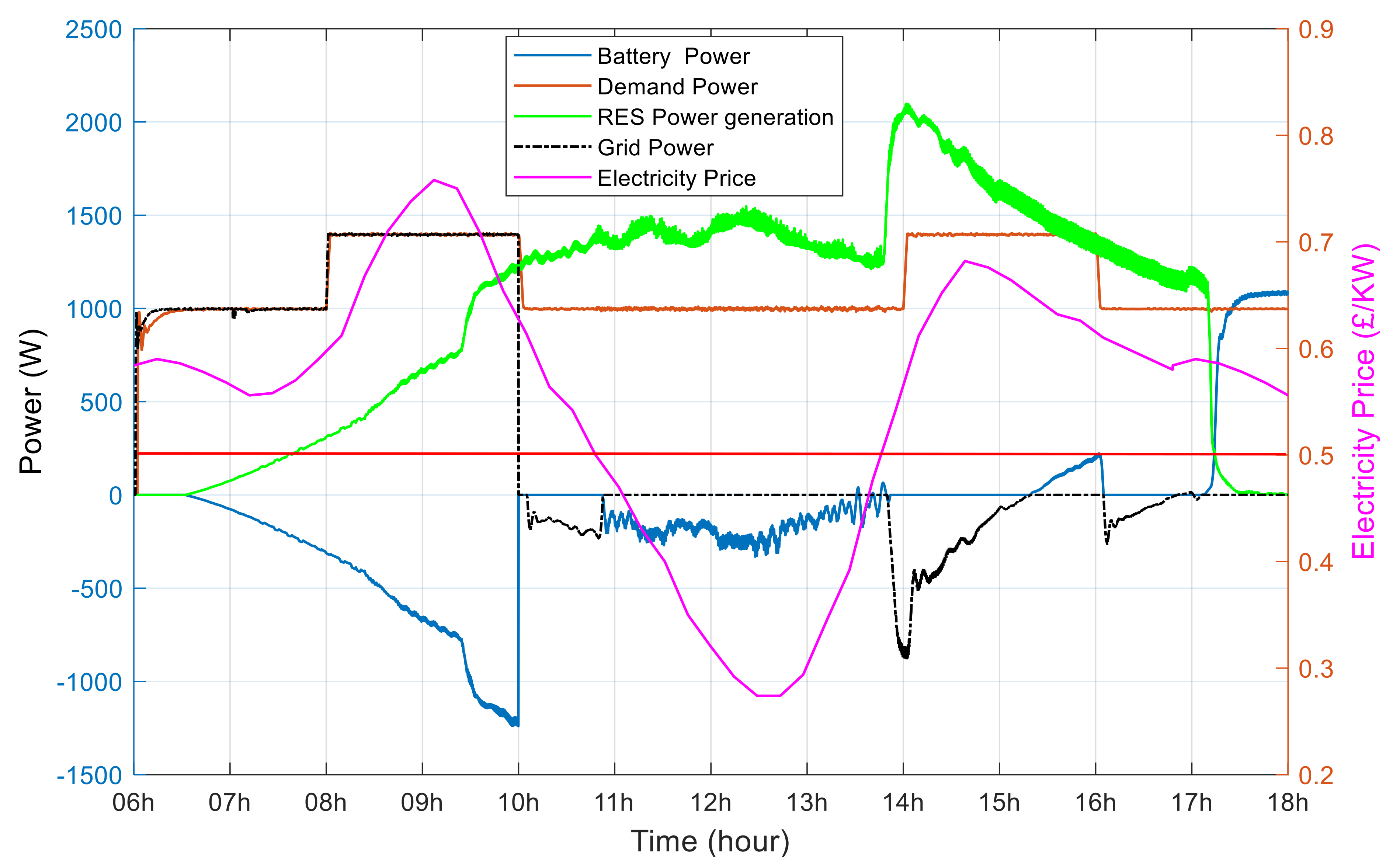
4.1. EM Scenarios Using GPC Control
4.2. The Benefit of GPC Model on the Electricity Price
4.3. State of the Art Synthesis and Our Contribution
4.4. GPC Controller for Power Quality Regulation
5. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elmouatamid, A.; NaitMalek, Y.; Ouladsine, R.; Bakhouya, M.; Elkamoun, N.; Khaidar, M.; Zine-Dine, K. A Micro-grid system infrastructure for efficient energy management in smart buildings. In Submitted to ATSPES’1 (Advanced Technologies for Solar Photovoltaics Energy Systems); Springer: Cham, Switzerland, 2020. [Google Scholar]
- Li, J.; Murphy, E.; Winnick, J.; Kohl, P.A. Studies on the cycle life of commercial lithium-ion batteries during rapid charge–discharge cycling. J. Power Sources 2001, 102, 294–301. [Google Scholar] [CrossRef]
- Elmouatamid, A. MAPCAST: An adaptive control approach using predictive analytics for energy balance in micro-grid systems. Int. J. Renew. Energy Res. 2020, 10, 945–954. [Google Scholar]
- Elmouatamid, A.; NaitMalek, Y.; Bakhouya, M.; Ouladsine, R.; Elkamoun, N.; Zine-Dine, K.; Khaidar, M. An energy management platform for micro-grid systems using internet of things and big-data technologies. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2019, 233, 904–917. [Google Scholar] [CrossRef]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; Zine-Dine, K.; Khaidar, M. A Control Strategy Based on Power Forecasting for Micro-Grid Systems. In Proceedings of the 2019 IEEE International Smart Cities Conference (ISC2), Casablanca, Morocco, 14–17 October 2019; pp. 735–740. [Google Scholar]
- Serale, G.; Fiorentini, M.; Capozzoli, A.; Bernardini, D.; Bemporad, A. Model predictive control (MPC) for enhancing building and HVAC system energy efficiency: Problem formulation, applications and opportunities. Energies 2018, 11, 631. [Google Scholar] [CrossRef] [Green Version]
- Elkhoukhi, H.; NaitMalek, Y.; Bakhouya, M.; Berouine, A.; Kharbouch, A.; Lachhab, F.; Essaaidi, M. A platform architecture for occupancy detection using stream processing and machine learning approaches. Concurr. Comput. Pract. Exp. 2020, 32, e5651. [Google Scholar] [CrossRef]
- NaitMalek, Y.; Najib, M.; Bakhouya, M.; Essaaidi, M. On the Use of Machine Learning for State-of-Charge Forecasting in Electric Vehicles. In Proceedings of the 2019 IEEE International Smart Cities Conference (ISC2), Casablanca, Morocco, 14–17 October 2019; pp. 408–413. [Google Scholar]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; El Kamoun, N.; Khaidar, M.; Zine-Dine, K. Review of control and energy management approaches in micro-grid systems. Energies 2020, 14, 168. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, J.; Guerrero, J.M. Model Predictive Control of Smart Microgrids. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 2815–2820. [Google Scholar]
- Dehghani-Pilehvarani, A.; Markou, A.; Ferrarini, L. A hierarchical distributed predictive control approach for microgrids energy management. Sustain. Cities Soc. 2019, 48, 101536. [Google Scholar]
- Marzband, M.; Yousefnejad, E.; Sumper, A.; Domínguez-García, J.L. Real time experimental implementation of optimum energy management system in standalone microgrid by using multi-layer ant colony optimization. Int. J. Electr. Power Energy Syst. 2016, 75, 265–274. [Google Scholar] [CrossRef] [Green Version]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; El Kamoun, N.; Zine-Dine, K.; Khaidar, M. A Model Predictive Control Approach for Energy Management in Micro-Grid Systems. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar]
- Hosseinzadeh, M.; Salmasi, F.R. Robust optimal power management system for a hybrid AC/DC micro-grid. IEEE Trans. Sustain. Energy 2015, 6, 675–687. [Google Scholar] [CrossRef]
- Luna, A.C.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Mixed-integer-linear-programming-based energy management system for hybrid PV-wind-battery microgrids: Modeling, design, and experimental verification. IEEE Trans. Power Electron. 2017, 32, 2769–2783. [Google Scholar] [CrossRef] [Green Version]
- Vergara, P.P.; López, J.C.; da Silva, L.C.; Rider, M.J. Security-constrained optimal energy management system for three-phase residential microgrids. Electr. Power Syst. Res. 2017, 146, 371–382. [Google Scholar] [CrossRef]
- Xiang, Y.; Liu, J.; Liu, Y. Robust energy management of microgrid with uncertain renewable generation and load. IEEE Trans. Smart Grid 2015, 7, 1034–1043. [Google Scholar] [CrossRef]
- Berouine, A.; Ouladsine, R.; Bakhouya, M.; Essaaidi, M. Towards a real-time predictive management approach of indoor air quality in energy-efficient buildings. Energies 2020, 13, 3246. [Google Scholar] [CrossRef]
- Buyak, N.A.; Deshko, V.I.; Sukhodub, I.O. Buildings energy use and human thermal comfort according to energy and exergy approach. Energy Build. 2017, 146, 172–181. [Google Scholar] [CrossRef]
- Rahmani-Andebili, M.; Shen, H. Cooperative Distributed Energy Scheduling for Smart Homes Applying Stochastic Model Predictive Control. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Hemmati, R.; Saboori, H. Stochastic optimal battery storage sizing and scheduling in home energy management systems equipped with solar photovoltaic panels. Energy Build. 2017, 152, 290–300. [Google Scholar] [CrossRef]
- Bordons, C.; Teno, G.; Marquez, J.J.; Ridao, M.A. Effect of the Integration of Disturbances Prediction in Energy Management Systems for Microgrids. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar]
- Petrollese, M. Optimal Generation Scheduling for Renewable Microgrids Using Hydrogen Storage Systems. Ph.D. Thesis, The University of Cagliari, Cagliari, Italy, 2015. [Google Scholar]
- Negenborn, R.R.; Houwing, M.; De Schutter, B.; Hellendoorn, J. Model Predictive Control for Residential Energy Resources Using a Mixed-Logical Dynamic Model. In Proceedings of the 2009 International Conference on Networking, Sensing and Control, Okayama, Japan, 26–29 March 2009; pp. 702–707. [Google Scholar]
- Mendes, P.R.; Isorna, L.V.; Bordons, C.; Normey-Rico, J.E. Energy management of an experimental microgrid coupled to a V2G system. J. Power Sources 2016, 327, 702–713. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Vilaplana, D.G.; Bordons, C.; Roncero-Sanchez, P.; Ridao, M.A. Optimal management of microgrids with external agents including battery/fuel cell electric vehicles. IEEE Trans. Smart Grid 2018, 10, 4299–4308. [Google Scholar] [CrossRef]
- Chen, H.; Chen, J.; Lu, H.; Yan, C.; Liu, Z. A modified MPC-based optimal strategy of power management for fuel cell hybrid vehicles. IEEE/ASME Trans. Mechatron. 2020, 25, 2009–2018. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Tzamalis, G.; Glielmo, L. Use of model predictive control for experimental microgrid optimization. Appl. Energy 2014, 115, 37–46. [Google Scholar] [CrossRef]
- Bozchalui, M.C.; Hashmi, S.A.; Hassen, H.; Canizares, C.A.; Bhattacharya, K. Optimal operation of residential energy hubs in smart grids. IEEE Trans. Smart Grid 2012, 3, 1755–1766. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Vazquez, S.; Moreno-Garcia, I.M.; Gil-de-Castro, A.; Roncero-Sanchez, P.; Moreno-Munoz, A. Microgrids power quality enhancement using model predictive control. Electronics 2021, 10, 328. [Google Scholar] [CrossRef]
- Bordons, C.; Montero, C. Basic principles of MPC for power converters: Bridging the gap between theory and practice. IEEE Ind. Electron. Mag. 2015, 9, 31–43. [Google Scholar] [CrossRef]
- Linder, A.; Kennel, R. Model Predictive Control for Electrical Drives. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 1793–1799. [Google Scholar]
- Rodriguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortés, P.; Ammann, U. Predictive current control of a voltage source inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Gregor, R.; Barrero, F.; Toral, S.; Arahal, M.R.; Prieto, J.; Durán, M.J. Enhanced Predictive Current Control Method for the Asymmetrical Dual—Three Phase Induction Machine. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 265–272. [Google Scholar]
- Cortes, P.; Wilson, A.; Kouro, S.; Rodriguez, J.; Abu-Rub, H. Model predictive control of multilevel cascaded H-bridge inverters. IEEE Trans. Ind. Electron. 2010, 57, 2691–2699. [Google Scholar] [CrossRef]
- Lezana, P.; Aguilera, R.; Quevedo, D.E. Model predictive control of an asymmetric flying capacitor converter. IEEE Trans. Ind. Electron. 2008, 56, 1839–1846. [Google Scholar] [CrossRef]
- Vargas, R.; Ammann, U.; Hudoffsky, B.; Rodriguez, J.; Wheeler, P. Predictive torque control of an induction machine fed by a matrix converter with reactive input power control. IEEE Trans. Power Electron. 2010, 25, 1426–1438. [Google Scholar] [CrossRef]
- Correa, P.; Rodríguez, J.; Rivera, M.; Espinoza, J.R.; Kolar, J.W. Predictive control of an indirect matrix converter. IEEE Trans. Ind. Electron. 2009, 56, 1847–1853. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Fontenot, H.; Dong, B. Modeling and control of building-integrated microgrids for optimal energy management—A review. Appl. Energy 2019, 254, 113689. [Google Scholar] [CrossRef]
- Villalón, A.; Rivera, M.; Salgueiro, Y.; Muñoz, J.; Dragičević, T.; Blaabjerg, F. Predictive control for microgrid applications: A review study. Energies 2020, 13, 2454. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Guerrero, J.M.; Ioinovici, A.; Chan, K.W.; Rodriguez, J. Model predictive control of microgrids–An overview. Renew. Sustain. Energy Rev. 2021, 136, 110422. [Google Scholar] [CrossRef]
- Jayachandran, M.; Ravi, G. Decentralized model predictive hierarchical control strategy for islanded AC microgrids. Electr. Power Syst. Res. 2019, 170, 92–100. [Google Scholar] [CrossRef]
- Tedesco, F.; Mariam, L.; Basu, M.; Casavola, A.; Conlon, M.F. Economic model predictive control-based strategies for cost-effective supervision of community microgrids considering battery lifetime. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1067–1077. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Arendt, K.; Kim, D.; Helsen, L. All you need to know about model predictive control for buildings. Annu. Rev. Control. 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Ławryńczuk, M. Computationally Efficient Model Predictive Control Algorithms; Springer: Berlin, Germany, 2014. [Google Scholar]
- Lv, J.; Wang, X.; Wang, G.; Song, Y. Research on control strategy of isolated DC microgrid based on SOC of energy storage system. Electronics 2021, 10, 834. [Google Scholar] [CrossRef]
- Grigg, C.; Wong, P.; Albrecht, P.; Allan, R.; Bhavaraju, M.; Billinton, R.; Li, W. The IEEE reliability test system-1996. A report prepared by the reliability test system task force of the application of probability methods subcommittee. IEEE Trans. Power Syst. 1999, 14, 1010–1020. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mohtadi, C. Properties of generalized predictive control. Automatica 1989, 25, 859–875. [Google Scholar] [CrossRef]
- Yi, X.; Zhang, J.; Wang, Z.; Li, T.; Zheng, Y. Deep Distributed Fusion Network for Air Quality Prediction. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 965–973. [Google Scholar] [CrossRef]
- Bruninx, K.; Delarue, E. A statistical description of the error on wind power forecasts for probabilistic reserve sizing. IEEE Trans. Sustain. Energy 2014, 5, 995–1002. [Google Scholar] [CrossRef]
- Camacho, E.F.; Alba, C.B. Model Predictive Control; Springer Science & Business Media: London, UK, 2013. [Google Scholar]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2016, 64, 935–947. [Google Scholar] [CrossRef] [Green Version]
- Cortes, P.; Rodriguez, J.; Silva, C.; Flores, A. Delay compensation in model predictive current control of a three-phase inverter. IEEE Trans. Ind. Electron. 2011, 59, 1323–1325. [Google Scholar] [CrossRef]
- Larrinaga, S.A.; Vidal, M.A.R.; Oyarbide, E.; Apraiz, J.R.T. Predictive control strategy for DC/AC converters based on direct power control. IEEE Trans. Ind. Electron. 2007, 54, 1261–1271. [Google Scholar] [CrossRef]
- IEEE Standard Association. Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE Standard Association: Piscataway, NJ, USA, 2018; pp. 1547–2018. [Google Scholar] [CrossRef]


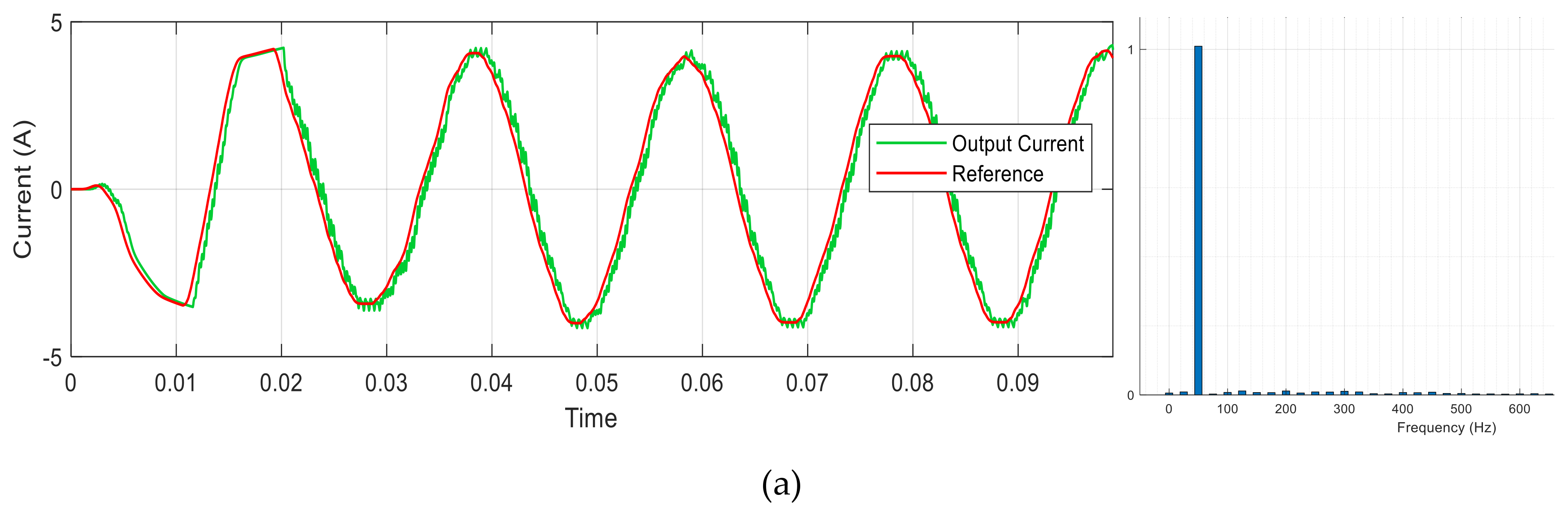
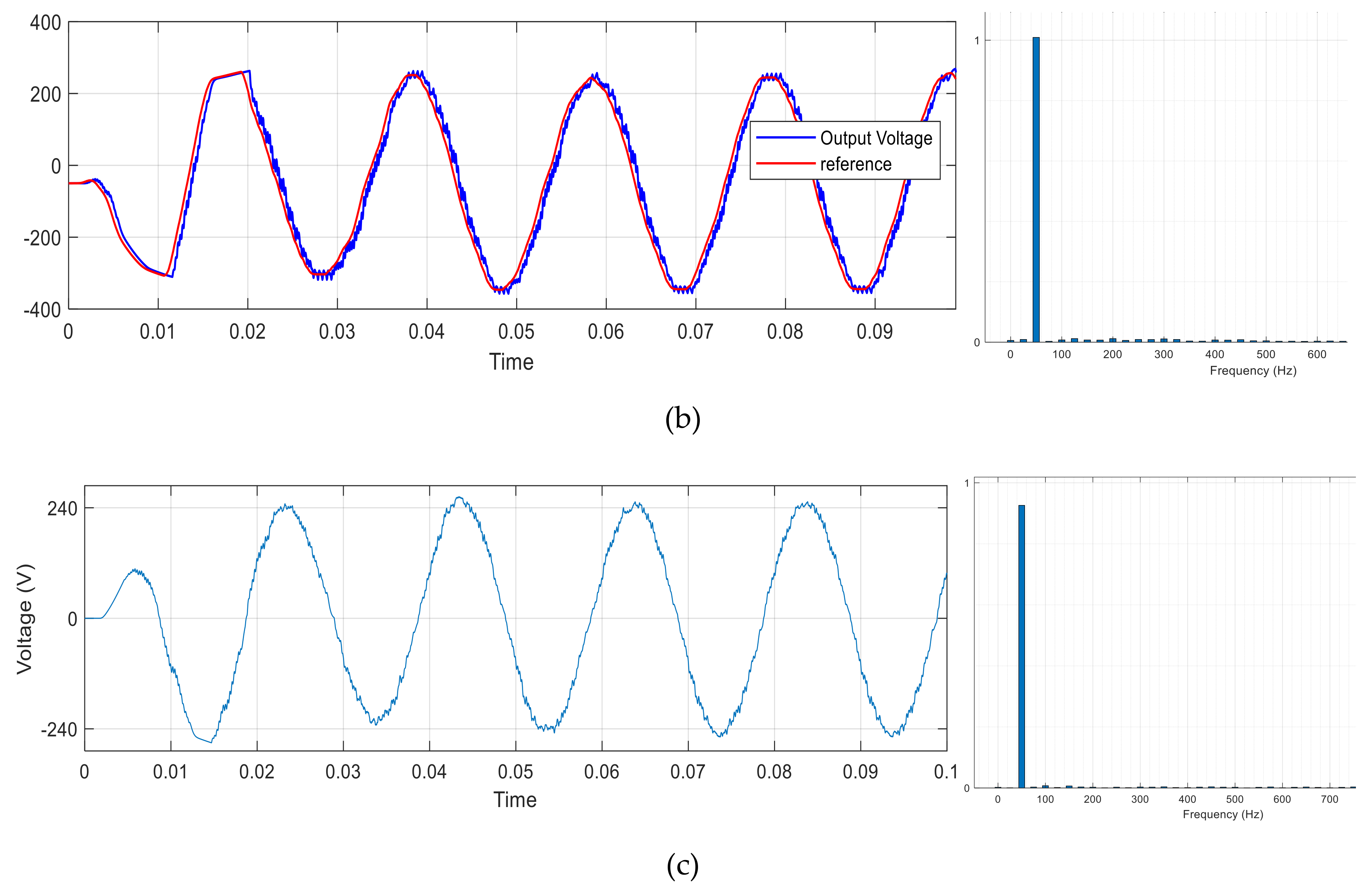
| Input Parameters | Control Horizon () | Prediction Horizon () | Sampling Time () | Weighting Control () |
|---|---|---|---|---|
| Value | 4 | 10 | 10 s | 0.6 |
| Description | Value |
|---|---|
| DC bus voltage | 320 V |
| Grid Nominal voltage | 240 V |
| System Nominal frequency | 50 Hz |
| DC link capacitance | 2.2 μF |
| LC Filter inductance | 0.4 μH |
| LC Filter capacitance | 6.85 μF |
| VSC rated power | 3 KW |
| Load capacitance | 100 mH |
| Load inductance | 1 pF |
| PWM carrier frequency | 10 KHz |
| Sampling frequency | 5 KHz |
| Battery capacity | 150 Ah |
| Maximum PV power | 1 KW |
| Maximum wind power | 1.5 KW |
| Battery | Grid | |||
|---|---|---|---|---|
| Time * | Cost Average (€) | Power Average (KWh) | Power Average (KWh) | Equivalent Cost Exchange |
| 06 h–07 h | 0.58 | −0.02 | 0.41 | 0.24 |
| 07 h–08 h | 0.56 | −0.19 | 0.50 | 0.28 |
| 08 h–09 h | 0.6 | −0.44 | 0.98 | 0.59 |
| 09 h–10 h | 0.72 | −0.69 | 1.00 | 0.73 |
| 10 h–11 h | 0.70 | −1.05 | 1.48 | 1.05 |
| 11 h–12 h | 0.57 | −1.35 | 1.48 | 0.84 |
| 12 h–13 h | 0.45 | −1.13 | 0.54 | 0.25 |
| 13 h–14 h | 0.33 | −0.46 | 0 | 0 |
| 14 h–15 h | 0.28 | −0.67 | 0 | 0 |
| 15 h–16 h | 0.43 | −0.47 | 0 | 0 |
| 16 h–17 h | 0.63 | −0.04 | −0.28 | −0.18 |
| 17 h–18 h | 0.66 | −0.65 | 0 | 0 |
| 18 h–19 h | 0.62 | −1.42 | 0 | 0 |
| 19 h–20 h | 0.59 | −1.17 | 0 | 0 |
| 20 h–21 h | 0.58 | −0.49 | 1.48 | 0.85 |
| 21 h–22 h | 0.58 | −0.45 | 1.48 | 0.85 |
| 22 h–23 h | 0.68 | −0.47 | 1.22 | 0.83 |
| 23 h–00 h | 0.74 | −0.51 | 1.22 | 0.90 |
| 00 h–01 h | 0.61 | −0.35 | 0.99 | 0.59 |
| 01 h–02 h | 0.49 | −0.05 | 0.98 | 0.48 |
| 02 h–03 h | 0.37 | −0.02 | 0.47 | 0.17 |
| 03 h–04 h | 0.27 | −0.02 | 0.47 | 0.12 |
| 04 h–05 h | 0.29 | −0.02 | 0.47 | 0.13 |
| 05 h–06 h | 0.48 | −0.0.2 | 0.47 | 0.22 |
| Total | - | −5.71 KWh | 15.36 KWh | 8.97 € |
| Battery | Grid | |||
|---|---|---|---|---|
| Time * | Cost Average (€) | Power Average (KWh) | Power Average (KWh) | Equivalent Cost Exchange |
| 06 h–07 h | 0.58 | 0.45 | 0 | 0 |
| 07 h–08 h | 0.56 | 0.38 | 0 | 0 |
| 08 h–09 h | 0.6 | 0.60 | 0 | 0 |
| 09 h–10 h | 0.72 | 0.41 | 0 | 0 |
| 10 h–11 h | 0.70 | 0.50 | 0 | 0 |
| 11 h–12 h | 0.57 | 0.25 | 0 | 0 |
| 12 h–13 h | 0.45 | −0.20 | 0 | 0 |
| 13 h–14 h | 0.33 | −0.36 | 0 | 0 |
| 14 h–15 h | 0.28 | −0.40 | 0 | 0 |
| 15 h–16 h | 0.43 | −0.37 | 0 | 0 |
| 16 h–17 h | 0.63 | −0.01 | −0.26 | −0.16 |
| 17 h–18 h | 0.66 | 0.65 | 0 | 0 |
| 18 h–19 h | 0.62 | 1.42 | 0 | 0 |
| 19 h–20 h | 0.59 | 1.17 | 0 | 0 |
| 20 h–21 h | 0.58 | −0.49 | 1.51 | 0.87 |
| 21 h–22 h | 0.58 | −0.45 | 1.51 | 0.87 |
| 22 h–23 h | 0.68 | −0.48 | 1.25 | 0.85 |
| 23 h–00 h | 0.74 | −0.51 | 1.25 | 0.92 |
| 00 h–01 h | 0.61 | −0.35 | 1.01 | 0.61 |
| 01 h–02 h | 0.49 | −0.05 | 1.01 | 0.49 |
| 02 h–03 h | 0.37 | −1.04 | 1.54 | 0.57 |
| 03 h–04 h | 0.27 | −1.02 | 1.51 | 0.40 |
| 04 h–05 h | 0.29 | −0.10 | 0.59 | 0.17 |
| 05 h–06 h | 0.48 | −0.004 | 0.50 | 0.24 |
| Total | -- | −0.0042 KWh | 11.42 KWh | 5.85 € |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; El kamoun, N.; Zine-Dine, K. A Predictive Control Strategy for Energy Management in Micro-Grid Systems. Electronics 2021, 10, 1666. https://doi.org/10.3390/electronics10141666
Elmouatamid A, Ouladsine R, Bakhouya M, El kamoun N, Zine-Dine K. A Predictive Control Strategy for Energy Management in Micro-Grid Systems. Electronics. 2021; 10(14):1666. https://doi.org/10.3390/electronics10141666
Chicago/Turabian StyleElmouatamid, Abdellatif, Radouane Ouladsine, Mohamed Bakhouya, Najib El kamoun, and Khalid Zine-Dine. 2021. "A Predictive Control Strategy for Energy Management in Micro-Grid Systems" Electronics 10, no. 14: 1666. https://doi.org/10.3390/electronics10141666
APA StyleElmouatamid, A., Ouladsine, R., Bakhouya, M., El kamoun, N., & Zine-Dine, K. (2021). A Predictive Control Strategy for Energy Management in Micro-Grid Systems. Electronics, 10(14), 1666. https://doi.org/10.3390/electronics10141666






