Single Step 2-Port Device De-Embedding Algorithm for Fixture-DUT-Fixture Network Assembly
Abstract
:1. Introduction
2. S-Parameter Cascade of Three Networks
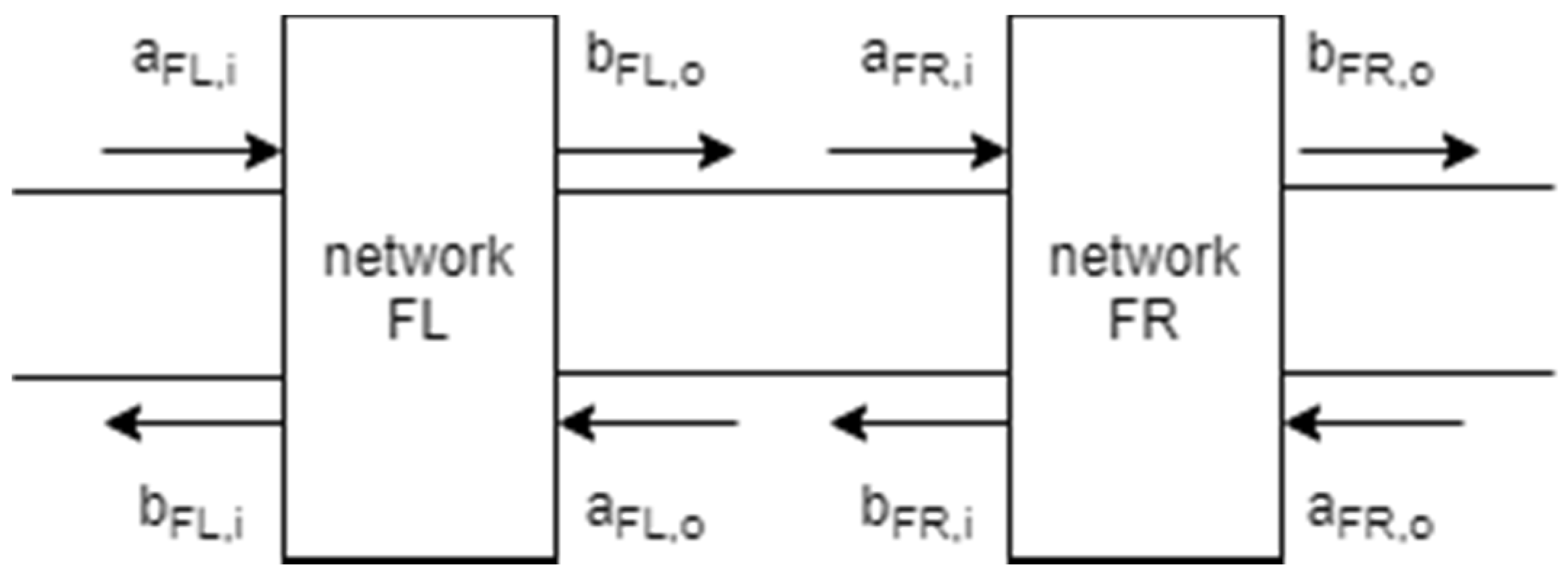
2.1. Review of Two-Network S-Parameter Cascading Algorithm
2.2. Single Step S-Parameter Cascading Algorithm for Three 2-Port Networks
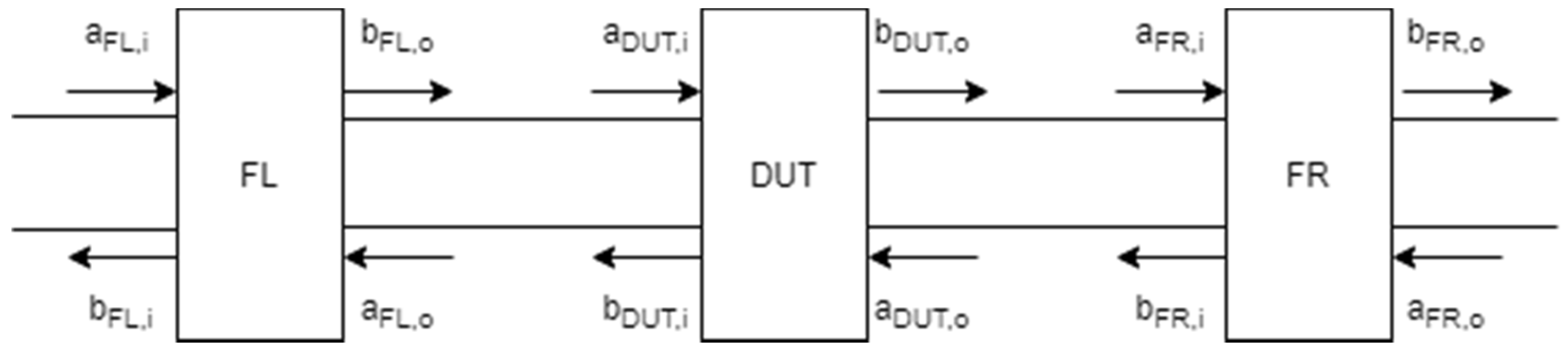
3. Single-Step Algorithm for Device under Test (DUT) De-Embedding
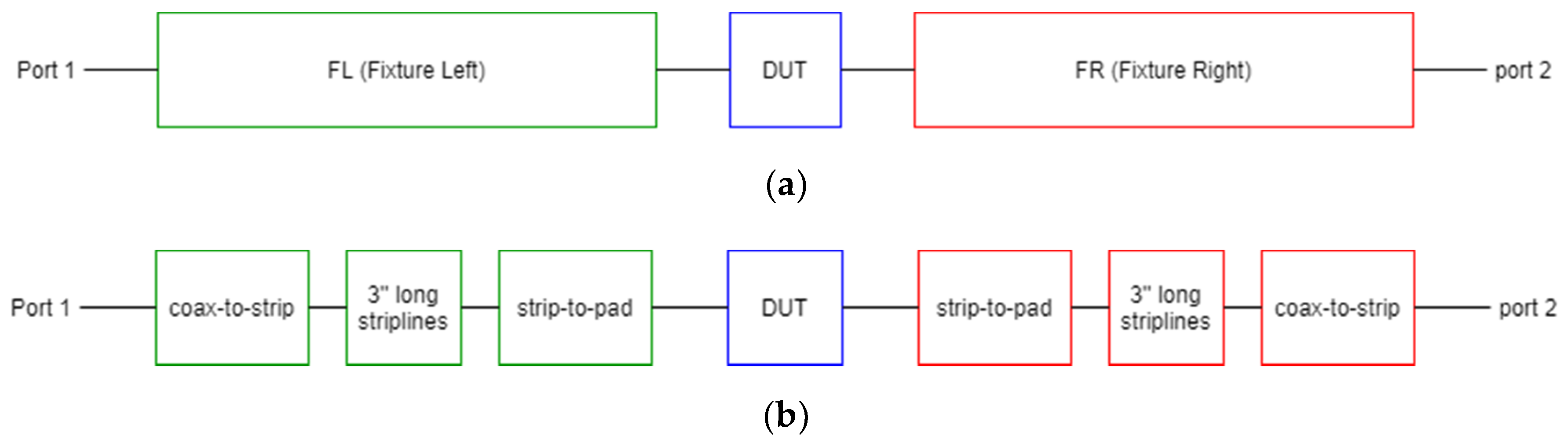
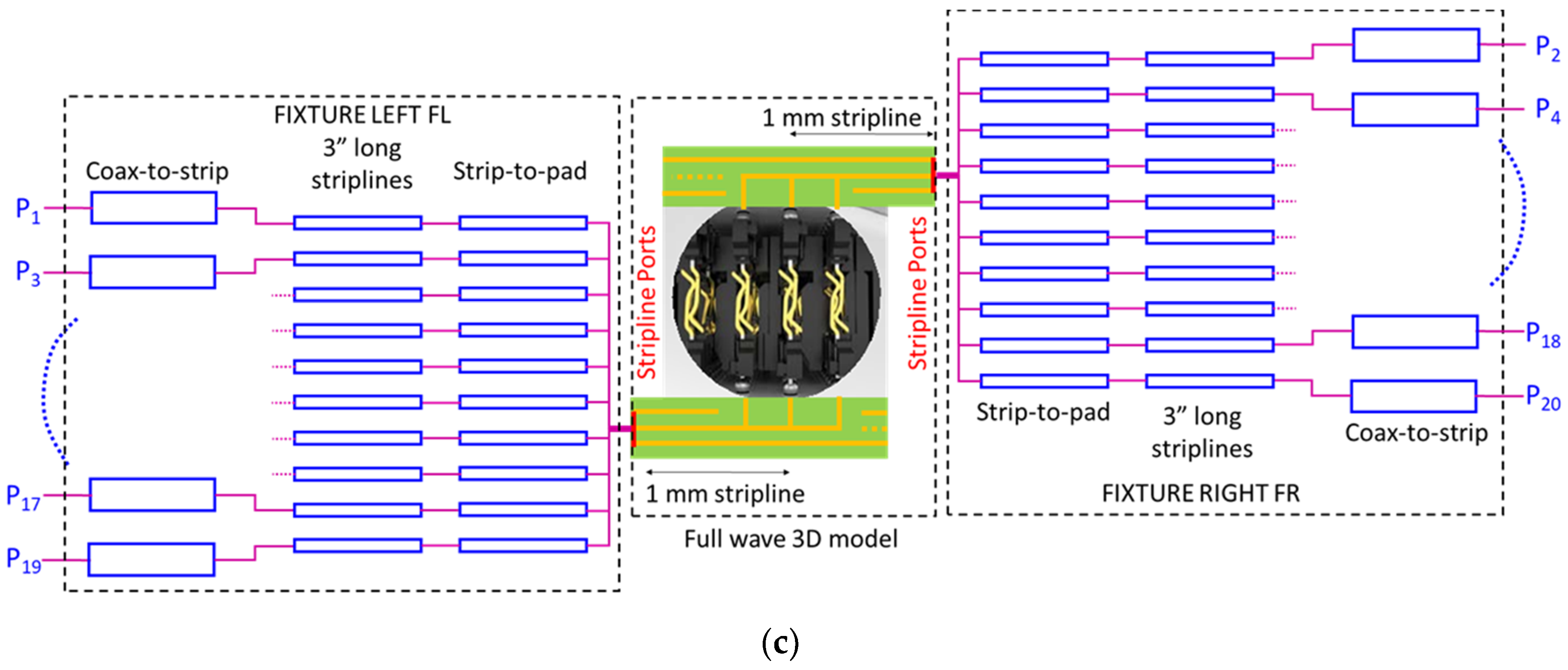
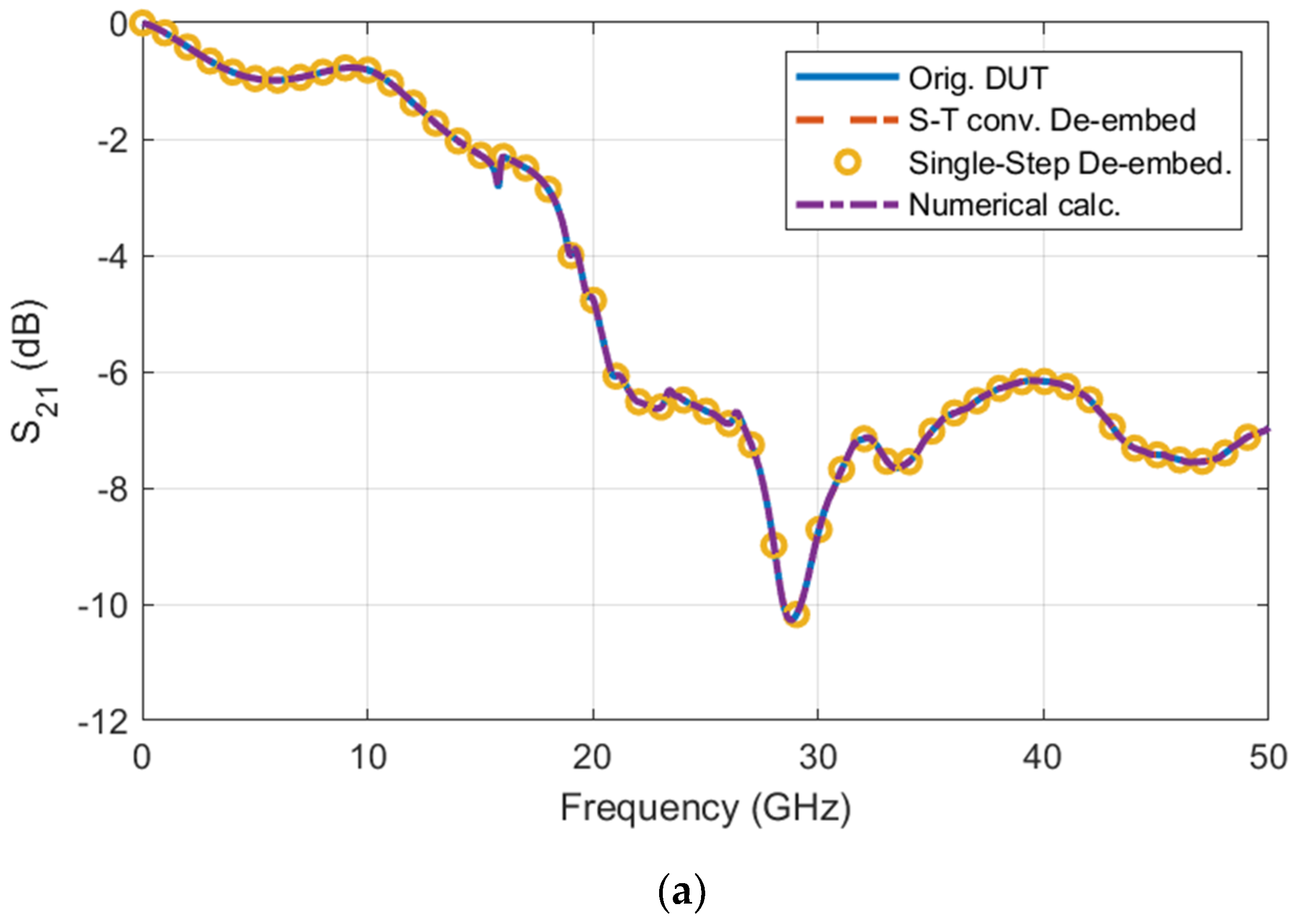
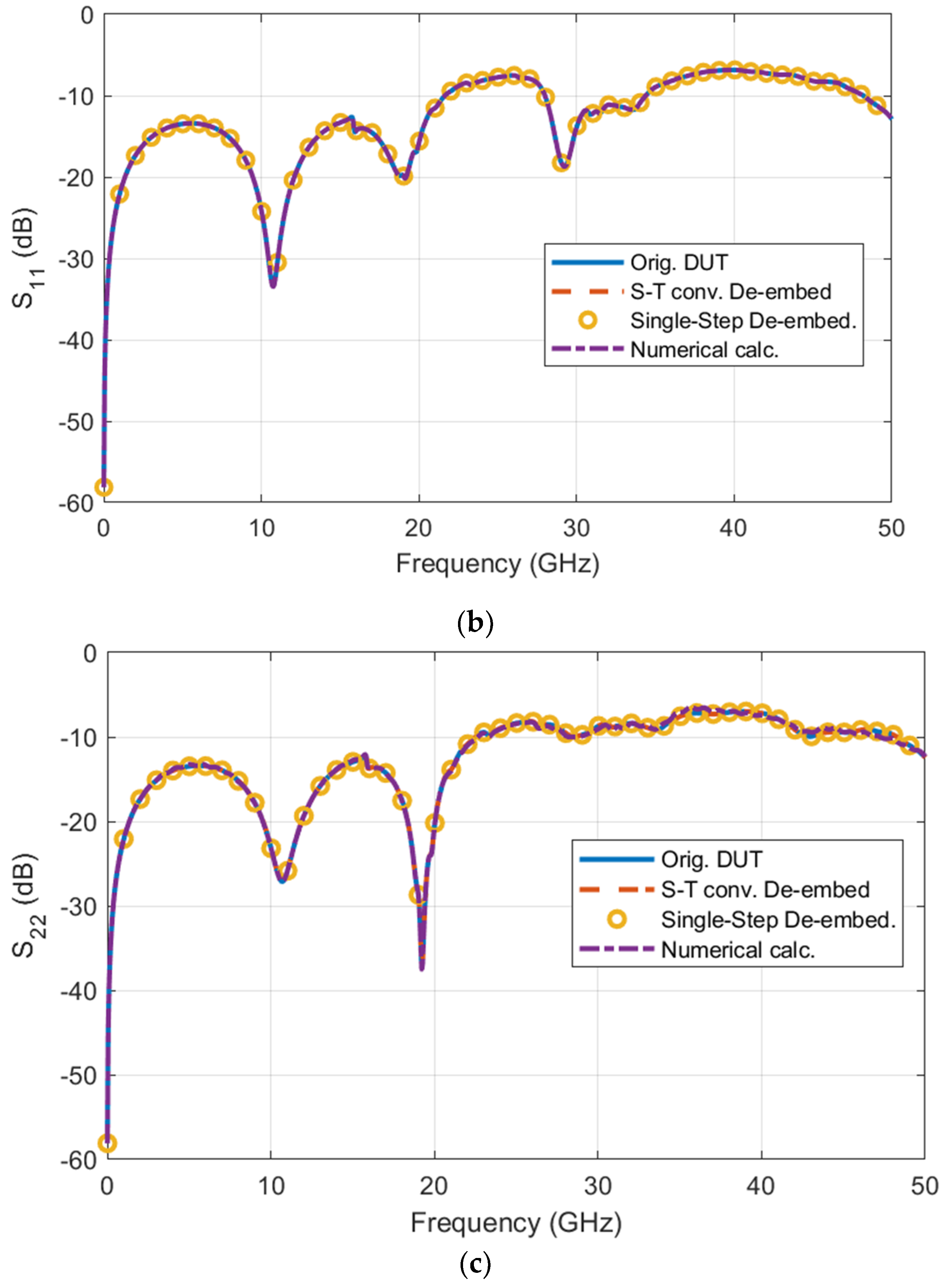
4. Validation of the Proposed Single-Step De-Embedding
- to those obtained by applying the classic standard two-step S-to-T and T-to-S parameter conversion named “S-T conv. De-embedding” in Figure 4;
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stenarson, J.; Yhland, K. An overview of VNA calibration and uncertainty evaluation techniques. Ger. Microw. Conf. 2008, 1, 1–4. [Google Scholar]
- Stumper, U. Uncertainties of VNA S-Parameter Measurements Applying the TAN Self-Calibration Method. IEEE Trans. Instrum. Meas. 2007, 56, 597–600. [Google Scholar] [CrossRef]
- Liu, Y.; Yong, S.; Gao, H.; Hinaga, S.; Padilla, D.; Yanagawa, D.; Drewniak, J.L.; Khilkevich, V. S-Parameter De-Embedding Error Estimation Based on the Statistical Circuit Models of Fixtures. IEEE Trans. Electromagn. Compat. 2020, 62, 1459–1467. [Google Scholar] [CrossRef]
- De Paulis, F.; Piersanti, S.; Wang, Q.; Cho, J.; Erickson, N.; Achkir, B.; Fan, J.; Drewniak, J.; Orlandi, A. TEM-Like Launch Geometries and Simplified De-embedding for Accurate Through Silicon Via Characterization. IEEE Trans. Instrum. Meas. 2017, 66, 792–801. [Google Scholar] [CrossRef]
- Resso, M.; Bogatin, E.; Vatsyayan, A. A new method to verify the accuracy of de-embedding algorithms. In Proceedings of the 2016 IEEE MTT-S Latin America Microwave Conference (LAMC), Puerto Vallarta, Mexico, 12–14 December 2016. [Google Scholar]
- Salnikov, A.S.; Dobush, I.M.; Bilevich, D.V.; Popov, A.A.; Kalentyev, A.A.; Goryainov, A.E. A Study of Connectors and Feed Lines De-Embedding Techniques for PCB Microwave Components S-Parameters Measurements Up To 50 Ghz. In Proceedings of the 2020 Dynamics of Systems, Mechanisms and Machines (Dynamics), Omsk, Russia, 10–12 November 2020. [Google Scholar]
- Chen, B.; Ye, X.; Samaras, B.; Fan, J. A novel de-embedding method suitable for transmission-line measurement. In Proceedings of the 2015 Asia-Pacific Symposium on Electromagnetic Compatibility (APEMC), Taipei, Taiwan, 25–29 May2015. [Google Scholar]
- Barnes, H.; Bogatin, E.; Moreira, J. Development of a PCB kit for s-parameter de-embedding algorithms verification. In Proceedings of the 2017 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Washington, DC, USA, 7–11 August 2017. [Google Scholar]
- Cho, H.; Burk, D. A three-step method for the de-embedding of high-frequency S-parameter measurements. IEEE Trans. Electron Devices 1991, 38, 1371–1375. [Google Scholar] [CrossRef]
- Mavaddat, R. Network Scattering Parameters; World Scientific: Jefferson, NJ, USA, 1996. [Google Scholar]
- Sadiku, M.N.O. Numerical Techniques in Electromagnetics, 2nd ed.; CRC: New York, NY, USA, 2000. [Google Scholar]
- De Paulis, F.; Zhang, Y.-J.; Fan, J. Signal/Power Integrity Analysis for Multilayer Printed Circuit Boards Using Cascaded S-Parameters. IEEE Trans. Electromagn. Compat. 2010, 52, 1008–1018. [Google Scholar] [CrossRef]
- De Paulis, F.; Wang-Lee, T.; Mellitz, R.; Resso, M.; Rabinovich, R.; Danzy, O.J. Backplane channel design exploration at 112 Gbps using channel operating margin (COM). In Proceedings of the 2020 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Reno, NJ, USA, 28 July–28 August 2020. [Google Scholar]
- SAMTEC. Available online: https://www.samtec.com/connectors/high-speed-board-to-board/high-density-arrays/novaray (accessed on 18 May 2021).
- De Paulis, F.; Wang-Lee, T.; Resso, M.; Mellitz, R.; Rabinovich, R.; Danzy, O. Validation and Performance Evaluation of High Speed Connector Model for Channel Design at 56 Gbps and Above. In Proceedings of the 2020 IEEE 24th Workshop on Signal and Power Integrity (SPI), Cologne, Germany, 17–20 May 2020. [Google Scholar]
- Mathworks. Matlab User Manual. Available online: https://it.mathworks.com/help/optim/ug/fsolve.html (accessed on 1 May 2021).
| Method | S11 | S22 | S21 |
|---|---|---|---|
| Classic standard three-step (S-T conv. De-embedding) | 6.15 × 10−9 + j × 1.08 × 10−8 | 1.09 × 10−9 + j × 3.9 × 10−9 | 2.04 × 10−8 + j × 3.8 × 10−9 |
| Proposed single step (Single-Step De-embed.) | 6.15 × 10−9 + j × 1.08 × 10−8 | 1.09 × 10−9 + j × 3.9 × 10−9 | 2.04 × 10−8 + j × 3.8 × 10−9 |
| Numerical solution (Numerical calc.) | 1.08 × 10−5 + j × 1.4 × 10−5 | 0.03 + j × 0.025 | 1.30 × 10−4 + j × 7.33 × 10−4 |
| Method | S11 | S22 | S21 |
|---|---|---|---|
| Classic standard three-step (S-T conv. De-embedding) | 9.26 × 10−18 | 7.76 × 10−18 | 2.09 × 10−17 |
| Proposed single step (Single-Step De-embed.) | 9.26 × 10−18 | 7.76 × 10−18 | 2.09 × 10−17 |
| Numerical solution (Numerical calc.) | 3.29 × 10−11 | 2.20 × 10−4 | 6.51 × 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scafati, S.; Pellegrino, E.; de Paulis, F.; Olivieri, C.; Drewniak, J.; Orlandi, A. Single Step 2-Port Device De-Embedding Algorithm for Fixture-DUT-Fixture Network Assembly. Electronics 2021, 10, 1275. https://doi.org/10.3390/electronics10111275
Scafati S, Pellegrino E, de Paulis F, Olivieri C, Drewniak J, Orlandi A. Single Step 2-Port Device De-Embedding Algorithm for Fixture-DUT-Fixture Network Assembly. Electronics. 2021; 10(11):1275. https://doi.org/10.3390/electronics10111275
Chicago/Turabian StyleScafati, Simone, Enza Pellegrino, Francesco de Paulis, Carlo Olivieri, James Drewniak, and Antonio Orlandi. 2021. "Single Step 2-Port Device De-Embedding Algorithm for Fixture-DUT-Fixture Network Assembly" Electronics 10, no. 11: 1275. https://doi.org/10.3390/electronics10111275
APA StyleScafati, S., Pellegrino, E., de Paulis, F., Olivieri, C., Drewniak, J., & Orlandi, A. (2021). Single Step 2-Port Device De-Embedding Algorithm for Fixture-DUT-Fixture Network Assembly. Electronics, 10(11), 1275. https://doi.org/10.3390/electronics10111275









