Multi-Step Learning-by-Examples Strategy for Real-Time Brain Stroke Microwave Scattering Data Inversion
Abstract
1. Introduction
2. Multi-Step Brain Stroke Diagnosis
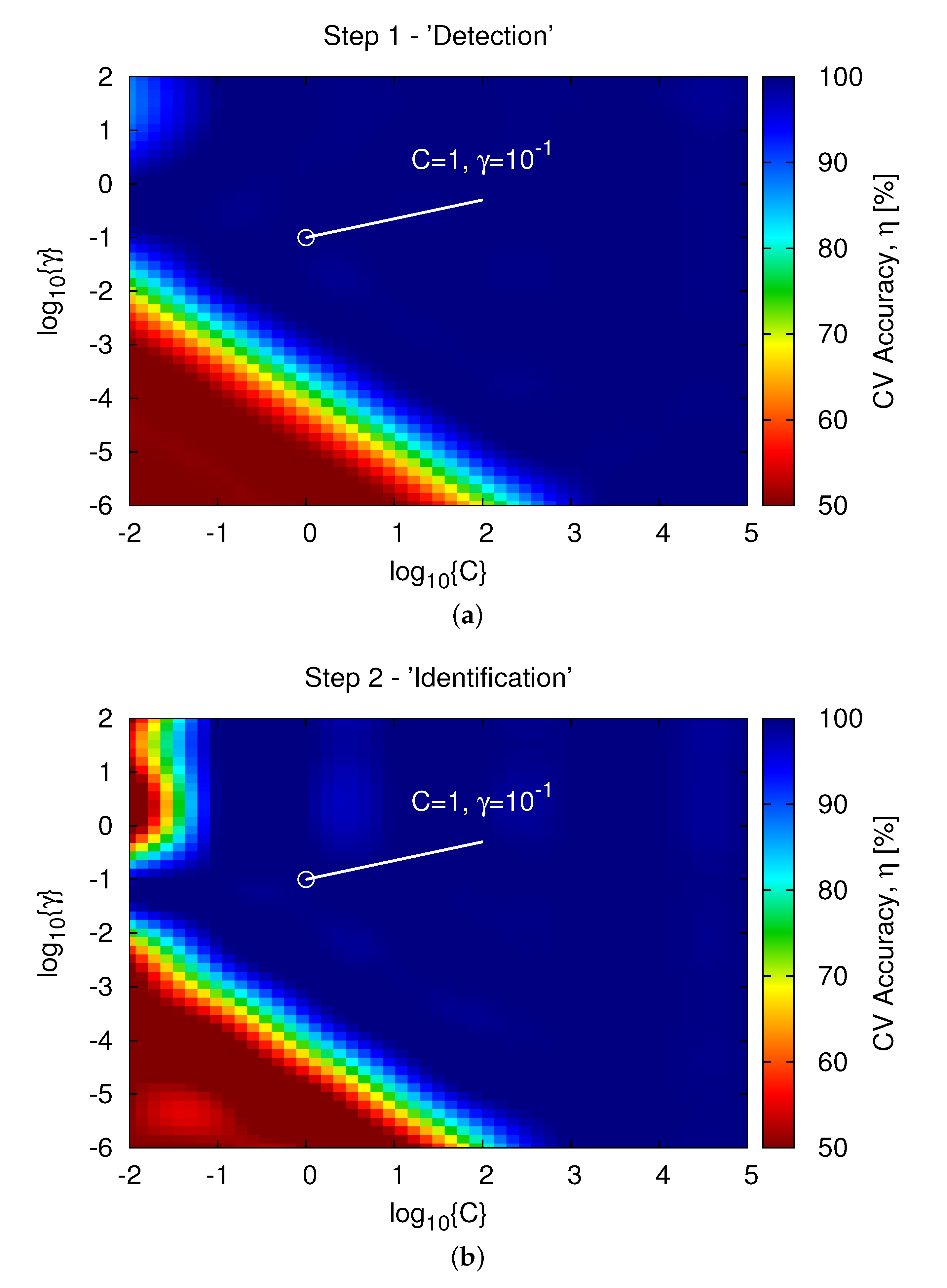
2.1. Step 1—“Detection”
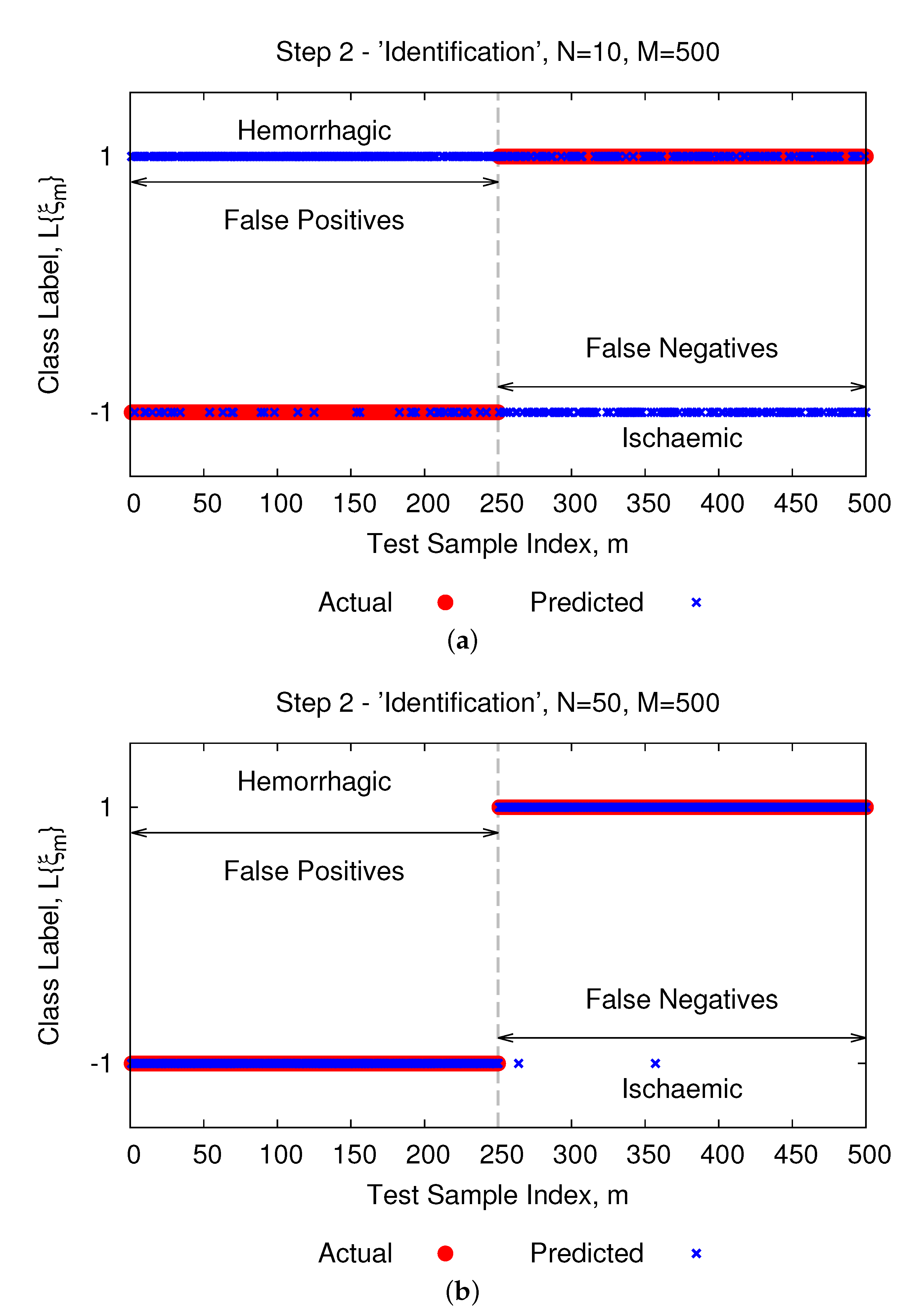
2.2. Step 2—“Identification”
2.3. Step 3—“Localization”
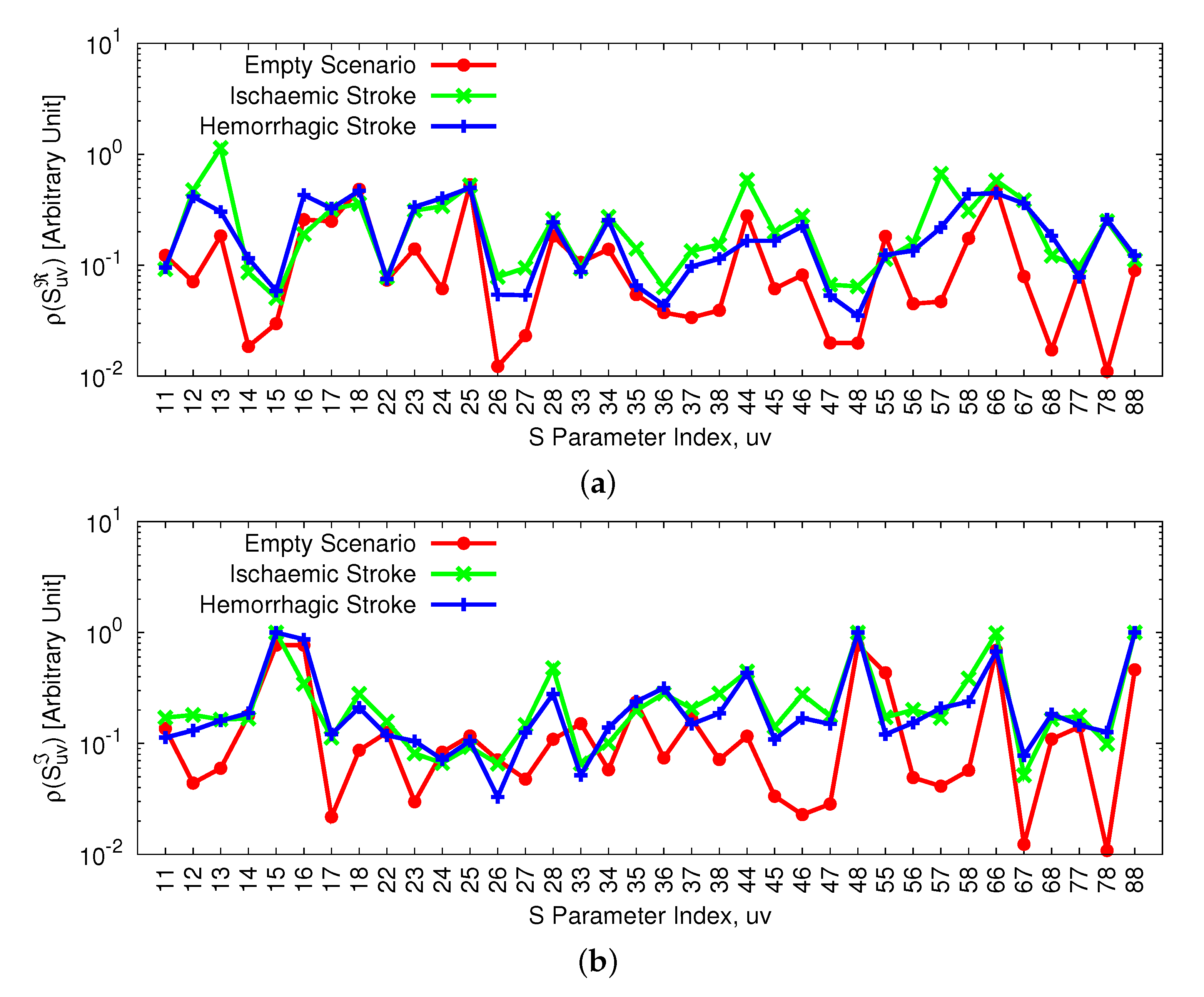
3. Experimental Validation
3.1. Acquisition Set-Up and Experimental Data Analysis
3.2. Inversion Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hagness, S.C.; Fear, E.C.; Massa, A. Guest editorial: Special cluster on microwave medical imaging. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1592–1597. [Google Scholar] [CrossRef]
- Fhager, A.; Candefjord, S.; Elam, M.; Persson, M. Microwave diagnostics ahead: Saving time and the lives of trauma and stroke patients. IEEE Microw. Mag. 2018, 19, 78–90. [Google Scholar] [CrossRef]
- Chiao, J.C.; Kissinger, D. Medical applications of RF and microwaves—Applications and events. IEEE Microw. Mag. 2015, 16, 14–18. [Google Scholar] [CrossRef]
- Tournier, P.-H.; Bonazzoli, M.; Dolean, V.; Rapetti, F.; Hecht, F.; Nataf, F.; Aliferis, I.; Kanfoud, I.E.; Migliaccio, C.; Buhan, M.; et al. Numerical modeling and high-speed parallel computing: New perspectives on tomographic microwave imaging for brain stroke detection and monitoring. IEEE Antennas Propag. Mag. 2017, 59, 98–110. [Google Scholar] [CrossRef]
- Hopfer, M.; Planas, R.; Hamidipour, A.; Henriksson, T.; Semenov, S. Electromagnetic tomography for detection, differentiation, and monitoring of brain stroke. IEEE Antennas Propag. Mag. 2017, 59, 86–97. [Google Scholar] [CrossRef]
- Semenov, S.; Corfield, D.R. Microwave tomography for brain imaging: Feasibility assessment for stroke detection. Int. J. Antennas Propag. 2008, 2008, 1–8. [Google Scholar] [CrossRef]
- Ireland, D.; Bialkowski, K.; Abbosh, A. Microwave imaging for brain stroke detection using Born iterative method. IET Microw. Antennas Propag. 2013, 7, 909–915. [Google Scholar] [CrossRef]
- Zamani, A.; Abbosh, A.; Mobashsher, A.T. Fast frequency-based multistatic microwave imaging algorithm with application to brain injury detection. IEEE Trans. Microwave Theory Technol. 2016, 64, 653–662. [Google Scholar] [CrossRef]
- Coli, V.L. Detection of simulated brain strokes using microwave tomography. IEEE J. Electromagn. RF Microw. Med. Biol. 2019, 3, 254–260. [Google Scholar] [CrossRef]
- Alqadami, A.S.M.; Trakic, A.; Stancombe, A.E.; Mohammed, B.; Bialkowski, K.; Abbosh, A. Flexible electromagnetic cap for head imaging. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1097–1107. [Google Scholar] [CrossRef]
- Persson, M.; Fhager, A.; Trefna, H.D.; Yu, Y.; McKelvey, T.; Pegenius, G.; Karlsson, J.-E.; Elam, M. Microwave-based stroke diagnosis making global pre-hospital thrombolytic treatment possible. IEEE Trans. Biomed. Eng. 2014, 61, 2806–2817. [Google Scholar] [CrossRef]
- Olesen, J.; Gustavsson, A.; Svensson, M.; Wittchen, H.-U.; Jonsson, B. on behalf of the CDBE2010 study group, and the European Brain Council, The economic cost of brain disorders in Europe. Eur. J. Neurol. 2012, 19, 155162. [Google Scholar] [CrossRef] [PubMed]
- European Stroke Organisation (ESO). Executive Committee and ESO Writing Committee, Guidelines for management of ischaemic stroke and transient ischaemic attack 2008. Cerebrovasc. Dis. 2008, 25, 457–507. [Google Scholar] [CrossRef] [PubMed]
- Massa, A.; Oliveri, G.; Salucci, M.; Anselmi, N.; Rocca, P. Learning-by-examples techniques as applied to electromagnetics. J. Electromagn. Waves Appl. 2018, 32, 516–541. [Google Scholar] [CrossRef]
- Gerazov, B.; Conceicao, R.C. Deep learning for tumour classification in homogeneous breast tissue in medical microwave imaging. In Proceedings of the IEEE EUROCON 2017—17th International Conference on Smart Technologies, Ohrid, Macedonia, 6–8 July 2017; pp. 564–569. [Google Scholar]
- Shah, P.; Moghaddam, M. Super resolution for microwave imaging: A deep learning approach. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 849–850. [Google Scholar]
- Song, H.; Li, Y.; Men, A. Microwave breast cancer detection using time-frequency representations. Med. Biol. Eng. Comput. 2017, 56, 571–582. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, L.G.; Teixeira, F.L.; Liu, C.; Cui, A.N.T.J. DeepNIS: Deep neural network for nonlinear electromagnetic inverse scattering. IEEE Trans. Antennas Propag. 2019, 67, 1819–1825. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, X. Deep-learning schemes for full-wave nonlinear inverse scattering problems. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1849–1860. [Google Scholar] [CrossRef]
- Ambrosanio, M.; Franceschini, S.; Baselice, F.; Pascazio, V. Machine learning for microwave imaging. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; pp. 1–4. [Google Scholar]
- Khoshdel, V.; Asefi, M.; Ashraf, A.; LoVetri, J. Full 3d microwave breast imaging using a deep-learning technique. J. Imaging 2020, 6, 80. [Google Scholar] [CrossRef]
- Salucci, M.; Vrba, J.; Merunka, I.; Massa, A. Real-time brain stroke detection through a learning-by-examples technique—An experimental assessment. Microw. Opt. Technol. Lett. 2017, 59, 2796–2799. [Google Scholar] [CrossRef]
- Salucci, M.; Gelmini, A.; Vrba, J.; Merunka, I.; Oliveri, G.; Rocca, P. Instantaneous brain stroke classification and localization from real scattering data. Microw. Opt. Technol. Lett. 2019, 61, 805–808. [Google Scholar] [CrossRef]
- Salucci, M.; Anselmi, N.; Oliveri, G.; Calmon, P.; Miorelli, R.; Reboud, C.; Massa, A. Real-time NDT-NDE through an innovative adaptive partial least squares SVR inversion approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6818–6832. [Google Scholar] [CrossRef]
- Salucci, M.; Oliveri, G.; Massa, A. Real-time electrical impedance tomography of the human chest by means of a learning-by-examples method. IEEE J. Electromagn. RF Microw. Med. Biol. 2019, 3, 88–96. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Balanis, C. Advanced Engineering Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Mathur, A.; Foody, G.M. Multiclass and Binary SVM Classification: Implications for Training and Classification Users. IEEE. Geosci. Remote Sens. Lett. 2008, 5, 241–245. [Google Scholar] [CrossRef]
- 1528-2013—IEEE Recommended Practice for Determining the Peak Spatial-Average Specific Absorption Rate (SAR) in the Human Head from Wireless Communications Devices: Measurement Techniques-Redline. Available online: https://ieeexplore.ieee.org/document/6719585/versionsversions (accessed on 6 September 2013).
- Everitt, B. The Cambridge Dictionary of Statistics; Cambridge Univ. Press: Cambridge, UK, 1999. [Google Scholar]








| Position, p | [mm] | Position, p | [mm] |
|---|---|---|---|
| 1 | 14 | ||
| 2 | 15 | ||
| 3 | 16 | ||
| 4 | 17 | ||
| 5 | 18 | ||
| 6 | 19 | ||
| 7 | 20 | ||
| 8 | 21 | ||
| 9 | 22 | ||
| 10 | 23 | ||
| 11 | 24 | ||
| 12 | 25 | ||
| 13 | - | - |
| Training Size | Multi-Class | Regression | |
|---|---|---|---|
| N | [%] | [mm] | [mm] |
| 50 | |||
| 100 | |||
| 250 | |||
| 400 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salucci, M.; Polo, A.; Vrba, J. Multi-Step Learning-by-Examples Strategy for Real-Time Brain Stroke Microwave Scattering Data Inversion. Electronics 2021, 10, 95. https://doi.org/10.3390/electronics10010095
Salucci M, Polo A, Vrba J. Multi-Step Learning-by-Examples Strategy for Real-Time Brain Stroke Microwave Scattering Data Inversion. Electronics. 2021; 10(1):95. https://doi.org/10.3390/electronics10010095
Chicago/Turabian StyleSalucci, Marco, Alessandro Polo, and Jan Vrba. 2021. "Multi-Step Learning-by-Examples Strategy for Real-Time Brain Stroke Microwave Scattering Data Inversion" Electronics 10, no. 1: 95. https://doi.org/10.3390/electronics10010095
APA StyleSalucci, M., Polo, A., & Vrba, J. (2021). Multi-Step Learning-by-Examples Strategy for Real-Time Brain Stroke Microwave Scattering Data Inversion. Electronics, 10(1), 95. https://doi.org/10.3390/electronics10010095







