How to Use the Normalized Hydrophilic-Lipophilic Deviation (HLDN) Concept for the Formulation of Equilibrated and Emulsified Surfactant-Oil-Water Systems for Cosmetics and Pharmaceutical Products
Abstract
1. Introduction
2. The Phenomena and Involved Variables in Equilibrated and Emulsified Surfactant-Oil-Water Systems
2.1. Principal Phenomena
- Phase behavior in one solvent fluid, i.e., the complete or partial solubility, in particular the concept of cloud point for nonionic surfactants in water that indicates the importance of temperature in the case of polyethoxylated species.
- Surfactant molecules’ self-association in a solvent fluid, e.g., the formation of micelles or other aggregates, either in aqueous or oily phases.
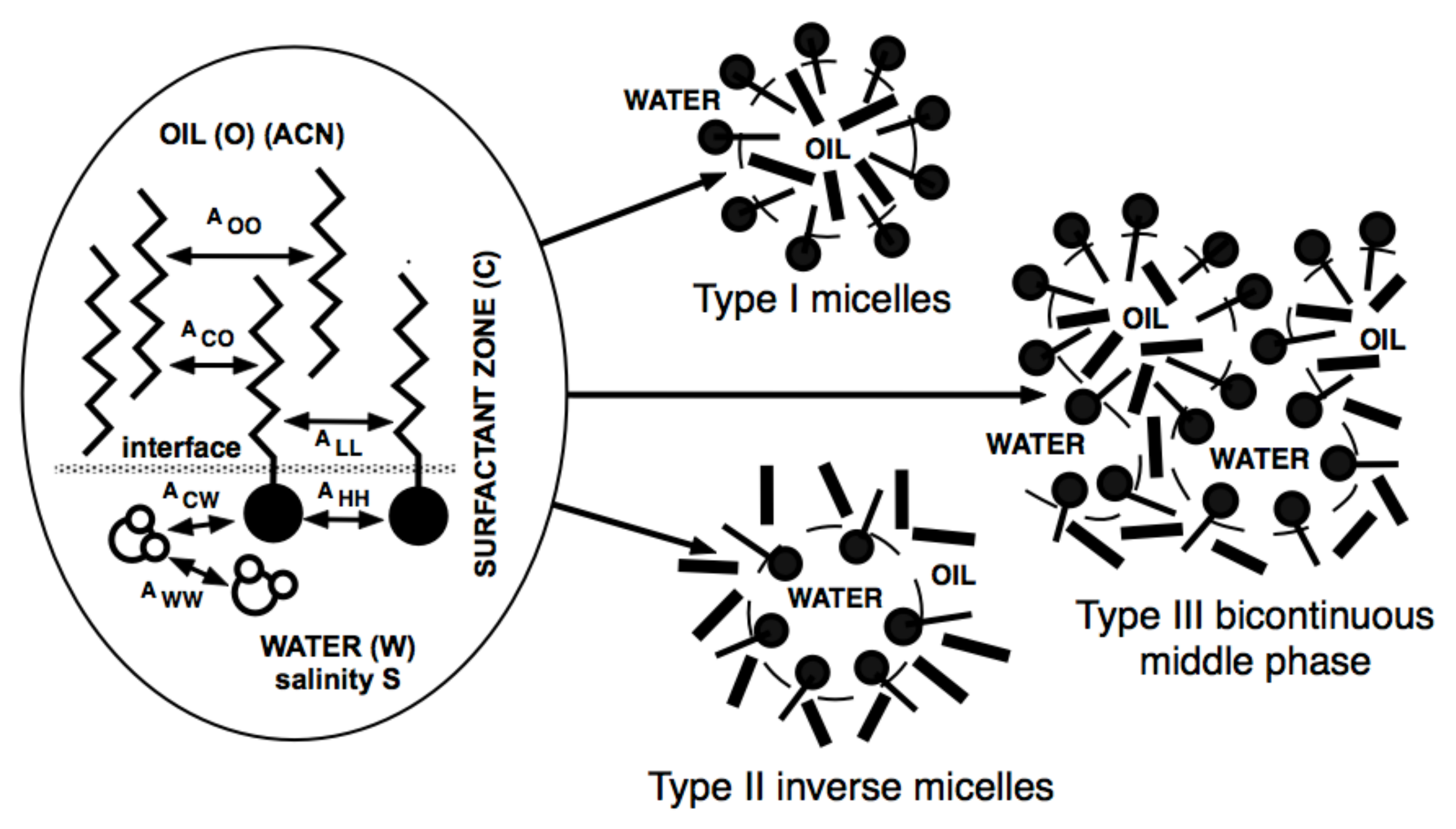
- The association structure of surfactants with two immiscible fluids, e.g., oil and water, as in an adsorbed single interface layer, or more complex arrangements like microemulsions, liquid crystals, vesicles, liposomes, etc.
2.2. Particularly Important Properties in Some Applications
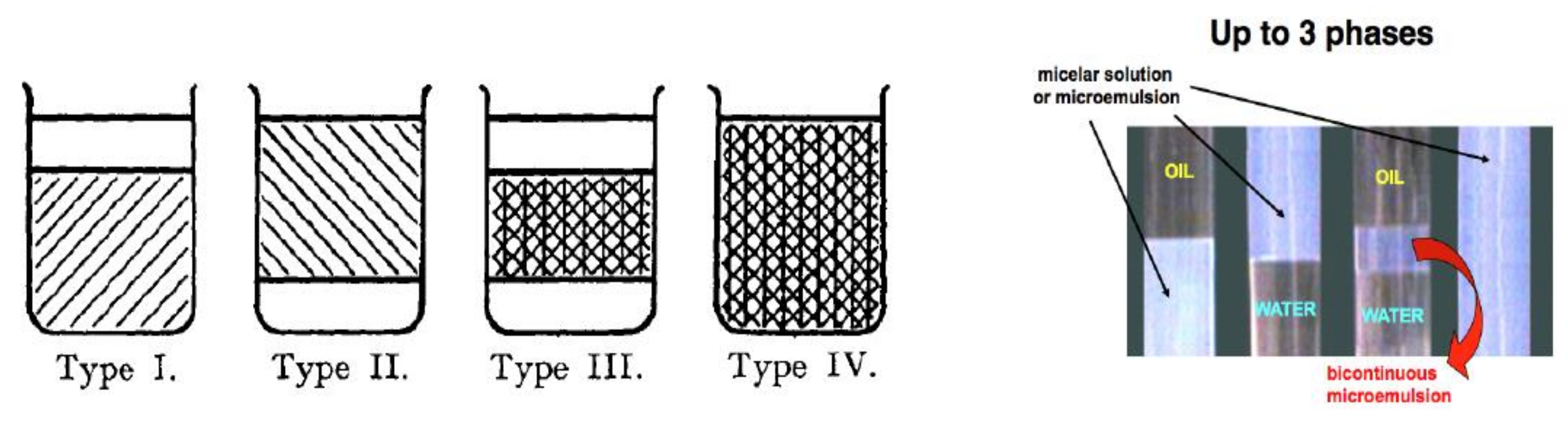
- Phase behavior, i.e., the occurrence of 1, 2 or 3 phases in a surfactant-oil-water (SOW) ternary or in a quaternary system when a second surfactant or a so-called cosurfactant, such as an alcohol, is added.
- The surface or interfacial tension at the fluid/fluid limit (e.g., air/water or oil/water) that varies with the nature of the ingredients, and their contents.
- Adsorption of amphiphilic substances, i.e., their location at interface, and its consequences as far as the wettability is concerned.
- Interfacial effects concerning dispersions with a high surface area, particularly the stability of emulsions, foams, and solid particle suspensions.
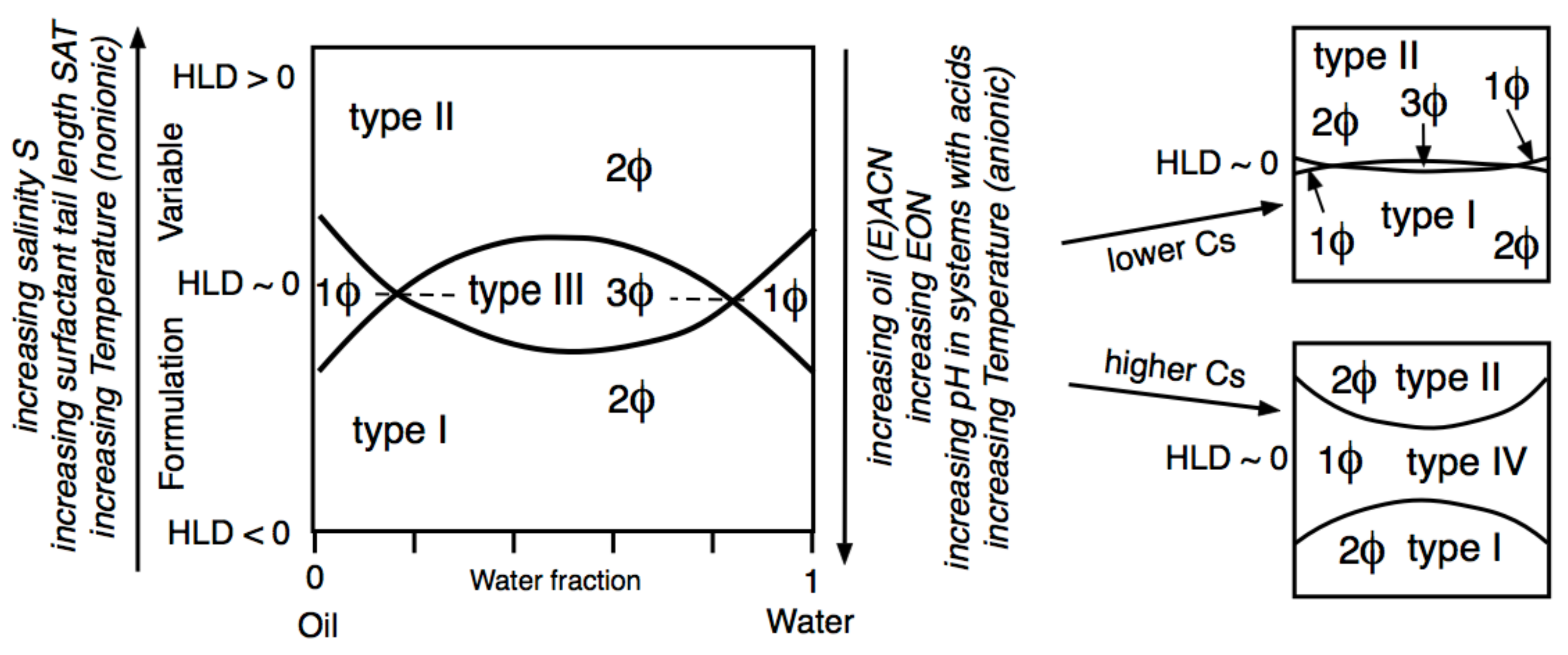
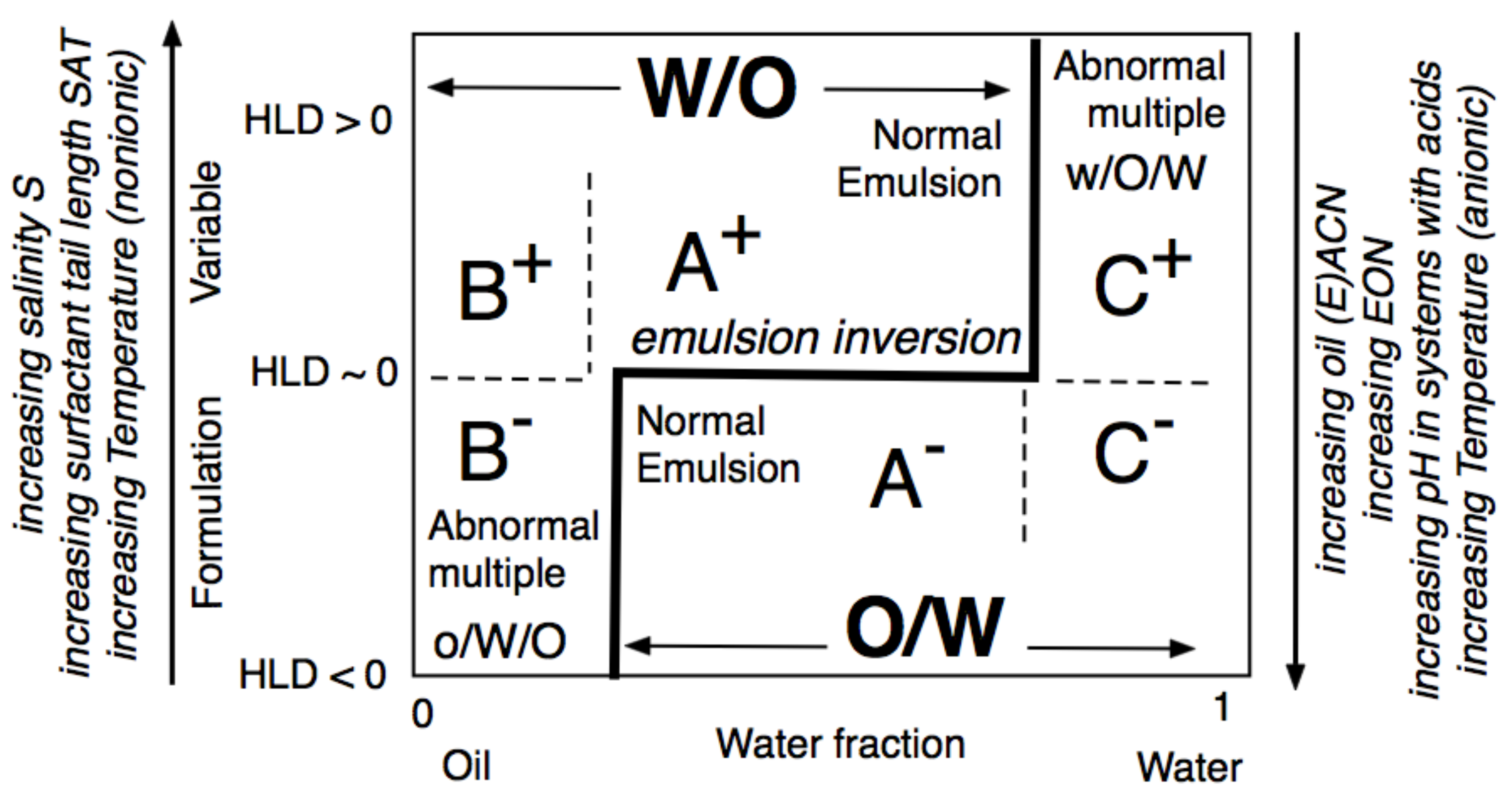
3. One-Dimensional Scan with Typical Formulation Variables
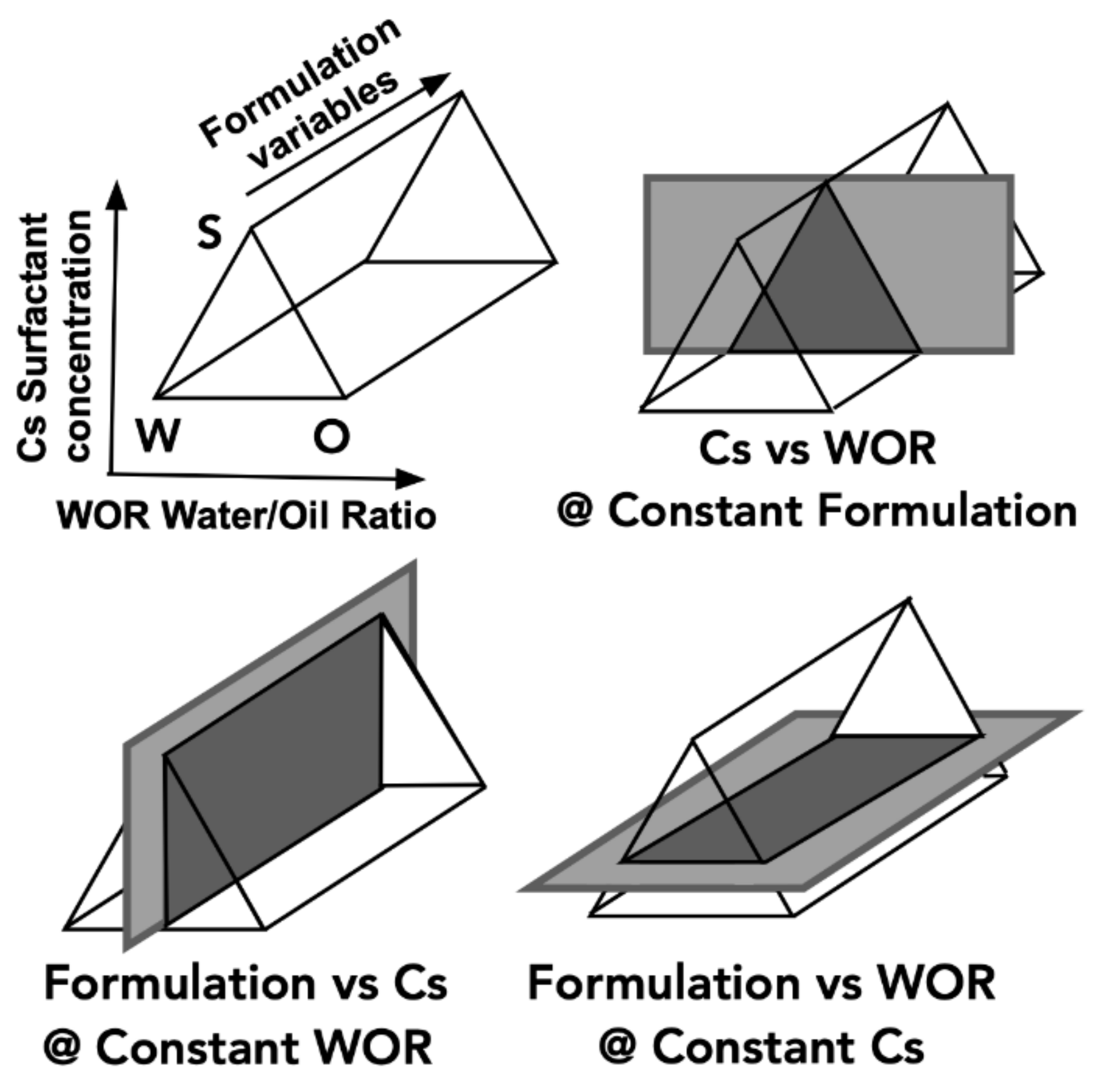
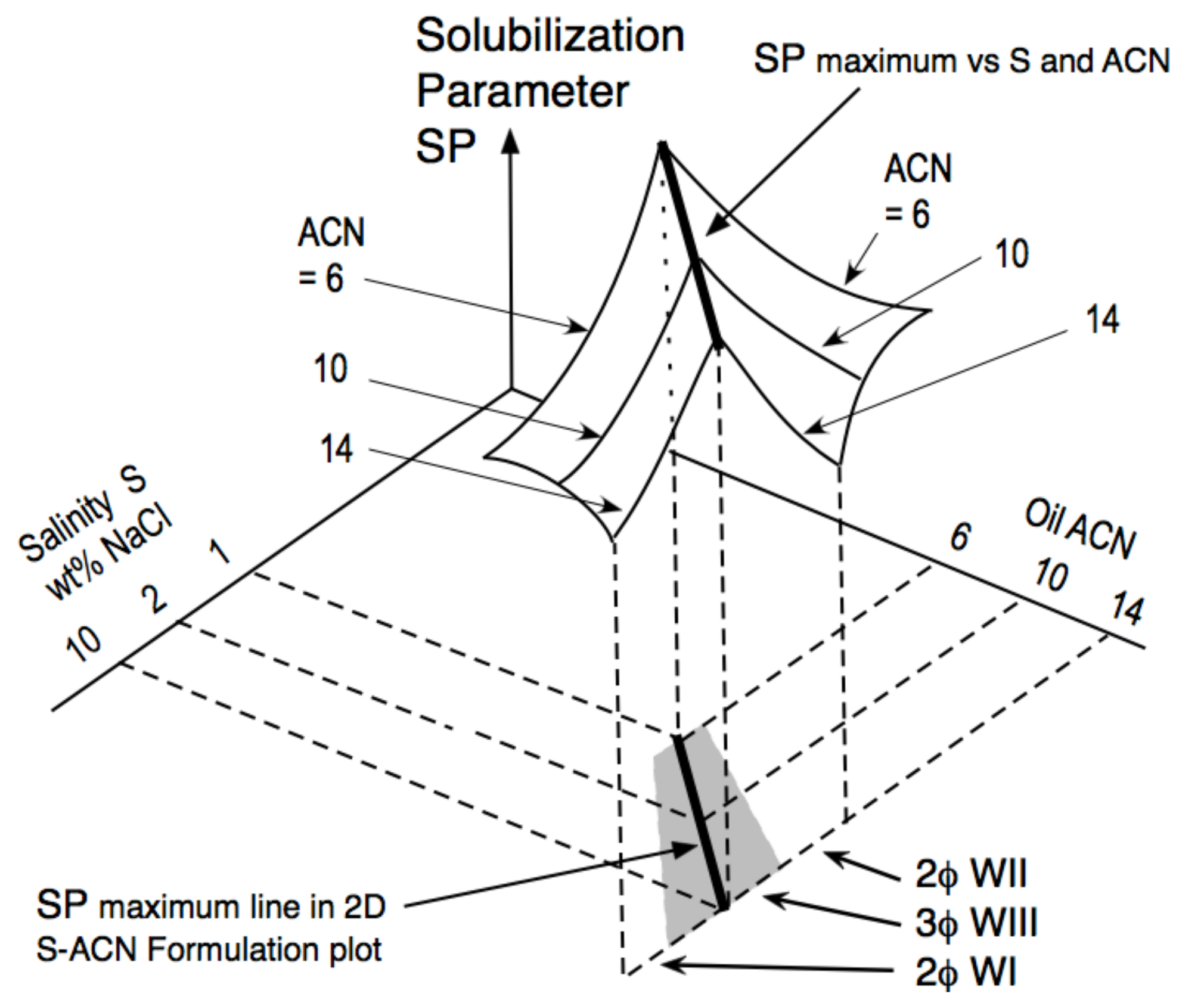
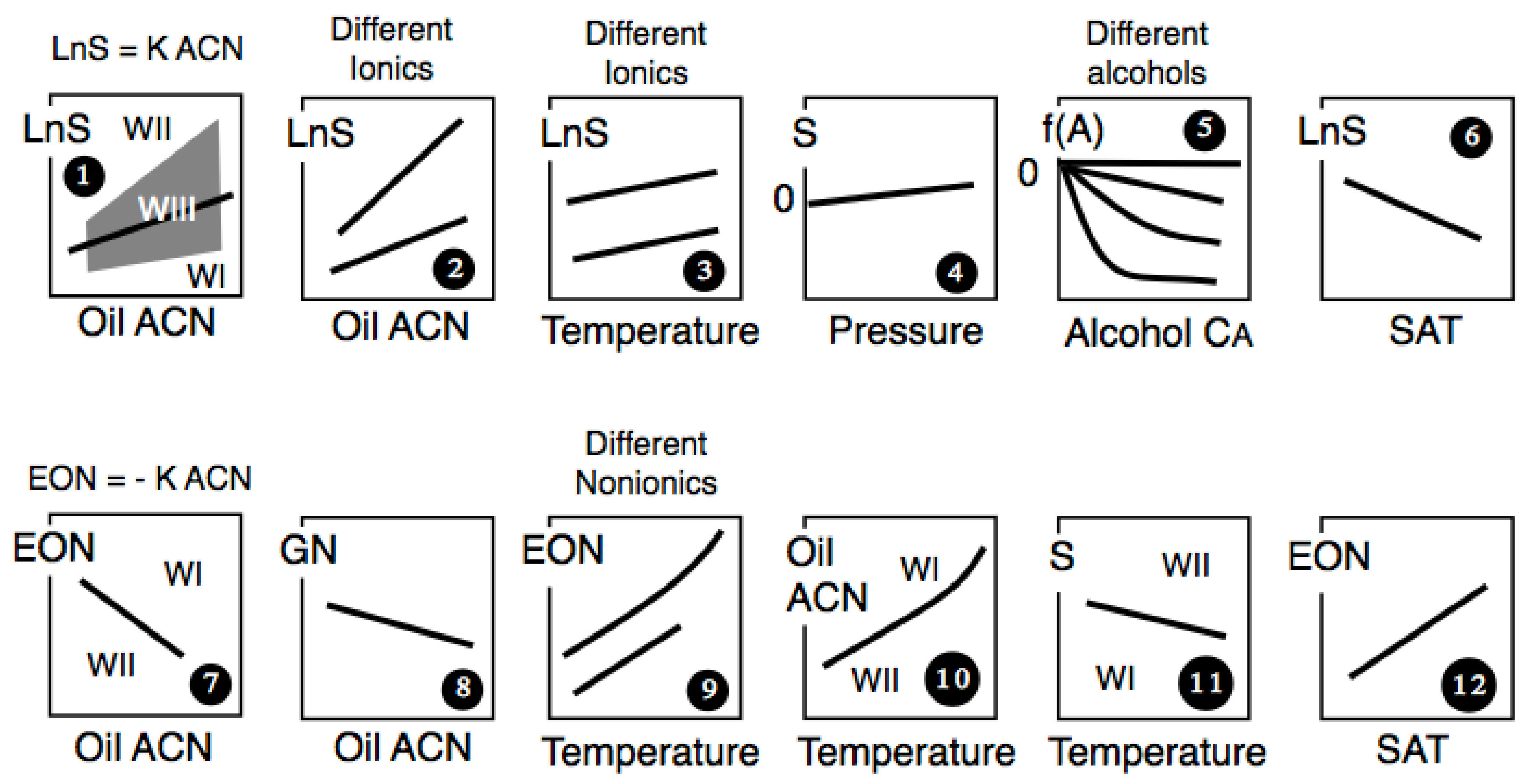
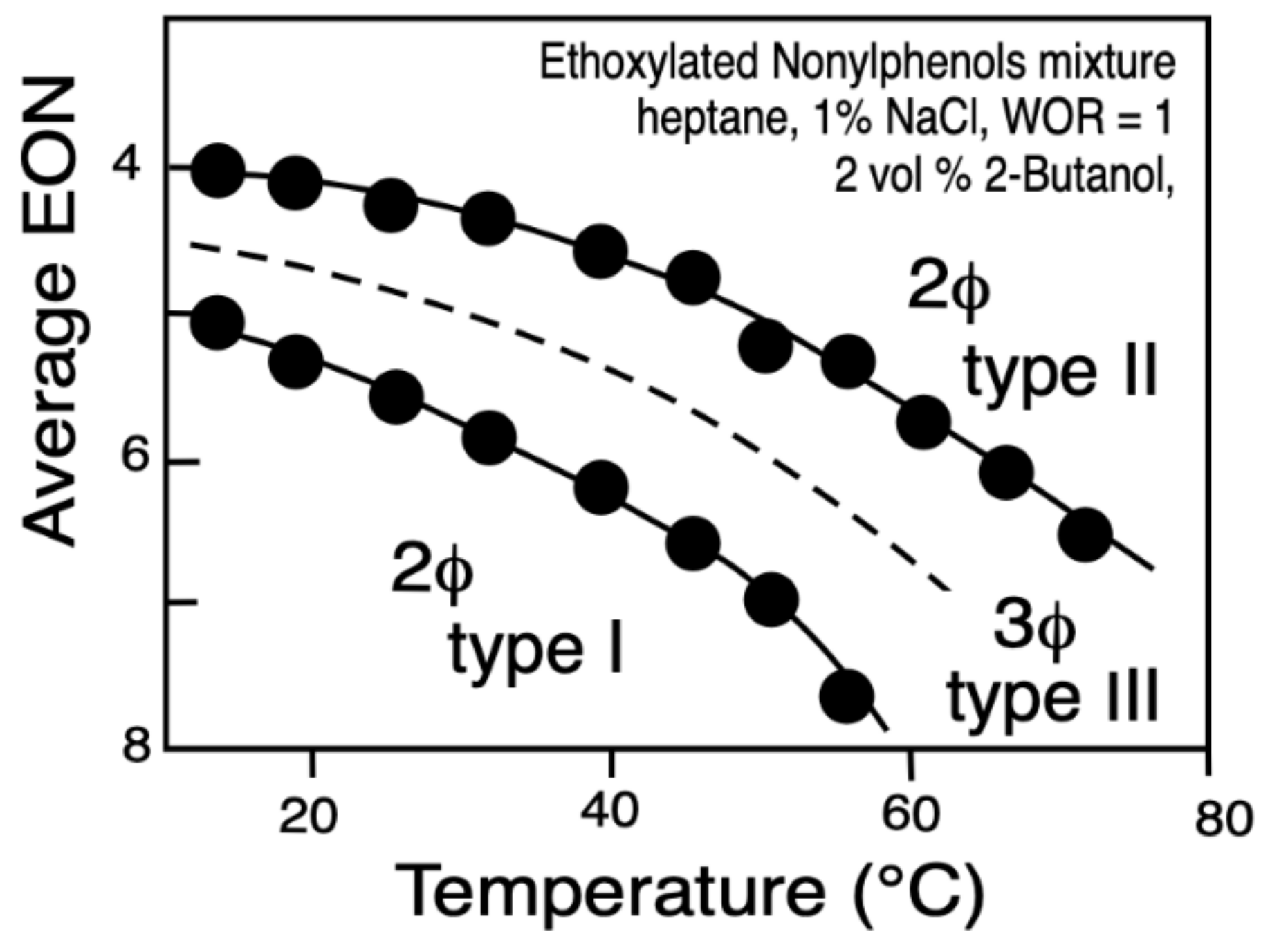
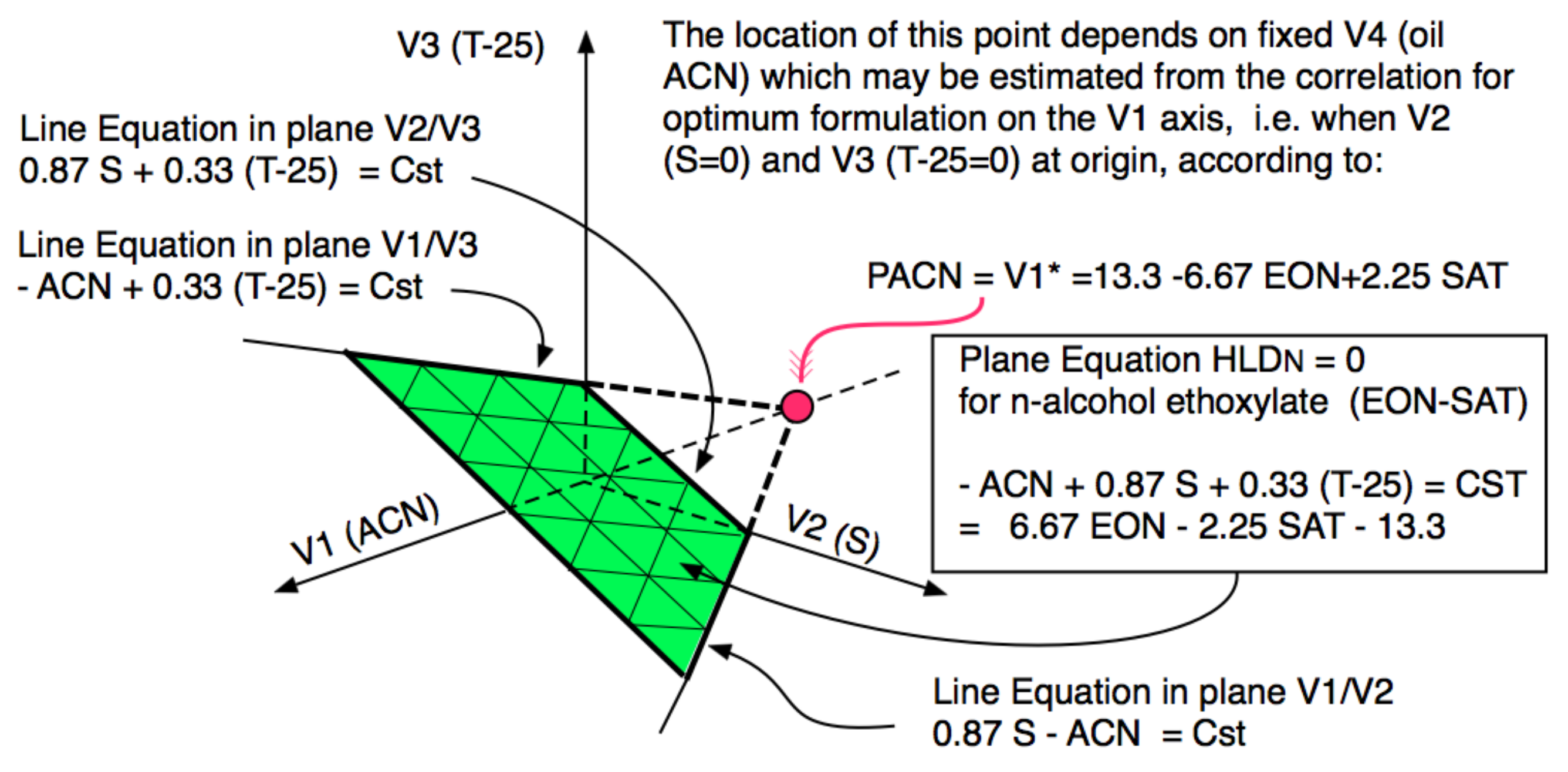
4. Multidimensional Scans and Optimum Formulation Events
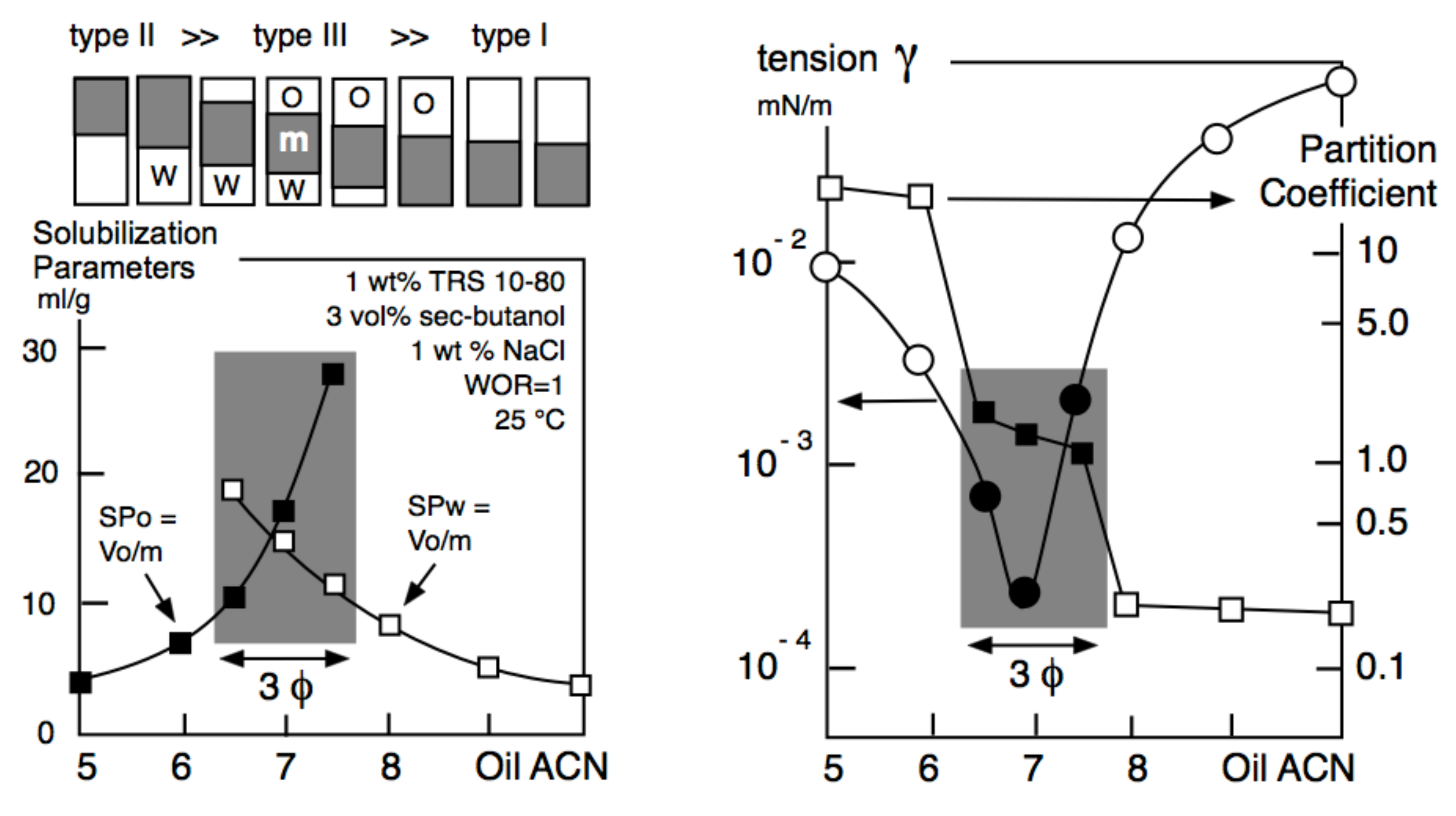
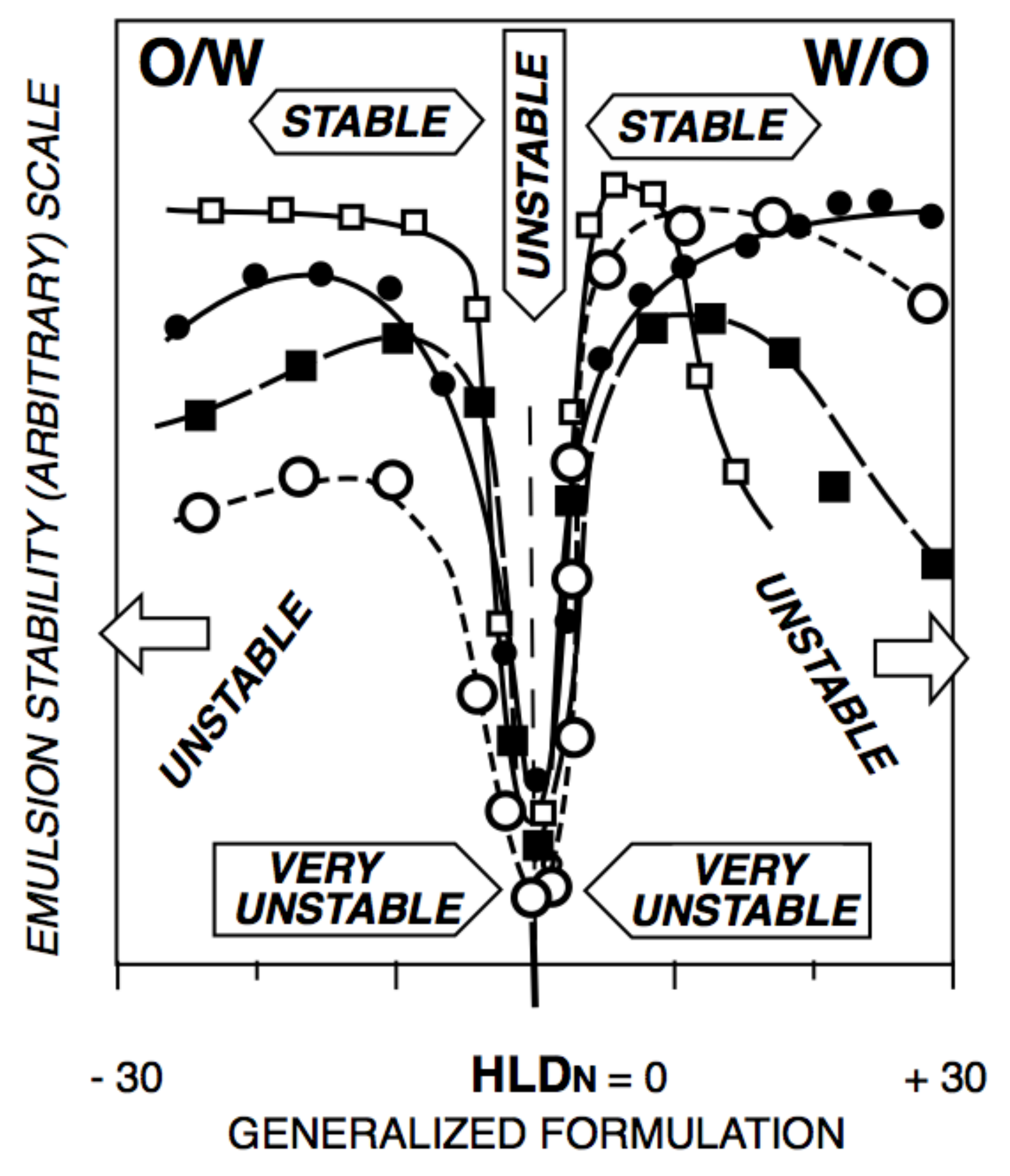
5. Relation of HLD Values with Micro-, Mini-, and Macroemulsion Properties
6. Additional Advantages and Complications with Complex Systems and Mixtures of Ingredients
6.1. Equivalent Oil Alkane Carbon Number (EACN)
6.2. Equivalent Salinity
6.3. Equivalent SCP in Surfactant Mixtures
6.4. Problems in Surfactant Mixtures with Interactions and Partitioning of Species
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Rosen, M.J. Surfactants and Interfacial Phenomena, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Rosen, M.J.; Dahanayake, M. Industrial Utilization of Surfactants. Principles and Practice; AOCS Press: Urbana, IL, USA, 2000; ISBN 893997111. [Google Scholar]
- Salager, J.L.; Bullon, J.; Pizzino, A.; Rondon-Gonzalez, M.; Tolosa, L. Emulsion Formulation Engineering for the Practitioner. In Encyclopedia of Surface and Colloid Science, 2nd ed.; Somasundaran, B., Ed.; Taylor & Francis: London, UK, 2010; Volume 1, Section 1; pp. 1–6. [Google Scholar] [CrossRef]
- Griffin, W.C. Classification of Surface Active Agents by HLB. J. Soc. Cosmet. Chem. 1949, 1, 311–326. [Google Scholar]
- Griffin, W.C. Calculation of HLB values of nonionic surfactants. J. Soc. Cosmet. Chem. 1954, 5, 249–256. [Google Scholar]
- Becher, P. Hydrophilic-lipophilic balance: An updated bibliography. In Encyclopedia of Emulsion Technology; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1985; Volume 2, Chapter 8. [Google Scholar]
- Davies, J.T. A quantitative kinetic theory of emulsion type I: Physical chemistry of the emulsifying agent. In Gas/Liquid and Liquid/Liquid Interfaces. Proceedings of the 2nd International Congress of Surface Activity; Butterworths: London, UK, 1957; Volume 1, pp. 426–438. [Google Scholar]
- Marszall, L. Dependence of hydrophilic-lipophilic balance of nonionic surfactants on the size of the molecule. Kolloid Z Z Polym. 1973, 251, 609–610. [Google Scholar] [CrossRef]
- Balson, T.G. HLB: Is it a valuable concept or a curiosity? In Industrial Applications of Surfactants IV; Karsa, D.R., Ed.; Royal Society of Chemistry: London, UK, 1999; pp. 175–192. [Google Scholar]
- Ontiveros, J.F.; Pierlot, C.; Catte, M.; Molinier, V.; Salager, J.L.; Aubry, J.M. A simple method to assess the hydrophilic lipophilic balance of food and cosmetic surfactants using the phase inversion temperature of C10E4/n-octane/water emulsions. Colloids Surf. A 2014, 458, 32–39. [Google Scholar] [CrossRef]
- Salager, J.L. Quantifying the concept of physico-chemical formulation in surfactant-oil-water systems. Progr. Colloid Polym. Sci. 1996, 100, 137–142. [Google Scholar] [CrossRef]
- Salager, J.L. Formulation concepts for the emulsion makers. In Pharmaceutial Emulsions and Suspensionfs; Nielloud, F., Marti-Mestres, G., Eds.; Marcel Dekker: New York, NY, USA, 2000; Chapter 2; pp. 19–72. [Google Scholar] [CrossRef]
- Salager, J.L. Emulsion properties and related know-how to attain them. In Pharmaceutial Emulsions and Suspensionfs; Nielloud, F., Marti-Mestres, G., Eds.; Marcel Dekker: New York, NY, USA, 2000; Chapter 3; pp. 73–125. [Google Scholar] [CrossRef]
- Bancroft, W.D. The Theory of Emusification VI. J. Phys. Chem. 1915, 19, 275–309. [Google Scholar] [CrossRef]
- Langmuir, I. The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 1917, 39, 1848–1906. [Google Scholar] [CrossRef]
- Winsor, P. Solvent Properties of Amphiphilic Compounds; Butterworth: London, UK, 1954. [Google Scholar]
- Winsor, P. Binary and multicomponent Solutions of amphiphilic compounds. solubilization and the formation, structure, and theoretical significance of liquid crystalline solutions. Chem. Rev. 1968, 68, 1–40. [Google Scholar] [CrossRef]
- Holtzscherer, C.; Candau, F. Application of the cohesive energy ratio concept (CER) to the formation of polymerizable microemulsions. Colloids Surf. 1988, 29, 411–423. [Google Scholar] [CrossRef]
- Hansen, C. The Three Dimensional Solubility Parameter—Key to Paint Component Affinities: I.; Solvents, Plasticizers, Polymer, and Resins. J. Paint Technol. 1967, 39, 104–117. [Google Scholar]
- Israelavilich, J.N. The science and applications of emulsions—An overview. Colloids Surf. A 1994, 91, 1–8. [Google Scholar] [CrossRef]
- Shinoda, K.; Arai, H. The correlation between phase inversion temperature in emulsion and cloud point in solution of nonionic emulsifier. J. Phys. Chem. 1964, 68, 3485–3490. [Google Scholar] [CrossRef]
- Shinoda, K.; Arai, H. The effect of phase volume on the phase inversion temperature of the emulsions stabilized by nonionic surfactants. J. Colloid Interface Sci. 1967, 25, 429–431. [Google Scholar] [CrossRef]
- Shinoda, K.; Kunieda, H. Conditions to produce so-called microemulsions: Factors To increase the mutual solubility of oil and water by solubilizer. J. Colloid Interface Sci. 1973, 42, 381–387. [Google Scholar] [CrossRef]
- Reed, R.L.; Healy, R.N. Some physicochemical aspects of microemulsion flooding—A review. In Improved Oil Recovery by Surfactant and Polymer Flooding; Shah, D.O., Schechter, R.S., Eds.; Academic Press: New York, NY, USA, 1977; pp. 347–383. [Google Scholar]
- Wade, W.H.; Schechter, R.S.; Morgan, J.C.; Jacobson, J.K.; Salager, J.L. Interfacial tension and Phase Behavior of Surfactant Systems. Paper SPE 6844 presented in Proceedings 52nd Fall Meeting Society of Petroleum Engineering, Denver (1977). Soc. Petroleum Eng. J. 1978, 18, 242–252. [Google Scholar] [CrossRef]
- Salager, J.L. Physico-Chemical Properties of Surfactant-Water-Oil Mixtures: Phase Behavior, Microemulsion Formation and Interfacial Tension. Ph.D. Thesis, University of Texas, Austin, TX, USA, 24 December 1977. [Google Scholar]
- Salager, J.L.; Morgan, J.; Schechter, R.S.; Wade, W.H.; Vasquez, E. Optimum formulation of surfactant-oil-water systems for minimum tension and phase behavior. Soc. Pet. Eng. J. 1979, 19, 107–115. [Google Scholar] [CrossRef]
- Bourrel, M.; Salager, J.L.; Schechter, R.S.; Wade, W.H. A correlation for phase behavior of nonionic surfactants. J. Colloid Interface Sci. 1980, 75, 451–461. [Google Scholar] [CrossRef]
- Salager, J.L.; Miñana-Perez, M.; Perez-Sanchez, M.; Ramirez-Gouveia, M.; Rojas, C. Surfactant-Oil-Water systems near the affinity inversion—Part III: The two kinds of emulsion inversion. J. Dispers. Sci. Technol. 1983, 4, 313–329. [Google Scholar] [CrossRef]
- Salager, J.L.; Marquez, N.; Graciaa, A.; Lachaise, J. Partitioning of ethoxylated octylphenol surfactants in microemulsion-oil-water systems: Influence of temperature and relation between partitioning coefficient and physicochemical formulation. Langmuir 2000, 16, 5534–5539. [Google Scholar] [CrossRef]
- Shinoda, K.; Kunieda, H. Phase properties of emulsions: PIT and HLB. In Encyclopedia of Emulsion Technology; Basic Theory; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1983; Volume 1, pp. 337–367. [Google Scholar]
- Bourrel, M.; Schechter, R.S. Microemulsions and Related Systems: Formulation, Solvency, and Physical Properties; Marcel Dekker: New York, NY, USA, 1988. [Google Scholar]
- Kunieda, H.; Solans, C. How to prepare microemulsions: Temperature insensitive microemulsions. In Industrial Applications of Microemulsions; Marcel Dekker: New York, NY, USA, 1997; ISBN 9780824797959. [Google Scholar]
- Stubenrauch, C. (Ed.) Microemulsions: Background, New Concepts, Applications and Perspectives; Wiley-Blackwell: Oxford, UK, 2009. [Google Scholar] [CrossRef]
- Shinoda, K.; Lindman, B. Organized surfactant systems: Microemulsions. Langmuir 1989, 3, 135–149. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A.; Bullon, J. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 1. Optimum formulation for simple surfactant-oil-water ternary systems. J. Surfactants Deterg. 2013, 16, 449–472. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A.; Marquez, L.; Manchego, L.; Bullon, J. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 2. Performance improvement trends from Winsor’s premise to currently proposed inter- and intramolecular mixtures. J. Surfactants Deterg. 2013, 16, 631–663. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A.; Rondon, M. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 3. Practical procedures to optimize the laboratory research according to the current state of the art in surfactant mixing. J. Surfactants Deterg. 2017, 20, 3–19. [Google Scholar] [CrossRef]
- Salager, J.L.; Anton, R.E.; Arandia, M.A.; Forgiarini, A. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 4. Robustness of optimum formulation zone through the insensibility to some variables and the occurrence of complex artifacts. J. Surfactants Deterg. 2017, 20, 987–1018. [Google Scholar] [CrossRef]
- Winsor, P. Hydrotropy, solubilization and related emulsification processs. Trans. Faraday Soc. 1948, 44, 376–382. [Google Scholar] [CrossRef]
- Hoar, T.P.; Schulman, J.H. Transparent water-in-oil dispersions: Oleopathic hydromicelle. Nature 1943, 182, 102–103. [Google Scholar] [CrossRef]
- Schulman, J.H.; Stoeckenius, W.; Prince, L.M. Mechanism of formation and structure of microemulsions by electron microscopy. J. Phys. Chem. 1959, 63, 1677–1680. [Google Scholar] [CrossRef]
- Scriven, L.E. Equilibrium bicontinuous structures. Nature 1976, 263, 123–125. [Google Scholar] [CrossRef]
- Clausse, M.; Peyrelasse, J.; Heil, J.; Boned, C.; Lagourette, B. Bicontinuous structure zones in microemulsions. Nature 1981, 293, 636–638. [Google Scholar] [CrossRef]
- Bourrel, M.; Verzaro, F.; Chambu, C. Effect of oil type on solubilization by amphiphiles. Soc. Pet. Eng. Reserv. Eng. 1987, 2, 41–53. [Google Scholar] [CrossRef]
- Kahlweit, M.; Strey, R. Phase Behavior of ternary systems of the type H20-oil-nonionic amphiphile microemulsions. Angew. Chem. Intern. Ed. Engl. 1988, 24, 654–668. [Google Scholar] [CrossRef]
- Kahlweit, M.; Strey, R.; Firman, P. Search for Tricritical points in ternary systems: Water-Oil-Nonionic amphiphile. J. Phys. Chem. 1986, 90, 671–677. [Google Scholar] [CrossRef]
- Lade, O.; Beizai, K.; Sottmann, T.; Strey, R. Polymerizable nonionic microemulsions: Phase Behavior of H2O-n-alkyl methacrylate-n-alkyl polyethylene glycol ether (CiEj). Langmuir 2000, 16, 4122–4130. [Google Scholar] [CrossRef]
- Lee, J.M.; Lim, K.H. Changes in two-phase emulsion morphology in temperature-amphiphile concentration or fish diagram for ternary amphiphile/oil/water systems. J. Colloid Interface Sci. 2005, 290, 241–249. [Google Scholar] [CrossRef] [PubMed]
- Pizzino, A.; Molinier, V.; Catte, M.; Salager, J.L.; Aubry, J.M. Bidimensional analysis of the phase behavior of a well-defined surfactant (C10E4)/oil (n-Octane)/water-temperature system. J. Phys. Chem. B 2009, 113, 16142–16150. [Google Scholar] [CrossRef] [PubMed]
- Pizzino, A.; Molinier, V.; Catte, M.; Ontiveros, J.F.; Salager, J.L.; Aubry, J.M. Relationship between phase behavior and emulsion inversion for a well-defined surfactant (C10E4)/n-octane/water ternary system at different temperatures and water/oil ratios. Ind. Eng. Chem. Res. 2013, 52, 4527–4538. [Google Scholar] [CrossRef]
- Burauer, S.; Sachert, T.; Sottmann, T.; Strey, R. On microemulsion phase behavior and the monomeric solubility of surfactant. Phys. Chem. Chem. Phys. 1999, 1, 4299–4306. [Google Scholar] [CrossRef]
- Solans, C.; Kunieda, H. (Eds.) Industrial Applications of Microemulsions; Marcel Dekker: New York, NY, USA, 1997. [Google Scholar]
- Kahlweit, M.; Lessner, E.; Strey, R. Phase behavior of quaternary systems of the type H2O-oil-nonionic surfactant inorganic electrolyte. J. Phys. Chem. 1984, 88, 1937–1944. [Google Scholar] [CrossRef]
- Strey, R. Microemulsion microstructure and interfacial curvature. Colloid Polym. Sci. 1994, 272, 1005–1019. [Google Scholar] [CrossRef]
- Graciaa, A.; Fortney, L.N.; Schechter, R.S.; Wade, W.H.; Yiv, S. Criteria for structuring surfactants to maximize solubilization of oil and water: Part 1—Commercial nonionics. Soc. Pet. Eng. J. 1982, 22, 743–749. [Google Scholar] [CrossRef]
- Barakat, Y.; Fortney, L.; Schechter, R.S.; Wade, W.H.; Yiv, S.H.; Graciaa, A. Criteria for structuring surfactants to maximize solubilization of oil and water. II. Alkyl benzene sodium sulfonates. J. Colloid Interface Sci. 1983, 92, 561–574. [Google Scholar] [CrossRef]
- Barakat, Y.; Fortney, L.; Schechter, R.S.; Wade, W.H. Alpha-Olefin sulfonates for oil recovery. In Proceedings of the 2nd European Symposium on Enhanced Oil Recovery, Paris, France, 8–10 November 1982. [Google Scholar]
- Huh, C. Interfacial tensions and solubilizing ability of a microemulsion phase that coexists with oil and brine. J. Colloid Interface Sci. 1979, 71, 408–426. [Google Scholar] [CrossRef]
- Salager, J.L.; Manchego, L.; Marquez, L.; Bullón, J.; Forgiarini, A. Trends to attain a lower interfacial tension in a revisited pure alkyl polyethyleneglycol surfactant-alkane-water ternary system. Basic concepts and straightforward guidelines for improving performance in enhanced oil recovery formulations. J. Surf. Deterg. 2014, 17, 199–213. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A.; Bullón, J. Surfactant formulation guidelines to reach an ultralow interfacial tension for enhanced oil recovery. In Topics in Colloidal Aggregation and Interfacial Phenomena; Garcia-Sucre, M., Lozsan, A., Castellanos-Suarez, A., Toro-Mendoza, J., Eds.; Research Signpost: Kerala, India, 2012; Chapter 5; pp. 125–160. ISBN 9788130804910. [Google Scholar]
- Salager, J.L.; Marquez, L.; Mira, I.; Peña, A.; Tyrode, E.; Zambrano, N. Principles of emulsion formulation engineering. In Adsorption and Aggregation of Surfactants in Solution; Surfactant Science Series; Mittal, K.L., Shah, D.O., Eds.; Marcel Dekker: New York, NY, USA, 2003; Volume 109, Chapter 24; pp. 501–524. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A.M.; Bullón, J. Progress over a century of designing emulsion properties—Emerging phenomenological guidelines from generalized formulation and prospects to transmute the knowledge into know-how. In Surfactant Science and Technology: Retrospects and Prospects; Romsted, L.S., Ed.; CRC Press: Boca Raton, FL, USA, 2014; Chapter 18; pp. 459–487. [Google Scholar] [CrossRef]
- Marquez, R.; Forgiarini, A.; Fernandez, J.; Langevin, D.; Salager, J.L. New interfacial rheology characteristics measured using a spinning-drop rheometer at the optimum formulation of a simple surfactant-oil-water system. J. Surf. Deterg. 2018, 21, 611–623. [Google Scholar] [CrossRef]
- Marquez, R.; Forgiarini, A.; Langevin, D.; Salager, J.L. Instability of emulsions made with surfactant-oil-water systems at optimum formulation with ultralow interfacial tension. Langmuir 2018, 34, 9252–9263. [Google Scholar] [CrossRef]
- Marquez, R.; Anton, R.E.; Vejar, F.; Salager, J.L.; Forgiarini, A. New Interfacial Rheology Characteristics Measured using a Spinning Drop Rheometer at the Optimum Formulation. Part 2. Surfactant-Oil-Water systems with a high volume of middle phase microemulsion. J. Surf. Deterg. 2019, 22, 177–188. [Google Scholar] [CrossRef]
- Cash, L.; Cayias, J.L.; Fournier, G.; MacAllister, D.; Shares, T.; Schechter, R.S.; Wade, W.H. The application of low interfacial tension scaling rules to binary hydrocarbon mixtures. J. Colloid Interface Sci. 1977, 59, 39–44. [Google Scholar] [CrossRef]
- Salager, J.L.; Anton, R.E.; Anderez, J.M.; Aubry, J.M. Formulation des micro-émulsions par la méthode HLD. Tech. Ing. Vol. Génie Procédés 2001, 157, 1–20. [Google Scholar]
- Salager, J.L.; Bourrel, M.; Schechter, R.S.; Wade, W.H. Mixing rules for optimum phase-behavior formulations of surfactant/oil/water systems. Soc. Pet. Eng. J. 1979, 19, 271–278. [Google Scholar] [CrossRef]
- Quintero, L.; Jones, T.A.; Clark, D.E.; Gabrysch, A.D.; Forgiarini, A.; Salager, J.L. Single Phase Microemulsions And in Situ Microemulsions for Cleaning Formation Damage. U.S. Patent 8,091,646 B2, 10 January 2012. [Google Scholar]
- Delgado-Linares, J.G.; Pereira, J.; Rondón, M.; Bullón, J.; Salager, J.L. Breaking of water-in-crude oil emulsions. 6. Estimating the demulsifier performance at optimum formulation from both the required dose and the attained instability. Energy Fuels 2016, 30, 5483–5491. [Google Scholar] [CrossRef]
- Delgado, J.G.; Alvarado, J.G.; Vejar, F.; Forgiarini, A.; Bullón, J.; Salager, J.-L. Breaking of water-in-crude oil emulsions. 7. Demulsifier performance at optimum formulation for various extended surfactant structures. Energy Fuels 2016, 30, 7065–7073. [Google Scholar] [CrossRef]
- Anton, R.E.; Anderez, J.M.; Bracho, C.; Vejar, F.; Salager, J.L. Practical surfactant mixing rules based on the attainment of microemulsion-oill-water three-phase behavior systems. In Interfacial Processes and Molecular Aggregation; Narayanan, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 218, pp. 83–113. [Google Scholar] [CrossRef]
- Bourrel, M.; Salager, J.L.; Schechter, J.L.; Wade, W.H. Properties of amphiphile oil-water systems at optimum formulation for phase behavior. In Proceedings of the 53rd Annual Fall Technical Conference Society Petroleum Engieneers, Preprints Paper SPE 7450, Houston, TX, USA, 1–3 October 1978. [Google Scholar] [CrossRef]
- Anton, R.E.; Salager, J.L. Effect of the electrolyte anion on the salinity contribution formulation of anionic surfactant microemulsions. J. Colloid Interface Sci. 1990, 1540, 75–81. [Google Scholar] [CrossRef]
- Witthayapanyanon, A.; Acosta, E.; Harwell, J.H.; Sabatini, D.A. Formulation of ultralow interfacial tension systems using extended surfactants. J. Surf. Deterg. 2006, 9, 331–339. [Google Scholar] [CrossRef]
- Salager, J.L.; Anton, R.E.; Sabatini, D.A.; Harwell, J.H.; Acosta, E.; Tolosa, L.I. Enhancing solubilization in microemulsion—State of the art and current trends. J. Surf. Deterg. 2005, 8, 3–21. [Google Scholar] [CrossRef]
- Witthayapanyanon, A.; Harwell, J.H.; Sabatini, D.A. Hydrophilic–Lipophilic deviation (HLD) method for characterizing conventional and extended surfactants. J. Colloid Interface Sci. 2008, 325, 259–266. [Google Scholar] [CrossRef]
- Solairaj, S.; Britton, C.; Lu, J.; Kim, D.H.; Weerasooriya, U.; Pope, G. New correlation to predict the optimum surfactant structure for EOR. Paper SPE 154262. In Proceedings of the 18th SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 14–18 April 2012. [Google Scholar] [CrossRef]
- Bourrel, M.; Koukounis, C.; Schechter, R.S.; Wade, W.H. Phase and interfacial tension behavior of nonionic surfactats. J. Dispers. Sci. Technol. 1980, 1, 13–35. [Google Scholar] [CrossRef]
- Anton, R.E.; Garces, N.; Yajure, A. A correlation for three-phase behavior of cationic surfactant-oil-water systems. J. Dispers. Sci. Technol. 1997, 18, 539–555. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Morgan, C.; Poindexter, L.; Fernandez, J. Application of the Hydrophilic–Lipophilic Deviation concept to surfactant characterization and surfactant selection for enhanced oil recovery. J. Surf. Deterg. 2019, 22, 983–999. [Google Scholar] [CrossRef]
- Torrealba, V.A.; Johns, R.T. Partition coefficient relations in surfactant-oil-brine systems for improved description of microemulsion phase behavior. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 26–28 March 2016. [Google Scholar] [CrossRef]
- Torrealba, V.; Johns, R. Coupled interfacial tension and phase behavior model based on micellar curvatures. Langmuir 2017, 33, 13603–13614. [Google Scholar] [CrossRef]
- Miñana-Perez, M.; Graciaa, A.; Lachaise, J.; Salager, J.L. Solubilization of polar oils in microemulsion systems. Progr. Colloid Polym. Sci. 1995, 98, 177–179. [Google Scholar] [CrossRef]
- Hammond, C.; Acosta, E.; Jakobs-Sauter, B. Effect of hydrocarbon branching on the packing of extended surfactants at oil-water interfaces. In Proceedings of the 5th World Congress on Emulsion, Lyon, France, 12–14 October 2010. [Google Scholar]
- Fotland, P.; Skauge, A. Ultralow interfacial tension as a function of pressure. J. Dispers. Sci. Technol. 1986, 7, 563–579. [Google Scholar] [CrossRef]
- Skauge, A.; Fotland, P. Effect of pressure and temperature on the phase behavior of microemulsions. Soc. Pet. Reserv. Eng. 1990, 5, 601–608. [Google Scholar] [CrossRef]
- Austad, T.; Strand, S. Chemical flooding of oil reservoir. 4. Effects of temperature and pressure on the middle phase solubilization parameters close to optimum flood conditions. Colloid Surf. A 1996, 108, 243–252. [Google Scholar] [CrossRef]
- Ghosh, S.; Johns, R.T. An equation-of-state model to predict surfactant/oil/brine-phase behavior. Soc. Pet. Eng. J. 2016, 21, 1106–1125. [Google Scholar] [CrossRef]
- Chailloux, N.; Nardello-Rataj, V.; Salager, J.L.; Aubry, J.M. Propriétés amphiphiles des tensioactifs de la famille du monolaurate de polyglycérol et application à la préparation de microémulsions à base d’esters gras. Ol. Corps Gras Lipides 2003, 10, 382–386. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A.; Marquez, R. Extended surfactants including an alkoxylated central part intermediate producing a gradual polarity transition—A review of the properties used in applications such as enhanced oil recovery and polar oil solubilization in microemulsions. J. Surfactants Deterg. 2019, 22, 935–972. [Google Scholar] [CrossRef]
- Miñana-Pérez, M.; Graciaa, A.; Lachaise, J.; Salager, J.L. Solubilization of polar oils with extended surfactants. Colloids Surf. A 1995, 100, 217–224. [Google Scholar] [CrossRef]
- Aoudia, M.; Wade, W.H.; Weerasooriya, V. Optimum microemulsions formulated with propoxylated Guerbet alcohol and propoxylated tridecyl alcohol sodium sulfates. J. Dispers. Sci. Technol. 1995, 16, 115–135. [Google Scholar] [CrossRef]
- Charoensaeng, A.; Sabatini, D.A.; Khaodhiar, S. Solubilization and adsolubilization of polar and nonpolar organic solutes by linker molecules and extended surfactants. J. Surfactants Deterg. 2009, 12, 209–217. [Google Scholar] [CrossRef]
- Velasquez, J.; Scorzza, C.; Vejar, F.; Forgiarini, A.; Anton, R.E.; Salager, J.L. Effect of the temperature and other variables on the optimum formulation of anionic extended surfactants-alkane-brine systems. J. Surfactants Deterg. 2010, 13, 69–73. [Google Scholar] [CrossRef]
- Forgiarini, A.M.; Scorzza, C.; Velasquez, J.; Vejar, F.; Zambrano, E.; Salager, J.-L. Influence of the mixed propoxy/ethoxy spacer arrangement order and of the ionic head group nature on the adsorption and aggregation of extended surfactants. J. Surfactants Deterg. 2010, 13, 451–458. [Google Scholar] [CrossRef]
- Klaus, A.; Tiddy, G.J.T.; Rachel, R.; Trinh, A.P.; Maurer, E.; Touraud, D.; Kunz, W. Hydrotrope-Induced inversion of salt effects on the cloud point of an extended surfactant. Langmuir 2011, 27, 4403–4411. [Google Scholar] [CrossRef] [PubMed]
- Zarate, S.; Troncoso, A.B.; Acosta, E. The cloud point of alkyl ethoxylates and its prediction with the hydrophilic-lipophilic difference (HLD) framework. Langmuir 2015, 31, 12000–12008. [Google Scholar] [CrossRef] [PubMed]
- Hammond, C.E.; Acosta, E. On the characteristic curvature of alkyl-polypropylene oxide sulfate extended surfactants. J. Surfactants Deterg. 2012, 15, 157–165. [Google Scholar] [CrossRef]
- Chen, J.; Hu, X.Y.; Fang, Y.; Liu, H.H.; Xia, Y.M. Comparative study of conventional/ethoxylated/extended n-alkylsulfate surfactants. Langmuir 2019, 35, 3116–3125. [Google Scholar] [CrossRef]
- Miñana-Perez, M.; Graciaa, A.; Lachaise, J.; Salager, J.L. Systems containing mixtures of extended surfactants and conventional nonionics. Phase behavior and solubilization in microemulsion. In Proceedings of the 4th World Surfactants Congress, Barcelona, Spain, 3–7 June 1996. Proceedings 2:226–234, Edited for AEPSAT by Roger de Llúria, Barcelona, Spain. [Google Scholar]
- Vera, R.; Salazar, F.; Marquez, R.; Forgiarini, A. How the influence of different salts on interfacial properties of surfactant-oil-water systems at optimum formulation matches the Hofmeister series ranking. J. Surfactants Deterg. 2020, 23, 603–615. [Google Scholar] [CrossRef]
- Kunieda, H.; Shinoda, K. Phase behavior in systems of nonionic surfactant-water-oil around the hydrophile-lipophile balance-temperature (HLB-Temperature). J. Dispers. Sci. Technol. 1982, 3, 233–244. [Google Scholar] [CrossRef]
- Aubry, J.M.; Ontiveros, J.F.; Salager, J.L.; Nardello-Rataj, V. Use of the normalized hydrophilic-lipophilic-deviation (HLDN) equation for determining the equivalent alkane carbon number (EACN) of oils and the preferred alkane carbon number (PACN) of nonionic surfactants by the fish-tail method (FTM). Adv. Colloid Interface Sci. 2020, 276, 102099. [Google Scholar] [CrossRef] [PubMed]
- Cayias, J.L.; Schechter, R.S.; Wade, W.H. Modeling crude oils for low interfacial tension. Soc. Pet. Eng. J. 1976, 16, 351–357. [Google Scholar] [CrossRef]
- Sottmann, T.; Strey, R. Ultralow interfacial tension in water-n-alkane-surfactant systems. J. Chem. Phys. 1997, 106, 8606–8615. [Google Scholar] [CrossRef]
- Acosta, E.; Yuan, J.S.; Bhakta, A.S. The characteristic curvature of ionic surfactants. J. Surfactants Deterg. 2008, 11, 145–158. [Google Scholar] [CrossRef]
- Abbott, S. Surfactant Science: Principles and Practice; Creative Commons BY-ND: Mountain View, CA, USA, 2015; ISBN 9781605954844. Available online: http://www.stevenabbott.co.uk/practical-surfactants/the-book.php (accessed on 14 July 2020).
- Acosta, E.; Bhakta, A.S. The HLD-NAC model for mixtures of ionic and nonionic surfactants. J. Surfactants Deterg. 2009, 12, 7–19. [Google Scholar] [CrossRef]
- Acosta, E.; Szekeres, E.; Sabatini, D.A.; Harwell, J. Net-Average curvature model for solubilization and supersolubilization in surfactant microemulsions. Langmuir 2003, 19, 186–195. [Google Scholar] [CrossRef]
- Hayes, M.; Bourrel, M.; El-Emary, M.; Schechter, R.S.; Wade, W.H. Interfacial tension and phase behavior of nonionic surfactants. Soc. Pet. Eng. J. 1979, 19, 349–356. [Google Scholar] [CrossRef]
- Graciaa, A.; Lachaise, J.; Cucuphat, C.; Bourrel, M.; Salager, J.L. Interfacial segregation of an ethyl oleate/hexadecane oil mixture in microemulsion systems. Langmuir 1993, 9, 1473–1478. [Google Scholar] [CrossRef]
- Salager, J.L.; Graciaa, A.; Lachaise, J. Improving solubilization in microemulsions with additives. 3. Lipophilic linker optimization. J. Surfactants Deterg. 1998, 1, 403–406. [Google Scholar] [CrossRef]
- Bourrel, M.; Chambu, C. The rules for achieving high solubilization of brine and oil by amphiphilic molecules. Soc. Pet. Eng. J. 1983, 23, 327–338. [Google Scholar] [CrossRef]
- Salager, J.L. Microemulsions. In Handbook of Detergents—Part A: Properties; Surfactant Science Series; Broze, G., Ed.; Marcel Dekker: New York, NY, USA, 1999; Volume 82, Chapter 8; pp. 253–302. [Google Scholar] [CrossRef]
- Budhathoki, M.; Hsu, T.P.; Lohateeraparp, P.; Roberts, B.L.; Shiau, B.-J.; Harwell, J.H. Design of an optimal middle phase microemulsion for ultra high saline brine using hydrophilic lipophilic deviation (HLD) method. Colloids Surf. A 2016, 488, 36–45. [Google Scholar] [CrossRef]
- Doe, P.H.; El-Emary, M.; Wade, W.H.; Schechter, R.S. Surfactants for producing low interfacial tensions: II. Linear alkylbenzene-sulfonates with additional alkyl substituents. J. Am. Oil Chem. Soc. 1978, 55, 505–512. [Google Scholar] [CrossRef]
- Doe, P.H.; El-Emary, M.; Wade, W.H.; Schechter, R.S. Surfactants for producing low interfacial tensions: III. Di and tri n-alkylbenzenesulfonates. J. Am. Oil Chem. Soc. 1978, 55, 513–520. [Google Scholar] [CrossRef]
- Doe, P.H.; El-Emary, M.; Wade, W.H. The influence of surfactant structure on low interfacial tension. In Chemistry of Oil Recovery; ACS Series 91; Johansen, R.T., Berg, R.L., Eds.; American Chemical Society: Washington, DC, USA, 1979; pp. 17–34. [Google Scholar] [CrossRef]
- Salager, J.L.; Anton, R.E. Ionic microemulsions. In Handbook of Microemulsion Science and Technology; Kumar, P., Mittal, K.L., Eds.; Marcel Dekker: New York, NY, USA, 1999; Chapter 8; pp. 247–280. ISBN 08247-1979-4. [Google Scholar]
- Acosta, E.; Kiran, S.; Hammond, C.E. The HLD-NAC model for extended surfactant microemulsions. J. Surfactants Deterg. 2012, 15, 495–504. [Google Scholar] [CrossRef]
- Schechter, R.S.; Wade, W.H.; Weerasooriya, U.; Weerasooriya, V.; Yiv, S. Synthesis and performance of isomer-free secondary alkane sulfonate surfactants. J. Dispers. Sci. Technol. 1985, 6, 223–235. [Google Scholar] [CrossRef]
- Johansson, I. Does hydrophobe branching make a surfactant more or less hydrophilic? Spec. Chem. Mag. 2004, 11, 38–40. [Google Scholar]
- Doe, P.H.; Wade, W.H.; Schechter, R.S. Alkylbenzene sulfonates for producing low interfacial tension between hydrocarbons and water. J. Colloid Interface Sci. 1977, 59, 525–531. [Google Scholar] [CrossRef]
- Trotter, B.; Baradaran, S.; Kadhum, M.; Shiau, B.; Harwell, J. Specific ion effects in Winsor III microemulsions. In Proceedings of the AOCS Annual Meeting, Orlando, FL, USA, 30 April–4 May 2017. [Google Scholar]
- Jeffreys, G.; Davies, A.C. Coalescence of liquid droplets and liquid dispersión. In Recent Advances in Liquid-Liquid Extraction; Hansen, C., Ed.; Pergamon Press: Oxford, UK, 1971; pp. 495–584. [Google Scholar] [CrossRef]
- Jones, T.J.; Neustadter, E.L.; Whittingham, K.P. Water-In-Crude oil emulsion stability and emulsion destabilization by chemical demulsifiers. J. Can. Pet. Technol. 1978, 17, 100–108. [Google Scholar] [CrossRef]
- Walstra, P. Formation of emulsions. In Encyclopedia of Emulsion Technology; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1983; Chapter 2; pp. 57–127. [Google Scholar]
- Bourrel, M.; Graciaa, A.; Schechter, R.S.; Wade, W.H. The relation of emulsion stability to phase behavior and interfacial tension of surfactant systems. J. Colloid Interface Sci. 1979, 72, 161–163. [Google Scholar] [CrossRef]
- Salager, J.L.; Quintero, L.; Ramos, E.; Anderez, J.M. Properties of surfactant/oil/water emulsified systems in the neighborhood of the three-phase transition. J. Colloid Interface Sci. 1980, 77, 288–289. [Google Scholar] [CrossRef]
- Milos, F.S.; Wasan, D.T. Emulsion stability of surfactant systems near the three-phase region. Colloids Surf. 1982, 4, 91–96. [Google Scholar] [CrossRef]
- Vinatieri, J.E. Correlation of emulsion stability with phase behavior in surfactant systems for tertiary oil recovery. Soc. Pet. Eng. J. 1980, 20, 402–406. [Google Scholar] [CrossRef]
- Anton, R.E.; Salager, J.L. Emulsion instability in the three-phase behavior region of surfactant-alcohol-oil-brine systems. J. Colloid Interface Sci. 1986, 111, 54–59. [Google Scholar] [CrossRef]
- Rieger, M.M.; Rhein, L.D. (Eds.) Surfactants in Cosmetics, 2nd ed.; Surfactant Science Series; Marcel Dekker: New York, NY, USA, 1997; Volume 68, ISBN 0824798058. [Google Scholar]
- Barel, A.O.; Paye, M.; Maibach, H.I. Handbook of Cosmetic Science and Technology; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Schueller, R.; Romanowski, P. Multifunctional Cosmetics; Marcel Dekker: New York, NY, USA, 2003; ISBN 9780203911044. [Google Scholar]
- Tadros, T. (Ed.) Encyclopedia of Colloid and Interface Science; Spinger: Berlin/Heidelberg, Germany, 2013; ISBN 9783642206665. [Google Scholar]
- Sivamani, R.K.; Jagdeo, J.R.; Elsner, P.; Maibach, H.I. (Eds.) Cosmeceuticals and Active Cosmetics, 3rd ed.; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2016. [Google Scholar]
- Tadros, T.F.; Vincent, B. Emulsion stability. In Encyclopedia of Emulsion Technology; Basic Theory; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1983; Volume 1, pp. 129–285. [Google Scholar]
- Zapryanov, Z.; Malhotra, A.K.; Aderangi, N.; Wasan, D.T. Emulsion stability: An analysis of the effects of bulk and interfacial properties on film mobility and drainage rate. Intern. J. Multiph. Flow 1983, 9, 105–129. [Google Scholar] [CrossRef]
- Shinoda, K.; Saito, H. The effect of temperature on the phase equilibria and the types of dispersions of the ternary system composed of water, cyclohexane and nonionic surfactant. J. Colloid Interface Sci. 1968, 26, 70–74. [Google Scholar] [CrossRef]
- Kunieda, H.; Shinoda, K. Evaluation of hydrophyle-lipophile balance (HLB) of nonionic surfactants. I. Multisurfactant systems. J. Colloid Interface Sci. 1985, 107, 107–121. [Google Scholar] [CrossRef]
- Kunieda, H.; Ishikawa, N. Evaluation of hydrophyle-lipophile balance (HLB) of nonionic surfactants. II. Commercial surfactant systems. J. Colloid Interface Sci. 1985, 107, 122–128. [Google Scholar] [CrossRef]
- Anton, R.E.; Castillo, P.; Salager, J.L. Surfactant-Oil-Water systems near the affinity inversion—Part IV: Emulsion Inversion Temperature. J. Dispers. Sci. Technol. 1986, 7, 319–329. [Google Scholar] [CrossRef]
- Miñana-Perez, M.; Jarry, P.; Perez-Sanchez, M.; Ramirez-Gouveia, M.; Salager, J.L.; Lopez-Castellanos, G.; Miñana-Perez, M. Surfactant-Oil-Water systems near the affinity inversion. Part 4. Emulsions with viscous hydrocarbons. J. Dispers. Sci. Technol. 1990, 11, 397–407. [Google Scholar] [CrossRef]
- Salager, J.L.; Lopez-Castellanos, G.; Miñana-Perez, M.; Parra, C. Surfactant-Oil-Water systems near the affinity inversion. Part 7. Phase inversion and emulsions with polar oils. J. Dispers. Sci. Technol. 1991, 12, 59–67. [Google Scholar] [CrossRef]
- Anton, R.E.; Rivas, H.; Salager, J.L. Surfactant-Oil-Water systems near the affinity inversion. Part 10. Emulsions made with anionic-nonionic surfactant mixtures. J. Dispers. Sci. Technol. 1996, 17, 553–566. [Google Scholar] [CrossRef]
- Mendez, Z.; Anton, R.E.; Salager, J.L. Surfactant-Oil-Water systems near the affinity inversion. Part 11. pH sensitive emulsions containing carboxylic acids. J. Dispers. Sci. Technol. 1999, 20, 883–892. [Google Scholar] [CrossRef]
- Perez, M.; Zambrano, N.; Ramirez, M.; Tyrode, E.; Salager, J.L. Surfactant-Oil-Water Systems near the affinity Inversion. 12. Emulsion Drop Size versus Formulation and Composition. J. Dispers. Sci. Technol. 2002, 23, 55–63. [Google Scholar] [CrossRef]
- Salager, J.L.; Anton, A.; Aubry, J.M. Formulation des émulsions par la méthode HLD. Tech. Ing. Vol. Génie Procédés 2006, 158, 1–15. [Google Scholar]
- Salager, J.L. Emulsion phase inversion phenomena. In Emulsions and Emulsion Stability, 2nd ed.; Sjoblöm, J., Ed.; Taylor & Francis: London, UK, 2006; Chapter 4; pp. 184–225. [Google Scholar]
- Aserin, A. (Ed.) Multiple Emulsions—Technology and Applications; Wiley: Hoboken, NJ, USA, 2008; ISBN 9780470170939. [Google Scholar]
- Frenkel, M.; Shwartz, R.; Garti, N. Multiple Emulsions. I. Stability: Inversion, apparent and weighted HLB. J. Colloid Interface Sci. 1983, 94, 174–178. [Google Scholar] [CrossRef]
- Garti, N. Double emulsions—Scope, limitations and new achievements. Colloids Surf. A 1997, 123, 233–246. [Google Scholar] [CrossRef]
- Salager, J.L. Phase transformation and emulsion inversion on the basis of catastrophe theory. In Encyclopedia of Emulsion Technology; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1988; Volume 3, Chapter 2; pp. 79–134. [Google Scholar]
- Salager, J.L. Applications of catastrophe theory to surfactant-oil-brine equilibrated and emulsified systems. In Surfactants in Solution; Mittal, K.L., Bothorel, P., Eds.; Plenum Press: New York, NY, USA, 1987; Volume 4, pp. 439–448. [Google Scholar] [CrossRef]
- Miller, D.J.; Henning, T.; Grunbein, W. Phase inversion of W/O emulsions by adding hydrophilic surfactant—A technique for making cosmetics products. Colloids Surf. A 2001, 183, 681–688. [Google Scholar] [CrossRef]
- Salager, J.L.; Anton, R.E.; Bracho, C.; Briceño, M.I.; Peña, A.; Rondon, M.; Salager, S. Attainment of emulsion properties on design. A typical case of formulation engineering. Récent Progrès Génie des Procédés. 1999, 13, 133–140. [Google Scholar]
- Salager, J.L.; Forgiarini, A.; Lopez, J.C.; Marfisi, S.; Alvarez, G. Dynamics of near-zero energy emulsification. In Proceedings of the 6th World Surfactant Congress CESIO, Berlin, Germany, 21–23 June 2004. [Google Scholar]
- Perazzo, A.; Preziosi, V.; Guido, S. Phase inversion emulsification: Current understanding and applications. Adv. Colloid Interface Sci. 2015, 222, 581–599. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A.; Marquez, L.; Peña, A.; Pizzino, A.; Rodriguez, M.P.; Rondon-Gonzalez, M. Using emulsion inversion in industrial processes. Adv. Colloid Interface Sci. 2004, 108, 259–272. [Google Scholar] [CrossRef]
- Tyrode, E.; Mira, I.; Zambrano, N.; Marquez, N.; Rondon-Gonzalez, M.; Salager, J.L. Emulsion catastrophic inversion from abnormal to normal morphology. 3. Conditions for triggering the dynamic inversion and application to industrial processes. Ind. Eng. Chem. Res. 2003, 42, 4311–4318. [Google Scholar] [CrossRef]
- Forster, T.; Schambil, F.; von Rybinski, W. Production of fine dispersed and long-term stable oil-in-water emulsions by the phase inversion temperature. J. Dispers. Sci. Technol. 1992, 13, 183–193. [Google Scholar] [CrossRef]
- Forster, T.; Von Rybinsky, W.; Wadle, A. Influence of microemulsion phases on the preparation of fine -dispersed emulsions. Adv. Colloid Interface Sci. 1995, 58, 119–149. [Google Scholar] [CrossRef]
- Cansellier, J.P.; Poux, M. Procédés d’émulsification—Méchanismes de formation des émulsions. Tech. Ing. 2000, 152, 1–12. [Google Scholar]
- Schubert, H.; Armbruster, H. Prinzipien der Herstellung und stabilität von emulsionen. Chem. Ing. Tech. 1989, 61, 701–711. [Google Scholar] [CrossRef]
- Grace, H.P. Dispersion phenomena in high viscosity inmiscible fluid systems and aplication of static mixers as dispersion devices in such systems. Chem. Eng. Commun. 1982, 14, 225–277. [Google Scholar] [CrossRef]
- Salager, S.E.; Tyrode, E.C.; Celis, M.T.; Salager, J.L. Influence of the stirrer initial position on emulsion morphology. Making use of the local water-to-oil ratio concept for formulation engineering purpose. Ind. Eng. Chem. Res. 2001, 40, 4808–4814. [Google Scholar] [CrossRef]
- Kunieda, K.; Miyajima, A. Effect of the mixing of oils on the Hydrophile-Lipophile-Balanced (HLB) temperature in a water/nonionic surfactant/oil system. J. Colloid Interface Sci. 1989, 128, 605–607. [Google Scholar] [CrossRef]
- Nardello, V.; Chailloux, N.; Poprawski, J.; Salager, J.L.; Aubry, J.M. HLD concept as a tool for the characterization of cosmetic hydrocarbon oils. Polym. Intern. 2003, 52, 602–609. [Google Scholar] [CrossRef]
- Queste, S.; Salager, J.L.; Strey, R.; Aubry, J.M. The EACN scale for oil classification revisited thanks to fish diagrams. J. Colloid Interface Sci. 2007, 312, 98–107. [Google Scholar] [CrossRef]
- Bouton, F.; Durand, M.; Nardello-Rataj, V.; Serry, M.; Aubry, J.M. Classification of terpene oils using the fish diagrams and the equivalent alkane carbon (EACN) scale. Colloids Surf. A 2009, 338, 142–147. [Google Scholar] [CrossRef]
- Bouton, F.; Durand, M.; Nardello-Rataj, V.; Borosy, A.P.; Quellet, C.; Aubry, J.M. A QSPR model for the prediction of the “fish-tail” temperature of CiE4/water/polar hydrocarbon oil systems. Langmuir 2010, 26, 7962–7970. [Google Scholar] [CrossRef]
- Tchakalova, V.; Fieber, W. Classification of fragrances and fragrance mixtures based on interfacial solubilization. J. Surfactants Deterg. 2012, 15, 167–177. [Google Scholar] [CrossRef]
- Ontiveros, J.F.; Pierlot, C.; Catte, M.; Molinier, V.; Pizzino, A.; Salager, J.L.; Aubry, J.M. Classification of ester oils according to their equivalent alkane carbon number (EACN) and asymmetry of fish diagrams of C10E4/ester oil/water systems. J. Colloid Interface Sci. 2013, 403, 67–76. [Google Scholar] [CrossRef]
- Baran, J.R.; Pope, G.A.; Schultz, C.; Wade, W.H.; Weerasooriya, V.; Yapa, A. Toxic spill remediation of chlorinated hydrocarons via microemulsion formation. In Surfactants in Solutions; Chattopadhay, A.K., Mittal, K.L., Eds.; Marcel Dekker: New York, NY, USA, 1996; pp. 393–411. [Google Scholar]
- Lukowicz, T.; Illous, E.; Nardello-Rataj, V.; Aubry, J.M. Prediction of the equivalent alkane carbon number (EACN) of aprotic polar oils with COSMO-RS sigma-moments. Colloids Surf. A 2018, 536, 53–59. [Google Scholar] [CrossRef]
- Rondon, M.; Bouriat, P.; Lachaise, J.; Salager, J.L. Breaking of water-in-crude oil emulsions. Part 1: Physico-chemical phenomenology of demulsifier action. Energy Fuels 2006, 20, 1600–1604. [Google Scholar] [CrossRef]
- Rondon, M.; Pereira, J.C.; Bouriat, P.; Graciaa, A.; Lachaise, J.; Salager, J.L. Breaking of water-in-crude oil emulsions. 2: Influence of asphaltene concentration and diluent nature on demulsifier action. Energy Fuels 2008, 22, 702–707. [Google Scholar] [CrossRef]
- Pereira, J.C.; Delgado, J.G.; Scorzza, C.; Rondon, M.; Salager, J.L. Breaking of water-in-crude emulsions. 4. Estimation of the demulsifier surfactant performance to destabilize the asphaltenes effect. Energy Fuels 2011, 25, 1045–1050. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A. Emulsion stabilization, breaking and inversion: Advantage or inconvenience in flow assurance. Energy Fuels 2012, 2, 4027–4033. [Google Scholar] [CrossRef]
- Gjayour, A.; Acosta, E. Characterizing the oil-like and surfactant-like behavior of polar oils. Langmuir 2019, 35, 15038–15050. [Google Scholar] [CrossRef]
- Vlachy, N.; Jagoda-Cwiklik, B.; Vácha, R.; Touraud, D.; Jungwirth, P.; Kunz, W. Hofmeister series and specific interactions of charged headgroups with aqueous ions. Adv. Colloid Interface Sci. 2009, 146, 42–47. [Google Scholar] [CrossRef]
- Graciaa, A.; Lachaise, J.; Sayous, J.G.; Grenier, P.; Yiv, S.; Schechter, R.S.; Wade, W.H. The Partitioning of complex surfactant mixtures between oil/water/microemulsion phases at high surfactant concentrations. J. Colloid Interface Sci. 1983, 93, 474–486. [Google Scholar] [CrossRef]
- Graciaa, A.; Lachaise, J.; Bourrel, M.; Osboren-Lee, I.; Schechter, R.S.; Wade, W.H. Partitioning of nonionic and anionic surfactant mixtures between oil/microemulsion/water phases. Soc. Pet. Eng. Reserv. Eng. 1987, 2, 305–314. [Google Scholar] [CrossRef]
- Graciaa, A.; Anderez, J.M.; Bracho, C.; Lachaise, J.; Salager, J.L.; Tolosa, L.; Ysambertt, F. The selective partitioning of the oligomers of polyethoxylated surfactant mixtures between interface and oil and water bulk phases. Adv. Colloid Interface Sci. 2006, 123, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Antón, R.E.; Gómez, D.; Graciaa, A.; Lachaise, J.; Salager, J.L. Surfactant-Oil-Water systems near the affinty inversion. Part 9. Optimum formulation and of mixed anionic-cationic systems phase behavior. J. Dispers. Sci. Technol. 1993, 14, 401–416. [Google Scholar] [CrossRef]
- Li, X.; Kunieda, H. Catanionic surfactants: Microemulsion formation and solubilization. Current Opin. Colloid Interface Sci. 2003, 8, 327–336. [Google Scholar] [CrossRef]
- Kunieda, H.; Hanno, K.; Yamaguchi, S.; Shinoda, K. The three-phase behavior of a brine/ionic surfactant/nonionic surfactant/oil system: Evaluation of the hydrophile-llipophile balance (HLB) of ionic surfactant. J. Colloid Interface Sci. 1985, 107, 129–137. [Google Scholar] [CrossRef]
- Anton, R.E.; Graciaa, A.; Lachaise, J.; Salager, J.L. Surfactant-Oil-Water system near the affinity inversion. Part 8. Optimum formulation and phase behavior of mixed anionic-nonionic system versus temperature. J. Dispers. Sci. Technol. 1992, 13, 565–579. [Google Scholar] [CrossRef]
- Lukowicz, T.; Maldonado, R.; Molinier, V.; Aubry, J.M.; Nardello-Rataj, V. Fragrance solubilization in temperature insensitive aqueous microemulsions based on synergistic mixtures of nonionicand anionic surfactants. Colloids Surf. A 2014, 458, 85–95. [Google Scholar] [CrossRef]
- Ontiveros, J.F.; Pierlot, C.; Catte, M.; Salager, J.L.; Aubry, J.M. Determining the Preferred Alkane Carbon Number (PACN) of nonionic surfactants using the PIT-slope method. Colloids Surfaces A 2018, 536, 30–37. [Google Scholar] [CrossRef]
- Ontiveros, J.F.; Pierlot, C.; Catte, M.; Molinier, V.; Salager, J.L.; Aubry, J.M. Structure-Interfacial properties relationship and quantification of the amphiphilicity of well-defined ionic and nonionic surfactants using the PIT-slope method. J. Colloid Interface Sci. 2015, 448, 222–230. [Google Scholar] [CrossRef]
- Salager, J.L.; Marquez, N.; Anton, R.E.; Graciaa, A.; Lachaise, J. Retrograde Transition in the Phase Behavior of surfactant-oil-water systems produced by an alcohol scan. Langmuir 1995, 11, 37–41. [Google Scholar] [CrossRef]
- Arandia, M.A.; Forgiarini, A.; Salager, J.L. Resolving an enhanced oil recovery challenge: Optimum formulation of a surfactant-oil-water system made insensitive to dilution. J. Surfactants Deterg. 2010, 13, 119–126. [Google Scholar] [CrossRef]
- Hirasaki, G.J. Interpretation of the change in optimal salinity with overall surfactant concentration. Soc. Pet. Eng. J. 1982, 22, 971–982. [Google Scholar] [CrossRef]
- Kunieda, H.; Yamagata, M. Three-Phase behavior in a mixed nonionic surfactant system. Colloid Polym. Sci. 1993, 271, 997–1004. [Google Scholar] [CrossRef]
- Engels, T.; Forster, T.; von Rybinski, W. The influence of coemulsifier type on the stability of oil-in-water emulsions. Colloids Surf. A 1995, 99, 141–149. [Google Scholar] [CrossRef]
- Marquez, R.; Bullon, J.; Marquez, L.; Cardenas, A.; Briceño, M.I.; Forgiarini, A. Rheological changes of parenteral emulsions during phase-inversion emulsification. J. Dispers. Sci. Technol. 2008, 29, 621–627. [Google Scholar] [CrossRef]
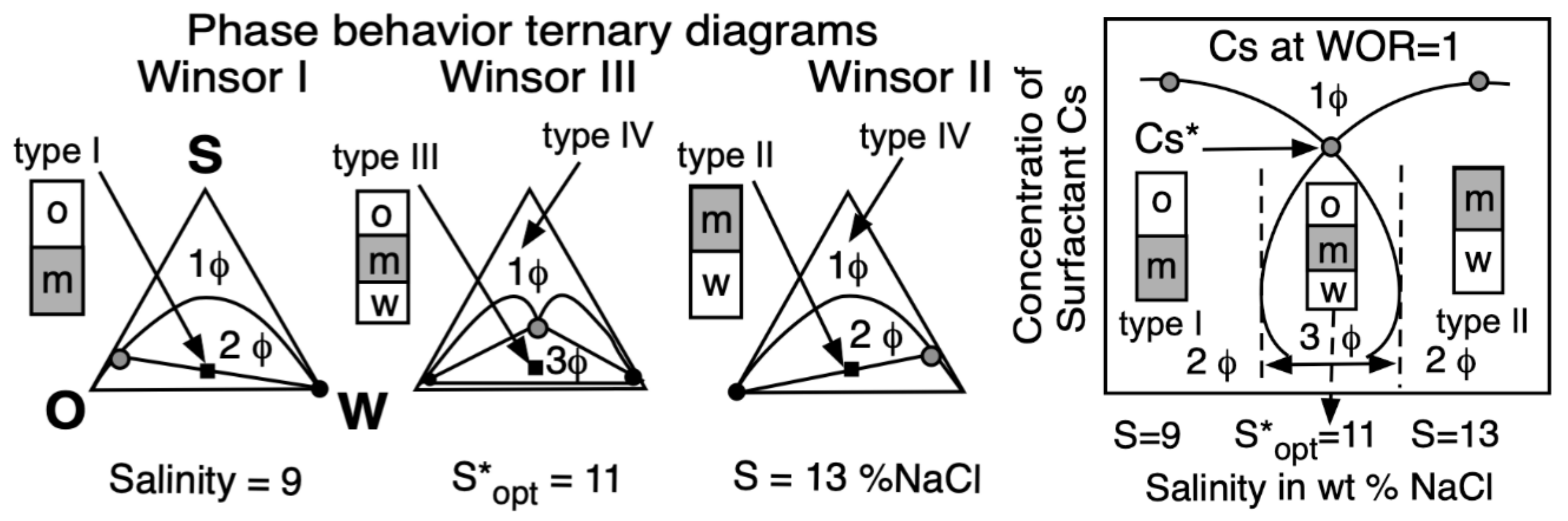
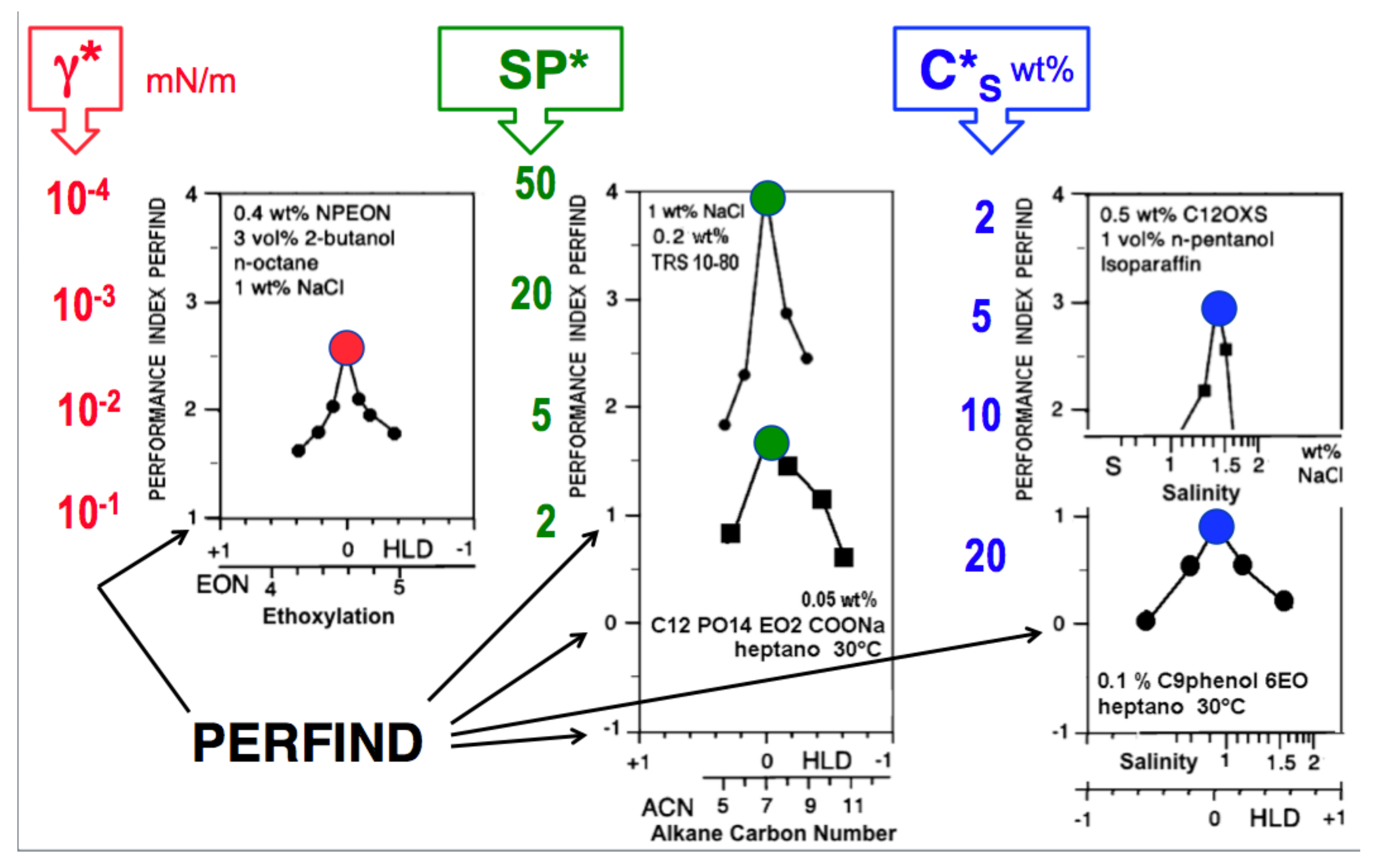
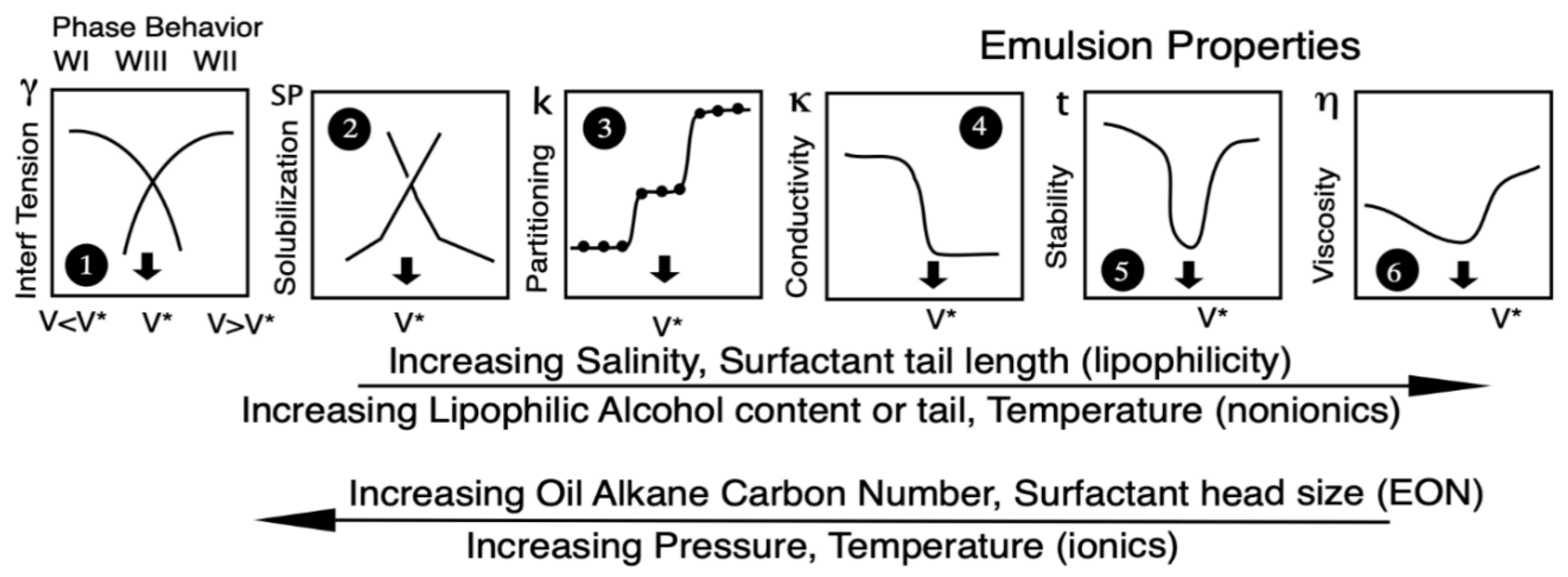
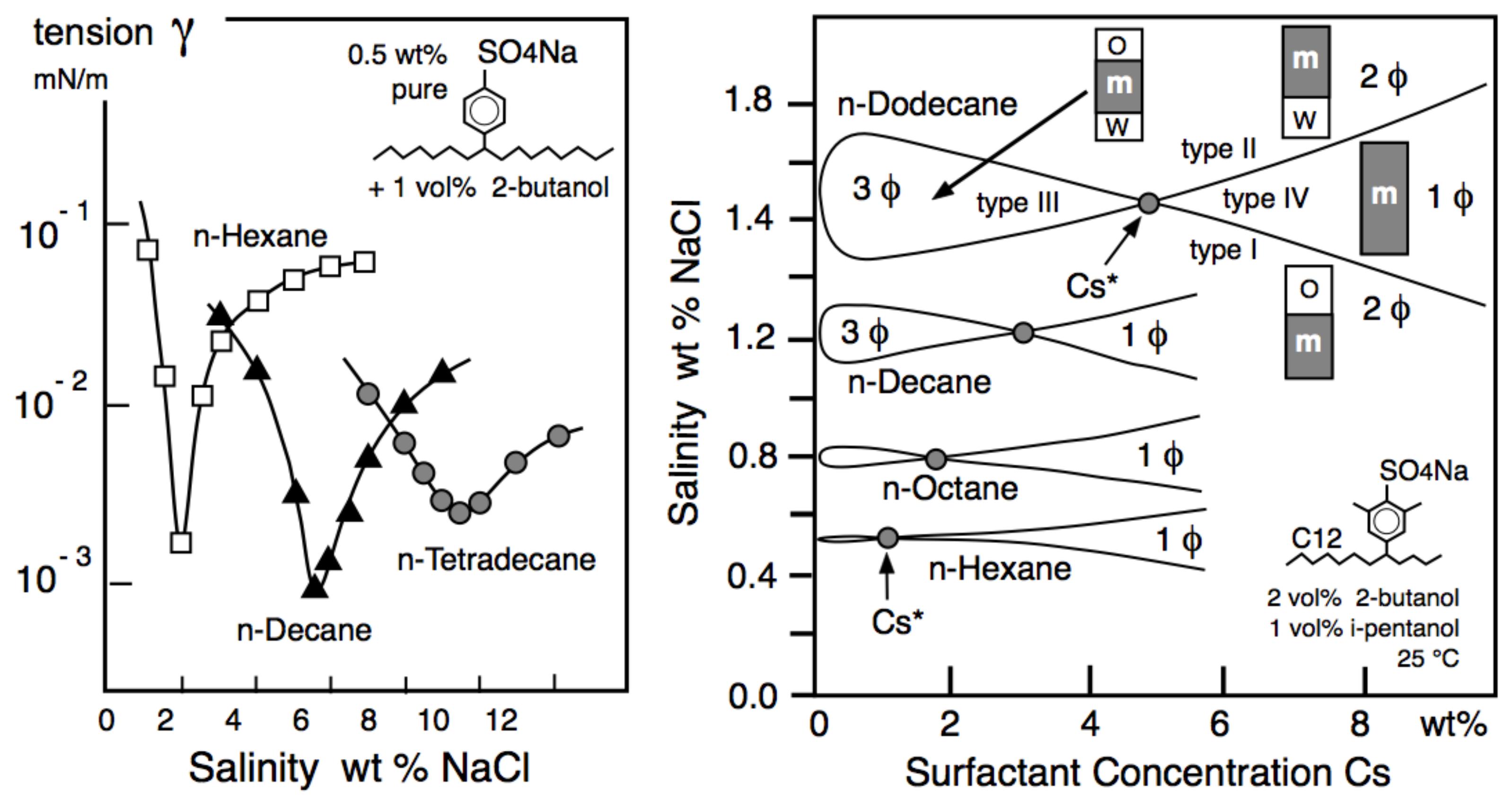
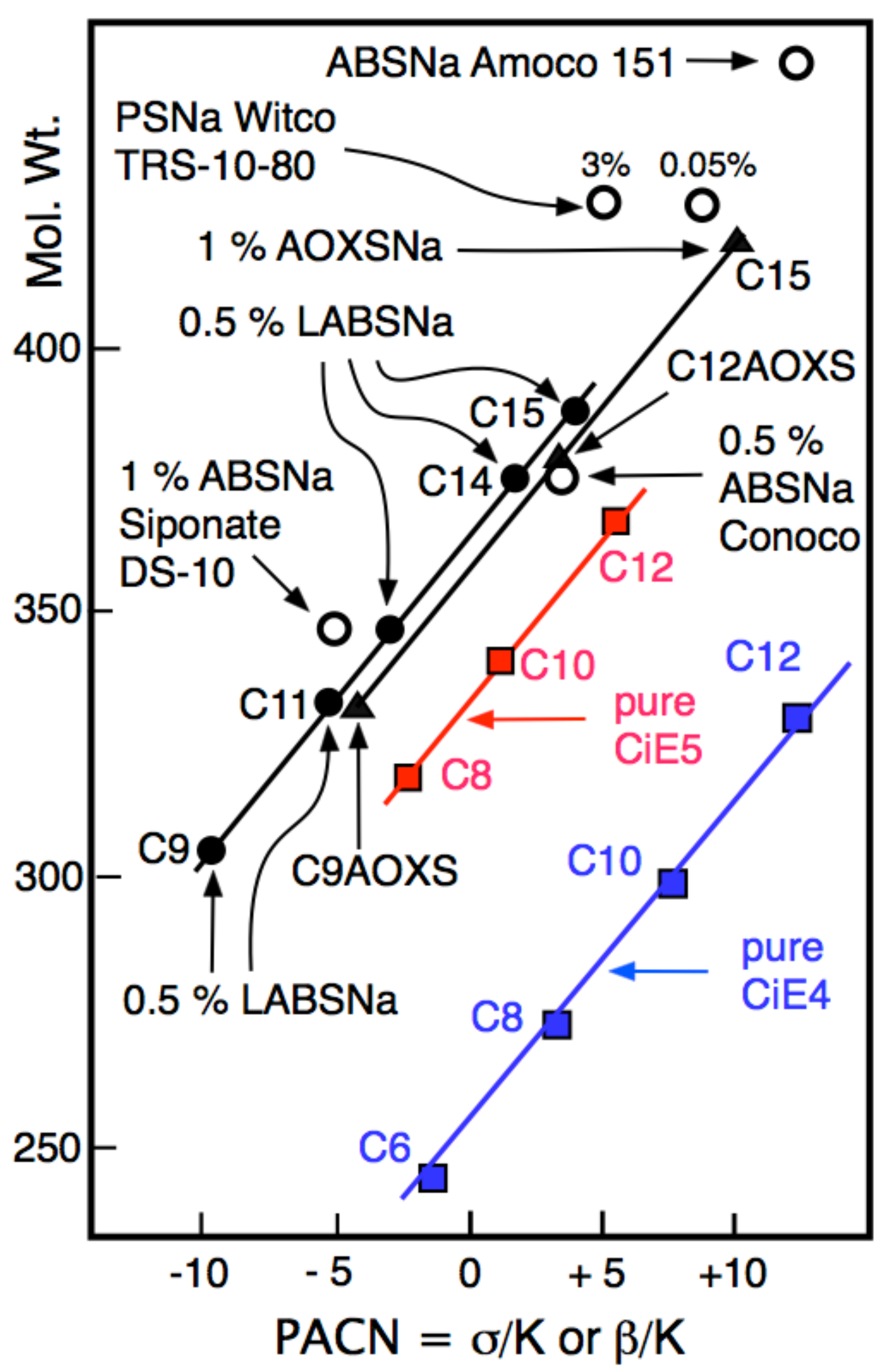
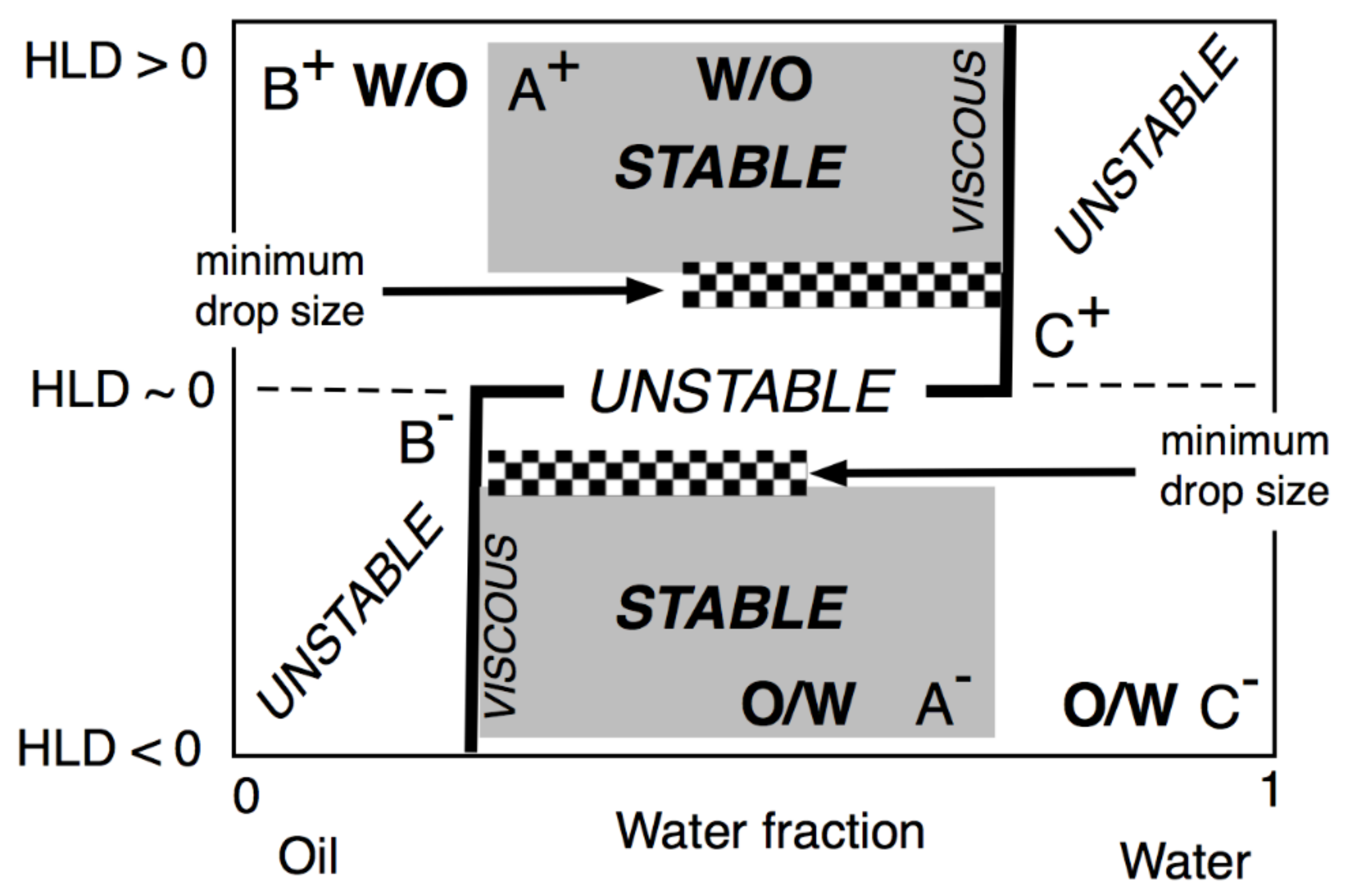
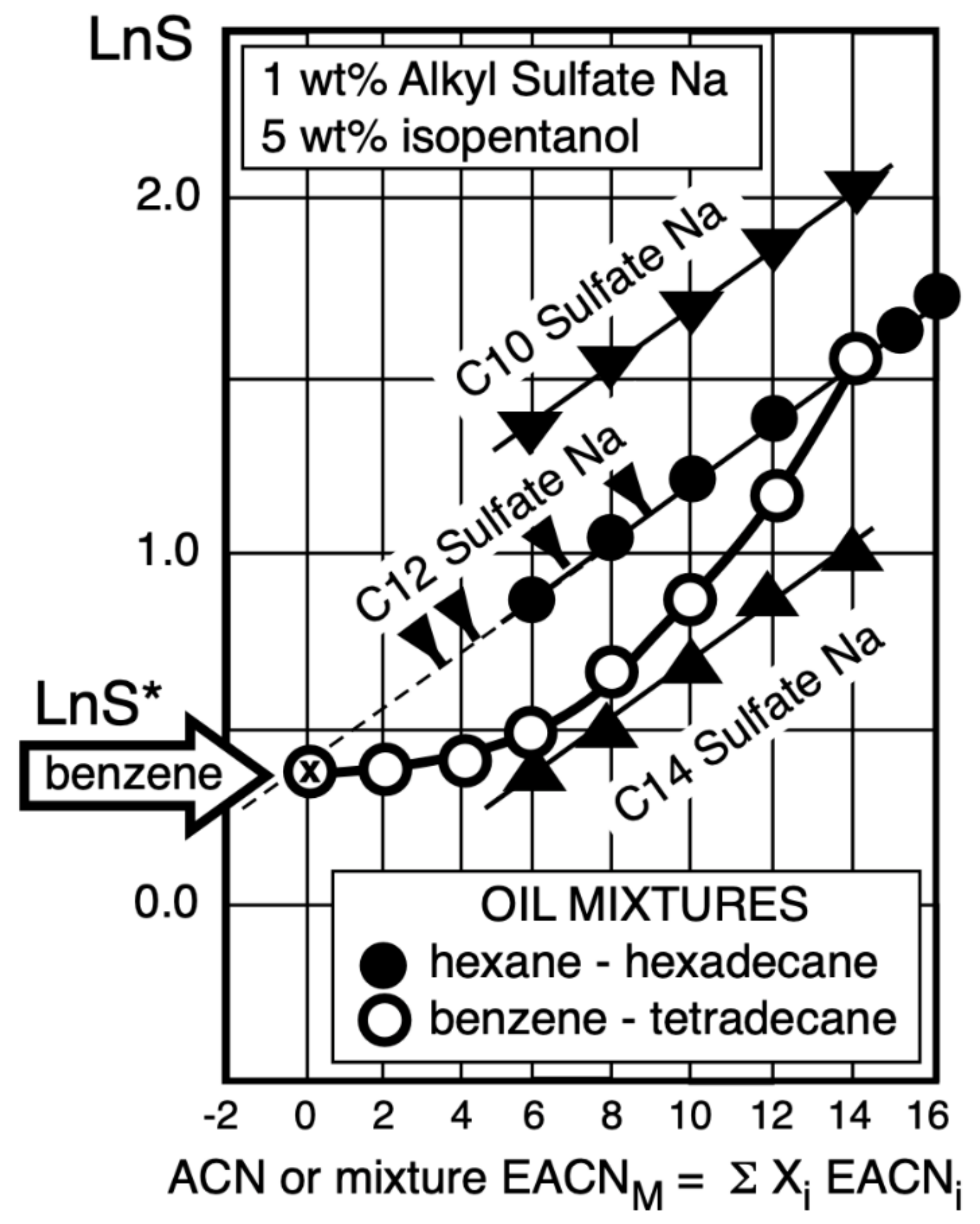
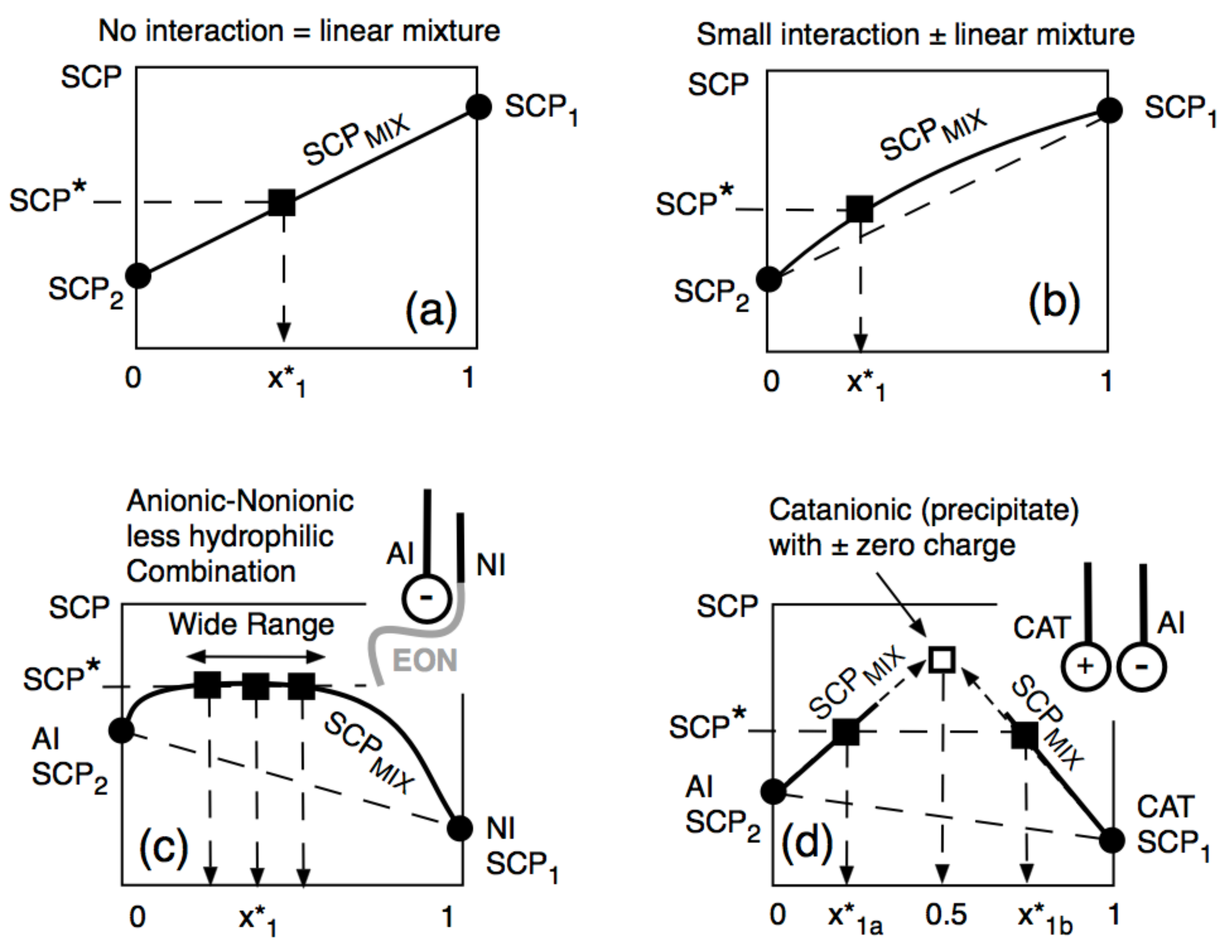
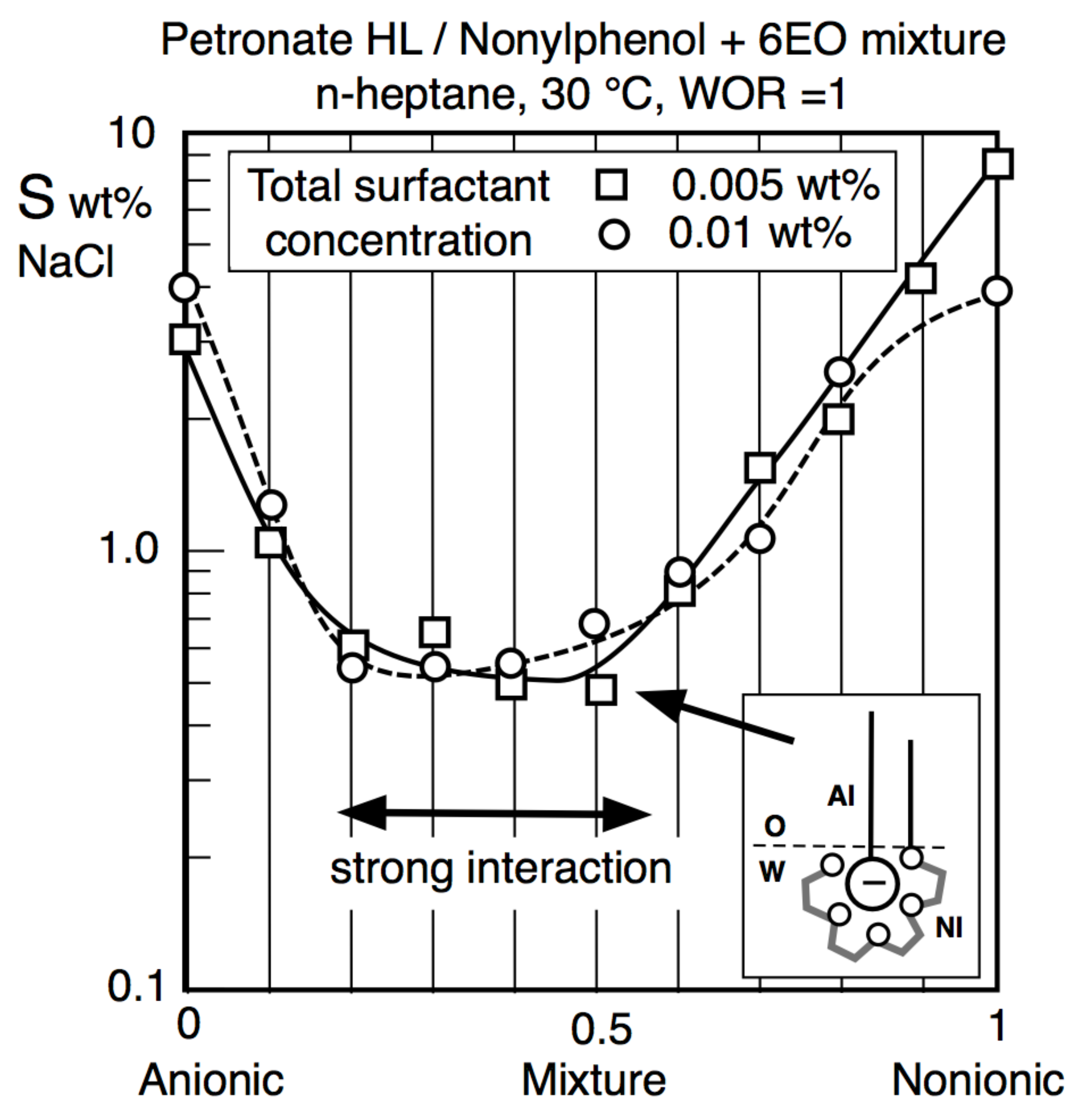
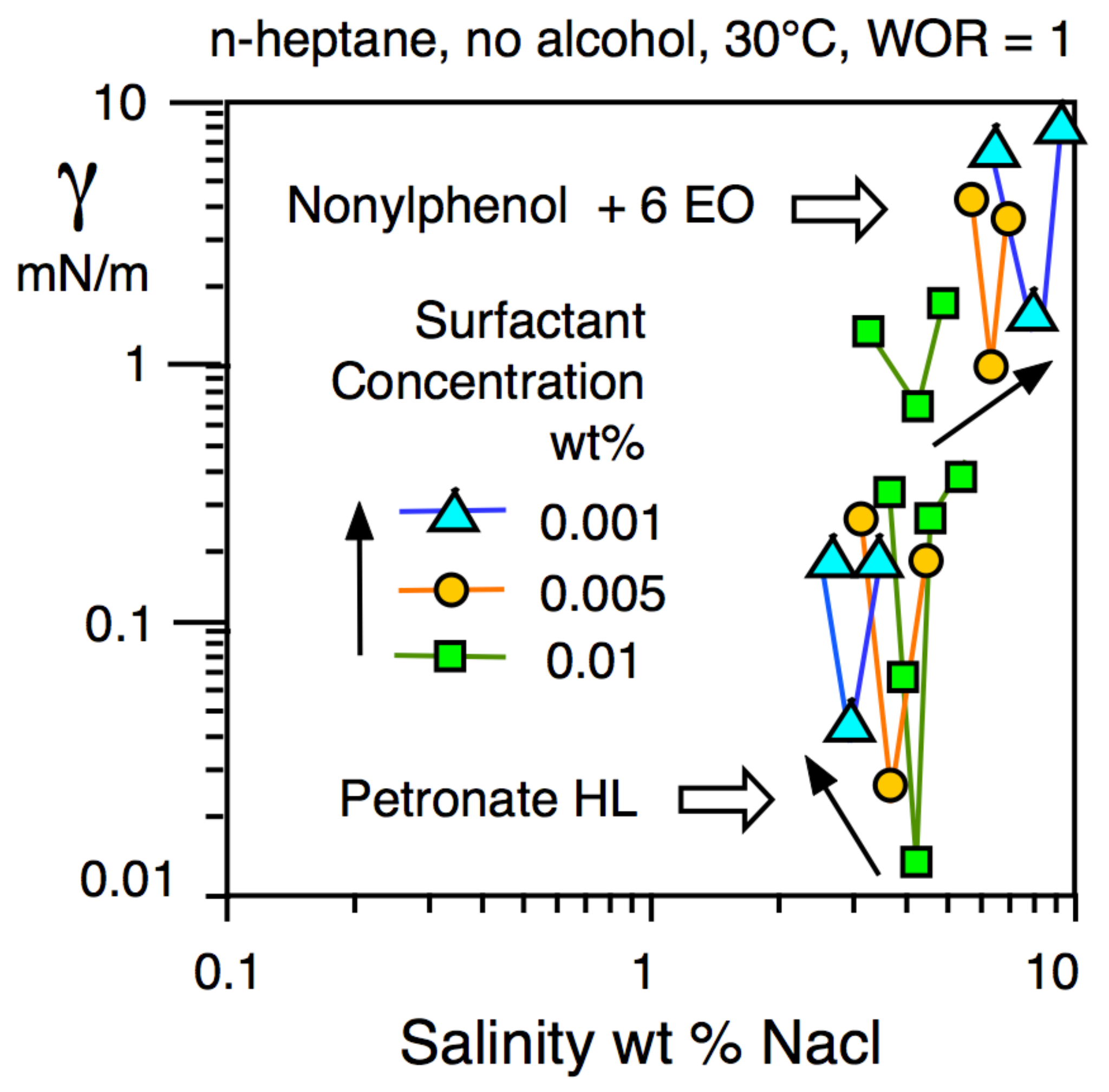
| Na n-alkyl carboxylate | PACN0 = −50 |
| Na n-alkyl sulfate | PACN0 = −57 |
| Na alkane sulfonate | PACN0 = −48 |
| Na iso-alkyl benzene sulfonate | PACN0 = −30 |
| Na alkyl orthoxylene sulfonate | PACN0 = −25 |
| Extended surfactants | no consistent data |
| Cl n-alkyl ammonium at pH = 3 | PACN0 = −32 |
| Cl n-alkyl trimethyl ammonium | PACN0 = −46 |
| Cl n-alkyl pyridinium | PACN0 = −47 |
| iso-alkyl phenol ethoxylate | PACN0 = + 23 − 6.67 EON |
| iso-alkyl phenol + 5 EO | PACN0 = −10 |
| n-alcohol ethoxylate | PACN0 = + 13 − 6.67 EON |
| n-alcohol + 5 EO | PACN0 = −20 |
| n-alcohol + 10 EO | PACN0 = −55 |
| iso-alcohol ethoxylate | PACN0 = −2 − 6.67 EON |
| iso-alcohol + 5 EO | PACN0 = −35 |
| iso-alcohol + 10 EO | PACN0 = −68 |
| n-alkyl carboxylic acid polyglycerol ester | PACN0 = + 34.5 − 10 GN |
| Oil | EACN | Oil | EACN |
|---|---|---|---|
| Myrcane | 9.5 | p-menthane | 6 |
| Cyclohexane | 2.5 | Cyclohexene | −1 |
| Ethylcyclohexane | 4.5 | Isopropylcyclohexane | 5.5 |
| Benzene | 0 or less | p-cymene | −0.5 |
| Limonene | 1.6 | terpinolene | 0.3 |
| Octyl benzene | 4 | decyl benzene | 6 |
| p-xylene | −2 | 1-decene | 5.5 |
| 1-octene | 4 | 1-octyne | −2 |
| 1-dodecene | 8 | 1-dodecyne | 2 |
| Squalane (branched C30) | 24 | Dibutyl ether | 3.4 |
| Ethyl myristate | 5 | Ethyl oleate | 7 |
| Hexyl octanoate | 6.2 | Hexyl dodecanoate | 9.3 |
| Hexyl methacrylate | 0 | Isopropylmyristate | 7.5 |
| Miglyol 840–diglyc. C11 | 9 | Miglyol 812 triglyc. C11 | 14 |
| Soya oil triglyceride C18 | 18 | Trilaurin | 16 |
| Triolein | 21 | Tristearin | 24 |
| Glycerol trioctanato | 12.3 | Glycerol tridecanoate | 14 |
| 1-Chlorodecane | 3.5 | 1–10 Dichloro decane | 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salager, J.-L.; Antón, R.; Bullón, J.; Forgiarini, A.; Marquez, R. How to Use the Normalized Hydrophilic-Lipophilic Deviation (HLDN) Concept for the Formulation of Equilibrated and Emulsified Surfactant-Oil-Water Systems for Cosmetics and Pharmaceutical Products. Cosmetics 2020, 7, 57. https://doi.org/10.3390/cosmetics7030057
Salager J-L, Antón R, Bullón J, Forgiarini A, Marquez R. How to Use the Normalized Hydrophilic-Lipophilic Deviation (HLDN) Concept for the Formulation of Equilibrated and Emulsified Surfactant-Oil-Water Systems for Cosmetics and Pharmaceutical Products. Cosmetics. 2020; 7(3):57. https://doi.org/10.3390/cosmetics7030057
Chicago/Turabian StyleSalager, Jean-Louis, Raquel Antón, Johnny Bullón, Ana Forgiarini, and Ronald Marquez. 2020. "How to Use the Normalized Hydrophilic-Lipophilic Deviation (HLDN) Concept for the Formulation of Equilibrated and Emulsified Surfactant-Oil-Water Systems for Cosmetics and Pharmaceutical Products" Cosmetics 7, no. 3: 57. https://doi.org/10.3390/cosmetics7030057
APA StyleSalager, J.-L., Antón, R., Bullón, J., Forgiarini, A., & Marquez, R. (2020). How to Use the Normalized Hydrophilic-Lipophilic Deviation (HLDN) Concept for the Formulation of Equilibrated and Emulsified Surfactant-Oil-Water Systems for Cosmetics and Pharmaceutical Products. Cosmetics, 7(3), 57. https://doi.org/10.3390/cosmetics7030057







