The Contribution of Energy Taxes to Climate Change Policy in the European Union (EU)
Abstract
1. Introduction
2. Literature Review
3. Data and Descriptive Statistics
4. Model and Estimation Method
5. Estimation Results
5.1. Time Series Data Analysis
5.2. Panel Data Analysis
6. Discussion and Policy Implications
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Fossil Energy Consumption | Energy Intensity | Share of Renewable Energy | GHG Emissions | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Country Code | Cointegration between TAX and FEC | Estimation of Equation (2) | Estimation of Equation (11) | Cointegration between TAX and EI | Estimation of Equation (3) | Estimation of Equation (12) | Cointegration between TAX and REN | Estimation of Equation (4) | Estimation of Equation (13) | Cointegration between TAX and GHG | Estimation of Equation (5) | Estimation of Equation (14) |
| AT | N | 0.003 (0.952) | N | 0.1394 (1.2080) | N | −0.0214 (−1.2260) | N | 0.0060 (0.5240) | ||||
| BE | N | −0.001 (−0.172) | N | −0.0321 (−0.1381) | N | −0.0029 (−0.3518) | N | 0.0016 (0.0917) | ||||
| BG | N | −0.003 (−1.47) | N | −0.8489 (−0.9641) | N | 0.0070 (0.3080) | N | −0.0173 (−1.0340) | ||||
| HR(1) | N | 0.001 (0.896) | N | 0.0823 (0.5813) | N | −0.0158 (−0.6950) | N | 0.0005 (0.0492) | ||||
| CY | N | −0.001 (−0.509) | N | −0.1517 ** (−2.1220) | N | −0.0022 (−0.5641) | N | −0.0089 (−1.0840) | ||||
| CZ | N | −0.001 (−0.114) | Y | 0.1686 (0.3606) −0.3666 (−1.0550) | N | 0.0020 (0.1653) | N | −0.0366 (−1.1960) | ||||
| DK | N | −0.001 (−0.305) | N | −0.0480 (−1.1540) | N | −0.0048 (−1.209) | N | −0.0080 (−0.7769) | ||||
| EE | N | −0.001 (−0.135) | N | 1.2240 (1.1910) | N | 0.0219 (0.6020) | N | 0.1201 (1.1170) | ||||
| FI | N | −0.003 (−0.857) | N | 0.0489 (0.2331) | N | 0.0033 (0.2058) | N | −0.0356 (−1.054) | ||||
| FR | N | −0.002 (−0.667) | N | 0.0063 (0.0792) | N | 0.0169 (1.730) | N | 0.0006 (0.1180) | ||||
| DE(1) | N | −0.469 (−2.116) | N | 0.0013 (0.5161) | N | −0.0011 (−0.1365) | N | 0.0060 NA | ||||
| EL | N | 0.001 (0.734) | N | 0.0253 (0.5880) | N | 0.0034 (0.6712) | N | −0.0057 (−1.049) | ||||
| HU(1) | N | 0.002 (0.471) | N | −0.5134 (−1.050) | N | −0.1774 * (−2.384) | N | 0.0033 (0.2601) | ||||
| IE | N | 0.004 (1.500) | N | 0.0161 (0.2179) | N | −0.0009 (−0.2391) | N | −0.0020 (−0.1665) | ||||
| IT | N | 0.001 (0.261) | Y | −0.0304 (0.9937) −0.890 ** (−2.4590) | N | 0.0046 (0.4766) | N | 0.0093 * (1.9150) | ||||
| LV | N | 0.001 (0.261) | N | 0.6148 (1.3930) | N | 0.0515 (1.1170) | N | −0.0060 (−0.2948) | ||||
| LT | N | −0.005* (−1.763) | Y | −0.4023 (−0.4044) 0.5225* (−2.0430) | N | 0.0443 (1.4540) | N | −0.0371 (−1.4330) | ||||
| LU | N | 0.003 (0.192) | N | 0.2493 (1.2100) | N | −0.0055 (−0.4328) | N | −0.0074 (−0.1391) | ||||
| MT | N | −0.001 (−0.094) | N | −0.0098 (−0.1138) | N | −0.0002 (−0.1195) | N | −0.014** (−2.775) | ||||
| NL | N | −0.005* (−1.874) | N | 0.1276 (0.7994) | N | 0.0047 (0.8766) | N | 0.0137 (0.9712) | ||||
| PL | N | −0.002 (−1.214) | N | −0.0910 (−0.2335) | N | −0.0015 (−0.1729) | N | −0.0130 (−1.0690) | ||||
| PT | N | 0.001 (0.280) | N | 0.0283 (0.4049) | N | 0.0099 (0.9494) | N | −0.0042 (−0.3525) | ||||
| RO | N | 0.0012 (1.0180) | N | −0.0590 (−0.2020) | N | −0.0374 (−1.4710) | N | 0.0131 (1.1720) | ||||
| SK | N | −0.0032 (−1.050) | N | 0.3349 (0.6304) | N | 0.0307 (1.2240) | N | −0.0057 (−0.5474) | ||||
| SI | N | −2.7·10−5 (−0.0181) | N | 0.3349 (0.6304) | N | −0.0127 (0.6329) | N | 0.0020 (0.3641) | ||||
| ES | Y | 0.0003 (0.1990) −0.1675 (−1.7890) | N | −0.0616 (−0.6824) | N | 0.0041 (0.3066) | N | 0.0142 (0.7275) | ||||
| SE | N | −0.0023 (−1.5800) | N | 0.0201 (0.1727) | N | 0.0099 (0.5232) | N | −0.0139* (−1.9300) | ||||
| UK | N | 0.0018* (2.1410) | N | −0.0291 (−0.6689) | N | −0.0004 (−0.1354) | N | 0.0032 (0.7620) | ||||
| Fossil Energy Consumption | Energy Intensity | Share of Renewable Energy | GHG Emissions | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Country Code | Cointegration between TAX and FEC | Estimation of Equation (2) | Estimation of Equation (11) | Cointegration between TAX and EI | Estimation of Equation (3) | Estimation of Equation (12) | Cointegration between TAX and REN | Estimation of Equation (4) | Estimation of Equation (13) | Cointegration between TAX and GHG | Estimation of Equation (5) | Estimation of Equation (14) |
| AT | N | 0.945 (1.1860) | N | 0.1543 (0.9764) | N | −0.4286 (−1.6580) | N | 0.1041 (0.6288) | ||||
| BE | N | −0.0362 (−0.1702) | N | −0.0147 (−0.0754) | N | −0.0321 (−0,0863) | N | 0.0153 (0.0874) | ||||
| BG | N | −0.0305 (−0.5877) | N | −0.0550 (−0.9588) | N | 0.0404 (0.2913) | N | −0.0503 (−0.9849) | ||||
| HR(1) | N | 0.1033 (0.8267) | N | 0.0504 (0.4552) | N | −0.1599 (−0.7536) | N | 0.0187 (0.0080) | ||||
| CY | N | −0.0296 (−0.5229) | N | −0.063 *** (−3.1420) | N | −0.0124 (−0.1255) | N | −0.0619 (−0.9885) | ||||
| CZ | N | 0.0429 (0.4053) | N | 0.0117 (0.0838) | N | 0.0340 (0.1788) | N | −0.0559 (−0.2301) | ||||
| DK | N | −0.0032 (−0.0329) | N | −0.1891 (−1.3350) | N | −0.1660 (−0.7855) | N | −0.2044 (−0.8613) | ||||
| EE | N | −0.0992 (−1.4080) | N | (−0.1431 (−1.6080) | N | 0.0003 (0.0024) | N | −0.1153 (−0.4694) | ||||
| FI | N | −0.1076 (−0.6910) | N | 0.0279 (0.1677) | N | 0.0071 (0.0538) | N | −0.4203 (−1.2200) | ||||
| FR | N | −0.1311 (−0.5745) | Y | 0.0419 (0.3521) −0.1990 (−1.6150) | N | 0.5390 * (1.7940) | N | 0.0210 (0.1691) | ||||
| DE(1) | N | −0.8702 (−1.9100) | N | 0.1222 (0.5304) | N | −0.0420 (−0.1330) | N | 0.1209 (N/A) | ||||
| EL | N | 0.0243 (0.2046) | N | 0.0685 (1.0800) | N | 0.1900 (1.2120) | N | −0.1033 (−1.1200) | ||||
| HU(1) | N | 0.1358 (0.4147) | N | −0.2346 (−0.9802) | N | −2.1490 * (−2.1200) | N | 0.0740 (0.3387) | ||||
| IE | N | 0.2719 (1.6420) | N | 0.0459 (0.2829) | N | −0.0382 (−0.1113) | Y | −0.0401 (−0.2801) −0.0328 (−0.1000) | ||||
| IT | N | 0.0407 (0.3158) | Y | 0.1167 (1.3230) −0.999 ** (−2.8860) | N | −0.0544 (−0.0726) | N | 0.3364 * (2.1270) | ||||
| LV | N | 0.0375 (1.5180) | N | −0.0473 (−0.5783) | N | 0.0872 (1.0120) | N | −0.2495 (−1.7120) | ||||
| LT | N | −0.2314 ** (−2.6040) | N | −0.1578 (−1.3370) | N | 0.3160 *** (3.8890) | N | −0.451 *** (−4.4150) | ||||
| LU | N | 0.2090 (0.5907) | N | 0.4870 (1.4980) | N | 0.2974 (0.1551) | N | 0.0551 (0.1336) | ||||
| MT | N | −0.1080 (−0.6068) | N | −0.0356 (−0.2643) | N | 0.0003 (0.0001) | N | −0.1868 * −2.110 | ||||
| NL | N | −0.2239 (−1.3750) | N | 0.0492 (0.2075) | N | 0.2280 (0.3894) | N | 0.0343 (0.1860) | ||||
| PL | N | −0.1280 (−1.6610) | N | −0.1168 (−1.4780) | N | −0.0102 (−0.1091) | N | −0.0934 (−0.9464) | ||||
| PT | N | 0.0277 (0.3905) | N | 0.0382 (0.5194) | N | 0.1006 (0.9068) | N | −0.0480 (−0.2141) | ||||
| RO | N | −0.0593 (−0.6948) | N | −0.0574 (−1.3700) | Y | −0.2016 (−1.6220) −0.4069) (−1.1650) | N | −0.0349 (−0.3785) | ||||
| SK | N | −0.0457 (−0.4981) | N | 0.0054 (0.0528) | N | 1.0946 (1.7390) | N | −0.0390 (−0.5808) | ||||
| SI | N | 0.0316 (0.2862) | N | 0.0117 (0.1927) | N | −0.6001 (−1.5280) | N | 0.0203 (0.2322) | ||||
| ES | Y | 0.0451 (0.2761) −0.1620 * (−1.7960) | N | −0.0903 (−0.6971) | N | 0.1220 (0.3303) | N | 0.2523 (0.7998) | ||||
| SE | N | −0.1245 (−1.0530) | N | 0.0387 (0.2309) | N | 0.1420 (0.5100) | N | −0.2931 (−1.4930) | ||||
| UK | N | 0.1758 * (2.0680) | N | −0.0273 (−0.3255) | N | −0.3962 (−0.6326) | N | 0.0589 (0.7052) | ||||
Appendix B
| Country | Series | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TAX | FEC | EI | REN | GHG | ||||||
| Col. (A) | Col. (B) | Col. (A) | Col. (B) | Col. (A) | Col. (B) | Col. (A) | Col. (B) | Col. (A) | Col. (B) | |
| AT | 0.399 | 0.044 | 0.185 | 0.015 | 0.097 | 0.010 | 0.212 | 0.011 | 0.328 | 0.003 |
| BE | 0.402 | 0.031 | 0.313 | 0.003 | 0.065 | 0.044 | 0.110 | 0.002 | 0.223 | 0.041 |
| BG | 0.315 | 0.010 | 0.271 | 0.000 | 0.192 | 0.000 | 0.068 | 0.026 | 0.059 | 0.034 |
| HR | 0.056 | 0.007 | 0.284 | 0.008 | 0.184 | 0.007 | 0.076 | 0.047 | 0.094 | 0.002 |
| CY | 0.259 | 0.006 | 0.185 | 0.036 | 0.239 | 0.017 | 0.091 | 0.044 | 0.335 | 0.029 |
| CZ | 0.302 | 0.049 | 0.310 | 0.045 | 0.320 | 0.028 | 0.313 | 0.004 | 0.273 | 0.023 |
| DK | 0.364 | 0.006 | 0.098 | 0.048 | 0.227 | 0.025 | 0.099 | 0.010 | 0.189 | 0.005 |
| EE | 0.363 | 0.009 | 0.338 | 0.049 | 0.346 | 0.004 | 0.075 | 0.030 | 0.131 | 0.035 |
| FI | 0.148 | 0.001 | 0.205 | 0.007 | 0.056 | 0.008 | 0.143 | 0.025 | 0.203 | 0.022 |
| FR | 0.119 | 0.041 | 0.219 | 0.015 | 0.072 | 0.030 | 0.360 | 0.003 | 0.102 | 0.029 |
| DE | 0.452 | 0.046 | 0.193 | 0.029 | 0.124 | 0.035 | 0.290 | 0.026 | 0.385 | 0.045 |
| EL | 0.445 | 0.004 | 0.388 | 0.003 | 0.055 | 0.015 | 0.323 | 0.004 | 0.065 | 0.002 |
| HU | 0.287 | 0.003 | 0.168 | 0.033 | 0.076 | 0.002 | 0.221 | 0.001 | 0.171 | 0.043 |
| IE | 0.183 | 0.047 | 0.283 | 0.046 | 0.225 | 0.013 | 0.275 | 0.048 | 0.243 | 0.048 |
| IT | 0.386 | 0.003 | 0.137 | 0.035 | 0.164 | 0.008 | 0.146 | 0.009 | 0.168 | 0.009 |
| LV | 0.400 | 0.036 | 0.057 | 0.011 | 0.115 | 0.030 | 0.073 | 0.006 | 0.205 | 0.007 |
| LT | 0.308 | 0.006 | 0.283 | 0.027 | 0.092 | 0.026 | 0.128 | 0.045 | 0.244 | 0.004 |
| LU | 0.135 | 0.024 | 0.212 | 0.047 | 0.194 | 0.028 | 0.380 | 0.018 | 0.058 | 0.007 |
| MT | 0.238 | 0.032 | 0.122 | 0.038 | 0.215 | 0.041 | 0.137 | 0.038 | 0.124 | 0.020 |
| NL | 0.147 | 0.010 | 0.143 | 0.005 | 0.100 | 0.046 | 0.305 | 0.012 | 0.317 | 0.040 |
| PL | 0.112 | 0.023 | 0.282 | 0.019 | 0.074 | 0.026 | 0.222 | 0.044 | 0.139 | 0.031 |
| PT | 0.067 | 0.008 | 0.394 | 0.017 | 0.083 | 0.031 | 0.136 | 0.014 | 0.144 | 0.008 |
| RO | 0.099 | 0.018 | 0.263 | 0.001 | 0.403 | 0.005 | 0.077 | 0.025 | 0.231 | 0.002 |
| SK | 0.357 | 0.004 | 0.135 | 0.008 | 0.165 | 0.007 | 0.094 | 0.008 | 0.401 | 0.011 |
| SI | 0.126 | 0.007 | 0.119 | 0.029 | 0.284 | 0.049 | 0.128 | 0.000 | 0.095 | 0.008 |
| ES | 0.245 | 0.030 | 0.325 | 0.049 | 0.272 | 0.000 | 0.096 | 0.006 | 0.094 | 0.020 |
| SE | 0.159 | 0.027 | 0.158 | 0.045 | 0.355 | 0.009 | 0.350 | 0.022 | 0.215 | 0.025 |
| UK | 0.269 | 0.009 | 0.390 | 0.046 | 0.440 | 0.011 | 0.193 | 0.010 | 0.187 | 0.026 |
| Country | p-Value of Testing Cointegration between TAX and | |||
|---|---|---|---|---|
| FEC | EI | REN | GHG | |
| AT | 0.267 | 0.095 | 0.303 | 0.007 |
| BE | 0.264 | 0.175 | 0.182 | 0.599 |
| BG | 0.356 | 0.090 | 0.220 | 0.414 |
| HR | 0.151 | 0.086 | 0.092 | 0.113 |
| CY | 0.241 | 0.208 | 0.065 | 0.248 |
| CZ | 0.075 | 0.016 | 0.077 | 0.444 |
| DK | 0.141 | 0.246 | 0.110 | 0.195 |
| EE | 0.176 | 0.196 | 0.132 | 0.122 |
| FI | 0.201 | 0.392 | 0.055 | 0.301 |
| FR | 0.349 | 0.172 | 0.228 | 0.099 |
| DE | 0.498 | 0.089 | 0.254 | 0.077 |
| EL | 0.265 | 0.169 | 0.086 | 0.294 |
| HU | 0.285 | 0.185 | 0.195 | 0.289 |
| IE | 0.232 | 0.079 | 0.247 | 0.387 |
| IT | 0.170 | 0.003 | 0.103 | 0.177 |
| LV | 0.073 | 0.165 | 0.227 | 0.313 |
| LT | 0.411 | 0.025 | 0.192 | 0.218 |
| LU | 0.111 | 0.348 | 0.378 | 0.304 |
| MT | 0.267 | 0.068 | 0.354 | 0.410 |
| NL | 0.474 | 0.262 | 0.097 | 0.165 |
| PL | 0.240 | 0.167 | 0.224 | 0.216 |
| PT | 0.449 | 0.177 | 0.060 | 0.092 |
| RO | 0.084 | 0.337 | 0.055 | 0.436 |
| SK | 0.433 | 0.095 | 0.123 | 0.064 |
| SI | 0.328 | 0.164 | 0.072 | 0.169 |
| ES | 0.028 | 0.212 | 0.342 | 0.397 |
| SE | 0.053 | 0.192 | 0.137 | 0.095 |
| UK | 0.127 | 0.412 | 0.327 | 0.478 |
References
- Rocchi, P.; Serrano, M.; Roca, J. The reform of the European energy tax directive: Exploring potential economic impacts in the EU 27. Energy Policy 2014, 75, 341–353. [Google Scholar] [CrossRef]
- Morley, B. Empirical evidence on the effectiveness of environmental taxes. Appl. Econ. Lett. 2012, 19, 1817–1820. [Google Scholar] [CrossRef]
- Borozan, D. Efficiency of Energy Taxes and the Validity of the Residential Electricity Environmental Kuznets Curve in the European Union. Sustainability 2018, 10, 2464. [Google Scholar] [CrossRef]
- Baumol, W.J. On taxation and the control of externalities. Am. Econ. Rev. 1972, 62, 307–322. [Google Scholar]
- Pigou, A.C. The Economics of Welfare, 1st ed.; Routledge: New York, NY, USA, 1932; ISBN 9781351304351. [Google Scholar]
- Bhandaria, V.; Giacomonic, A.M.; Wollenberga, B.F.; Wilsona, E.J. Interacting policies in power systems: Renewable subsidies and a carbon tax. Electr. J. 2017, 30, 80–84. [Google Scholar] [CrossRef]
- Donga, H.; Daib, H.; Genga, Y.; Fujitad, T.; Liue, Z.; Xied, Y.; Wuf, R.; Fujiid, M.; Masuid, T.; Tangg, L. Exploring impact of carbon tax on China’s CO2 reductions and provincial disparities. Renew. Sustain. Energy Rev. 2017, 77, 596–603. [Google Scholar] [CrossRef]
- Freedman, M.; Freedman, O.; Stagliano, A.J. Greenhouse gas disclosures. Evidence from the EU response to Kyoto. Int. J. Crit. Account. 2012, 4, 237–264. [Google Scholar] [CrossRef]
- Stram, B.N. A new strategic plan for a carbon tax. Energy Policy 2014, 73, 519–523. [Google Scholar] [CrossRef][Green Version]
- Lin, B.; Li, X. The effect of carbon tax on per capita CO2 emissions. Energy Policy 2011, 39, 5137–5146. [Google Scholar] [CrossRef]
- Liang, Q.M.; Fan, Y.; Wei, Y.M. Carbon taxation policy in China: How to protect energy- and trade-intensive sectors? J. Policy 2007, 29, 311–333. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Li, Y. The impact of carbon tax on economic growth in China. Energy Procedia 2011, 5, 1757–1761. [Google Scholar] [CrossRef][Green Version]
- Eurostat. Environmental Statistics and Accounts in Europe; Publications Office of the European Union: Luxembourg, 2010. [Google Scholar]
- Goulder, L.H. Carbon Taxes vs. Cap and Trade; Working Paper; Stanford University: Stanford, CA, USA, 2009. [Google Scholar]
- Taylor, D.D.J.; Paiva, S.; Slocum, A.H. An alternative to carbon taxes to finance renewable energy systems and offset hydrocarbon based greenhouse gas emissions. Sustain. Energy Technol. Assess. 2017, 19, 136–145. [Google Scholar] [CrossRef]
- Friedrich, R.J. In defense of multiplicative terms in multiple regression equations. Am. J. Pol. Sci. 1982, 26, 797–833. [Google Scholar] [CrossRef]
- Barker, T.; Lutz, C.; Meyer, B.; Polliitt, H.; Speck, S. Modelling an ETR for Europe. In Environmental Tax Reform (ETR): A Policy for Green Growth; Ekins, P., Speck, S., Eds.; Oxford University Press: Oxford, UK, 2011; ISBN 9780199584505. [Google Scholar]
- Sargan, J.D. Wages and Prices in the United Kingdom: A Study in Econometric Methodology, 16. In Econometric Analysis for National, Economic Planning; Hart, P.E., Mills, G., Whittaker, J.N., Eds.; Butterworths: London, UK, 1964; pp. 25–54. [Google Scholar]
- Fang, G.; Tian, L.; Fu, M.; Sun, M. The impacts of carbon tax on energy intensity and economic growth—A dynamic evolution analysis on the case of China. Appl. Energy 2013, 110, 17–28. [Google Scholar] [CrossRef]
- Liang, Q.M.; Wei, Y.M. Distributional impacts of taxing carbon in China: Results from the CEEPA model. Appl. Energy 2012, 92, 545–551. [Google Scholar] [CrossRef]
- Kim, H.G. On the Views of Carbon Tax in Korea. Am. J. Appl. Sci. 2008, 5, 1558–1561. [Google Scholar] [CrossRef][Green Version]
- Lu, C.; Tong, Q.; Liu, X. The impacts of carbon tax and complementary policies on Chinese economy. Energy Policy 2010, 38, 7278–7285. [Google Scholar] [CrossRef]
- Conefrey, T.; Fitz Gerald, J.D.; Malaguzzi Valeri, L.; Tol, R.S.J. The impact of a carbon tax on economic growth and carbon dioxide emissions in Ireland. J. Environ. Plan. Manag. 2012, 1–19. [Google Scholar] [CrossRef]
- Cabalu, H.; Koshy, P.; Corong, E.; Rodriguez, U.-P.E.; Endriga, B.A. Modelling the impact of energy policy on the Philippine economy: Caron tax, energy efficiency, and changes in the energy mix. Econ. Anal. Pol. 2015, 48, 222–237. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, A.; Wang, D.; Li, A.; Song, H. How to improve the performance of carbon tax in China? J. Clean. Prod. 2017, 142, 2060–2072. [Google Scholar] [CrossRef]
- Gonseth, C.; Cadot, O.; Mathys, N.A.; Thalmann, P. Energy-tax changes and competitiveness: The role of adaptive capacity. Energy Econ. 2015, 48, 127–135. [Google Scholar] [CrossRef]
- Peretto, P.F. Energy taxes and endogenous technological change. J. Environ. Econ. Manag. 2009, 57, 29–283. [Google Scholar] [CrossRef]
- Cosmo, V.D.; Hyland, M. Carbon tax scenarios and their effects on the Irish energy sector. Energy Policy 2013, 59, 404–414. [Google Scholar] [CrossRef]
- Dissou, Y.; Siddiqui, M.S. Can carbon taxes be progressive? Energy Econ. 2014, 42, 88–100. [Google Scholar] [CrossRef]
- Oueslati, W.; Zipperer, V.; Rousselière, D.; Dimitropoulos, A. Energy taxes, reforms and income inequality: An empirical cross-country analysis. Int. Econ. 2017, 150, 80–95. [Google Scholar] [CrossRef]
- Eisemack, K.; Edenhofter, O.; Kalkuhl, M. Resource rents: The effects of energy taxes and quantity instruments for climate protection. Energy Policy 2012, 48, 159–166. [Google Scholar] [CrossRef]
- Wesseh, P.K.; Lin, B.; Atsagli, P. Carbon taxes, industrial production, welfare and the environment. Energy 2017, 123, 305–313. [Google Scholar] [CrossRef]
- Vera, S.; Sauma, E. Does a carbon tax make sense in countries with still a high potential for energy efficiency? Comparison between the reducing-emissions effects of carbon tax and energy efficiency measures in the Chilean case. Energy 2015, 88, 478–486. [Google Scholar] [CrossRef]
- Oikonomou, V.; Jemta, C.; Becchis, F.; Russolillo, D. White certificates for energy efficiency improvement with energy taxes: A theoretical economic model. Energy Econ. 2008, 30, 3044–3062. [Google Scholar] [CrossRef]
- Kuo, T.C.; Hong, I.H.; Lin, S.C. Do carbon taxes work? Analysis of government policies and enterprise strategies in equilibrium. J. Clean. Prod. 2016, 139, 337–346. [Google Scholar] [CrossRef]
- Carl, J.; Fedor, D. Tracking global carbon revenues: A survey of carbo taxes versus cap-and-trade in the real world. Energy Policy 2016, 96, 50–77. [Google Scholar] [CrossRef]
- Komanoff, C.; Gordon, M. British Columbia’s Carbon Tax: By the Numbers; Carbon Tax Centre: New York, NY, USA, 2015; Available online: https://www.carbontax.org/wp-content/uploads/CTC_British_Columbia’s_Carbon_Tax_By_The_Numbers-2.pdf (accessed on 8 August 2018).
- Bruvoll, A.; Larsen, B.M. Greenhouse gas emissions in Norway: Do carbon taxes work? Energy Policy 2004, 32, 493–505. [Google Scholar] [CrossRef]
- Vollebergh, H.R.J. Lessons from the polder: Energy tax design in the Netherlands from a climate change perspective. Ecol. Econ. 2008, 64, 660–672. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Liu, D.; Fang, Z.; Xu, H. Modelling and forecasting CO2 emissions in the BRICS (Brazil, Russia, India, China, and South Africa) countries using a novel multi-variable grey model. Energy 2015, 79, 489–495. [Google Scholar] [CrossRef]
- Antanasijevic, D.; Pocajt, V.; Ristic, M.; Peric-Grujic, A. Modeling of energy consumption and related GHG (greenhouse gas) intensity and emissions in Europe using general regression neural networks. Energy 2015, 84, 816–824. [Google Scholar] [CrossRef]
- Hwang, J.J. Policy review of greenhouse gas emission reduction in Taiwan. Renew. Sustain. Energy Rev. 2011, 15, 1392–1402. [Google Scholar] [CrossRef]
- Jeffrey, C.; Perkins, J.D. The association between energy taxation, participation in an emissions trading system, and the intensity of carbon dioxide emissions in the European Union. Int. J. Account. 2015, 50, 397–417. [Google Scholar] [CrossRef]
- Webster, A.; Ayatakshi, S. The effect of fossil energy and other environmental taxes on profit incentives for change in an open economy: Evidence from the UK. Energy Policy 2013, 61, 1422–1431. [Google Scholar] [CrossRef][Green Version]
- Eide, J.; De Sisternes, F.J.; Herzog, H.J.; Webster, M.D. CO2 emission standards and investment in carbon capture. Energy Econ. 2014, 45, 53–65. [Google Scholar] [CrossRef]
- Markandya, A.; Ortiz, R.A.; Mudgal, S.; Tinetti, B. Analysis of tax incentives for energy-efficiency durables in the EU. Energy Policy 2009, 37, 5662–5674. [Google Scholar] [CrossRef]
- Orlov, A.; Grethe, H.; McDonald, S. Carbon taxation in Russia: Prospects for a double dividend and improved energy efficiency. Energy Econ. 2013, 37, 128–1240. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Baranzinic, A. What do we know about carbon taxes? An inquiry into their impacts on competitiveness and distribution of income. Energy Policy 2004, 32, 507–518. [Google Scholar] [CrossRef]
- Enervoldsen, M.K.; Ryelund, A.; Andersen, M.S. The impact of energy taxes on competitiveness: A panel regression study of 56 European industry sectors. In Carbon-Energy Taxation: Lessons from Europe; Andersen, M.S., Ekins, P., Eds.; Oxford University Press: New York, NY, USA, 2009; pp. 100–119. [Google Scholar]
- Choi, J.K.; Bakshi, B.R.; Hubacek, K.; Nader, J. A sequential input-output framework to analyze the economic and environmental implications of energy policies: Gas taxes and fuel subsidies. Appl. Energy 2016, 384, 830–839. [Google Scholar] [CrossRef]
- Telli, C.; Voyvoda, E.; Yeldan, E. Economics of environmental policy in Turkey: A general equilibrium investigation of the economic evaluation of sectoral emission reduction policies for climate change. J. Policy Model. 2008, 30, 321–340. [Google Scholar] [CrossRef]
- Sterner, T. Distributional effects of taxing transport fuel. Energy Policy 2012, 41, 75–83. [Google Scholar] [CrossRef]
- Yoshino, N.; Taghizadeh-Hesary, F. Alternatives to Private Finance: Role of Fiscal Policy Reforms and Energy Taxation in Development of Renewable Energy Projects. Financing for Low-carbon Energy Transition: Unlocking the Potential of Private Capital; Anbumozhi, V., Kalirajan, K., Kimura, F., Eds.; Springer: Tokyo, Japan, 2018; pp. 335–357. [Google Scholar]
- Tchórzewska-Cieślak, B.; Pietrucha-Urbanik, K.; Urbanik, M.; Rak, J.R. Approaches for Safety Analysis of Gas-Pipeline Functionality in Terms of Failure Occurrence: A Case Stdudy. Energies 2018, 11, 1589. [Google Scholar] [CrossRef]
- Tchórzewska-Cieślak, B.; Pietrucha-Urbanik, K. Approaches to Methods of Risk Analysis and Assessment Regarding the Gal Supply to a City. Energies 2018, 11, 3304. [Google Scholar] [CrossRef]
- Lapinskiene, G.; Peleckis, K.; Nedelko, Z. Testing environmental Kuznets curve hypothesis: The role of enterprise’s sustainability and other factors on GHG in European countries. J. Bus. Econ. Manag. 2017, 18, 54–67. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Shmelev, S.E.; Speck, S.U. Green fiscal reform in Sweden: Econometric assessment of the carbon and energy taxation scheme. Renew. Sustain. Energy Rev. 2018, 90, 969–981. [Google Scholar] [CrossRef]
- Abdullah, S.; Morley, B. Environmental taxes and economic growth: Evidence from panel causality tests. Energy Econ. 2014, 42, 27–33. [Google Scholar] [CrossRef]
- Wang, M. A Granger Causality Analysis between the GDP and CO2 Emissions of Major Emitters and Implications for International Climate Governance. Chin. J. Urban Environ. Stud. 2018, 6, 1850004. [Google Scholar] [CrossRef]
- Granger, C.W.J. Time Series Analysis, Cointegration, and Applications. Am Econ Rev. 2004, 94, 421–425. [Google Scholar] [CrossRef]
- Vance, M.; Stan, H.; David, H. Econometric Modelling with Time Series; Cambridge University Press: New York, NY, USA, 2013; pp. 662–711. ISBN 978-0-521-13981-6. [Google Scholar]
- Arellano, M.; Bond, S. Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Rev. Econ. Stud. 1991, 58, 277–297. [Google Scholar] [CrossRef]
- Alonso-Borrego, C.; Arellano, M. Symmetrically Normalized Instrumental Variable Estimation Using Panel Data. J. Bus. Econ. Stat. 1999, 17, 36–49. [Google Scholar] [CrossRef]
- Blundell, R.; Bond, S. Initial conditions and moment restrictions in dynamic panel-data models. J. Econ. 1998, 87, 115–143. [Google Scholar] [CrossRef]
- Arellano, M.; Bover, O. Another Look at the Instrumental Variable Estimation of Error-components Models. J. Econ. 1995, 68, 29–51. [Google Scholar] [CrossRef]
- Bond, S.; Bowsher, C.; Windmeijer, F. Criterion-based Inference for GMM in Autoregressive Panel Data Models. Econ. Lett. 2001, 73, 379–388. [Google Scholar] [CrossRef]
- Hauk, W.; Wacziarg, R. A Monte Carlo study of growth regressions. J. Econ. Growth 2009, 14, 103–147. [Google Scholar] [CrossRef]
- Windmeijer, F. A finite sample correction for the variance of linear efficient two-step GMM estimators. J. Econ. 2005, 126, 25–51. [Google Scholar] [CrossRef]
- Yao, C.; Feng, K.; Hubacek, K. Driving forces of CO2 emissions in the G20 countries: An index decomposition analysis from 1971 to 2010. Ecol. Inf. 2015, 26, 93–100. [Google Scholar] [CrossRef]
- Bölük, G.; Mert, M. Fossil and renewable energy consumption, GHGs (greenhouse gases) and economic growth: Evidence from a panel of EU (European Union) countries. Energy 2014, 74, 439–446. [Google Scholar] [CrossRef]
- Sebri, M.; Ben-Salha, O. On the causal dynamics between economic growth, renewable energy consumption, CO2 emissions and trade openness: Fresh evidence from BRICS countries. Renew Sustain Energy Rev. 2014, 39, 4–23. [Google Scholar] [CrossRef]
- Marrero, G.A. Greenhouse gases emissions, growth and the energy mix in Europe. Energy Econ. 2010, 32, 1356–1363. [Google Scholar] [CrossRef]
- Wang, S.; Li, Q.; Fang, C.; Zhou, C. The relationship between economic growth, energy consumption, and CO2 emissions: Empirical evidence from China. Sci. Total Environ. 2016, 542, 360–371. [Google Scholar] [CrossRef]
- Pacesila, M.; Burcea, S.G.; Colesca, S.E. Analysis of renewable energies in European Union. Renew. Sustain. Energy Rev. 2016, 56, 156–170. [Google Scholar] [CrossRef]
- Ghouli, Y.Z.; Belmokaddem, M.; Sahraoui, M.A.; Guellil, M.S. Factors Affecting CO2 Emissions in the BRICS Countries: A panel data analysis procedia. Econ. Financ. 2015, 26, 114–125. [Google Scholar] [CrossRef]
- Liobikienė, G.; Butkus, M. The European Union possibilities to achieve targets of Europe 2020 and Paris agreement climate policy. Renew. Energy 2017, 106, 298–309. [Google Scholar] [CrossRef]
- Liobikienė, G.; Butkus, M. Environmental Kuznets Curve of greenhouse gas emissions including technological progress and substitution effects. Energy 2017, 135, 237–248. [Google Scholar] [CrossRef]
- Hong, S.; Sim, S. Inelastic Supply of Fossil Energy and Competing Environmental Regulatory Policies. Sustainability 2018. [Google Scholar] [CrossRef]
- Hintermann, B. Allowance price drivers in the first phase of the EU ETS. J. Environ. Econ. Manag. 2010, 59, 43–56. [Google Scholar] [CrossRef]
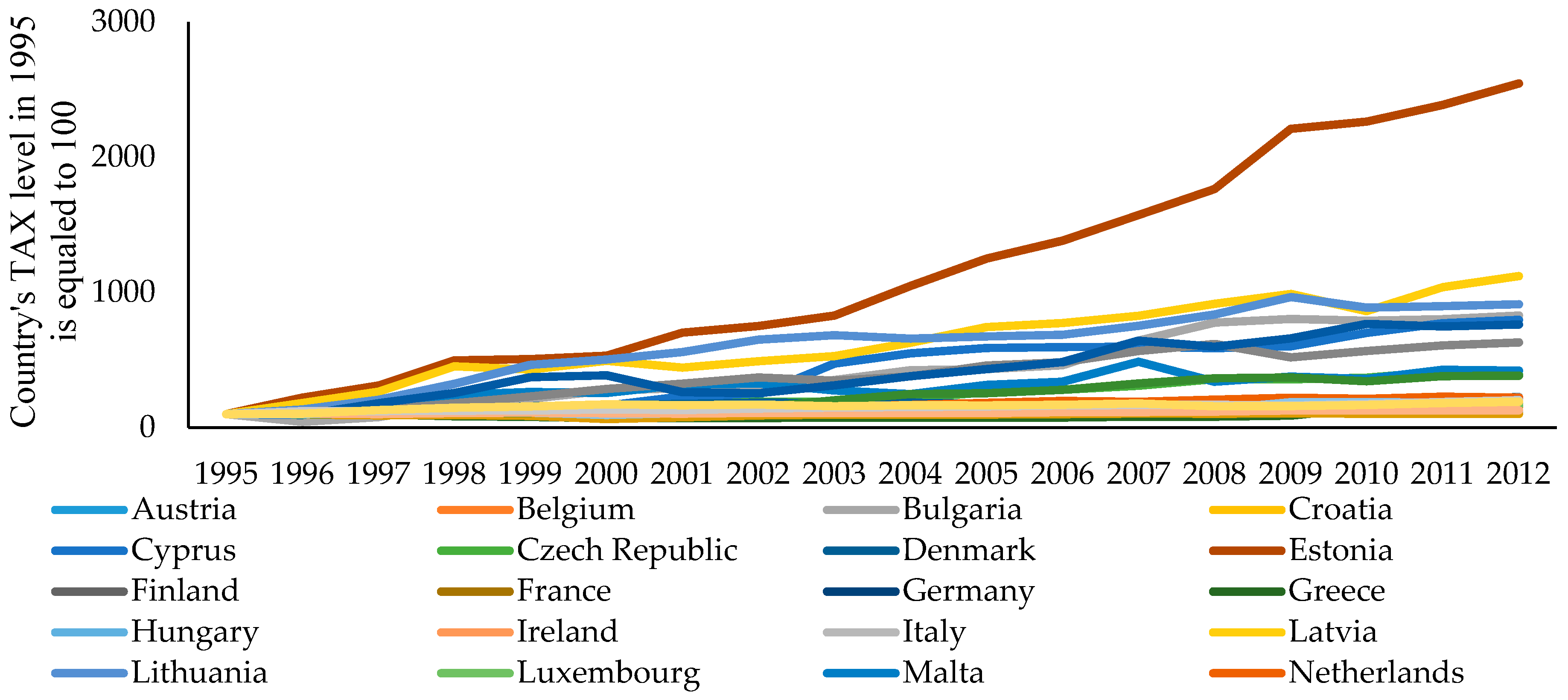
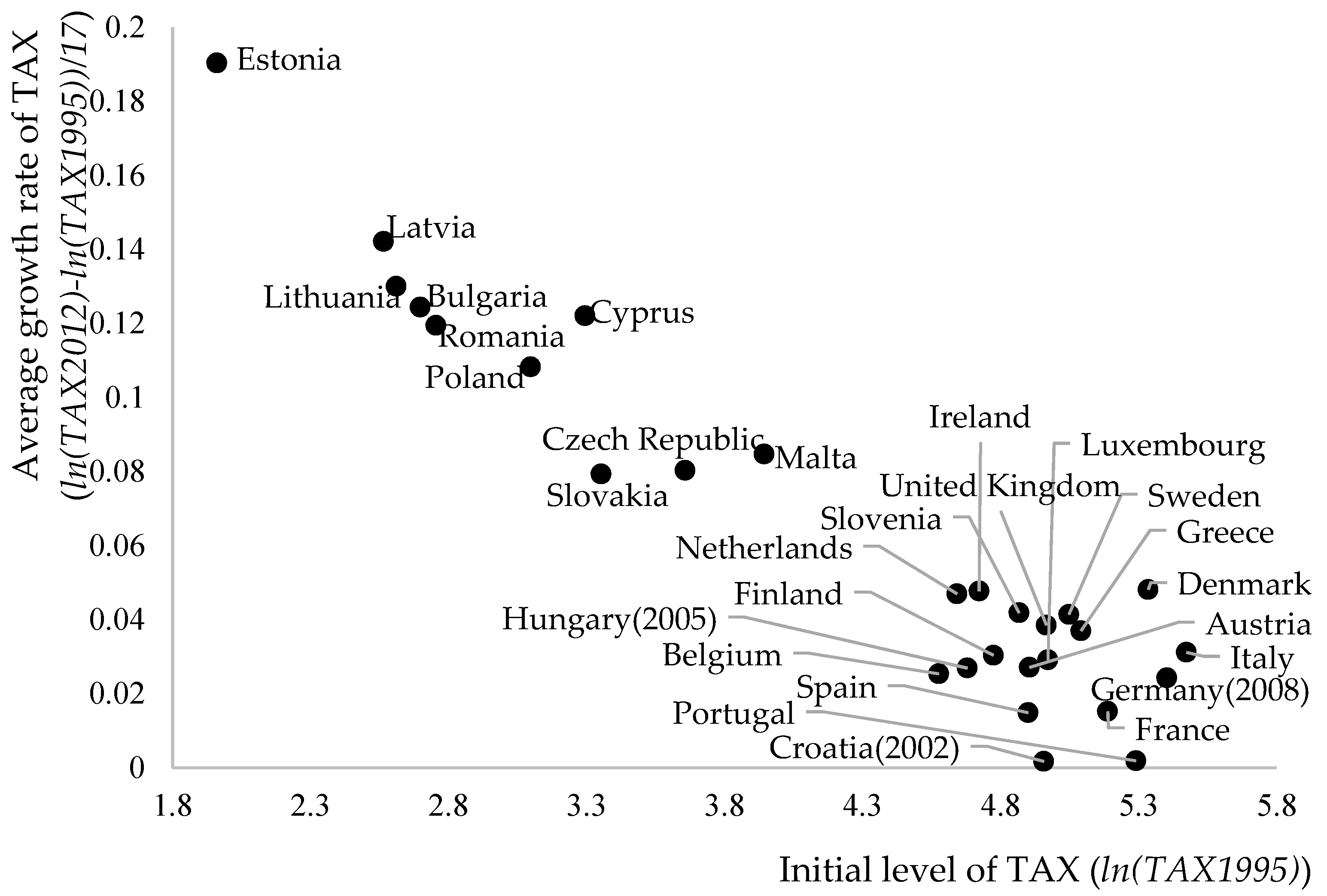
| Variable Name | Short Variable Name | Explanation and Measurement Unit |
|---|---|---|
| Energy taxes | TAX | Euros per energy (except renewable and nuclear) ton of oil equivalent (TOE) consumed |
| Fossil energy consumption | FEC | Final energy (except renewable and nuclear) consumption per capita (tons of oil equivalent TOE) |
| Energy intensity | EI | Energy intensity of the economy (gross inland consumption of energy divided by gross domestic product (GDP) (kg of oil equivalent per 1000 EUR)) |
| Renewable energy | REN | Share of renewable energy in gross inland consumption of energy (%) |
| Greenhouse gas emissions | GHG | Total greenhouse gas emissions per capita (tons of CO2 equivalent) |
| Variable | Mean | Std. Dev. | Minimum | Maximum |
|---|---|---|---|---|
| TAX | 162.7 | 83.0 | 6.6 | 502.9 |
| FEC | 7.1 | 25.1 | 0.9 | 163.2 |
| EI | 212.5 | 139.9 | 2.4 | 951.1 |
| REN | 8.49 | 6.5 | 0.1 | 27.2 |
| GHG | 11.03 | 4.2 | 4.9 | 28.9 |
| Level–Level Type Model | Log–Log Type Model | ||||||
|---|---|---|---|---|---|---|---|
| Null Hypothesis is not Rejected for * | Null Hypothesis is Rejected with | Null Hypothesis is not Rejected for | Null Hypothesis is Rejected with | ||||
| Negative Correlation for | Positive Correlation for | Negative Correlation in | Positive Correlation in | ||||
| Null hypothesis: | TAX does not Granger cause FEC | AT, BE, BG, HR, CY, CZ, DK, EE, FI, FR, DE, EL, HU, IE, IT, LV, LU, MT, PL, PT, RO, SK, SI, ES(2), SE | LT(1)(4), NL(1)(4) | UK(1)(4) | AT, BE, BG, HR, CY, CZ, DK, EE, FI, FR, DE, EL, HU, IE, IT, LV, LU, MT, NL, PL, PT, RO, SK, SI, SE | LT(4), ES(1)(3), | UK(1)(4) |
| TAX does not Granger cause EI | AT, BE, BG, HR, CZ(2), DE, EE, FI, FR, DE, EL, HU, IE, LV, LU, MT, NL, PL, PT, RO, SK, SI, ES, SE, UK | CY(4), IT(3) | LT(1)(3) | AT, BE, BG, HR, CZ, DE, EE, FI, FR(2), DE, EL, HU, IE, LV, LT, LU, MT, NL, PL, PT, RO, SK, SI, SE, UK | CY(4), IT(3), | ||
| TAX does not Granger cause REN | AT, BE, BG, HR, CY, CZ, DE, EE, FI, FR, DE, EL, IE, IT, LV, LT, LU, MT, NL, PL, PT, RO, SK, SI, ES, SE, UK | HU(1)(4) | AT, BE, BG, HR, CY, CZ, DE, EE, FI, DE, EL, IE, IT, LV, LU, MT, NL, PL, PT, RO(2), SK, SI, SE, UK | HU(1)(4), | LT(4), FR(1)(4), | ||
| TAX does not Granger cause GHG | AT, BE, BG, HR, CY, CZ, DK, EE, FI, FR, DE, EL, HU, IE, LV, LT, LU, NL, PL, PT, RO, SK, SI, ES, UK | MT(4), SE(1)(3) | IT(1)(4) | AT, BE, BG, HR, CY, CZ, DE, EE, FI, FR, DE, EL, HU, IE(2), LV, LU, NL, PL, PT, RO, SK, SI, SE, UK | LT(4), MT(1)(4) | IT(1)(4) | |
| Variables | (I) | (II) | (III) | (IV) |
|---|---|---|---|---|
| Y(−1) | 0.7999 *** (13.2505) | 0.7469 *** (10.7328) | 0.7455 *** (11.1713) | 0.7201 *** (10.6530) |
| Const. | 0.0670 (0.5521) | −0.2181 (−0.7935) | −0.3092 (−1.1728) | −0.2335 (−0.9707) |
| Fossil energy Consumption | 0.1396 ** (2.2714) | 0.1400 *** (2.7330) | 0.1454 *** (2.9286) | 0.1593 *** (3.1568) |
| Energy intensity | 0.0963 ** (2.0435) | 0.1013 ** (2.1963) | 0.1110 ** (2.4624) | 0.1131 *** (2.7101) |
| RENewable energy | −0.0194 ** (−2.1374) | −0.0196 ** (−2.1042) | −0.0190 ** (−2.0397) | −0.0203 ** (−2.0209) |
| relative TAXation on energy | 0.0431 (1.4287) | |||
| (−1) | 0.0533 * (1.9444) | |||
| (−2) | 0.0459 * (1.9205) | |||
| Sample size | 435 | 411 | 408 | 405 |
| Number of countries | 28 | 28 | 28 | 28 |
| Number of instruments | 26 | 26 | 23 | 27 |
| Error AR (2) test | 0.7346 | 0.7345 | 0.7420 | 0.5984 |
| Sargan test | 0.5151 | 0.8020 | 0.7402 | 0.8207 |
| Pesaran CD test | 0.0626 | 0.0816 | 0.0591 | 0.0517 |
| Kao test | 0.3744 | 0.4022 | 0.2975 | 0.1883 |
| Pedroni test | 0.1403 | 0.1005 | 0.1598 | 0.1701 |
| Variables | (V) | (VI) | (VII) | (VIII) | (IX) | (X) |
|---|---|---|---|---|---|---|
| Y(−1) | 0.6367 *** (9.2912) | 0.8450 *** (15.5058) | 0.6884 *** (11.2957) | 0.8164 *** (16.3240) | 0.7708 *** (11.2318) | 0.8322 *** (16.0842) |
| Const. | −0.4274 (−1.5066) | 0.0603 (0.6627) | 0.8665 (1.1760) | 0.1856 ** (1.9928) | −0.2775 (−0.9927) | 0.0993 (1.0229) |
| Fossil Energy Consumption | 0.7623 (0.7673) | 0.1491 *** (3.8035) | 0.1562 *** (2.8163) | 0.1312 *** (2.6379) | 0.1485 ** (2.3817) | |
| Energy intensity | 0.1152 *** (2.6747) | 0.12084 * (1.8876) | 0.0701 (0.5940) | 0.1012 ** (2.2909) | 0.1138 ** (2.0399) | |
| Renewable energy | −0.0207 ** (−1.9927) | −0.0181 ** (−2.0021) | −0.0225 ** (−2.0089) | −0.0199 ** (−2.1413) | −0.0272 (−0.4062) | |
| relative TAXation on energy (−1) | 0.1058 *** (3.8149) | −0.1687 (−1.2961) | 0.0462 (1.2746) | |||
| FECˣTAX (−1) | −0.1102 *** (−3.0753) | 0.0156 (1.1610) | ||||
| EIˣTAX(-1) | 0.0387 * (1.9534) | 0.0090 * (1.8908) | ||||
| RENˣTAX(-1) | 0.0021 (1.2746) | 0.0420 (0.6607) | ||||
| Sample size | 408 | 408 | 408 | 408 | 408 | 408 |
| Number of countries | 28 | 28 | 28 | 28 | 28 | 28 |
| Number of instruments | 25 | 24 | 26 | 28 | 27 | 27 |
| Error AR (2) test | 0.6396 | 0.7487 | 0.7214 | 0.7907 | 0.7497 | 0.7377 |
| Sargan test | 0.7695 | 0.6020 | 0.5645 | 0.5451 | 0.5738 | 0.6709 |
| Pesaran CD test | 0.0814 | 0.0755 | 0.0792 | 0.0638 | 0.0729 | 0.0521 |
| Kao test | 0.3853 | 0.3002 | 0.4187 | 0.3749 | 0.4460 | 0.4093 |
| Pedroni test | 0.0932 | 0.1287 | 0.1638 | 0.1033 | 0.1857 | 0.1052 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liobikienė, G.; Butkus, M.; Matuzevičiūtė, K. The Contribution of Energy Taxes to Climate Change Policy in the European Union (EU). Resources 2019, 8, 63. https://doi.org/10.3390/resources8020063
Liobikienė G, Butkus M, Matuzevičiūtė K. The Contribution of Energy Taxes to Climate Change Policy in the European Union (EU). Resources. 2019; 8(2):63. https://doi.org/10.3390/resources8020063
Chicago/Turabian StyleLiobikienė, Genovaitė, Mindaugas Butkus, and Kristina Matuzevičiūtė. 2019. "The Contribution of Energy Taxes to Climate Change Policy in the European Union (EU)" Resources 8, no. 2: 63. https://doi.org/10.3390/resources8020063
APA StyleLiobikienė, G., Butkus, M., & Matuzevičiūtė, K. (2019). The Contribution of Energy Taxes to Climate Change Policy in the European Union (EU). Resources, 8(2), 63. https://doi.org/10.3390/resources8020063






