Optimal Pump Scheduling for Urban Drainage under Variable Flow Conditions
Abstract
1. Introduction
Aim of the Paper and Methodology
- Formulating a complete mathematical model of a drainage pumping system
- Optimizing the pumping system aiming at reducing the required energy
- Showing the benefit of such an optimization comparing the results with a classical CS plant.
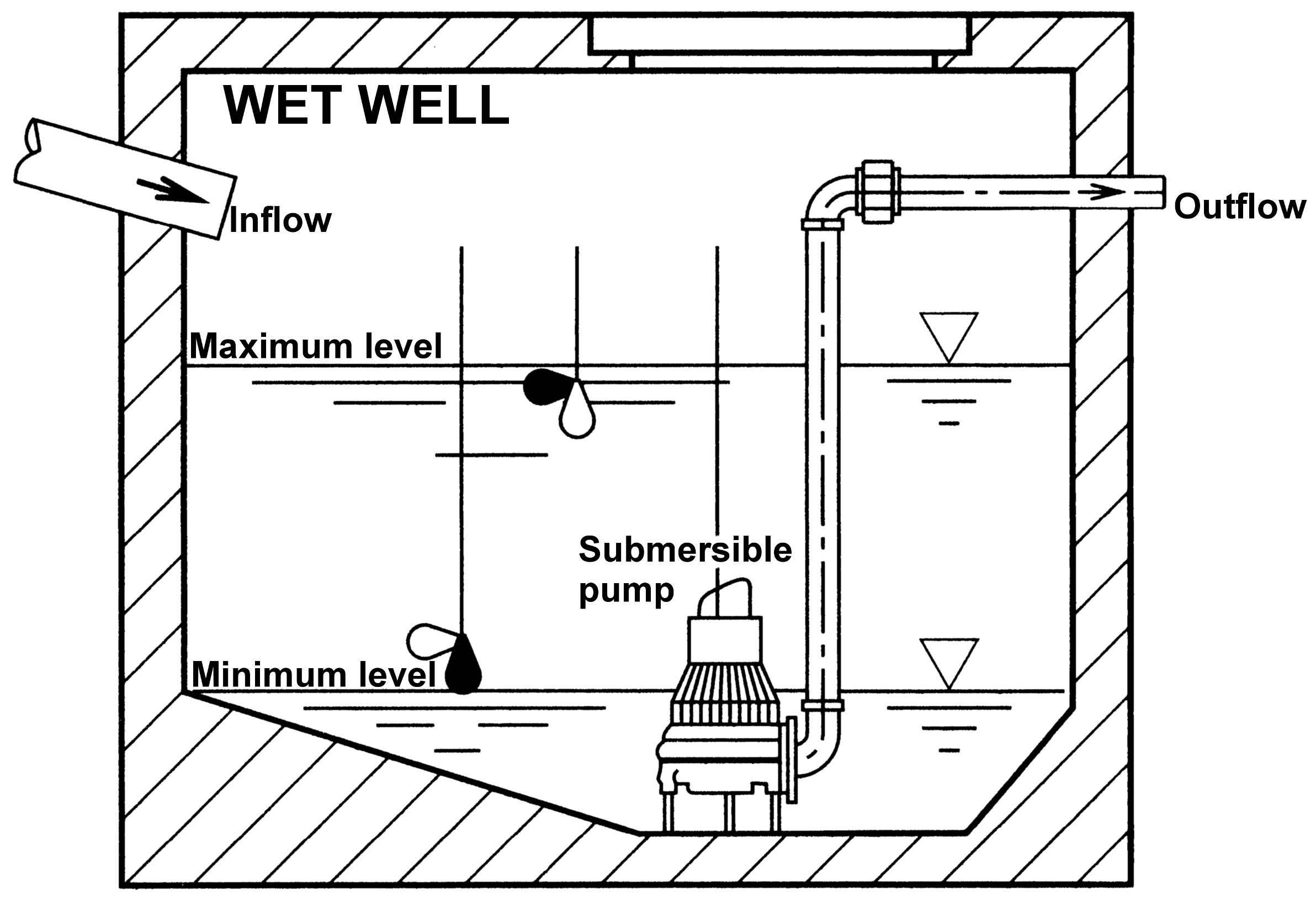
2. Pumping Station Description and Case Study
2.1. Classical Design
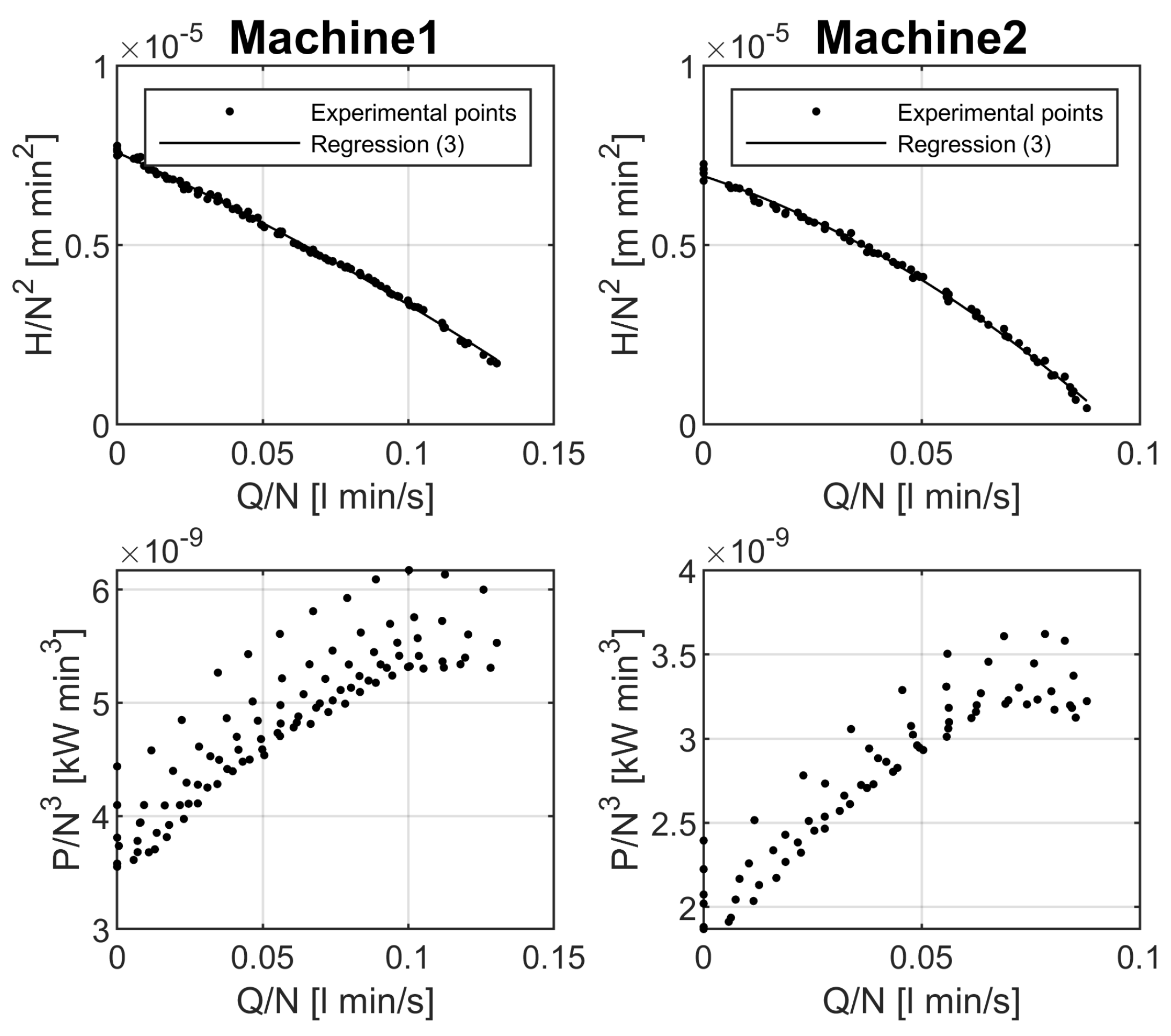
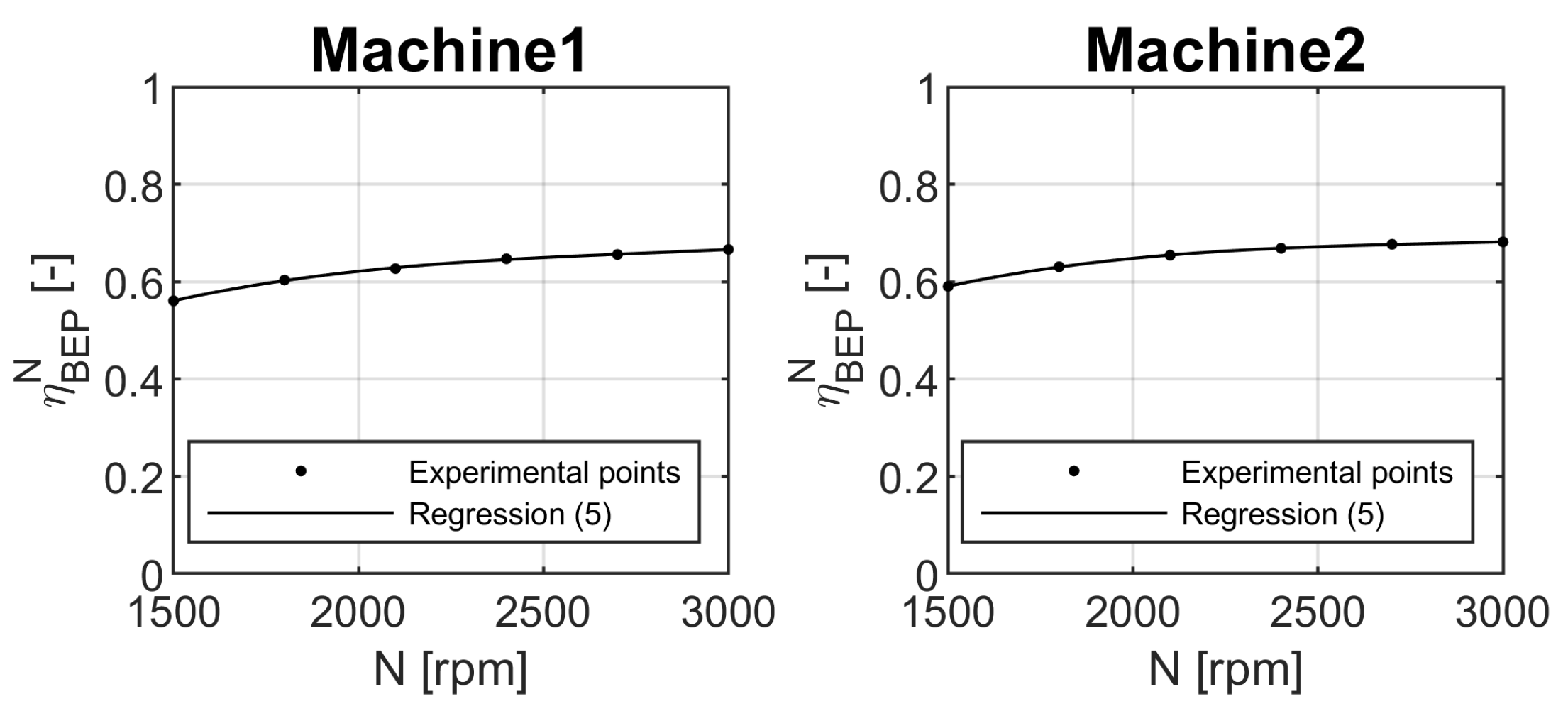
2.2. Experimental Investigation of the Behaviour of Two Submersible Pumps
2.3. Input Discharge Pattern
2.4. Plant Behaviour
3. Optimization Model
Resolution of the Optimization Model
4. Application and Results
5. Conclusions
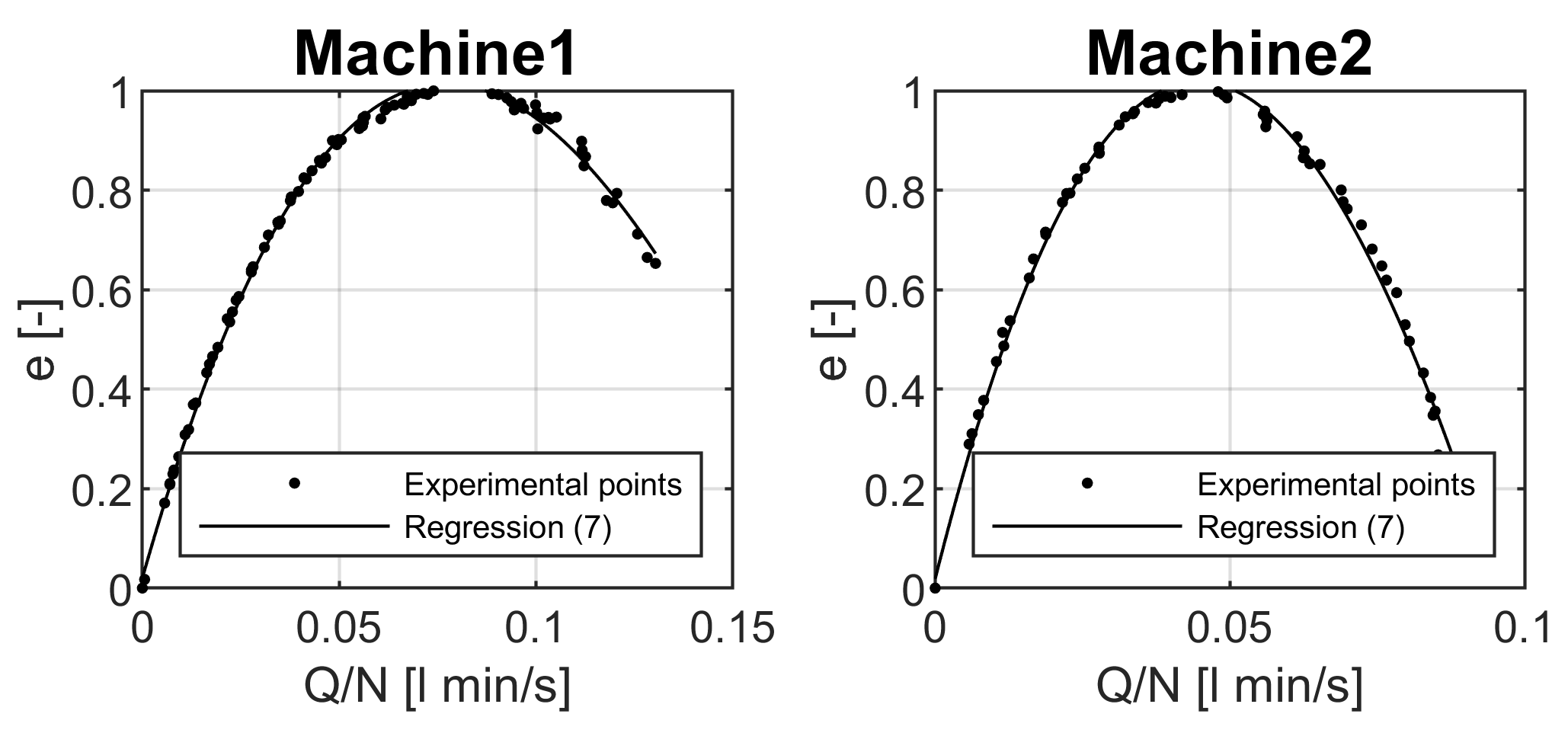
- An experimental campaign is undertaken to explore the effects of variable speed on the pumping efficiency. Specifically, in accordance with the affinity laws, an empirical equation is provided to compute the pumping head (Equation (7)), whereas a novel approach based on the concept of relative efficiency (Equation (10)) is provided to compute the pumping power under variable speed conditions (Equation (12)).
- On the basis of the above-mentioned theoretical framework, a mixed-integer optimization problem (Equation (30)) is built that is made up of an objective function (the overall pumping energy) to be minimized and a set of constraints for the variables of interest. The model is also able to comply with the ON/OFF switch of the pump, and two parameters ( and ) are introduced to simulate different scenarios for the inflow discharge and the plant configuration. The influence of the time window and step for computations is also discussed.
- The model is solved for a case study (a literature sewage daily pattern provided for the City of Naples, Italy) relying on a literature algorithm, and some indicators are analyzed to test the computational performance of the algorithm and the overall energy savings given by the optimal solution for the different scenarios. The case study was developed assuming a known inflow pattern and a constant energy cost during the day.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Ratio between and | |
| Ratio between static head and | |
| Length of the timestep | |
| Efficiency of the pump at its BEP | |
| Efficiency of the pump at its BEP for the maximum rotational speed | |
| Efficiency of the pump at its BEP at N rotational speed | |
| Efficiency of the CS operation | |
| Efficiency of optimal scheduling | |
| Efficiency of the pump at N rotational speed | |
| Time interval between two consecutive starts of the pump | |
| Ratio between and | |
| Benefit of the optimal operation, when compared to the CS mode | |
| Best Efficiency Point | |
| Regression coefficients of the head curve | |
| Regression coefficients of the power curve | |
| Regression coefficients of the efficiency curve | |
| Regression coefficients of the relative efficiency curve | |
| Computational time | |
| Constant Speed operation | |
| e | Relative efficiency |
| E | Required pumping energy |
| Daily required pumping energy for the CS operation | |
| Daily required pumping energy resulting from the optimization | |
| Daily reference energy | |
| Required pumping energy for each time window | |
| f | Electrical frequency |
| H | Pumped head |
| Pumped head at rotational speed at the BEP of the pump | |
| Required pumping head | |
| Pumped head at rotational speed | |
| Static head | |
| Pumped head at N rotational speed | |
| Water level in the wet well | |
| Maximum allowable water level in the wet well | |
| Minimum allowable water level in the wet well | |
| Subscript indicating the i-th timestep | |
| I | Switch of the pump |
| K | Head loss coefficient |
| Number of timesteps in the time window | |
| Number of time windows within the whole day | |
| N | rotational speed of the pump |
| Maximum rotational speed of the pump | |
| P | Pumped power |
| Pumped power at rotational speed | |
| Pumped power at N rotational speed | |
| Number of pole pairs of the motor | |
| Ratio between and | |
| Q | Pumped discharge |
| Non dimensional inflow pattern | |
| Discharge of the pump at its BEP for the maximum rotational speed | |
| Maximum inflow discharge | |
| Measured drainage discharge | |
| Inflow discharge | |
| Outflow discharge | |
| S | Cross section of the wet well |
| Maximum allowable number of starts per hour | |
| Number of starts per hour | |
| t | Time |
| T | Time window |
| W | Storage volume of the wet well |
| Volume of water inside the wet well |
References
- Carravetta, A.; Fecarotta, O.; Golia, U.M.; La Rocca, M.; Martino, R.; Padulano, R.; Tucciarelli, T. Optimization of Osmotic Desalination Plants for Water Supply Networks. Water Resour. Manag. 2016, 30, 3965–3978. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H. A new low-cost installation scheme of PATs for pico-hydropower to recover energy in residential areas. Renew. Energy 2018. [Google Scholar] [CrossRef]
- Vairavamoorthy, K.; Lumbers, J. Leakage Reduction in Water Distribution Systems: Optimal Valve Control. J. Hydraul. Eng. 1998, 124, 1146–1154. [Google Scholar] [CrossRef]
- Castro-Gama, M.; Pan, Q.; Lanfranchi, E.A.; Jonoski, A.; Solomatine, D.P. Pump Scheduling for a Large Water Distribution Network Milan, Italy. Procedia Eng. 2017, 186, 436–443. [Google Scholar] [CrossRef]
- Goldstein, R.; Smith, W. Water & Sustainability: U.S. Electricity Consumption for Water Supply & Treatment—The Next Half Century. Water Supply 2002, 4, 93. [Google Scholar] [CrossRef]
- Bunn, S.M.; Reynolds, L. The energy-efficiency benefits of pump-scheduling optimization for potable water supplies. IBM J. Res. Dev. 2009, 53, 5:1–5:13. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X.; Kusiak, A. Data-driven minimization of pump operating and maintenance cost. Eng. Appl. Artif. Intell. 2015, 40, 37–46. [Google Scholar] [CrossRef]
- Plappally, A.K.; Lienhard, V.J.H. Energy requirements for water production, treatment, end use, reclamation, and disposal. Renew. Sustain. Energy Rev. 2012, 16, 4818–4848. [Google Scholar] [CrossRef]
- Zhang, Z.; Kusiak, A.; Zeng, Y.; Wei, X. Modeling and optimization of a wastewater pumping system with data-mining methods. Appl. Energy 2016, 164, 303–311. [Google Scholar] [CrossRef]
- Boulos, P.F.; Wu, Z.; Orr, C.H.; Moore, M.; Hsiung, P.; Thomas, D. Optimal Pump Operation of Water Distribution Systems Using Genetic Algorithms. Available online: https://pdfs.semanticscholar.org/30bd/0b8898b9c7eede6581df60fe8aaf2964d0f7.pdf?_ga=2.184499744.767898400.1542030914-596395705.1542030914 (accessed on 12 November 2018).
- Ostojin, S.; Mounce, S.R.S.; Boxall, J.B.J. An artificial intelligence approach for optimizing pumping in sewer systems. J. Hydroinform. 2011, 13, 295–306. [Google Scholar] [CrossRef]
- Carravetta, A.; Antipodi, L.; Golia, U.; Fecarotta, O. Energy saving in a water supply network by coupling a pump and a Pump As Turbine (PAT) in a turbopump. Water 2017, 9, 62. [Google Scholar] [CrossRef]
- Carravetta, A.; Conte, M.; Antipodi, L. Energy efficiency index for water supply systems. In Proceedings of the AEIT International Annual Conference (AEIT), Naples, Italy, 14–16 October 2015; pp. 1–4. [Google Scholar]
- Jowitt, P.W.; Germanopoulos, G. Optimal Pump Scheduling in Water? Supply Networks. J. Water Resour. Plan. Manag. 1992, 118, 406–422. [Google Scholar] [CrossRef]
- Little, K.W.; McCrodden, B.J. Minimization of raw water pumping costs using MILP. J. Water Resour. Plan. Manag. 1989, 115, 511–522. [Google Scholar] [CrossRef]
- Ormsbee, L.E.; Walski, T.M.; Chase, D.V.; Sharp, W.W. Methodology for Improving Pump Operation Efficiency. J. Water Resour. Plan. Manag. 1989, 115, 148–164. [Google Scholar] [CrossRef]
- Tabesh, M. Scheduling and operating costs in water distribution networks. Proc. Inst. Civ. Eng. 2013, 166, 432. [Google Scholar]
- Lansey, K.; Awumah, K. Optimal Pump Operations Considering Pump Switches. J. Water Resour. Plan. Manag. 1994, 120, 17–35. [Google Scholar] [CrossRef]
- Van Zyl, J.E.; Savic, D.A.; Walters, G.A. Operational optimization of water distribution systems using a hybrid genetic algorithm. J. Water Resour. Plan. Manag. 2004, 130, 160–170. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Tabesh, M.; Ataeekia, B. Ant-colony optimization of pumping schedule to minimize the energy cost using variable-speed pumps in water distribution networks. Urban Water J. 2014, 11, 335–347. [Google Scholar] [CrossRef]
- De Paola, F.; Fontana, N.; Giugni, M.; Marini, G.; Pugliese, F. An application of the Harmony-Search Multi-Objective (HSMO) optimization algorithm for the solution of pump scheduling problem. Procedia Eng. 2016, 162, 494–502. [Google Scholar] [CrossRef]
- De Paola, F.; Fontana, N.; Giugni, M.; Marini, G.; Pugliese, F. Optimal solving of the pump scheduling problem by using a Harmony Search optimization algorithm. J. Hydroinform. 2017, 19, 879–889. [Google Scholar] [CrossRef]
- Shamir, U.; Salomons, E. Optimal Real-Time Operation of Urban Water Distribution Systems Using Reduced Models. J. Water Resour. Plan. Manag. 2008, 134, 181–185. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M.; Marinelli, A. A short-term, pattern-based model for water-demand forecasting. J. Hydroinform. 2007, 9, 39. [Google Scholar] [CrossRef]
- Jamieson, D.G.; Shamir, U.; Martinez, F.; Franchini, M. Conceptual design of a generic, real-time, near-optimal control system for water-distribution networks. J. Hydroinform. 2007, 9, 3. [Google Scholar] [CrossRef]
- Martínez, F.; Hernández, V.; Alonso, J.M.; Rao, Z.; Alvisi, S. Optimizing the operation of the Valencia water-distribution network. J. Hydroinform. 2007, 9, 65. [Google Scholar] [CrossRef]
- Rao, Z.; Alvarruiz, F. Use of an artificial neural network to capture the domain knowledge of a conventional hydraulic simulation model. J. Hydroinform. 2007, 9, 15. [Google Scholar] [CrossRef]
- Barán, B.; Von Lücken, C.; Sotelo, A. Multi-objective pump scheduling optimisation using evolutionary strategies. Adv. Eng. Softw. 2005, 36, 39–47. [Google Scholar] [CrossRef]
- Wang, J.Y.; Chang, T.P.; Chen, J.S. An enhanced genetic algorithm for bi-objective pump scheduling in water supply. Expert Syst. Appl. 2009, 36, 10249–10258. [Google Scholar] [CrossRef]
- Kougias, I.P.; Theodossiou, N.P. Multiobjective Pump Scheduling Optimization Using Harmony Search Algorithm (HSA) and Polyphonic HSA. Water Resour. Manag. 2013, 27, 1249–1261. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, Z.; Kusiak, A.; Tang, F.; Wei, X. Optimizing wastewater pumping system with data-driven models and a greedy electromagnetism-like algorithm. Stoch. Environ. Res. Risk Assess. 2016, 30, 1263–1275. [Google Scholar] [CrossRef]
- Giacomello, C.; Kapelan, Z.; Nicolini, M. Fast Hybrid Optimization Method for Effective Pump Scheduling. J. Water Resour. Plan. Manag. 2013, 139, 175–183. [Google Scholar] [CrossRef]
- Sperlich, A.; Pfeiffer, D.; Burgschweiger, J.; Campbell, E.; Beck, M.; Gnirss, R.; Ernst, M. Energy Efficient Operation of Variable Speed Submersible Pumps: Simulation of a Ground Water Well Field. Water 2018, 10, 1255. [Google Scholar] [CrossRef]
- Behandish, M.; Wu, Z.Y. Concurrent pump scheduling and storage level optimization using meta-models and evolutionary algorithms. Procedia Eng. 2014, 70, 103–112. [Google Scholar] [CrossRef]
- Chabal, L.; Stanko, S. Sewerage pumping station optimization under real conditions. Geosci. Eng. 2014, 60, 19–28. [Google Scholar] [CrossRef][Green Version]
- Boon, A.G. Septicity in sewers: Causes, consequences and containment. Water Sci. Technol. 1995, 31, 237–253. [Google Scholar] [CrossRef]
- Fecarotta, O.; Ramos, H.M.; Derakhshan, S.; Del Giudice, G.; Carravetta, A. Fine Tuning a PAT Hydropower Plant in a Water Supply Network to Improve System Effectiveness. J. Water Resour. Plan. Manag. 2018, 144, 04018038. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Performance of vertical-axis pumps as turbines. J. Hydraul. Res. 2018, 1–12. [Google Scholar] [CrossRef]
- Fecarotta, O.; Carravetta, A.; Ramos, H.M.; Martino, R. An improved affinity model to enhance variable operating strategy for pumps used as turbines. J. Hydraul. Res. 2016, 54, 332–341. [Google Scholar] [CrossRef]
- Simpson, A.R.; Marchi, A. Evaluating the approximation of the affinity laws and improving the efficiency estimate for variable speed pumps. J. Hydraul. Eng. 2013, 139, 1314–1317. [Google Scholar] [CrossRef]
- Carravetta, A.; Conte, M.C.; Fecarotta, O.; Ramos, H.M. Evaluation of PAT performances by modified affinity law. Procedia Eng. 2014, 89, 581–587. [Google Scholar] [CrossRef]
- Morani, M.; Carravetta, A.; Del Giudice, G.; McNabola, A.; Fecarotta, O. A Comparison of Energy Recovery by PATs against Direct Variable Speed Pumping in Water Distribution Networks. Fluids 2018, 3, 41. [Google Scholar] [CrossRef]
- Padulano, R.; Del Giudice, G. A Mixed Strategy Based on Self-Organizing Map for Water Demand Pattern Profiling of Large-Size Smart Water Grid Data. Water Resour. Manag. 2018, 32, 3671–3685. [Google Scholar] [CrossRef]
- Del Giudice, G.; Padulano, R. Sensitivity analysis and calibration of a rainfall-runoff model with the combined use of EPA-SWMM and genetic algorithm. Acta Geophys. 2016, 64, 1755–1778. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Pump as turbine (PAT) design in water distribution network by system effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef]
- Belotti, P.; Kirches, C.; Leyffer, S.; Linderoth, J.; Luedtke, J.; Mahajan, A. Mixed-integer nonlinear optimization. Acta Numer. 2013, 22, 1–131. [Google Scholar] [CrossRef]
- Bonami, P.; Biegler, L.T.; Conn, A.R.; Cornuéjols, G.; Grossmann, I.E.; Laird, C.D.; Lee, J.; Lodi, A.; Margot, F.; Sawaya, N.; et al. An algorithmic framework for convex mixed integer nonlinear programs. Discret. Optim. 2008, 5, 186–204. [Google Scholar] [CrossRef]
- Fecarotta, O.; McNabola, A. Optimal Location of Pump as Turbines (PATs) in Water Distribution Networks to Recover Energy and Reduce Leakage. Water Resour. Manag. 2017. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Schoenemann, T. Computing optimal alignments for the IBM-3 translation model. In Proceedings of the Fourteenth Conference on Computational Natural Language Learning, Uppsala, Sweden, 15–16 July 2010; Association for Computational Linguistics: Stroudsburg, PA, USA, 2010; pp. 98–106. [Google Scholar]
- Bonami, P.; Lee, J. BONMIN Users’ Manual. 2009. Available online: https://projects.coin-or.org/Bonmin/browser/stable/0.1/Bonmin/doc/BONMIN_UsersManual.pdf?format=raw (accessed on 12 November 2018).
- Burer, S.; Letchford, A.N. Non-convex mixed-integer nonlinear programming: A survey. Surv. Oper. Res. Manag. Sci. 2012, 17, 97–106. [Google Scholar] [CrossRef]

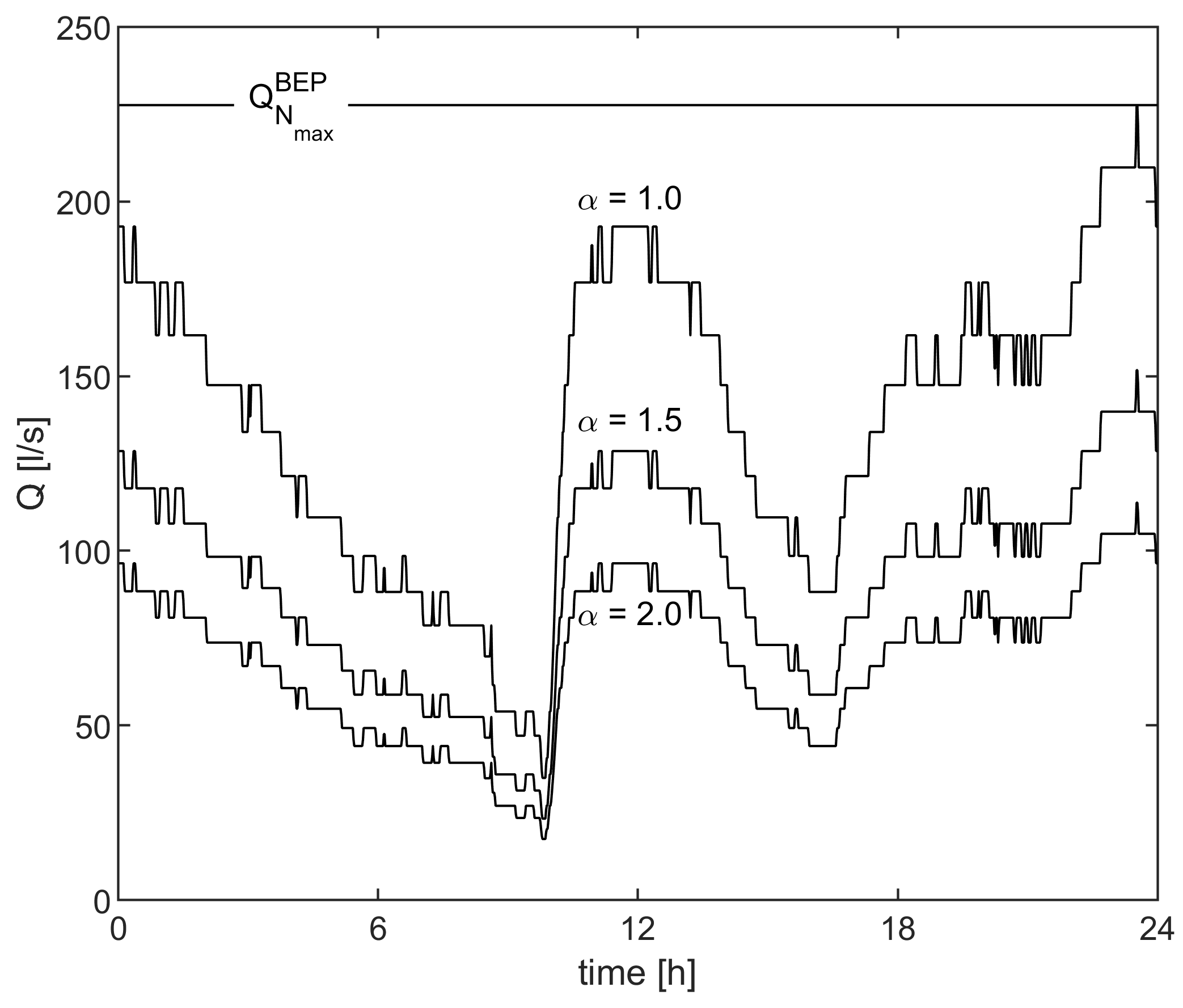

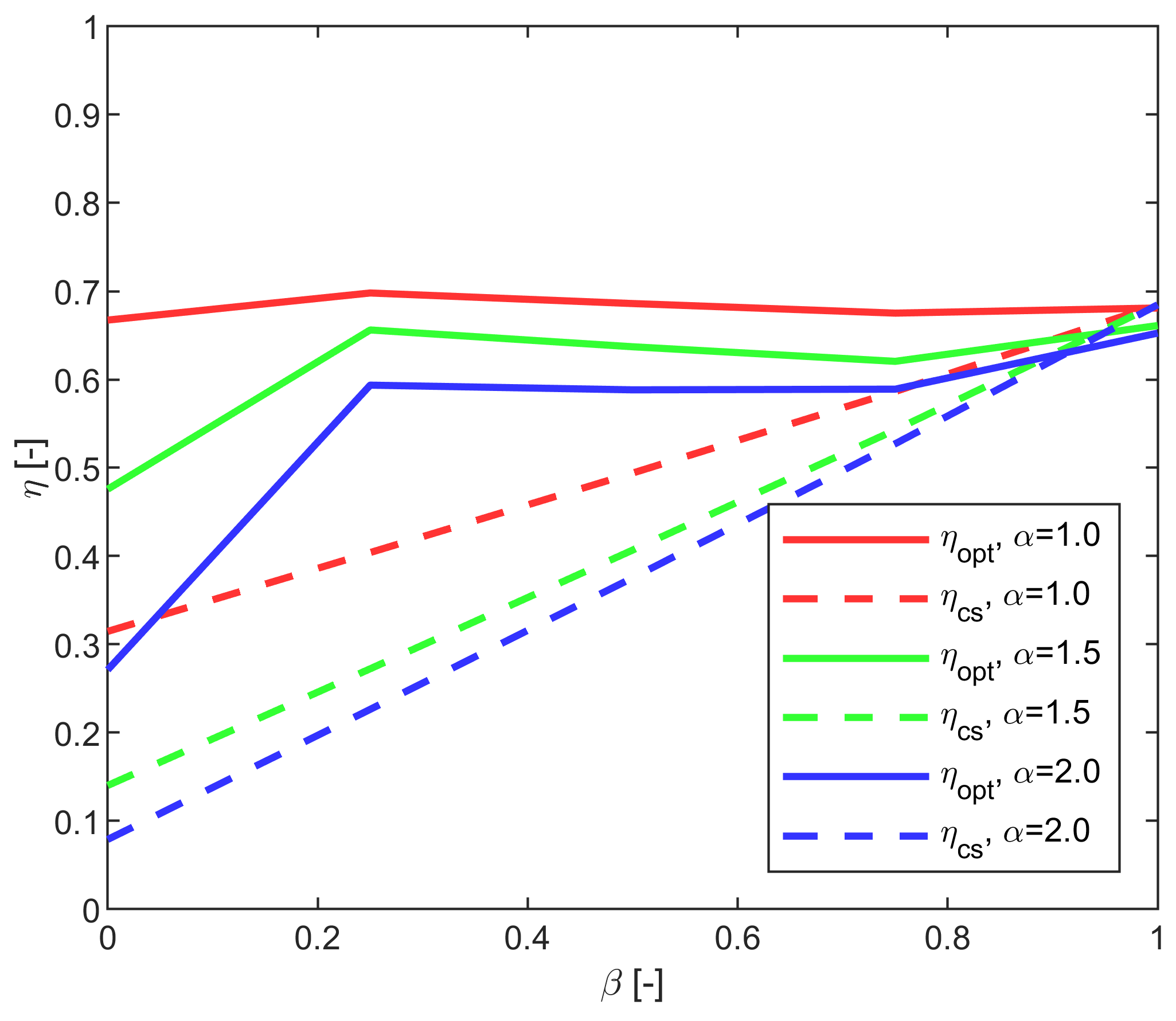
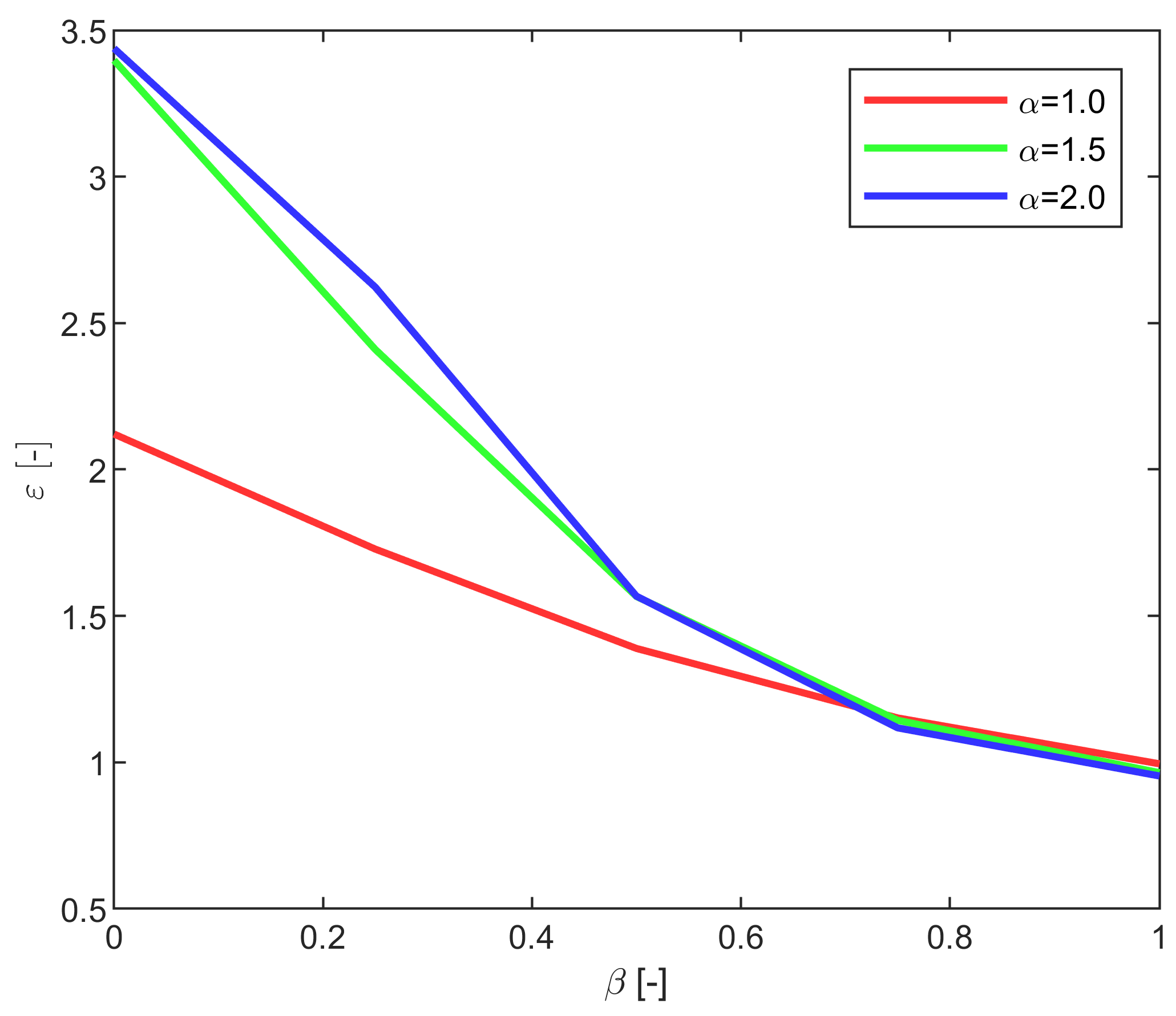
| Machine | ||||||
|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [L/s] | [m] | kWh/day | kWh/day |
| 1 | 1.00 | 0.00 | 236.66 | 0.00 | 616.9 | 1960.8 |
| 1 | 1.00 | 0.25 | 236.66 | 9.71 | 790.4 | 1956.7 |
| 1 | 1.00 | 0.50 | 236.66 | 19.42 | 963.9 | 1951.0 |
| 1 | 1.00 | 0.75 | 236.66 | 29.13 | 1137.4 | 1939.4 |
| 1 | 1.00 | 1.00 | 236.66 | 38.84 | 1310.8 | 1914.4 |
| 1 | 1.50 | 0.00 | 157.78 | 0.00 | 182.8 | 1305.5 |
| 1 | 1.50 | 0.25 | 157.78 | 9.71 | 355.6 | 1306.0 |
| 1 | 1.50 | 0.50 | 157.78 | 19.42 | 528.3 | 1298.8 |
| 1 | 1.50 | 0.75 | 157.78 | 29.13 | 701.1 | 1291.5 |
| 1 | 1.50 | 1.00 | 157.78 | 38.84 | 873.9 | 1274.7 |
| 1 | 2.00 | 0.00 | 118.33 | 0.00 | 77.1 | 978.1 |
| 1 | 2.00 | 0.25 | 118.33 | 9.71 | 221.7 | 979.5 |
| 1 | 2.00 | 0.50 | 118.33 | 19.42 | 366.3 | 975.6 |
| 1 | 2.00 | 0.75 | 118.33 | 29.13 | 510.8 | 969.0 |
| 1 | 2.00 | 1.00 | 118.33 | 38.84 | 655.4 | 957.2 |
| 2 | 1.00 | 0.00 | 135.04 | 0.00 | 356.5 | 1112.8 |
| 2 | 1.00 | 0.25 | 135.04 | 9.83 | 456.7 | 1113.7 |
| 2 | 1.00 | 0.50 | 135.04 | 19.67 | 557.0 | 1110.7 |
| 2 | 1.00 | 0.75 | 135.04 | 29.50 | 657.2 | 1106.2 |
| 2 | 1.00 | 1.00 | 135.04 | 39.33 | 757.5 | 1098.3 |
| 2 | 1.50 | 0.00 | 90.03 | 0.00 | 105.6 | 743.7 |
| 2 | 1.50 | 0.25 | 90.03 | 9.83 | 205.5 | 741.7 |
| 2 | 1.50 | 0.50 | 90.03 | 19.67 | 305.3 | 739.3 |
| 2 | 1.50 | 0.75 | 90.03 | 29.50 | 405.2 | 738.7 |
| 2 | 1.50 | 1.00 | 90.03 | 39.33 | 505.0 | 732.2 |
| 2 | 2.00 | 0.00 | 67.52 | 0.00 | 44.6 | 557.0 |
| 2 | 2.00 | 0.25 | 67.52 | 9.83 | 128.1 | 556.3 |
| 2 | 2.00 | 0.50 | 67.52 | 19.67 | 211.7 | 554.5 |
| 2 | 2.00 | 0.75 | 67.52 | 29.50 | 295.2 | 554.7 |
| 2 | 2.00 | 1.00 | 67.52 | 39.33 | 378.7 | 549.5 |
| Machine | C.T. | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [kWh/day] | [kWh/day] | [kWh/day] | [-] | [-] | [-] | [min] |
| 1 | 1.0 | 0.00 | 616.9 | 1960.8 | 924.5 | 0.315 | 0.667 | 2.121 | 1.8 |
| 1 | 1.0 | 0.25 | 790.4 | 1956.7 | 1132.3 | 0.404 | 0.698 | 1.728 | 1.3 |
| 1 | 1.0 | 0.50 | 963.9 | 1951.0 | 1404.9 | 0.494 | 0.686 | 1.389 | 1.6 |
| 1 | 1.0 | 0.75 | 1137.4 | 1939.4 | 1684.4 | 0.586 | 0.675 | 1.151 | 1.4 |
| 1 | 1.0 | 1.00 | 1310.8 | 1914.4 | 1924.8 | 0.685 | 0.681 | 0.995 | 2.4 |
| 1 | 1.5 | 0.00 | 182.8 | 1305.5 | 384.2 | 0.140 | 0.476 | 3.398 | 6.6 |
| 1 | 1.5 | 0.25 | 355.6 | 1306.0 | 541.9 | 0.272 | 0.656 | 2.410 | 1.6 |
| 1 | 1.5 | 0.50 | 528.3 | 1298.8 | 829.3 | 0.407 | 0.637 | 1.566 | 21.2 |
| 1 | 1.5 | 0.75 | 701.1 | 1291.5 | 1129.8 | 0.543 | 0.621 | 1.143 | 904.6 |
| 1 | 1.5 | 1.00 | 873.9 | 1274.7 | 1321.8 | 0.686 | 0.661 | 0.964 | 3.0 |
| 1 | 2.0 | 0.00 | 77.1 | 978.1 | 284.5 | 0.079 | 0.271 | 3.438 | 5.4 |
| 1 | 2.0 | 0.25 | 221.7 | 979.5 | 373.5 | 0.226 | 0.594 | 2.623 | 1.4 |
| 1 | 2.0 | 0.50 | 366.3 | 975.6 | 622.6 | 0.375 | 0.588 | 1.567 | 2906.8 |
| 1 | 2.0 | 0.75 | 510.8 | 969.0 | 867.2 | 0.527 | 0.589 | 1.117 | 383.3 |
| 1 | 2.0 | 1.00 | 655.4 | 957.2 | 1004.3 | 0.685 | 0.653 | 0.953 | 3.5 |
| 2 | 1.0 | 0.00 | 356.5 | 1112.8 | 538.5 | 0.320 | 0.662 | 2.067 | 2.3 |
| 2 | 1.0 | 0.25 | 456.7 | 1113.7 | 660.5 | 0.410 | 0.692 | 1.686 | 1.2 |
| 2 | 1.0 | 0.50 | 557.0 | 1110.7 | 817.6 | 0.501 | 0.681 | 1.358 | 28.6 |
| 2 | 1.0 | 0.75 | 657.2 | 1106.2 | 975.0 | 0.594 | 0.674 | 1.135 | 1.4 |
| 2 | 1.0 | 1.00 | 757.5 | 1098.3 | 1093.7 | 0.690 | 0.693 | 1.004 | 2.5 |
| 2 | 1.5 | 0.00 | 105.6 | 743.7 | 218.8 | 0.142 | 0.483 | 3.399 | 2.2 |
| 2 | 1.5 | 0.25 | 205.5 | 741.7 | 316.9 | 0.277 | 0.648 | 2.340 | 1.6 |
| 2 | 1.5 | 0.50 | 305.3 | 739.3 | 484.7 | 0.413 | 0.630 | 1.525 | 16,559.1 |
| 2 | 1.5 | 0.75 | 405.2 | 738.7 | 643.4 | 0.548 | 0.630 | 1.148 | 1.6 |
| 2 | 1.5 | 1.00 | 505.0 | 732.2 | 740.0 | 0.690 | 0.682 | 0.990 | 2.6 |
| 2 | 2.0 | 0.00 | 44.6 | 557.0 | 159.3 | 0.080 | 0.280 | 3.496 | 2.5 |
| 2 | 2.0 | 0.25 | 128.1 | 556.3 | 214.4 | 0.230 | 0.598 | 2.595 | 1.3 |
| 2 | 2.0 | 0.50 | 211.7 | 554.5 | 362.8 | 0.382 | 0.583 | 1.529 | 977.0 |
| 2 | 2.0 | 0.75 | 295.2 | 554.7 | 486.9 | 0.532 | 0.606 | 1.139 | 2.1 |
| 2 | 2.0 | 1.00 | 378.7 | 549.5 | 562.0 | 0.689 | 0.674 | 0.978 | 2.5 |
| T | C.T. | |||
|---|---|---|---|---|
| [min] | [kWh/day] | [-] | [-] | [min] |
| 30 | 924.5 | 0.667 | 2.121 | 1.8 |
| 30 | 1132.3 | 0.698 | 1.728 | 1.3 |
| 30 | 1404.9 | 0.686 | 1.389 | 1.6 |
| 30 | 1684.4 | 0.675 | 1.151 | 1.4 |
| 30 | 1924.8 | 0.681 | 0.995 | 2.4 |
| 60 | 920.8 | 0.670 | 2.129 | 1.8 |
| 60 | 1127.9 | 0.701 | 1.735 | 1.5 |
| 60 | 1399.3 | 0.689 | 1.394 | 2.0 |
| 60 | 1676.7 | 0.678 | 1.157 | 1.8 |
| 60 | 1910.2 | 0.686 | 1.002 | 2.2 |
| 120 | 918.6 | 0.672 | 2.135 | 6.6 |
| 120 | 1125.7 | 0.702 | 1.738 | 2.4 |
| 120 | 1396.5 | 0.690 | 1.397 | 3.4 |
| 120 | 1672.6 | 0.680 | 1.159 | 2.0 |
| 120 | 1902.0 | 0.689 | 1.007 | 3.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fecarotta, O.; Carravetta, A.; Morani, M.C.; Padulano, R. Optimal Pump Scheduling for Urban Drainage under Variable Flow Conditions. Resources 2018, 7, 73. https://doi.org/10.3390/resources7040073
Fecarotta O, Carravetta A, Morani MC, Padulano R. Optimal Pump Scheduling for Urban Drainage under Variable Flow Conditions. Resources. 2018; 7(4):73. https://doi.org/10.3390/resources7040073
Chicago/Turabian StyleFecarotta, Oreste, Armando Carravetta, Maria Cristina Morani, and Roberta Padulano. 2018. "Optimal Pump Scheduling for Urban Drainage under Variable Flow Conditions" Resources 7, no. 4: 73. https://doi.org/10.3390/resources7040073
APA StyleFecarotta, O., Carravetta, A., Morani, M. C., & Padulano, R. (2018). Optimal Pump Scheduling for Urban Drainage under Variable Flow Conditions. Resources, 7(4), 73. https://doi.org/10.3390/resources7040073








