Abstract
Stochastic computing (SC) is an emerging low-cost computation paradigm for efficient approximation. It processes data in forms of probabilities and offers excellent progressive accuracy. Since SC’s accuracy heavily depends on the stochastic bitstream length, generating acceptable approximate results while minimizing the bitstream length is one of the major challenges in SC, as energy consumption tends to linearly increase with bitstream length. To address this issue, a novel energy-performance scalable approach based on quasi-stochastic number generators is proposed and validated in this work. Compared to conventional approaches, the proposed methodology utilizes a novel algorithm to estimate the computation time based on the accuracy. The proposed methodology is tested and verified on a stochastic edge detection circuit to showcase its viability. Results prove that the proposed approach offers a 12–60% reduction in execution time and a 12–78% decrease in the energy consumption relative to the conventional counterpart. This excellent scalability between energy and performance could be potentially beneficial to certain application domains such as image processing and machine learning, where power and time-efficient approximation is desired.
1. Introduction
With rapidly advancing technology, energy efficiency has become one of the major design challenges in digital circuits and systems. Studies demonstrate that energy efficiency can be improved by reducing both the computational time and power consumption [1]. However, reducing these factors affects the performance of the system. In other words, reducing the power consumption affects the overall performance of the system. This challenge intensifies the current demand for low-power high-performance systems, and therefore a novel methodology to handle this challenge is required.
One such promising technique that exploits probability theory “stochastic computation” can address these limitations [1]. Stochastic computing (SC), which was invented in the 1960s by Gaines [2,3], recently regained significant attention mainly due to its approximate computation method. This computation method offers progressive accuracy scalability [4] that can be well exploited in the applications where approximated accuracy is accepted. This includes media processing, neural networks, factor graphs, LDPC codes, fault-tree analysis, image processing, and filters [5,6,7,8,9,10].
However, mainstream adoption of SC is limited due to the long run-time and inaccuracy [1]. As explained in [11], a random number generator (RNG), also known as a stochastic number generator (SNG), plays a significant role in determining the area and energy consumption. The commonly used SNG is the linear feedback shift register (LFSR), and several optimization techniques to improve the output accuracy of the LFSR-based SNGs are presented in the literature [12,13,14,15,16,17,18]. As presented in [19], increasing the length of stochastic sequences (SS) increases operating time and power consumption.
To address this issue, [11] introduced a quasi-stochastic bit sequence generation (QSNG) that utilizes the distributed memory elements of a field-programmable gate array (FPGA) for designing the SNGs. However, no comment on energy reduction has been reported in [11]. Therefore, in this work a detailed analysis and methodology for energy reduction is presented to improve the overall performance.
In this paper, a novel energy-performance scalable methodology based on quasi-stochastic number generators is proposed and validated. Compared to the conventional approaches, the proposed methodology utilizes a novel algorithm to estimate the computation time based on the accuracy. Finally, a comprehensive simulation-based study is presented in this paper to demonstrate the reductions in operating time and energy consumption. Overall, a 12–60% reduction in the operating time and a 12–78% saving in terms of the energy consumption relative to the conventional LFSR counterpart are observed.
This paper is organized as follows. In Section 2, background of Stochastic computing and quasi-stochastic bit sequence generation are discussed. Section 3 provides a novel energy-efficient quasi-stochastic computing algorithm to calculate the number of clock cycles based on the peak signal-to-noise ratio. The simulation results to validate the proposed approach are presented in Section 4. Finally, Section 5 asserts the conclusion.
2. Background
2.1. Stochastic Computing
SC is a computation technique that uses finite length binary bitstreams to encode stochastic numbers [19]. The length of the bitstream and the number of 1s and 0s in the binary bitstream determine the encoded probability value [1]. The basic circuits used in stochastic computation are shown in Figure 1. The operation of these circuits rely on the type of number interpretations, namely unipolar (UP), bipolar (BP) or inverted bipolar (IBP) formats as presented in [19]. The unipolar format represents the real number x in the range of , using bipolar x is represented in between [−1, 1] and IBP ranges from , where the Boolean values 0 and 1 are represented as 1 and in the stochastic number (SN) [11]. Detailed explanations of various SN formats are clearly discussed in [14].
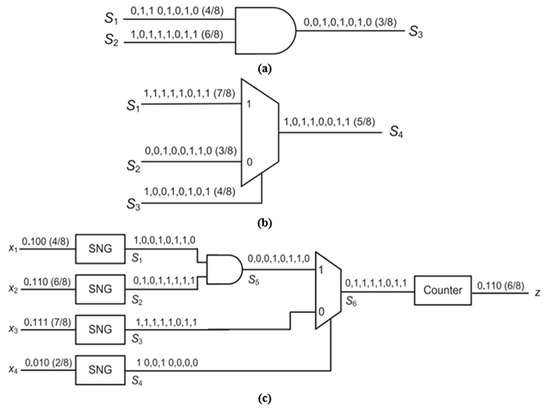
Figure 1.
Basic circuits used in stochastic computation: (a) AND gate used as a stochastic multiplier. (b) Multiplexer used as a scaled stochastic adder. (c) Stochastic circuit for realizing the arithmetic function [19].
The probability value in SC is represented by a binary bitstream of 0s and 1s with specific length L [19]. For the binary representation of 0.5, in the bitstream of length L, half of the bits are represented by 1s and the other half with 0s [11]. For example, one way of representing with a bitstream of 8 bits is 01010101. Dependency or correlation between the inputs also plays an important role in representing a stochastic number [19].This inherent feature of SC limits its performance over certain applications compared to conventional binary implementations [20]. For example, an AND gate is used as a multiplier in SC. If two input SS (x and y, namely) are identical (e.g., ), output z will also be , which is not an accurate result because the accurate output stochastic bitstream should have three 0’s and one 1 (i.e., 0.25). Another extreme case can happen when , where output will be .
As shown in these two examples, stochastic bitstream length should be large enough to have the output stream to converge to an accurate value. Therefore, SC is considered to be viable for applications such as image processing and machine learning where fast and efficient approximate computation is desired. To achieve acceptable accuracy, bitstream length L should be large enough to have the final result converged to a value with acceptable approximation error. To address this limitation, a new approach quasi-stochastic bit sequence generation, leveraging FPGA implementation of low-discrepancy (LD) bitstreams for faster convergence has been proposed in [11].
2.2. Quasi-Stochastic Bit Sequence Generation
In this approach, the LD sequence and distributed memory elements of the FPGAs (i.e., the LUTs are used for designing the SNGs) [11]. Compared to conventional hardware pseudo random number generation scheme such as LFSR methodology, LD sequences prevent the occurrence of random fluctuation by uniformly spicing the and in the stochastic bit streams [21]. They allow a fraction of the points inside any subset of to be as close as possible, such that uniformity is maintained between the low-discrepancy points [11]. This helps to reduce gaps and clustering points as illustrated in Figure 2.

Figure 2.
Distribution of pseudo-random points (top) and LD points (bottom) in the unit square [22].
In this QSNG methodology, the stochastic sequence is obtained by multiplying the pre-computed fixed direction vectors with binary numbers [11]. The general structure for generating the binary base two LD sequence consists of bit-wise XOR gates, a multiplication circuit, and RAM to store the directional vectors. In the multiplication circuit, each bit from the counter output is multiplied by each n-bit direction vector to produce n-bit intermediate direction vectors [11].
The bit-wise XOR-ing of these n-bit intermediate direction vectors will result in n-bit LD sequence. At the comparator, these LD sequences are compared with the input binary numbers to generate stochastic number [11]. For example, to generate an SS of bit length of 256 (), eight-bit length direction vectors, which can generate an eight-bit length LD sequence every clock cycle, are required. In summary, SNG plays an important role in determining the SC properties such as size and computation time. In a LFSR-based SNG, L clock cycles are required to fully generate an SS of length L bits [19]. On the other hand, the length of the SS in QSNG methodology determines the size of the binary counter, which in turn determines the computation time [11].
Furthermore, the extensive study of prior literature indicates that SC is beneficial in image processing [8,9,11,19], yet its application is limited due to accuracy and high-energy consumption. With energy becoming the predominant factor in the current computing systems, novel techniques to address this limitation is required.
Therefore, the primary focus of this work is to present an energy-efficient SC approach for image processing application based on the proposed QSNG methodology. A systematic approach called EQSNG (energy-efficient quasi-stochastic number generation) is proposed that minimizes the energy consumption by detecting the lowest number of clock cycles for a specified accuracy. This methodology is used to assess SC’s accuracy in various test images. To the best of our knowledge, this is the only SC design that outperforms its conventional LFSR-based SC in terms of energy-performance scalability. The energy-performance scalability of SC based on QSNG is discussed in detail in Section 3.
3. Energy Performance Scalability of Novel Quasi-Stochastic Computing Approach
We begin this section by discussing major factors affecting the accuracy of a processed image. Next, the effect of computation time on accuracy and energy consumption is demonstrated. Lastly, the proposed energy efficient algorithm that introduces energy-performance scalability in SC is discussed in detail.
In most of the image processing techniques, the quality of the processed image is determined by its accuracy. Accuracy can be quantified using several error metrics, such as maximum error, mean square error (MSE), and so on [23]. In this work, PSNR is used to quantify the acceptability of noisy image. It is measured in the unit of and determines the similarities between two images (e.g., input image and processed output image). PSNR value can be calculated by Equation (1) [23]:
where = is the mean square error between the error-free and the erroneous image, is the maximum image pixel value (e.g., 255 in 8-bit grayscale image), m and n represent the width and height of the target image in terms of the number of pixels, and and represent the pixel values of the error-free image and the erroneous/noisy image, respectively. For the gray scale images, MSE is determined based on their brightness values.
As seen from Equation (1), plays an important role in determining the accuracy of the image and the length of the SS. According to [11,19], high precision (in terms of accuracy) output can be achieved when an SC circuit operates on a large number of stochastic bit streams. Since each bit of an SS takes a clock cycle to be processed, computation time linearly increases with the increase in the size of the stochastic bit stream. Therefore, with increasing accuracy, computation time tends to increase. Note the computation time refers to the total number of clock cycles required to generate output SS. In physics, power is how fast energy is used or transmitted and power is calculated as the amount of energy divided by the time it took to use the energy. Its unit is the watt, which is one joule per second of energy used. Likewise, power is the amount of energy used per each unit time (i.e., 126 clock cycles) in a clocked digital circuits. Then, energy can be calculated by multiplying power by the total number of clock cycles used. Therefore, the number of clock cycles and energy consumption are proportional. In a conventional digital circuit designed to process data given in binary radix encoding, energy-performance scalable computing is quite limited, as the total number of clock cycles needed to process inputs to generate output is solely determined by how the circuit is designed and optimized. Also, power consumed per clock cycle is purely dependent upon the complexity of the circuit. Besides, Stochastic computing has much higher inherent potential for efficient utilization of energy-performance scalability. The term energy-performance scalability in this paper refers to the fact that when accuracy is high, energy consumption will be high. However, for many image processing applications, a desirable accuracy is more than enough. Therefore, savings in energy can be achieved for acceptable accuracy. If more clock cycles are used, more energy will be needed, but higher quality output will result and vice versa. Such an inherent tradeoff can be beneficial in certain application domains such as image processing and artificial neural networks where quick low-power approximation is desired. The proposed quasi-stochastic computing approach is to address the slow convergence problem of conventional Stochastic computing while offering excellent energy-performance scalability.
To prove that the proposed approach is viable, an edge detection scheme is performed on the gray scale image “clock.” The impact of computation time on accuracy and energy is depicted in Figure 3. As seen from the graph, the accuracy in terms of PSNR of the image and the energy consumption tends to increase linearly with the number of clock cycles. Hence, it is practical to choose the minimum number of clock cycles that can satisfy the minimum required accuracy for the best possible energy-performance balance. To address this energy-accuracy trade-off, we propose an energy-accuracy scalable EQSNG design that can determine the number of iterations based on the acceptable PSNR threshold for an image.
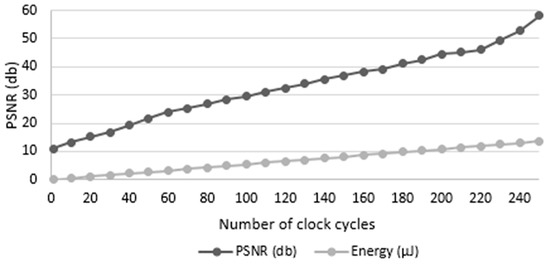
Figure 3.
Accuracy and energy consumption during edge detection of clock test image.
The acceptability of the target image can be achieved by just comparing the equivalent error rate with the corresponding acceptable error rate threshold. This acceptable error rate threshold is assumed to be a user-defined value in this work. The general design of the energy efficient QSNG model (EQSNG) is depicted in Figure 4. The optimal number of iterations is calculated based on the user-defined peak signal-to-noise ratio (PSNR).
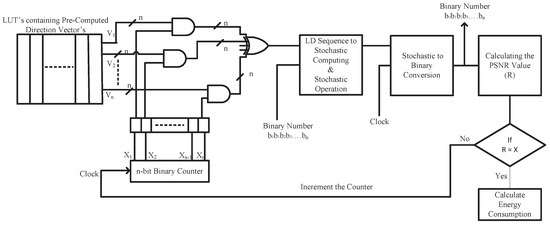
Figure 4.
Structure of EQSNG.
The process to estimate optimal number of iterations is shown in Algorithm 1. The first step is to store the pre-computed direction vectors in the random-access memory (e.g., look up tables of the FPGA). Then, each bit of n-bit directional vectors is multiplied with the n-bit binary counter output using an AND gate. The resulting binary numbers are XORed up to obtain the final LD sequence. This LD sequence is compared to the binary input value to generate an SS on which stochastic operations are performed. The resultant stochastic output is again converted to binary number at the stochastic binary conversion block. This post-processed binary output is processed in MATLAB to determine the image quality (i.e., accuracy).
| Algorithm 1: EQSNG Algorithm |
 |
To determine the image accuracy, the mean square error (MSE) that accurately measures the error in the reference image is calculated first. The resultant MSE value is used for calculating PSNR (). If the calculated is less than the user defined target PSNR value (), the counter is incremented and the whole process is carried out till the desired is achieved. Since the counter is incremented by increasing the clock cycles, the total energy consumption is calculated by multiplying the power by the number of clock cycles. As the proposed approach can converge at a much faster rate, they require few clock cycles to achieve the desired PSNR value, which in turn further reduces the energy consumption.
Hence, the proposed approach provides acceptable image quality with fewer clock cycles and less energy consumption. Compared to the conventional SC approach based on LFSR, the EQSNG methodology can generate an acceptable quality edge detection image with excellent energy efficiency. To demonstrate and verify the energy-performance scalability of the EQSNG approach, the proposed methodology is implemented on a stochastic edge detection circuit for 8-bit grayscale image processing. In the next section, the proposed methodology is applied to several test images and comparative results are presented and analyzed.
4. Simulation-Based Energy-Performance Scalability Analysis
This section compares the results for various test images implemented using conventional LFSR and EQSNG approaches. These test images on which edge detection is performed are shown in Figure 5, which are called clock, crowd, and aerial. The edge detection circuit based on Robert’s cross algorithm [5] was used for the proposed energy-performance scalability analysis. To study the impact of the proposed approach on energy consumption, target PSNR values are arbitrarily selected. Next, the computation time (i.e., number of clock cycles) required to achieve the specified accuracy is determined and corresponding energy consumption is calculated.

Figure 5.
Open source test images used for edge detection: (a) clock. (b) crowd. (c) aerial.
The circuits have been realized on a Xilinx Virtex 4 SF FPGA (XC4VLX15) device and synthesized using Xilinx ISE 12.1 design suite. The QSNG uses the LD sequence and distributed memory elements (LUTS) of the FPGAs for designing the SNGs. Therefore, an FPGA is used. The performance of the proposed technique has been extensively evaluated using a 8-bit grayscale images (i.e., each pixel value is represented using a stochastic bit-length of = 256 bits) as an example in this section. A cycle-accurate simulator has been implemented in MATLAB to generate simulation results for the proposed technique. The pixel values of the images were extracted using MATLAB and were given as the 8-bit binary input to the stochastic edge detection circuit. Then, the output extracted from the post-synthesis simulation results was processed in MATLAB to determine the accuracy.
To quantitatively demonstrate and verify the performance of the proposed approach, energy consumption is determined by using the following simulation parameters: 8-bit grayscale images and its desired PSNR value. Table 1 shows the number of clock cycles and energy consumed for achieving the desired quality of image. As per the results shown in the table, energy consumption for the proposed EQSNG methodology is significantly lower than the traditional approach (LFSR) for the same target PSNR. As seen from the Table 1, the number of clock cycles for EQSNG to achieve the desired quality of the image is considerably less than LFSRs. The proposed EQSNG implementation of the edge detection circuit reduces the computation time by a factor of 3.5 times on average when compared to LFSR based approach. For instance, to achieve a PSNR of 31.53 dB for the Aerial test image, the energy consumed by the EQSNG and LFSR approach are 0.14 J and 0.63 J, which is a substantial saving.

Table 1.
Table showing the no of clock cycles and energy consumption for various PNSR values.
To quantitatively demonstrate and verify the performance of the proposed approach, energy consumption is determined by using the following simulation parameters: 8-bit grayscale images and their desired PSNR value. Table 1 shows the number of clock cycles and amount of energy consumed for achieving the desired quality of image. As per the results shown in the table, energy consumption for the proposed EQSNG methodology is significantly lower than the traditional approach (LFSR) for the same target PSNR. As seen from Table 1, the number of clock cycles for EQSNG to achieve the desired quality of the image is considerably less than LFSRs. The values in Table 1, are obtained by designing both the LFSR and EQSNG models and verified via simulation studies.
The proposed EQSNG implementation of the edge detection circuit reduces the computation time by a factor of 3.5 times on average when compared to the LFSR based approach. For instance, to achieve a PSNR of 31.53 dB for the aerial test image, the energy consumed by the EQSNG and LFSR approach are 0.14 J and 0.63 J, which is a substantial saving. Therefore, the energy consumption reduces by 77.7%. Similarly, the energy consumed by LFSR and EQSNG methodologies to achieve a PSNR of 28 dB for the clock test image is 0.054 J and 0.05 J energy. Thus, the proposed approach reduces energy consumption by 12.2% as presented. Compared to the LFSR approach, for the Crowd test image with a PSNR of 40.30 dB, the EQSNG approach saves about 18.6% of energy. The, reduction in energy consumption for various PSNR values by using the proposed approach is depicted in Figure 6.
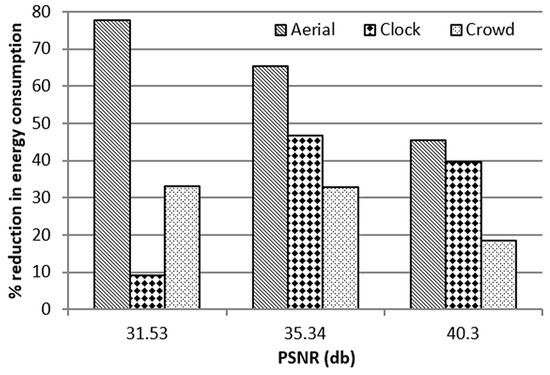
Figure 6.
Reduction in energy consumption for various PSNR values using EQSNG methodology compared to LFSR approach.
From Table 1, it should be noticed that as the PSNR (i.e., accuracy) increases the number (#) of clock cycles utilized also increases. Therefore, the higher the computation time, the better the quality of the image as illustrated in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, and Figure 12. These figures show that the proposed approach utilizes a smaller number of clock cycles to achieve the same accuracy as the LFSR approach due to faster stochastic value convergence. Therefore, using the proposed EQSNG methodology, execution time and energy consumed can be reduced while achieving an acceptable level of accuracy.

Figure 7.
Edge detection on the clock test image using the proposed EQSNG SC apporach: (a) PSNR = 22.2 dB; 4 clock cycles. (b) PSNR = 25.13 dB; 7 clock cycles. (c) PSNR = 28.12 dB; 10 clock cycles. (d) PSNR = 31.53 dB; 18 clock cycles. (e) PSNR = 35.34 dB; 35 clock cycles. (f) PSNR = 40.30 dB; 55 clock cycles.

Figure 8.
Edge detection on the clock test image using conventional LFSR-based SC apporach: (a) PSNR = 22.2 dB; 4 clock cycles. (b) PSNR = 25.13 dB; 10 clock cycles. (c) PSNR = 28.12 dB; 18 clock cycles. (d) PSNR = 31.53 dB; 37 clock cycles. (e) PSNR = 35.34 dB; 95 clock cycles. (f) PSNR = 40.30 dB; 151 clock cycles.

Figure 9.
Edge detection on the crowd test image using the proposed EQSNG SC apporach: (a) PSNR = 22.2 dB; 8 clock cycle. (b) PSNR = 25.13 dB; 13 clock cycles. (c) PSNR = 28.12 dB; 18 clock cycles. (d) PSNR = 31.53 dB; 28 clock cycles. (e) PSNR = 35.34 dB; 45 clock cycles. (f) PSNR = 40.30 dB; 80 clock cycles.

Figure 10.
Edge detection on the Crowd test image using conventional LSFR’s apporach: (a) PSNR = 22.2 dB; 14 clock cycles. (b) PSNR = 25.13 dB; 22 clock cycles. (c) PSNR = 28.12 dB; 50 clock cycles. (d) PSNR = 31.53 dB; 70 clock cycles. (e) PSNR = 35.34 dB; 112 clock cycles. (f) PSNR = 40.30 dB; 165 clock cycles.

Figure 11.
Edge detection on the aerial test image using EQSNGs SC apporach: (a) PSNR = 22.2 dB; 7 clock cycles. (b) PSNR = 25.13 dB; 10 clock cycles. (c) PSNR = 28.12 dB; 15 clock cycles. (d) PSNR = 31.53 dB; 26 clock cycles. (e) PSNR = 35.34 dB; 47 clock cycles. (f) PSNR = 40.30 dB; 77 clock cycles.

Figure 12.
Edge detection on the aerial test image using conventional LSFR’s apporach: (a) PSNR = 22.2 dB; 17 clock cycles. (b) PSNR = 25.13 dB; 23 clock cycles. (c) PSNR = 28.12 dB; 100 clock cycles. (d) PSNR = 31.53 dB; 198 clock cycles. (e) PSNR = 35.34 dB; 225 clock cycles. (f) PSNR = 40.30 dB; 248 clock cycles.
In summary, 12%–78% reduction in the energy consumption is observed. Moreover, compared to LFSR based approach, the proposed EQSNG implementation on average reduces the computation time by a factor of 2.5 times. This excellent energy-quality scalability of the proposed approach may also be beneficial to the other application domains (e.g., signal processing, machine vision, and deep learning) where efficient reduced-precision computation is desired.
5. Conclusions
In this paper, a novel EQSNG is introduced and verified via extensive simulation-based analysis where low computation time and energy consumption are achieved. The proposed approach is efficient enough to offer 12–60% reduction in execution time and a 12–78% decrease in energy consumption relative to the conventional LFSR counterpart. This considerable enhancement in terms of time and energy will further promote the viability of SC over conventional approaches in application domains such as image processing and machine learning where fast low-power approximation is desired.
Author Contributions
All authors contributed equally to this work.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alaghi, A.; Qian, W.; Hayes, J.P. The promise and challenge of stochastic computing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2017, 37, 1515–1531. [Google Scholar] [CrossRef]
- Gaines, B.R. Stochastic computing. In Proceedings of the Spring Joint Computer Conference, Atlantic City, NY, USA, 18–20 April 1967; ACM: New York, NY, USA, 1967; pp. 149–156. [Google Scholar]
- Gaines, B. Stochastic computing systems. In Advances in Information Systems Science; Springer: Berlin, Germany, 1969; pp. 37–172. [Google Scholar]
- Moons, B.; Verhelst, M. Energy-Efficiency and Accuracy of Stochastic Computing Circuits in Emerging Technologies. Emerg. Sel. Top. Circuits Syst. IEEE J. 2014, 4, 475–486. [Google Scholar] [CrossRef]
- Alaghi, A.; Li, C.; Hayes, J.P. Stochastic circuits for real-time image-processing applications. In Proceedings of the 50th Annual Design Automation Conference, Austin, TX, USA, 29 May–7 June 2013; ACM: New York, NY, USA, 2013; p. 136. [Google Scholar]
- Naderi, A.; Mannor, S.; Sawan, M.; Gross, W.J. Delayed stochastic decoding of LDPC codes. IEEE Trans. Signal Process. 2011, 59, 5617–5626. [Google Scholar] [CrossRef]
- Aliee, H.; Zarandi, H.R. Fault tree analysis using stochastic logic: A reliable and high speed computing. In Proceedings of the IEEE 2011 Proceedings-Annual Reliability and Maintainability Symposium (RAMS), Lake Buena Vista, FL, USA, 24–27 January 2011; pp. 1–6. [Google Scholar]
- Li, P.; Lilja, D.J. Using stochastic computing to implement digital image processing algorithms. In Proceedings of the 2011 IEEE 29th International Conference on Computer Design (ICCD), Amherst, MA, USA, 9–12 October 2011; pp. 154–161. [Google Scholar]
- Chang, Y.N.; Parhi, K. Architectures for digital filters using stochastic computing. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 2697–2701. [Google Scholar]
- Saraf, N.; Bazargan, K.; Lilja, D.J.; Riedel, M.D. IIR filters using stochastic arithmetic. In Proceedings of the 2014 IEEE Design, Automation and Test in Europe Conference and Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 1–6. [Google Scholar]
- Seva, R.; Metku, P.; Choi, M. Energy-Efficient FPGA-Based Parallel Quasi-Stochastic Computing. J. Low Power Electron. Appl. 2017, 7, 29. [Google Scholar] [CrossRef]
- Li, P.; Lilja, D.J. Accelerating the performance of stochastic encoding-based computations by sharing bits in consecutive bit streams. In Proceedings of the 2013 IEEE 24th International Conference on Application-Specific Systems, Architectures and Processors (ASAP), Washington, DC, USA, 5–7 June 2013; pp. 257–260. [Google Scholar]
- Ichihara, H.; Ishii, S.; Sunamori, D.; Iwagaki, T.; Inoue, T. Compact and accurate stochastic circuits with shared random number sources. In Proceedings of the 2014 32nd IEEE International Conference on Computer Design (ICCD), Seoul, Korea, 19–22 October 2014; pp. 361–366. [Google Scholar]
- Alaghi, A.; Hayes, J.P. A spectral transform approach to stochastic circuits. In Proceedings of the 2012 IEEE 30th International Conference on Computer Design (ICCD), Montreal, QC, Canada, 30 September–3 October 2012; pp. 315–321. [Google Scholar]
- Alaghi, A.; Hayes, J. STRAUSS: Spectral Transform Use in Stochastic Circuit Synthesis. IEEE Trans. Comput.-Aided Des. Integr. Circ. Syst. 2012, 34, 1770–1783. [Google Scholar] [CrossRef]
- Chen, T.H.; Hayes, J.P. Equivalence among Stochastic Logic Circuits and its Application to Synthesis. IEEE Trans. Emerg. Top. Comput. 2016, 7, 67–79. [Google Scholar] [CrossRef]
- Kwok, S.H.; Lam, E.Y. FPGA-based high-speed true random number generator for cryptographic applications. In Proceedings of the TENCON 2006—2006 IEEE Region 10 Conference, Hong Kong, China, 14–17 November 2006; pp. 1–4. [Google Scholar]
- Majzoobi, M.; Koushanfar, F.; Devadas, S. FPGA-Based True Random Number Generation Using Circuit Metastability with Adaptive Feedback Control; CHES; Springer: Berlin, Germany, 2011; pp. 17–32. [Google Scholar]
- Alaghi, A.; Hayes, J.P. Survey of stochastic computing. ACM Trans. Embed. Comput. Syst. (TECS) 2013, 12, 92. [Google Scholar] [CrossRef]
- Manohar, R. Comparing Stochastic and Deterministic Computing. Available online: https://www.computer.org/csdl/journal/ca/2015/02/07059235/13rRUx0gebQ (accessed on 15 November 2019).
- Alaghi, A.; Hayes, J.P. Fast and accurate computation using stochastic circuits. In Proceedings of the Conference on Design, Automation & Test in European Design and Automation Association, Dresden, Germany, 24–28 March 2014; p. 76. [Google Scholar]
- Wikipedia. Low-Discrepancy Sequence. Available online: https://en.wikipedia.org/wiki/Low-discrepancy_sequence (accessed on 15 November 2019).
- Hsieh, T.Y.; Peng, Y.H.; Ku, C.C. An Efficient Test Methodology for Image Processing Applications Based on Error-Tolerance. In Proceedings of the 2013 22nd Asian Test Symposium, Jiaosi Township, Taiwan, 18–21 November 2013; pp. 289–294. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).