Starting Framework for Analog Numerical Analysis for Energy-Efficient Computing
Abstract
:1. Introduction
2. Why Analog Numerical Analysis?
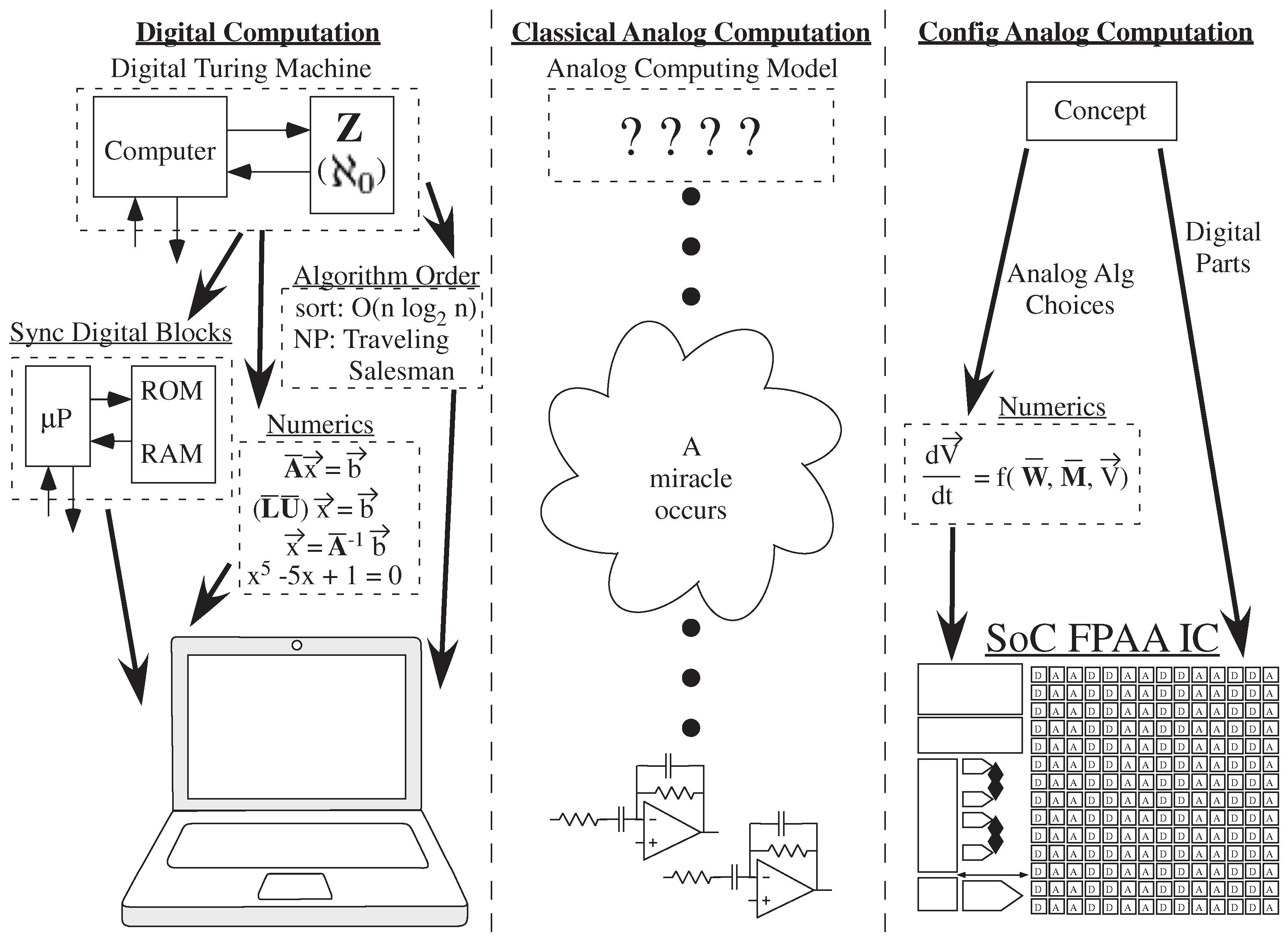
2.1. Digital Framework Enables Ubiquitous Numerical Computation
2.2. Analog Computing Has Arrived, But Lacks a Framework
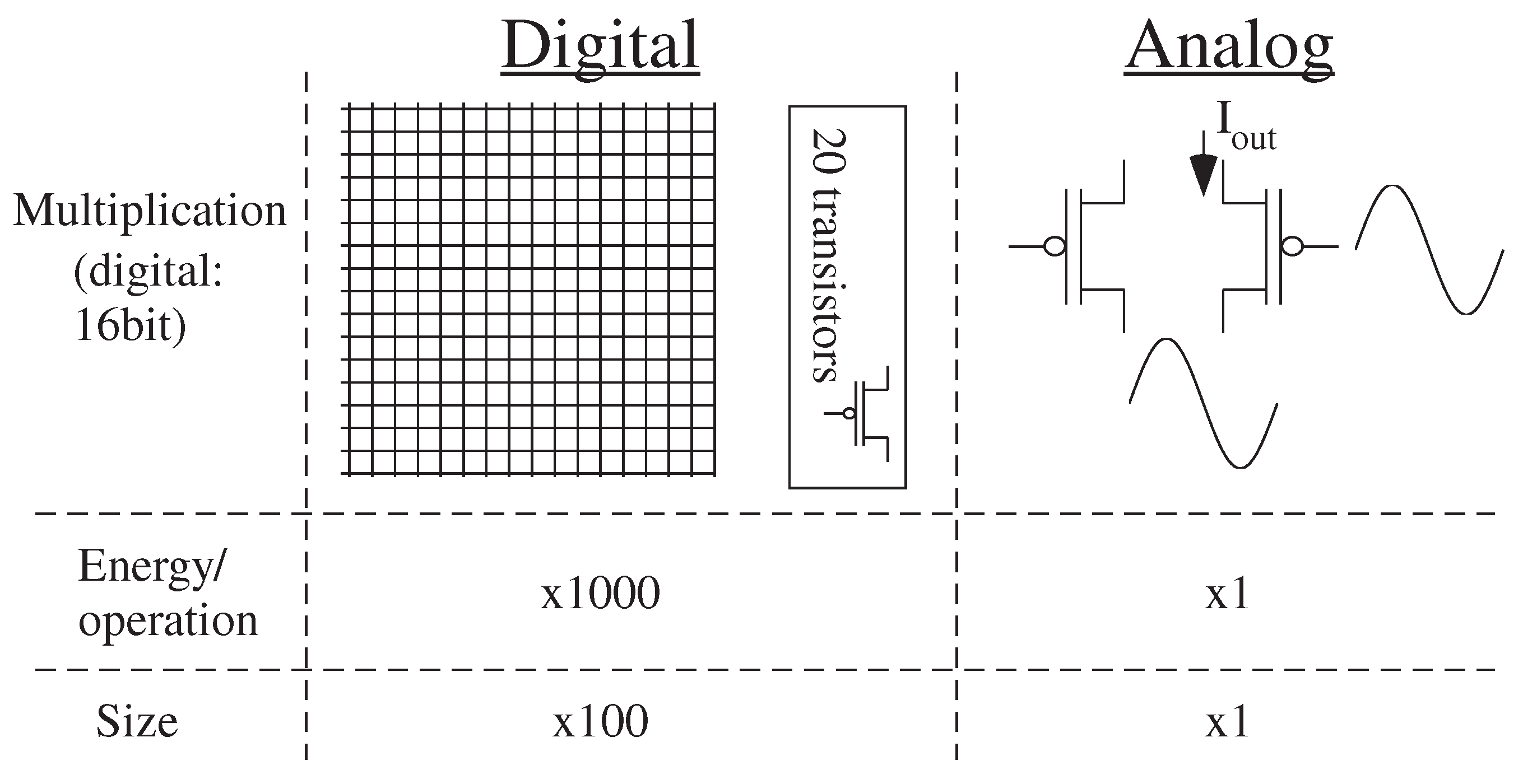
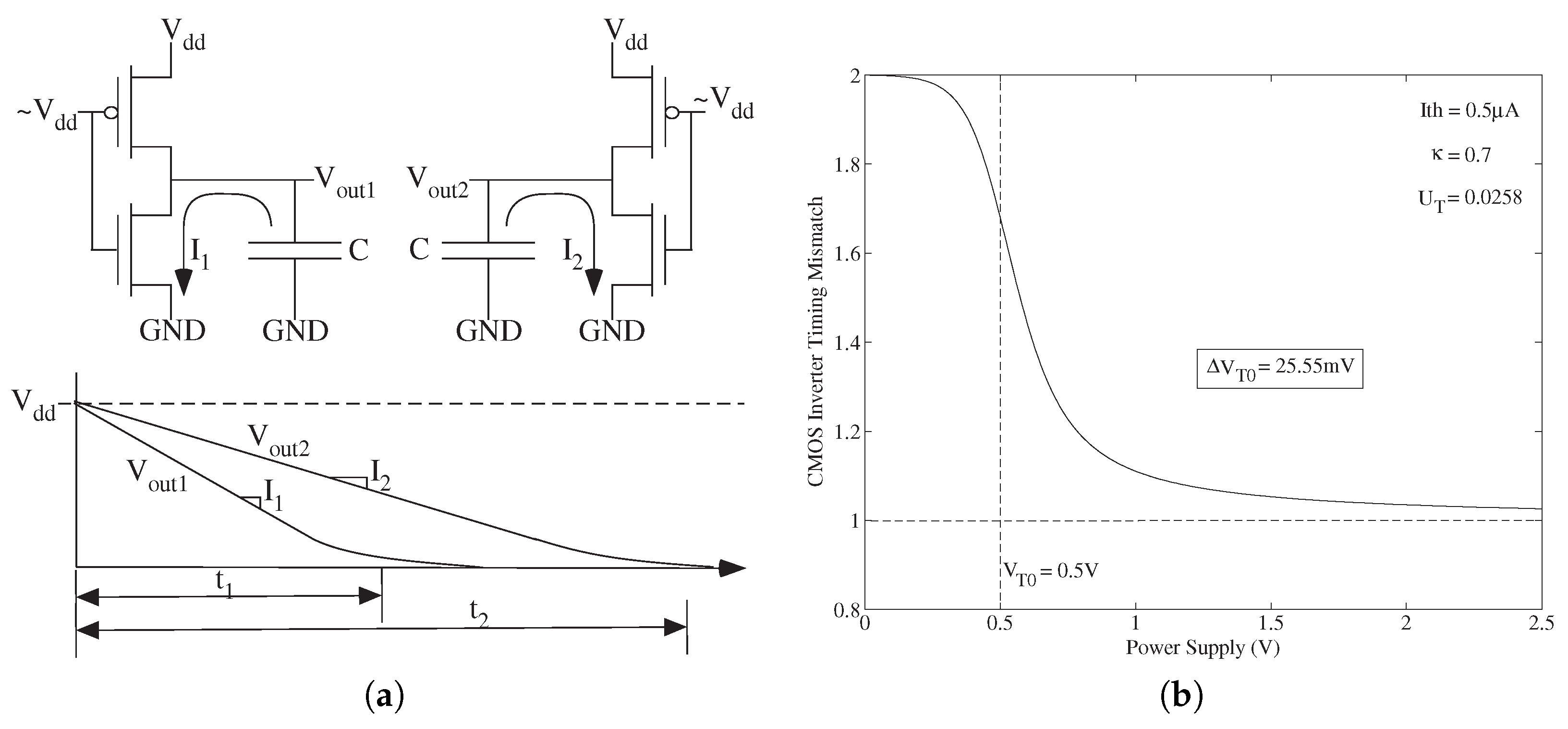
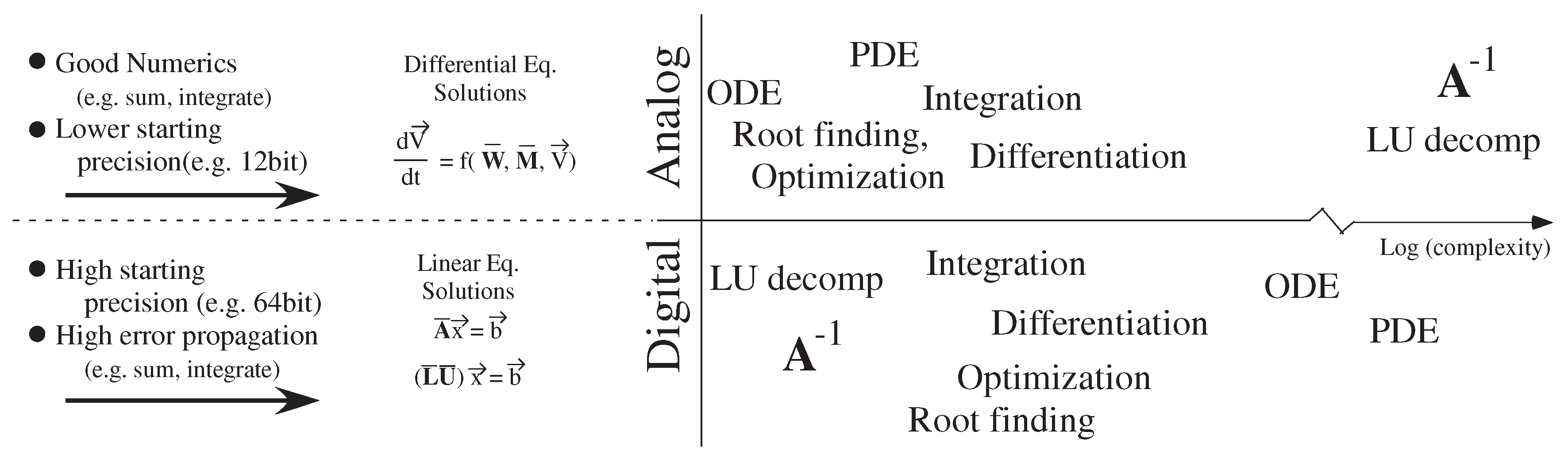
3. Digital Strength: Lower Cost Numerical Precision
4. Analog Strength: Better Numerical Operations
4.1. LU Decomposition as the Basis of Digital Numerics
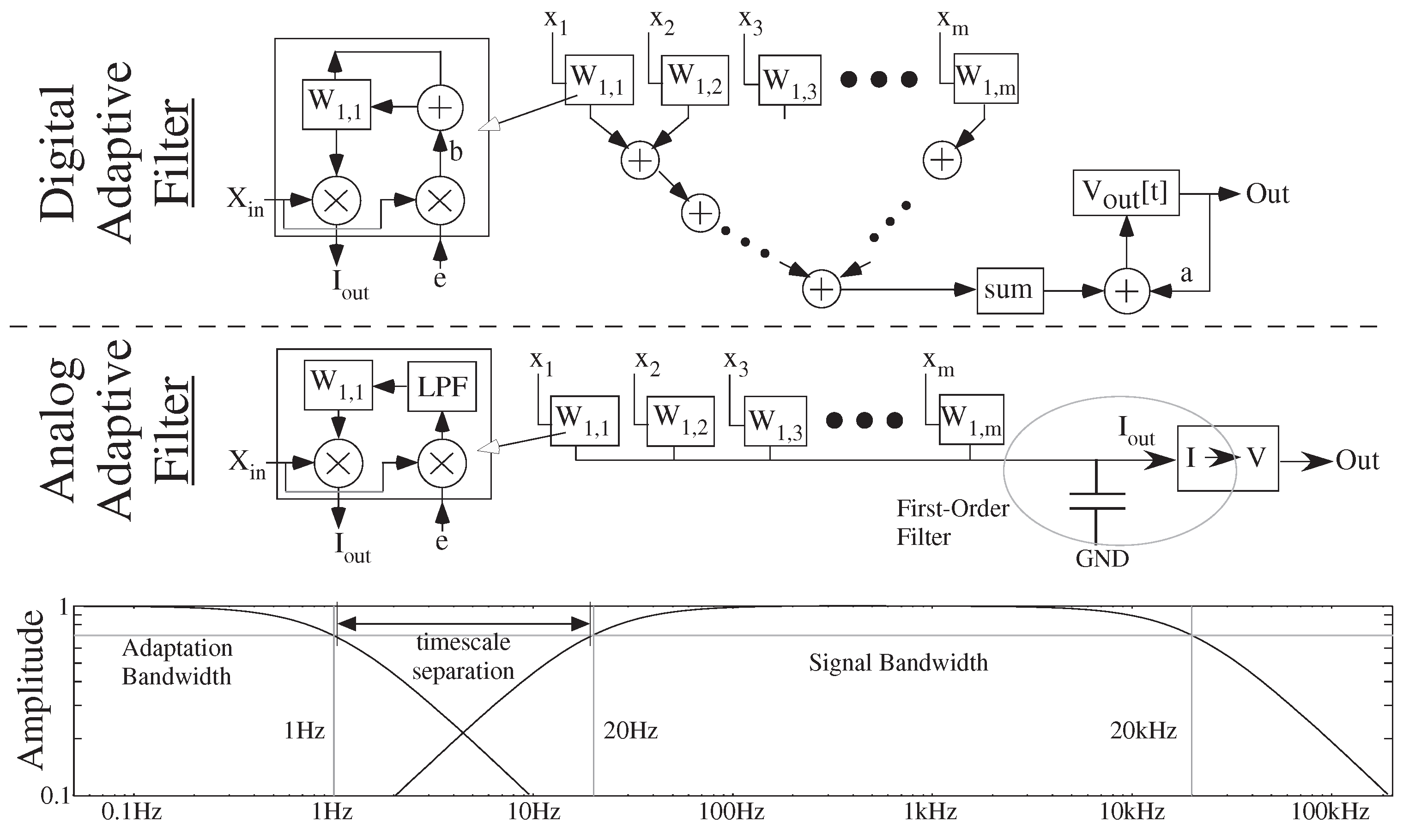
4.2. ODE Solutions as the Basis of Analog Numerics
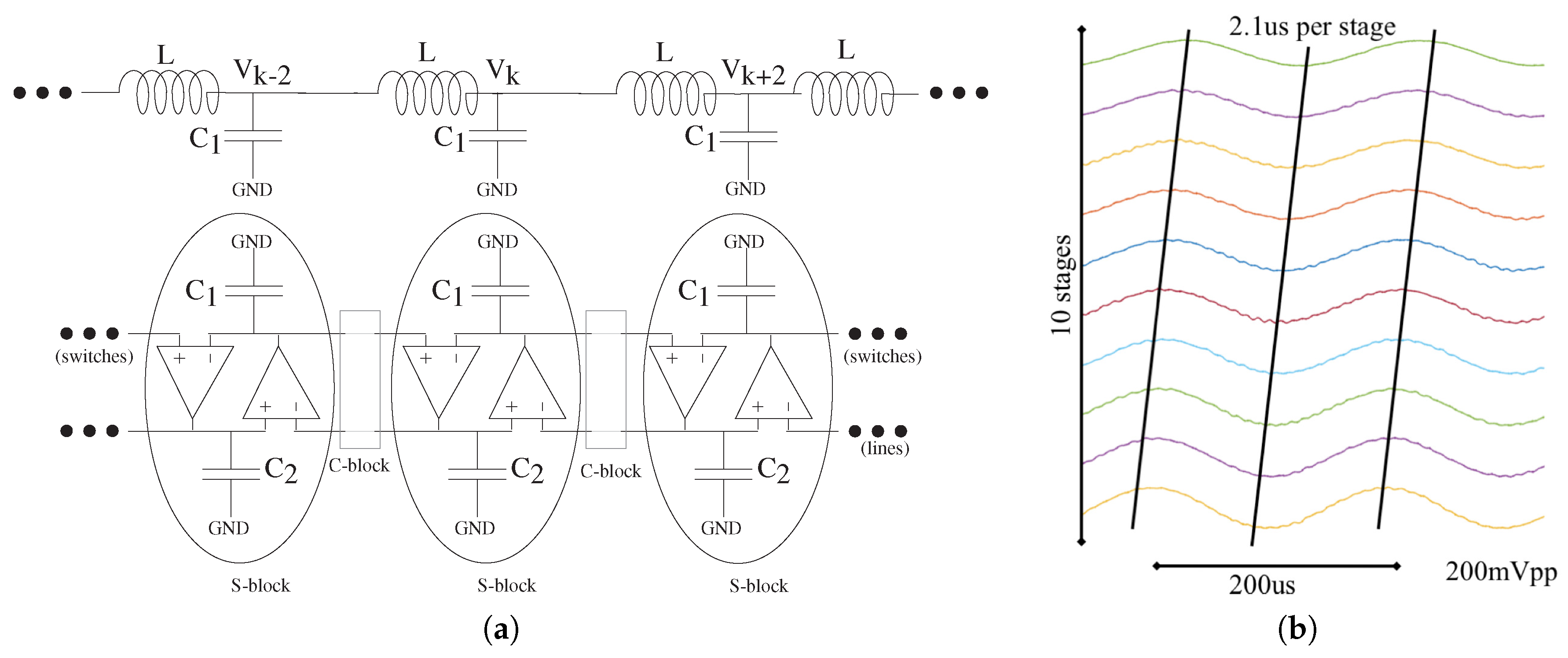
4.3. Analog Numerics for PDE Solutions
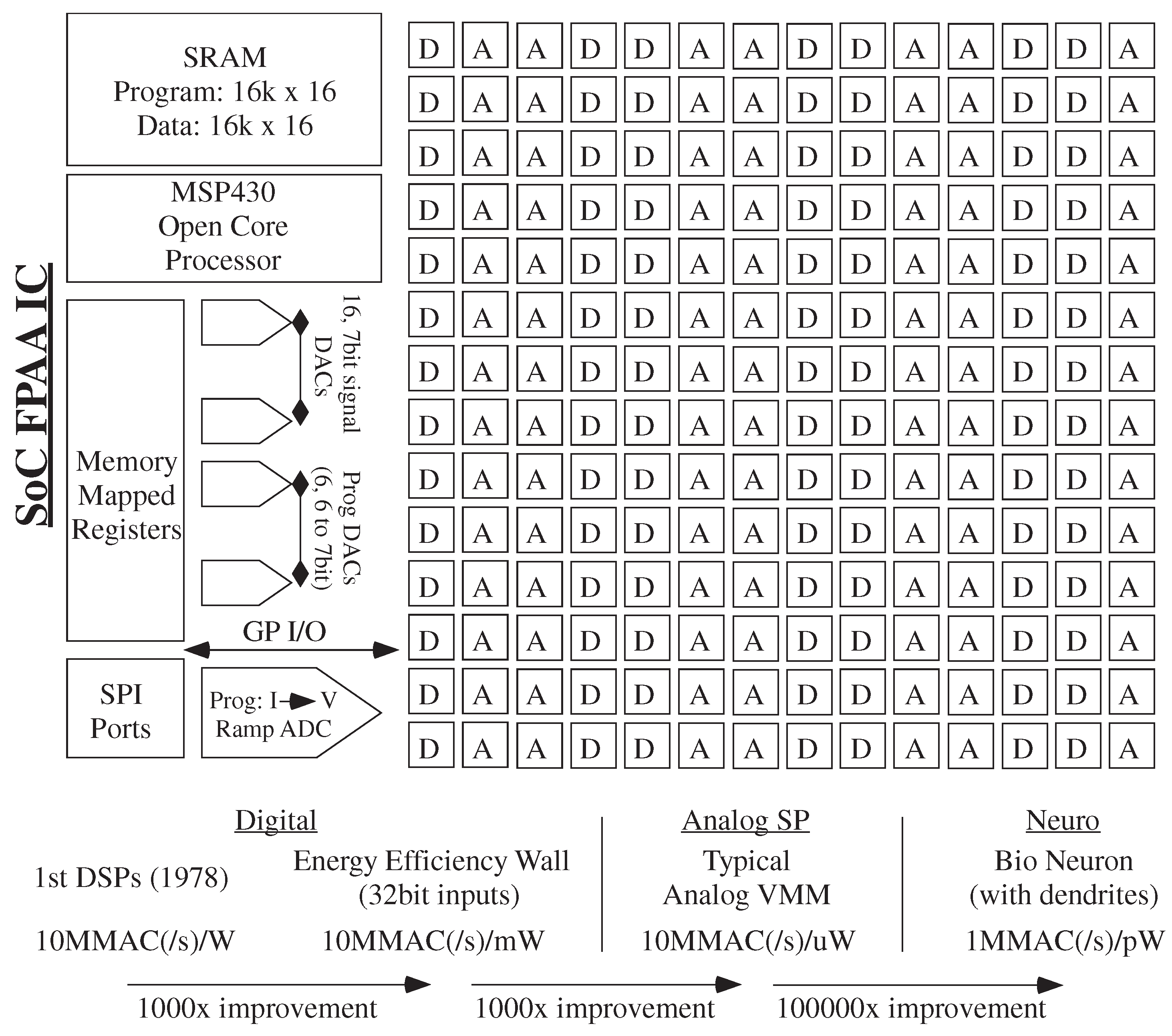
5. Analog Strength: Computational Effort (Energy) as a Metric for Digital and Analog Numerical Computation
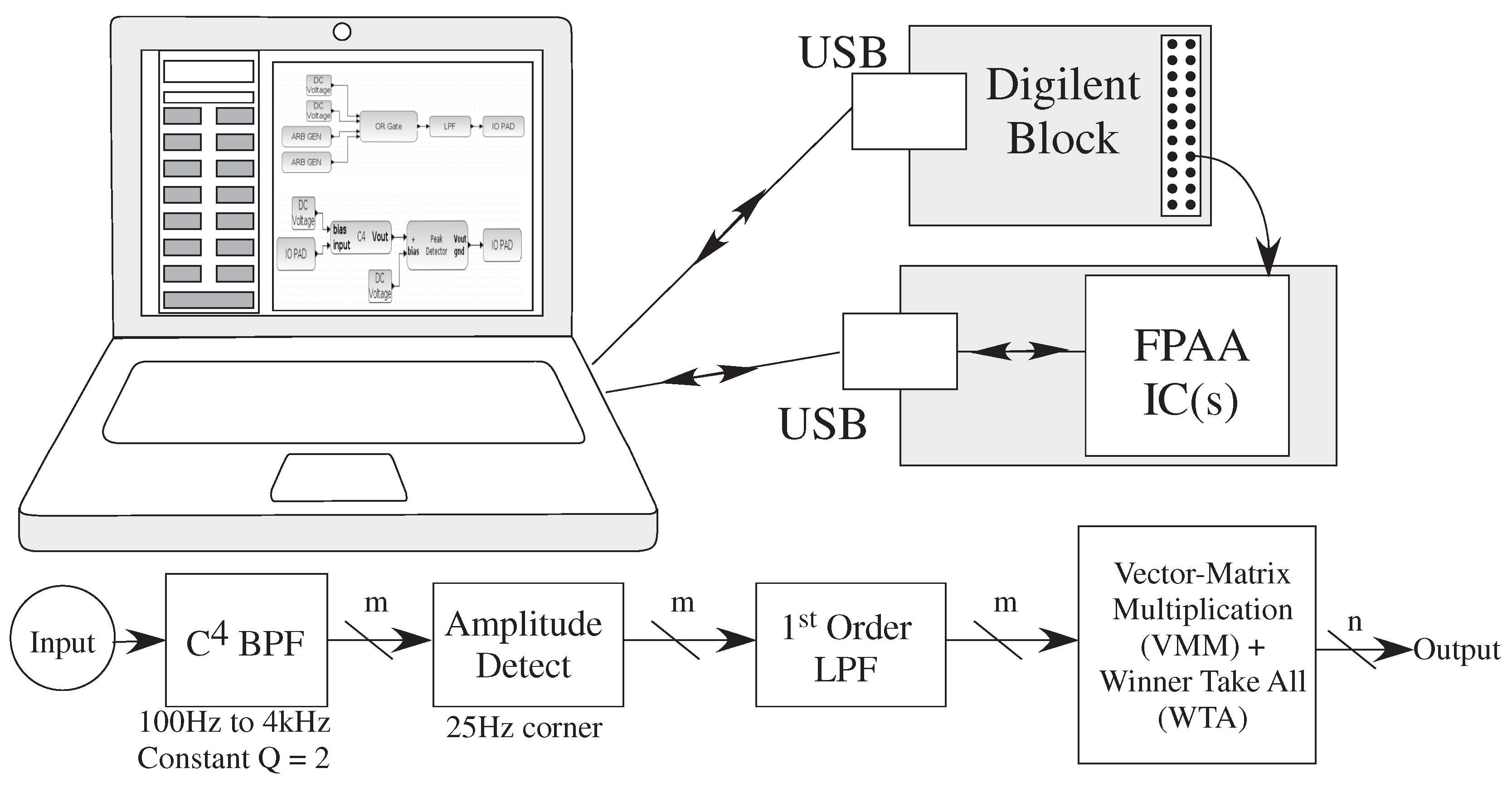
6. Simulation Tool Impact of Analog and Digital Numerics
7. Comparing Analog and Digital Numerical Analysis Complexity
8. Summary and Discussion
Acknowledgments
Conflicts of Interest
References
- George, S.; Kim, S.; Shah, S.; Hasler, J.; Collins, M.; Adil, F.; Wunderlich, R.; Nease, S.; Ramakrishnan, S. A Programmable and Configurable Mixed-Mode FPAA SoC. IEEE Trans. Very Large Scale Integr. Syst. 2016, 24, 2253–2261. [Google Scholar] [CrossRef]
- Wolf, W. Hardware-software co-design of embedded systems. Proc. IEEE 1994, 82, 967–989. [Google Scholar] [CrossRef]
- Jerraya, A.A.; Wolf, W. Hardware/Software Interface Codesign for Embedded Systems. IEEE Comput. 2005, 38, 63–69. [Google Scholar] [CrossRef]
- Teich, J. Hardware/Software Codesign: The Past, the Present, and Predicting the Future. Proc. IEEE 2012, 100, 1411–1430. [Google Scholar] [CrossRef]
- Sampson, A.; Bornholt, J.; Ceze, L. Hardware—Software Co-Design: Not Just a Cliché. In Advances in Programming Languages (SNAPL—15); Leibniz-Zentrum für Informatik: Wadern, Germany, 2015; pp. 262–273. [Google Scholar]
- Rossi, D.; Mucci, C.; Pizzotti, M.; Perugini, L.; Canegallo, R.; Guerrieri, R. Multicore Signal Processing Platform with Heterogeneous Configurable hardware accelerators. IEEE Trans. Very Large Scale Integr. Syst. 2014, 22, 1990–2003. [Google Scholar] [CrossRef]
- Zhao, Q.; Amagasaki, M.; Iida, M.; Kuga, M.; Sueyoshi, T. An Automatic FPGA Design and Implementation Framework. In Proceedings of the 23rd International Conference on Field Programmable Logic and Applications (FPL), Porto, Portugal, 2–4 September 2013; pp. 1–4. [Google Scholar]
- Weinhardt, M.; Krieger, A.; Kinder, T. A Framework for PC Applications with Portable and Scalable FPGA Accelerators. In Proceedings of the International Conference on Reconfigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 9–11 December 2013; pp. 1–6. [Google Scholar]
- Marr, B.; Degnan, B.; Hasler, P.; Anderson, D. Scaling Energy Per Operation via an Asynchronous Pipeline. IEEE Trans. Very Large Scale Integr. Syst. 2013, 21, 147–151. [Google Scholar] [CrossRef]
- Degnan, B.; Marr, B.; Hasler, J. Assessing trends in performance per Watt for signal processing applications. IEEE Trans. Very Large Scale Integr. Syst. 2016, 24, 58–66. [Google Scholar] [CrossRef]
- Mead, C. Neuromorphic electronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef]
- Frantz, G.; Wiggins, R. Design case history: Speak and spell learns to talk. IEEE Spectr. 1982, 19, 45–49. [Google Scholar] [CrossRef]
- Hasler, J. Opportunities in Physical Computing driven by Analog Realization. In Proceedings of the IEEE International Conference on IEEE ICRC, San Deigo, CA, USA, 17–19 October 2016; pp. 1–8. [Google Scholar]
- Conte, S.D.; de Boor, C. Elementary Numerical Analysis: An Algorithmic Approach; McGraw Hill: New York, NY, USA, 1980. [Google Scholar]
- Butcher, J.C. Numerical Analysis of Ordinary Differential Equations: Runga Kutta and General Linear Methods; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Mitchell, A.R.; Griffiths, D.F. The Finite Difference Method in Partial Differential Equations; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Turing, R. On Computable Numbers. Proc. Lond. Math. Soc. 1937, 2, 230–265. [Google Scholar] [CrossRef]
- Mead, C.; Conway, L. VLSI Design; Addison Wesley: Boston, MA, USA, 1980. [Google Scholar]
- MacKay, D.M.; Fisher, M.E. Analogue Computing at Ultra-High Speed: An Experimental and Theoretical Study; John Wiley and Sons: New York, NY, USA, 1962. [Google Scholar]
- Karplus, W.J. Analog Simulation: Solution of Field Problems; McGraw Hill: New York, NY, USA, 1958. [Google Scholar]
- MacLennan, B.J. A Review of Analog Computing; Technical Report for University of Tennessee: Knoxville, TN, USA, 2007. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J. Neurons with graded responses have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [PubMed]
- Mead, C. Analog VLSI and Neural Systems; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Hasler, P.; Diorio, C.; Minch, B.A.; Mead, C.A. Single transistor learning synapses. In Advances in Neural Information Processing Systems 7; Tesauro, G., Touretzky, D.S., Todd, K.L., Eds.; MIT Press: Cambridge, MA, USA, 1994; pp. 817–824. [Google Scholar]
- Kim, S.; Hasler, J.; George, S. Integrated Floating-Gate Programming Environment for System-Level ICs. IEEE Trans. Very Large Scale Integr. Syst. 2016, 24, 2244–2252. [Google Scholar] [CrossRef]
- Srinivasan, V.; Serrano, G.J.; Gray, J.; Hasler, P. A precision CMOS amplifier using floating-gate transistors for offset cancellation. IEEE J. Solid-State Circuits 2007, 42, 280–291. [Google Scholar] [CrossRef]
- Srinivasan, V.; Serrano, G.; Twigg, C.M.; Hasler, P. A floating-gate- based programmable CMOS reference. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 3448–3456. [Google Scholar] [CrossRef]
- Hasler, P. Continuous-time feedback in floating-gate MOS circuits. IEEE Trans. Circuits Syst. Analog Digit. Signal Process. 2001, 48, 56–64. [Google Scholar] [CrossRef]
- Hasler, P.; Minch, B.; Diorio, C. An autozeroing floating-gate amplifier. IEEE Trans. Circuits Syst. Analog Digit. Signal Process. 2001, 48, 74–82. [Google Scholar] [CrossRef]
- Brink, S.; Hasler, J.; Wunderlich, R. Adaptive floating-gate circuit enabled large-scale FPAA. IEEE Trans. Very Large Scale Integr. Syst. 2014, 22, 2307–2315. [Google Scholar] [CrossRef]
- Laiho, M.; Hasler, J.; Zhou, J.; Du, C.; Lu, W.; Lehtonen, E.; Poikonen, J. FPAA/memristor hybrid computing infrastructure. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 906–915. [Google Scholar] [CrossRef]
- Hasler, J.; Shah, S. Reconfigurable Analog PDE Computation for Baseband and RF Computation. In Proceedings of the GOMAC, Reno, NV, USA, 20–23 March 2017. [Google Scholar]
- Ozalevli, E.; Huang, W.; Hasler, P.E.; Anderson, D.V. A reconfigurable mixed-signal VLSI implementation of distributed arithmetic used for finite impulse response filtering. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 510–521. [Google Scholar] [CrossRef]
- Gregorian, R.; Temes, G.C. Analog MOS Integrated Circuits for Signal Processing; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar]
- Ramakrishnan, S.; Wunderlich, R.; Hasler, J.; George, S. Neuron array with plastic synapses and programmable dendrites. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 631–642. [Google Scholar] [CrossRef] [PubMed]
- Wunderlich, R.; Adil, F.; Hasler, P. Floating gate-based field programmable mixed-signal array. IEEE Trans. Very Large Scale Integr. Syst. 2013, 21, 1496–1505. [Google Scholar] [CrossRef]
- Schlottmann, C.; Hasler, J. High-level modeling of analog computational elements for signal processing applications. IEEE Trans. Very Large Scale Integr. Syst. 2014, 22, 1945–1953. [Google Scholar] [CrossRef]
- Collins, M.; Hasler, J.; George, S. An Open-Source Toolset Enabling Analog–Digital Software Codesign. J. Low Power Electron. Appl. 2016, 6, 3. [Google Scholar] [CrossRef]
- Hasler, J.; Kim, S.; Shah, S.; Adil, F.; Collins, M.; Koziol, S.; Nease, S. Transforming Mixed-Signal Circuits Class through SoC FPAA IC, PCB, and Toolset. In Proceedings of the IEEE European Workshop on Microelectronics Education, Southampton, UK, 11–13 May 2016. [Google Scholar]
- Hasler, J.; Kim, S.; Adil, F. Scaling Floating-Gate Devices predicting behavior for Programmable and Configurable Circuits and Systems. J. Low Power Electron. Appl. 2016, 6, 13. [Google Scholar] [CrossRef]
- Hasler, J.; Shah, S. Learning for VMM + WTA Embedded Classifiers; GOMAC: Orlando, FL, USA, March 2016. [Google Scholar]
- Hasler, J.; Marr, H.B. Finding a roadmap to achieve large neuromorphic hardware systems. Front. Neurosci. 2013, 7. [Google Scholar] [CrossRef] [PubMed]
- Hall, T.; Twigg, C.; Gray, J.; Hasler, P.; Anderson, D. Large-scale Field-Programmable Analog Arrays for analog signal processing. IEEE Trans. Circuits Syst. 2005, 52, 2298–2307. [Google Scholar] [CrossRef]
- Peng, S.Y.; Gurun, G.; Twigg, C.M.; Qureshi, M.S.; Basu, A.; Brink, S.; Hasler, P.E.; Degertekin, F.L. A large-scale Reconfigurable Smart Sensory Chip. In Proceedings of the IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 2145–2148. [Google Scholar]
- Twigg, C.M.; Gray, J.D.; Hasler, P. Programmable floating gate FPAA switches are not dead weight. In Proceedings of the IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 27–30 May 2007; pp. 169–172. [Google Scholar]
- Schlottmann, C.; Hasler, P. A highly dense, low power, programmable analog vector-matrix multiplier: The FPAA implementation. IEEE J. Emerg. Sel. Top. Circuits Syst. 2011, 1, 403–411. [Google Scholar] [CrossRef]
- Rumberg, B.; Graham, D.W. Reconfiguration Costs in Analog Sensor Interfaces for Wireless Sensing Applications. In Proceedings of the International Midwest Symposium on Circuits and Systems (MWSCAS), Columbus, OH, USA, 4–7 August 2013; pp. 321–324. [Google Scholar]
- Guo, N.; Huang, Y.; Mai, T.; Patil, S.; Cao, C.; Seok, M.; Sethumadhavan, S.; Tsividis, Y. Energy-efficient hybrid analog/digital approximate computation in continuous time. IEEE J. Solid-State Circuits 2016, 51, 1514–1524. [Google Scholar] [CrossRef]
- Shyu, J.B.; Temes, G.C.; Krummenacher, F. Random error effects in matched MOS capacitors and current sources. IEEE J. Solid-State Circuits 1984, 19, 948–956. [Google Scholar] [CrossRef]
- Lyon, R.F.; Mead, C. An analog electronic cochlea. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1119–1134. [Google Scholar] [CrossRef]
- Watts, L.; Kerns, D.A.; Lyon, R.F.; Mead, C.A. Improved implementation of the silicon cochlea. IEEE J. Solid-State Circuits 1992, 27, 692–700. [Google Scholar] [CrossRef]
- Van Schaik, A.; Fragniere, E.; Vittoz, E.A. Improved silicon cochlea using compatible lateral bipolar transistors. In Neural Information Processing Systems; Touretzky, D.S., Hasselmo, M.E., Eds.; MIT Press: Cambridge, MA, USA, 1996; pp. 671–677. [Google Scholar]
- Hosticka, B.J. Performance comparison of analog and digital circuits. Proc. IEEE 1985, 73, 25–29. [Google Scholar] [CrossRef]
- Vittoz, E.A. Future of analog in the VLSI environment. In Proceedings of the International Symposium on Circuits and Systems, New Orleans, LA, USA, 1–3 May 1990; Volume 2, pp. 1347–1350. [Google Scholar]
- Sarpeshkar, R. Analog Versus Digital: Extrapolating from Electronics to Neurobiology. Neural Comput. 1998, 10, 1601–1638. [Google Scholar] [CrossRef] [PubMed]
- Abshire, P.A. Sensory Information Processing under Physical Constraints. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2001. [Google Scholar]
- Hasler, P.; Smith, P.; Graham, D.; Ellis, R.; Anderson, D. Analog floating-gate, on-chip auditory sensing system interfaces. IEEE Sens. J. 2005, 5, 1027–1034. [Google Scholar] [CrossRef]
- Vittoz, E.A. Low-power design: Ways to approach the limits. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 6–18 February 1994; pp. 14–18. [Google Scholar]
- Sarpeshkar, R.; Delbruck, T.; Mead, C. White noise in MOS transistors and resistors. IEEE Circuits Devices Mag. 1993, 9, 23–29. [Google Scholar] [CrossRef]
- Kim, S.; Shah, S.; Hasler, J. Calibration of Floating-Gate SoC FPAA System. IEEE Trans. Very Large Scale Integr. Syst. 2017. in Press. [Google Scholar]
- Shapero, S.; Hasler, P. Mismatch characterization and calibration for accurate and automated analog design. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 548–556. [Google Scholar] [CrossRef]
- Vittoz, E.A. Analog VLSI Signal Processing: Why, Where and How? J. VLSI Signal Process. 1994, 8, 27–44. [Google Scholar] [CrossRef]
- Dongarra, J.J.; Luszczek, P.; Petitet, A. The LINPACK Benchmark: Past, present and future. Concurr. Comput. Pract. Exp. 2003, 15, 803–820. [Google Scholar] [CrossRef]
- Widrow, B. Adaptive Filters I: Fundamentals; Technical Report No. 6764-6; Stanford University: Stanford, CA, USA, 1966. [Google Scholar]
- Widrow, B.; Lehr, M.A. 30 Years of Adaptive Neural Networks: Perceptrons, Madaline, and Backpropagation. Proc. IEEE 1990, 78, 1415–1442. [Google Scholar] [CrossRef]
- Schneider, C.; Card, H. CMOS implementation of analog hebbian synaptic learning circuits. In Proceedings of the IEEE IJCNN-91-Seattle International Joint Conference on Neural Networks, Seattle, WA, USA, 8–12 July 1991; pp. 437–442. [Google Scholar]
- Hasler, P.; Akers, L. Circuit implementation of trainable neural networks employing both supervised and unsupervised techniques. In Proceedings of the IEEE International Joint Conference on Neural Networks, San Diego, CA, USA, 10–13 May 1992; pp. 1565–1568. [Google Scholar]
- Hasler, P.; Dugger, J. An analog floating-gate node for supervised learning. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 834–845. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Hasler, J. Vector-Matrix Multiply and WTA as an Analog Classifier. IEEE Trans. Very Large Scale Integr. Syst. 2014, 22, 353–361. [Google Scholar] [CrossRef]
- Morton, K.W.; Mayers, D.F. Numerical Solution of Partial Differential Equations; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- George, S.; Hasler, J.; Koziol, S.; Nease, S.; Ramakrishnan, S. Low power dendritic computation for wordspotting. J. Low Power Electron. Appl. 2013, 3, 73–98. [Google Scholar] [CrossRef]
- Koziol, S.; Brink, S.; Hasler, J. A neuromorphic approach to path planning using a reconfigurable neuron array IC. IEEE Trans. Very Large Scale Integr. Syst. 2014, 22, 2724–2737. [Google Scholar] [CrossRef]
- Koziol, S.; Wunderlich, R.; Hasler, J.; Stilman, M. Single-Objective Path Planning for Autonomous Robots Using Reconfigurable Analog VLSI. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1301–1314. [Google Scholar] [CrossRef]
- Nease, S.; George, S.; Hasler, P.; Koziol, S.; Brink, S. Modeling and implementation of voltage-mode CMOS dendrites on a reconfigurable analog platform. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley: Hoboken, NJ, USA, 1973. [Google Scholar]
- Kevorkian, J.; Cole, J.D. Perturbation Methods in Applied Mathematics; Springer: New York, NJ, USA, 1981. [Google Scholar]
- Asadi, P.; Navi, K. A New Low Power 32 × 32-bit Multiplier. World Appl. Sci. J. 2007, 2, 341–347. [Google Scholar]
- Fuketa, H.; Iida, S.; Yasufuku, T.; Takamiya, M.; Nomura, M.; Shinohara, H.; Sakurai, T. A Closed-form Expression for Estimating Minimum Operating Voltage (VDDmin) of CMOS Logic Gates. In Proceedings of the Design Automation Conference, San Diego, CA, USA, 5–10 June 2011; pp. 984–989. [Google Scholar]
- Fuketa, H.; Yasufuku, T.; Iida, S.; Takamiya, M.; Nomura, M.; Shinohara, H.; Sakurai, T. Device-Circuit Interactions in Extremely Low Voltage CMOS Designs. In Proceedings of the 2011 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 5–7 December 2011; pp. 559–562. [Google Scholar]
- Degnan, B.P.; Wunderlich, R.B.; Hasler, P. Programmable floating-gate techniques for CMOS inverters. In Proceedings of the IEEE International Symposium on Circuits and Systems, Kobe, Japan, 23–26 May 2005; pp. 2441–2444. [Google Scholar]
- Enz, C.C.; Krummenacher, F.; Vittoz, E.A. An analytical MOS transistor model valid in all regions of operation and dedicated to low-voltage and low-current applications. Analog Integr. Circuits Signal Process. 1995, 8, 83–114. [Google Scholar] [CrossRef]
- Pelgrom, M.J.M.; Duinmaijer, A.C.J.; Welbers, A.P.G. Matching Properties of MOS Transistors. IEEE J. Solid State Circuits 1989, 24, 1433–1440. [Google Scholar] [CrossRef]
- Adil, F.; Serrano, G.; Hasler, P. Offset removal using floating-gate circuits for mixed-signal systems. In Proceedings of the Southwest Symposium on Mixed-Signal Design, Las Vegas, NV, USA, 23–25 February 2003; pp. 190–195. [Google Scholar]
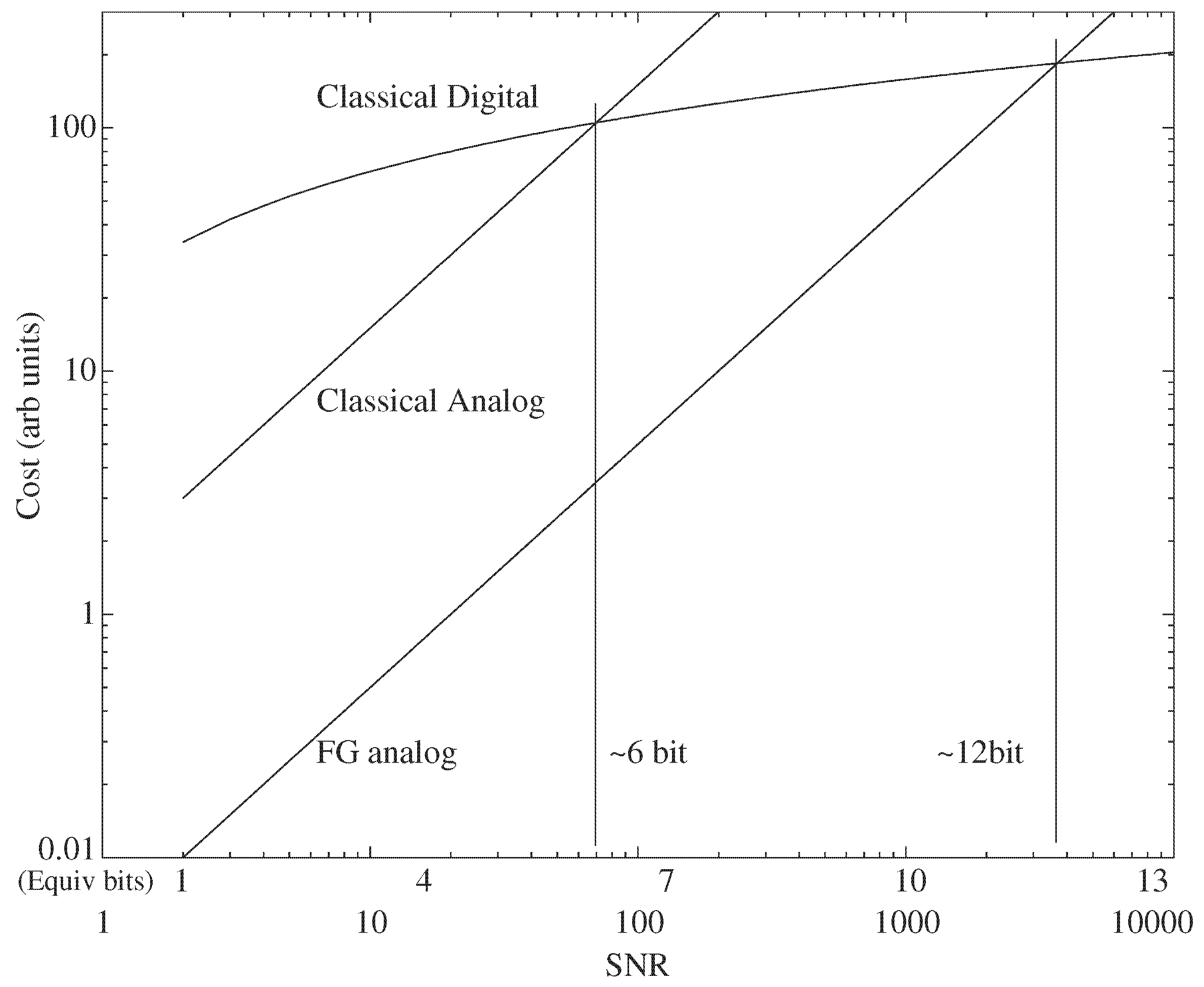
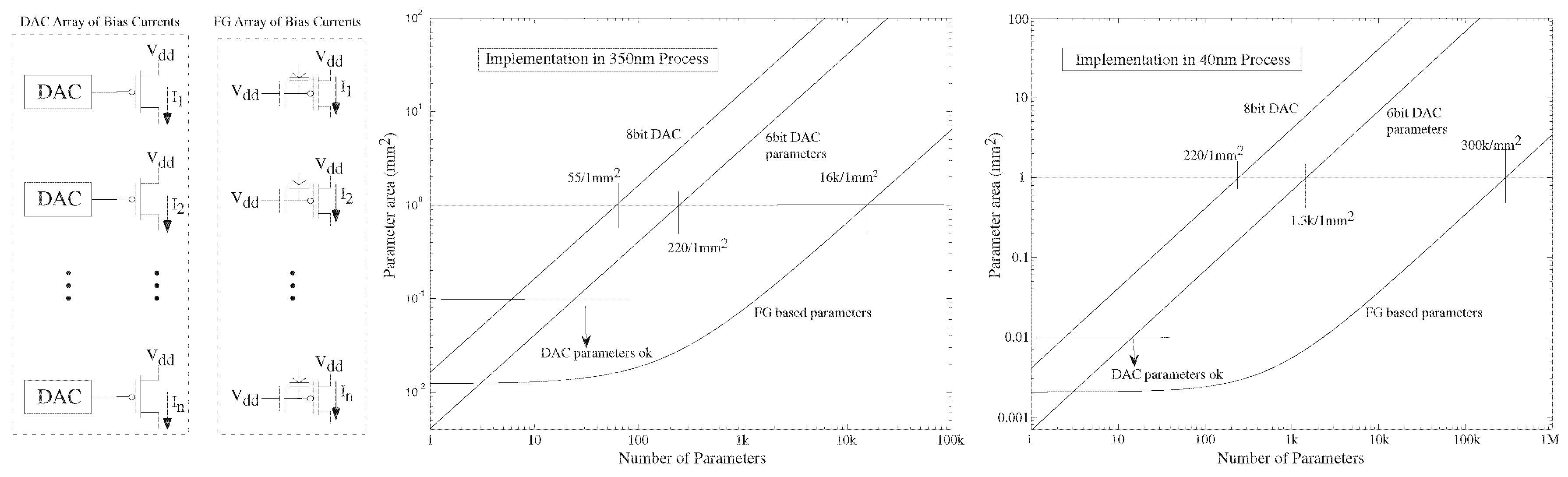
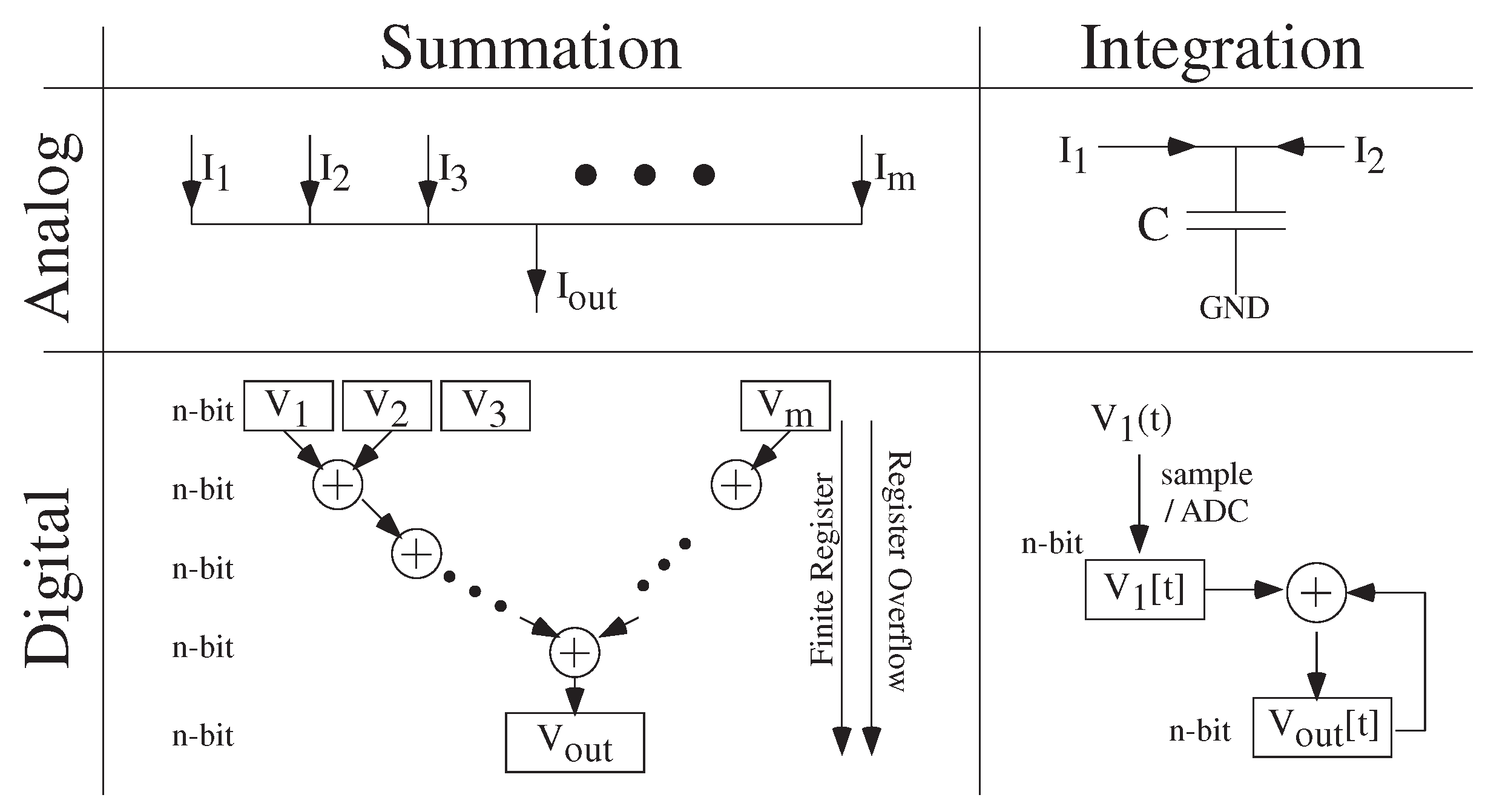
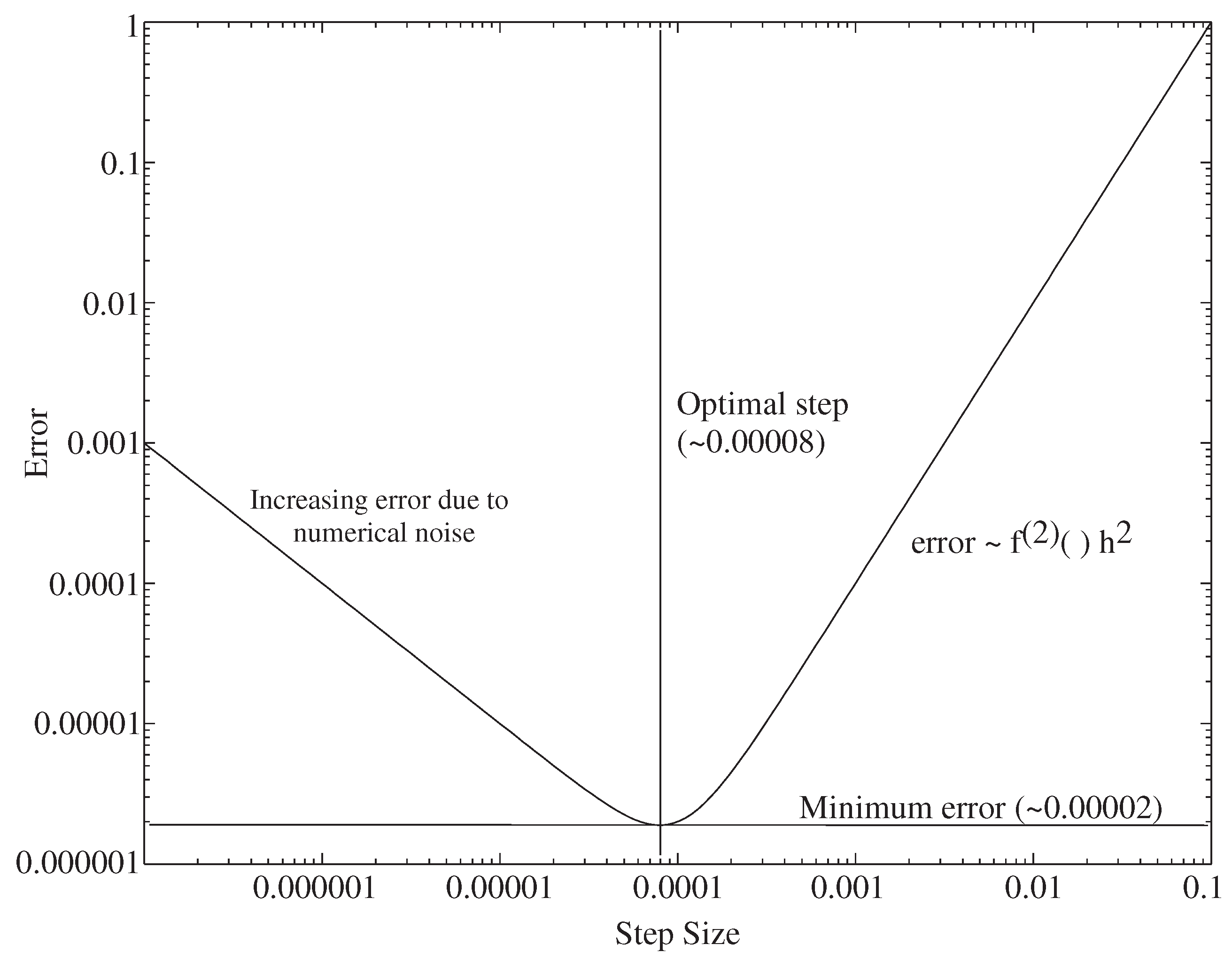
| Digital | Analog | |
|---|---|---|
| Precision | High starting precision, low cost adding more | lower starting precision (e.g., 10, 12, 14 bit) |
| Summation Noise | High numerical noise accumulation (summation) | ideal summation |
| Latency | computational latency (need for pipelining) | minimal latency |
| Computational Efficiency (VMM) | 10 MMAC (/s)/mW (32 bit) | 10 MMAC (/s)/W (×1000, 12 bit) |
| Intellectual Tradition | Long numerical tradition | a few artistic experts, sometimes agree |
| Digital Strength | Analog Strength | |
|---|---|---|
| Lower Cost Numerical Precision | X | FG helps |
| Low Error Numerical Operations | X | |
| Core Numerical Algorithm | LU decomposition | ODE solutions |
| Computational Energy Required | X | |
| Designer Knowledge, Number | Tools now | |
| of Designers, CAD tools | X | being developed |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasler, J. Starting Framework for Analog Numerical Analysis for Energy-Efficient Computing. J. Low Power Electron. Appl. 2017, 7, 17. https://doi.org/10.3390/jlpea7030017
Hasler J. Starting Framework for Analog Numerical Analysis for Energy-Efficient Computing. Journal of Low Power Electronics and Applications. 2017; 7(3):17. https://doi.org/10.3390/jlpea7030017
Chicago/Turabian StyleHasler, Jennifer. 2017. "Starting Framework for Analog Numerical Analysis for Energy-Efficient Computing" Journal of Low Power Electronics and Applications 7, no. 3: 17. https://doi.org/10.3390/jlpea7030017
APA StyleHasler, J. (2017). Starting Framework for Analog Numerical Analysis for Energy-Efficient Computing. Journal of Low Power Electronics and Applications, 7(3), 17. https://doi.org/10.3390/jlpea7030017




