Energy Efficiency Effects of Vectorization in Data Reuse Transformations for Many-Core Processors—A Case Study †

Abstract

Thread-level and data-level parallel architectures have become the design of choice in many of today’s energy-efficient computing systems. However, these architectures put substantially higher requirements on the memory subsystem than scalar architectures, making memory latency and bandwidth critical in their overall efficiency. Data reuse exploration aims at reducing the pressure on the memory subsystem by exploiting the temporal locality in data accesses. In this paper, we investigate the effects on performance and energy from a data reuse methodology combined with parallelization and vectorization in multi- and many-core processors. As a test case, a full-search motion estimation kernel is evaluated on Intel^® Core^TM i7-4700K (Haswell) and i7-2600K (Sandy Bridge) multi-core processors, as well as on an Intel^® Xeon Phi^TM many-core processor (Knights Landing) with Streaming Single Instruction Multiple Data (SIMD) Extensions (SSE) and Advanced Vector Extensions (AVX) instruction sets. Results using a single-threaded execution on the Haswell and Sandy Bridge systems show that performance and EDP (Energy Delay Product) can be improved through data reuse transformations on the scalar code by a factor of ≈3× and ≈6×, respectively. Compared to scalar code without data reuse optimization, the SSE/AVX2 version achieves ≈10×/17× better performance and ≈92×/307× better EDP, respectively. These results can be improved by 10% to 15% using data reuse techniques. Finally, the most optimized version using data reuse and AVX512 achieves a speedup of ≈35× and an EDP improvement of ≈1192× on the Xeon Phi system. While single-threaded execution serves as a common reference point for all architectures to analyze the effects of data reuse on both scalar and vector codes, scalability with thread count is also discussed in the paper.

1. Introduction

The continuously-increasing computational demands of advanced scientific problems, combined with limited energy budgets, has motivated the need to reach exascale computing center systems under reasonable power budgets (below 20 MW) by the year 2020. Such systems will require huge improvements in energy efficiency at all system levels. Indeed, system efficiency needs to increase from the current 33 Pflops/17 MW (515 pJ/op ) to 1 Eflops/20 MW (20 pJ/op) [2]. Most performance and energy improvements will come from heterogeneity combined with coarse-grained parallelism, through Simultaneous Multithreading (SMT) and Chip Multiprocessing (CMP), as well as fine-grained parallelism, through Single Instruction Multiple Data (SIMD) or vector units.

Streaming SIMD Extensions (SSE) and Advanced Vector Extensions (AVX) are SIMD instruction sets supported by Intel. SSE, AVX and AVX512 support 128-bit, 256-bit and 512-bit vector computations respectively. Additionally, NEON and SVE in ARM , AltiVec in Motorola and IBM and 3DNow! in AMD are examples of SIMD instruction sets to enable vectorization in different platforms. Many applications can potentially benefit from using SIMD instructions for better performance, higher energy efficiency and greater resource utilization [3]. However, modern compilers do not yet have adequate auto-vectorization support for complex codes to maximize the potential of SIMD instructions [4,5]. Consequently, when code efficiency is required, the vectorization is often written manually in assembly language or using SIMD intrinsics.

In addition, while processor performance has increased significantly, the memory subsystem has not improved at the same rate. SIMD architectures push the limits of the memory subsystem even further, since now, a single instruction works with N data elements simultaneously, which need to be transferred along the memory hierarchy. Such architectures can even turn CPU-bound applications into memory-bound, depending on the vector length and the arithmetic intensity of the computations (seen as floating point operations per byte of data). Improvements in memory latency/bandwidth (the amount of data that can be accessed in a given period of time), reduction of the energy cost when accessing the data, alongside with better data reuse strategies, are now considered as the key challenges in contemporary computer architectures.

For data-dominated and memory-bound applications such as multimedia algorithms, the Data Transfer and Storage Exploration (DTSE) is a complete methodology for obtaining and evaluating a set of data reuse code transformations [6]. The fundamental idea behind these transformations is to systematically move data accesses from background memories to smaller foreground memory blocks using less energy. Smaller memories can have reduced access latency, while dissipating less power. This approach eventually results in significant improvements in performance and energy savings.

To sum up, it is becoming crucial to exploit both parallelization via multithreading and through the use of vectorization (i.e., multilevel parallelism) to achieve the required performance on current and future multi-core and many-core processors that run memory bound applications. This paper presents a case-study of the effects of multilevel parallelism combined with the DTSE methodology. The contributions of the paper can be summarized as follows:

• We present a set of data reuse transformation strategies and evaluate the effect of data-parallelism using vectorization on these transformation methodologies on a single core. We further extend our study by analyzing the effects of parallelism at different granularities by combining vectorization with multithreading. For coarse-grained parallelism, the OpenMP parallel programming model is used to provide multithreading across multiple cores. On the other hand, SSE-/AVX-based vectorization on each core is used for fine-grained data parallelism.
• We consider both multi-core and many-core system architectures in our study. For multi-core architecture, Intel Sandy Bridge and Haswell multi-core CPUs are used. For many-core architecture, the Intel Xeon Phi Knights Landing (KNL) processor is used. A full-search motion estimation kernel is used as a test application.

This paper is organized as follows: Section 2 describes related work. Section 3 presents the applied methodology to improve energy efficiency, and Section 4 illustrates the use of the methodology on the motion estimation algorithm. Section 5 presents and discusses our results. Finally, we conclude the paper in Section 6.

2. Related Work

A large body of research on data reuse exploration methodologies for multimedia applications has led to numerous approaches for improving memory latency and reducing their energy footprint. Wuytack et al. [6] presented almost 20 years ago a formalized methodology for data reuse exploration. The idea is to exploit temporal locality of memory accesses using an optimized custom memory hierarchy. It is taken further and oriented towards predefined memory organization in [7]. The authors in [8,9] study the effects of data reuse decisions on power, performance and area in embedded processing systems. The effect of data reuse transformations on a general purpose processor has been explored in [10]. In [11], the authors presented the effect of data reuse transformations on multimedia applications using an application-specific processor. The research described so far focuses on single-core systems and mainly relies on simulation-based modeling when estimating energy efficiency.

In [12], Kalva et al. studied parallel programming on multimedia applications, but lacked energy-efficiency analysis. In [13], Chen et al. presented different optimization opportunities of the Fast Fourier Transform (FFT) to improve performance on the IBM Cyclops-64 chip architecture. In [14], Zhang et al. studied both intra-core and inter-core data reuse and presented a technique to exploit all of the available cores to boost overall application performance. In [15], He et al. proposed a bilinear quarter approximation strategy for fractional motion estimation design together with a data reuse strategy for ultrahigh definition video applications. Lifflander et al. in [16] presented a work-stealing algorithm for fork-/join-based parallel programming models to gain performance boost-up though improving the data locality property.

These earlier studies on parallel architectures emphasized performance rather than energy efficiency. In contrast, our work is not limited to performance analysis only; rather, it is extended by energy efficiency analysis on three different state-of-the-art multi- or many-core processors, namely Sandy Bridge and Haswell CPUs and the Xeon Phi KNL processor.

In [17], Marchal et al. presented an approach for integrated task-scheduling and data-assignment for reducing SDRAM costs for multithreaded applications. However, this work did not couple the data reuse analysis with a parallel programming model the way we do here. Here, we extend our previous work presented in [1], where we analyzed the effect on the performance and energy efficiency of coupling multithreaded parallelism with the data reuse transformations. However, [1] was limited to a single multi-core platform, and the effect of fine-grained data-parallelism through vectorization was not covered.

Data reuse techniques (mainly blocking) and other low level optimizations for Intel’s many-core architectures are covered in [18]. A combination of programming language features, compiler techniques and operating system interfaces are presented in [19] that can effectively hide memory latency for the processing lanes. Their study is based on the active memory cube system, a novel heterogeneous computing system, substantially different from our test platforms. Dong et al. in [20] made a custom implementation of linear algebra kernels for GPUs to obtain ≈10% power savings for a hydrometric kernel. In [21], the authors presented a micro-architectural technique to approximate load values on load misses so as to reduce the cost of memory accesses. In [22], the authors provided emphasis on making efficient use of hardware vector units in order to achieve optimal performance on multi- and many-core architectures. They also demonstrated the limitations of auto-vectorization over hand-tuned intrinsic-based vectorization for the applications with irregular memory accesses on a Xeon Phi co-processor. Furthermore, the authors in [23] argued for Cray-style temporal vector processing architectures as an attractive means of exploiting parallelism for the future high performance embedded devices.

Though these articles demonstrated the importance of vector processing in achieving better performance as we do in this paper, they do not provide energy efficiency or DTSE-like analysis for a full-search motion estimation or similar kernels.

3. Energy-Efficient Methodology for Multi-Core and Many-Core Processor

The approach presented in this paper is a combination of three techniques: the data reuse transformation methodology, parallelization by dividing computational work on several cores and vectorization by using the SIMD instructions available in each core. Note that vectorization is also a technique for parallelization. For example, an application divided onto four cores each using a four-way vectorization exhibits, in total, a 16-way parallelization.

3.1. Approaches to Improve Performance and Energy Efficiency

3.1.1. Data Reuse Transformation

The most central concept of a data reuse transformation is the use of a memory hierarchy that exploits the temporal locality of the data accesses [6]. This memory hierarchy consists of smaller memories where copies of data from larger memories that expose high data reuse are stored. For data-intensive applications, this approach causes significant energy savings since smaller memories built on similar technology consume less energy per access and have significantly shorter access times. In addition, the average access latency to data is reduced, since the transformations act as a complex software prefetching mechanism.

3.1.2. Parallelization

Multi-core processors can potentially achieve higher performance with lower energy consumption compared to uni-processor system. However, there are challenges in exploiting the available hardware parallelism without adding too much overhead. Different parallel programming models have been developed for speeding up applications by using multiple threads or processes [24]. Parallel programs can be developed by using specific programming models (e.g., OpenMP, OmpSs, Cilk) [25] or can use explicit threading support from the operating system (e.g., POSIX (Portable Operating System Interface) threads).

3.1.3. Vectorization

Vectorization using SIMD constructs is very efficient in exploring data level parallelism since it executes multiple data operations concurrently using a single instruction. Therefore, SIMD-computations often result in significant performance improvements and reduced memory accesses, eventually leading to higher energy efficiency for an application [26]. However, extracting performance from SIMD-based computations is not trivial as it can be significantly affected by irregular data access. In multi-core programming memory bandwidth often becomes a critical bottleneck, as the data movement from memory to the register bank increases with both vectorization and parallelization [3]. On the other hand, memory latency can sometimes be hidden by optimization techniques, such as SIMD prefetching or improved data locality (e.g., cache blocking).

3.2. Data Reuse Transformations with Parallelization and Vectorization

In our case-study, we combine the aforementioned approaches to further optimize the performance and energy efficiency of data reuse transformations. Our approach consists of the following main steps.

• In the first step, the sequential optimized algorithm is translated into a parallel algorithm that follows a typical parallel workflow:

  -

  The original workload is divided into a number of p smaller sub-workloads. Each of the p sub-workloads is assigned to a thread for completion.

  -

  Multiple threads are executed simultaneously on different cores, and each thread operates independently on its own sub-workload.

  -

  When all of the sub-workloads are completed by the threads, an implicit barrier ensures that all of the local results of the completed sub-workloads are combined together through a reduction step.

  At this stage, coarse-grained parallelism is applied through multithreading/simultaneous multithreading on multiple cores.
• Next, to exploit the data parallelism support available in the systems, we use SIMD computations on each thread. Since modern compilers still do not have adequate auto-vectorization support for complex codes [4,5], we use the SSE, AVX2 and AVX512 intrinsics to manually perform the SIMD computations. We ensure that the data layout of the demonstrator application is properly aligned with the boundaries of the vector registers. SIMD prefetching is used to copy the copy-candidates described below into smaller buffers to hide the latency of the memory transfer.
• In the final step, we apply the proposed model for data reuse transformations as presented in [6]. Here, we identify the datasets that are reused multiple times within a short period of time. These are called copy-candidates. In this study, the copy-candidate tree from [6] is used for the scalar version of the demonstrator kernel, whereas it has been slightly changed when SIMD computations are used. Depending on their size and position in the tree, the copy-candidates are mapped into appropriate layers of the system’s memory hierarchy. To map a data block into its layer, we use the SIMD-prefetch intrinsic (i.e., _mm_prefetch) with the appropriate hint options for both scalar and vectorized codes. Generally, _MM_HINT_T0, _MM_HINT_T1 and _MM_HINT_T2 options can be used for prefetching data into L1, L2 and L3 caches, respectively [27]. Compiler-assisted software prefetching is disabled to avoid auto-prefetching of data from memory. Furthermore, we also use SIMD stream intrinsics (_mm_stream_load and _mm_stream) in our vectorized codes to limit cache pollution due to movement of data across the memory hierarchy.

4. Demonstrator Application: Full-Search Motion Estimation Algorithm

To evaluate the efficiency of the combined approach, we have used a full-search motion estimation algorithm as a case-study. In this section, we use it to describe the main steps of the approach.

4.1. Sequential Motion Estimation Algorithm

Motion Estimation (ME) is used in most video compression algorithms as it can be used to find temporal redundancy in a video sequence. In a block-matching ME algorithm, a video frame (W × H) is divided into a number of (n × n) non-overlapping blocks called Macro-Blocks (MBs), where the value of n can be {2,4,8,16, …}. Next, for each MB in the Current frame (Cur), a matching MB within the search area (m × m) in the Reference frame (Ref) is selected having the least cost value. There are several possible cost functions. The Sum of Absolute Difference (SAD) is widely used and computationally inexpensive and so selected for this study. The SAD between an MB in Cur and an MB in Ref is given by,

$$SAD=\sum _{i=1}^{i=n}\sum _{j=1}^{j=n}\mid Cu{r}_{ij}-Re{f}_{ij}\mid$$

(1)

where $Cu{r}_{ij}$ and $Re{f}_{ij}$ are the pixel values at position $(i,j)$ in the MBs of Cur and Ref, respectively.

Finally, the relative displacement of the current MB and its matching MB is the motion vector. A full-search ME algorithm performs an exhaustive search over the entire search region to find the best match. Running this algorithm is computationally intensive and can account for as much as 80% of the encoding time [12]. This computationally-intensive algorithm exhibits the properties of data reuse and parallelization and is therefore well suited as a test application for our approach.

The full-search ME kernel used in our work is presented in Algorithm 1 [6,28]. The implementation consists of a number of nested loops. The basic operation at the innermost loop consists of an accumulation of pixel differences (i.e., the SAD computation), while the basic operation two levels higher in the loop hierarchy consists of the calculation of the new minimum. In our experiments, we use the parameters of the QCIF (Quarter Common Intermediate Format) format $(W=176,H=144,m=16,n=8)$ on the multi-core system and the Full HD format $(W=1920,$ $H=1080,m=16,n=8)$ on the many-core platform [29]. In the remainder of this paper, we simply refer to this as the ME application.

4.2. Parallel ME Application across Multiple Cores

In the process of ME algorithm parallelization, we design a multi-core computing model to exploit the data parallelism properties inherent in the ME algorithm. In the algorithm, there is no data dependency between two macro-blocks’ SAD. Thus, the SADs of different macro-blocks can be computed in parallel. Considering this, we divide Cur into the same number of subsections as there are threads and assign each subsection to a particular thread. Eventually, all of the threads run in parallel across multiple cores to execute the SAD processing. The benefit of this division into subsections is to make full use of the available cores on the underlying platforms. Figure 1 illustrates a four-threaded computation model for an 8 × 8 frame.

Algorithm 1: Motion estimation kernel (source: [6,28]).
Input: Current frame (Cur), Reference frame (Ref), frame Height (H), frame Width (W), search range (m), block size (n).
Output: motion vector (${\mathrm{\Delta }}_{opt}$).
1:	for g=0; g<H/n; g++ do	▹ Vertical current block counter
2:	for h=0; h<W/n; h++ do	▹ Horizontal current block counter
3:	${\mathrm{\Delta }}_{opt}\left[g\right]\left[h\right]={\mathrm{\Delta }}_{opt}\left[g\right]\left[h\right]+\infty$
4:	for i= -m; i<m; i++ do	▹ Vertical searching of reference window
5:	for j= -m; j<m; j++ do	▹ Horizontal searching of reference window
6:	$\mathrm{\Delta }=0$
7:	for k=0; k<n; k++ do	▹ Vertical traversal of MB
8:	for l=0; l<n; l++ do	▹ Horizontal traversal of MB
9:	Δ = Δ + ∣ Cur[g×n+k][h×n+l] − Ref[g×n+i+k][h×n+j+l]) ∣
10:	end for
11:	end for
12:	${\mathrm{\Delta }}_{opt}\left[g\right]\left[h\right]=min(\mathrm{\Delta },{\mathrm{\Delta }}_{opt}\left[g\right]\left[h\right])$
13:	end for
14:	end for
15:	end for
16:	end for

Algorithm 2 represents our parallel ME algorithm, which shows OpenMP parallel programming constructs used to achieve thread-level parallelism across multiple cores [25]. As we can see, the #pragma omp parallel for collapse(2) directive of the OpenMP programming model is used at the outermost for-loop. The inclusion of this directive will instruct the compiler to fuse the next two loops into a single loop, increasing the amount of work that can be assigned to all processors (cores) of the system. We have also set the KMP_AFFINITY environment variable to bind each thread, i.e., each instance of the for-loop, to a specific core. We further use the OMP_NUM_THREADS environment variable to control the number of threads to be created at a particular time. Note that though we have used loop-based work-sharing constructs of OpenMP here, other types of work sharing constructs, such as OpenMP tasking constructs (#pragma omp parallel, #pragma omp task) can be used, as well.

Algorithm 2: Optimized parallel motion estimation algorithm.
Input: Current frame (Cur), Reference frame (Ref), frame Height (H), frame Width (W), search range (m), block size (n).
Output: motion vector (${\mathrm{\Delta }}_{opt}$)
1:	#pragma omp parallel for schedule(static, <chunksize>) collapse(2)
2:	for g=0; g<H/n; g++ do	▹ Vertical current block counter
3:	for h=0; h<W/n; h++ do	▹ Horizontal current block counter
4:	for k=0; k<2m+n-1; k++ do	▹ Copy-candidates are copied to a smaller memory block
5:	for l=0; l<2m+n-1; l++ do
6:	Buffer_ref[k][l] = Ref[g×n-m+k][h×n-m+l]
7:	end for
8:	end for
9:	for k=0; k<n; k++ do	▹ Copy-candidates are copied to a smaller memory block
10:	for l=0; l<n; l++ do
11:	Buffer_cur[k][l] = Cur[g×n+a][h×n+b]
12:	end for
13:	end for
14:	${\mathrm{\Delta }}_{opt}\left[g\right]\left[h\right]={\mathrm{\Delta }}_{opt}\left[g\right]\left[h\right]+\infty$
15:	for i=0; i<2m-1; i++ do	▹ Vertical searching of reference window
16:	for j=0; j<2m-1; j++ do	▹ Vertical searching of reference window
17:	$\mathrm{\Delta }=0$
18:	for k=0; k<n; k++ do	▹ Vertical traversal of MB
19:	for l=0; l<n; l++ do	▹ Horizontal traversal of MB
20:	Δ += ∣ (Buffer_cur[k][l]- Buffer_ref[i+k][j+l]) ∣
21:	end for
22:	end for
23:	${\mathrm{\Delta }}_{opt}\left[g\right]\left[h\right]=min(\mathrm{\Delta },{\mathrm{\Delta }}_{opt}\left[g\right]\left[h\right])$
24:	end for
25:	end for
26:	end for
27:	end for

4.3. Data Parallelism in Each Core through Vectorization

The use of SIMD intrinsics will help to reduce the number of memory accesses and instructions in comparison to the sequential execution on both of the considered architectures. The inner loop of the SAD calculation of one macro-block (SSE/AVX2) or two macro-blocks (AVX512) can be partially executed in parallel by using SIMD instructions. Within each iteration of the loop over all block rows, one complete cache-line of the reference and one of the candidate block are loaded into two separate vector registers, and their row-wise SAD value is accumulated over all rows. The AVX512 and SSE/AVX2 instruction-set extensions of the Intel architecture feature a single instruction, computing the element-wise absolute difference of two vector registers and internally reducing each vector of eight consecutive absolute difference values to one 32-bit element. Finally, the accumulated 32-bit SAD value, which is generated for each row of the current block, needs to be extracted from the vector register into a scalar register.

Table 1. Required C/C++ intrinsics to implement the Motion Estimation (ME) algorithm. Streaming Single Instruction Multiple Data (SIMD) Extensions (SSE), Advanced Vector Extensions (AVX) 2 and AVX512 are the SIMD instruction sets that operate on 128-bit, 256-bit and 512-bit vector registers, respectively.

Operation	SSE	AVX2	AVX512
bitwise OR	$\_mm\_or\_si128$	$\_mm256\_or\_si256$	$\_mm512\_or\_si512$
bitwise AND	$\_mm\_and\_si128$	$\_mm256\_and\_si256$	$\_mm512\_and\_si512$
shift right by a number of bytes	$\_mm\_srli\_si128$	$\_mm256\_srli\_si256$	$\_mm512\_srli\_si512$
shift left by a number of bytes	$\_mm\_slli\_si128$	$\_mm256\_slli\_si256$	$\_mm512\_slli\_si512$
add four 32-bit integers	$\_mm\_add\_epi32$	$\_mm256\_add\_epi32$	$\_mm512\_add\_epi32$
shuffle four 32-bit integers	_mm_shuffle_epi32	_mm256_shuffle_epi32	_mm512_shuffle_epi32
compare four 32-bit integers	$\_mm\_cmpgt\_epi32$	$\_mm256\_cmpgt\_epi32$	$\_mm512\_cmpgt\_epi32$
store a 128-bit register	$\_mm\_storeu\_si128$	$\_mm256\_storeu\_si256$	$\_mm512\_storeu\_si512$
load to 128-bit register	$\_mm\_loadu\_si128$	$\_mm256\_loadu\_si256$	$\_mm512\_loadu\_si512$
unpack and interleave 32-bit integers	$\_mm\_unpacklo\_epi32$	$\_mm256\_unpacklo\_epi32$	$\_mm512\_unpacklo\_epi32$
convert 8-bit integers to 32-bit integers	$\_mm\_cvtepi8\_epi32$	$\_mm256\_cvtepi8\_epi32$	$\_mm512\_cvtepi8\_epi32$
element-by-element bitwise AND on 32-bit integers	-	-	$\_mm512\_mask\_and\_epi32$
compare packed 32-bit integers, and store the results in mask vector k	-	-	$\_mm512\_cmpgt\_epi32\_mask$
compare packed 32-bit integers, and store the results in mask vector k	-	-	$\_mm512\_cmplt\_epi32\_mask$
reduce 32-bit integers in a by addition using mask k	-	-	$\_mm512\_mask\_reduce\_add\_epi32$
store a 128-bit register	$\_mm\_strea{m}_{l}oad\_si128$	$\_mm256\_strea{m}_{l}oad\_si256$	$\_mm512\_strea{m}_{l}oad\_si512$
store to 128-bit register	$\_mm\_stream\_si128$	$\_mm256\_stream\_si256$	$\_mm512\_stream\_si512$
Reduce 32-bit integers by addition using mask k and returns the sum	-	-	${}_{m}m512\_mask\_reduc{e}_{a}d{d}_{e}pi32$

lists a set of SSE, AVX2 and AVX512 intrinsics used in the ME algorithm implementations.

4.4. ME Optimization Using Data Reuse Transformation

In the final stage of the optimization process, we integrate data reuse transformation strategies into our optimized ME kernel to gain further performance and energy efficiency improvements. Our study is based on a research work of Wuytack et al., who used the DTSE methodology for data reuse transformations and presented a number of different possible transformations using a copy-candidate tree for the ME algorithm [6]. However, in this study, we only consider the subset of transformations reported to be the more energy efficient in [6] and which also fit to the memory hierarchy of our test systems. Figure 2 presents different possible transformations that are considered to optimize the ME algorithm in this work.

In Figure 2, each branch in the copy-candidate tree corresponds to a potential memory hierarchy for a given data-reuse transformation. The vertical dashed lines in the figure indicate the levels of the hierarchy. Each rectangle in the hierarchy is a copy-candidate and corresponds to a block of data to be stored in memory. Each block is annotated with its size. The highlighted branches in the figure (i.e., the branching option with the blue rectangular boxes) indicate a two-layer memory hierarchy for a possible data reuse transformation in each of the frames. For the reference frame, the hierarchy is comprised of an H × W block and a $(2m+n-1)$ × $(2m+n-1)$ block memory. These blocks are mapped into the L3 and L2 caches of our test platforms. In addition, a two-layer memory hierarchy for the current frame with an H × W and an n × n memory block is also introduced. The blocks are mapped into the L3 and L1 caches, respectively. Among the different possible transformation options presented in the copy candidate tree, the options that are labeled with E are analyzed in detail in the Results section.

To evaluate the performance and energy efficiency of the different data-reuse transformations presented in Figure 2, the basic ME algorithm (Algorithm 1) has been modified into different versions to exploit different possible transformations. This modification is done by introducing smaller memory blocks (Buffer_cur, Buffer_ref) to which the copy-candidates (e.g., each line in the reference window) of the reference frame are copied. The algorithm illustrated in Algorithm 2 presents the most effective solution in terms of performance and energy among the different transformation options we have analyzed in this study. The solution introduces two small buffers for two copy-candidates; one of them is for the Current frame (Cur), and the other one is for the Reference frame (Ref).

It is also important to note that the copy-candidate tree presented in Figure 2 is used in all of our experiments, except the experiments with AVX512. Architectures supporting AVX512 intrinsics (e.g., KNL) are featured with 512-bit SIMD registers, that operate with 512-bits of data at the same time. Therefore, AVX512 intrinsics access the pixels in two macro-blocks of size $8\times 8$ at the same time. Consequently, a copy candidate of size n × n becomes less efficient for AVX512-based computations. To address this problem, instead of defining a copy-candidate of size n × n, we define a copy-candidate of size $2n\times n$ for AVX512 computations.

5. Results and Discussion

In this section, we present several experiments to study the effect of vectorization on data reuse transformations. We implement ten different variants of the ME kernel following the data reuse transformation techniques illustrated in Figure 6. The experiment names reflect the different copy-candidates ($E0$ through $E3$) in Figure 6. The kernels are implemented in C++ using SSE, AVX2 and AVX512 intrinsics. The ten variants are:

• Scalar_E0: Implementation of the ME kernel (Algorithm 1) without any of the optimization techniques covered in this study (i.e., no data reuse transformations or vectorization). This sequential implementation is the baseline to which we make a comparative study of different kernel implementations.
• Scalar_E1: Non-vectorized ME kernel with data reuse transformation using the n × n copy-candidate.
• Scalar_E2: Non-vectorized ME kernel with data reuse transformation using the $(2m+n+1)$ × $(2m+n+1)$ copy-candidate.
• Scalar_E3: Non-vectorized ME kernel with data reuse transformation using the $(2m+n+1)$ × $(2m+n+1)$ and n × n copy-candidates.
• SSE_E0: SSE-vectorized ME kernel without any data reuse transformations.
• SSE_E2: SSE-vectorized ME kernel with data reuse transformation using the $(2m+n+1)$ × $(2m+n+1)$ copy-candidate.
• AVX2_E0: AVX2-vectorized ME kernel without any data reuse transformations.
• AVX2_E2: AVX2-vectorized ME kernel with data reuse transformation using the $(2m+n+1)$ × $(2m+n+1)$ copy-candidate.
• AVX512_E0: AVX512-vectorized ME kernel without any data reuse transformations.
• AVX512_E2: AVX512-vectorized ME kernel with data reuse transformation using the ($2m+n+1)$ × $(2m+n+1)$ copy-candidate.

5.1. Test System Architecture

This subsection describes the platforms used in our evaluation. It is important to note that since we conduct our experiment on multi- and many-core systems with a memory hierarchy of fixed sized cache-blocks, the copy-candidates are mapped into system caches according to their sizes (

Table 2. Hardware specifications of the test platforms.

Processor	Intel® CoreTM i7-2600K	Intel® CoreTM i7-4700K	Intel® Xeon Phi 7250
Architecture	Sandy Bridge	Haswell	Knights Landing (pre-production)
Clock Speed	1.6 to 3.4 GHz	0.8 to 3.5 GHz	1.4 Ghz
# of Cores	4 cores/8 threads		68 cores/272 threads
L1 Cache	32 KB data + 32 KB inst, 8-way private
L2 Cache	256 KB, 8-way private		1 MB, 16-way per 2 cores

).

5.1.1. Intel^® Core^TM CPUs

In our experiments, we have used the Intel^® Core^TM i7-4700K (Haswell) and i7-2600K (Sandy Bridge) processors consisting of four physical cores. Both support Hyper-Threading (HT), which allows the CPU to simultaneously process up to eight threads (i.e., two threads per core). The memory hierarchy consists of a 32-KB Level-1 cache, a 256-KB Level-2 cache and a 8192-KB Level-3 cache. Level-1 and Level-2 caches are private to each core, while the Level-3 cache is shared among the cores. Note that this is a memory hierarchy with a fixed number of levels and sizes, typical for a standard processor. This is different from the assumption in [6], where an application-specific memory hierarchy is assumed. The base clock speeds of the processors are 3.5 GHz and 3.4 GHz, respectively, but it can go as high as 3.9 GHz when Turbo Boost is enabled [27]. However, we disabled dynamic frequency scaling (SpeedStep and Turbo Boost) to get more stable results from the experiments. The systems run under Ubuntu 14.04.3 LTS. All of the kernels are compiled using Intel C++ compiler (ICC Version 14.0.1) with the -O2 option.

5.1.2. Intel Xeon Phi Processor

Xeon Phi: Knights Landing (KNL) is the second revision of Intel’s Many Integrated Core Architecture (MIC). Many-core architectures offer a high number of cores (68 in our evaluation platform) with up to four threads per core and a potential peak performance close to 6 Tflops for single precision floating point. These cores are based on the Silvermont Atom architecture. Cores are out of order and tiled in pairs. Each core contains two Vector Processing Units (VPUs), which work with vector registers up to 512 bits wide. The VPUs are compatible with SSE, AVX/AVX2 and AVX512.

Each tile in the processor shares 1 MB of L2 memory, using a 2D mesh interconnect (or NOC (Network On Chip)) for communication. This interconnect also links the tiles to two DDR4 memory controllers, with a capacity of up to 384 GB and a bandwidth of 90 GB/s. In addition, some KNL models feature a High Bandwidth Memory Multi-Channel DRAM (HBM-MCDRAM), which is accessed using the NOC. This memory is divided into eight stacks, adding up to 16 GB of capacity, and has a bandwidth close to 400 GB/s. The HBM memory can work in different modes, as a scratchpad memory, as an additional cache level or in hybrid mode (combination of the previous two modes).

Our evaluated Xeon Phi platform is based on the Xeon Phi 7250 processor. This processor features 68 cores running at 1.40 GHz. The system runs SUSE Linux Enterprise Server 12 SP1, and the binaries are generated using Intel C++ compiler (Version 17.0.035) with the -O2 optimization level and the -xMIC-AVX512 flag to generate AVX512 code. The devices are configured to work in cache mode, where the HBM acts as an L3.

5.2. Metrics Used for Analysis

We use execution time (in micro-seconds) as the metric for performance evaluation. To estimate on-chip energy consumption, we read the Model-Specific Registers (MSRs) that provide energy measurements for the cores in Haswell and Sandy Bridge [27], since package measurements include the integrated GPU power, and we are not interested in that. For KNL, we measure the whole package energy (including core power and DRAM controller traffic), since the core energy counter is not available in our pre-production system. In addition, we have not found any accurate description of what the DRAM controller actually measures as the measurements might include memory controller and caches, or the accesses to the DDR modules (it should not, since manufacturers can have any brand/technology attached to the system and dissipate different power). We decided to go for the isolated core energy (PP0 i.e. Power-Plane 0) and Package energy (PKG) since both are properly defined. These counters can be accessed either by the RAPL (Running Average Power Limit ) interface (root-level) or the powercap interface (user-level). We report both core/package-energy consumption and Energy Delay Product (EDP: Joule × Second) [30,31] to perform energy efficiency analysis. For both, lower values corresponds to better energy efficiency. Speedup, relative on-chip energy and relative EDP at a certain frequency are all computed with respect to the baseline kernel (Scalar_E0). The PAPI (Performance Application Programming Interface) [32] is used to track cache- and memory-related events.

5.3. Performance Analysis on the Haswell and Sandy Bridge Platforms

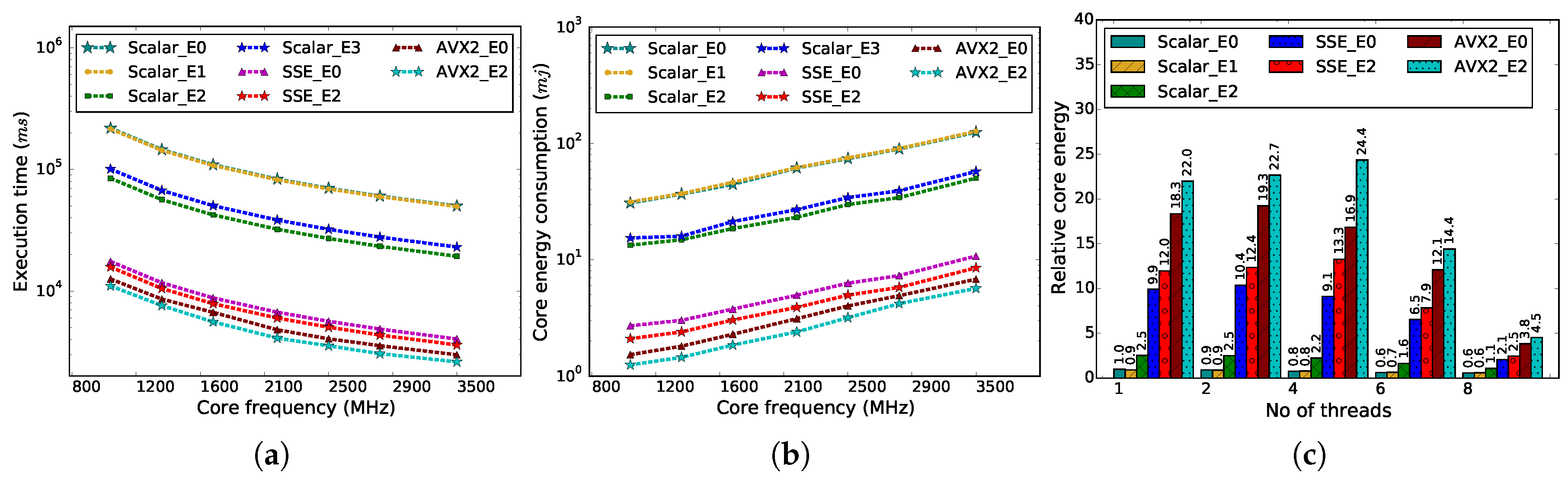
In the first set of experiments, our goal is to gain insight into the effects of vectorization on data reuse transformations. Figure 3a compares the performance of different kernel implementations at different core frequencies on the Haswell platform.

In Figure 3a, we observe a linear impact of core frequency on the performance of the implemented kernels. The kernel execution time decreases with increasing core frequency. The figure also confirms that the performance of the kernel can be improved by using data reuse transformation techniques despite the overhead of copying the copy-candidates into the buffers. Among the three different data reuse transformation techniques (E1, E2 and E3), E2 appeared to be more effective than the other two transformations, and it (i.e., Scalar_E2) provides more than a two-fold performance gain over the unoptimized (i.e., Scalar_E0) solution when integrated with the scalar ME kernel in a single core on the Haswell system. 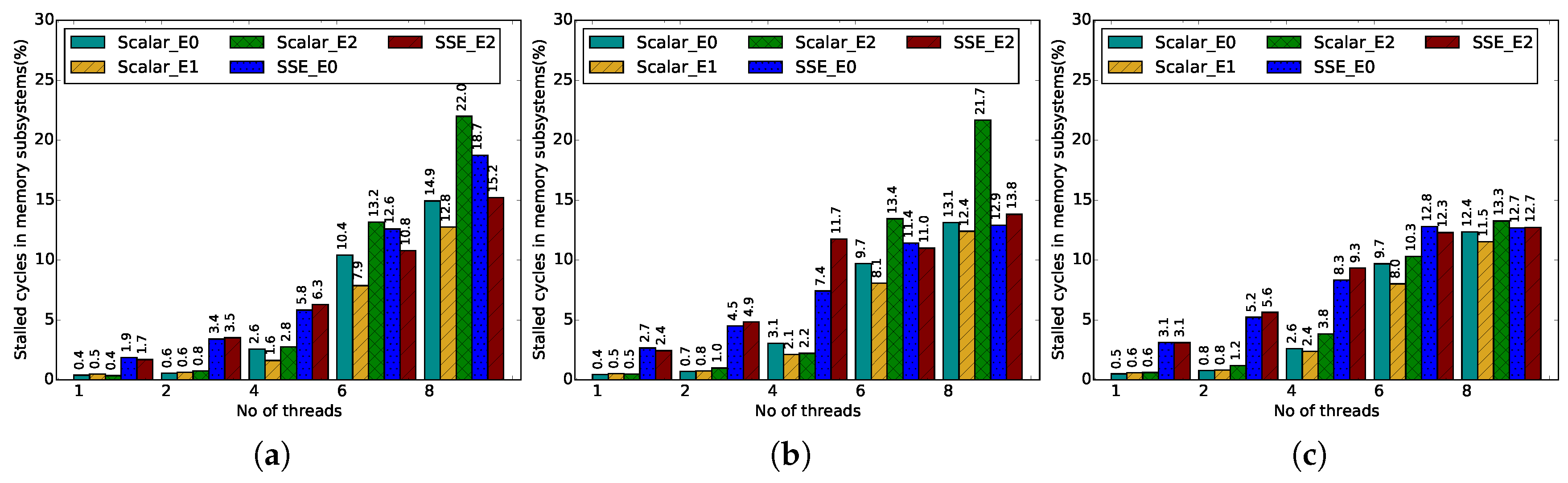This improvement is attributed to the use of a smaller block size, since a block of $(2m+n-1)$ × $(2m+n-1)$ unsigned-characters corresponds to 2209 (47 × 47 ×1) bytes, which is less than the Level-1 cache size in our system. Therefore, a full block is brought into the Level-1 cache during computation, which significantly reduces the cost of expensive memory accesses. This cost reduction is evident in the data presented in

Table 3. Average execution time and energy consumption of sequential kernel implementations at a peak core frequency on the Haswell system. EDP, Energy Delay Product.

ME kernel	Execution Time	Stalled CPU Cycles	Total CPU Cycles	Core Energy Consumption		EDP	Instruction Count	Relative Energy		Cache Miss Rate (L2)
Scalar_E0	48480	564838	164147540	132	13	6256000	631036879	1	1	28%
Scalar_E1	50745	403386	165314558	136	158	6292469	631292899	1	1	21%
Scalar_E2	20491	120485	67881181	49	56	966100	187288526	3	2	12%
Scalar_E3	23008	1828712	80570952	57	66	1311456	199778723	2	2	11%
SSE_E0	5422	148615	14696743	13	14	44341	54934069	11	9	35%
SSE_E2	4597	150375	12574005	9	10	32445	37939611	14	13	29%
AVX2_E0	2991	119285	10616947	7	6	20937	30518927	18	21	42%
AVX2_E2	2619	121012	9672043	6	5	15714	22057913	21	25	37%

, as the total number of stalled CPU cycles on memory subsystems is reduced to one third of the stalled cycles for Scalar_E0. It is also interesting to note that the L1D/L2 cache miss rate for SIMD computations is much higher than the scalar computations, and the cache miss rates increase as the width of SIMD register increases. This observation leaves us room for further optimization, particularly for the systems with wider SIMD registers, such as Scalable Vector Extensions (SVE) [33], which are designed to support up to 2048-bit registers.

Now, comparing the performance of the vectorized kernels with the scalar kernels, the vectorized kernels clearly outperform the scalar kernels by a significant margin (≈10× and ≈17× for SSE and AVX2, respectively). This performance improvement is expected as SIMD computation provides two-fold benefits in this circumstance. First, it reduces the number of instructions needed to be executed for completing the task by simultaneously processing multiple data points using the vector registers. Since the SSE registers are 128-bit wide, SSE-based SIMD computations can process up to 16 unsigned characters (8-bit) at a time. Therefore, we can potentially achieve 16× performance speedup using SSE-based vectorization in the ME kernel. However, due to the inherent complexity of the algorithm (e.g., 8-bit values need to be converted into 32-bit values to continue further computations), we ended up with ≈10× speedup for SSE_E0 over Scalar_E0. Similarly, using 256-bit SIMD registers for AVX2-based computations, we have achieved speedup ≈17× for AVX2_E0 over Scalar_E0. This speedup is shown in Figure 4, and the reduction of instruction counts are presented in Table 3. Second, the SIMD computation also reduces the required number of cache/memory accesses by simultaneously loading/storing multiple data points using a single load/store operation. This can eventually reduce the CPU waiting time for the memory subsystems and improve the overall system’s performance. On the other hand, for bandwidth-bound applications, the increased bandwidth demand caused by the SIMD computations can limit the potential performance improvements if the memory subsystem cannot sustain such demand. Indeed, the data presented in Table 3 shows that the absolute number of stalled CPU cycles on the memory system for the vectorized ME kernels is reduced, but represents a higher percentage of the overall execution (estimated to be Figure 5).

Another important observation is the fact that the impact of data reuse transformation is greater for the performance of the scalar ME than for the vectorized ME. As shown in Figure 4, the data reuse transformations provide two-fold performance gain as we move from E0 to E2 optimizations for the scalar ME kernel. However, with the vectorized ME, the performance is improved by only 10% to 15% on the Haswell system. Three factors can contribute to this limited improvement. First, the total number of memory accesses is greatly reduced by the vectorized computations (e.g., ≈10× less number of memory accesses for SSE). Second, the copy-candidate sizes can also be affected by the length of the vector register and may increase the overhead of copying the data into the buffer. Finally, the relative stalled CPU cycles on the memory subsystems are increased due to the increased bandwidth demands of SIMD computations, which can be clearly seen in Figure 5.

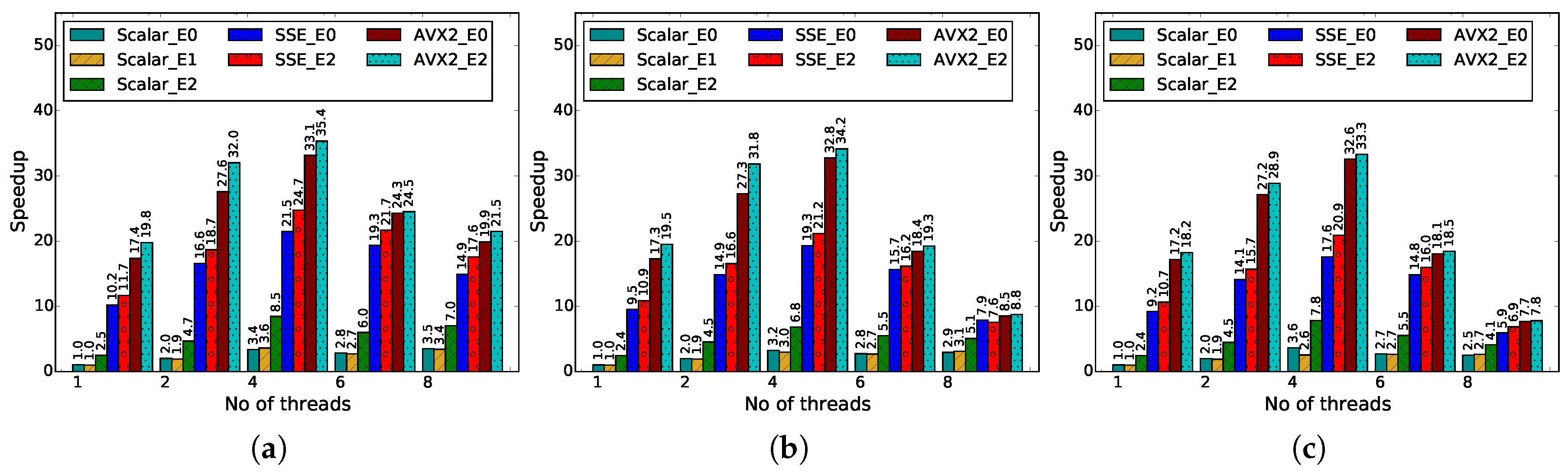
Figure 4 and

Table 4. Average execution time and core-energy consumption of multi-threaded kernel implementations on the Haswell system at peak core frequency.

ME	Execution Time				Core Energy
Kernel	1 Thread	2 Threads	4 threads	8 Threads	1 Thread	2 Threads	4 Threads	8 Threads
Scalar_E0	48480.38	25384.31	13714.04	19854.64	131.66	135.28	162.45	216.62
Scalar_E1	50745.10	26383.63	19607.79	18884.49	136.00	138.97	157.97	203.58
Scalar_E2	20491.06	11200.93	6394.28	12140.29	49.35	49.80	55.82	113.85
SSE_E0	5421.62	3547.64	2844.55	8445.98	12.60	12.02	13.67	60.22
SSE_E2	4697.03	3188.25	2395.11	7292.13	10.42	10.10	9.41	50.97
AVX2_E0	2991.48	1842.71	1535.45	6510.13	6.21	6.49	7.41	32.52
AVX2_E2	2619.03	1733.14	1502.45	6412.13	5.18	5.51	5.13	27.58

present the multithreaded performance of different kernel implementations at different core frequencies. From the figure, we can observe that the performance of all of the kernels increases with the increasing number of threads as long as only one thread runs on a given physical-core. AVX2_E2 provides the best performance in all cases and can provide speedup up to 34× on the Haswell system over the unoptimized scalar kernel (SSE_E0) when four threads are used. However, beyond four threads, when hyper-threading is used, the performance is degraded. This performance is less than what we could potentially achieve with the combination of multithreading (≈4×), vectorization (≈16× using SSE and ≈32× using AVX2 for an 8-bit value) and data reuse transformations.

In summary, based on our observation, we can conclude that vectorization accelerates the performance of the motion estimation kernel by reducing the total number of instructions and memory accesses through data parallelization. On top of that, data reuse transformations reduce expensive memory accesses to upper cache levels, by improving locality on lower levels. When combined with vectorization, data reuse transformation helps to keep the amount of stalled cycles due to memory accesses low, despite the extra pressure on the memory system. Finally, thread-level parallelism provides further performance improvements on multi-core platforms regardless of the frequency, as long as physical cores are used.

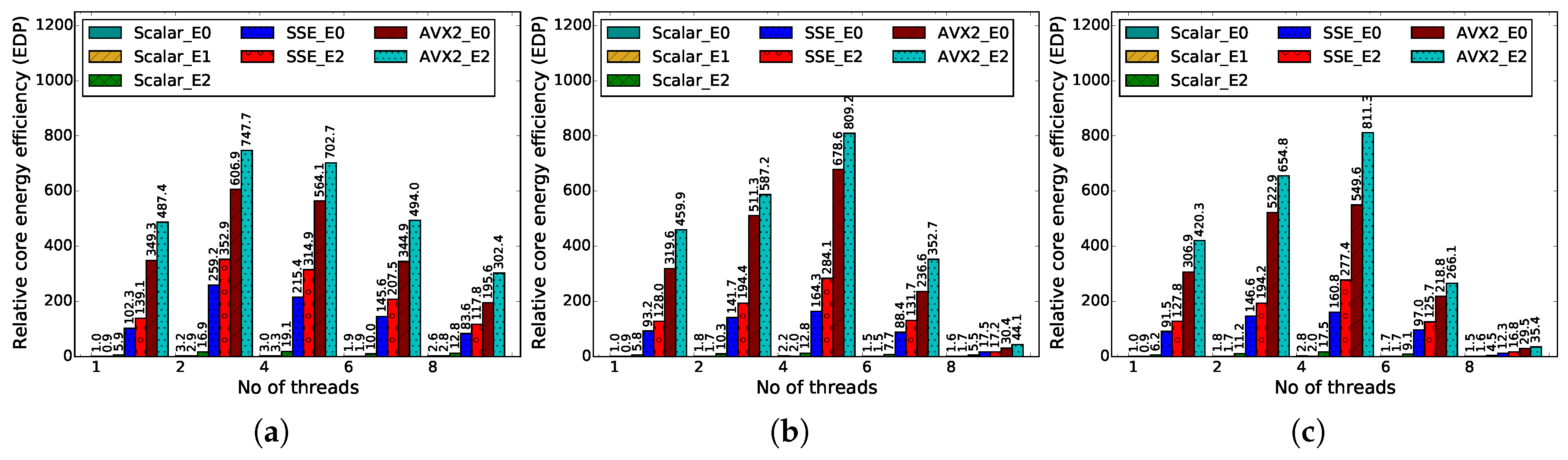
5.4. Energy Efficiency Analysis on the Haswell and Sandy Bridge Platforms

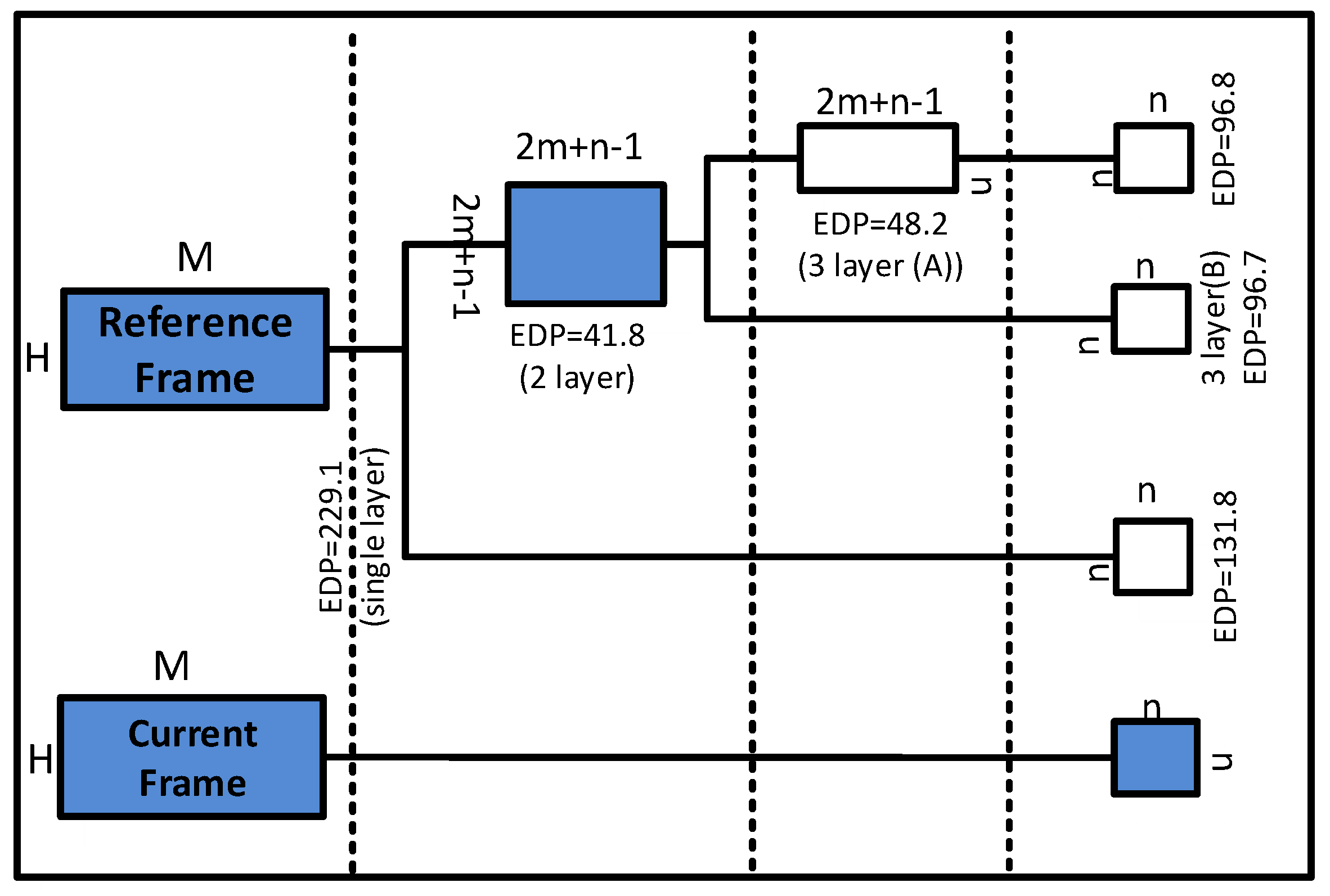
In this section, we present the implications of different strategies on improving the energy efficiency. Figure 6 presents the EDP measurements on the Sandy Bridge system for the different data reuse transformation options presented in Figure 2 for a sequential ME kernel.

Figure 6. Energy-efficiency optimization using different possible data-reuse transformations on the Sandy Bridge system.

Figure 6. Energy-efficiency optimization using different possible data-reuse transformations on the Sandy Bridge system.

The use of data reuse transformations in the motion estimation kernel reduces the accesses to the larger memories in the memory hierarchy. Therefore, it is expected that the kernels with data reuse transformations consume less energy than the unoptimized kernels. Indeed, Figure 6 shows a significant improvement in energy efficiency due to the data-reuse transformation techniques. The core energy consumption of the sequential motion estimation kernel is reduced to one-third of its original energy consumption by the deployment of data reuse transformations (in

Table 5. Results of different data reuse transformations on the Sandy Bridge system.

Version	Execution Time	Energy	Energy Efficiency	Relative	Relative
	Milliseconds	Millijoules	(EDP) Js $\times {10}^{-9}$	Energy	EDP
Scalar_E0	0.01379	378.71	5224.4	1.00	1.00
Scalar_E2	0.00461	130.29	608.8	2.91	8.58
Scalar_E3	0.00488	137.93	673.2	2.74	7.76
Parallel_E0	0.00143	141.03	201.1	2.69	25.98
Parallel_E2	0.00135	139.18	187.9	2.72	27.80

). In terms of the energy-delay product, the EDP of Scalar_E0 is 5224.4 Js$\times {10}^{-9}$, whereas the EDP of the Scalar_E2 kernel that uses an additional memory hierarchy of block size $(2m+n-1)$ × $(2m+n-1)$ is 608.8 Js$\times {10}^{-9}$, which is an ≈9× improvement in energy efficiency in terms of EDP.

An important observation from Figure 6 is that the efficiency peaks with a two-layer memory hierarchy of $(2m+n-1)$ × $(2m+n-1)$ block memory and degrades with the introduction of any additional layers of smaller memory blocks. Two factors that can contribute to this result are: (i) data-reuse transformations generally make the code more complex and increase the code size; (ii) due to fixed-size caches, smaller data blocks are mapped to relatively larger cache blocks, which negate the advantage of using additional memory layers.

On the Haswell system, we also see that relative EDP measurements are improved by the data-reuse transformations techniques. Figure 7 illustrates that both parallelization and vectorization improve the energy efficiency in terms of EDP for the optimized (that exploits the data-reuse transformation methodology), as well as the unoptimized ME kernels (that does not use data-reuse transformations). Among the different possible ME kernels, AVX2_E2 consumes the least amount of core energy (shown in Figure 3b), and the relative EDP values are improved rapidly with increasing number of threads and reach the maximum value when the total number of threads is four (in Figure 7). However, once the number of threads exceeds four, relative EDP begins to decline.

It is also interesting to note that the multithreaded parallelization of the motion estimation kernel does not lead to core-energy savings despite the reduction in execution time due to parallelization at a peak core frequency on the Haswell system. This is an expected behavior if proper power saving mechanisms are in place, meaning that idle cores go into low power mode and do not contribute significantly to the total energy consumed during the application run. This is illustrated in Figure 3c. In contrast, vectorization results in quite a significant amount of core energy savings for the motion estimation kernel. This is due to several reasons. First, Intel processors do not have a separate vector unit or separate vector registers. This translates into a small increase in the power dissipated by the ALUs/register bank working with SIMD instructions instead of scalar. In fact, GCC/ICC compilers no longer generate the scalar assembly, but rather SIMD instructions working only with the lowest vector lane. In addition, when working with vectors, the system spends more idle waiting time for memory, and therefore, cores can go into low power mode more often. This demonstrates that vectorization can lead to significant core energy savings if they can be applied effectively.

Table 5 gives a summary of our results for the Sandy Bridge platform. They show that data reuse transformations significantly improve the energy efficiency of the ME algorithm. The Relative EDP column in the table presents EDP values of different approaches normalized with respect to the EDP value of optimized parallel ME kernel. Relative EDP values indicate that the best energy efficiency can be achieved by using the parallel-optimized solution. Compared to the optimized serial solution (Scalar_E2), the parallel optimized solution (Parallel_E2) gives 3× better EDP, and the serial unoptimized solution (Scalar_E0) provides 28× higher EDP.

5.5. Performance and Energy Efficiency Analysis on the KNL Coprocessor

In our last set of experiments, we study the same problem in the many-core context. To this end, the best performing transformation options (E2 kernels) are chosen along with the baseline (E0) to carry out scalability tests on the Intel Xeop Phi Co-processor (KNL). However, unlike the experiments done on the multi-core platforms, experiments on the KNL platform deal with full HD frames (1920 × 1080) as an input rather than the QCIF format. 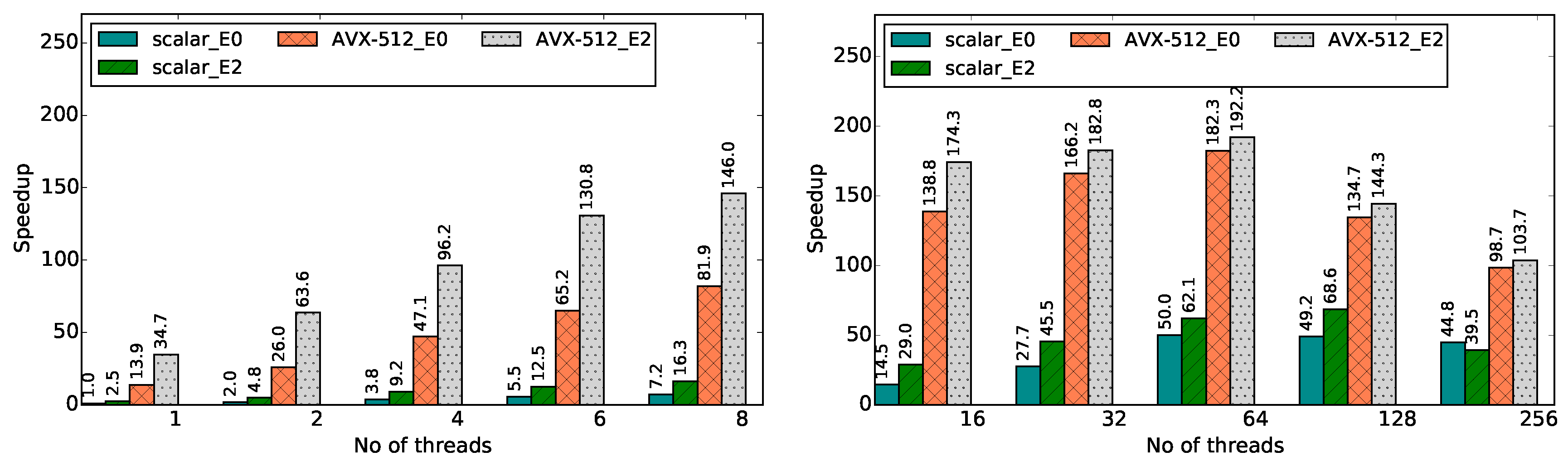Figure 8 and Figure 9 present improvements for the speedup and energy efficiency metrics that can be achieved through the optimized kernels when run on up to 256 threads on KNL (64 cores running four threads each; the rest of the cores are reserved to manage the operating system). In Figure 8, observations on the single core performance highlight two interesting aspects of the kernels being investigated. First, Scalar_E0 (i.e., unoptimized) and Scalar_E2 (i.e., optimized using data reuse transformations) kernels exhibit ≈3× performance increase, which is similar to what was observed on the Haswell system. Therefore, we can conclude that the data reuse transformations on a single core in a KNL coprocessor are as effective as the transformations on a single core in the Haswell system. Second, once again, the performance difference between a non-vectorized and vectorized kernel is quite significant; for example, the single-threaded AVX512_E2) kernel is ≈35× faster than the single-threaded (Scalar_E0) kernel on the Haswell system (Figure 4c). Third, a significant amount of performance improvement can be observed by the deployment of data reuse transformations in conjunction with the AVX512 vectorization technique. Particularly for lower number of threads (i.e., <8), AVX512_E2 provides ≈2× better performance than AVX512_E0. Furthermore, we can also observe that the performance is increased with the increasing number of threads until it passes 64 threads and simultaneous multithreading takes place.

In terms of energy efficiency, we have also achieved improved results as shown in Figure 9. This metric is also scalable across multiple threads as long as only one thread runs per core. The energy efficiency improvements on the KNL platform are much larger than for the Haswell platform, which may seem surprising. The governor for our KNL system is set to performance, and it will therefore never throttle the core frequency down. In addition, there is probably not enough time to disable cores. According to Intel, it takes around one minute for an idle KNL core to go completely offline. On low core count, the OS may be jumping/sending system processes to different cores, so none will ever go offline. At best, the OS could use DVFS (Dynamic voltage and frequency scaling) to reduce core frequency, but our governor prevents this. Since we do not have root access, we cannot test shield cores (prevent scheduling of OS processes into specific cores), nor bind all OS processes into a single core, nor change the governor. Nevertheless, this would be the common case for most end users.

5.6. Summary of Findings

We now summarize the key results and observations from our performance and energy efficiency evaluation of different data reuse transformations on Intel multi- and many-core systems.

• Use of data reuse transformations together with vectorization is a promising approach to improve the performance and energy efficiency of massively parallel data-dominated applications (such as motion estimation) on multi- and many-core systems. Significant energy improvements can be achieved from throughput-oriented architectures that rely on low-power processing cores (e.g., KNL cores), especially if those cores provide SIMD/vector capabilities. These architectures have better energy efficiency (simple cores with low clock frequency) than complex cores available in commodity CPUs.
• As compared to multi-threaded parallelism, data-parallelism through vector processing results in better energy savings even at peak core frequency. While doubling the number of cores results in approximately double the average power dissipated by the CPU, using vector units in Intel comes almost “for free” in terms of average power. Similar results have also been reported for several Intel and ARM CPUs in [3]. As a consequence, vector processing can be an attractive solution to improve energy efficiency without sacrificing performance, especially in a situation where performance trade-off is not desirable.
• The deployment order of different optimization techniques has a great impact on the application performance. First, we apply multithreading to exploit explicit parallelism across multiple cores, which is followed by fine-grained parallelism through vectorization at each core. Finally, data reuse transformations are applied as it depends on both multithreading and vectorization for further improvement. However, on applications that face scalability issues, users may want to limit the amount of threads running in their application and rely more on SIMD units, since the energy cost of running on extra physical cores is much higher than using SIMD instructions.
• In contrast to the results of Wuytack et al. in [6] where they have shown that a three-layer memory hierarchy is the most energy-efficient scheme for the ME algorithm, our results show that a two-layer memory hierarchy is more energy efficient. However, there exists a fundamental difference between these two experiments: First, we conduct our experiment on multi-core and many-core systems with a memory hierarchy of fixed sized cache-blocks, and thus, the copy-candidates are mapped into these fixed-size system caches. Since we cannot manually turn off the part of the caches not being used, our measurements include the energy consumed by both used and idle cache lines. Wuytack et al. avoided this extra energy consumption by conducting their experiment in a simulation environment where they created a hierarchy of memory blocks perfectly fitting the data blocks.

6. Conclusions

In this paper, we have investigated the performance and energy efficiency effects of applying data-reuse transformations on a multi-core processor running a motion estimation algorithm. We have shown that the performance can be improved up to 35×, and core energy consumption can be reduced by 25× on multi-core platforms (Haswell and Sandy Bridge) using appropriate data-reuse transformation techniques in combination with parallelization and vectorization. For a KNL many-core processor platform, this improvement can reach up to 192× and 185× (EDP 35,662×) for performance and core energy efficiency respectively when it runs with 64 threads. This gives clear indications that a data reuse methodology in combination with a parallel programming model can significantly save energy, as well as improve the performance of this type of application running on multi- and many-core processors.

In our experiments, simultaneous multithreading causes performance degradation. As our study was only limited to static and dynamic scheduling (in the KNL coprocessor), we plan to further extend our study to analyze the effect of using a more advanced scheduling method (e.g., guided scheduling) along with compiler-assisted selected lock assignment on the data reuse transformations in the simultaneous multithreading environment.

In the future, we will extend our study by running the experiments on an execution platform supporting a concept like drowsy cache [34] that powers down the unused parts of the cache. This would give more comparable results against the results of Wuytack et al.