Completing the Complete ECC Formulae with Countermeasures
Abstract
:1. Introduction
2. Background Information
2.1. Formulas
2.2. Side-Channel Analysis and Countermeasures
2.2.1. Countermeasures
2.2.2. Test Vector Leakage Assessment Methodology
3. Related Work
ECC Hardware Implementations
4. Experimental Setup
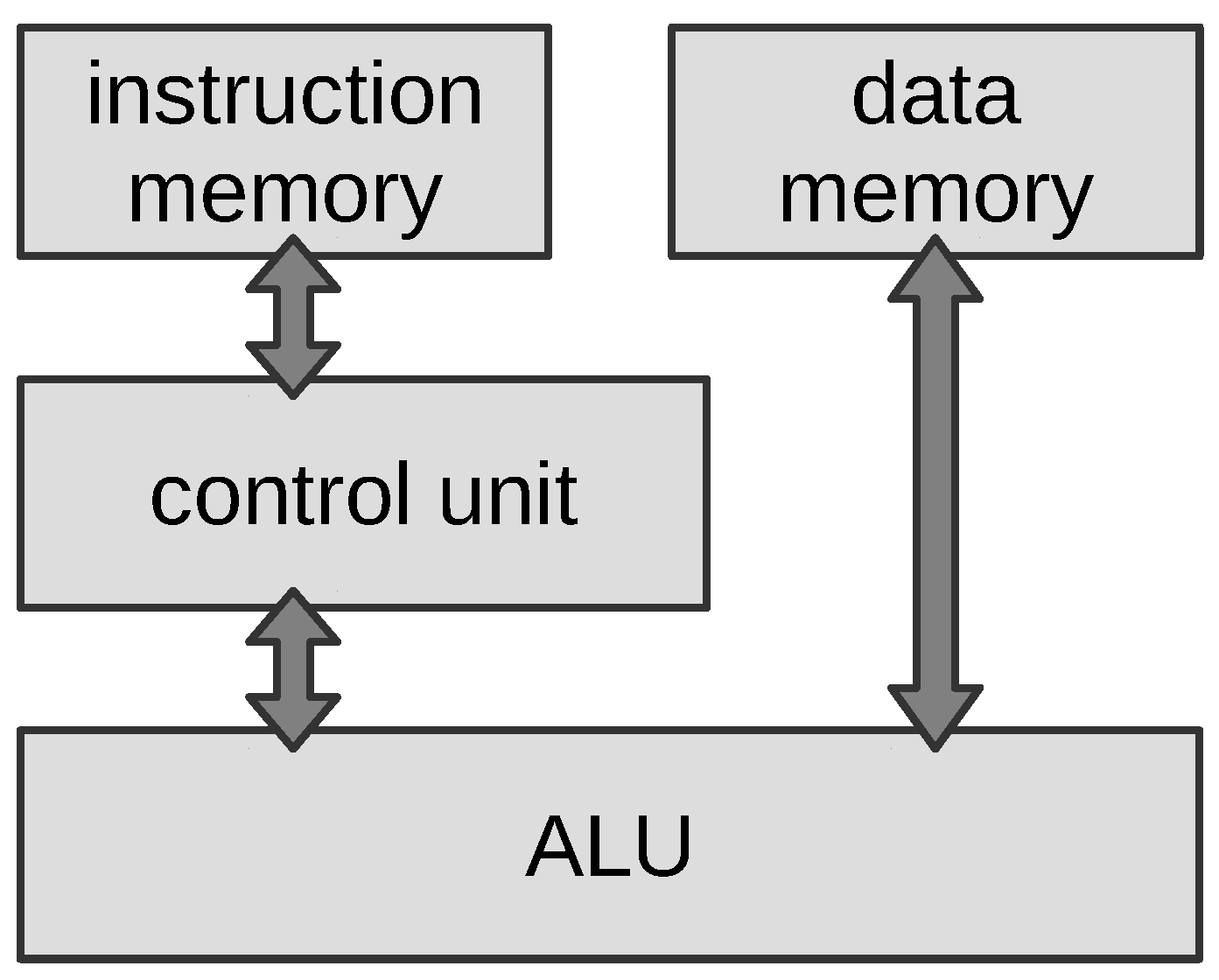
4.1. Hardware Architecture
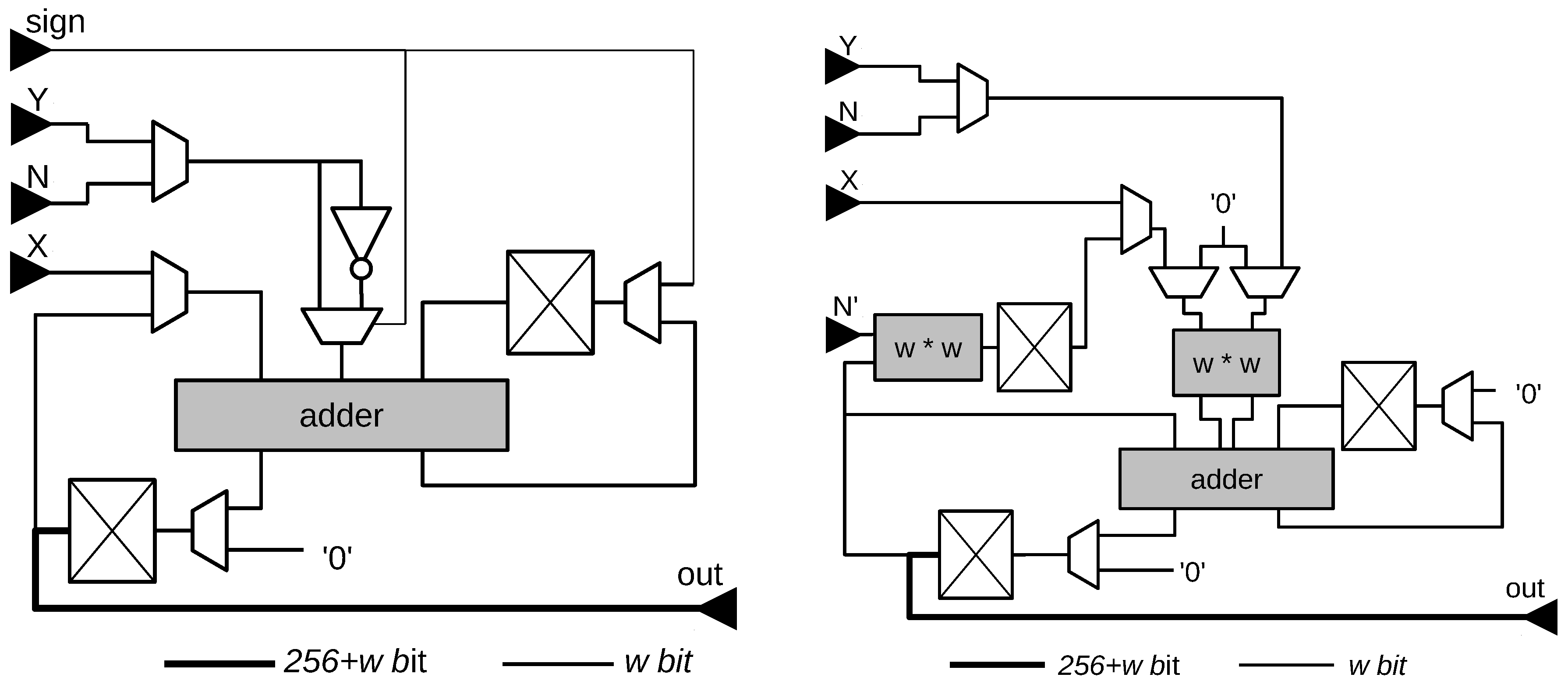
- conversion of the coordinates of the point to Montgomery form and to homogeneous coordinates:
- initialization of S:
- execution of the Montgomery ladder [28], performing a scalar multiplication of a hard coded scalar with P
- calculation of the modular inverse of
- conversion of Q back to affine coordinates and undoing the Montgomery form
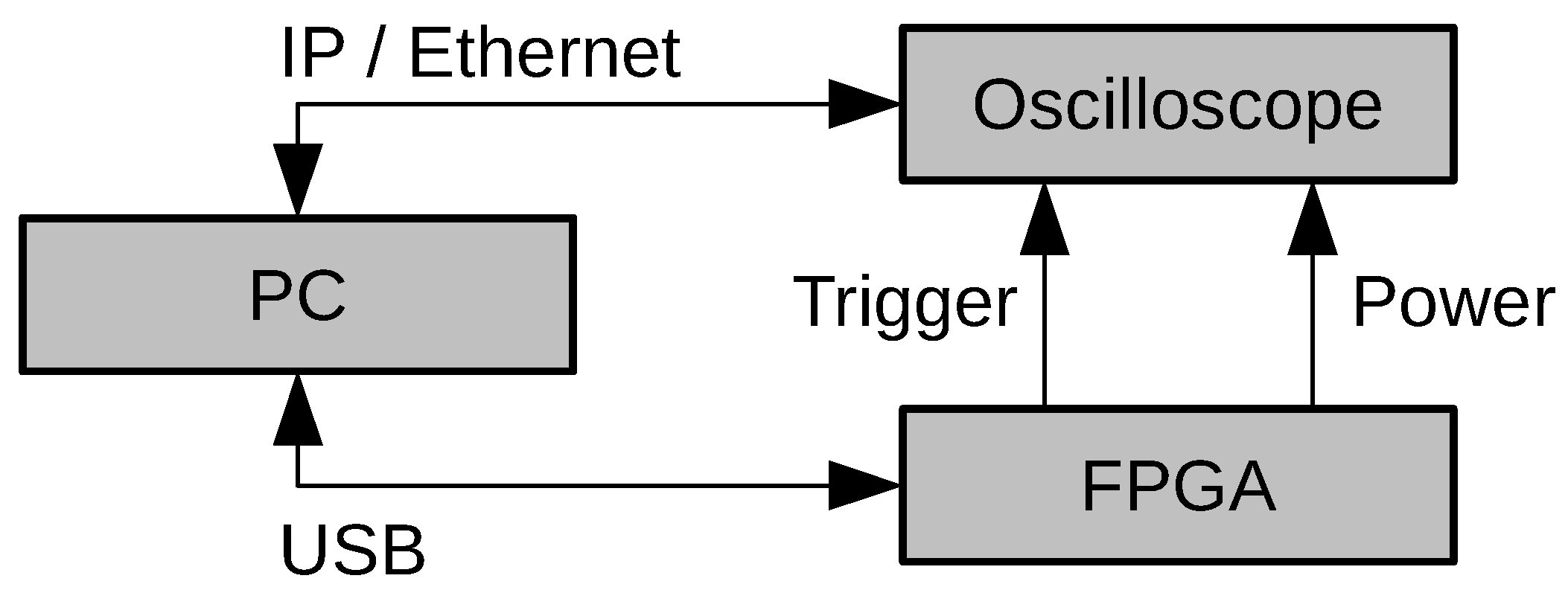
4.2. Measurement Setup
5. Side-Channel Analysis
5.1. Application of the TVLA Methodology to ECC
5.2. Leakage Analysis
5.3. Analysis Results
5.3.1. Timing Analysis
5.3.2. TVLA Analysis
- with no countermeasures applied;
- with point randomization;
- with point randomization and scalar randomization.
Unprotected Implementation
- ,
- randomly selected subset of of size T and.
Implementation protected with coordinate randomization:
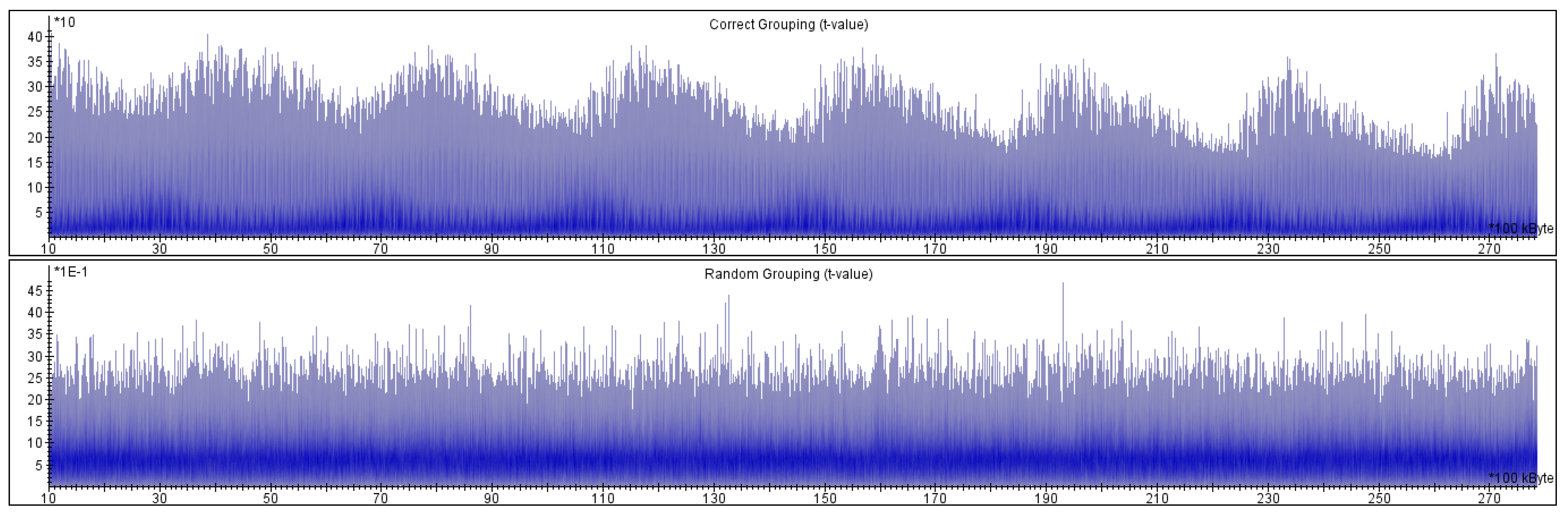
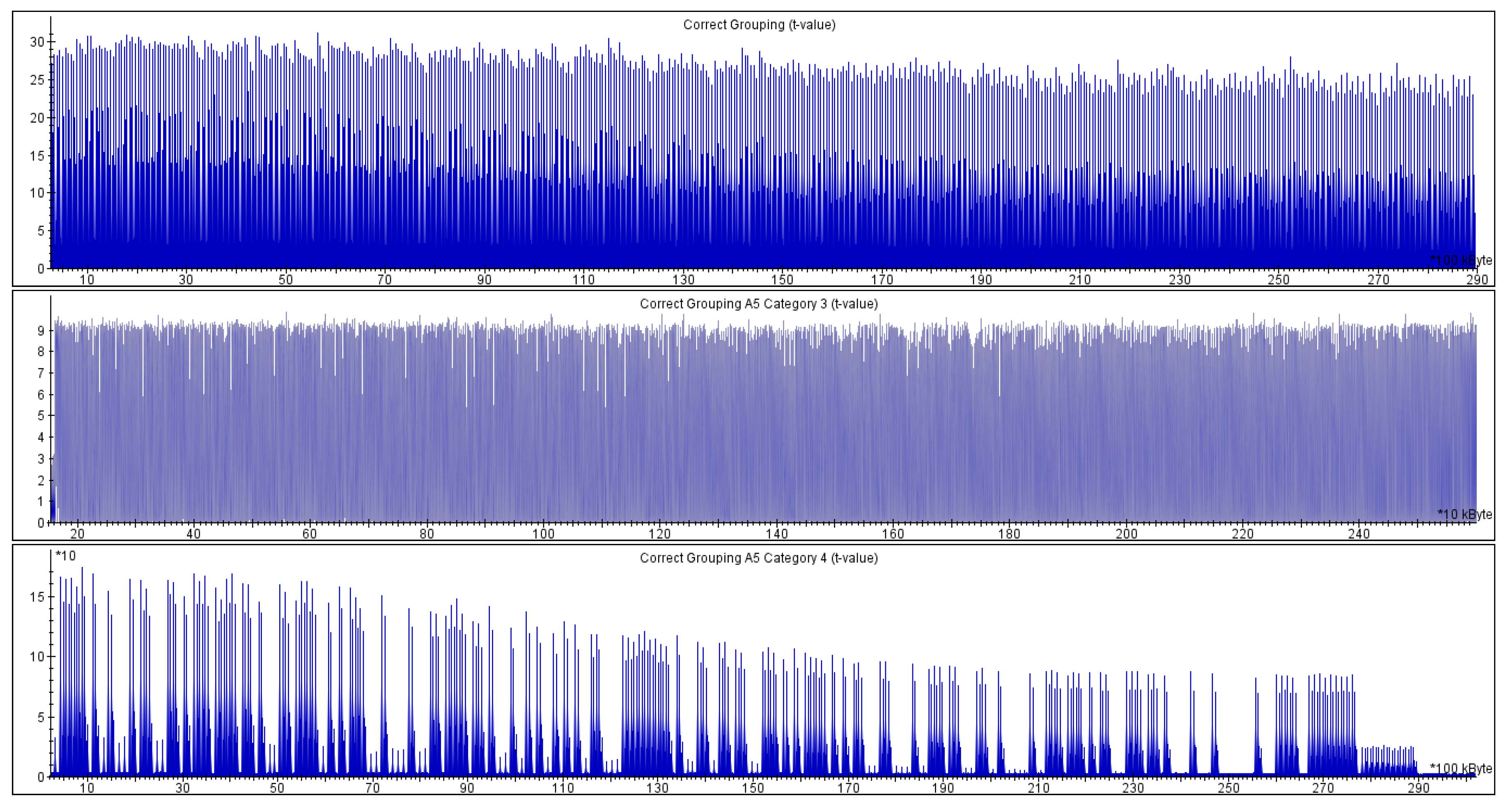
- the t-statistics values for the groups and (both categories) are way above , as presented in Figure 5; the values reach for , for and Category 3 and for and Category 4.
- the t-statistics for the group and the group are almost always less than , and they rarely reach the threshold (never significantly).
Implementation protected with coordinate randomization and scalar splitting:
6. Results and Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Miller, V. Use of Elliptic Curves in Cryptography. In Advances in Cryptology—CRYPTO 85 Proceedings; Springer: Berlin/Heidelberg, Germany, 1986; Volume 218, pp. 417–426. [Google Scholar]
- Kocher, P.; Jaffe, J.; Jun, B. Differential Power Analysis. In Advances in Cryptology—CRYPTO’ 99; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1666, pp. 388–397. [Google Scholar]
- Coron, J. Resistance against Differential Power Analysis for Elliptic Curve Cryptosystems. In Proceedings of the First International Workshop on Cryptographic Hardware and Embedded Systems, CHES’99, Worcester, MA, USA, 12–13 August 1999; pp. 292–302.
- Bernstein, D.J.; Lange, T. Faster Addition and Doubling on Elliptic Curves. In Proceedings of the 13th International Conference on the Theory and Application of Cryptology and Information Security, Advances in Cryptology—ASIACRYPT 2007, Kuching, Malaysia, 2–6 December 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 29–50. [Google Scholar]
- Batina, L.; Mentens, N.; Preneel, B.; Verbauwhede, I. Side-Channel Aware Design: Algorithms and Architectures for Elliptic Curve Cryptography over GF(2n). In Proceedings of the 16th IEEE International Conference on Application-Specific Systems, Architectures, and Processors (ASAP 2005), Samos, Greece, 23–25 July 2005; pp. 350–355.
- Renes, J.; Costello, C.; Batina, L. Complete Addition Formulas for Prime Order Elliptic Curves. In Proceedings of the 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Advances in Cryptology—EUROCRYPT 2016, Vienna, Austria, 8–12 May 2016.
- Bernstein, D.J.; Lange, T. Explicit-Formulas Database. Available online: http://hyperelliptic.org/EFD/index.html (accessed on 21 February 2015).
- Batina, L.; Chmielewski, L.; Papachristodoulou, L.; Schwabe, P.; Tunstall, M. Online Template Attacks. In Proceedings of the 15th International Conference on Cryptology in India, Progress in Cryptology—INDOCRYPT 2014, New Delhi, India, 14–17 December 2014; pp. 21–36.
- Joye, M.; Yen, S. The Montgomery Powering Ladder. In Proceedings of the 4th International Workshop, Cryptographic Hardware and Embedded Systems—CHES 2002, Redwood Shores, CA, USA, 13–15 August 2002; pp. 291–302.
- Goodwill, G.; Jun, B.; Jaffe, J.; Rohatgi, P. A Testing Methodology for Side-Channel Resistance Validation; NIST Non-Invasive Attack Testing Workshop: Nara, Japan, 2011. [Google Scholar]
- Jaffe, J.; Rohatgi, P.; Witteman, M. Efficient Side-Channel Testing for Public Key Algorithms: RSA Case Study. Available online: http://csrc.nist.gov/news_events/non-invasive-attack-testing-workshop/papers/09_Jaffe.pdf (accessed on 22 January 2017).
- Tunstall, M.; Goodwill, G. Applying TVLA to Public Key Cryptographic Algorithms. Cryptology ePrint Archive, Report 2016/513, 2016. Available online: http://eprint.iacr.org/2016/513 (accessed on 24 May 2016).
- Nascimento, E.; López, J.; Dahab, R. Efficient and Secure Elliptic Curve Cryptography for 8-bit AVR Microcontrollers. In Proceedings of the 5th International Conference, Security, Privacy, and Applied Cryptography Engineering, SPACE 2015, Jaipur, India, 3–7 October 2015; Springer International Publishing: Cham, Switzerland, 2015; pp. 289–309. [Google Scholar]
- Marzouqi, H.; Al-Qutayri, M.; Salah, K. Review of Elliptic Curve Cryptography processor designs. Microprocess. Microsyst. 2015, 39, 97–112. [Google Scholar] [CrossRef]
- Roy, D.B.; Das, P.; Mukhopadhyay, D. ECC on Your Fingertips: A Single Instruction Approach for Lightweight ECC Design in GF (p). In Proceedings of the 22nd International Conference, Selected Areas in Cryptography, Sackville, NB, Canada, 12–14 August 2015; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Pöpper, C.; Mischke, O.; Güneysu, T. MicroACP—A Fast and Secure Reconfigurable Asymmetric Crypto-Processor. In Reconfigurable Computing: Architectures, Tools, and Applications; Springer International Publishing: Cham, Switzerland, 2014; Volume 8405, pp. 240–247. [Google Scholar]
- Vliegen, J.; Mentens, N.; Genoe, J.; Braeken, A.; Kubera, S.; Touhafi, A.; Verbauwhede, I. A Compact FPGA-Based Architecture for Elliptic Curve Cryptography over Prime Fields. In Proceedings of the 2010 21st IEEE International Conference on Application-Specific Systems Architectures and Processors (ASAP), Rennes, France, 7–9 July 2010; pp. 313–316.
- Alrimeih, H.; Rakhmatov, D. Fast and Flexible Hardware Support for ECC Over Multiple Standard Prime Fields. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2014, 22, 2661–2674. [Google Scholar] [CrossRef]
- Guillermin, N. A High Speed Coprocessor for Elliptic Curve Scalar Multiplications over . In Proceedings of the 12th International Workshop, Cryptographic Hardware and Embedded Systems, CHES 2010, Santa Barbara, CA, USA, 17–20 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6225, pp. 48–64. [Google Scholar]
- Esmaeildoust, M.; Schinianakis, D.; Javashi, H.; Stouraitis, T.; Navi, K. Efficient RNS Implementation of Elliptic Curve Point Multiplication Over GF(p). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2013, 21, 1545–1549. [Google Scholar] [CrossRef]
- Sasdrich, P.; Güneysu, T. Efficient Elliptic-Curve Cryptography Using Curve25519 on Reconfigurable Devices. In Reconfigurable Computing: Architectures, Tools, and Applications; Springer International Publishing: Cham, Switzerland, 2014; Volume 8405, pp. 25–36. [Google Scholar]
- Baldwin, B.; Moloney, R.; Byrne, A.; McGuire, G.; Marnane, W.P. A Hardware Analysis of Twisted Edwards Curves for an Elliptic Curve Cryptosystem. In Reconfigurable Computing: Architectures, Tools and Applications; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5453, pp. 355–361. [Google Scholar]
- Järvinen, K.; Miele, A.; Azarderakhsh, R.; Longa, P. Four on FPGA: New Hardware Speed Records for Elliptic Curve Cryptography over Large Prime Characteristic Fields. In Proceedings of the 18th International Conference on Cryptographic Hardware and Embedded Systems—CHES 2016, Santa Barbara, CA, USA, 17–19 August 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 517–537. [Google Scholar]
- Ghosh, S.; Mukhopadhyay, D.; Roychowdhury, D. Petrel: Power and Timing Attack Resistant Elliptic Curve Scalar Multiplier Based on Programmable GF(p) Arithmetic Unit. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1798–1812. [Google Scholar] [CrossRef]
- Montgomery, P.L. Modular Multiplication without Trial Division. Math. Comput. 1985, 44, 519–521. [Google Scholar] [CrossRef]
- Walter, C.D. Montgomery Exponentiation Needs No Final Subtraction. Electron. Lett. 1999, 35, 1831–1832. [Google Scholar] [CrossRef]
- Montgomery, P.L. Speeding the Pollard and Elliptic Curve Methods of Factorization. Math. Comput. 1987, 48, 243–264. [Google Scholar] [CrossRef]
- Guntur, H.; Ishii, J.; Satoh, A. Side-channel Attack User Reference Architecture Board SAKURA-G. In Proceedings of the 2014 IEEE 3rd Global Conference on Consumer Electronics (GCCE), Tokyo, Japan, 7–10 October 2014; pp. 271–274.
- Itoh, K.; Izu, T.; Takenaka, M. A Practical Countermeasure against Address-Bit Differential Power Analysis. In Cryptographic Hardware and Embedded Systems—CHES 2003; Walter, C.D., Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2779, pp. 382–396. [Google Scholar]
- Nascimento, E.; Chmielewski, Ł.; Oswald, D.; Schwabe, P. Attacking Embedded ECC Implementations through cmov Side Channels. In Selected Areas in Cryptology—SAC 2016; Avanzi, R., Heys, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Chari, S.; Jutla, C.S.; Rao, J.R.; Rohatgi, P. Towards Sound Approaches to Counteract Power-Analysis Attacks. In Proceedings of the 19th Annual International Cryptology Conference, Advances in Cryptology—CRYPTO’ 99, Santa Barbara, CA, USA, 15–19 August 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 398–412. [Google Scholar]
- Clavier, C.; Joye, M. Universal Exponentiation Algorithm A First Step towards Provable SPA-Resistance. In Proceedings of the Third International Workshop on Cryptographic Hardware and Embedded Systems—CHES 2001, Paris, France, 14–16 May 2001; Springer: Berlin/Heidelberg, , 2001; pp. 300–308. [Google Scholar]
- Witteman, M.; van Woudenberg, J.; Menarini, F. Defeating RSA Multiply-Always and Message Blinding Countermeasures. In Proceedings of the Topics in Cryptology—CT-RSA 2011, San Francisco, CA, USA, 14–18 February 2011; Kiayias, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6558, pp. 77–88. [Google Scholar]
- Hanley, N.; Kim, H.; Tunstall, M. Exploiting Collisions in Addition Chain-Based Exponentiation Algorithms Using a Single Trace. In Proceedings of the Topics in Cryptology–CT-RSA 2015, San Francisco, CA, USA, 20–24 April 2015; Nyberg, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9048, pp. 431–448. [Google Scholar]
- Perin, G.; Chmielewski, Ł. A Semi-Parametric Approach for Side-Channel Attacks on Protected RSA Implementations. In Smart Card Research and Advanced Application; Homma, N., Medwed, M., Eds.; Springer: Cham, Switzerland, 2015; Volume 9514, pp. 102–114. [Google Scholar]

| FPGA Resource | ECPOnly | Full |
|---|---|---|
| Number of slice registers | 2274 | 2892 |
| Number of slice LUTs | 2421 | 2752 |
| Number of RAMB16 | 9 | 9 |
| Number of DSP48A1 | 7 | 7 |
| Set # | Properties | Rationale |
|---|---|---|
| 1 | constant k, constant P | This is the baseline. The tests compare power consumption from the other sets against it. |
| 2 | constant k, varying P | The goal is to detect systematic relationships between the power consumption and the P value. |
| 3 | varying k, constant P | The goal is to detect systematic relationships between the power consumption and the k value. |
| 4 | constant k, special P | Edge cases of the algorithms used. |
| 5 | special k, constant P | Edge cases of the algorithms used. |
| Set # | Category # | Properties |
|---|---|---|
| 4 | 1x | . |
| 4 | 1y | . |
| 4 | 2x | . |
| 4 | 2y | . |
| 5 | 3 | . |
| 5 | 4 | . |
| 4 | 5x | x has a low Hamming Weight (≤25). |
| 4 | 5y | y has a low Hamming Weight (≤25). |
| 4 | 6x | x has a high Hamming Weight (≥230). |
| 4 | 6y | y has a high Hamming Weight (≥230). |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chmielewski, Ł.; Massolino, P.M.C.; Vliegen, J.; Batina, L.; Mentens, N. Completing the Complete ECC Formulae with Countermeasures. J. Low Power Electron. Appl. 2017, 7, 3. https://doi.org/10.3390/jlpea7010003
Chmielewski Ł, Massolino PMC, Vliegen J, Batina L, Mentens N. Completing the Complete ECC Formulae with Countermeasures. Journal of Low Power Electronics and Applications. 2017; 7(1):3. https://doi.org/10.3390/jlpea7010003
Chicago/Turabian StyleChmielewski, Łukasz, Pedro Maat Costa Massolino, Jo Vliegen, Lejla Batina, and Nele Mentens. 2017. "Completing the Complete ECC Formulae with Countermeasures" Journal of Low Power Electronics and Applications 7, no. 1: 3. https://doi.org/10.3390/jlpea7010003
APA StyleChmielewski, Ł., Massolino, P. M. C., Vliegen, J., Batina, L., & Mentens, N. (2017). Completing the Complete ECC Formulae with Countermeasures. Journal of Low Power Electronics and Applications, 7(1), 3. https://doi.org/10.3390/jlpea7010003





