Fast Energy Recovery During Motor Braking: Analysis and Simulation
Abstract
1. Introduction
2. Principle of Energy Braking Recovery
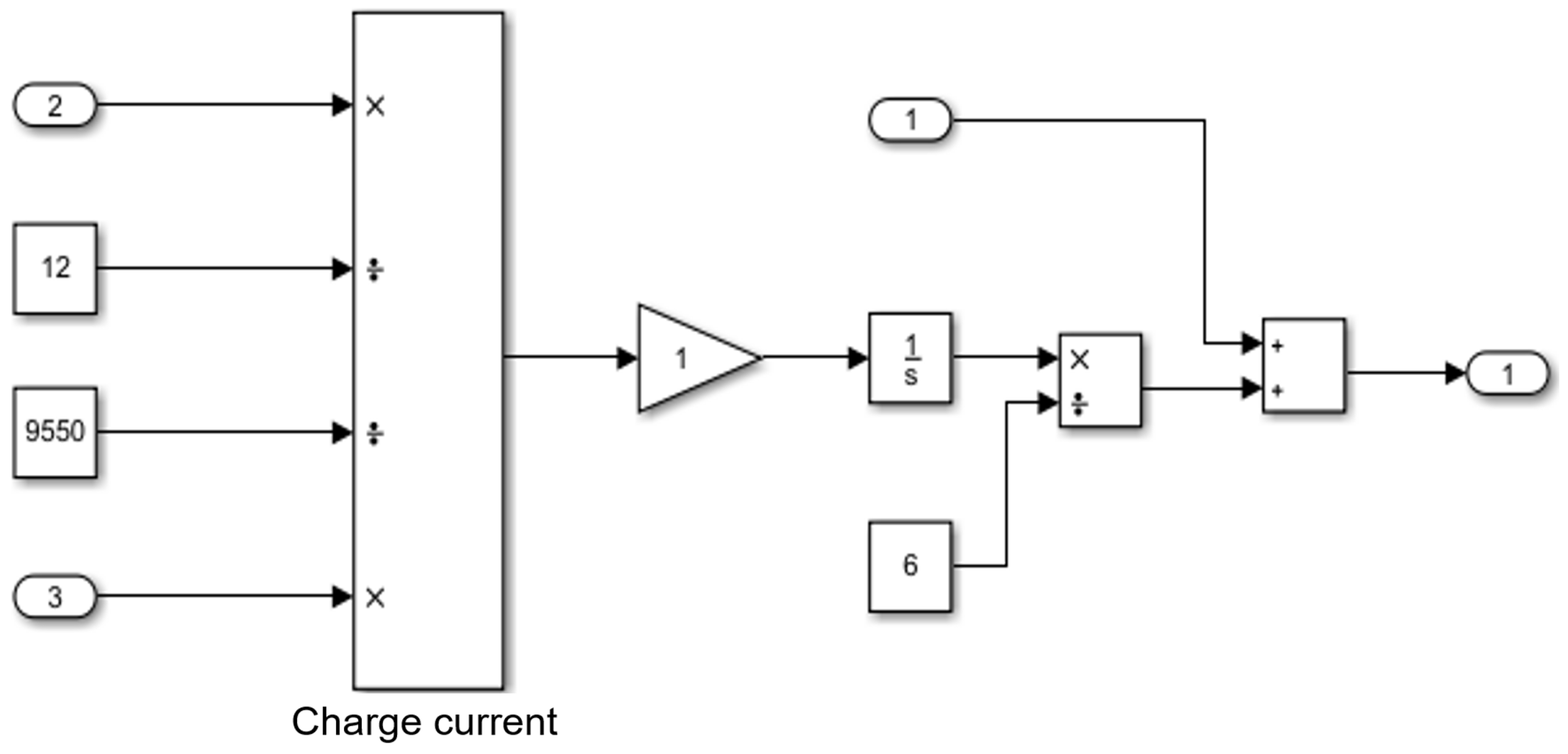
2.1. SOC Estimation Method
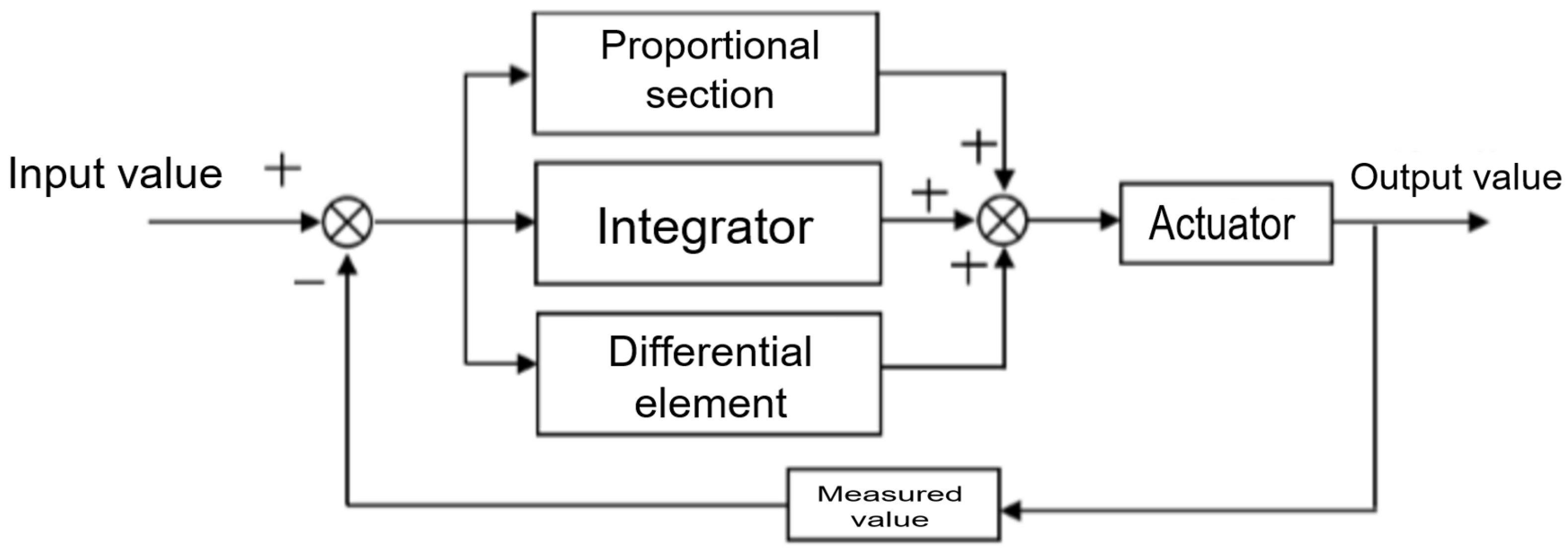
2.2. PID Control Method
3. Simulation of Energy Brake Recovery
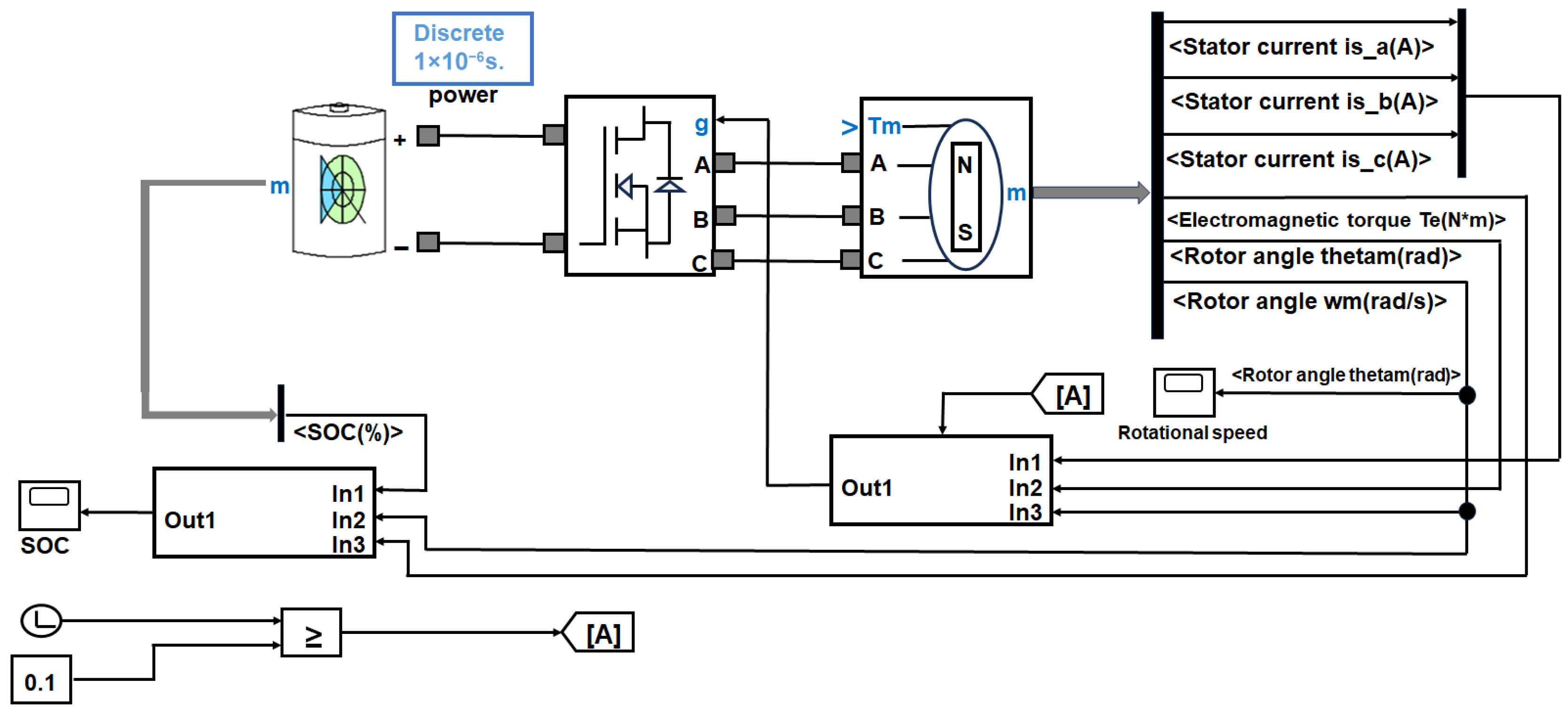
3.1. Main Module
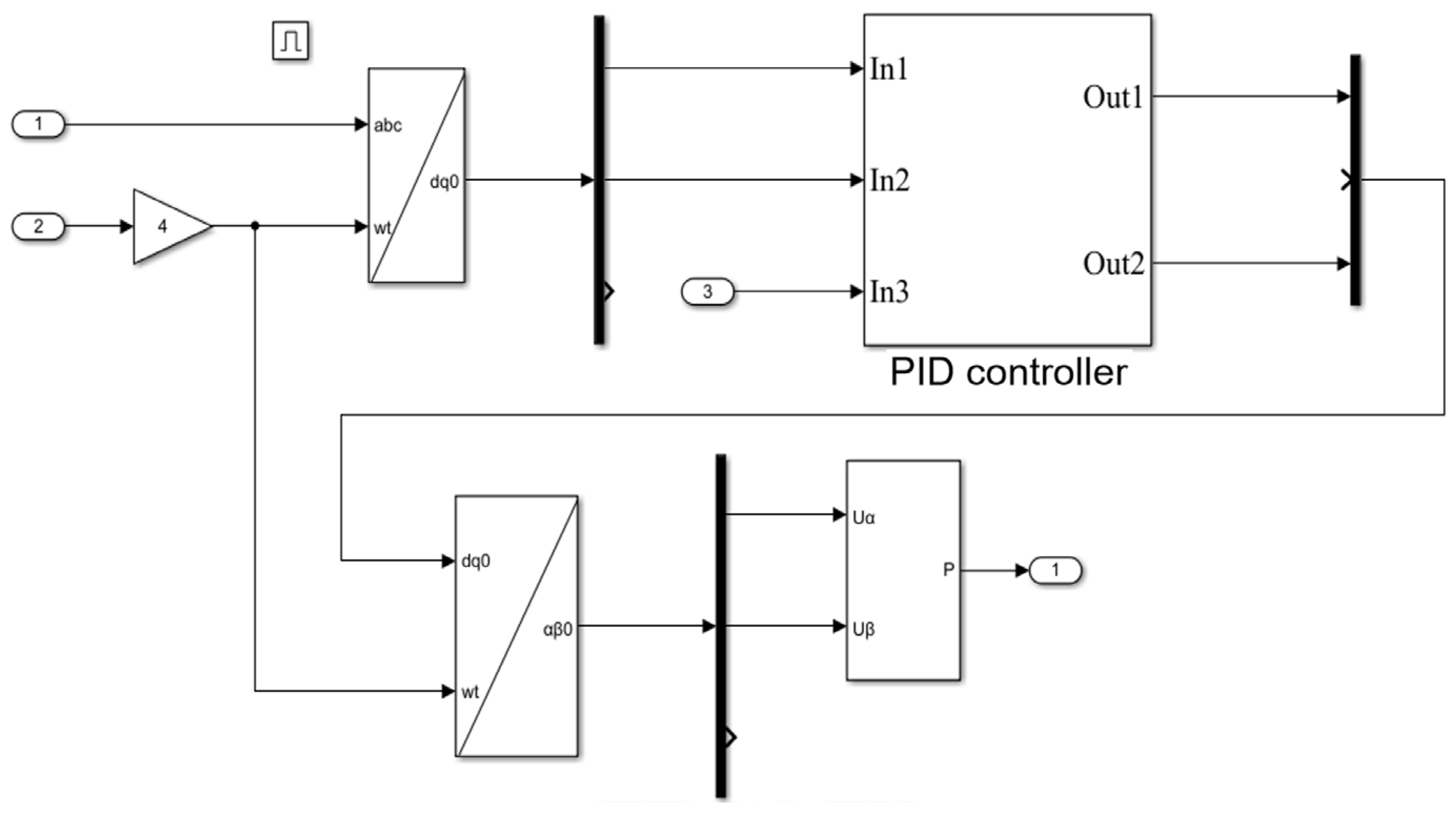
3.2. Control Module
3.3. Recovery Module
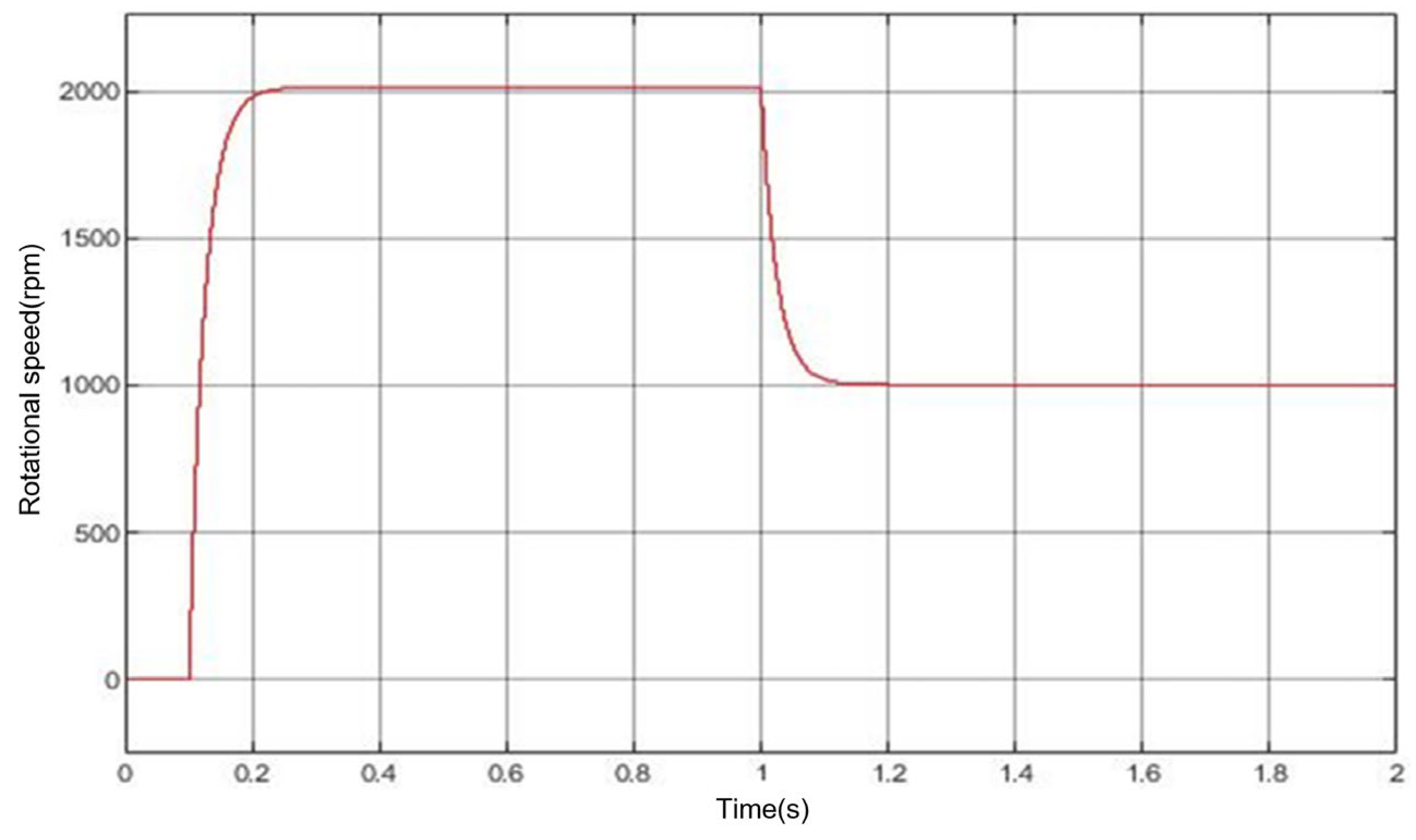
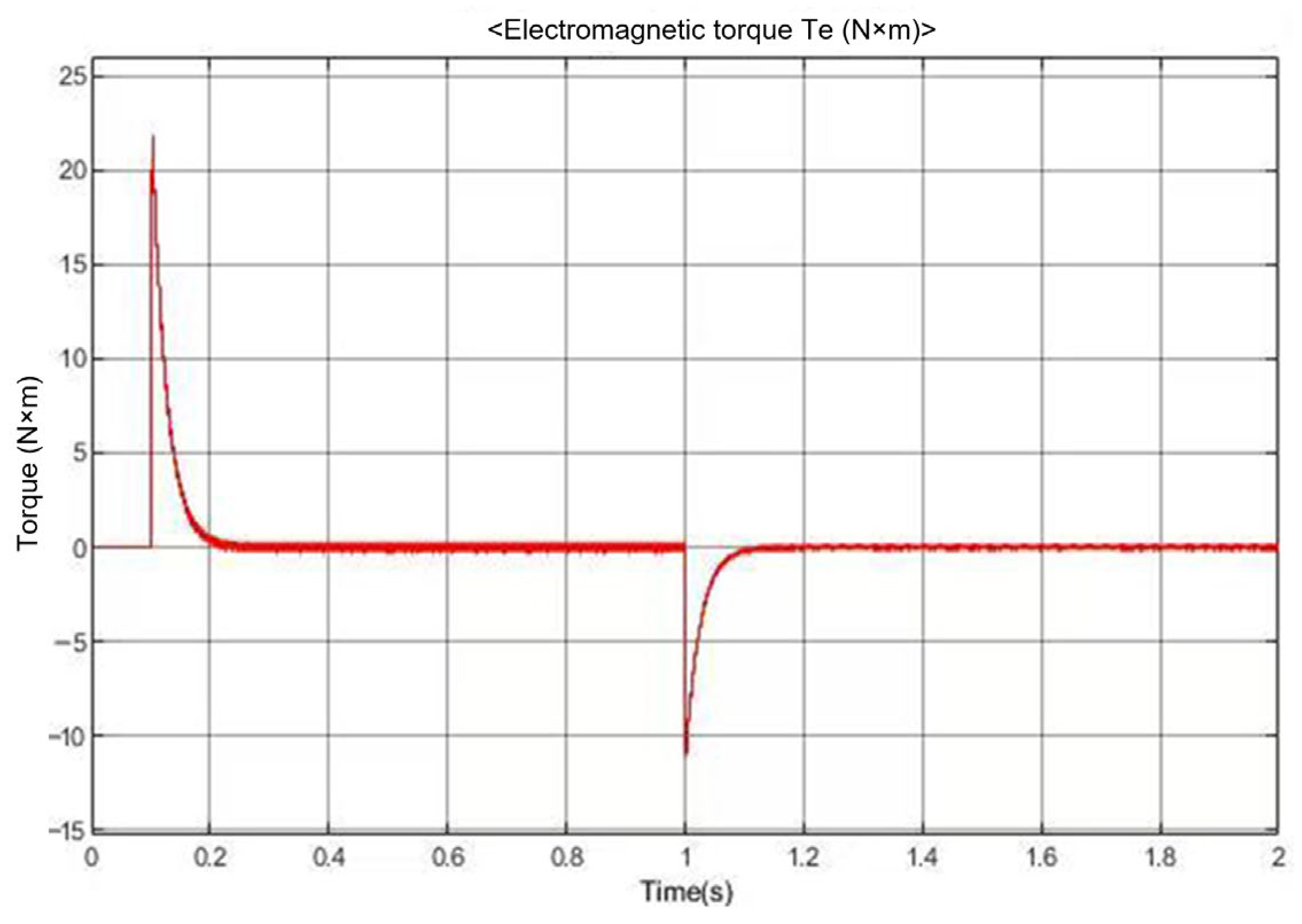
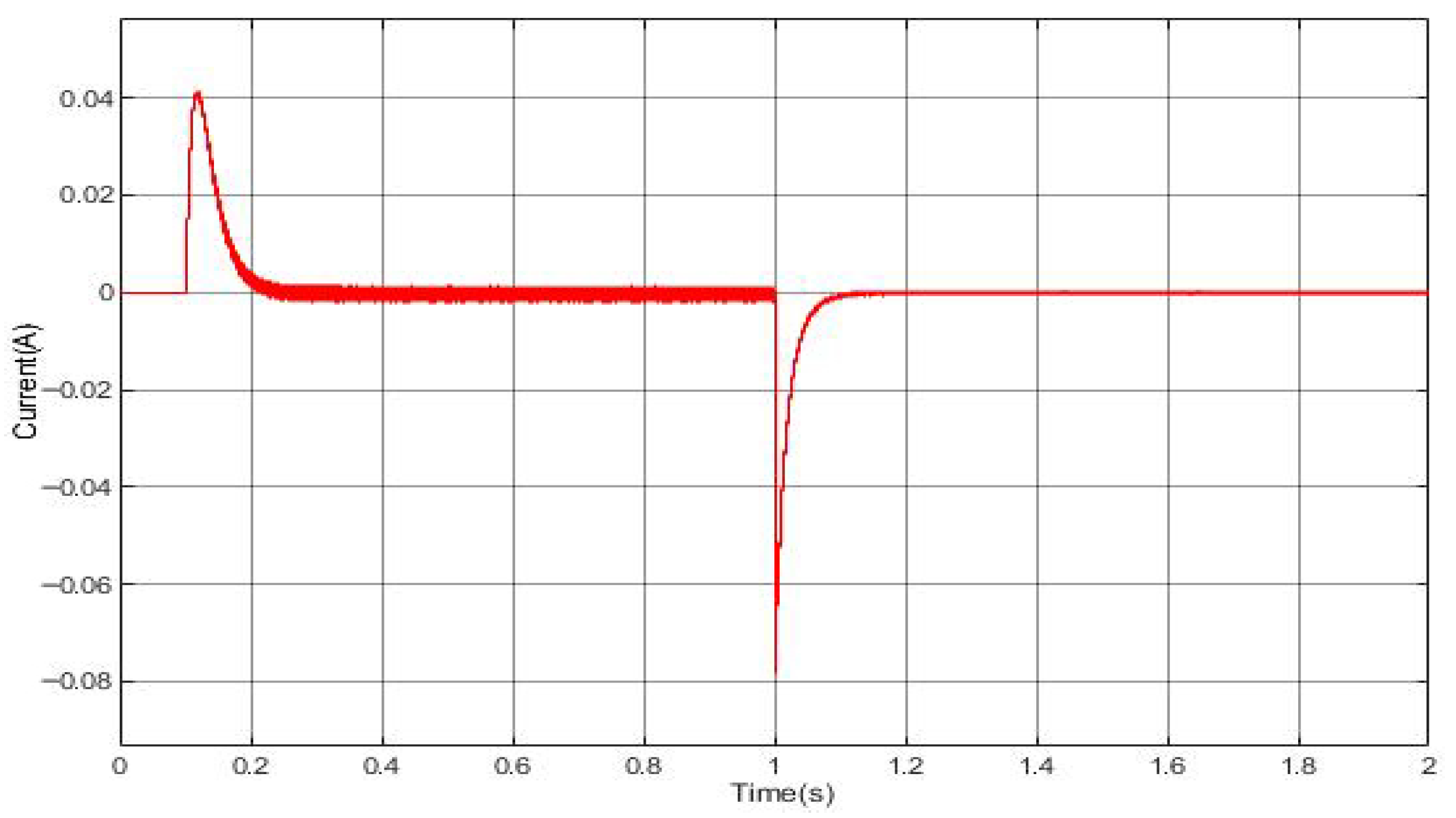
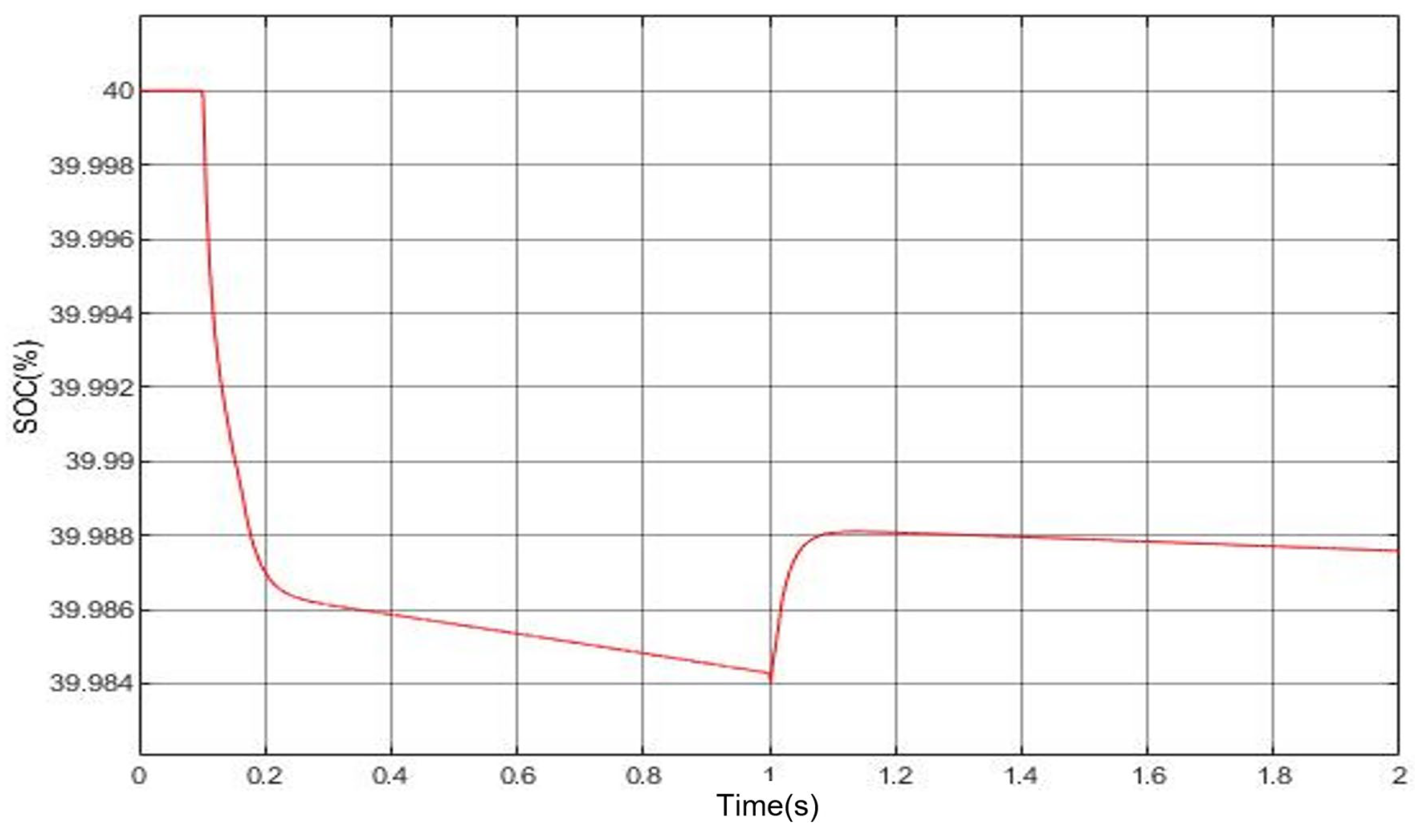
3.4. Analysis of Simulation Results
3.5. Analysis of Test Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Heydari, S.; Fajri, P.; Rasheduzzaman, M. Maximizing regenerative braking energy recovery of electric vehicles through dynamic low-speed cutoff point detection. IEEE Trans. Transp. Electrif. 2019, 5, 262–270. [Google Scholar] [CrossRef]
- Hardman, S.; Chandan, A.; Tal, G. The effectiveness of financial purchase incentives for battery electric vehicles–A review of the evidence. Renew. Sustain. Energy Rev. 2017, 80, 1100–1111. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Liu, P.; Zhang, Z. Energy consumption analysis and prediction of electric vehicles based on real-world driving data. Appl. Energy 2020, 275, 115408. [Google Scholar] [CrossRef]
- Lv, S.; Li, X. A Review of Regenerative Braking Energy Recovery Research for Pure Electric Vehicles. In Proceedings of the 2024 IEEE 5th International Conference on Advanced Electrical and Energy Systems (AEES), Lanzhou, China, 29 November–1 December 2024; pp. 468–472. [Google Scholar]
- Ko, J.; Ko, S.; Son, H. Development of brake system and regenerative braking cooperative control algorithm for automatic-transmission-based hybrid electric vehicles. IEEE Trans. Veh. Technol. 2014, 64, 431–440. [Google Scholar] [CrossRef]
- Chougale, R.G.; Lakade, C.R. Regenerative braking system of electric vehicle driven by brushless DC motor using fuzzy logic. In Proceedings of the 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; IEEE: Chennai, India, 2017; pp. 2167–2171. [Google Scholar]
- Satzger, C.; de Castro, R.; Bünte, T. A model predictive control allocation approach to hybrid braking of electric vehicles. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 286–292. [Google Scholar]
- Hwang, M.H.; Lee, G.S.; Kim, E.; Kim, H.W.; Yoon, S.; Talluri, T.; Cha, H.R. Regenerative braking control trategy based on AI algorithm to improve driving comfort of autonomous vehicles. Appl. Sci. 2023, 13, 946. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H. Braking energy recuperation performance of input coupled power-split hydraulic hybrid powertrain. Trans. Chin. Soc. Agric. Eng. 2013, 29, 23–30. [Google Scholar]
- Zhou, J.; Lu, D.; Yi, F.; Shen, Y.; Lin, H.; Yang, T. Research on Control Strategy of Flywheel Energy Storage Pure Electric Vehicle Braking Energy Recovery System. In Proceedings of the 2020 4th CAA International Conference on Vehicular Control and Intelligence (CVCI), Hangzhou, China, 18–20 December 2020; pp. 536–542. [Google Scholar]
- Yang, Z.; Tan, G.; Ling, H.; Zeng, P.; Li, C.; Liu, L. Research on braking energy recovery strategy of pure electric vehicle. In Proceedings of the Brake Colloquium & Exhibition—39th Annual, Orlando, FL, USA, 17–20 October 2021; Technical Paper. SAE: Warrendale, PA, USA, 2021; Volume 1, p. 1264. [Google Scholar]
- Duong, T.-T.; Huynh, P.-S.; Ngo, Q.-T. Research to Evaluate the Regenerative Braking System Effect on Fuel Consumption of Hybrid Vehicle. In Proceedings of the 2021 International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 26–28 August 2021; pp. 252–256. [Google Scholar]
- Yuan, X.; Li, L.; Gou, H.; Dong, T. Energy and environmental impact of battery electric vehicle range in China. Appl. Energy 2015, 157, 75–84. [Google Scholar] [CrossRef]
- Fu, S.; Lyu, T.; Min, F.; Luo, W.; Luo, C.; Wu, L.; Xie, J. Review of estimation methods on SOC of lithium-ion batteries in electric vehicles. Energy Storage Sci. Technol. 2021, 10, 1127–1136. [Google Scholar] [CrossRef]
- Chen, G.; Jiang, S.; Xie, M.; Yang, F. A hybrid DNN-KF model for real-time SOC estimation of lithium-ion batteries under different ambient temperatures. In Proceedings of the 2022 Global Reliability and Prognostics and Health Management (PHM-Yantai), Yantai, China, 13–16 October 2022; pp. 1–5. [Google Scholar]
- Labiri, H.; Farhat, S.; Nadir, E.; Chekoubi, Z.; Elihssini, H. SoC Estimation in Electric Cars using Ampere-Hour and Fuzzy Logic Approaches. In Proceedings of the 2025 5th International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Fez, Morocco, 15–16 May 2025; pp. 1–4. [Google Scholar]
- Zhu, D.; Chikkannanavar, S.; Tao, J. SOC Estimation Error Analysis for Li Ion Batteries. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; pp. 479–483. [Google Scholar]
- Doicin, B.; Popescu, M.; Patrascioiu, C. PID Controller optimal tuning. In Proceedings of the 2016 8th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Ploiesti, Romania, 30 June–2 July 2016; pp. 1–4. [Google Scholar]
- Chen, W.; Du, Z. Nonlinear adaptive control with integral-PID adaptive law. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010; pp. 2125–2128. [Google Scholar]
- Yue, X.L.; Bai, P. Modeling and Simulation of Brushless DC Motor Speed Control System Based on MATLAB/SIMULINK. Adv. Mater. Res. 2014, 998, 755–758. [Google Scholar] [CrossRef]
- Long, B.; Lim, S.T.; Ryu, J.H.; Chong, K.T. Energy-regenerative braking control of electric vehicles using three-phase brushless direct-current motors. Energies 2013, 7, 99–114. [Google Scholar] [CrossRef]
- Kumar, D.; Gupta, R.A.; Gupta, N. Modeling and simulation of four switch three-phase BLDC motor using anti-windup PI controller. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017; pp. 1–6. [Google Scholar]
- Cheng, J.; Zhang, G.; Lu, C.; Wu, C.; Xu, Y. Research of brushless DC motor control system based on RBF neural network. In Proceedings of the 2017 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; IEEE: Hefei, China, 2017; pp. 521–524. [Google Scholar]
- Wang, P.; Duan, X.; Chen, C.; Liu, S. Experimental investigation on the exhaust emissions and performance of a hybrid electric motor coupled with an energy recovery system. Case Stud. Therm. Eng. 2023, 45, 102994. [Google Scholar] [CrossRef]
- Dasi, S.; Sandiri, R.; Anuradha, T.; Sri, T.S.; Majji, S.; Murugan, K. The State-of-the-art Energy Management Strategy in Hybrid Electric Vehicles for Real-time Optimization. In Proceedings of the 2023 International Conference on Inventive Computation Technologies (ICICT), Lalitpur, Nepal, 26–28 April 2023; pp. 1637–1643. [Google Scholar]
- Abraham, P.K.; Namboodiry, J. Ultracapacitor based Constant Torque Regenerative Braking System for a Brushless DC Motor. In Proceedings of the 2021 IEEE International Power and Renewable Energy Conference (IPRECON), Kollam, India, 24–26 September 2021; IEEE: Kollam, India, 2021; pp. 1–5. [Google Scholar]
- Shi, C.; Wang, W.; Li, W. Analysis of Evaluation Indicators for Regenerative Braking Energy Recovery in Hybrid Electric Vehicles. In Proceedings of the 2025 IEEE 8th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 14–16 March 2025; pp. 952–957. [Google Scholar]
- Sakai, M.; Takeshita, T. Power Control Using Sub-Battery for Electric Motorcycle. In Proceedings of the 2024 27th International Conference on Electrical Machines and Systems (ICEMS), Fukuoka, Japan, 26–29 November 2024; pp. 3757–3762. [Google Scholar]
- Szumska, E.M. Regenerative Braking Systems in Electric Vehicles: A Comprehensive Review of Design, Control Strategies, and Efficiency Challenges. Energy 2025, 18, 2422. [Google Scholar] [CrossRef]
- Abdelfattah, W.; Abdelhamid, A.S.; Hasanien, H.M.; Rashad, B.A.-E. Smart Vehicle-to-Grid Integration Strategy for Enhancing Distribution System Performance and Electric Vehicle Profitability. Energy 2024, 302, 131807. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Operating voltage | 12 V |
| Rated speed | 2000 rpm |
| Number of poles | 6 |
| Hall installation angle | 120° |
| Parameter | Value |
|---|---|
| Battery voltage | 12 V |
| Battery capacity | 6 Ah |
| Current (Stationary Charging) | ≤0.6 A |
| Current (Motor Acceleration) | ≤90 A |
| Current (Regenerative Braking) | ≤20 A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Li, W.; Zhao, Z.; Meng, F. Fast Energy Recovery During Motor Braking: Analysis and Simulation. J. Low Power Electron. Appl. 2025, 15, 49. https://doi.org/10.3390/jlpea15030049
Xu L, Li W, Zhao Z, Meng F. Fast Energy Recovery During Motor Braking: Analysis and Simulation. Journal of Low Power Electronics and Applications. 2025; 15(3):49. https://doi.org/10.3390/jlpea15030049
Chicago/Turabian StyleXu, Lin, Wengan Li, Zenglong Zhao, and Fanyi Meng. 2025. "Fast Energy Recovery During Motor Braking: Analysis and Simulation" Journal of Low Power Electronics and Applications 15, no. 3: 49. https://doi.org/10.3390/jlpea15030049
APA StyleXu, L., Li, W., Zhao, Z., & Meng, F. (2025). Fast Energy Recovery During Motor Braking: Analysis and Simulation. Journal of Low Power Electronics and Applications, 15(3), 49. https://doi.org/10.3390/jlpea15030049







