Event-Triggered Model Predictive Control of Buck Converter with Disturbances: Design and Experimentation
Abstract
1. Introduction
- (1)
- RESO is used to estimate state and total disturbance for tracking the error state equation of the DC-DC buck converter.
- (2)
- An ET condition in steady state is designed based on RESO to reduce unnecessary computation and energy consumption in the control chip during the steady state of the buck converter.
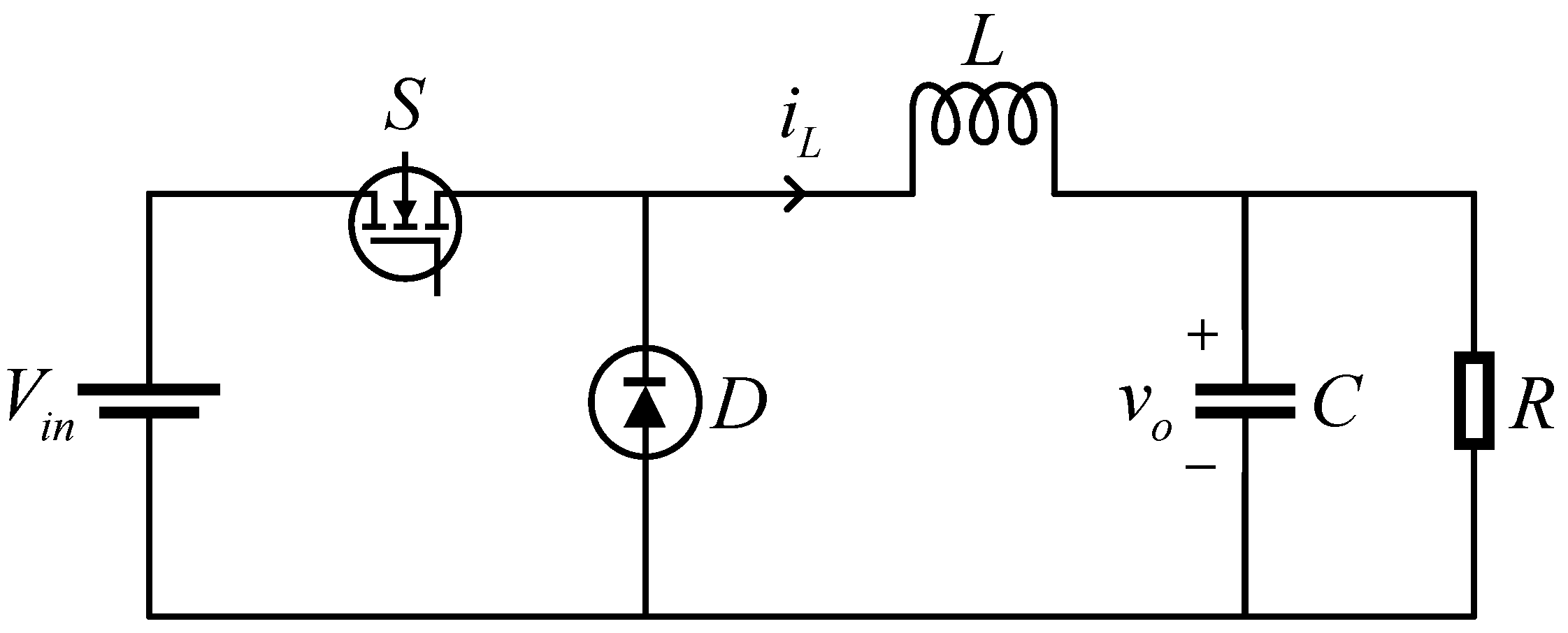
2. Modeling and Prediction of Buck Converter
2.1. Modeling of Buck Converter
2.2. Prediction of the Buck Converter
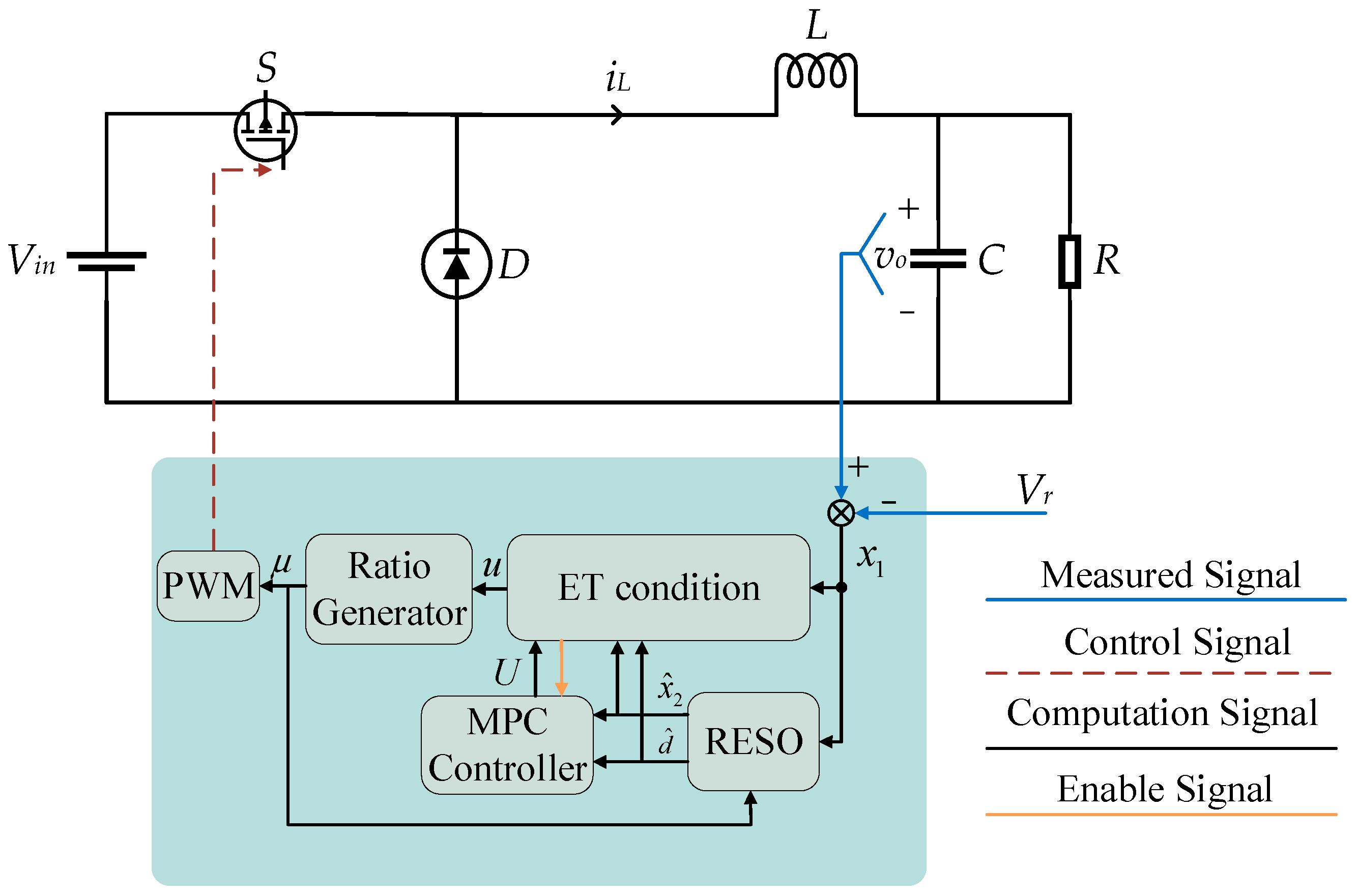
3. Control Strategy Design and Analysis
3.1. Design and Convergence Analysis of Reduced-Order Extended State Observer
3.2. Model Predictive Controller Design
3.3. Triggering Condition of ET-MPC
- (1)
- Parameter initialization: sequence pointer k, state quantities x1 and x2, and total disturbance d.
- (2)
- The state quantities x1, x2 and the total perturbation d are obtained by sampling and partial processing (including RESO).
- (3)
- Substitute the state quantity x1 and the control increment Δu(k) left over from the previous cycle into (35). If Equation (35) is satisfied, continue to the next step; if not, skip to step 5.
- (4)
- Continue to use the control quantity u of the previous moment and update the pointer k = N, and skip to step 11.
- (5)
- Determine whether k is equal to N + 1. If it is satisfied, skip to step 7; if not, continue to the next step.
- (6)
- Substitute the state quantities x1 and x2 and the total disturbance d into (34). If (34) is satisfied, continue to the next step; if not, skip to step 9.
- (7)
- The sequence of optimal control increments ΔU is calculated by model predictive controller.
- (8)
- Replace the original control sequence with the newly calculated control sequence and set the sequence pointer k to 1. Then skip to step 10.
- (9)
- The optimal control increment sequence ΔU remains unchanged and the sequence pointer k is increased by 1.
- (10)
- The kth control increment of the control increment sequence ΔU is taken and added to the control quantity of the previous cycle to obtain the control quantity u of this cycle.
- (11)
- Processing the control quantity u as a duty cycle and applying it to the DC-DC buck converter.
- (12)
- Determine whether the system needs to end the work. If so, stop the work; if not, return to step 2 and wait for the next cycle to start.
3.4. Stability Analysis of Closed-Loop System
4. Experimental Verifications and Results Analysis
4.1. Experimental Set-Up
- (1)
- Variations in load equivalent resistance: The load equivalent resistance undergoes a sudden increase from 4 Ω to 8 Ω, followed by a precipitous decline to 3 Ω.
- (2)
- Variations in input voltage: The input voltage plummets from 24 V to 22 V at a rate of change of −21.67 V/s and surges from 22 V to 25 V at a rate of change of 18.75 V/s.
- (3)
- Variations in reference voltage: The reference voltage undergoes a step change from 12 V to 15 V, before returning to 12 V.
4.2. Experimental Results and Analyses
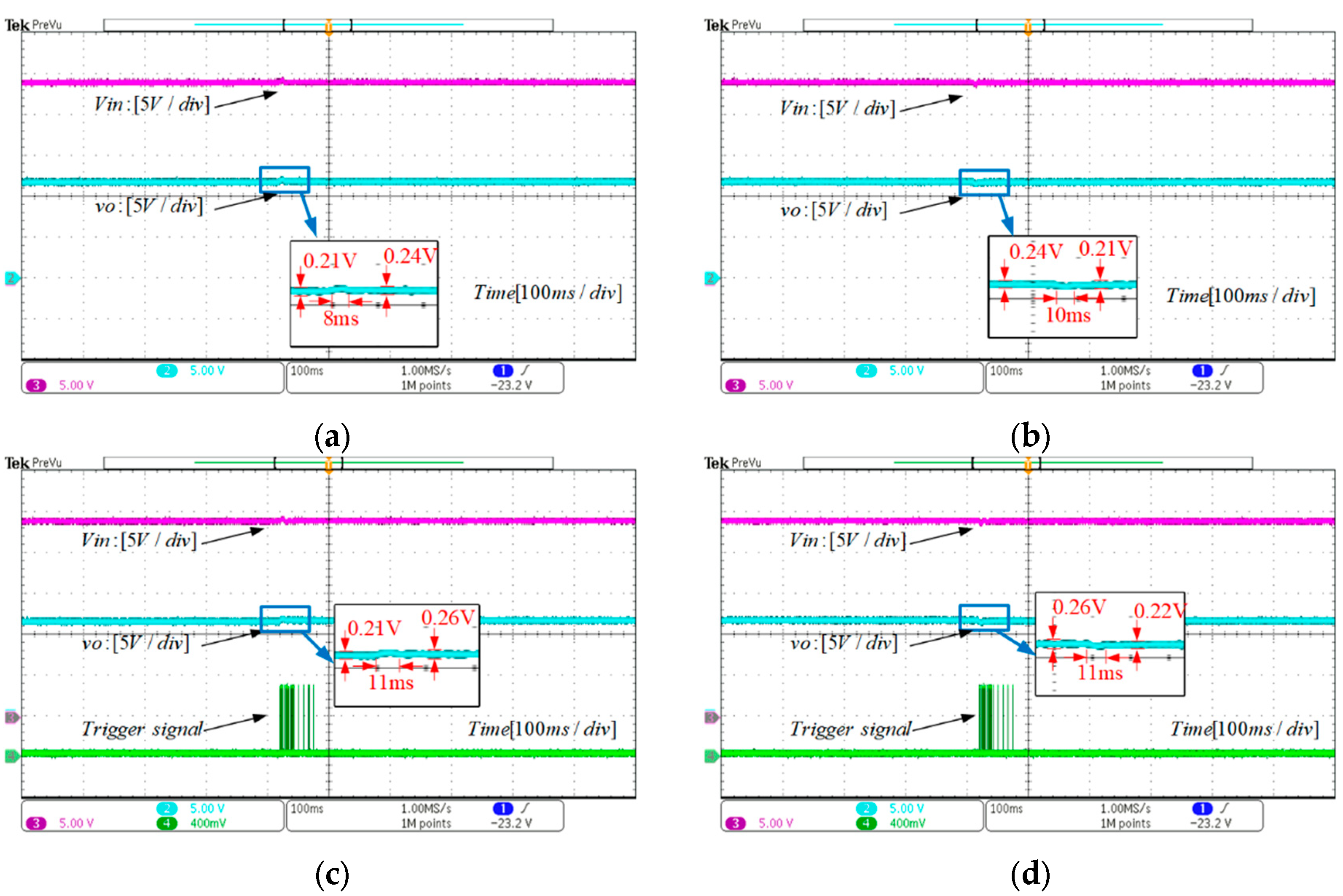
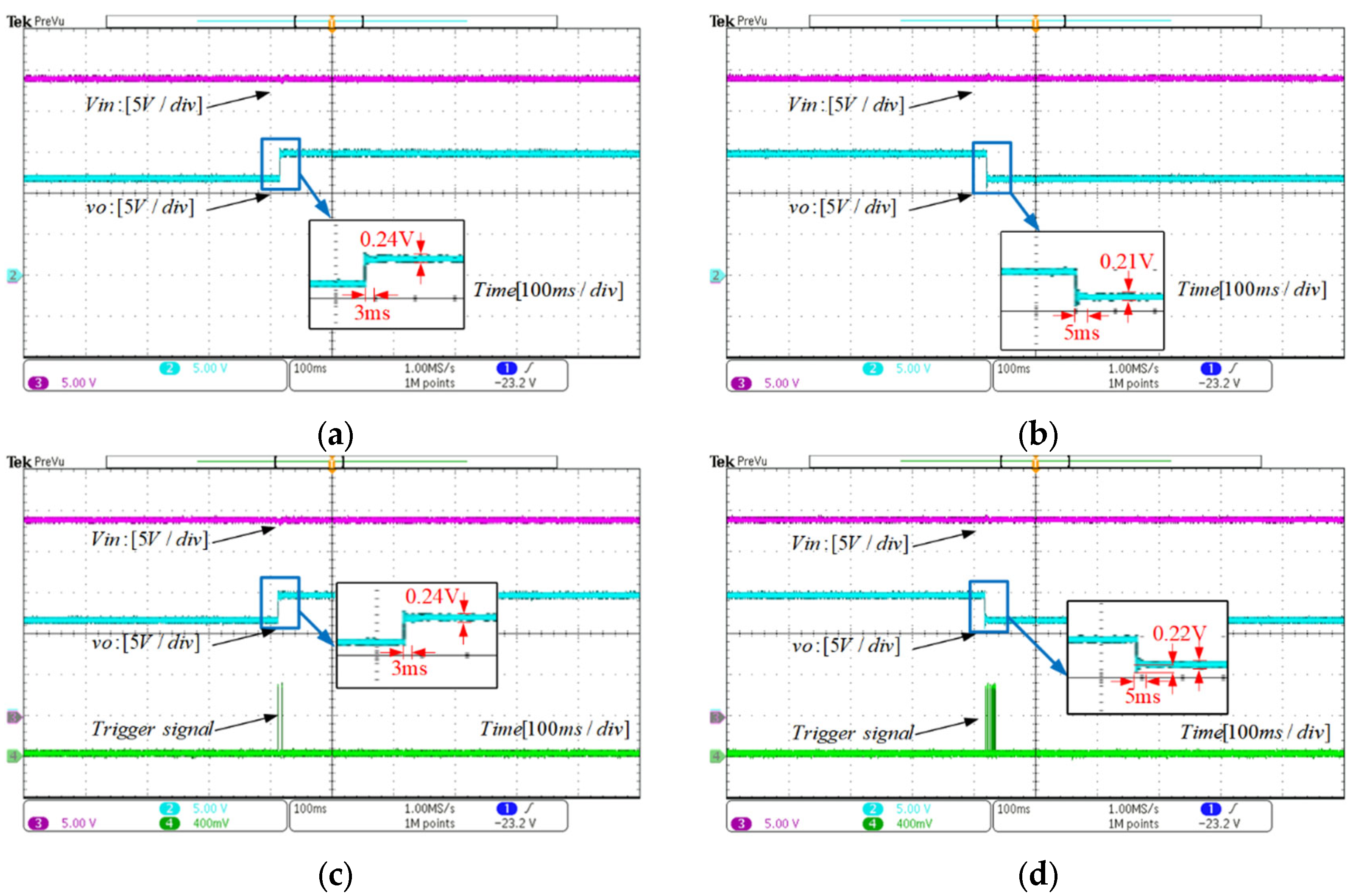
4.2.1. Experiment 1: Load Resistance Variations
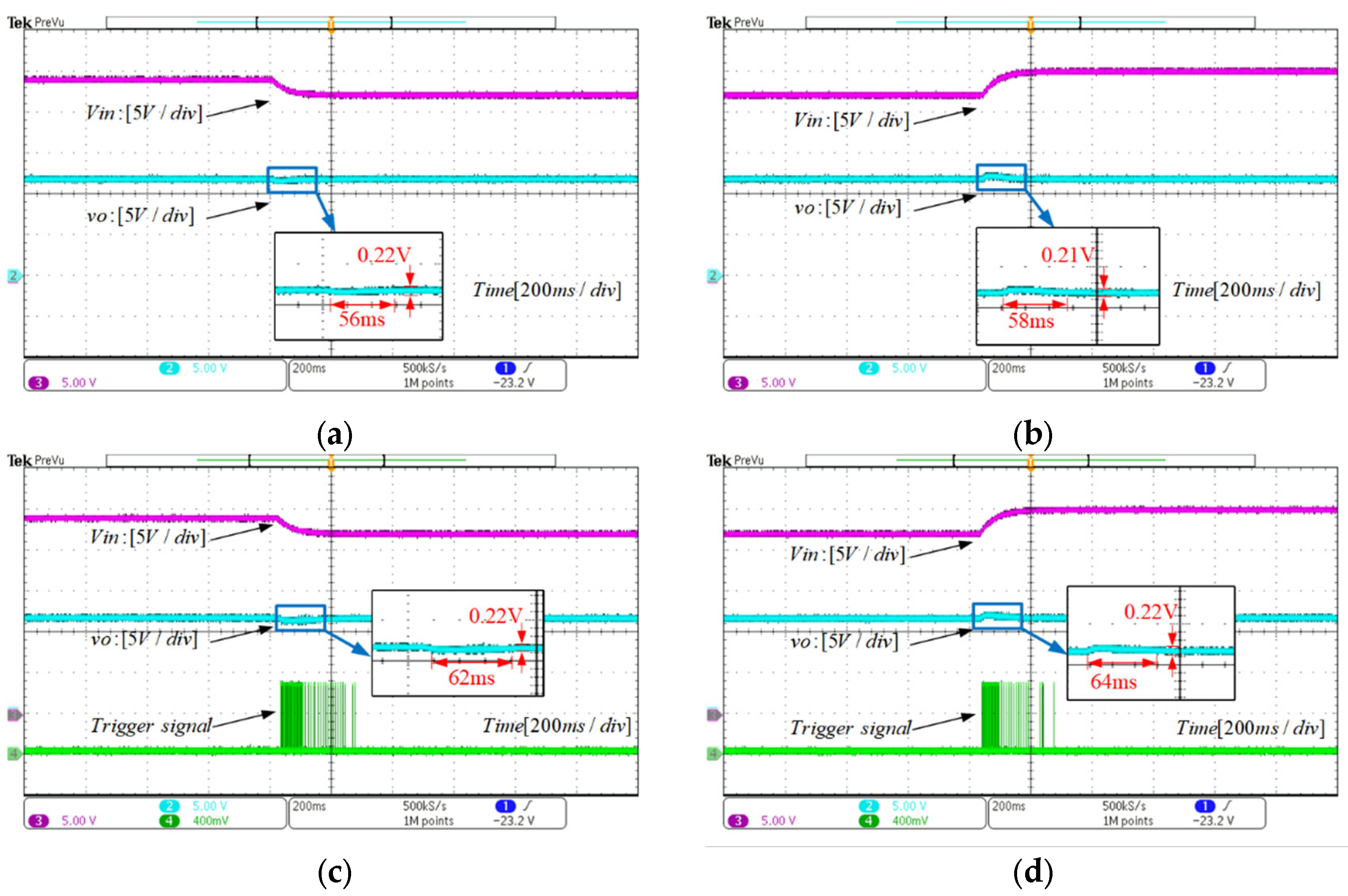
4.2.2. Experiment 2: Input Voltage Variations
4.2.3. Experiment 2: Reference Voltage Variations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohammed, D.M.; Hassan, R.F.; Yasin, N.M.; Alruwaili, M.; Ibrahim, M.A. A Comparative study of direct power control strategies for STATCOM using three-level and five-level diode-clamped inverters. Energies 2025, 18, 3582. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, G.; He, M.; Mao, S.; Zhao, H.; Liu, G. Stability effect of different modulation parameters in voltage-mode PWM control for CCM switching DC-DC converter. IEEE Trans. Transp. Electrif. 2024, 10, 2408–2422. [Google Scholar] [CrossRef]
- Shrivastava, A.; Calhoun, B.H. A DC–DC converter efficiency model for system level analysis in ultra low power applications. J. Low Power Electron. Appl. 2013, 3, 215–232. [Google Scholar] [CrossRef]
- Veerabathini, A.; Furth, P.M. High-Efficiency Switched-Capacitor DC-DC Converter with Three Decades of Load Current Range Using Adaptively-Biased PFM. J. Low Power Electron. Appl. 2020, 10, 5. [Google Scholar] [CrossRef]
- Garcés-Ruiz, A.; Riffo, S.; González-Castaño, C.; Restrepo, C. Model predictive control with stability guarantee for second-order DC/DC converters. IEEE Trans. Ind. Electron. 2024, 71, 5157–5165. [Google Scholar] [CrossRef]
- Wang, S.; Li, S.; Su, J.; Li, J.; Zhang, L. Extended state observer based nonsingular terminal sliding mode controller for a DC-DC buck converter with disturbances: Theoretical analysis and experimental verification. Int. J. Control 2023, 96, 1661–1671. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, W.X.; Ding, S. An adaptive SOSM controller design by using a sliding-mode-based filter and its application to buck converter. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2409–2418. [Google Scholar] [CrossRef]
- Peng, Q.; Zhou, S.; Ma, F.; Huang, G.; Fan, R. A model predictive control of three-level cascaded noninverting buck–boost converter for energy storage system. IEEE Trans. Ind. Electron. 2025, 72, 4933–4942. [Google Scholar] [CrossRef]
- Wang, B.; Kanamarlapudi, V.R.K.; Xian, L.; Peng, X.; Tan, K.T.; So, P.L. Model predictive voltage control for single-inductor multiple-output DC–DC converter with reduced cross regulation. IEEE Trans. Ind. Electron. 2016, 63, 4187–4197. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, R. An improved model predictive voltage control for PMSM drives without motor parameters. CES Trans. Electr. Mach. Syst. 2024, 8, 471–480. [Google Scholar] [CrossRef]
- Rosolia, U.; Guastella, D.C.; Muscato, G.; Borrelli, F. Model predictive control in partially observable multi-modal discrete environments. IEEE Control Syst. Lett. 2023, 7, 2161–2166. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S. Fractional-order linear active disturbance rejection control strategy for DC-DC BUCK converters. Electronics 2025, 14, 2226. [Google Scholar] [CrossRef]
- Kitaba, T. Modeling the system for hybrid renewable energy using highly efficient converters and generator. CES Trans. Electr. Mach. Syst. 2024, 8, 356–366. [Google Scholar] [CrossRef]
- Lu, H.; Li, J.; Li, S.; Wang, S.; Xiao, Y. Finite-time extended state observer enhanced nonsingular terminal sliding mode control for buck converters in the presence of disturbances: Design, analysis and experiments. Nonlinear Dyn. 2024, 112, 7113–7127. [Google Scholar] [CrossRef]
- Sun, J.; Xu, S.; Ding, S.; Pu, Z.; Yi, J. Adaptive conditional disturbance negation-based nonsmooth-integral control for PMSM drive system. IEEE/ASME Trans. Mechatron. 2024, 29, 3602–3613. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-free predictive current control of PMSM drives based on extended state observer using ultralocal model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Wu, W.J.; Ma, J.; Fang, Y.T.; Peng, Z.H.; Wang, D.; Rodríguez, J. Event-triggered ESO-based robust MPC for power converters. IEEE Trans. Ind. Electron. 2023, 70, 2144–2152. [Google Scholar] [CrossRef]
- Sun, C.; Wang, R.; Sun, Q.; Zhang, H. A novel synchronous rectification scheme with low computational burden for LLC resonant converter in EV charger applications. IEEE Trans. Ind. Electron. 2023, 70, 8991–9003. [Google Scholar] [CrossRef]
- Wang, J.; Rong, J.; Yu, L. Reduced-order extended state observer based event-triggered sliding mode control for DC–DC buck converter system with parameter perturbation. Asian J. Control 2021, 23, 1591–1601. [Google Scholar] [CrossRef]
- Peng, C.; Li, F. A survey on recent advances in event-triggered communication and control. Inf. Sci. 2018, 457, 113–125. [Google Scholar] [CrossRef]
- Wang, B.; Huang, J.; Wen, C.; Rodriguez, J.; Garcia, C.; Gooi, H.B.; Zeng, Z. Event-triggered model predictive control for power converters. IEEE Trans. Ind. Electron. 2021, 68, 715–720. [Google Scholar] [CrossRef]
- Tabuada, P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans. Autom. Control 2007, 52, 1680–1685. [Google Scholar] [CrossRef]
- Hu, Z.R.; Shi, P.; Wu, L.G. Polytopic event-triggered robust model predictive control for constrained linear systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2594–2603. [Google Scholar] [CrossRef]
- Qin, B.; Yan, H.; Zhang, H.; Wang, Y.; Yang, S.X. Enhanced reduced-order extended state observer for motion control of differential driven mobile robot. IEEE Trans. Cybern. 2023, 53, 1299–1310. [Google Scholar] [CrossRef]
- Li, S.Q.; Lu, H.; Li, J.; Zheng, T.; He, Y. Fractional-order sliding mode controller based on ESO for a buck converter with mismatched disturbances: Design and experiments. IEEE Trans. Ind. Electron. 2025, in press. [CrossRef]
- Wang, B.Z.; Li, S.Q.; Kan, S.Q.; Li, J. Enhanced tracking of DC-DC buck converter systems using reduced-order extended state observer-based model predictive control. Int. J. Intell. Syst. 2023, 2, 143–152. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, S. Output regulation of switched singular systems based on extended state observer approach. Appl. Math. Comput. 2021, 399, 126020. [Google Scholar] [CrossRef]
- Ma, C.; Wang, J. Applicability analysis of extended state observer-based control for systems subject to parametric disturbances. ISA Trans. 2022, 130, 226–234. [Google Scholar] [CrossRef]
- Karami, Z.; Shafiee, Q.; Sahoo, S.; Yaribeygi, M.; Bevrani, H.; Dragicevic, T. Hybrid model predictive control of DC-DC boost converters with constant power load. IEEE Trans. Energy Convers. 2021, 36, 1347–1356. [Google Scholar] [CrossRef]
- Li, N.; Zhang, S.; Jiang, Y. Junction temperature estimation model of power MOSFET device based on photovoltaic power enhancer. J. Low Power Electron. Appl. 2025, 15, 17. [Google Scholar] [CrossRef]


| Parameters | Symbol | Value |
|---|---|---|
| Input voltage | E | 24 V |
| Desire output voltage | vr | 12 V |
| Inductance | L | 50 μH |
| Capacitance | C | 67.5 μF |
| Load equivalent resistance | R | 4 Ω |
| Control Strategy | Parameters | Load Step Change | Input Step Change | Reference Voltage Step Change | |||
|---|---|---|---|---|---|---|---|
| Decline | Rise | Decline | Rise | Decline | Rise | ||
| RESO-MPC | Settling time | 10 ms | 8 ms | 56 ms | 58 ms | 5 ms | 3 ms |
| Count of calculations | 100 times | 100 times | 100 times | 100 times | 100 times | 100 times | |
| ET-MPC | Settling time | 11 ms | 11 ms | 62 ms | 64 ms | 5 ms | 3 ms |
| Count of calculations | 17 times | 21 times | 39 times | 43 times | 10 times | 2 times | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Li, S.; Cao, K.; Chen, D.; Li, J.; Cao, W. Event-Triggered Model Predictive Control of Buck Converter with Disturbances: Design and Experimentation. J. Low Power Electron. Appl. 2025, 15, 45. https://doi.org/10.3390/jlpea15030045
Yang Z, Li S, Cao K, Chen D, Li J, Cao W. Event-Triggered Model Predictive Control of Buck Converter with Disturbances: Design and Experimentation. Journal of Low Power Electronics and Applications. 2025; 15(3):45. https://doi.org/10.3390/jlpea15030045
Chicago/Turabian StyleYang, Ziyuan, Shengquan Li, Kaiwen Cao, Donglei Chen, Juan Li, and Wei Cao. 2025. "Event-Triggered Model Predictive Control of Buck Converter with Disturbances: Design and Experimentation" Journal of Low Power Electronics and Applications 15, no. 3: 45. https://doi.org/10.3390/jlpea15030045
APA StyleYang, Z., Li, S., Cao, K., Chen, D., Li, J., & Cao, W. (2025). Event-Triggered Model Predictive Control of Buck Converter with Disturbances: Design and Experimentation. Journal of Low Power Electronics and Applications, 15(3), 45. https://doi.org/10.3390/jlpea15030045







