Optimized Coupling Coil Geometry for High Wireless Power Transfer Efficiency in Mobile Devices
Abstract
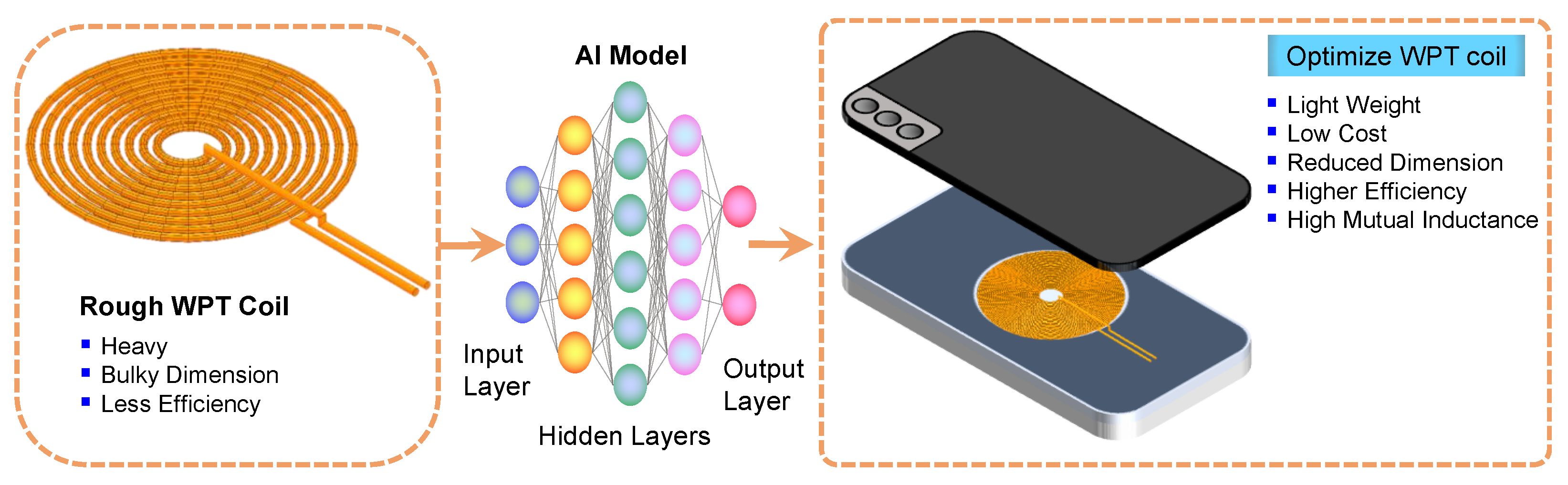
1. Introduction
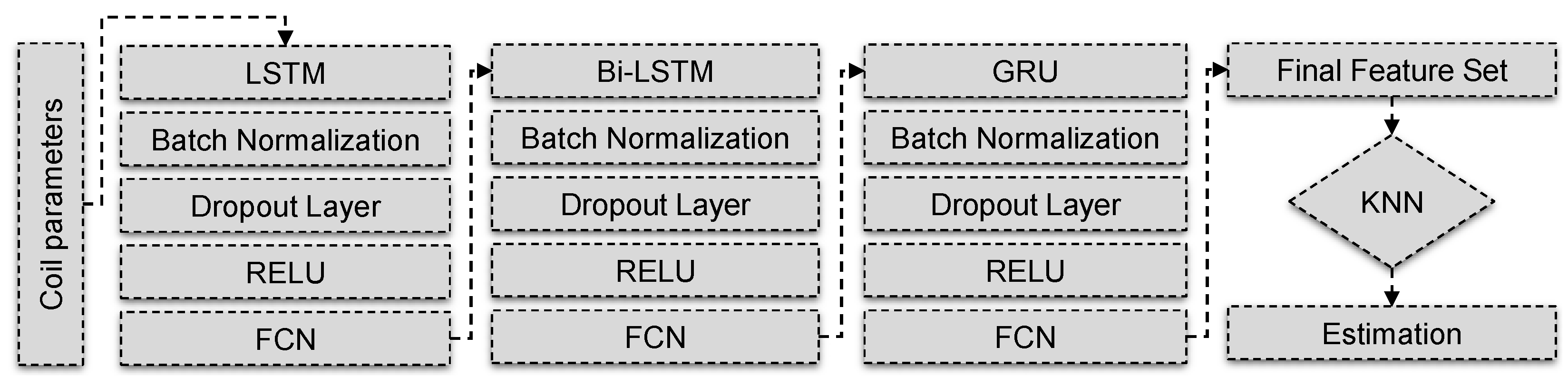
- This work introduces ResML-HybNN, an innovative hybrid neural architecture that combines GRU, LSTM, and BiLSTM units within a residual multi-layer framework. The model incorporates ReLU activation, normalization, and dropout techniques to improve training stability, generalization, and optimization efficiency. The architecture incorporates skip connections, enabling direct feature propagation across parallel and cascaded blocks, mitigating vanishing gradients, and strengthening feature representation in deep network layers.
- An iterative approach is utilized to improve the generation of training data through Ansys simulations. Additionally, the architecture of the ResML-HybNN model is refined through iterative simulations, where key hyperparameters—such as hidden unit count, dropout probability, learning rate, and number of training epochs—are systematically optimized using parametric analysis.
- A stratified clustering approach is employed to obtain a uniformly distributed sample from the design space, providing an effective starting point for model training and mitigating training bias. The optimized designs are further validated through experimental measurements following fabrication.
2. Related Work
3. Methodology
3.1. Design Setup and Constraints
3.2. Deep Learning Model for Wireless Power Transfer Efficiency Prediction
4. Results and Discussion
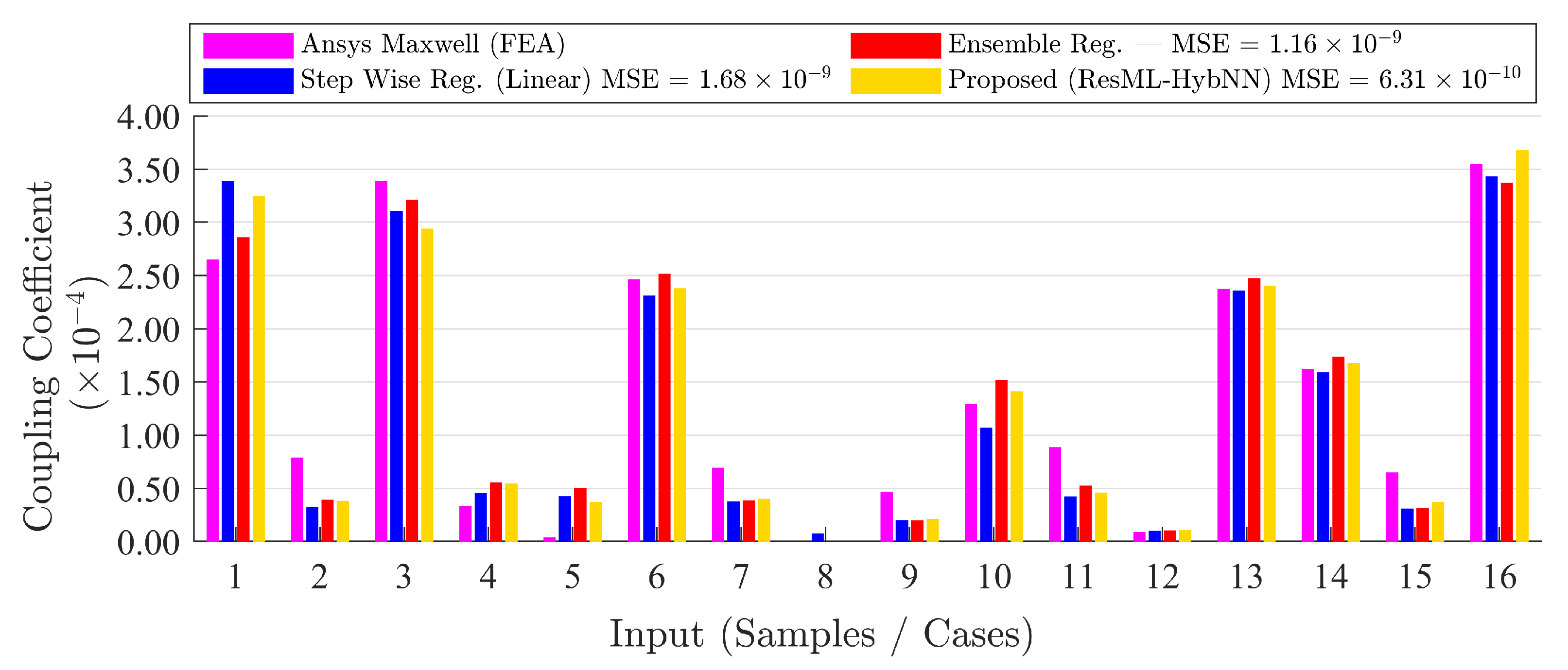
4.1. Simulation Results
4.2. ResML-HybNN Optimization Performance
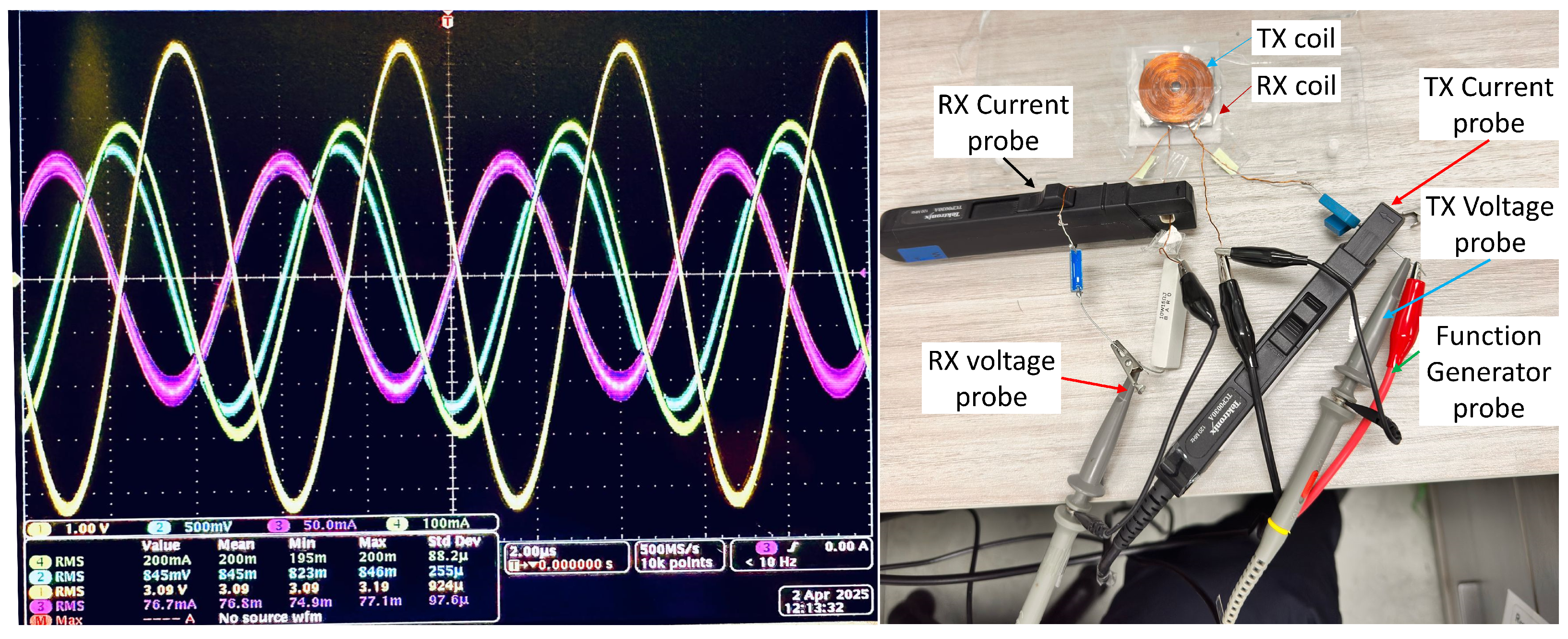
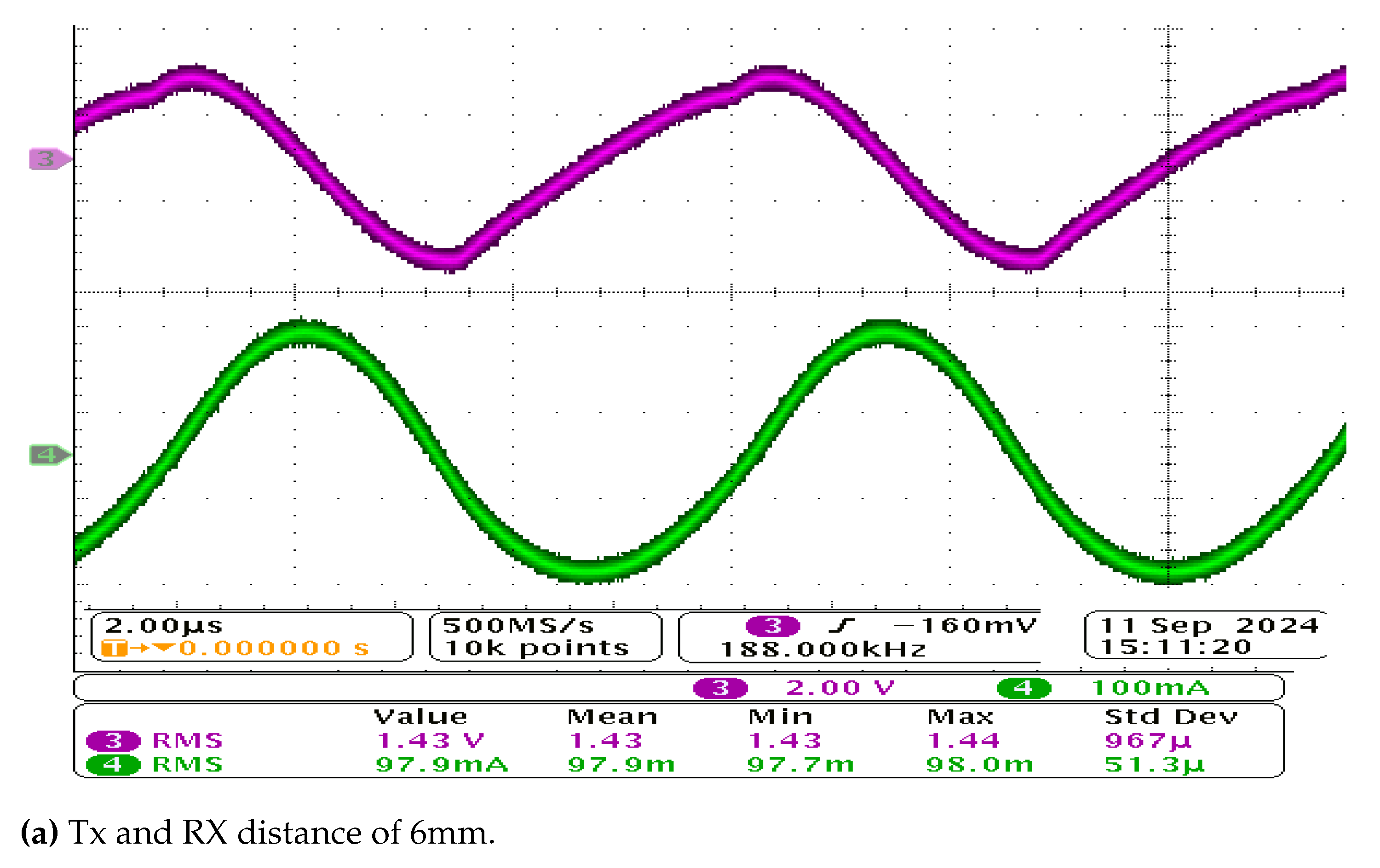
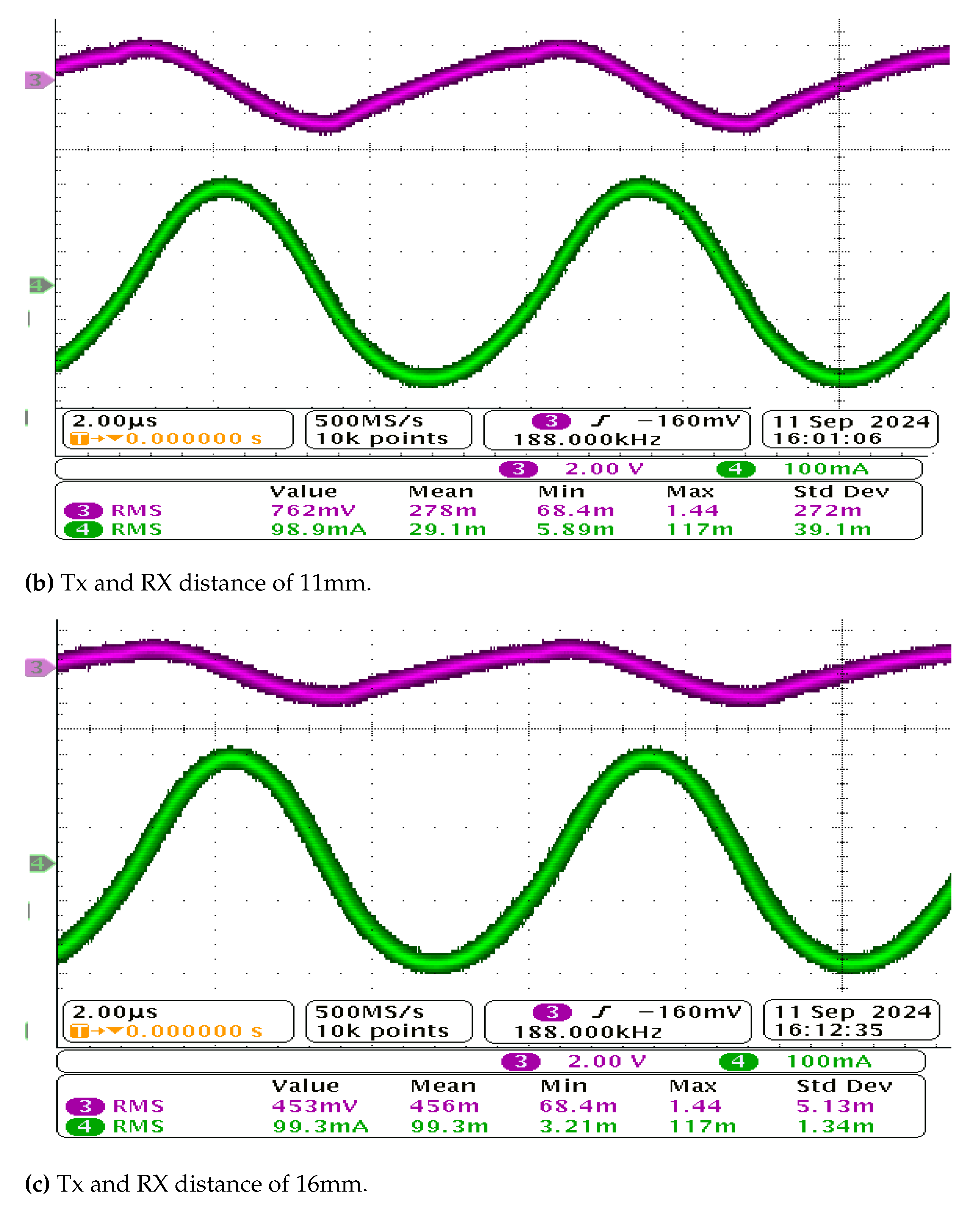
5. Experimental Verification
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Budhia, M.; Covic, G.A.; Boys, J.T. Design and optimization of circular magnetic structures for lumped inductive power transfer systems. IEEE Trans. Power Electron. 2011, 26, 3096–3108. [Google Scholar] [CrossRef]
- Shen, H.; Tan, P.; Song, B.; Gao, X.; Zhang, B. Receiver position estimation method for multitransmitter WPT system based on machine learning. IEEE Trans. Ind. Appl. 2021, 58, 1231–1241. [Google Scholar] [CrossRef]
- Zhang, W.; Mi, C.C. Compensation topologies of high-power wireless power transfer systems. IEEE Trans. Veh. Technol. 2015, 65, 4768–4778. [Google Scholar] [CrossRef]
- Pahlavan, S.; Shooshtari, M.; Jafarabadi Ashtiani, S. Star-shaped coils in the transmitter array for receiver rotation tolerance in free-moving wireless power transfer applications. Energies 2022, 15, 8643. [Google Scholar] [CrossRef]
- Zhang, X.; Kan, T.; You, C.; Mi, C. Modeling and analysis of AC output power factor for wireless chargers in electric vehicles. IEEE Trans. Power Electron. 2016, 32, 1481–1492. [Google Scholar] [CrossRef]
- Adepoju, W.O.; Bhattacharya, I.; Bima, M.E.; Banik, T. Novel metamaterial and ai-based multi-objective optimization of coil parameters for efficient wireless power transfer. In Proceedings of the 2021 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 25–28 October 2021; pp. 1–6. [Google Scholar]
- Dinis, H.; Mendes, P. A comprehensive review of powering methods used in state-of-the-art miniaturized implantable electronic devices. Biosens. Bioelectron. 2021, 172, 112781. [Google Scholar] [CrossRef] [PubMed]
- Karimi, M.J.; Schmid, A.; Dehollain, C. Wireless power and data transmission for implanted devices via inductive links: A systematic review. IEEE Sens. J. 2021, 21, 7145–7161. [Google Scholar] [CrossRef]
- Benjamens, S.; Dhunnoo, P.; Meskó, B. The state of artificial intelligence-based FDA-approved medical devices and algorithms: An online database. NPJ Digit. Med. 2020, 3, 118. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image matching from handcrafted to deep features: A survey. Int. J. Comput. Vis. 2021, 129, 23–79. [Google Scholar] [CrossRef]
- Fawad; Khan, M.J.; Riaz, M.A.; Shahid, H.; Khan, M.S.; Amin, Y.; Loo, J.; Tenhunen, H. Texture representation through overlapped multi-oriented tri-scale local binary pattern. IEEE Access 2019, 7, 66668–66679. [Google Scholar]
- Shakoor, M.H.; Boostani, R. A novel advanced local binary pattern for image-based coral reef classification. Multimed. Tools Appl. 2018, 77, 2561–2591. [Google Scholar] [CrossRef]
- Shihavuddin, A.; Gracias, N.; Garcia, R.; Gleason, A.C.; Gintert, B. Image-based coral reef classification and thematic mapping. Remote Sens. 2013, 5, 1809–1841. [Google Scholar] [CrossRef]
- Shrestha, A.; Mahmood, A. Review of deep learning algorithms and architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Sarkar, D.; Khan, T.; Talukdar, F.A.; Rengarajan, S.R. Computational Intelligence for Modeling and Optimization of RFEH and WPT Systems: A Comprehensive Survey: Computational Intelligence for RFEH and WPT Systems. IEEE Microw. Mag. 2023, 24, 46–60. [Google Scholar] [CrossRef]
- Ali, A.; Mohd Yasin, M.N.; Jusoh, M.; Ahmad Hambali, N.A.M.; Abdul Rahim, S.R. Optimization of wireless power transfer using artificial neural network: A review. Microw. Opt. Technol. Lett. 2020, 62, 651–659. [Google Scholar] [CrossRef]
- Shimokawa, S.; Oshima, H.; Shimizu, K.; Uehara, Y.; Fujisaki, J.; Furuya, A.; Igarashi, H. Fast 3-D optimization of magnetic cores for loss and volume reduction. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Pretorius, K.; Pillay, N. Neural network crossover in genetic algorithms using genetic programming. Genet. Program. Evolvable Mach. 2024, 25, 1–30. [Google Scholar] [CrossRef]
- Jeong, M.S.; Jang, J.H.; Lee, E.S. Optimal IPT core design for wireless electric vehicles by Reinforcement Learning. IEEE Trans. Power Electron. 2023, 38, 13262–13272. [Google Scholar] [CrossRef]
- Dixit, P.; Silakari, S. Deep learning algorithms for cybersecurity applications: A technological and status review. Comput. Sci. Rev. 2021, 39, 100317. [Google Scholar] [CrossRef]
- Vinayakumar, R.; Alazab, M.; Soman, K.; Poornachandran, P.; Al-Nemrat, A.; Venkatraman, S. Deep learning approach for intelligent intrusion detection system. IEEE Access 2019, 7, 41525–41550. [Google Scholar] [CrossRef]
- Liu, G.; Bao, H.; Han, B. A stacked autoencoder-based deep neural network for achieving gearbox fault diagnosis. Math. Probl. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Alrawashdeh, K.; Purdy, C. Fast hardware assisted online learning using unsupervised deep learning structure for anomaly detection. In Proceedings of the 2018 International Conference on Information and Computer Technologies (ICICT), DeKalb, IL, USA, 23–25 March 2018; pp. 128–134. [Google Scholar]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent trends in deep learning based natural language processing. IEEE Comput. IntelligenCe Mag. 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Reddi, V.J. Deep reinforcement learning for cyber security. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3779–3795. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Shi, Y.; Xue, Z. Idsgan: Generative adversarial networks for attack generation against intrusion detection. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2022; pp. 79–91. [Google Scholar]


| Methods | Kernel | MSE | ||
|---|---|---|---|---|
| Coupling Coeff. | Mag. Flux | Mutual Ind. | ||
| BiLSTM → LSTM → FC1 | - | 1.76 | 2.01 | 4.34 |
| Gaussian Process Regression | Gaussian | 1.71 | 1.53 | 3.23 |
| MLP Regression | - | 2.55 | 2.21 | 2.66 |
| SVM Regression | Linear | 1.59 | 1.52 | 2.34 |
| GRU → BiLSTM → LSTM | - | 7.72 | 1.11 | 2.09 |
| GRU | - | 6.91 | 8.16 | 1.86 |
| GRU → BiLSTM | - | 9.68 | 3.45 | 1.82 |
| LSTM | - | 3.54 | 1.48 | 1.79 |
| SVM Regression | Gaussian | 1.29 | - | 1.77 |
| Ensemble Regression | - | 1.16 | 5.67 | 1.68 |
| Linear Regression | Linear | 1.68 | 5.43 | 1.66 |
| StepWise Regression | Linear | 1.10 | 5.69 | 1.59 |
| SVM Regression | Quadratic | 3.12 | 1.52 | 1.57 |
| ResML-HybNN | - | 6.31 | 5.68 | 1.51 |
| Wire Thickness (mm) | Start Radius (mm) | Radius Change (mm) | Total Turns | Mutual Inductance H |
| 0.45 | 2.8 | 0.1 | 40 | 12.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, F.M. Optimized Coupling Coil Geometry for High Wireless Power Transfer Efficiency in Mobile Devices. J. Low Power Electron. Appl. 2025, 15, 36. https://doi.org/10.3390/jlpea15020036
Alotaibi FM. Optimized Coupling Coil Geometry for High Wireless Power Transfer Efficiency in Mobile Devices. Journal of Low Power Electronics and Applications. 2025; 15(2):36. https://doi.org/10.3390/jlpea15020036
Chicago/Turabian StyleAlotaibi, Fahad M. 2025. "Optimized Coupling Coil Geometry for High Wireless Power Transfer Efficiency in Mobile Devices" Journal of Low Power Electronics and Applications 15, no. 2: 36. https://doi.org/10.3390/jlpea15020036
APA StyleAlotaibi, F. M. (2025). Optimized Coupling Coil Geometry for High Wireless Power Transfer Efficiency in Mobile Devices. Journal of Low Power Electronics and Applications, 15(2), 36. https://doi.org/10.3390/jlpea15020036






