Abstract
In a photovoltaic power enhancer system, when it is operated in current-control mode, significant nonuniform temperature distribution occurs in the converter due to thermal coupling effects, dissipative boundary conditions, and differences in device losses within the in-phase bridge. Accurate on-site estimation of the power device’s junction temperature is critical in the system design. To address this problem, a novel thermal behavior estimation model based on electro-thermal analysis is proposed in this paper, which can be used for asymmetric power MOSFETs in a photovoltaic power enhancer system. Thermal coupling effects and dissipative boundary conditions are, firstly, analyzed in a three-dimensional finite element model. A coupling impedance matrix is constructed through step power response extraction to describe the significant thermal coupling effects among devices. The complete heat sink is decoupled into several sub-parts representing different dissipative boundary conditions. A compact RC network model for estimating junction temperature is established based on the combination of the coupling impedance and the sub-heat-sink impedance. The proposed model is verified by finite element simulation and experimental measurement.
1. Introduction
The junction temperature of devices is of great significance in reliability assessment, such as thermal fatigue degradation and lifespan prediction []. Since measuring the internal junction temperature is nearly impossible, researchers have employed various techniques over the past few decades, such as the finite element method (FEM), thermal parameter extraction methods, and thermal impedance model methods, to extensively study power devices to estimate accurate junction temperature [,]. Although the FEM can provide relatively precise results, its computational process is time-consuming and requires substantial computational resources [,]. On the other hand, for the thermal parameter extraction method, a set of measurement process is needed [,]. In contrast, the thermal impedance model method not only is suitable for predicting dynamic thermal behavior but also can be used for analyzing long-term load profiles, with the merit of less cost []. However, the application of the thermal impedance model requires consideration of coupling effects and heat dissipation boundary conditions [,,,].
The thermal coupling effect between the power module chip and the key substrate layers can be characterized with the bypass resistance extracted from the step power response []. The relevant literature shows a method of connecting a voltage source in series with the coupling impedance to establish a three-dimensional RC block thermal model []. However, the process of extracting all coupling impedances is relatively complex and especially unsuitable for multicomponent converters. In practice, the coupling effect of individual devices is varied in different circumstances [,].
On the other hand, in practical applications of the converters, including photovoltaic inverters, onboard inverters, and wind power converters, the power loss of the modules always exhibits symmetrical distribution of the temperature []. The substrate can be treated as a uniform RC block, which may enable the neglect of boundary conditions for temperature distribution []. The relevant literature changed these boundary conditions by analyzing the shell junction impedance at different positions on the substrate [].
In order to simulate the dynamic thermal behavior of power MOSFET modules in the converter, three typical thermal models are usually used, including the numerical model, analytical model, and thermal network model. Numerical simulation is a technique widely used to solve thermodynamic problems with complex geometries and boundary conditions. Commercial thermal simulation software, such as COMSOL 6.3 and ANSYS 10.0/ICEPAK 4.2, provides powerful computational fluid dynamics tools for electronic thermal management. The finite volume method, finite difference method, or finite element method are adopted in the software to solve partial differential equations, which can accurately simulate the actual thermal behavior but with the sacrifice of timeliness. Although the model reduction method can improve the computational efficiency, it often sacrifices a certain accuracy [].
The analysis model is based on the thermal diffusion equation with physical meaning to study the thermal behavior of the power module. In order to solve the heat equation, a variety of methods are proposed, including the boundary element method, three-dimensional transmission line matrix method, Green’s equation [], Fourier series expansion method [], and finite difference method []. The analytical model achieves faster calculation speed by simplifying the actual physical structure, which requires researchers to have a solid mathematical and physical foundation.
Compared with the above two models, the thermal network model is easy to integrate with a circuit simulator and digital signal processor (DSP), and it is especially suitable for long-term load distribution analysis and online temperature estimation []. The reasons are as follows: (1) Model simplification and efficiency: The thermal network can simplify the complex heat transfer process into a relatively simple structure, which makes the model calculation more efficient and maintains high accuracy. Similar to the circuit model, the structure and principle of the thermal network model are similar to a network composed of resistors, capacitors, and other components in a circuit. (2) Modularization and flexibility: The thermal network model can be modularly constructed according to actual needs. Different components or regions can be represented by corresponding thermal network modules, which has high flexibility. (3) Real-time detection and feedback: The thermal network model can calculate and give feedback on the temperature change at each point in the system in real time.
The thermal network model includes the Foster thermal network and Kaur thermal network []. Under certain boundary conditions, the data of the Foster thermal network can be obtained from a data table. However, when the temperature of the reference point changes, the junction temperature in the traditional Foster thermal network is changed synchronously with the reference temperature, which may introduce errors. The traditional Kaur thermal network shows higher accuracy. It is a one-dimensional model that does not consider the thermal coupling effect [,].
The compact thermal network can reflect the dynamic change in junction temperature more accurately. However, it is challenging to construct a compact thermal network. The extraction of thermal resistance and heat capacity parameters usually depends on the finite element simulation method. The power MOSFET is mainly distributed in the fields of motor drives, new energy vehicle photovoltaics, and so on. As a heating element, the difference between different modules is fitted as the coupled thermal impedance. Therefore, this paper uses the junction temperature change of a power MOSFET in a photovoltaic power module to verify the junction temperature measurement method proposed in this paper. In this paper, an assessment of the coupling degree of the MOSFET module in the photovoltaic power optimizer is conducted, leading to the derivation of a critical coupling impedance matrix. This matrix can be used to decrease the complexity of thermal modeling and enable the accurate estimation of the junction temperature.
Developing compact thermal networks for multichip power modules remains a significant technical challenge. While finite element method (FEM) simulations are conventionally employed for extracting thermal resistance and heat capacity parameters, existing modeling approaches present notable limitations. Schweitzer [] demonstrated dynamic compact thermal modeling for multisource semiconductor devices through nonlinear optimization algorithms, but the methodology demands extensive computational iterations to achieve convergence. Bahman et al. [] implemented step response analysis to establish 3D lumped thermal models accounting for thermal coupling and boundary conditions, yet their approach exhibits a labor-intensive nature and limited scalability for multichip configurations. Li et al. [] developed a three-step curve-fitting method to extract physically meaningful resistor–capacitor (RC) parameters from FEM results, effectively addressing Foster network limitations in multichip applications. However, the substantial parameter space (multiple R and C values) complicates the identification process. To overcome these collective challenges, this work proposes a novel two-step methodology for constructing optimized compact thermal models in multichip power modules.
In this paper, we mainly establish the FEM based on the power MOSFET module in a photovoltaic power enhancer. The correctness of the model is verified by probe detection. The coupling effect between the MOSFET devices and the influence of the boundary conditions on the temperature are analyzed. The results of the thermal network model of the power device are mainly due to the power loss and cooling conditions of the device. In this paper, they are simulated and verified to further improve the correctness of the model. The model-building method in this paper can be used on the power MOSFET devices, which are commonly adopted in the photovoltaic power enhancers. In different application environments, the corresponding thermal network model can be extracted only by modifying the parameters of each material layer in FEM, which simplifies the junction temperature measurement with small error.
2. Heat Distribution Analysis
There are many reports on the thermal modeling of photovoltaic grid-connected inverters and wind power converters []. Most of the converters are designed with integrated modules. In a modular device, the chips are assembled on a PCB substrate so that the heat flow generated by the device junction can be dissipated through the same thermal path, thereby realizing the symmetry of the temperature distribution. In contrast, a photovoltaic power optimizer typically works in conjunction with discrete devices, with their respective substrates at different locations in the radiator []. Because of different cooling paths, the junction temperatures of the power devices are different even under the same thermal load, resulting in uneven heat dissipation distribution [,].
In order to explore the nonuniform heat distribution of the asymmetric photovoltaic power optimizer, the steady-state thermal simulation of the power MOSFET module of a photovoltaic power enhancer is carried out by using the finite element method (FEM). Based on the calculation of power loss, the boundary conditions of the heat dissipation and the coupling effect are studied, and a junction temperature estimation model of the power MOSFET is extracted. The measurement principle is shown in Figure 1. The input current vin is output through an inductor, resistor, capacitor, 4MOSFET, and Bluetooth module. The thermal modeling process is illustrated in Figure 2.
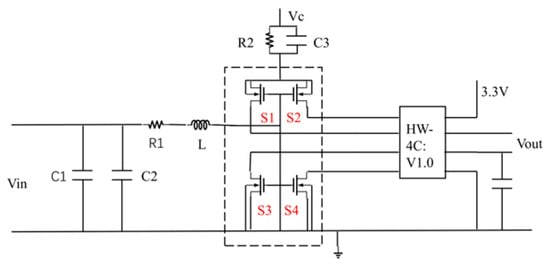
Figure 1.
Photovoltaic power device schematic diagram.
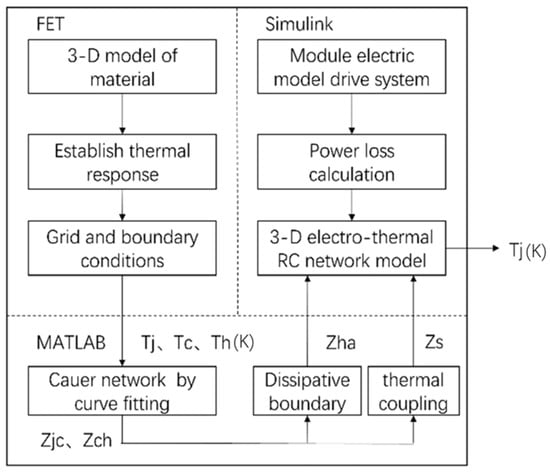
Figure 2.
Thermal modeling process proposed in this paper.
In the photovoltaic power enhancer, a large amount of energy loss is generated by the power module. The thermal dissipation approach for the power module with high power density should be studied carefully. Advanced packaging and heat dissipation technologies can improve the heat dissipation efficiency of the power module. The structure of the photovoltaic optimizer is shown in Figure 3. The schematic of the JMSH1004BGQ module is shown in Figure 4, with the simulation result on the module. In addition, assuming that the ambient temperature is a constant value (20 °C), the convection heat transfer coefficient on the heat-sink surface is set as h = 6.8 × 10−6 W/(mm·°C) with the emissivity as e = 0.4, and the simulation time is selected as 300 s. And in different applications, as long as the convection of the radiator is modified in comsol, there is no need to redesign the extraction method.

Figure 3.
Structure of the photovoltaic power enhancer. (a) Top view of photovoltaic power enhancer. (b) Set-up model of the photovoltaic power enhancer.
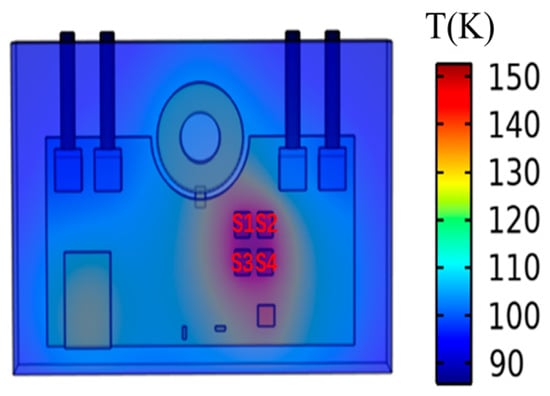
Figure 4.
FEM simulation results of JMSH1004BGQ module.
Finite element simulation plays an irreplaceable role in the thermal analysis of photovoltaic power enhancer systems. Thermal behavior can be simulated by a meshing process and setting strict boundary conditions. A MOSFET JMSH1004BGQ (Made by Jie Jie Microelectronics Co., LTD, Suzhou, China) module is taken as the prototype, which is divided into the aluminum electrode layer, silicon chip layer, copper metal layer, epoxy resin layer, and PCB layer, as shown in Figure 5. The lateral dimensions of different materials are marked: the silicon layer is 0.6 mm, the copper is 2.5 mm, the aluminum is 1 mm, the epitaxial is 5 mm, and the PCB is 70 mm.

Figure 5.
Three-dimensional FEM model layers of MOSFET.
As shown in Table 1, the material properties of the three-dimensional finite element model are listed, including thermal conductivity, specific heat capacity, thickness, etc.

Table 1.
Thermal Properties of MOSFET Materials.
The thermal impedance Zjc(t) from the junction to the shell as the key layer plays an important role in thermal modeling, which is defined as follows:
where Tj(t) and Tc(t) are expressed with time as the junction and case temperatures of the MOSFETs, respectively, and Pstep(t) represents the heat source of the device. Thus, a step power loss is loaded as heat flow on the MOSFET die layer (Node J) in FEM, and the transient temperature Tj(t) and Tc(t) can be obtained by probe. Figure 6a depicts the temperature response result, and FEM results are plotted in log coordinates with dotted lines. It is in good consistency with the datasheet, which indicates that the FEM model established in this paper is certainly effective.
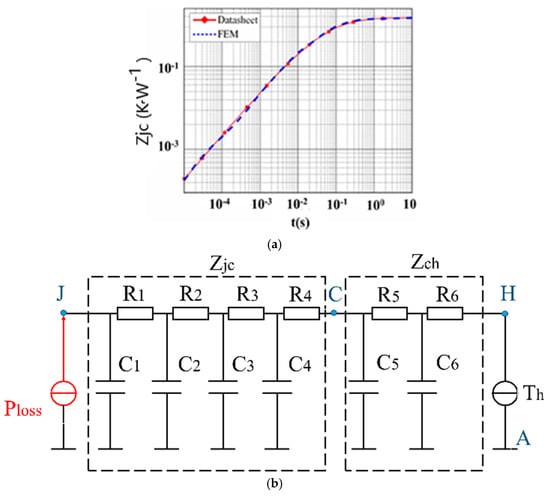
Figure 6.
FEM model of MOSFET. (a) Transient impedance curve with FEM result. (b) Cauer network model of MOSFET.
Thermal impedance can be denoted with an RC network, which is mainly divided into the Foster model and Cauer model. The Foster model can be obtained from the step thermal response, but its structure is inconsistent with the physical meaning. The Cauer model can reflect the actual thermal path and has more effective cascade characteristics. In this paper, the Cauer network model is used to represent the heat conduction of the MOSFET, as shown in Figure 6b. The heat flow generated by the power loss of the device, from the module point J to the chassis node C, is conducted between the inner layers. The heat is dissipated to the environmental node A through the impedance Zch of the grease and the radiator, and the temperature is constant at room temperature (20 °C).
In order to describe the thermal impedance in the form of an RC network, Zjc can be interpreted as
where ri and ci are the thermal resistance and heat capacity of the Foster network, respectively.
Using the same method, the thermal response curve of oil impedance Zch can be extracted from the finite element method. Then, the Foster network can be converted to the Cauer network for ri and ci values. Considering that the time constants of a MOSFET and thermal grease in the step thermal response are different, the Zjc of a MOSFET device is fitted by the fourth order, and the Zch of thermal grease is fitted by the second order to meet the accuracy requirements. The ri and ci values of the MOSFET module in the Cauer network are shown in Table 2.

Table 2.
Thermal Impedance Parameters in the Cauer Model.
The radiator is one of the main components on the thermal path from node J to node A, and its heat dissipation characteristics have a decisive influence on the temperature distribution. Studies have shown that when a power device is installed at different positions on the surface of a radiator, the heat dissipation paths may be unequal [], which is one of the reasons for the uneven temperature distribution.
Considering the geometric symmetry of the converter structure, the points (node H) S1, S2, and S3 are defined as three typical positions for analyzing the heat dissipation of the radiator, with the points as shown in Figure 4. The junction temperature response can be extracted in a FEM simulation by loading the same step power loss on the device at four typical positions, as shown in Figure 6. In the case of the same impedance of a MOSFET and grease, the junction temperature curves shown in Figure 7 are different, especially in the stable state after 90 s, which can only be caused by the uneven dissipation boundary conditions of the radiator.
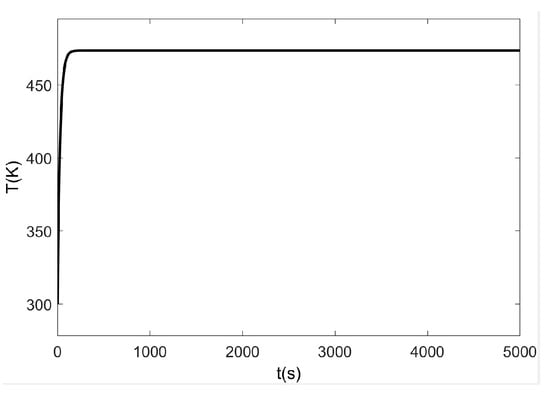
Figure 7.
Thermal impendence parameters in Cauer model.
For a photovoltaic power enhancer, although the power losses of the loads on the same functional devices (such as S1 and S3) are equal, the junction temperature distribution of the devices is not uniform. Therefore, in order to accurately estimate the junction temperature, it is necessary to consider the heat dissipation boundary conditions. The difference between dissipative boundary conditions is mainly reflected in the stable junction temperature and time constant. The stable junction temperature is determined by the thermal conductivity, and the response time constant is affected by the specific heat capacity.
For traditional power converters, such as photovoltaic grid-connected inverters and wind power converters, power losses and thermal circuits are generally symmetrically distributed in an integrated module []. Therefore, in the process of radiator modeling, even if the boundary conditions can be considered, the thermal path is generally regarded as a unified thermal impedance. However, in this paper, a complete radiator is decoupled into multiple sub-radiators for each device. These subdivisions have unequal thermal conductivity and specific heat, so the difference in dissipative boundary conditions can be represented by the corresponding sub-radiators.
For example, Zha(S1) and Zha(S2) (Zha(S1) and Zha(S2) are the thermal impedances of the H-A node of the S1 and S2 devices in Figure 4, respectively) represent the thermal impedances of the sub-radiator below S1 and S2, from node h to a, respectively. According to the thermal response curves of four typical positions, the Cauer RC network of the sub-radiator is extracted by curve fitting in MATLAB 2023. The fitting order can be selected as the second order to meet the accuracy requirements. Table 2 describes the thermal impedance of the sub-radiator under different boundary conditions at four typical locations.
Based on the analysis of power loss and uneven heat dissipation boundary conditions, a set of actual loss distribution values, shown in Table 1, can be loaded into the FEM to obtain the steady-state temperature of the converter. When multiple components work together, the heat flow generated by the power loss not only causes its own temperature rise but also causes the temperature rise of surrounding devices. The device would be affected by the thermal coupling from other devices. In order to further explore the accurate junction temperature, it is necessary to study the coupling effect of thermal behavior.
Due to the special loss distribution of asymmetric MOSFETs, the coupling effects among devices are different. Therefore, the actual power loss is used in this paper instead of the step thermal response, which can reduce the complexity of thermal modeling and meet the accuracy requirements. When the ambient temperature is 22 °C, the heat transfer coefficient is 3000 W·m−2·°C−1, and the Ploss = 1, 1.5, 2 W is applied to the S1 device, the Tj of S1 changes with time as shown in Figure 8a. When the heat loss is higher, the temperature peak is higher. When the ambient temperature is 22 °C, the heat transfer coefficient is 3000 W·m−2·°C−1, and the Ploss = 1 W is applied to the S1 device, the Tj of S1 changes with time at different flow rates of 1.5, 2, and 2.5 m/s, respectively, as shown in Figure 8b. The larger the flow rate, the lower the temperature peak.
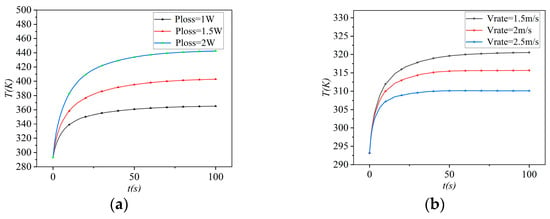
Figure 8.
Comparison of Tj of thermal models with the FEM simulation at Ta = 20 °C and HTC (heat transfer coefficient) = 3000 W·m−2·°C−1. (a) With different Ploss values. (b) With different Vrate values.
When the simulation of Ploss = 1 W is applied to the S1 and S2 devices at the same time, the stable state is shown in Figure 9. The two devices are coupled and the peak temperature is greatly improved. When Ploss = 1 W is applied to S1 and S2, respectively; Ploss = 1 W is applied to S1 and S3; and when Ploss = 1 W is applied to S1 and S4, the temperature curve is shown in Figure 10. The power MOSFET is affected by the coupling effect. The farther the distance is, the smaller the coupling effect is.
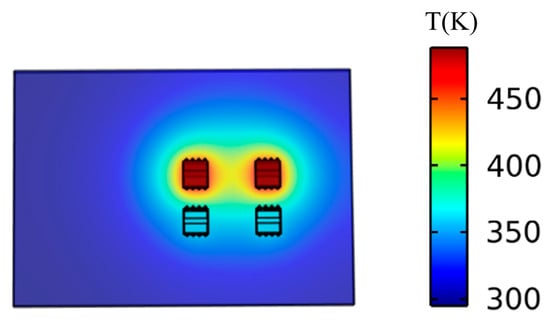
Figure 9.
Load PS1 on device S1and PS2 on device S2.
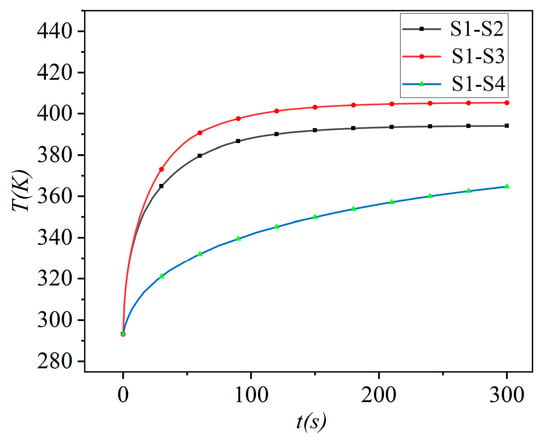
Figure 10.
Junction temperature of S1 under coupling effect with different devices.
3. Loss Model and Heat Network Model
As the input of the heating network, including conduction loss and switching loss, the power loss includes the following parts.
Firstly, switching loss should be considered. The switching loss in a MOSFET includes conduction loss and turn-off loss, while the switching loss in a diode is given by recovery loss. Compared with conduction loss, the switching loss is closely related to many variables, such as DC bus voltage, current, junction temperature, gate drive resistance, and voltage. A double pulse test is carried out to calibrate the switching loss under different working conditions. In the actual switching loss measurement, the switching energy can be obtained by the integral function of the digital oscilloscope.
The second part is conduction loss. In an electrical excitation cycle, the junction temperature fluctuation of the power module cannot be ignored. Therefore, a model of average conduction loss in a period is established [,,,,].
In order to understand the junction temperature estimation approach, a three-dimensional compact RC network model of an asymmetric power MOSFET for a photovoltaic power optimizer is proposed in this paper [,,]. The model can reflect the nonuniform distribution of power loss and can be used to estimate the heat dissipation boundary conditions and thermal coupling effects. However, the junction temperature should be regarded as the superposition result of temperature rise caused by self-loss and coupling effect under different dissipative boundary conditions. Figure 11 shows the RC network model.
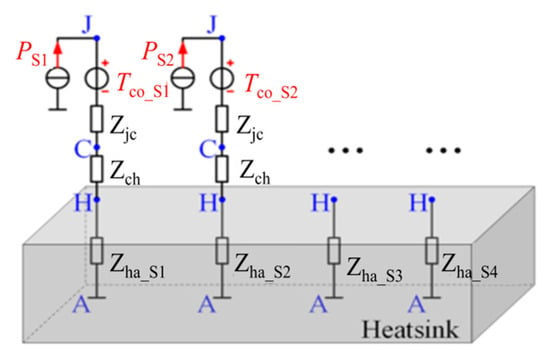
Figure 11.
Compact RC network model of photovoltaic power optimizer.
As shown in Figure 11, the current source presents the heat flow generated by the power loss of the device itself. The thermal impedance Zjc and silicon grease Zch of the device are arranged on the surface of the radiator in turn, forming a thermal path from node J to node A. In contrast, the thermal coupling effect is modeled as a voltage source between the insertion node J and the impedance Zjc, and the magnitude of the source voltage is controlled by the degree of the coupling effect of other devices. In the model, various dissipative boundary conditions are expressed as four typical sub-radiator impedances connected in series at the end of the thermal path and exposed to ambient temperature.
4. Experimental Verification
The experimental test is carried out to test the validity and the accuracy of the proposed thermal model. The experimental setup is shown in Figure 12, including an oscilloscope (such as Vsd) for electrical signal acquisition, a programmable DC power supply for generating test current, a DC power supply for generating gate signals for testing Si MOSFET modules, a liquid recirculation cooler for cooling the module through the cold plate, an infrared camera (FLIR) for collecting the junction temperature in real time, and a thermo-couple connected to the bottom of the module for measuring Tc.

Figure 12.
Test platform.
The MOSFET module is placed in an environment with a temperature of 20 °C, a cooling flow rate of 1 m/s is added, and Ploss = 1, 1.5, 2 W is applied to the S1 device, respectively. After the device is stable, the infrared thermal imager is used to measure the temperature, and the experimental results are compared with the temperature curve obtained by the thermal network model, with an error of ±5 °C. As shown in Figure 13, the MOSFET module is placed in an environment with a temperature of 20 °C, a Ploss = 0.5 W is added to the S1 device, a cooling flow rate of 1, 1.5, 2 m/s is applied to the module, respectively, and the infrared thermal imager is used to measure the temperature after the device is stable. Comparing the experimental results with the temperature curve obtained by the thermal network model, the error is ±5 °C, as shown in Figure 14.
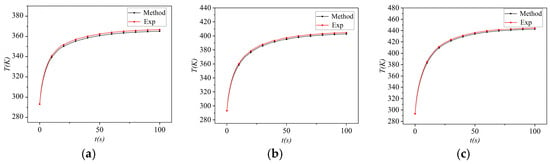
Figure 13.
Comparison of experiments when the ambient temperature of thermal model Tj is 20 °C and flow rate is 1 m/s: (a) Ploss = 1 W. (b) Ploss = 1.5 W. (c) Ploss = 2 W.
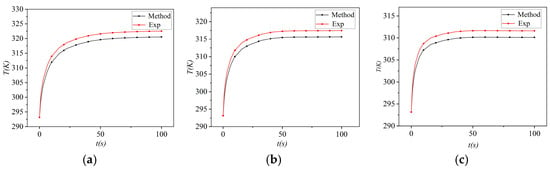
Figure 14.
Comparison of experiments when the ambient temperature of thermal model Tj is 20 °C and P is 0.5 W: (a) Flow rate = 1 m/s. (b) Flow rate: 1.5 m/s. (c) The flow rate is 2 m/s.
The results are shown in Figure 13 with different thermal flow rates. The errors of the proposed thermal models are estimated to be less than 4 °C. Then, the influence of cooling conditions on the model is shown in Figure 14. The maximum error is less than 1.5 °C under different cooling conditions. Because of many variations, such as the distance between the infrared camera and the chip surface, the reflection temperature during measurement, and other factors, some errors exist in the experiment. The proposed temperature-dependent thermal model with different boundary conditions can be applied to different practical applications and has high junction temperature estimation accuracy.
5. Conclusions
In this article, a 3D compact thermal model considering thermal boundary conditions extracted from a complex FEM model was proposed to improve computation efficiency for the inverters in a power.MOSFET. A novel method to extract the parameters in a compact thermal model was developed, and the accuracy of the reduced-order model was verified by FEM simulation. The effects of thermal boundary conditions including flow rate and coolant temperature on the thermal network were studied through many simulation experiments in ANSYS/ICEPAK. A temperature-dependent physical RC network model of a MOSFET module considering boundary conditions is proposed. With the help of finite element steady-state thermal simulation, the extraction process of RC parameters is greatly simplified.
- The temperature-sensitive thermal parameters can play an important role in the thermal behavior modeling of high-temperature modules.
- The effective heat dissipation area of each layer is optimized based on FEM simulation results. High accuracy of junction temperature estimation can be achieved.
- The influence of boundary conditions on the heat flow path is quantified, and the thermal analysis of the boundary conditions is carried out. The results show that the thermal model based on temperature and boundary can well characterize the thermal behavior of the power module under different working conditions.
The thermal model has the advantages of simple establishment, fast calculation speed, and strong adaptive ability, and it can be widely used to accurately estimate the long-term mission life of Si MOSFET modules. For the majority of power MOSFETs, based on the package and material parameters, this method can be utilized to conduct online measurement of the junction temperature. Subsequently, research will be carried out on the practicability of this method for MOSFETs fabricated from semiconductor materials such as SiC.
Author Contributions
Conceptualization, N.L., S.Z. and Y.J.; methodology, N.L., S.Z. and Y.J.; software, N.L. and S.Z.; validation, N.L., S.Z. and Y.J.; formal analysis, N.L.; investigation, N.L.; resources, S.Z. and Y.J.; data curation, N.L. and S.Z.; writing—original draft preparation, N.L.; writing—review and editing, S.Z. and Y.J.; visualization, S.Z. and Y.J.; supervision, Y.J.; project administration, Y.J.; funding acquisition, Y.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by in part by Leading Technology Pre-Research Project (No.XD23008, Wuxi Industrial Innovation Research Institute and Jiangsu JITRI IC Application Technology Innovation Center).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, U.M.; Blaabjerg, F.; Lee, K.B. Study and Handling Methods of Power IGBT Module Failures in Power Electronic Converter Systems. IEEE Trans. Power Electron. 2014, 30, 2517–2533. [Google Scholar] [CrossRef]
- Baker, N.; Liserre, M.; Dupont, L.; Avenas, Y. Improved reliability of power modules: A review of online junction temperature measurement methods. IEEE Ind. Electron. Mag. 2014, 8, 17–27. [Google Scholar] [CrossRef]
- Qian, C.; Gheitaghy, A.M.; Fan, J.; Tang, H.; Sun, B.; Ye, H.; Zhang, G. Thermal Management on IGBT Power Electronic Devices and Modules. IEEE Access 2018, 6, 12868–12884. [Google Scholar] [CrossRef]
- Williams, R.; Suggs, J.; Rea, A.; Sheldon, L.; Rodes, C.; Thornburg, J. The Research Triangle Park particulate matter panel study: Modeling ambient source contribution to personal and residential PM mass concentrations. Atmos. Environ. 2003, 37, 5365–5378. [Google Scholar] [CrossRef]
- Blackburn, D.L. Semiconductor devices and circuits: Smaller, faster, denser and what it all means. In Proceedings of the IEEE Fifteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium. SEMI-THERM. Fifteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium (Cat. No.99CH36306)—Semicond, San Diego, CA, USA, 9–11 March 1999; p. 73. [Google Scholar]
- Nick, B.; Stig, M.N.; Francesco, I.; Marco, L. IGBT Junction Temperature Measurement via Peak Gate Current. IEEE Trans. Power Electron. 2016, 31, 3784–3793. [Google Scholar]
- Niu, H.; Lorenz, R.D. Sensing Power MOSFET Junction Temperature Using Gate Drive Turn-on Current Transient Properties. IEEE Trans. Ind. Appl. 2015, 52, 1677–1687. [Google Scholar] [CrossRef]
- Bahman, A.S.; Ma, K.; Blaabjerg, F. A Lumped Thermal Model Including Thermal Coupling and Thermal Boundary Conditions for High Power IGBT Modules. IEEE Trans. Power Electron. 2018, 33, 2518–2530. [Google Scholar] [CrossRef]
- Eiser, S.; Bernardoni, M.; Nelhiebel, M.; Kaltenbacher, M. Finite-Element Analysis of Coupled Electro-Thermal Problems with Strong Scale Separation. IEEE Trans. Power Electron. 2016, 32, 561–570. [Google Scholar] [CrossRef]
- Ji, B.; Pickert, V.; Cao, W.; Zahawi, B. In Situ Diagnostics and Prognostics of Wire Bonding Faults in IGBT Modules for Electric Vehicle Drives. IEEE Trans. Power Electron. 2013, 28, 5568–5577. [Google Scholar] [CrossRef]
- Bing, J.; Xueguan, S.; Wenping, C.; Pickert, V.; Yihua, H.; Mackersie, J.W.; Pierce, G. In Situ Diagnostics and Prognostics of Solder Fatigue in IGBT Modules for Electric Vehicle Drives. IEEE Trans. Power Electron. 2014, 30, 1535–1543. [Google Scholar] [CrossRef]
- Peiró, J.; Sherwin, S. Finite Difference, Finite Element and Finite Volume Methods for Partial Differential Equations. In Handbook of Materials Modeling; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Li, J.; Castellazzi, A.; Eleffendi, M.A.; Gurpinar, E.; Johnson, C.M.; Mills, L. A Physical RC Network Model for Electro-Thermal Analysis of a Multichip SiC Power Module. IEEE Trans. Power Electron. 2017, 33, 2494–2508. [Google Scholar] [CrossRef]
- Bahman, A.S.; Ma, K.; Ghimire, P.; Iannuzzo, F.; Blaabjerg, F. A 3D Lumped Thermal Network Model for Long-term Load Profiles Analysis in High Power IGBT Modules. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1050–1063. [Google Scholar] [CrossRef]
- Khatir, Z.; Dupont, L.; Ibrahim, A. Investigations on junction temperature estimation based on junction voltage measurements. Microelectron. Reliab. 2010, 50, 1506–1510. [Google Scholar] [CrossRef]
- Chen, H.; Yang, J.; Xu, S. Electrothermal-Based Junction Temperature Estimation Model for Converter of Switched Reluctance Motor Drive System. IEEE Trans. Ind. Electron. 2020, 67, 874–883. [Google Scholar] [CrossRef]
- Li, H.; Hu, Y.; Liu, S.; Li, Y.; Liao, X.; Liu, Z. An Improved Thermal Network Model of the IGBT Module for Wind Power Converters Considering the Effects of Base-Plate Solder Fatigue. IEEE Trans. Device Mater. Reliab. 2016, 16, 570–575. [Google Scholar] [CrossRef]
- Wang, Z.; Qiao, W. A Physics-Based Improved Cauer-Type Thermal Equivalent Circuit for IGBT Modules. IEEE Trans. Power Electron. 2016, 31, 6781–6786. [Google Scholar] [CrossRef]
- Luo, Z.; Ahn, H.; Nokali, M.A.E. A thermal model for insulated gate bipolar transistor module. IEEE Trans. Power Electron. 2004, 19, 902–907. [Google Scholar]
- Xu, Y.; Chen, H.; Gu, J. Power loss analysis for switched reluctance motor converter by using electrothermal model. IET Power Electron. 2014, 8, 130–141. [Google Scholar] [CrossRef]
- Gerstenmaier, Y.C.; Castellazzi, A.; Wachutka, G.K. Electrothermal simulation of multichip-modules with novel transient thermal model and time-dependent boundary conditions. IEEE Trans. Power Electron. 2006, 21, 45–55. [Google Scholar] [CrossRef]
- Du, B.; Hudgins, J.L.; Santi, E.; Bryant, A.T.; Palmer, P.R.; Mantooth, H.A. Transient electrothermal simulation of power semiconductor devices. IEEE Trans. Power Electron. 2009, 25, 237–248. [Google Scholar]
- Reichl, J.; Ortiz-Rodriguez, J.M.; Hefner, A.; Lai, J.-S. 3-D thermal component model for electrothermal analysis of multichip power modules with experimental validation. IEEE Trans. Power Electron. 2014, 30, 3300–3308. [Google Scholar] [CrossRef]
- Reggiani, S.; Gnani, E.; Rudan, M. A New Numerical and Experimental Analysis Tool for ESD Devices by Means of the Transient Interferometric Technique. IEEE Electron Device Lett. 2005, 26, 916–918. [Google Scholar]
- Ma, K.; He, N.; Liserre, M.; Blaabjerg, F. Frequency-Domain Thermal Modeling and Characterization of Power Semiconductor Devices. IEEE Trans. Power Electron. 2016, 31, 7183–7193. [Google Scholar]
- Sakr, A.H.; Hossain, E. Cognitive and Energy Harvesting-Based D2D Communication in Cellular Networks: Stochastic Geometry Modeling and Analysis. IEEE Trans. Commun. 2015, 63, 1867–1880. [Google Scholar] [CrossRef]
- Schweitzer, D. Generation of multisource dynamic compact thermal models by RC-network optimization. In Proceedings of the 29th IEEE Semiconductor Thermal Measurement and Management Symposium, San Jose, CA, USA, 17–21 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 116–123. [Google Scholar]
- Liserre, M.; Andresen, M.; Costa, L.; Buticchi, G. Power Routing in Modular Smart Transformers: Active Thermal Control Through Uneven Loading of Cells. IEEE Ind. Electron. Mag. 2016, 10, 43–53. [Google Scholar] [CrossRef]
- Ivanova, M.; Avenas, Y.; Schaeffer, C.; Dezord, J.B.; Schulz-Harder, J. Heat Pipe Integrated in Direct Bonded Copper (DBC) Technology for Cooling of Power Electronics Packaging. IEEE Trans. Power Electron. 2006, 21, 1541–1547. [Google Scholar] [CrossRef]
- Lutz, J.; Schlangenotto, H.; Scheuermann, U.; Doncker, R.D. Semiconductor Power Devices; Springer: Cham, Switzerland, 2011. [Google Scholar]
- Broeck, C.H.V.D.; Ruppert, L.A.; Doncker, R.W.D. Spatial Electro-Thermal Modeling and Simulation of Power Electronic Modules. In Proceedings of the Energy Conversion Congress and Exposition, ECCE 2016, Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Bahman, A.S.; Ma, K.; Blaabjerg, F. General 3D Lumped Thermal Model with Various Boundary Conditions for High Power IGBT Modules. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016. [Google Scholar]
- Gachovska, T.K.; Tian, B.; Hudgins, J.L.; Qiao, W.; Donlon, J.F. A Real-Time Thermal Model for Monitoring of Power Semiconductor Devices. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 September 2013. [Google Scholar]
- Sciascera, C.; Giangrande, P.; Papini, L.; Gerada, C.; Galea, M. Analytical Thermal Model for Fast Stator Winding Temperature Prediction. IEEE Trans. Ind. Electron. 2017, 64, 6116–6126. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).