An Ultra-Low-Power 0.8 V, 60 nW Temperature Sensor for Battery-Less Wireless Sensor Networks

Abstract

This work presents a nano-watt digital output temperature sensor featuring a supply-insensitive, self-biased current source. Second-order temperature dependencies of the MOS diode are canceled to produce a stable reference and a linear temperature-sensitive voltage. The sensor integrates a sensing unit, voltage-controlled differential ring oscillators, and a low-power frequency-to-digital converter, utilizing a resistor-less design to minimize power and area. The delay element in the ring oscillator reduces stage count, improving noise performance and compactness. Fabricated in 65 nm CMOS, the sensor occupies 0.02 mm² and consumes 60 nW at 25 °C and 0.8 V. Measurements show an inaccuracy of +1.5/−1.6 °C from −20 °C to 120 °C after two-point calibration, with a resolution of 0.2 °C (rms) and a resolution FoM of 0.022 nJ·K⁻². Consuming 0.55 nJ per conversion with a 9.2 ms conversion time, the sensor was tested in a battery-less wireless sensor node, demonstrating its suitability for wireless sensing systems.

1. Introduction

In the last decade, battery-less and wireless sensors have enabled large-scale, energy-efficient, and cost-effective monitoring systems. The rapid expansion of wireless sensor networks (WSNs) and the Internet of Things (IoT) has driven the demand for self-powered sensors reliant on environmental energy harvesting. Temperature sensors, widely used in industries such as farming, healthcare, supply chain, climate monitoring, smart homes, and automation [1,2,3], are increasingly required to function in remote and challenging environments, making high-accuracy, area-efficient, and low-power designs crucial [1,2].

Designing ultra-low-power temperature sensors for battery-less systems poses challenges, including efficient energy use to handle intermittent harvesting [4], maintaining accuracy across wide temperature ranges without regular calibration [5], and compact designs for cost-effective mass production. Fully integrated sensors must also generate all biases internally, removing reliance on external references.

A wide range of temperature sensors have been developed using CMOS technology [6], employing bipolar junction transistors (BJTs) [7,8,9], resistors [10,11], or MOSFETs [12,13,14]. BJT-based sensors leverage the complementary-to-absolute-temperature (CTAT) behavior of the base-emitter voltage (V_BE) and the proportional-to-absolute-temperature (PTAT) difference (ΔV_BE) between transistors with varying current densities to generate a temperature-insensitive reference voltage [9]. Accurate digital measurements are achieved by comparing this reference voltage with the PTAT voltage using an analog to digital converter (ADC) [8,15]. While BJTs provide a wide sensing range (−55 °C to 125 °C), they face challenges like limited dynamic range [16], non-linearity at high temperatures [7,9], and sensitivity to process variations, which can lead to errors mitigated by one-point calibration (±0.1 °C) [17]. Their high turn-on voltage (>0.7 V) and µW-level power consumption make them unsuitable for low-power, battery-less applications [8].

Resistor-based temperature sensors provide low power consumption, linear responses, and simple designs, but are prone to self-heating inaccuracies [18] and high process sensitivity, often requiring 2-point calibration [11]. They can operate across wide temperature ranges (−55 °C to 125 °C) [10] using Wheatstone bridge configurations with resistors of opposite temperature coefficients. However, the process sensitivity of on-chip resistors’ temperature coefficients limits their suitability for many applications [19].

Voltage references using 2T and 4T structures [20] use MOS threshold and thermal voltages (VT) for low power consumption (~pWs) but require special common-mode voltage considerations for o-perational transconductance amplifiers (OTAs). Another design introduces voltage reference and dummy structures to address these requirements, albeit with increased complexity [21]. Resistor-based PTAT and reference current generation demand large resistors (~7 MΩ), which consume significant chip area (42%) and limit integration.

Efforts to reduce power consumption and supply voltage include resistorless current [22] and voltage [23] references consuming under 50 nW and <1 V, respectively. Frequency-to-digital converters, while advantageous, require a reference clock, which may not be available in wireless systems and can increase power consumption. Leakage-dominated ring oscillator (LDRO) sensors [24] offer low power (9.3 µW) and modest accuracy (±0.7 °C from −40 to 125 °C) but depend on external clocks. Time-domain sensors [14] with on-chip clocks achieve lower power consumption (196 nW at 0.95 V). However, many of these designs rely on multiple current sources or large resistors, limiting their integration efficiency and often requiring external references. In contrast, our work introduces a single-branch resistorless approach that significantly reduces both power and area overheads, eliminates the need for external references, and enables fully integrated, battery-less operation.

This work introduces a resistorless, fully integrated MOSFET-based temperature sensor. It employs a single current source to generate temperature-sensitive and reference voltages, using voltage-controlled, current-starved VCOs for digital temperature measurement. A modified Oguey current source [25]—featuring improved supply rejection through active control of internal node voltages—generates all bias currents, enabling low-power operation. Additionally, we adopt a differential pair structure in the ring oscillator to improve noise immunity and achieve a wide tuning range at low supply voltages. Fabricated in a 65 nm CMOS process, the sensor occupies 0.02 mm², consumes 60 nW at 0.8 V, and achieves ±1.5/−1.6 °C inaccuracy (3σ) from −20 to 120 °C with 2-point calibration, covering a 140 °C span. It offers a 0.2 °C (rms) resolution with a resolution FoM of 0.022 nJ·K⁻², consuming 0.54 nJ per conversion over a 9.2 ms conversion time. Although this broad temperature range and short conversion time can introduce challenges for maintaining uniform accuracy, the sensor remains competitive for battery-less IoT applications due to its extremely low power consumption and small footprint.

This paper is structured as follows. Section 2 discusses the architecture of the proposed sensor and provides a mathematical analysis and detailed design of all the functional blocks. Section 3 presents post-silicon measurement results. Section 4 describes the integration of the temperature sensor in a battery-less wireless sensor node. Section 5 concludes the paper.

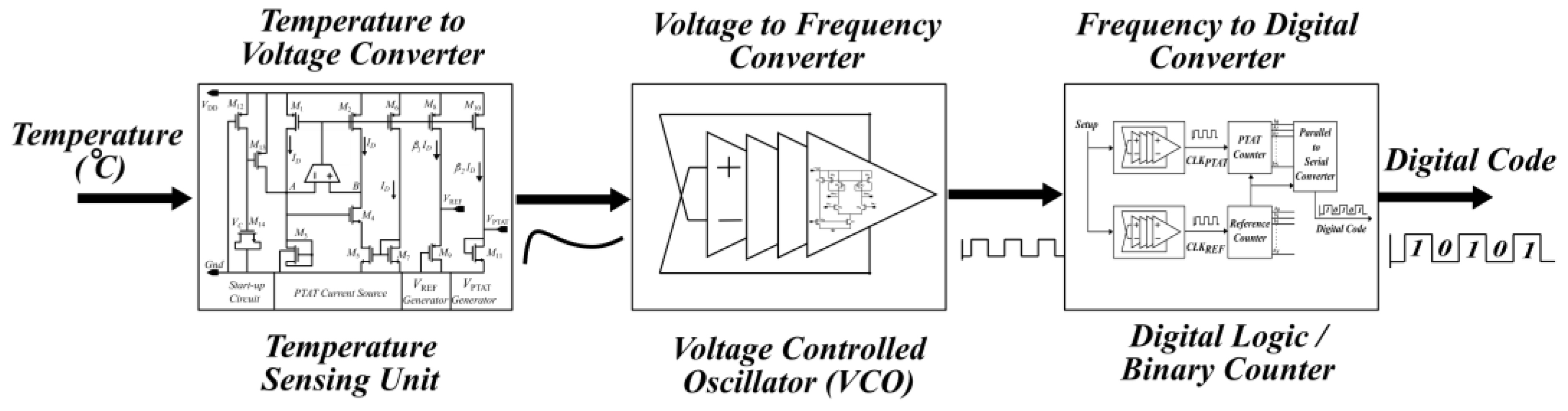
2. Architecture of the Proposed Temperature Sensor

A temperature sensor detects the ambient temperature and converts it into a digital code. Figure 1 illustrates the proposed architecture of this sensor with three main functional blocks: (1) a temperature sensing unit, (2) a voltage-to-frequency converter, and (3) frequency-to-digital converter logic.

The temperature sensing unit produces a PVT-tolerant reference voltage (V_REF) and a temperature-sensitive voltage (V_PTAT), which controls a VCO to create a temperature-dependent frequency (F_PTAT). A second VCO generates a reference frequency (F_REF) from the V_REF. A digital logic circuit then compares the F_REF and F_PTAT frequencies to produce a binary temperature code.

To achieve low power consumption (nano-watt) in each block, special design considerations are necessary, particularly in the temperature sensing unit. The voltage ranges of the V_PTAT and V_REF determine the oscillation frequency range, directly impacting the dynamic power consumption of the digital logic. Therefore, it is critical to have a strictly defined range for the generated voltages in all the process, temperature, and supply corners.

2.1. Temperature Sensing Unit

The temperature sensing unit outputs V_PTAT and V_REF voltages. Figure 2 shows a conventional way to generate such voltages using a couple of current sources and resistors. While this method is simple, it has limitations. To achieve low-power operation, a low VCO frequency is desired, requiring a low control voltage (~200 mV). If the current source outputs <10 nA, the resistor must be very large (>5 MΩ). Reducing the resistor size requires higher current, creating a trade-off between power and area. This design challenge arises from balancing power efficiency and minimizing area.

A key challenge in the conventional approach is the need for current sources with well-defined PVT dependencies to maintain the linearity of resistors, requiring two sources with different temperature dependencies to generate V_PTAT and V_REF. This increases design complexity and strains power and area. To address this, we propose a resistorless design (Figure 3) using a single current source with a square temperature dependency (PTAT)². The current is copied to a branch with a diode-connected MOSFET whose second-order non-linearities are compensated by the square temperature dependency, resulting in linear V_PTAT and stable V_REF. This design reduces power consumption by 25% (eliminating one of the current-carrying branches) and saves chip area by removing bulky resistors. The use of a single current source ensures identical process variations for both control voltages, simplifying cancellation in the frequency-to-digital converter.

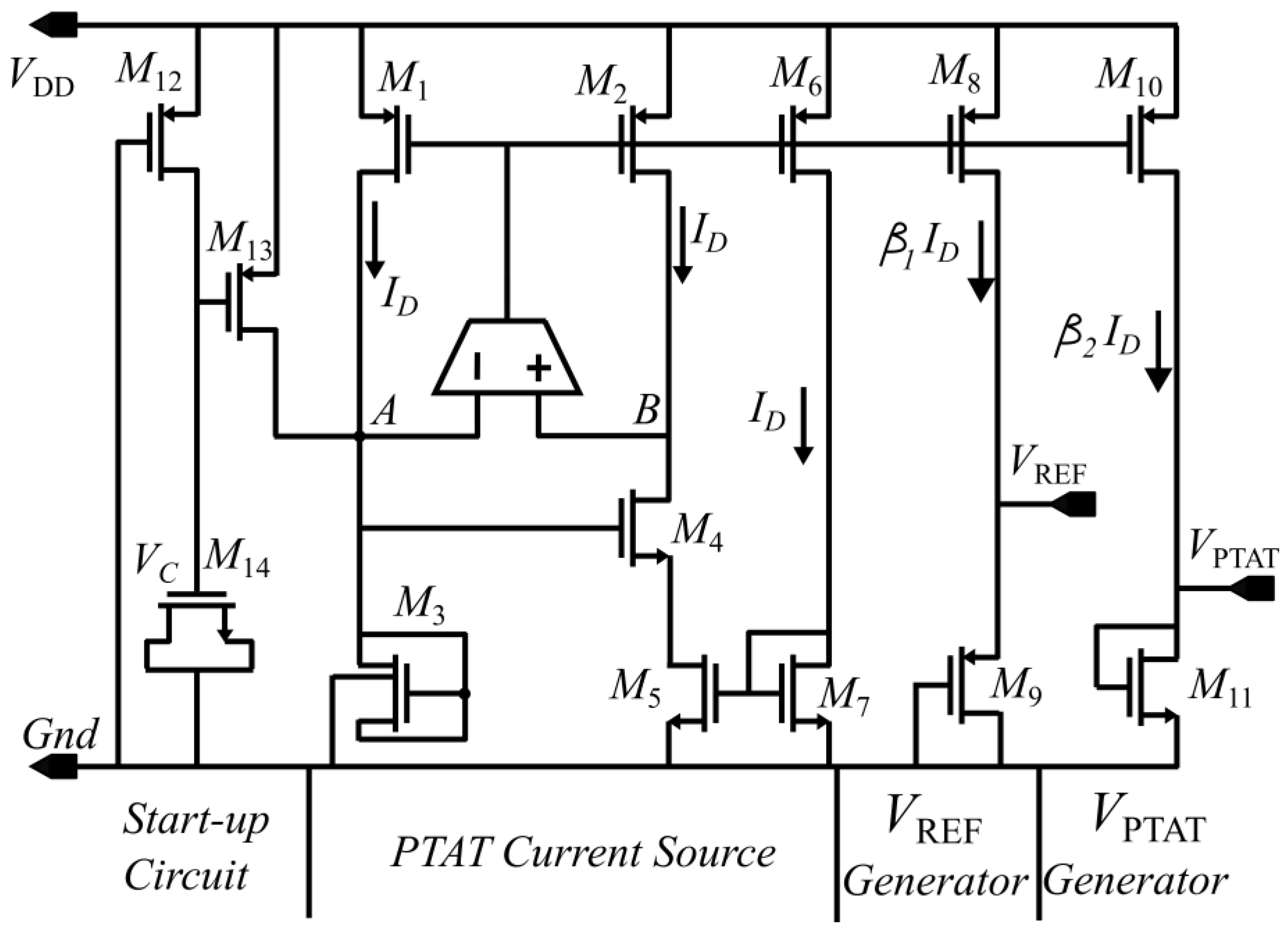
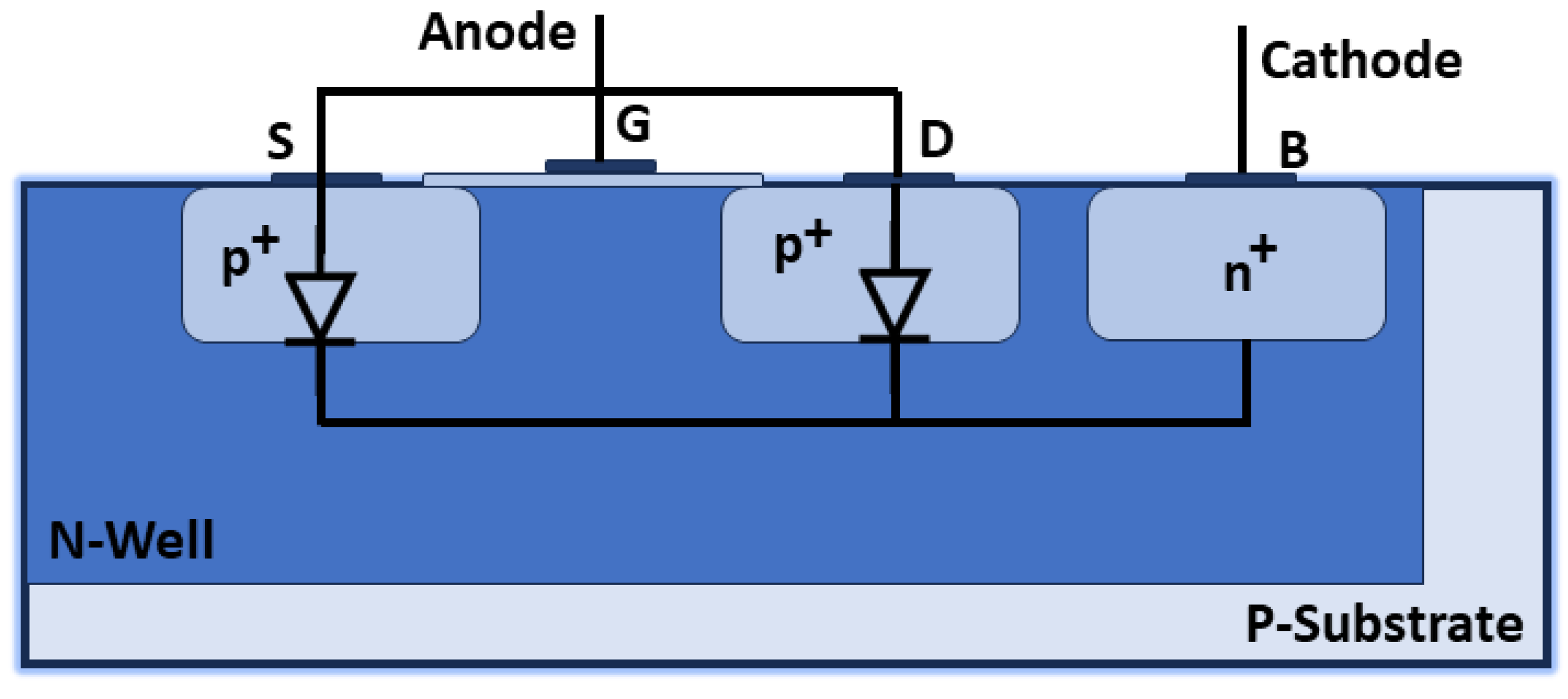
2.1.1. Temperature Sensing Circuit

As mentioned in the previous section, the voltages V_PTAT and V_REF are generated by passing a bias current (I_D) through a diode-connected MOSFET operating in the subthreshold region. The drain current of a diode-connected MOSFET in subthreshold is expressed as [26]:

$$I_D={\displaystyle \frac{W}{L}}\mu C_{ox}{V}_T^2 exp\left({\displaystyle \frac{V_{GS-}{V}_{TH}}{\eta V_T}}\right)\left[1-\mathit{exp}\left({\displaystyle \frac{V_{DS}}{V_T}}\right)\right]$$

(1)

where W/L is the width-to-length ratio of the MOSFET, µ is the carrier mobility, C_ox = ɛ_ox/t_ox is the gate oxide capacitance per unit area, t_ox is the oxide thickness, and ɛ_ox is the oxide permittivity. V_T is the thermal voltage, which is denoted by V_T = KT/q, where K is the Boltzmann Constant, T the temperature, and q the charge of an electron. V_GS denotes the gate-source voltage of the MOSFET, V_TH is the threshold voltage of the MOSFET, and η is the subthreshold slope factor. V_DS is the drain-to-source voltage drop.

The size of the MOSFET is kept such that V_DS ≥ 4 V_T, which is necessary to keep a subthreshold MOSFET in saturation. Setting V_DS ≥ 4 V_T, (1) can be solved and expressed in terms of the V_GS (MOS diode drop) as:

$$V_{GS}=\eta V_T\mathit{ln}\left[{\displaystyle \frac{I_D}{\left(\frac{W}{L}\right)\mu C_{ox}{V}_T^2}}\right]+V_{TH}$$

(2)

In (2) V_T has a positive temperature coefficient (TC), while µ and V_TH have a negative TC. These temperature-dependent coefficients can set the temperature behavior of the diode drop if the I_D is of the form:

$$I_D=\beta \mu C_{ox}{V}_T^2$$

(3)

where β is an arbitrary variable. The mobility that is a process/temperature term is canceled out, and as a result, better process tolerance is achieved. Note that the current I_D in (3) should have a square dependency on the temperature to effectively cancel out the nonlinear term in (2). Substituting (3) in (2) gives:

$$V_{DS}=V_{GS}=\eta V_T ln\left({\displaystyle \frac{\beta }{\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$L$}\right.}}\right)+V_{TH}$$

(4)

The value of the β variable, the sizing, and the choice of the MOS diode with a suitable temperature dependence can be used to generate V_PTAT and V_REF, as illustrated in Figure 3. The value of the subthreshold slope factor (η) is about 1.3, and the thermal voltage V_T has a well-defined temperature coefficient (TC) of 0.086 mV/K. The threshold voltages (V_TH) have a negative TC of −4 to −2 mV/K, which varies from device to device. The temperature coefficient of V_T is significantly weaker than that of V_TH; thus, to compensate for the negative TC of V_TH, a high value of the β/(W/L) >> 1 is needed. After determining the MOSFET size and value of β of the current source, an appropriate choice of MOS diodes is used to generate V_PTAT and V_REF. A PMOS diode tends to have a more significant temperature dependence in terms of V_TH compared to the NMOS diode; hence, a PMOS diode is used to generate V_REF, and an NMOS diode is used to generate V_PTAT. V_TH is the only process-dependent term remaining in (4), but since both the V_PTAT and V_REF are simultaneously influenced by this variation, it can easily be nullified in the digital logic when comparing the frequencies of their VCOs.

2.1.2. Current Source Design

As we established by the mathematical representation in (3), we require a current source that has a square dependency on the absolute temperature. The current source must be self-biased, low voltage, and immune to supply variation. To meet all those requirements, we present the design of a current source based on Oguey’s topology. The design has been optimized to improve the power supply rejection ratio (PSRR). The Oguey current reference [25] is based on a PTAT current source shown in Figure 4.

The design achieves low-power operation by keeping M₃ and M₄ in the subthreshold region. M₁ and M₂ act as current mirrors. The voltage across the resistor determines the magnitude of the current, which is given by:

$$V_{S4}=V_T ln\left({\displaystyle \frac{k_4{k}_1}{k_3{k}_2}}\right)$$

(5)

where V_T is the thermal voltage and k₁, k₂, k₃ and k_4, respectively, are dimensions (W/L) of the MOSFETs. It shows that the voltage across the resistor is PTAT because of its dependence on thermal voltages. The voltage remains insensitive to supply variation as long as the voltage drop across M₃ remains greater than 4 V_T, keeping M₃ and M₄ in saturation. Oguey eliminates a major drawback from the design by replacing the resistor with a MOSFET (M₅) working in the triode region (linear region). A branch is introduced in the circuit to supply bias M₅, as shown in Figure 5.

M₅ determines the bias current I_D, which is kept in the deep-triode region (i.e., the V_DS of M₅ is much less than its overdrive voltage (V_GS − V_TH). The current flowing in M₅ can be expressed as:

$$I_D=\mu C_{ox}{k}_5 \left[\left(V_{G5}-V_{TH5}\right)V_{DS5}-{\displaystyle \frac{1}{2}}-V_{DS}^2\right]$$

(6)

and the voltage V_DS5 = V_GS3 − V_GS4 can be expressed as [25]:

$$V_{DS5}=\eta V_T ln\left({\displaystyle \frac{k_4}{k_3}}\right)$$

(7)

where K_n is the W/L ratio of the nth MOSFET. The MOSFET M₇ is diode-connected and operates in saturation. Its current can be expressed as:

$$I_{D7}={\displaystyle \frac{1}{2}}\mu C_{ox} k_7{\left( V_{TH}-V_{TH}\right)}^2$$

(8)

Equations (6)–(8) can be solved to give the current I_D as:

$$I_D={\displaystyle \frac{1}{2}}\mu C_{ox} k_7 V_T^2 K_{eff}$$

(9)

with:

$$K_{eff}=\left[S_2 -{\displaystyle \frac{1}{2}}+\sqrt{S_2\left(S_2-1\right)}\right]{\ln }^2\left(S_1\right)$$

(10)

where:

$$S_1={\displaystyle \frac{k_4}{k_3}} , S_1=Q{\displaystyle \frac{k_5}{k_7}} .$$

(11)

The current I_D in (9) is proportional to the square of absolute temperature and the carrier mobility (µ), which meets all the requirements of I_D shown in (3). The factor K_eff is a function of device sizes and, therefore, can easily be adjusted for (3).

Keeping the NMOS pair (M₃ and M₄) in the subthreshold region is crucial to ensure insensitivity to supply variation. We propose modifying the Oguey current source to improve the supply rejection by actively controlling the voltage of nodes A and B, as shown in Figure 6. An operational transconductance amplifier (OTA) is used to form a closed loop around nodes A and B with V_DD [23]. The OTA gets its bias current from the same current generator block. The OTA is biased at only 2.5 nA to keep the power consumption low. The OTA controls the voltages of nodes A and B so that the change in supply voltage can be directed to the drain-source voltages of M₁ and M_2, keeping a constant drop across the M₃ and M₄. When the V_DD variation causes the voltage of node B to increase, the input to the non-inverting terminal of the OTA increases, which causes the output of the OTA to rise. This increase in the output of the OTA decreases V_GS2 and causes an increase in V_DS2, and the voltage of node B falls again and vice versa. It can also be seen in Figure 6 that the OTA creates a virtual short between nodes A and B. These nodes define V_DS2, and thus, virtual shorting together the drain and source terminal of M₄ makes it diode connected, keeping it in saturation. Node A, however, is connected to the inverting terminal of the OTA and does not benefit from the closed loop. We also replaced the diode-connected MOS (M3) with PMOS-based N-well diodes to achieve improved voltage regulation at node A, further enhancing PSRR. The N-Well diodes are formed by connecting the drain, source, and gate terminal of M₃ and utilizing the P-N junctions formed between the N-well (body connection) and the source/drain terminals of the PMOS, as shown in Figure 7. As compared to the original diode-connected MOS in the Oguey current source, the N-Well diodes formed in M₃ exhibit a superior voltage regulation across it [27]. By keeping a constant voltage drop at node A, the overall line sensitivity of the generated current is improved. The channel length of the PMOS current mirrors (M₁, M₂, M₆, M₈, and M₁₀) are kept long to maintain a high output impedance that provides passive immunity to supply variation, and using long channel length prevents second-order effects like channel length modulation.

The current source is self-biased, so during the power-up, the circuit can settle in two possible stable states. One of the stable states is when the bias current I_D is zero, while the other possible state is when I_D is of the form in (9). A start-up circuit is introduced in the modified source to prevent the zero-bias current state, as shown in Figure 6. The start-up circuit is simple and comprises M₁₂, M₁₃, and M₁₄. M₁₄ is connected in a MOS-CAP configuration and serves as a delay element keeping M₁₂ and M₁₃ from turning off during the startup. At startup (t = 0), the node voltage VC is zero and transistors M₁₂ and M₁₃ are turned on in strong inversion. The MOS-CAP M₁₄ starts charging through M₁₂ until its voltage reaches up to the supply voltage V_DD, causing M₁₂ and M₁₃ to eventually turn off. During startup, M₁₃ ensures that the current source is in a stable state with a finite current flowing in its branches. The start-up circuit consumes power only during a short duration of start-up time. The complete design of the proposed temperature sensing unit is shown in Figure 6. Both M₉ and M₇ are diode-connected as previously established.

Figure 8 and Figure 9 show the simulation results of V_REF and V_PTAT across the process corners. The sensing unit consumes 15 nW at 25 °C and achieves a low variability across process corners.

2.2. Voltage-to-Frequency Converter

The voltages from the temperature sensing unit are translated into frequency using a voltage-controlled ring oscillator (VCO). The design of the differential delay element for the proposed VCO is shown in Figure 10. Instead of relying on a conventional approach of using an inverter as a delay element, our work proposes a new differential pair to control the frequency of the ring oscillator. In our approach, the tail current and an extra active load are varied using the control voltage. This variation provides better control and a wide frequency variation with a small change in control voltages. Differential circuits provide good rejection of common-mode supply and substrate noise. Noise sensitivity is a crucial aspect of the design of our temperature sensor; hence, the differential structure of the delay element is a preferable choice to improve noise immunity. In addition to being noise-tolerant, differential ring oscillators also let us employ an even number of stages in the oscillator’s loop. If we want oscillations using single-ended inverters, the stages must be in odd numbers. In our design, we use four differential stages and obtain the necessary inversion by crossing outputs between stages.

As shown in Figure 11, the propagation delay (t_d) of a single differential stage can be estimated using a simple RC model. The simple RC model is driven from the half-circuit small-signal model during the low-to-high transition, and it can be mathematically expressed as:

$$t_d=C_T{R}_T$$

(12)

with R_T approximately

$$R_T\cong {\displaystyle \frac{1}{G_m}}={\displaystyle \frac{1}{g_{m1}+g_{m2}}}$$

(13)

$$t_d={\displaystyle \frac{C_T}{G_m}}$$

(14)

where C_T is the total load capacitance seen by the output of a stage (including parasitic capacitances) and gm₁ and gm₂ are the transconductance of M₁ and M₂, respectively. It can be noted that variation of the active load M₁ using the control voltages changes the delay of each stage.

The time it takes for a single transition to propagate twice around the ring of the oscillator determines its oscillation frequency. From [28] the frequency of oscillation F_OSC can be expressed as:

$$F_{OSC}={\displaystyle \frac{1}{2N{t}_d}}={\displaystyle \frac{G_m}{2N{C}_T}}$$

(15)

The outputs V_PTAT and V_REF from the sensing unit control the frequency of their respective ring oscillators, giving us F_PTAT and F_REF. It can be noted that the delay of the differential stage depends on transconductance (G_m), and G_m is sensitive to both temperature and supply voltage. The ring oscillator with fixed control voltage shows a simulated supply sensitivity of +1.1 to −1.8 °C (temperature reading error) across a supply variation of 0.8 to 1.4 V and a mean temperature coefficient of 85 ppm/°C. Although the ring oscillator is sensitive to both supply and temperature variations, we mitigate these issues by comparing the two frequencies in the digital section, which cancels much of the common-mode drift. The temperature sensing accuracy may also suffer due to process variation; therefore, careful layout considerations are adopted to minimize this variation. Long-channel devices are used along with common centroid layouts to minimize mismatches.

2.3. Frequency-to-Digital Converter

A digital logic circuit is designed to convert the frequencies F_PTAT and F_REF into digital outputs using two asynchronous counters configured as 12-bit binary counters. F_PTAT and F_REF serve as the clock sources Clk_PTAT and Clk_REF for the PTAT- counter and reference counter, respectively. The frequencies are chosen such that the reference frequency is always greater than the PTAT frequency at all temperature, supply, and process corners. As shown in Figure 12, the ‘Setup’ signal triggers the oscillation in both oscillators and resets the counters, making them increment with each clock pulse. Since the reference frequency is higher, its counter overflows first, raising its ‘overflow’ signal. This overflow signal triggers the transfer of the count from the PTAT counter to the parallel-to-serial converter. To prevent metastability, we introduce a short chain of inverters/buffers after the PTAT counter stops, ensuring its output stabilizes before latching. The ‘Setup’ signal then clears and starts both counters again for a new temperature reading. At high temperatures, more counts are accumulated in the PTAT counter, and at low temperatures, the accumulated count is low. Hence, the PTAT count serves as the binary representation of the measured temperature. Conversion can be set to continuous mode using the internal ‘Setup’ signal or, to conserve power, the conversion can be triggered from an external signal when needed. Circuit level optimization is achieved by carefully considering the device sizing in each switching stage of the counters to minimize short circuit currents and leakages. We use only one differential output of the final (fourth) VCO stage to clock each counter, simplifying the clock distribution. Capacitive loading of the counter is also minimized at the layout level to reduce the charging and discharging currents, leading to efficient power consumption.

3. Experimental Results

The micrograph of the temperature sensor chip is shown in Figure 13. The design is fabricated in a 65 nm CMOS process and occupies an area of 0.02 mm².

The measurement setup is shown in Figure 14. Twelve dies were selected and packaged in a QFP package to test the temperature sensor.

Figure 15 shows the output voltage V_PTAT over the range of −20 to 120 °C. The V_PTAT output shows a linear output with minimal dependence on process variation. The average temperature sensitivity of V_PTAT was measured to be 0.19 mV/°C. A mean value of 266.4 mV was observed at a supply voltage of 0.8 V @ 25 °C, with a standard deviation of 13.19 mV across samples. The output voltage V_REF is shown in Figure 12. V_REF showed an average temperature sensitivity of 0.95 µV/°C, and a mean value of 601.5 mV was observed at 0.8 V supply @ 25 °C. V_REF showed a standard deviation of 25 mV across samples.

The average power consumption of the sensing unit was measured to be 18 nW. The measured average F_PTAT varied from 168 KHz to 308 KHz across the temperature range, and the measured average F_REF was 442 KHz @ 25 °C, as shown in Figure 16.

The average RMS resolution of the temperature sensor across samples was measured to be 0.2 °C_rms. The resolution showed an inverse relation with conversion time, as shown in Figure 17; however, this improvement in resolution increased the energy expenditure per conversion.

A supply voltage change from 0.8 to1.2 V produced an error of +1.5/−2.1 °C in the temperature measurement. Figure 18 shows the measured error of 1.5 °C/−1.6 °C across the temperature range after 2-point calibration at 25 °C and 105 °C.

The average power consumption of the complete sensor over the 12 dies at ambient temperature, and 0.8 V supply is 59 nW. The overall power breakdown is shown in Figure 19, which shows that the ring oscillator accounts for about 50% of the power consumption while generating V_REF, and V_PTAT consumes about 30% of the total power budget.

Table 1. Comparison with state-of-the-art.

	This Work	TCAS-I’ 21 [14]	TCAS-I’ 23 [29]	TCAS-II’ 19 [15]	JSSC’ 19 [13]	TCAS-II’ 22 [30]
Process (nm)	65	130	180	180	180	180
Type	MOSFET	MOSFET	MOSFET	MOSFET	MOSFET	MOSFET
Area (mm2)	0.02	0.07	0.055	0.007	0.074	0.049
Supply Range (V)	0.8	0.95	1	0.6–1.2	0.8	0.35
Temperature Range (°C)	−20–120	0–80	0–100	0–100	−20–80	0–100
Resolution (°C−1)	0.2	0.1	0.12	0.55	0.14	0.27
Conversion Time (ms)	9.2 ms	59 ms	50 ms	300 ms	839 ms	33 ms
Calibration Points	2	2	2	2	2	2
Error (°C)	+1.5/ −1.6	+0.44/ −0.4	+0.8/−0.8	+0.67/ −1.64	+1.2/ −0.9	+3/ −3
Fully Integrated	yes	yes	Yes	yes	yes	yes
Power (nW)	60	196	20	3.92	11	14
Energy per Conversion (nJ)	0.55	11.56	1.0	1.2	8.9	0.46
FOM [nJ·K2]	0.022	0.12	0.014	0.36	0.19	0.034

shows the comparison of the design with other low-power temperature sensors reported in the literature. The comparison is based on a figure of merit (FoM) derived from [6]. A lower FoM means better performance and is calculated as follows:

$$FoM\left[nJ.K^2\right]=Energy/Conv\times {\left(Resolution\right)}^2$$

(16)

Different process nodes (e.g., 180 nm vs. 65 nm) significantly impact achievable accuracy, power, and supply voltage ranges. Although some sensors in Table 1 achieve slightly tighter accuracy, they often operate over narrower temperature spans or at longer conversion times, thereby trading off speed or range for accuracy. The design in [30] achieves the lowest energy per conversion due to its reduced power and short conversion time, yet it exhibits the highest inaccuracy among the compared solutions. In comparison, our sensor covers a larger temperature range, −20 to 120 °C, and uses only 9.2 ms conversion time, balancing power efficiency with operational speed while still achieving a moderate inaccuracy level. We also employ two-point calibration, which is standard in many reported designs. Notably, only [29] demonstrates a better FoM due to its higher resolution, but it requires a higher supply voltage than the other references. By contrast, our proposed design offers significantly better performance in terms of area, supply voltage, conversion time, and energy per conversion. Future improvements may include exploring single-point calibration or advanced process compensation to further reduce calibration overhead and improve accuracy.

4. Integration with the Wireless Sensor Node

A wireless-powered sensing node is fabricated separately to integrate with our proposed temperature sensor. The goal is to achieve a fully integrated ultra-low-power wireless temperature sensor node. Figure 20 shows the block diagram of the WSN and its integration with the temperature sensor. The WSN works by harvesting power from the ISM band (915 MHz). The system operates in a cycle of two phases. During phase I, the antenna is connected to an RF rectifier through an RF switch. The transmitter and the temperature sensor are in sleep mode during phase I to conserve power. The harvested power is stored in an external storage capacitor. As soon as the voltage on the storage capacitor reaches a specific threshold, the power management circuit switches the RF switch and wakes up the temperature sensor and transmission circuit. During phase II, the 915 MHz signal is directed to the carrier extractor and frequency synthesizer through the RF switch. The carrier extractor boosts the amplitude of the received 915 MHz and divides it by a factor of 3 to down-convert it to a 305 MHz square signal. The down-converted signal then goes through an 8× frequency multiplier, resulting in a 2.44 GHz signal that is suitable to be used as the carrier for ISM band transmission. The 2.44 GHz signal is modulated using the on–off keying (OOK) scheme by the serial data coming from our proposed temperature sensor. Finally, a power amplifier transmits the modulated signal.

The temperature sensor was tested after integration in WSN. The measurement results showed a degradation in temperature measurement accuracy with an error of 1.8 °C/−2.1 °C across the temperature range after 2-point calibration at 25 °C and 105 °C, while the resolution of the sensor was preserved. The degradation in measurement accuracy could be a result of the noise from the WSN system.

5. Conclusions

This work presents an ultra-low-power temperature sensor suitable for battery-less wireless sensor nodes. By employing a resistorless design, the sensor is both power-efficient and area-efficient. Both the reference and temperature-sensitive voltages are derived from the same current source to enhance process sensitivity. Operating at just 60 nW at room temperature, the sensor covers a temperature range of −20 to 120 °C with an inaccuracy of +1.5/−1.6 °C (3σ) after 2-point calibration. It achieves a conversion rate of 108 samples/second, consuming 0.55 nJ per conversion. The sensor’s integration into a wireless sensor node demonstrates its suitability for WSNs.