A 0.064 mm² 16-Channel In-Pixel Neural Front End with Improved System Common-Mode Rejection Exploiting a Current-Mode Summing Approach

Abstract

In this work, we introduce the design of a 16-channel in-pixel neural analog front end that employs a current-based summing approach to establish a common-mode feedback loop. The primary aim of this novel structure is to enhance both the system common-mode rejection ratio (SCMRR) and the common-mode interference (CMI) range. Compared to more conventional designs, the proposed front end utilizes DC-coupled inverter-based main amplifiers, which significantly reduce the occupied on-chip area. Additionally, the current-based implementation of the CMFB loop obviates the need for voltage buffers, replacing them with simple common-gate transistors, which, in turn, decreases both area occupancy and power consumption. The proposed architecture is further examined from an analytical standpoint, providing a comprehensive evaluation through design equations of its performance in terms of gain, common-mode rejection, and noise power. A 50 $\mathsf{\mu }$m × 65 $\mathsf{\mu }$m compact layout of the pixel amplifiers that make up the recording channels of the front end was designed using a 180 nm CMOS process. Simulations conducted in Cadence Virtuoso reveal an SCMRR of 80.5 dB and a PSRR of 72.58 dB, with a differential gain of 44 dB and a bandwidth that fully encompasses the frequency range of the bio-signals that can be theoretically captured by the neural probe. The noise integrated in the range between 1 Hz and 7.5 kHz results in an input-referred noise (IRN) of 4.04 $\mathsf{\mu }{V}_{rms}$. Power consumption is also tested, with a measured value of 3.77 $\mathsf{\mu }$W per channel, corresponding to an overall consumption of about 60 $\mathsf{\mu }$W. To test its robustness with respect to PVT and mismatch variations, the front end is evaluated through extensive parametric simulations and Monte Carlo simulations, revealing favorable results.

1. Introduction

Understanding the intricate correlation between individual neuron activities is pivotal for advancing the development of numerous applications within the realm of neuroscience [1,2]. Among these, a notable area of research focuses on investigating the mechanisms underlying the effects of neurodegenerative diseases such as Parkinson’s or Alzheimer’s, in light of their increasing global spread and the corresponding rise in treatment costs [3,4,5,6]. Additionally, ongoing research endeavors center around the development of efficient brain–machine interfaces (BMIs) for diagnostic and neuro-prosthetic purposes [7,8,9].

However, to achieve breakthroughs in these and other areas of neuroscientific research, reliance solely on non-invasive methods of neural recording (i.e., EEG or fMRI) has proven to be insufficient. Although affordable and safe to perform, such techniques are hampered by limited spatial and temporal resolutions and exhibit a low signal-to-noise ratio (SNR) due to the filtering effect of the intermediate layers between the scalp and the source of the bio-signals [10,11]. Invasive neural recording through implantable neural probes, on the other hand, allows for the isolation of spike events from single neurons with sub-millisecond time precision by recording the neuronal activity directly from the extracellular space of the membrane [12].

Multi-channel neural probes can be fabricated using a variety of techniques and materials. Most notably, silicon is widely favored on account of its cost-effectiveness, compatibility with standard fabrication processes, and the ability to integrate CMOS circuits on the same substrate [13,14]. Taking advantage of this aspect, recently introduced active neural probes have been a key factor in contributing to the gradual increase in the density of recording channels that can be implemented in a single probe’s shank. In turn, the number of individual neurons that can be simultaneously recorded has also experienced a steady rise [15]. At the forefront of neural recording, devices such as Neuropixels 2.0, Neuroseeker, and SiNAPS have produced groundbreaking results when applied to small mammals and non-human primates [16,17,18,19,20].

Designing CMOS neural probes presents a multifaceted challenge, involving various disciplines such as electronics, material science, and biology [21,22,23]. While implanted micro-electrodes provide superior access to fine-grained neural activity, they inherently cover a smaller volume of brain tissue compared to standard non-invasive methods. Thus, future advancements must prioritize increasing the density and number of integrated recording sites to achieve large-scale brain coverage. Moreover, reducing the area occupied by neural probes can significantly decrease their invasiveness, which, in turn, decreases the risk of tissue damage during the probe’s insertion and reduces the chances of inflammatory response under chronic recording conditions [24,25,26]. It is worth noting that down-scaling the technology to achieve a smaller area introduces short-channel effects of the MOS transistors, resulting in a reduction in transconductance and an increase in gate leakage current, flicker, and thermal noise power [27].

Furthermore, optimizing power consumption in neural recording devices, and thus managing potential heat generation through dissipation, is a critical parameter [28,29]. Recent studies have shown that power consumption exceeding 40 mW leads to a temperature increase of over 2 °C, which, in turn, triggers neural cell death within a few days [30].

Another important aspect to consider when designing neural probes is the ability of the circuit to effectively reject interferences, that is, the common-mode rejection ratio (CMRR) and the power supply rejection ratio (PSRR). To preserve the integrity of the acquired bio-signals and maintain a high SNR, both the common-mode signals, typically fed through the micro-electrodes, and the power supply noise, such as wall-mounted 50/60 Hz interference, should be rejected accordingly [31]. Although various methods have been employed to ensure a high CMRR for the amplifiers employed in multi-channel neural probes, few studies have centered on the system CMRR in analog front ends [32,33,34]. Typically, the system common-mode rejection ratio (SCMRR) in systems with a high channel count N decreases as N itself increases and is also dependent on the mismatch between the impedance of the reference electrode and the impedance of the signal-acquiring electrode.

In this regard, the novel approach introduced in [34] aims to raise the SCMRR and the common-mode interference (CMI) range of a DC-coupled neural recording front end through the implementation of a shared voltage-averaging circuit (VAC) and a floating-rail common-mode feedback loop (CMFB). The latter employs an error amplifier with an open-loop gain of 45 dB that accepts as input the mean of the voltage outputs of the multiple input amplifiers and, in turn, produces a feedback voltage, used to retroactively cancel out any common-mode interference.

Similarly, in this work, we introduce the architecture of a DC-coupled analog front end designed for high-channel-count in-pixel neural recording systems. The described structure features 15 recording channels alongside a single reference channel. It incorporates a CMFB loop, which operates on the sum of individual channel currents to enhance both the SCMRR and the CMI range. In addition, the proposed design focuses on minimizing the on-chip area footprint of the front end, aligning with the demand for compact and efficient neural recording devices set by the state of the art.

The remainder of this paper is organized as follows. Section 2 delves into the architecture of the front end, highlighting its innovative features. The topologies of the various components that make up the front end are presented in detail in Section 3, while Section 4 concerns the analytical aspects of the circuit’s performance. The results obtained through simulations are subsequently presented in Section 5, along with a final table to compare the results with current state-of-the-art devices. The conclusions are drawn in Section 6.

2. System Architecture

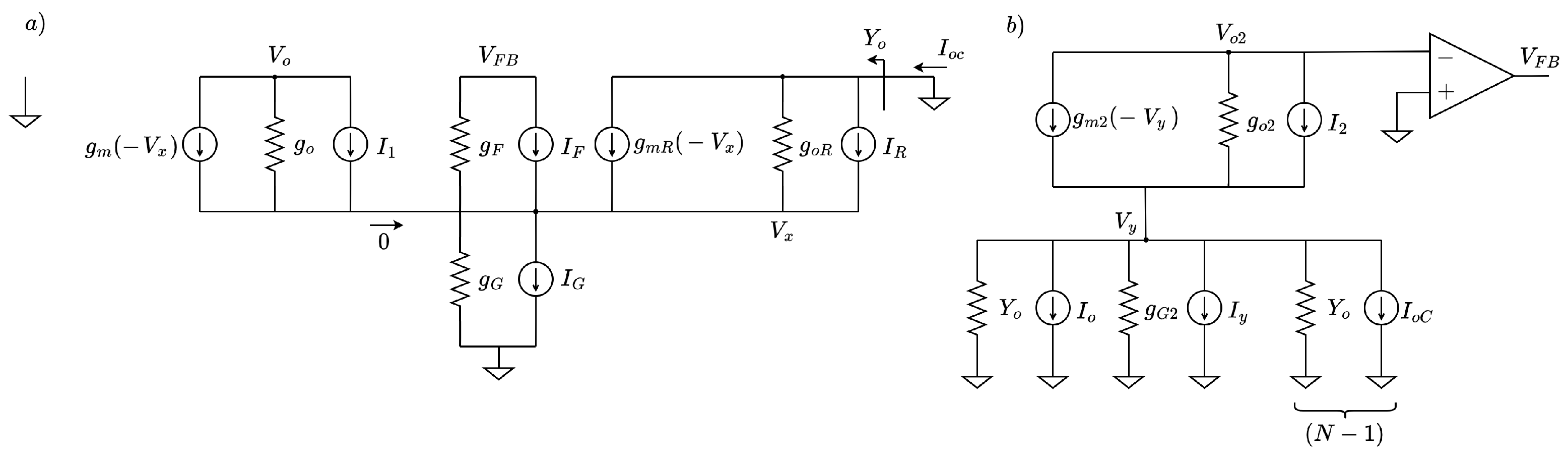
In order to effectively contextualize the novel contributions brought forth by the analog front end proposed in this document, it is necessary to first provide a characterization of the fundamental workings of the circuit outlined in [34], thereby establishing a baseline for comparison. In this regard, the circuit depicted in Figure 1 comprises 16 recording channels, 15 of which serve as input channels, while the remaining one acts as a reference channel. For local conditioning of the acquired bio-signals, each front-end channel integrates an in-pixel low-noise neural amplifier with a bandwidth of 7.5 kHz, ensuring coverage of both the action potentials and local field potentials recorded in the extracellular space. In a conventional IC multi-channel recording system, the total common-mode rejection ratio is dependent on the intrinsic CMRR of the input amplifiers, as well as the number of employed channels, as demonstrated in [33]:

$$SCMRR={\left(\frac{1}{ICMRR}+{\left(\frac{1+2\left(\left|\frac{Z_{IN}}{Z_E}\right|+Nϵ\right)}{2\left(Nϵ-1\right)}\right)}^{-1}\right)}^{-1}$$

(1)

Here, $Z_{IN}$ represents the input impedance of the low-noise amplifier, while $Z_E$ denotes the impedance of the recording electrode. The term $ϵ$ is used to quantify the difference in impedance between the reference electrode and the signal electrode, with a value of one indicating a condition of a perfect match. With the goal of improving the SCMRR and, therefore, increasing the CMI range in high-channel-count systems, the solution presented in [34] employs a common-mode feedback loop based on the average sum of the output voltages of the input amplifiers.

The CMFB consists of a voltage-averaging circuit and an error amplifier. In relation to the single recording channel, the former is composed of a voltage buffer, necessary to eliminate the loading effect to the main amplifier, and a resistor $R_a$. Assuming the same value for all 16 resistors, the voltage fed to the inverting input of the error amplifier can be expressed as follows:

$$V_{in\_i}=\frac{\frac{V_{out\_1}}{R_a}+\frac{V_{out\_2}}{R_a}+\dots +\frac{V_{out\_N}}{R_a}}{\frac{N}{R_a}}=\frac{1}{N}\sum _{i=1}^N{V}_{out,i}.$$

(2)

To complete the CMFB loop, the output of the error amplifier, denoted as $V_{FB}$, is fed back to the pixel amplifiers. As previously mentioned, the implementation of this kind of common-mode feedback loop enhances the SCMRR. However, it is important to acknowledge that including a voltage buffer for each recording channel results in a substantial increase in the on-chip area occupation, which is a critical aspect to consider in the context of neural recording devices.

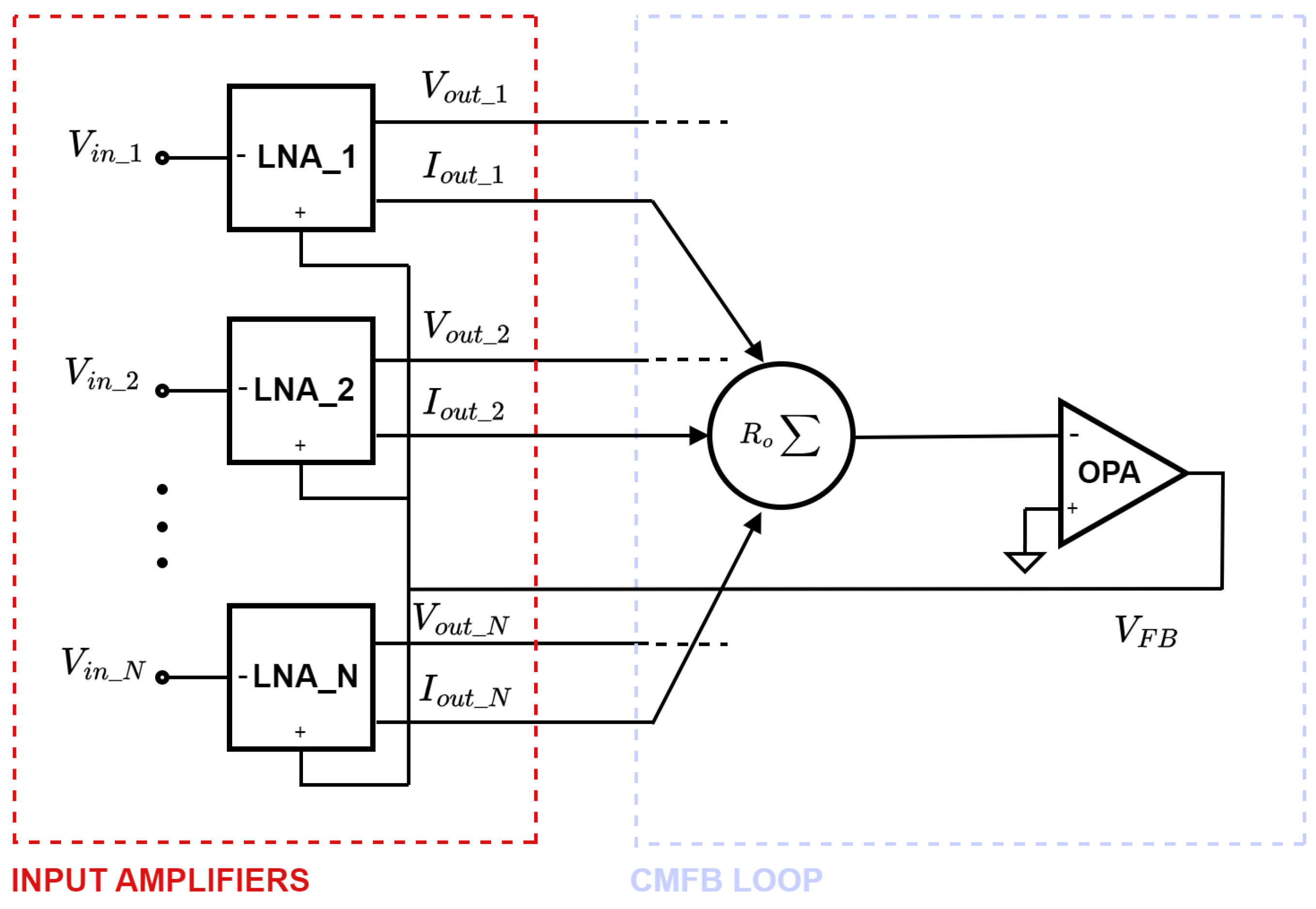
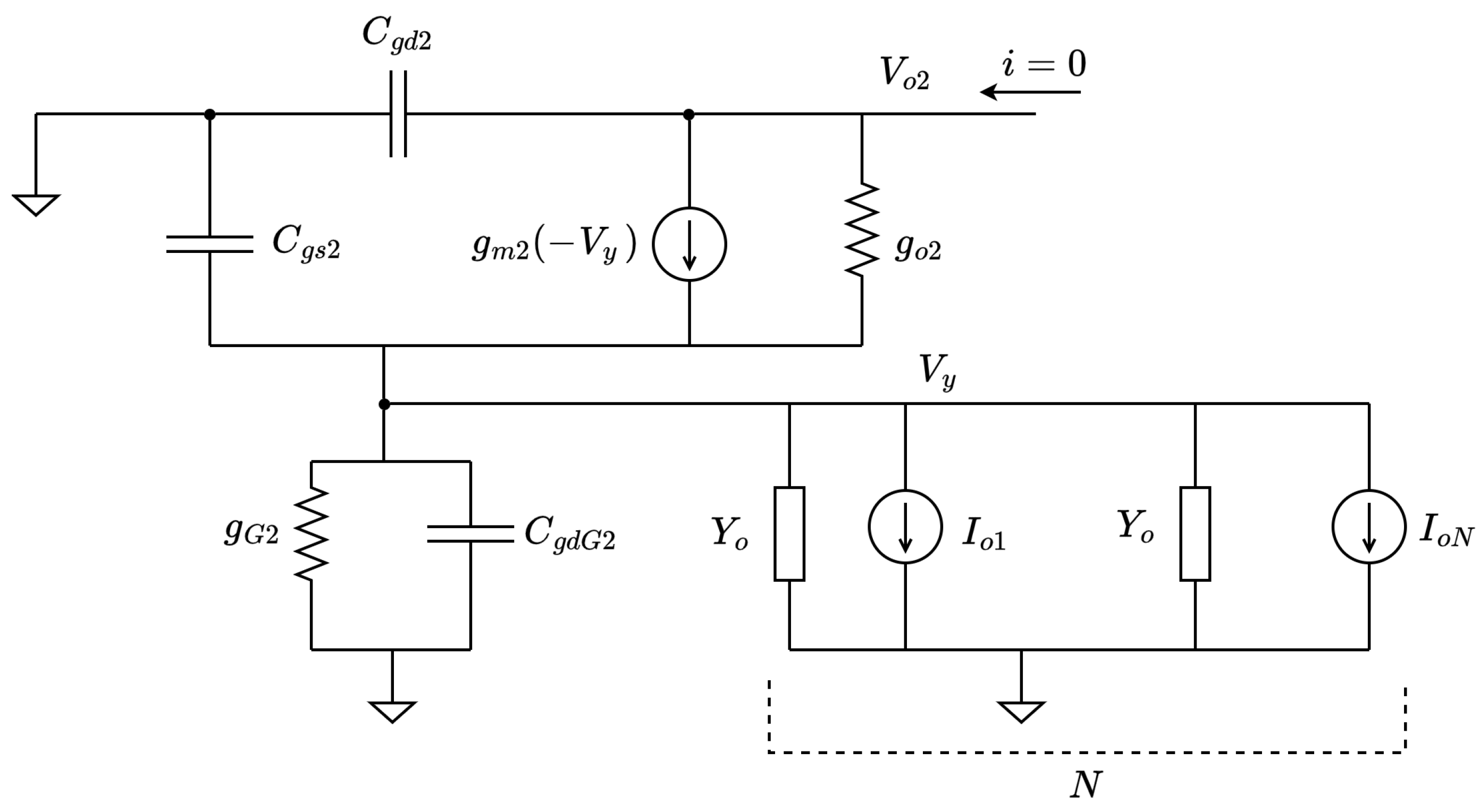
To address this limitation, we devised a variation of the aforementioned front end, designed with the aim of significantly reducing its area occupation without compromising the system’s performance. As depicted in the block diagram in Figure 2, this modified version of the front end maintains the same number of recording channels. Its distinctive feature lies in the operation mode of the CMFB loop: in place of the mean calculation of the output voltages, a sum of the output currents is conducted instead.

Summing the output signals as currents eliminates the need for voltage buffers and resistors, resulting in a significant reduction in the on-chip area occupation per recording channel. In particular, for each input amplifier, the voltage-averaging circuit is replaced with two much smaller transistors, while the current sum is made possible by implementing two common-gate transistors. In doing so, the voltage buffers and the resistors depicted in Figure 1 are no longer required. As a result, the on-chip area occupation is significantly reduced.

3. Circuit Design

The following section of the paper delves deeper into the topologies of the various stages that comprise the proposed multi-channel neural recording front end, providing insight into the mechanisms underlying the amplifying stage and the CMFB loop.

3.1. Pixel DC-Coupled Amplifiers

The schematic of the primary low-noise amplifier utilized in each recording channel is depicted in Figure 3. Following the topology proposed in [34], transistors M1 and M2 form the DC-coupled inverter-based amplifier of the system. In contrast to commonly used configurations employing differential amplifiers, the utilization of single-ended amplifiers offers notable benefits, such as reduced area occupancy and power dissipation, albeit at the cost of a decreased system rejection to interfering common-mode signals and power supply variations.

For the i-th channel, the output current produced by the main inverter-based amplifier is duplicated by utilizing the replicating transistors M8 and M9, which share the same source and gate nodes as the transistors comprising the inverter itself. The magnitude of the duplicated current is determined by the transconductance of M8 and M9. As such, by adjusting the aspect ratios of M8 and M9 to a fraction of the ratios of transistors M1 and M2, it is possible to replicate a scaled current with precision. This is done to ensure a more efficient occupation of the on-chip area and a reduction in power consumption.

With reference to the schematic in Figure 3, transistors M3 and M4 provide a way to set the voltages of the floating rails of the input pixel amplifier. Acting as the terminal of the CMFB loop of the system, these transistors are diode-connected to avoid strong variations in the output high-impedance node, which would otherwise require Miller compensation. Additionally, the pairs M3–M4 and M1–M2 must be sized equally in order to effectively reject common-mode interference and also to prevent an increase in the IRN caused by the eventual mismatch.

Biasing of the amplifier is achieved through the voltages $V_{bp}$ and $V_{bn}$ applied to the gates of transistors M5 and M6–M7, which, respectively, act as a current source and a current sink for the inverter. Concerning the pair M6–M7 in particular, connecting the gate nodes and the body nodes of the two transistors allows us to virtually obtain a transistor with a channel length capable of exceeding the upper limit set by the specific adopted technology [35].

3.2. Common-Mode Feedback Stage

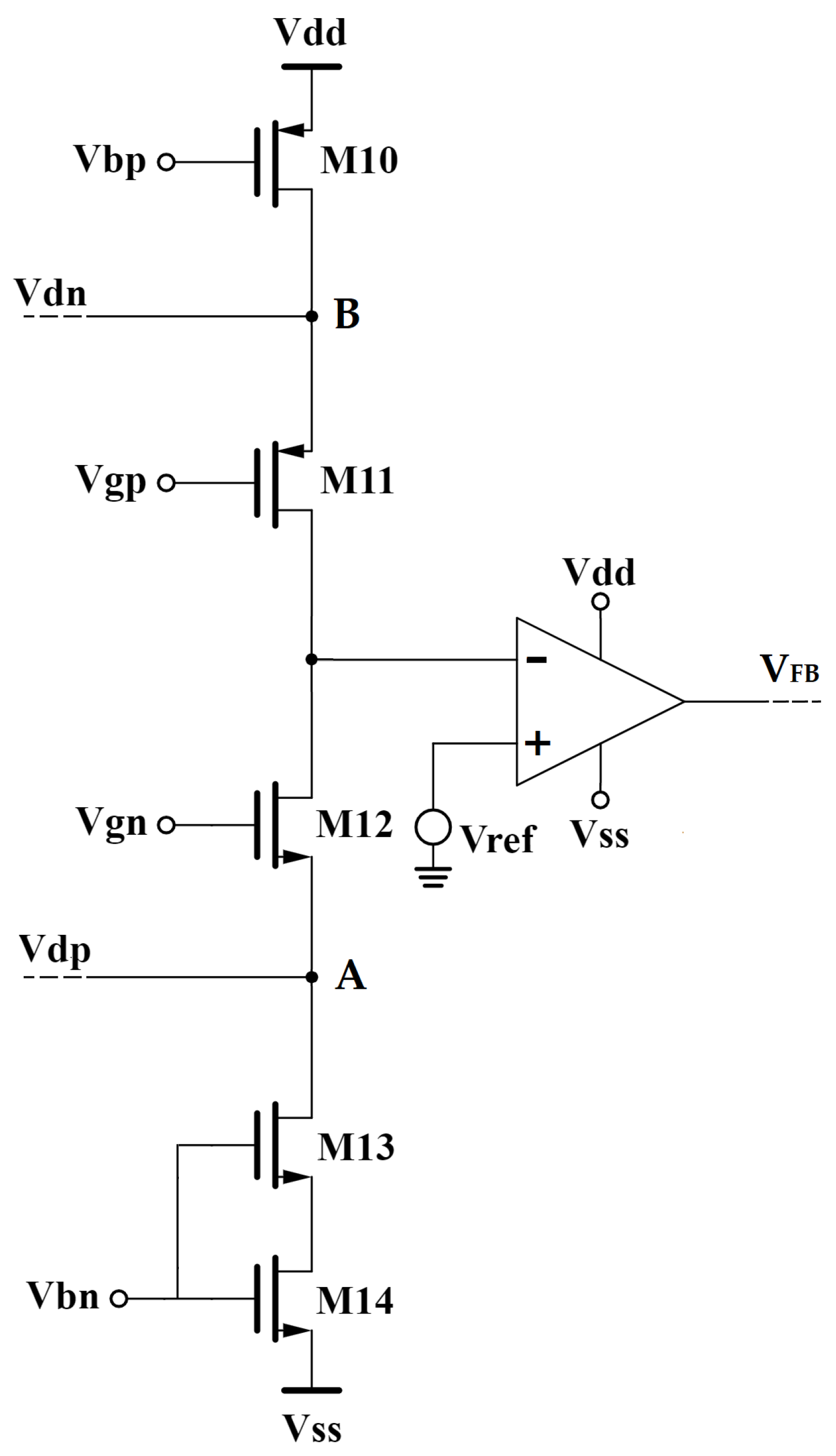
The topology of the CMFB stage in the front end is structured around two common-gate transistors, namely M11 and M12, which are used to establish a low-impedance node for summing the scaled duplicated currents. Referring to the schematic presented in Figure 4, node A serves as the summing node for the currents duplicated by the 16 NMOS replicating transistors, while node B provides the same function for the currents duplicated by the PMOS replicating transistors connected to the main amplifiers.

Transistors M11 and M12 effectively form two folded cascode structures, with the total scaled output current being converted into the input voltage of the error amplifier through the output resistance at their shared drain node. This voltage is subsequently amplified and fed back to the gate of the feedback amplifiers introduced in Section 3.1.

In terms of biasing, transistors M10 and M13–M14 act as current sources and are employed to set the bias current for the branch of the CMFB stage. It must be noted that the pair M13–M14 is designed following the same principle as the pair M6–M7 that makes up one of the two current generators used to bias the inverter-based amplifier.

3.3. Error Amplifier

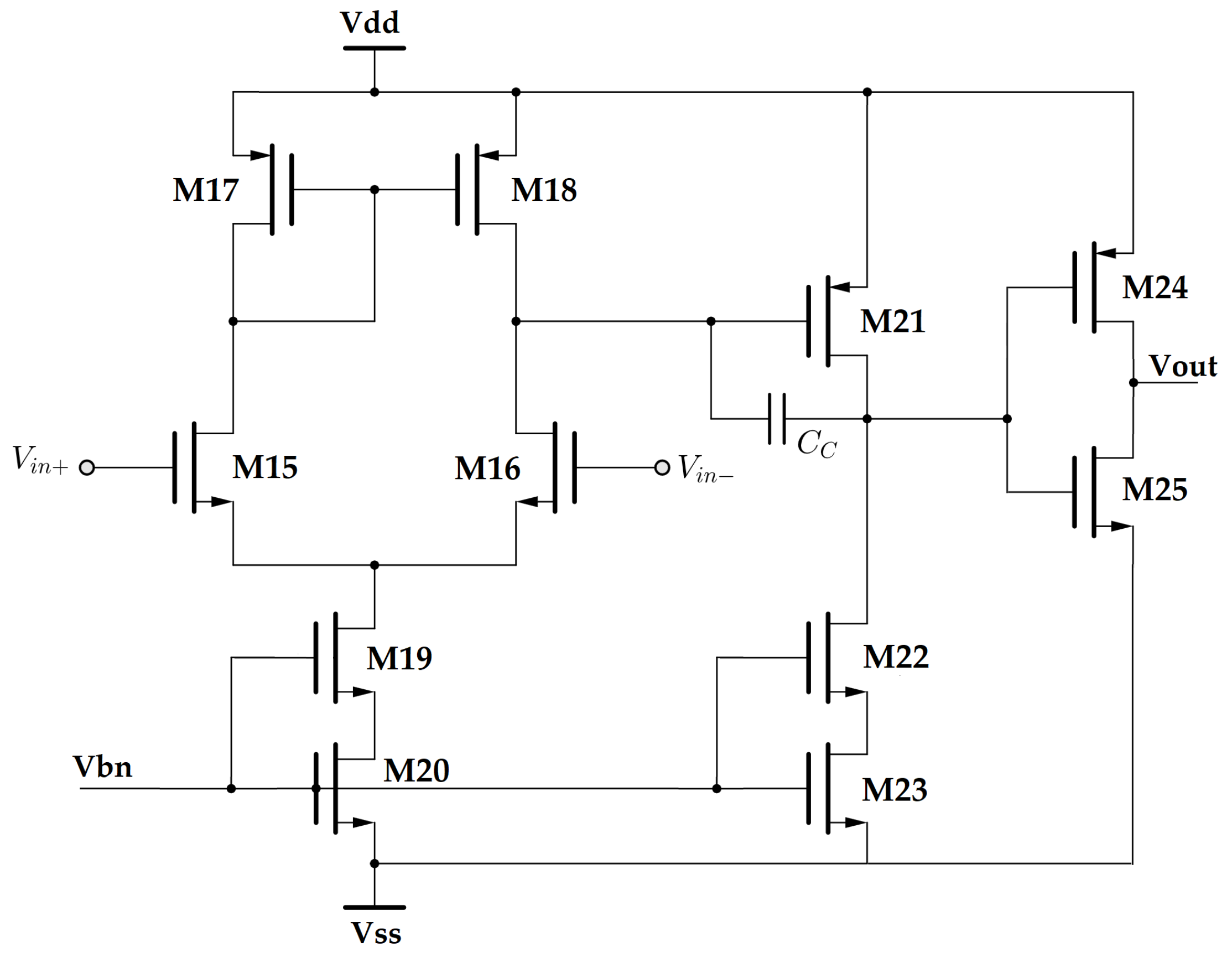
The topology of the error amplifier utilized to implement the CMFB loop is illustrated in Figure 5. Designed to operate in weak inversion mode, the amplifier comprises three stages; transistors M15, M16, M17, M18, M19, and M20 form a differential active-load amplifying stage, with the signal coming from the inverting input. Note that a reference voltage is applied to the non-inverting input instead. Transistors M19 and M20 ensure the correct biasing of the stage and are driven by a voltage $V_{bn}$ applied to the shared gate node.

The second stage of the amplifier is made up of a common-source transistor, M21, biased through the composite transistors M22–M23. A compensation feedback capacitor $C_C$ is connected between the drain and the gate of M21 to ensure the stability of the amplifier, as well as to provide a sufficient gain bandwidth product according to the following formula [36]:

$$C_C=\frac{g_{m1}}{2\pi ·GBW}.$$

(3)

The final class AB stage implemented through M24–M25 guarantees a rail-to-rail output swing, which, in turn, allows for the overall front end to achieve a high CMI value.

4. Circuit Analysis

The following section aims to provide an analytical overview of the circuit’s small-signal performance. The proposed design equations mainly focus on parameters such as the differential gain, common-mode gain, and SCMRR. Additionally, the circuit’s noise performance is evaluated.

4.1. Gain and SCMRR

Despite being classified as a single-ended amplifier, the pixel amplifier effectively operates with an inverting input for the acquired signal and a non-inverting input for the feedback voltage due to the diode-connected pair of transistors that closes the CMFB loop. For the k-th recording channel, the gain of the former is $A_L$, while the gain of the latter is defined as $A_R$. Therefore, the output voltage of the amplifier can be expressed as

$$V_o=-A_L{V}_i+A_R{V}_{FB}\simeq -A_1(V_i-V_{FB}),$$

(4)

where $A_R$ and $A_L$ are assumed to be approximately equal to each other. Referring to the small-signal model of the pixel amplifier (Figure 6), the gain $A_1$ can be computed as

$$A_1\simeq A_0\frac{g_{mF}}{g_{mF}+g_{mR}}\frac{1+s/{\omega }_{TF}}{1+s/{\omega }_1},$$

(5)

where $A_0$ corresponds to

$$A_0=\frac{g_m}{g_0},$$

(6)

and ${\omega }_{TF}$ and ${\omega }_1$ are defined as

$${\omega }_{TF}=\frac{g_{mF}}{C_{gsF}};$$

(7)

$${\omega }_1=\frac{g_{mR}+g_{mF}}{C_{gs}+C_{gsR}+C_{gsF}}<{\omega }_{TF}.$$

(8)

It is important to note that the expressions presented here are based on several approximations. Firstly, to simplify the calculations, the parameters of the NMOS and PMOS transistors are assumed to be identical to each other. As such, the small-signal parameters $g_{*}$ and $C_{*}$ are equivalent to $g_{\ast n}+g_{\ast p}$ and $C_{\ast n}+C_{\ast p}$, respectively. Furthermore, the computation of $V_o$ assumes the output of the system to be an open circuit, while the capacitance $C_{gd}$ has been disregarded in the node equations of the first stage. By applying Norton’s theorem, the output current of the equivalent circuit is found to be equal to

$$I_o\simeq -\frac{g_{mR}}{A_0}{V}_o,$$

(9)

with the equivalent Norton’s admittance being denoted as

$$Y_o=\frac{g_{mF}}{g_{mF}+g_{oR}}{g}_{oR}\frac{1+s/{\omega }_2}{1+s/{\omega }_1},$$

(10)

where

$${\omega }_2=\frac{g_{mF}}{C_{gs}+C_{gsF}+C_{gsR}}$$

(11)

is smaller than ${\omega }_1$. The small-signal model of the current summing stage of the circuit is presented in Figure 7. The output voltage $V_{o2}$ can be derived as

$$V_{o2}=-A_2(V_{ic}-V_{FB})$$

(12)

with $V_{ic}=\left(1/N\right){\sum }_{j=1}^N{V}_i$.

The gain $A_2$ is computed as follows:

$$A_2=\frac{g_{m2}+g_{o2}}{g_{o2}}\frac{g_{mR}{g}_{mF}(1+s/{\omega }_{TF})}{d_0+d_{1}s+d_2{s}^2}N.$$

(13)

In this case, N indicates the number of recording channels that make up the front end. Coefficients $d_0$, $d_1$, and $d_2$ can be expressed as (see Appendix A):

$$\begin{array}{c}{d}_0=N{g}_{mF}{g}_{oR}+g_{mF}{g}_{G2}+g_{mR}{g}_{G2}\\ d_1=N(C_{gsF}+C_{gs}+C_{gsR})g_{oR}+g_{G2}(C_{gsF}+C_{gs}+C_{gsR})+C_{gs2}(g_{mF}+g_{mR})\\ d_2=C_{gs2}(C_{gs}+C_{gsR}+C_{gsF})\end{array}$$

(14)

Voltage $V_{o2}$ is subsequently fed to the inverting input of the error amplifier. We may assume $V_{REF}=0$ for the small-signal analysis. The resulting feedback voltage is equal to

$$V_{FB}=-A_E{V}_{o2}.$$

(15)

The single-pole error amplifier is characterized by a gain $A_E$ that can be denoted by the following expression:

$$A_E=\frac{A_{E0}}{1+s{\tau }_E}.$$

(16)

By replacing $V_{o2}$ in (15) with the expression defined in (12), the feedback voltage can be rewritten as

$$V_{FB}=\frac{A_2{A}_E}{1+A_2{A}_E}{V}_{ic}=\frac{LG}{1+LG}{V}_{ic}.$$

Particularly, the loop gain $LG=A_2{A}_E$ is equivalent to

$$LG=\frac{g_{m2}+g_{o2}}{g_{o2}}\frac{g_{mR}}{g_{oR}}\frac{(1+s/{\omega }_{TF})}{1+\frac{d_1}{d_0}s+\frac{d_2}{d_0}{s}^2}\frac{A_{E0}}{1+s{\tau }_E}$$

(17)

Under the hypothesis that the pole $1/{\tau }_E$ is dominant and that $1/{\tau }_E<<{\omega }_{TF}$, the expression for the loop gain can be further simplified. As a result, $LG$ can be expressed as

$$LG\simeq \frac{A_{E0}}{1+s{\tau }_E}{A}_{02}{A}_{0R},$$

(18)

where $A_{02}=g_{m2}/g_{o2}$ and $A_{0R}=g_{mR}/g_{oR}$. Considering an input voltage $V_i=V_{ic}+{\widehat{V}}_i$, the output voltage, as defined in (4), becomes

$$V_o=-A_1\left(V_{ic}+{\widehat{V}}_i-\frac{LG}{1+LG}{V}_{ic}\right)=-A_1\left({\widehat{V}}_i+\frac{V_{ic}}{1+LG}\right).$$

(19)

By setting ${\widehat{V}}_i=0$, the common-mode gain of the system can be evaluated accordingly. From (19), it is found that $A_{cm}$ can be computed as

$$A_{cm}=\frac{V_o}{V_{ic}}{|}_{{\widehat{V}}_i=0}=-\frac{A_1}{1+LG}.$$

(20)

It is evident from Equation (20) that the common-mode gain presents a zero in $1/{\tau }_E$, which is set by the error amplifier employed in the CMFB loop. In order to compute the SCMRR of the front end, the expression for the single-channel gain must be derived as well. By imposing $V_{ic}=0$ in (4), we obtain the following:

$$A_{ch}=\frac{V_o}{{\widehat{V}}_i}{|}_{V_{ic}=0}=-A_1.$$

(21)

Therefore, the $SCMRR$ can be derived from (20) and (21) as

$$SCMRR=A_{ch}/A_{cm}=1+LG.$$

(22)

According to (22), the SCMRR’s behavior in frequency is dependent on the error amplifier, with a pole in $1/{\tau }_E$.

4.2. Noise Analysis

For the purpose of noise analysis, each transistor has been modeled by a single noise current source that encompasses both thermal and flicker noise. With reference to the model presented in Figure 8, $g_F=g_{mF}+g_{oF}\simeq g_{mF}$. Concerning the CMFB stage of the front end, the noise current generator $I_y$ represents the noise of $g_{G2}$, as well as the noise of the other channels.

The equilibrium equation at $V_x$ results in

$$G_D{V}_x=g_F{V}_{FB}+g_{oR}{V}_y+I_F-I_G+I_R,$$

(23)

with $G_D=g_F+g_{mR}+g_{oR}+g_G\simeq g_{mF}+g_{mR}$. Hence, the output admittance $Y_o$ and the output current $I_o$ can be expressed as

$$\begin{array}{c}{Y}_o\simeq g_{oR}\frac{g_F}{G_D};\end{array}$$

(24)

$$\begin{array}{c}{I}_o=I_{onoise}+I_{oc}.\end{array}$$

(25)

Regarding the expression in (25), the output current’s terms are defined as follows:

$$\begin{array}{c}{I}_{onoise}=\frac{g_F{I}_R-g_{mR}(I_F-I_G)}{G_D};\end{array}$$

(26)

$$\begin{array}{c}{I}_{oc}=-G_C{V}_{FB},\end{array}$$

(27)

where $G_C\simeq \frac{g_{mR}{g}_F}{G_D}$. Noise sources make it so that $V_y\ne 0$, which, in turn, causes $V_{FB}\ne 0$. This affects the channel under consideration and the other recording channels, whose $I_{oc}$ affects $V_y$. The analysis of the second stage provides

$$V_{o2}\simeq A_{02}{V}_y-\frac{I_2}{g_{o2}}.$$

(28)

Considering that $V_{FB}=-A_E{V}_{o2}$ and, therefore, $I_{oc}=G_C{A}_E{V}_{FB}$, voltage $V_y$ can be derived as

$$V_y\simeq \frac{I_2}{g_{m2}}-\frac{I_y+I_{onoise}}{N{A}_E{A}_{02}{G}_C},$$

(29)

where $I_y=I_{G2}+(N-1)I_{onoise}$. By substituting $V_y$ in Equation (23) and considering $V_o=A_o{V}_x-I_1/g_o$, the output noise voltage is computed as

$$V_{onoise}\simeq \frac{A_o}{G_D}\left[-\frac{G_D}{g_m}{I}_1+\frac{N-1}{N}(I_F-I_G)+\left(1+\frac{g_F}{N{g}_{mR}}\right)I_R+\frac{g_{oR}}{g_{m2}}{I}_2+\frac{G_D}{N{g}_{mR}}{I}_y\right].$$

(30)

The input noise can be calculated by dividing the expression in (30) by the gain $A_1$, as defined in (5), as follows:

$$V_{inoise}\simeq \frac{1}{g_F}\left[-\frac{G_D}{g_m}{I}_1+\frac{N-1}{N}(I_F-I_G)+\left(1+\frac{g_F}{N{g}_{mR}}\right)I_R+\frac{g_{oR}}{g_{m2}}{I}_2+\frac{G_D}{N{g}_{mR}}{I}_y\right],$$

(31)

By looking at Equation (31), it is apparent that the contribution of $I_2$ to the IRN is negligible, as its coefficient is much lower than one. Additionally, it can be noticed that $I_F$, $I_G$, and $I_R$ contribute to the overall input noise due to the presence of the CMFB loop. Other recording channels affect $V_{inoise}$ through the term $I_y$.

5. Simulation Results

The proposed analog front end was designed and simulated following the 180 nm CMOS process from TSMC. This section delves into the layout design aspects of the DC-coupled pixel input amplifiers and provides sizing information concerning the various components. Additionally, it showcases the results obtained through extensive simulations.

5.1. Layout and Transistor Sizing

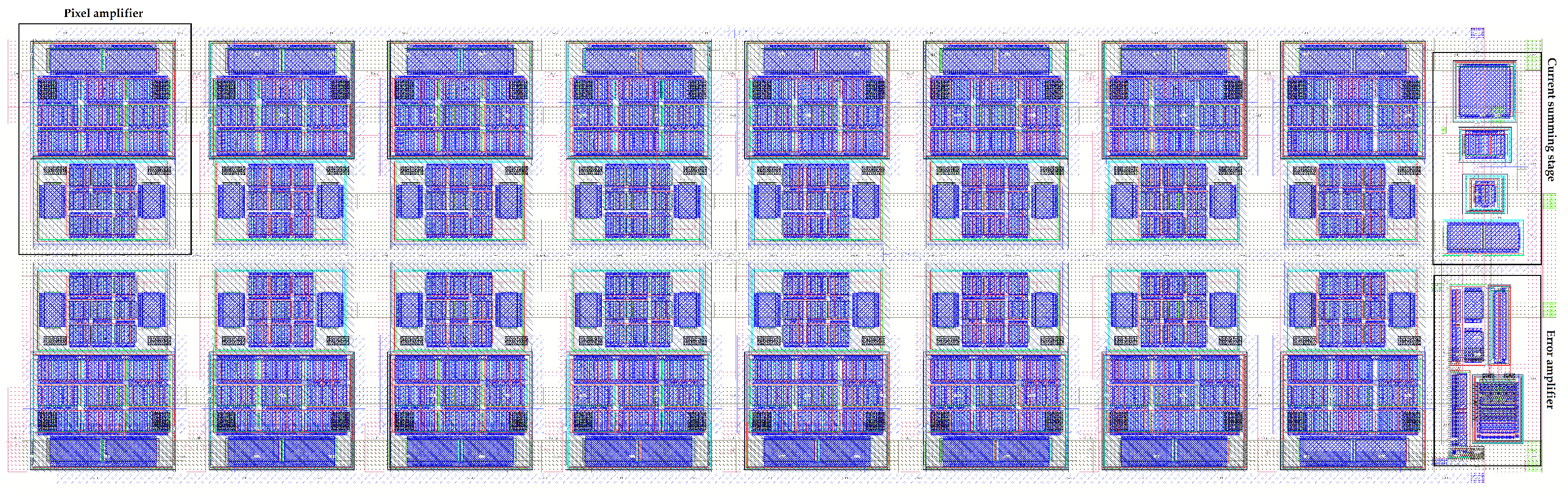
The layout of the analog front end is depicted in Figure 9, showing the 16-pixel amplifiers, each with an area footprint of 50 $\mathsf{\mu }$m × 65 $\mathsf{\mu }$m, placed along two rows. Utilizing six metal layers, this compact layout encompasses all the transistors described in detail in Section 3. Notably, the smaller transistors (M8–M9 in Figure 3), responsible for replicating the scaled currents, are surrounded by the transistors of the main inverter and the feedback transistors to mitigate potential mismatch between the devices. Overall, the area occupation per channel is lower than 0.004 mm².

With reference to Figure 3 and Figure 4,

Table 1. Transistor sizes for the pixel amplifier and the CMFB stage.

MOSFET	Width	Length
M1–M3	175 $\mathsf{\mu }$m	1 $\mathsf{\mu }$m
M2–M4	40 $\mathsf{\mu }$m	1 $\mathsf{\mu }$m
M8–M11	43.75 $\mathsf{\mu }$m	1 $\mathsf{\mu }$m
M9–M12	20 $\mathsf{\mu }$m	1 $\mathsf{\mu }$m
M5	12.70 $\mathsf{\mu }$m	15 $\mathsf{\mu }$m
M6–M7	5 $\mathsf{\mu }$m	10 $\mathsf{\mu }$m
M10	15 $\mathsf{\mu }$m	14.1 $\mathsf{\mu }$m
M13–M14	10 $\mathsf{\mu }$m	6.91 $\mathsf{\mu }$m

summarizes the size parameters of the MOS transistors used in both the pixel amplifier and the CMFB stage that make up the closed loop. As stated previously, the transistors that make up the inverter and the feedback transistors are sized equally by design. In order to accurately scale the currents of the main amplifiers, feedback transistors M8 and M9 are sized with a width scaled by a factor of 4. Transistors M5 and M6–M7 are sized with the intent of producing a bias current of 2.5 $\mathsf{\mu }$A for the main amplifying branch. Regarding the common-gate transistors implemented in the current-summing branch of the front end, the sizes are chosen to be equal to the replicating transistors to minimize area occupation. For biasing purposes, the W and L parameters of transistors M10 and M13–M14 are chosen to generate a current at least equal to the sum of the scaled, replicated currents.

Table 2. Transistor sizes for the error amplifier.

MOSFET	Width	Length
M15–M16	8 $\mathsf{\mu }$m	5 $\mathsf{\mu }$m
M17–M18	20 $\mathsf{\mu }$m	1 $\mathsf{\mu }$m
M19–M20	1 $\mathsf{\mu }$m	10 $\mathsf{\mu }$m
M21	150 $\mathsf{\mu }$m	500 nm
M22–M23	3 $\mathsf{\mu }$m	10 $\mathsf{\mu }$m
M24	10 $\mathsf{\mu }$m	180 nm
M25	3 $\mathsf{\mu }$m	180 nm

displays the sizing choices made with respect to the error amplifier. In this case, the parameters of the transistors are set with the aim of obtaining a high open-loop gain for the amplifier of at least 80 dB, with a phase margin of 60°.

5.2. Circuit Simulations

The proposed front end’s nominal behavior was simulated within the Cadence Virtuoso environment. To achieve results that closely resemble the actual implementation of the neural recording system, simulations were conducted using the post-layout netlist with extracted parasitics. The circuit was biased with a dual voltage supply ($Vdd$ = $-Vss$ = 0.5 V), while the total current used to bias a single channel was set at 3.5 $\mathsf{\mu }$A.

Figure 10 shows that the inverter-based pixel amplifiers integrated into each recording channel boasted a differential gain of 44.16 dB, alongside a high cutoff frequency exceeding 100 kHz. These metrics highlight the amplifiers’ ability to capture and amplify neural signals across the entire frequency spectrum, encompassing both local field potentials and action potentials as measured from the extracellular space.

As shown in Figure 11, further simulations revealed a favorable SCMRR of 80.5 dB at low frequencies. Particularly noteworthy was the performance of the front end within the range between 0.1 Hz and 100 Hz, where the SCMRR maintained a value of at least 80 dB. A moderately high level of rejection was maintained at higher frequencies, with the SCMRR exceeding 60 dB up to a frequency of 2 kHz.

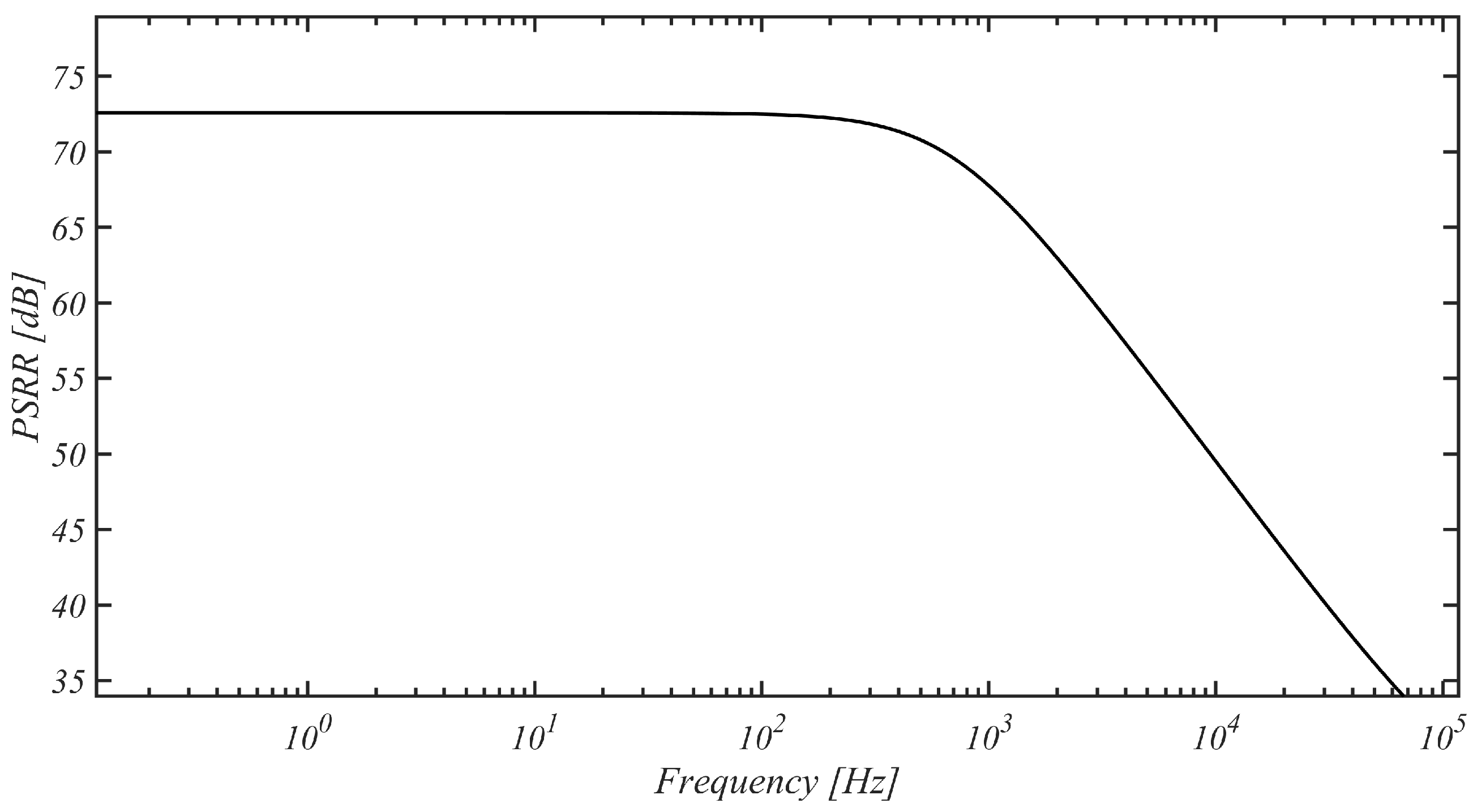
The PSRR of the front end, as indicated in Figure 12, exhibited a value of 72.55 dB at frequencies in the range spanning from 0.1 Hz to 100 Hz. For higher frequencies, the measured PSRR exhibited a similar behavior to the SCMRR, maintaining a level above 60 dB up until 2 kHz.

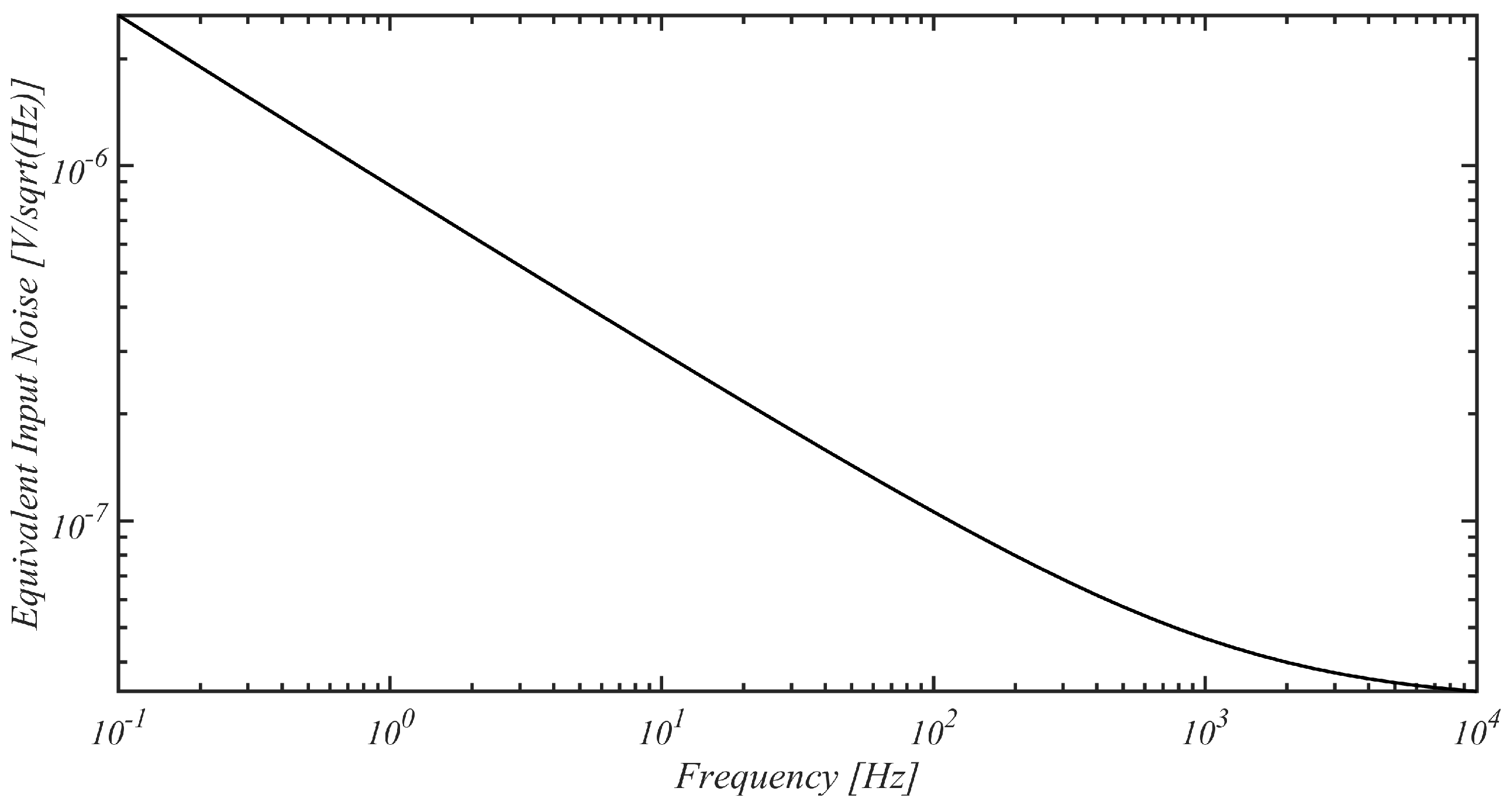
The input-referred noise spectrum of the input amplifier is presented in Figure 13, showing a noise level of 100 nV/$\sqrt{\mathrm{Hz}}$ at 100 Hz and a value of 50 nV/$\sqrt{\mathrm{Hz}}$ at 1 kHz. By integrating the noise spectrum across various frequency intervals, the noise performance of the amplifier was evaluated in terms of the IRN. Specifically, the considered frequency bands are those associated with the LFP signals (1 Hz–300 Hz), the action potentials (300 Hz–7.5 kHz), and the overall spectrum that characterizes the bio-signals recorded from the extracellular space (1 Hz–7.5 kHz). The resulting measurements, acquired by varying the number of channels, are reported in

Table 3. IRN values measured in different frequency intervals.

N° of Ch.	${\mathit{IRN}}_{\mathit{LFP}}$ $\mathbf{(}\mathsf{\mu }$${\mathit{V}}_{\mathit{rms}}\mathbf{)}$	${\mathit{IRN}}_{\mathit{AP}}$ $\mathbf{(}\mathsf{\mu }$${\mathit{V}}_{\mathit{rms}}\mathbf{)}$	${\mathit{IRN}}_{\mathit{TOT}}$ $\mathbf{(}\mathsf{\mu }$${\mathit{V}}_{\mathit{rms}}\mathbf{)}$
2	$6.44$	$8.72$	$10.83$
4	$3.57$	$4.90$	$6.059$
8	$2.71$	$3.77$	$4.64$
16	$2.36$	$3.30$	$4.04$

.

As seen in the results reported in Table 3, the IRN exhibited an increasing trend as the number of recording channels decreased. This is consistent with Equation (31), highlighting the significance of the contribution of $I_R$, the noise source associated with the smaller replicating transistors, which became negligible when using at least eight channels.

A widely used figure of merit that allows us to relate the noise performance of the circuit with its power consumption and bandwidth is the noise efficiency factor (NEF) [37], expressed as follows:

$$NEF=IRN·\sqrt{\frac{2·I_{TOT}}{\pi ·V_T·4k_{b}T·BW}},$$

(32)

where $V_T$ is the thermal voltage, $I_{TOT}$ is the total supply current of the amplifier, and $BW$ is the amplifier’s bandwidth in Hz. By substituting the values of the total current required to bias the individual recording channel, the IRN, and the bandwidth into (32), we obtain

$$NEF=3.32.$$

In addition, the power efficiency factor (PEF) can be computed as

$$PEF=NE{F}^2·\left(Vdd-Vss\right)=11.02.$$

(33)

5.3. Process and Mismatch Simulations

To assess the robustness of the front end against PVT (Process, Voltage, and Temperature) and mismatch variations, the system underwent comprehensive testing via multiple simulations. Specifically, a Monte Carlo simulation comprising 200 iterations was conducted. The outcomes of these simulations are outlined in

Table 4. Performance under mismatch variations.

Parameter	Min	Max	Mean	Std. Dev.
$G_D$ (dB)	$44.05$	$44.24$	$44.16$	$0.04$
$G_{CM}$ (dB)	$-41.06$	$-34.00$	$-36.38$	$1.42$
$SCMRR$ (dB)	$78.07$	$85.33$	$80.53$	$1.45$
$PSRR$ (dB)	$64.89$	$94.52$	$74.11$	$6.27$
$V_{out\_DC}$ (mV)	$-24.52$	$30.54$	$1.99$	$11.38$

.

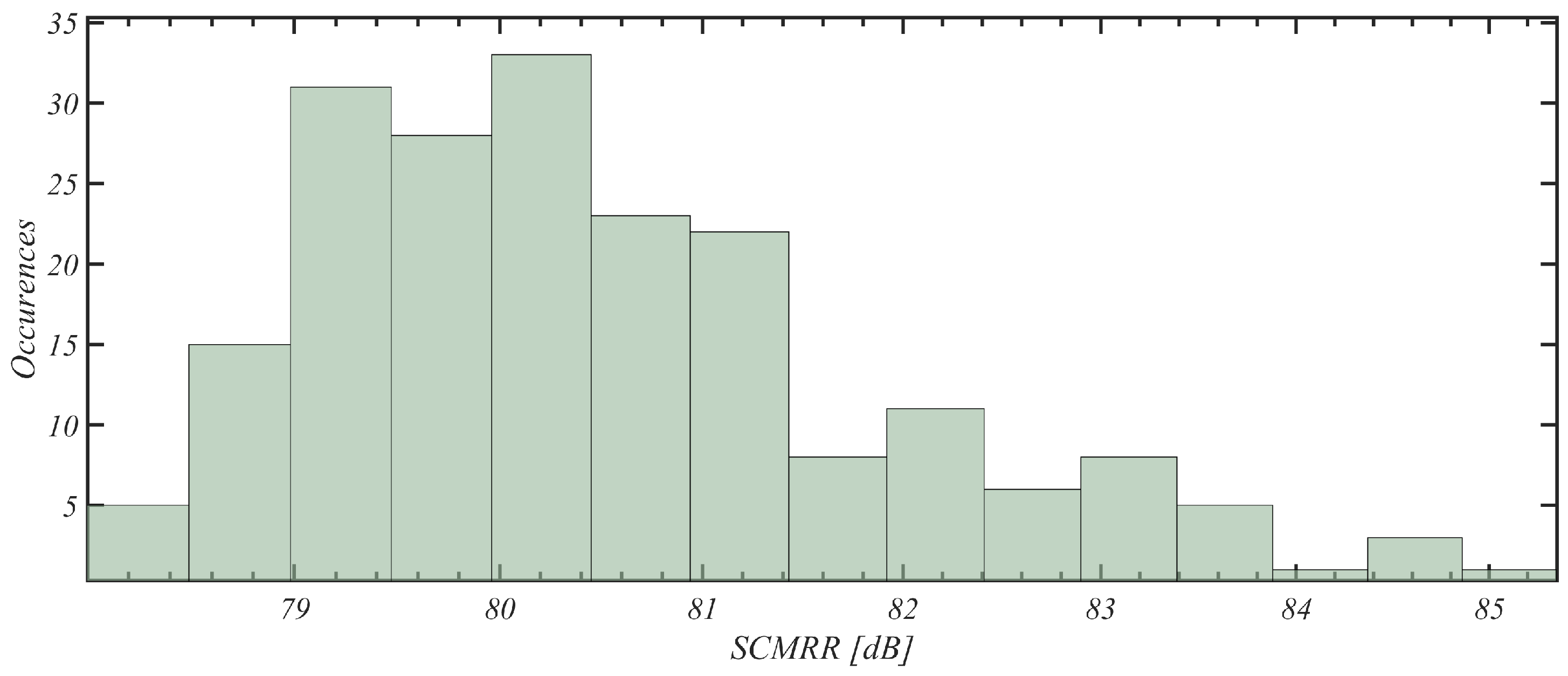
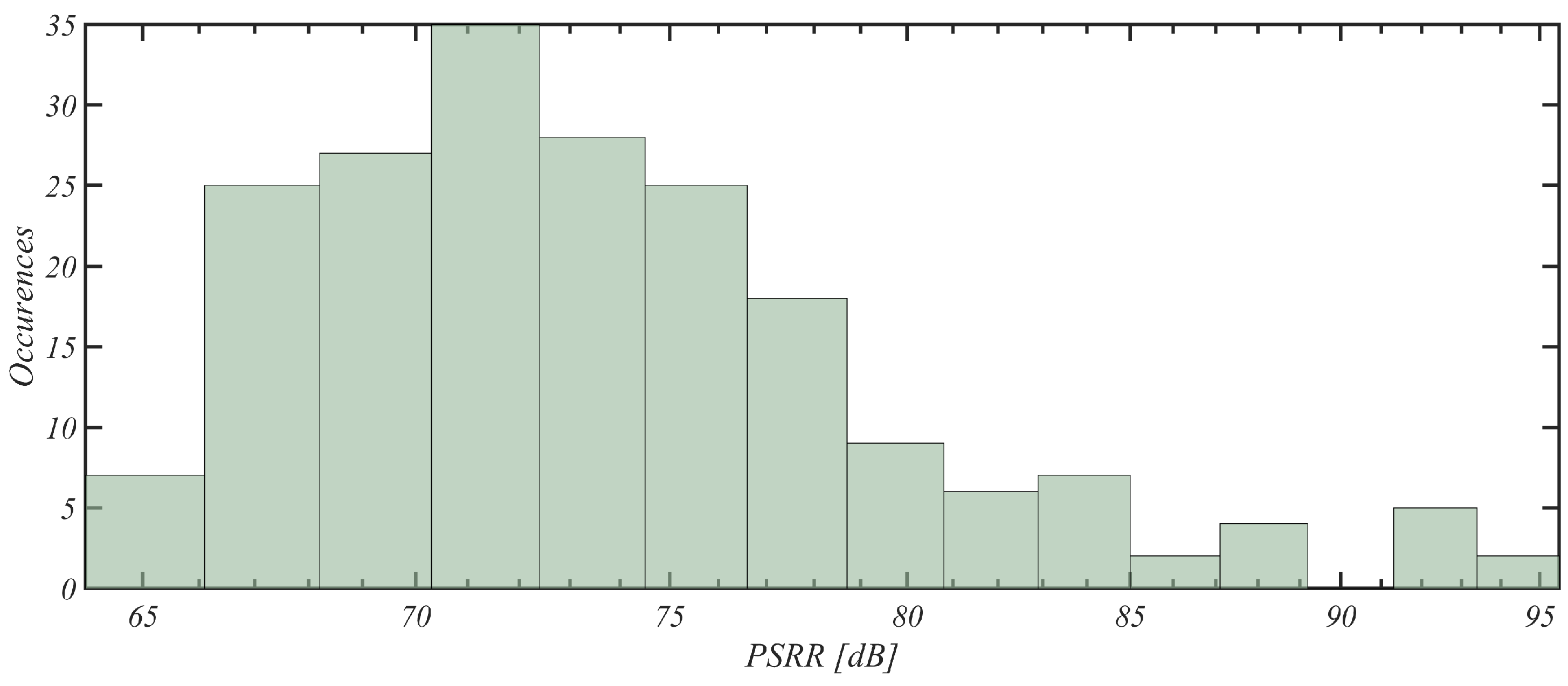
It must be noted that both the differential gain and the common-mode gain of the front end demonstrated standard deviations within a 2 dB interval, consequently maintaining a similarly constrained SCMRR. Particularly, the differential gain exhibited minimal fluctuations around its mean value of 44.16 dB. Although the PSRR (power supply rejection ratio) variance was marginally higher, it remained moderately limited, with a mean of 74.11 dB and a variance of 6.30 dB. In both instances, the tested performance metrics yielded favorable results, with both figures of merits exceeding 70 dB on average.

Concerning the SCMRR and PSRR, histograms related to the distribution of results over the 200 Monte Carlo iterations are presented in Figure 14 and Figure 15.

To further test the robustness of the proposed front end, a parametric simulation focusing on temperature variations was conducted. By gradually varying the operating temperature within the range [0 °C–50 °C], the front end’s gain and noise parameters, along with the rejection parameters, were evaluated accordingly (

Table 5. Performance under temperature variations.

Temp. (°C)	0.00	10.50	21.00	31.60	42.10	50.00
$G_D$ (dB)	$44.64$	$44.45$	$44.30$	$44.07$	$43.38$	$43.73$
$G_{CM}$ (dB)	$-29.89$	$-32.20$	$-34.60$	$-37.33$	$-40.37$	$-43.99$
$SCMRR$ (dB)	$74.53$	$76.65$	$78.90$	$81.40$	$84.25$	$86.72$
$PSRR$ (dB)	$90.46$	$79.17$	$74.37$	$71.28$	$68.92$	$67.42$
$V_{out\_DC}$ (mV)	$1.64$	$1.86$	$1.95$	$1.95$	$1.90$	$1.84$
$IR{N}_{LFP}$ ($\mathsf{\mu }$$V_{rms}$)	$2.27$	$2.30$	$2.34$	$2.38$	$2.41$	$2.44$
$IR{N}_{AP}$ ($\mathsf{\mu }$$V_{rms}$)	$3.14$	$3.20$	$3.27$	$3.33$	$3.40$	$3.45$
$IR{N}_{TOT}$ ($\mathsf{\mu }$$V_{rms}$)	$3.87$	$3.95$	$4.02$	$4.10$	$4.17$	$4.23$

).

Regarding the differential gain of the input amplifiers, minimal fluctuations were observed; however, the common-mode gain of the system exhibited a gradual decrease in value as the test temperature rose. Consequently, the SCMRR displayed an increasing trend with rising temperatures, reaching a maximum value of 86.72 dB at 50 °C. Conversely, the PSRR of the system tended to decrease in value with rising temperatures. In the range corresponding to the physiological conditions of the brain [38 °C–41 °C], both the PSRR and SCMRR were characterized by relatively minor variations, maintaining values of around 70 dB and 80 dB, respectively. When examining the noise performance of the front end amidst temperature variations, it was expected that the IRN of the system would experience a gradual rise. Nevertheless, at 4.23 $\mathsf{\mu }$$V_{rms}$, considering the total bandwidth [1 Hz–7.5 kHz], $IR{N}_{TOT}$ barely exceeded its nominal value measured at 27 °C.

Continuing with the evaluation of the front end, the following batch of simulations was conducted by varying the power supply voltage ±10% of its nominal value. By consulting the results displayed in

Table 6. Performance under supply voltage variations.

Vdd − Vss (V)	0.90	0.94	0.97	1.02	1.07	1.10
$G_D$ (dB)	$44.18$	$44.17$	$44.16$	$44.15$	$44.15$	$44.15$
$G_{CM}$ (dB)	$-32.36$	$-33.93$	$-35.54$	$-37.03$	$-38.34$	$-39.21$
$SCMRR$ (dB)	$76.54$	$78.10$	$79.70$	$81.18$	$82.49$	$83.36$
$PSRR$ (dB)	$59.78$	$65.66$	$70.81$	$74.96$	$77.80$	$79.01$
$V_{out\_DC}$ (mV)	$1.25$	$0.99$	$1.65$	$2.63$	$3.66$	$4.39$
$IR{N}_{LFP}$ ($\mathsf{\mu }$$V_{rms}$)	$2.32$	$2.34$	$2.36$	$2.37$	$2.39$	$2.41$
$IR{N}_{AP}$ ($\mathsf{\mu }$$V_{rms}$)	$3.45$	$3.38$	$3.32$	$3.28$	$3.25$	$3.23$
$IR{N}_{TOT}$ ($\mathsf{\mu }$$V_{rms}$)	$4.16$	$4.11$	$4.07$	$4.05$	$4.03$	$4.03$

, it can be seen that variations in the differential gain were once again minimal. In a similar manner, the common-mode gain of the system varied between a minimum of −39.21 dB for (Vdd − Vss) = 1.1 V and a maximum of −32.36 for (Vdd − Vss) = 0.9 V. Integrating the input noise spectrum across the bandwidths of interest revealed a minor increasing trend in the band related to the local field potentials [1 Hz–300 Hz] and a minor decreasing trend in the band related to the action potentials [300 Hz–7.5 kHz]. Overall, the IRN measured across the total frequency band exhibited a negligible decrease.

To conclude with the PVT analysis, the results of the simulations under corner variations are compiled in

Table 7. Performance under process variations.

Temp. (°C)	TT	FF	SS	SF	FS
$G_D$ (dB)	$44.16$	$43.59$	$44.73$	$44.09$	$44.17$
$G_{CM}$ (dB)	$-36.04$	$-40.47$	$-32.38$	$-35.56$	$-24.97$
$SCMRR$ (dB)	$80.20$	$84.06$	$77.11$	$79.65$	$69.14$
$PSRR$ (dB)	$72.55$	$72.38$	$71.58$	$68.75$	$91.49$

. Generally, it can be observed that the front end’s robustness is quite favorable.

Table 8. Performance comparison against state-of-the-art front ends.

	[33] *	[38] *	[39] **	B	This Work **
Year	2016	2018	2019	2022	2024
Process	65 nm	180 nm	180 nm	180 nm	180 nm
N° Channels	16	4	4	15	15
Supply (V)	1	$1.8$	$\pm 1.2$	$\pm 0.5$	$\pm \mathbf{0.5}$
P/Ch ($\mathsf{\mu }$W)	$3.28$	$4.50$	$7.68$	$1.20$	3.77
A/Ch (mm2)	$0.042$	$0.072$	$0.0214$	$0.012$	0.004
NEF/PEF	$3.19/10.2$	$1.94/6.77$	$2.65/8.43$	$2.65/7.02$	3.32/11.04
SCMRR (dB)	90	76	>50	75	80.50
PSRR (dB)	78	80	>53	74	72.55
CMI (${\mathrm{mV}}_{pp}$)	220	–	–	300	400
IRN ($\mathsf{\mu }$$V_{rms}$)	$4.13$	$3.20$	$3.87$	$5.30$	4.04
THD (%(@ ${\mathrm{mV}}_{pp}$))	1 (0.7)	–	–	1.6 (2)	1 (1.2)

*: Results obtained by testing a physical chip. **: Results obtained through post-layout simulations.

shows a comparison between the front end proposed in this work and various analog front ends introduced in recent years. In terms of noise, SCMRR, PSRR, and power consumption per channel (P/Ch), the simulation results presented in this section are comparable with modern state-of-the-art findings. Of particular importance is the area occupation per recording channel (A/Ch), which, for our devised front end, was reduced by a factor of 3 with respect to the front end introduced in [34], and was approximately one-tenth of the area occupied by the work presented in [33]. Additionally, thanks to the implemented closed CMFB loop, the CMI range of the front end described here was significantly higher than those measured for other devices.

6. Conclusions

In this work, we have presented a 16-channel in-pixel neural front-end architecture utilizing a common-mode feedback loop to enhance the SCMRR and the CMI range. The closed loop was achieved by scaling and summing the input currents of DC-coupled inverter-based amplifiers on low-impedance nodes provided by common-gate transistors. Designed using a 180 nm CMOS process from TSMC, post-layout simulations demonstrated a DC gain of 44.16 dB, with nominal values for the SCMRR and PSRR measured at 80.50 dB and 72.55 dB, respectively. The front end was shown to consume 3.77 $\mathsf{\mu }$W per recording channel, totaling about 60 $\mathsf{\mu }$W. Noise analysis indicated an IRN of 4.06 $\mathsf{\mu }$$V_{rms}$ in the frequency range [1 Hz–7.5 kHz]. Further simulations confirmed the system’s robustness against PVT and mismatch variations. Overall, the front end exhibited comparable results with other state-of-the-art devices in terms of rejection, noise, and power consumption. Thanks to the implementation of DC-coupled amplifiers and a current-based CMFB loop, the occupied area per channel was minimized to 0.004 mm².