Intelligent Control of Seizure-Like Activity in a Memristive Neuromorphic Circuit Based on the Hodgkin–Huxley Model

Abstract

Memristive neuromorphic systems represent one of the most promising technologies to overcome the current challenges faced by conventional computer systems. They have recently been proposed for a wide variety of applications, such as nonvolatile computer memory, neuroprosthetics, and brain–machine interfaces. However, due to their intrinsically nonlinear characteristics, they present a very complex dynamic behavior, including self-sustained oscillations, seizure-like events, and chaos, which may compromise their use in closed-loop systems. In this work, a novel intelligent controller is proposed to suppress seizure-like events in a memristive circuit based on the Hodgkin–Huxley equations. For this purpose, an adaptive neural network is adopted within a Lyapunov-based nonlinear control scheme to attenuate bursting dynamics in the circuit, while compensating for modeling uncertainties and external disturbances. The boundedness and convergence properties of the proposed control scheme are rigorously proved by means of a Lyapunov-like stability analysis. The obtained results confirm the effectiveness of the proposed intelligent controller, presenting a much improved performance when compared with a conventional nonlinear control scheme.

1. Introduction

Neuromorphic circuits are based on the underlying principles of the nervous system and are intended to be employed in brain-inspired machines. They represent an important alternative to deal with contemporary challenges faced by conventional computer systems, such as the von Neumann bottleneck and the end of both Moore’s law and Dennard scaling [1,2,3,4]. Standard computer systems are commonly based on classic von Neumann architecture, where the memory part is separate from the central processing unit (CPU). This continuous data transfer between the CPU and the memory unit generates unavoidable latency and power consumption issues [3]. As matter of fact, along with the increased energy consumption caused by the von Neumann bottleneck, scaling problems related to Moore’s law also cause overheating. Neuromorphic systems, on the other hand, are considered low-power devices and allow for a much lower thermal budget [5]. In this context, they have recently been employed in a wide range of applications, from robotics [6] and computer vision [7] to neuroprosthetics and brain–machine interfaces [5,8].

Among the available options for hardware deployment of neuromorphic systems, memristive devices have been recognized as one of the most promising technologies [2,3,9,10,11]. Memristors can be defined as two-terminal electrical components that are characterized by a state-dependent Ohm’s law [11]. They were theoretically proposed by Leon O. Chua in 1971 [12], but their first physical realization had to wait until 2008, when R. Stanley Williams and his team at the Hewlett-Packard laboratories introduced a resistive switching device based on nanoscale titanium dioxide (TiO₂ and TiO_2−x) films [13,14]. Memristive (or resistive switching) neuromorphic devices present a stimulus response comparable to the synaptic strengthening/weakening process, being intrinsically capable of emulating important brain learning mechanisms, such as short- and long-term plasticity [10,11,15].

Due to their ability to store resistance values indefinitely, requiring energy only to switch or read their states, memristive systems can be used as nonvolatile resistive random-access memory (RRAM), which are (much) more energy efficient than capacitor-based dynamic random access memory (DRAM) devices [14]. Furthermore, for the same reason, they also represent the most natural choice for the physical implementation of artificial neural networks (ANN) [3,4,16]. However, despite the promising prospects of using memristive neuromorphic circuits, they are still subject to accuracy issues due to their nonlinear dynamic behavior [3] and disturbances caused by sneak-path currents [17].

In addition to proposing the existence of memristors, Leon O. Chua and his colleagues also suggested that memristive components are essential for an accurate representation of the Hodgkin–Huxley (HH) model [18,19]. The HH model consists of a set of nonlinear differential equations that quantitatively describe current flow through the neuronal membrane [20]. It was introduced seventy years ago from studies carried out with the giant axon of the Loligo squid [21,22,23,24,25] and represents the basis of modern neuroscience [26]. Because of its capacity to describe the excitable dynamics of action potentials in neurons and to emulate a diversity of spiking patterns [27], the HH model plays an essential role in the research of epilepsy [28,29,30,31], Parkinson’s disease [32,33,34], and other neuropathies [35,36,37]. However, its rich and nonlinear dynamics can also exhibit self-sustained oscillations [38,39], seizure-like events [29,40], and chaotic behavior [41,42], which in fact challenges the adoption of conventional control strategies.

In this work, we introduce a novel intelligent controller for the suppression of seizure-like events in a memristive neuromorphic circuit based on the Hodgkin–Huxley model. For this purpose, an adaptive neural network is incorporated into a Lyapunov-based nonlinear control scheme, which allows the attenuation of bursting dynamics, even assuming that there is no prior knowledge of the mathematical model of the circuit. By means of a Lyapunov-like stability analysis, the boundedness and convergence properties of the closed-loop signals are rigorously proved. The obtained numerical results confirm that the intelligent control law is capable of dealing with the nonlinear behavior of memristive components, as well as with uncertainties and external disturbances, presenting a much superior performance when compared with a conventional nonlinear controller.

The remainder of this paper is structured as follows: Section 2 presents the adopted memristive Hodgkin–Huxley model; Section 3 introduces the novel intelligent controller for the neuromorphic circuit and presents the Lyapunov-like stability analysis; Section 4 presents the obtained numerical results; and Section 5 summarizes the concluding remarks.

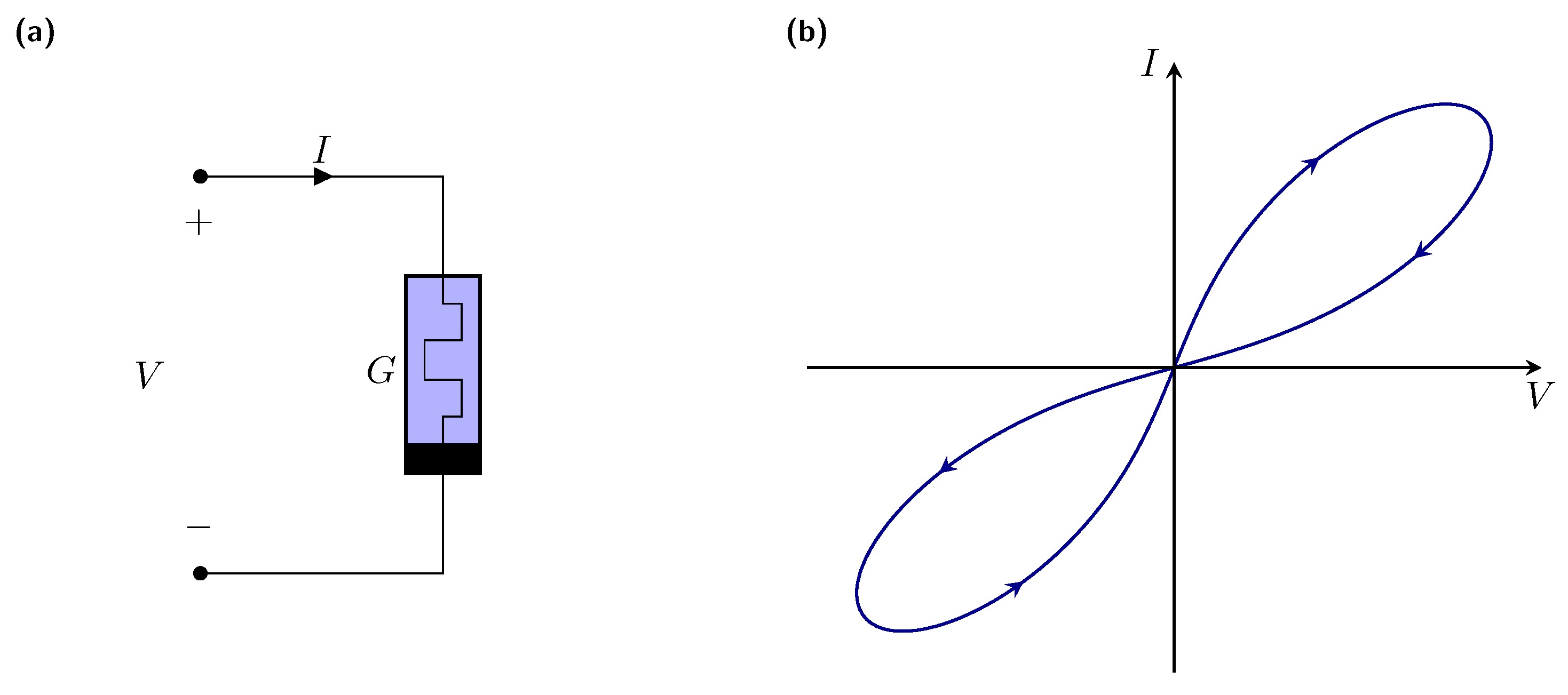
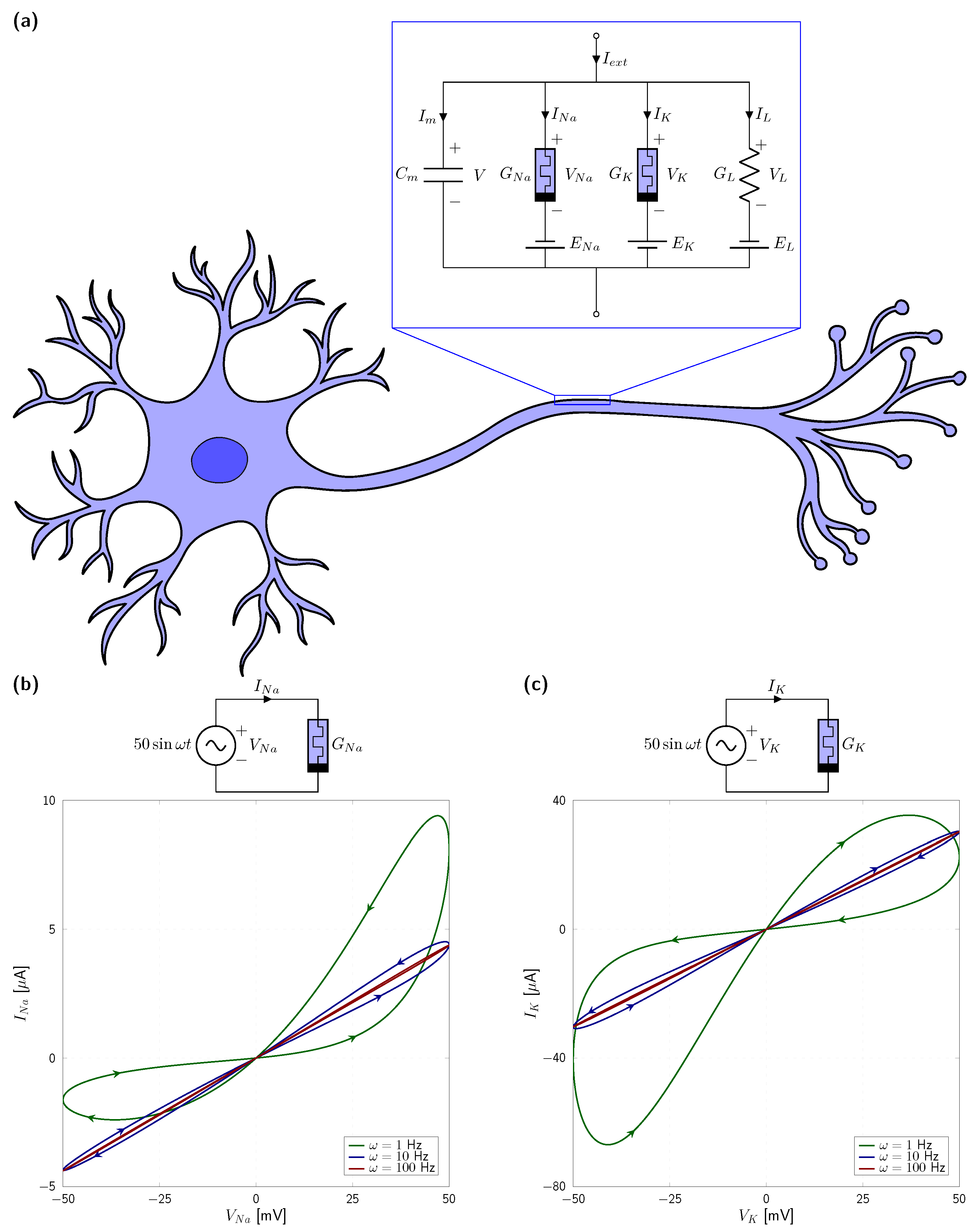
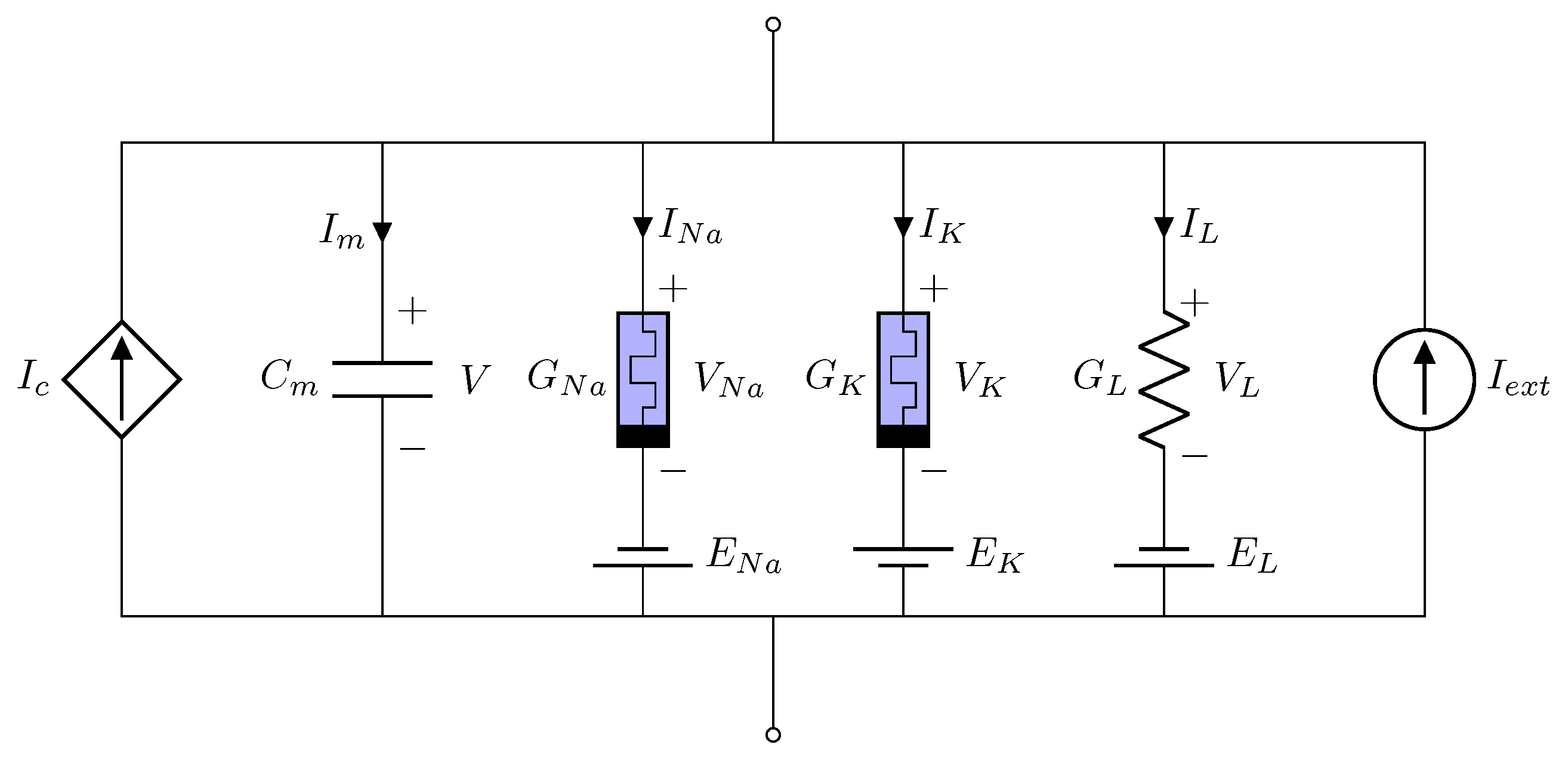
2. Memristive Neuromorphic Circuit

The memristor was originally introduced in 1971 by Leon O. Chua [12] as the missing fourth passive circuit element whose properties could not be obtained by any combination considering only the other three, namely resistor, inductor, and capacitor. Following the modern definition, a memristor can be understood as a 2-terminal resistive switching component with an associated state-dependent Ohm’s law [43,44]:

$$I=G(x_1,x_2,\dots ,x_n)V$$

(1)

where V is the voltage between the two terminals, I represents the electric current, and G stands for the conductance (or memductance) that depends on the state variables $x_n$, with n representing a measure of the order of complexity of the memristor dynamics.

The state variables $x_n$, in turn, can be described by a set of n autonomous ordinary differential equations:

$$\begin{array}{cc}\hfill {\dot{x}}_1& =f_1(x_1,x_2,\dots ,x_n;V)\hfill \\ \hfill {\dot{x}}_2& =f_2(x_1,x_2,\dots ,x_n;V)\hfill \\ \hfill & ⋮\hfill \\ \hfill {\dot{x}}_n& =f_n(x_1,x_2,\dots ,x_n;V)\hfill \end{array}$$

(2)

By applying a periodic voltage with positive and negative values to the memristor terminals, a pinched hysteresis loop is formed in the corresponding $V\times I$ plane. According to Chua [11,44], this is the main property of the memristor and can be considered its fingerprint. Figure 1 depicts the memristor symbol and a typical pinched hysteresis loop.

Furthermore, Chua and his colleagues have also suggested that memristors are the ideal components for the correct implementation of the Hodgkin–Huxley equations [18,19]. The HH model was introduced seventy years ago by Alan Hodgkin and Andrew Huxley to mathematically describe the flow of electric current through the axon membrane [25]. Originally, Hodgkin and Huxley represented the voltage-gated ion channels of the membrane by means of time-varying resistances. This assumption is actually not consistent with basic circuit theory and has led to some paradoxes and anomalous phenomena, as reported in the literature over the years [19]. By replacing the time-varying resistors with time-invariant memristors, however, it became possible to obtain a rigorous biophysical basis for the HH model.

Figure 2 shows the memristive HH circuit and the pinched hysteresis loops associated with the two voltage-gated ion channels. For the circuit presented in Figure 2a: $C_m$ stands for the membrane capacitance and V its corresponding voltage; $G_{Na}$, $V_{Na}$, $I_{Na}$, and $E_{Na}$ represent, respectively, the memductance, the voltage, the current, and the battery voltage related to the sodium-gated channel; $G_K$, $V_K$, $I_K$, and $E_K$ are, respectively, the memductance, the voltage, the current, and the battery voltage associated with the potassium-gated channel; $G_L$, $V_L$, $I_L$, and $E_L$ stand for the leakage conductance, voltage, current, and battery voltage, respectively.

Thus, recalling the Kirchhoff’s Current Law to the memristive circuit shown in Figure 2a, and considering an external current $I_{ext}$ through the axon membrane, we obtain the following ordinary differential equation [18,19]:

$$C_m\frac{dV}{dt}=-G_{Na}(V+E_{Na})-G_K(V-E_K)-G_L(V+E_L)+I_{ext}$$

(3)

where the memductance functions are given by

$$G_{Na}(x_1,x_2)=g_{Na}{x}_1^3{x}_2$$

(4)

$$G_K(x_3)=g_K{x}_3^4$$

(5)

with the dynamics of the internal states $x_1$, $x_2$, and $x_3$ being defined according to

$${\dot{x}}_1=\frac{(1-x_1)(V+25)}{\exp [0.1(V+25)]-1}-4\exp (V/18)x_1$$

(6)

$${\dot{x}}_2=0.07(1-x_2)\exp (0.05V)-\frac{x_2}{\exp [0.1(V+30)]+1}$$

(7)

$${\dot{x}}_3=\frac{0.1(1-x_3)(V+10)}{\exp [0.1(V+10)]-1}-0.125\exp (V/80)x_3$$

(8)

Equations (3)–(8) represent the four-dimensional vector field that mathematically describes the memristive Hodgkin–Huxley circuit shown in Figure 2a. Regarding the memristors, note that by applying a sinusoidal voltage of $50\sin \omega t$ mV across their terminals, the typical pinched hysteresis loop can be clearly observed for both sodium and potassium ion channels, shown in Figure 2b and Figure 2c, respectively. Moreover, as stated by Chua [19], the shape of their pinched hysteresis loops tends to a straight line as the frequency $\omega$ increases.

Table 1. Parameters for the memristive circuit.

${\mathit{C}}_{\mathit{m}}$	${\mathit{E}}_{\mathit{Na}}$	${\mathit{E}}_{\mathit{K}}$	${\mathit{E}}_{\mathit{L}}$	${\mathit{g}}_{\mathit{Na}}$	${\mathit{g}}_{\mathit{K}}$	${\mathit{G}}_{\mathit{L}}$
1 µF	115 mV	12 mV	$10.599$ mV	120 mS	36 mS	$0.3$ mS

presents the parameters for the memristive circuit.

It is worth recalling that the conductances given by Equations (4) and (5) were first proposed by Hodgkin and Huxley in 1952 [25] and later were also adopted by Chua to mathematically describe the memristors in the memristive version of the Hodgkin–Huxley circuit [11,18,19,44]. As defined by Hodgkin and Huxley [25], the internal states $x_1$, $x_2$, and $x_3$ are dimensionless variables, which can vary between 0 and 1. Thus, the proper dimension of the conductances is actually given by the parameters $g_{Na}$ and $g_K$, as can be seen in Table 1. Moreover, the nonlinearities present in the Hodgkin–Huxley model provide its rich and complex dynamic behavior, which is indeed essential for neuroscience and epilepsy research, as it allows a wide range of spiking and burst-firing patterns [27,42]. As a matter of fact, bursting dynamics can be easily emulated with HH equations. By applying an external electric current such as $I_{ext}=-28\mathrm{sgn}\{\cos (2\pi t/T)\cos [-2\pi t/(3T)]\}\mu$A, with $T={10}^3$, it is possible to observe the emergence of seizure-like events, as seen in Figure 3. The membrane voltages presented in Figure 3 were obtained from Equations (3)–(8) by means of a C++ implementation of the Euler–Maruyama method, using a time step of ${10}^{-3}$ s and considering Gaussian noise of null mean and variance of $0.4{\mathrm{mV}}^2$.

Brain electrical activity usually has irregular waveforms, but during seizure events, high-amplitude burst patterns can be clearly observed [28]. The bursting activity observed in Figure 3 is in fact quite similar to those previously reported in the literature for both numerical [29,40] and experimental procedures [45,46]. The ability to precisely control the bursting dynamics of the HH model plays an essential role for a better understanding of the treatment of many neuropathies [37]. For this reason, a novel intelligent control scheme is introduced in the next section to suppress seizure-like events in a memristive Hodgkin–Huxley circuit.

3. Intelligent Control

Due to its ability to deal with highly uncertain systems, adequately compensating for modeling inaccuracies and external disturbances, intelligent control presents itself as a very suitable approach for bio-inspired devices [47]. Intelligent control schemes are able to adapt, learn from experience, and predict the dynamic behavior of the controlled system. They have been successfully employed in the control of robotic [48], underactuated [49] and chaotic systems [50].

Thus, let us start by assuming that the memristive neuromorphic circuit can be described by an uncertain first-order nonlinear system:

$$\dot{V}=f+b{I}_c$$

(9)

where $I_c$ represents the control input, b stands for the input gain, and f is a nonlinear function that represents the plant dynamics.

The input signal $I_c$ is introduced to the memristive circuit by means of a controlled current source, as shown in Figure 4.

It should be noted that when choosing the first-order plant (9) to represent the entire fourth-order memristive circuit, it is necessary to ensure that the controller is capable of handling not only parametric uncertainties and the unknown external electric current $I_{ext}$ but also the unmodeled dynamics of the internal states of the memristors, as in Equations (6)–(8).

Then, considering that the plant is subject to modeling uncertainties, i.e., $f=\widehat{f}+\mathsf{\Delta }f$ and $b=\widehat{b}+\mathsf{\Delta }b$, with $\widehat{f}$ and $\widehat{b}$ being estimates of f and b, respectively, Equation (9) can be rewritten as follows:

$$\dot{V}=\widehat{f}+\widehat{b}{I}_c+d$$

(10)

where d comprises the modeling uncertainties $\mathsf{\Delta }f$ and $\mathsf{\Delta }b$.

By evoking the universal approximation properties of artificial neural networks [51], we propose the adoption of an ANN to deal with both modeling inaccuracies and unmodeled dynamics. The chosen network architecture considers one input and one output, in addition to a hidden layer with n neurons, as shown in Figure 5.

The single-hidden layer network depicted in Figure 5 is mathematically described by

$$\widehat{d}={\mathit{w}}^{\top }\mathbf{\psi }(\tilde{V})$$

(11)

where $\mathit{w}=[w_1\dots w_n]$ is the weight vector and $\mathbf{\psi }=[{\psi }_1\dots {\psi }_n]$ stands for the vector of activation functions ${\psi }_i$.

Now, following the feedback linearization method [52], a nonlinear control law for the uncertain first-order system (9) can be designed as follows:

$$I_c={\widehat{b}}^{-1}(-\widehat{f}-\widehat{d}+{\dot{V}}_d-\lambda \tilde{V})$$

(12)

with $\lambda$ being a strictly positive constant and $\tilde{V}=V-V_d$ representing the control error associated with the desired state $V_d$.

By applying the control law (12) to (10), the closed-loop dynamics becomes

$$\dot{\tilde{V}}+\lambda \tilde{V}=d-\widehat{d}$$

(13)

Equation (13) shows that the error dynamics are constantly driven by the approximation error $d-\widehat{d}$. However, recalling that the adopted ANN is a universal approximator, an arbitrary precision $ϵ$ can be ensured for the uncertainty/disturbance estimation:

$$d={\widehat{d}}^{*}+ϵ$$

(14)

with ${\widehat{d}}^{*}$ being the optimal estimate and $|ϵ|\le \epsilon$.

Let us now evaluate the boundedness and convergence properties of the closed-loop signals by defining positive definite Lyapunov candidate function L:

$$L(t)=\frac{1}{2}{\tilde{V}}^2+\frac{1}{2\eta }{\mathbf{\delta }}^{\top }\mathbf{\delta }$$

(15)

where $\eta$ is a strictly positive constant and $\mathbf{\delta }=\mathit{w}-{\mathit{w}}^{*}$, with ${\mathit{w}}^{*}$ being the optimal weight vector that minimizes the approximation error.

Since $\dot{\mathbf{\delta }}=\dot{\mathit{w}}$, the time derivative of L is

$$\begin{array}{cc}\hfill \dot{L}(t)& =\tilde{V}\dot{\tilde{V}}+{\eta }^{-1}{\mathbf{\delta }}^{\top }\dot{\mathit{w}}\hfill \\ \hfill & =\tilde{V}[-\lambda \tilde{V}+d-\widehat{d}]+{\eta }^{-1}{\mathbf{\delta }}^{\top }\dot{\mathit{w}}\hfill \\ \hfill & =\tilde{V}[-\lambda \tilde{V}+{\widehat{d}}^{*}+ϵ-\widehat{d})] + {\eta }^{-1}{\mathbf{\delta }}^{\top }\dot{\mathit{w}}\hfill \\ \hfill & =\tilde{V}[-\lambda \tilde{V}+ϵ-{(\mathit{w}-{\mathit{w}}^{*})}^{\top }\mathbf{\psi }]+{\eta }^{-1}{\mathbf{\delta }}^{\top }\dot{\mathit{w}}\hfill \\ \hfill & =\tilde{V}[-\lambda \tilde{V}+ϵ-{\mathbf{\delta }}^{\top }\mathbf{\psi }]+{\eta }^{-1}{\mathbf{\delta }}^{\top }\dot{\mathit{w}}\hfill \\ \hfill & =-[\lambda \tilde{V}-ϵ]\tilde{V}+{\eta }^{-1}{\mathbf{\delta }}^{\top }[\dot{\mathit{w}}-\eta \tilde{V}\mathbf{\psi }]\hfill \end{array}$$

Hence, by updating $\mathit{w}$ according to $\dot{\mathit{w}}=\eta \tilde{V}\mathbf{\psi }$, the time derivative becomes

$$\dot{L}(t)=-[\lambda \tilde{V}-ϵ]\tilde{V}\le -[\lambda |\tilde{V}|-\epsilon ]|\tilde{V}|$$

(16)

According to (16), it can be seen that $\dot{V}$ is negative definite only when $|\tilde{V}| >\epsilon /\lambda$. In order to ensure an upper bound on $\mathit{w}$ when $|\tilde{V}| \le \epsilon /\lambda$, the projection algorithm [53] can be employed:

$$\dot{\mathit{w}}=\left\{\begin{array}{cc}\eta \tilde{V}\mathbf{\psi }& {\mathrm{if}\parallel \mathit{w}\parallel }_2<\mu \mathrm{or}\hfill \\ & {\mathrm{if}\parallel \mathit{w}\parallel }_2=\mu \mathrm{and}\eta \tilde{V}{\mathit{w}}^{\top }\mathbf{\psi }<0\hfill \\ \left(\mathit{I}-{\displaystyle \frac{\mathit{w}{\mathit{w}}^{\top }}{{\mathit{w}}^{\top }\mathit{w}}}\right)\eta \tilde{V}\mathbf{\psi }& \mathrm{otherwise}\hfill \end{array}\right.$$

(17)

with $\mu$ being the desired upper bound for ${\parallel \mathit{w}\parallel }_2$ (the Euclidean norm of $\mathit{w}$).

By adopting (17), we ensure that the weight vector always remains within the convex region $\mathcal{W}=\{\mathit{w}\in {\mathbb{R}}^n:{\mathit{w}}^{\top }\mathit{w}\le {\mu }^2\}$ as long as ${\parallel \mathit{w}(0)\parallel }_2\le \mu$, and the control error converges to the closed region $\mathcal{V}=\{\tilde{V}\in \mathbb{R}:|\tilde{V}|\le \epsilon /\lambda \}$ as $t\to \infty$.

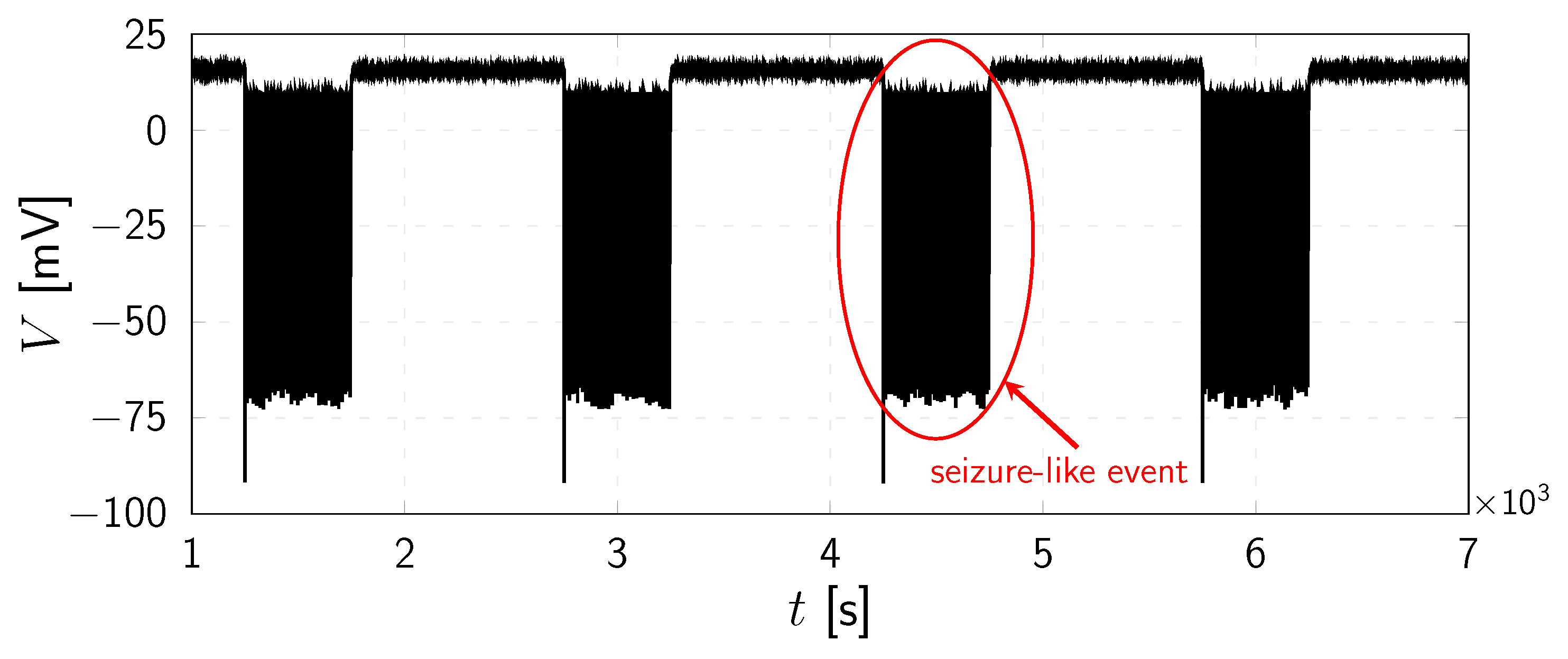
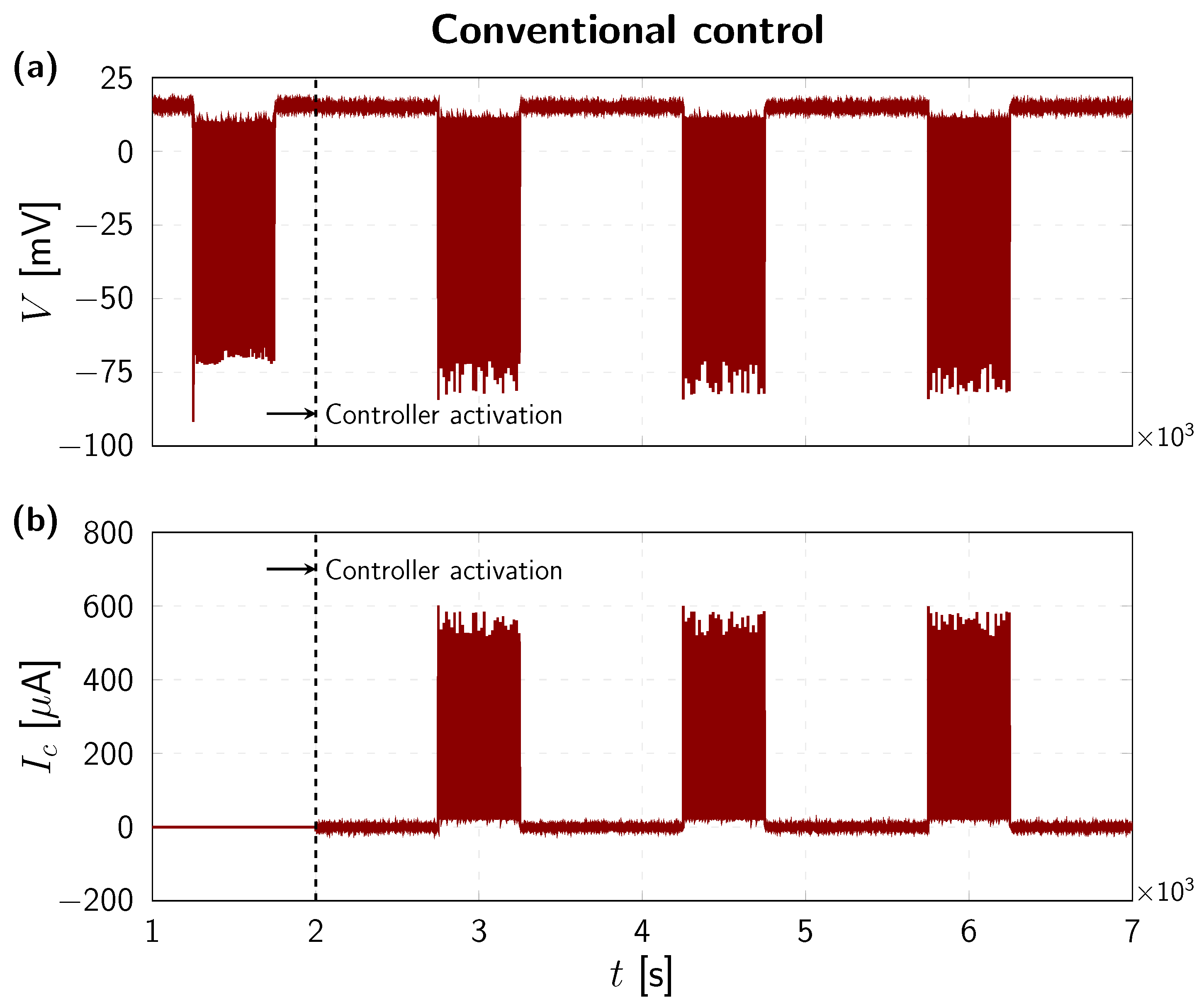
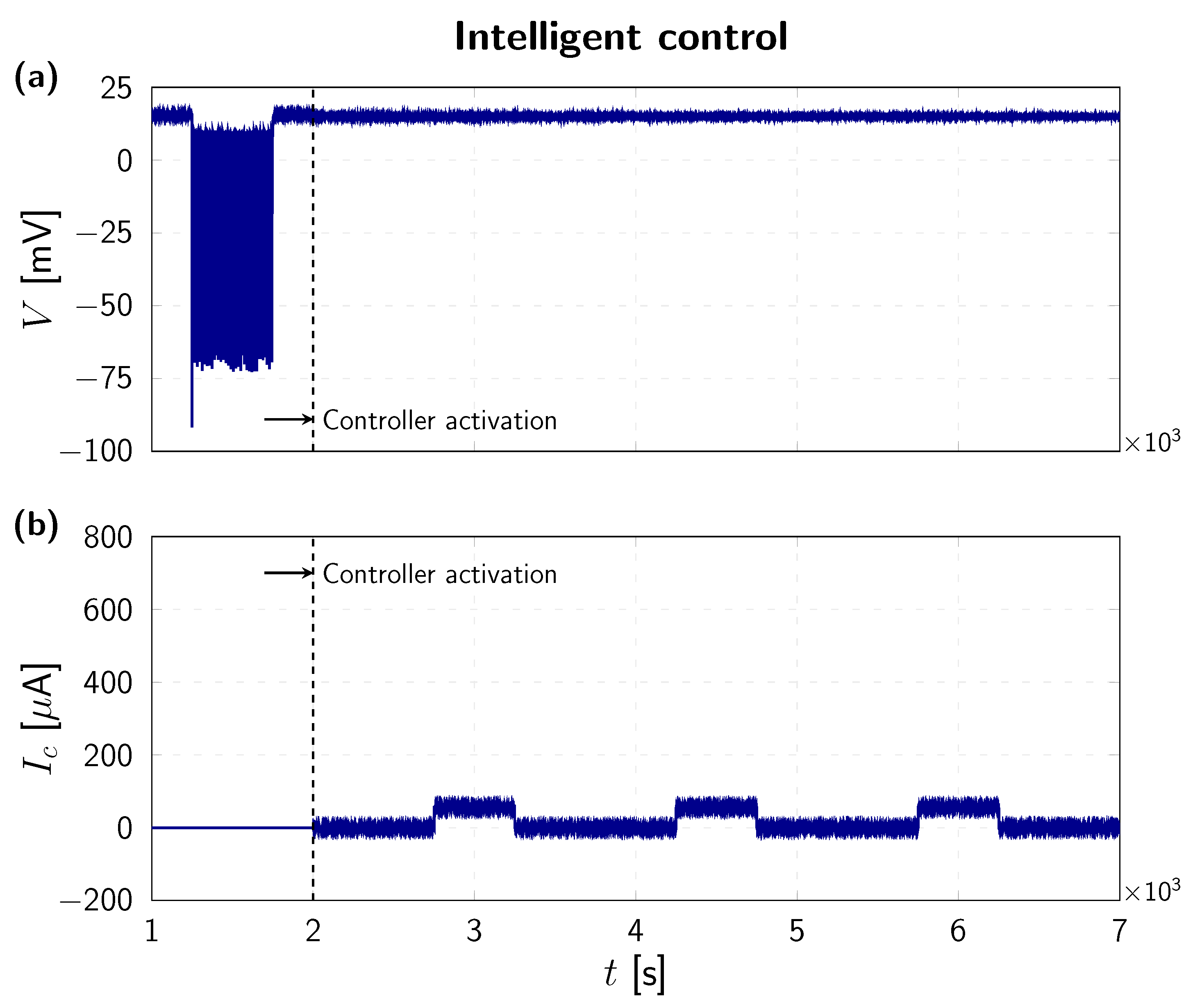
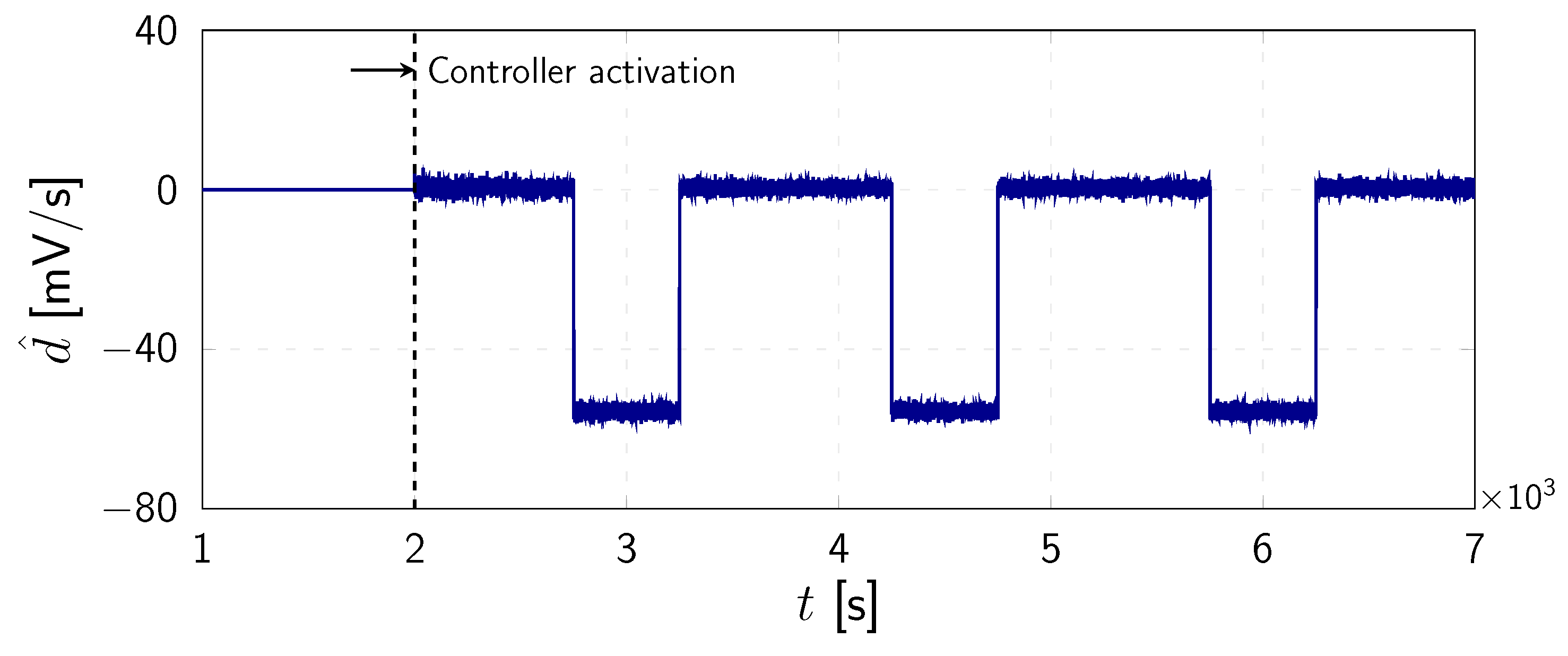
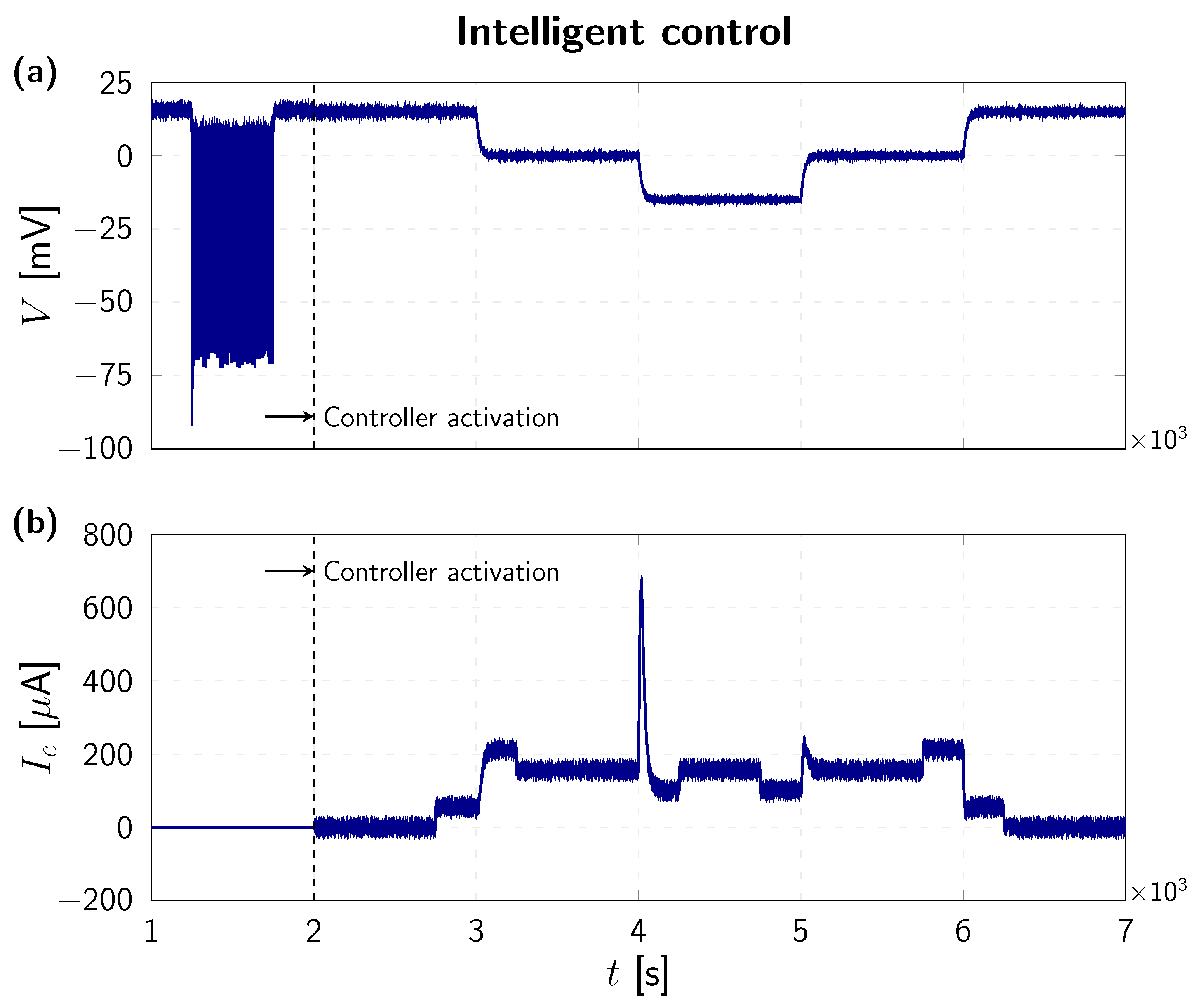
4. Numerical Results

The efficacy of the proposed intelligent controller was evaluated by means of numerical simulations carried out at a sampling rate of 100 Hz. As in the numerical studies presented in Section 2, the memristive circuit represented by Equations (3)–(8), now including a controlled current source being defined by the intelligent scheme, were simulated using a C++ implementation of the Euler–Maruyama method, with a time step of ${10}^{-3}$ s and a Gaussian noise of null mean and variance of $0.4{\mathrm{mV}}^2$. Assuming that no prior knowledge about the plant was available to the control system designer, we defined $\widehat{b}=1$ and $\widehat{f}=0$. The control parameter $\lambda$ was set to 6.

Regarding the artificial neural network, the weight vector was initialized as $\mathit{w}=\mathbf{0}$ and is updated according to (17), with learning rate $\eta =300$. The activation functions were of the Gaussian type:

$${\psi }_i(\tilde{V};c_i,{\sigma }_i)=\exp \left[-\frac{1}{2}{\left(\frac{\tilde{V}-c_i}{{\sigma }_i}\right)}^2\right],i=1,\dots ,6$$

(18)

with corresponding centers $c_i$ and widths ${\sigma }_i$ being defined as in

Table 2. Parameters of the Gaussian-type activation functions.

	${\mathit{\psi }}_1$	${\mathit{\psi }}_2$	${\mathit{\psi }}_3$	${\mathit{\psi }}_4$	${\mathit{\psi }}_5$	${\mathit{\psi }}_6$
Centers	$-10.00$	$-2.50$	$-1.25$	$1.25$	$2.50$	$10.00$
Widths	$10.00$	$6.67$	$3.33$	$3.33$	$6.67$	$10.00$

.

Figure 6 and Figure 7 show the obtained results.

The influence of the adaptive neural network on the control performance is evaluated by comparing the proposed intelligent approach with a conventional nonlinear controller, namely the feedback linearization scheme. In fact, the feedback linearization controller can be easily obtained from the intelligent scheme by simply disregarding the contribution of the neural network to the control signal, i.e., by setting $\widehat{d}=0$.

Comparing the results obtained with a conventional nonlinear controller and the intelligent scheme, Figure 6 and Figure 7 respectively, the effectiveness of the proposed intelligent approach can be clearly ascertained. As a matter of fact, the conventional controller was not able to suppress the bursting activity, shown in Figure 6a, despite the higher amplitude of the associated control signal, shown in Figure 6b. The proposed intelligent controller, on the other hand, was able to successfully suppress seizure-like events, as shown in Figure 7a, with a much lower amplitude of the associated control signal, shown in Figure 7b, when compared with the conventional approach.

In order to allow a quantitative comparison of the performance obtained with the two control schemes, the Integral Absolute Error (IAE) and the Integral Absolute Control Input (IACI) were calculated for the numerical results presented in Figure 6 and Figure 7.

$$\mathrm{IAE}={\int }_{t_1}^{t_2}|\tilde{V}(t)|\mathrm{d}t\mathrm{and}\mathrm{IACI}={\int }_{t_1}^{t_2}|I_c(t)|\mathrm{d}t$$

Table 3. Integral Absolute Error (IAE) and the Integral Absolute Control Input (IACI) for both conventional and intelligent controllers with corresponding achieved percentage reductions.

	Conventional	Intelligent	Percentage Reduction
IAE [mV s]	$1151.00$	$4.67$	$99.59\%$
IACI [$\mu$C]	$6907.27$	$4330.15$	$37.31\%$

shows the IAE and IACI obtained for the conventional and intelligent controllers, taking into account the numerical results presented in Figure 6 and Figure 7 for $t_1=2$ ks and $t_2=7$ ks.

From Table 3, it can be seen that the intelligent controller provided a total control error (IAE) $99.59\%$ lower and also granted a reduction of $37.31\%$ in the overall control effort (IACI). These results confirm the efficiency of the intelligent scheme, being able to drastically reduce the error with a total control effort even lower than the conventional one.

As a matter of fact, the improved performance of the intelligent controller is due to the adaptive neural network, which is able to recognize the dynamics of the memristive neuromorphic circuit and adequately compensate the disturbance caused by the unknown external current. Figure 8 shows the estimate $\widehat{d}$, as computed by the adaptive neural network.

Now, to show that the intelligent scheme is also capable of tracking different references, the desired output is changed during the control phase, causing the controller to stabilize the voltage at distinct setpoints. Figure 9 shows the obtained results.

Figure 9a shows that, after activating the controller, the setpoint is then intentionally changed to different voltage levels: $V_d=15$ mV, $V_d=0$ mV, $V_d=-15$ mV, $V_d=0$ mV, and $V_d=15$ mV, successively. As can be verified, the controller is not only able to suppress seizure-like events but also manages to drive the voltage to the desired levels. The control signal, in this case, is adjusted as needed for the different setpoints, as can be seen in Figure 9b. Once again, it is important to emphasize that this stabilization capability is granted by the neural network embedded into the intelligent controller. By interacting with the plant, the adaptive neural network is able to learn online how to ensure that the desired voltage levels are properly achieved.

Finally, based on the obtained results, the main features of the proposed intelligent controller can be highlighted as follows:

• The intelligent control scheme can adequately handle the unknown external electric current $I_{ext}$ and the uncertainties associated with the unmodeled internal states of the memristors, which in fact may allow other different memristive circuits to be controlled by means of the same control framework;
• Online learning, rather than offline training, is adopted to allow the controller to continuously improve its overall performance, even when subjected to dynamically changing circumstances;
• The neural network can learn to compensate for uncertainties and disturbances by minimizing the control error, making direct measurements of the signal to be estimated (which is not possible in real applications) completely unnecessary;
• By combining the artificial neural network with a nonlinear control method, the computational demands on the ANN are minimized, which allows its implementation on low-power embedded hardware and the adoption of the online learning scheme.

5. Concluding Remarks

This work introduces a novel intelligent control scheme for the suppression of seizure-like events in a memristive neuromorphic circuit. The neuromorphic circuit is based on the Hodgkin–Huxley equations, with memristors representing the voltage-gated ion channels. Regarding the intelligent controller, an adaptive neural network is embedded within a Lyapunov-based nonlinear control law. Moreover, even by assuming that no prior knowledge about the plant is available to the control system designer, the proposed model-free controller is able to identify the unmodeled dynamics of the memristors, as well as the unknown external current, and compensate them accordingly. The boundedness and convergence properties of the closed-loop signals are rigorously addressed through a Lyapunov-like stability analysis. The improved performance of the intelligent controller is confirmed by means of a comparative numerical study. It is important to note that by combining the artificial neural network with a nonlinear control method, the computational demands on the ANN are minimized, which allows its implementation on low-power embedded hardware and the adoption of an online learning scheme. In fact, the reduced complexity of the proposed control scheme makes it a promising candidate for the development of neuroprostheses and brain–machine interfaces. Finally, the online learning feature of the adaptive neural network enables proper identification and automatic compensation of unknown plant dynamics, which allows the proposed control scheme to be employed in a wide variety of memristive neuromorphic systems.